Area of Parallelograms and Triangles
Multiple Choice Questions(MCQs)
1. The median of a triangle divides it into two
(A) triangles of equal area
(B) congruent triangles
(C) right triangles
(D) isosceles triangles
Show Answer
Solution
A median of a triangle divides it into two triangles of equal area.
Hence, the correct option is (A).
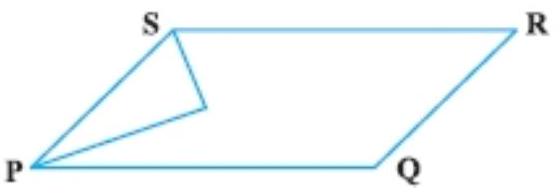
2. In which of the following figures, you find two polygons on the same base and between the same parallels?
(A)
(B)
(C)

(D)
Show Answer
Solution
In figure (d), we find two polygons (PQRA and BQRS) on the same base and between the same parallels.
Hence, the correct option is (D).
3. The figure obtained by joining the mid-points of the adjacent sides of a
rectangle of sides $8 ~cm$ and $6 ~cm$ is:(A) a rectangle of area $24 ~cm^{2}$.
(B) a square of area $25 ~cm^{2}$.
(C) a trapezium of area $24 ~cm^{2}$.
(D) a rhombus of area $24 ~cm^{2}$.
Show Answer
Solution
According to the question,
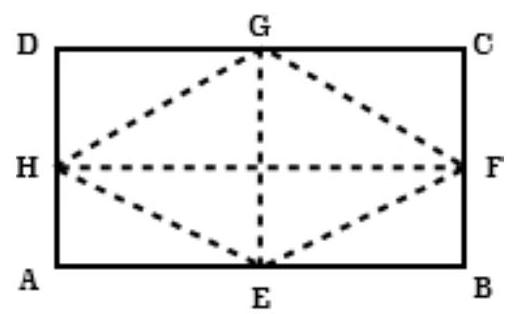
$ABCD$ is a rectangle and $E, F, G$ and $H$ are the mid-point of the sides $AB, BC, CD$ and $DA$ respectively. The figure formed is rhombus hose area:
$ \begin{aligned} & =\dfrac{1}{2} \times E G \times F H \\ & =\dfrac{1}{2} \times 6 ~cm \times 8 ~cm \\ & =24 ~cm^{2} \end{aligned} $
Hence, the correct option is (D).
4. In Fig., the area of parallelogram $A B C D$ is:
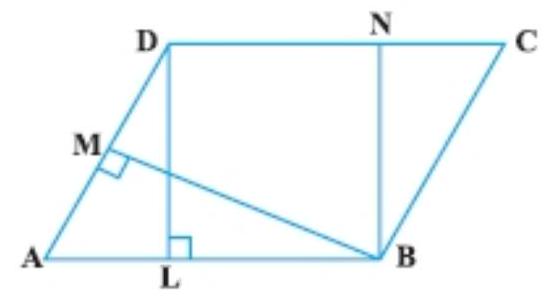
(A) $A B \times B M$
(B) $BC \times BN$
(C) $DC \times DL$
(D) $AD \times DL$
Show Answer
Solution
Area of parallelogram $=$ Base $\times$ Corresponding altitude
$=A B \times D L=D C \times D L$
[Since, AB = DC (opposite side of a parallelogram)]
Hence, the correct option is (C).
5. In Fig., if parallelogram $ABCD$ and rectangle $ABEF$ are of equal area, then:
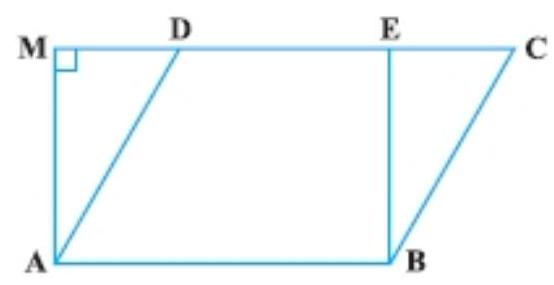
(A) Perimeter of $ABCD=$ Perimeter of $ABEM$
(B) Perimeter of $A B C D<$ Perimeter of ABEM
(C) Perimeter of $A B C D>$ Perimeter of ABEM
(D) Perimeter of $ABCD=\dfrac{1}{2}$ (Perimeter of $.ABEM)$
Show Answer
Solution
If parallelogram $ABCD$ and rectangle $ABEF$ are of equal area then perimeter of $ABCD>$ Perimeter of ABEM because:
As we know that, the perpendicular distance between two parallel sides of a parallelogram is always less than the length of the other parallel sides.
$BE<BC$ and $AM<AD$.
Hence, the correct option is (C).
6. The mid-point of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
(A) $\dfrac{1}{2} ar(ABC)$
(B) $\dfrac{1}{3} ar(ABC)$
(C) $\dfrac{1}{4} ar(ABC)$
(D) $ar(ABC)$
Show Answer
Solution
We know that, median of a triangle divides it into two triangle of equal area.
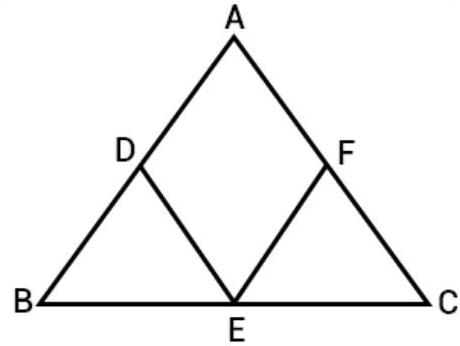
So, area $(\triangle A D E)=area(\triangle B D E)$
$area(\triangle A E F)=area(\triangle E F C)$
Now, $AE$ is the diagonal of a parallelogram ADEF. That is divides it into two triangles of equal area.
So, $area(\triangle A D E)=area(\triangle A F E)$
Now, from equation (I), (II), and (III), get:
$area(\triangle A D E)=area(\triangle B D E)=area(\triangle A E E)=area(\triangle E F C)$
Hence, $area(\triangle A D E F)=\dfrac{1}{2} area(\triangle A B C)$
Therefore, the correct option is (A).
7. Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is
(A) $1: 2$
(B) $1: 1$
(C) $2: 1$
(D) $3: 1$
Show Answer
Solution
As we know that parallelogram on the same or equal bases and between the same parallels are equal in area.
So, the ratio of these area is $1: 1$.
Hence, the correct option is (B).
8. $ABCD$ is a quadrilateral whose diagonal $AC$ divides it into two parts, equal in area, then $A B C D$
(A) is a rectangle
(B) is always a rhombus
(C) is a parallelogram
(D) need not be any of (A), (B) or (C)
Show Answer
Solution
The quadrilateral $ABCD$ need not be any of rectangle, rhombus and parallelogram because if quadrilateral $ABCD$ is a square then its diagonal $AC$ also divides it into two parts which are equal in area.
Hence, the correct option is (D).
9. If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is
(A) $1: 3$
(B) $1: 2$
(C) $3: 1$
(D) $1: 4$
Show Answer
Solution
As we know that, if a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram. Therefore, the ratio of the area of the triangle to the area of parallelogram is 1:2.
Hence, the correct option is (B).
10. $ABCD$ is a trapezium with parallel sides $AB=a ~cm$ and $DC=b ~cm \cdot E$ and $F$ are the mid-points of the non-parallel sides. The ratio of ar (ABFE) and ar (EFCD) is
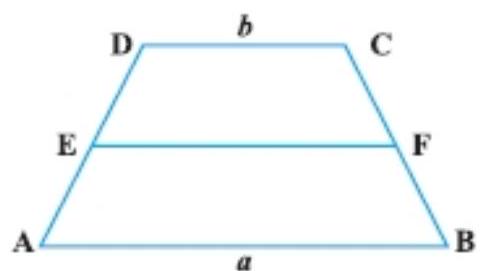
(A) $a: b$
(B) $(3 a+b):(a+3 b)$
(C) $(a+3 b):(3 a+b)$
(D) $(2 a+b):(3 a+b)$
Show Answer
Solution
Given:
$ABCD$ is a trapezium with parallel sides such that $AB || DC$ and $AB=a ~cm$ and $DC=b ~cm . E$ and $F$ are the mid-points of the non-parallel sides that are $AD$ and $BC$. So,
$ E F=\dfrac{1}{2}(a+b) $
$ABEF$ and EFCD are also trapezium.
$ \begin{aligned} & area(A B E F)=\dfrac{1}{2}[\dfrac{1}{2}(a+b)+a] \times h=\dfrac{h}{4}(3 a+b) \\ & area(E F C D)=\dfrac{1}{2}[b+\dfrac{1}{2}(a+b)] \times h=\dfrac{h}{4}(a+3 b) \end{aligned} $
So,
$\dfrac{area(A B E F)}{area(E F C D)}=\dfrac{\dfrac{h}{4}(3 a+b)}{\dfrac{h}{4}(a+3 b)}=\dfrac{3 a+b}{a+3 b}$
So, the required ratio is $(3 a+b):(a+3 b)$.
Hence, the correct option is (B).
Short Answer Questions with Reasoning
Write True or False and justify your answer:
1. $A B C D$ is a parallelogram and $X$ is the mid-point of $A B$. If $ar(AXCD)=24 ~cm^{2}$, then $ar(ABC)=24 ~cm^{2}$.
Show Answer
Solution
Given in the question, $ABCD$ is a parallelogram and $X$ is the mid-point of $AB$.
So, $area(A B C D)=area(A X C D)+area(\triangle X B C)$
Now, diagonal $AC$ of a parallelogram divides it into two triangles of equal area.
area $(A B C D)=2 area(\triangle A B C)$
Similarly, $X$ is the mid-point of $AB$, So,
area $(\triangle C X B)=\dfrac{1}{2}$ area $(\triangle A B C) \quad \ldots$ (III) [Median divides the triangle in two triangles of equal area]
2area $(\triangle A B C)=24+\dfrac{1}{2} area(\triangle A B C) \quad$ [By using equation (I), (II) and (III)]
Now, 2area $(\triangle A B C)-\dfrac{1}{2} area(\triangle A B C)=24$
$\dfrac{3}{2} area(\triangle A B C)=24$
Therefore, $area(\triangle A B C)=\dfrac{2 \times 24}{3}=16 ~cm^{2}$.
2. $P Q R S$ is a rectangle inscribed in a quadrant of a circle of radius $13 ~cm$. A is any point on $P Q$. If $P S=5 ~ c m$, then $ar(P A S)=30 ~cm^{2}$
Show Answer
Solution
Given: A is any point on PQ. Since, $PA<PQ$
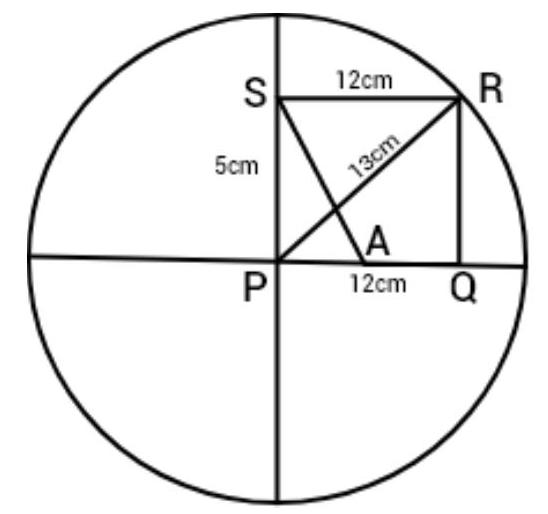
Now, area of triangle PQR is:
area $(\triangle P Q R)=\dfrac{1}{2} \times$ base $\times$ height
So, $area(\triangle P Q R)=\dfrac{1}{2} \times P Q \times Q R=\dfrac{1}{2} \times 12 \times 5=30 ~cm^{2}[PQRS$ is a rectangle, $RQ=SP=5 ~cm]$
As $PA<PQ$
So, area $(\triangle P A S)<area(\triangle P Q R)$
Or area $(\triangle P A S)<30 ~cm^{2} \quad[area(\triangle P Q R)=30 ~cm^{2}]$
Hence, the given statement is false.
3. PQRS is a parallelogram whose area is $180 ~cm^{2}$ and $A$ is any point on the diagonal QS. The area of $\triangle ASR=90 ~cm^{2}$.
Show Answer
Solution
Given: PQRS is a parallelogram.
As we know that diagonal of a parallelogram divides parallelogram into two triangles of equal area.
So,
$ \begin{aligned} area(\triangle Q R S) & =\dfrac{1}{2} area(P Q R S) \\ & =\dfrac{1}{2} \times 180=90 ~cm^{2} \end{aligned} $
Now, $A$ is any point on SQ. So, area $(\triangle A S R)<area(\triangle Q R S)$
Therefore, $area(\triangle A S R)<90 ~cm^{2}$
Hence, the given statement is false.
4. $A B C$ and $B D E$ are two equilateral triangles such that $D$ is the mid-point of BC. Then $ar(BDE)=\dfrac{1}{4} ar(ABC)$.
Show Answer
Solution
Given: $\triangle ABC$ and $\triangle BDE$ are two equilateral triangles.
Suppose that each sides of triangle $ABC$ be $x$.
Similarly, D is the mid-point of BC. So, each side of triangle BDE is $\dfrac{x}{2}$.
Now,
$\dfrac{area(\triangle B D E)}{area(\triangle A B C)}=\dfrac{\dfrac{\sqrt{3}}{4} \times(\dfrac{x}{2})^{2}}{\dfrac{\sqrt{3}}{4} \times x^{2}}=\dfrac{x^{2}}{4 x^{2}}=\dfrac{1}{4}$
Therefore, area $(\triangle B D E)=\dfrac{1}{4} area(\triangle A B C)$.
Hence, the given statement is true.
5. In Fig., ABCD and EFGD are two parallelograms and $G$ is the mid-point of CD. Then $ar(DPC)=\dfrac{1}{4} ar(EFGD)$.
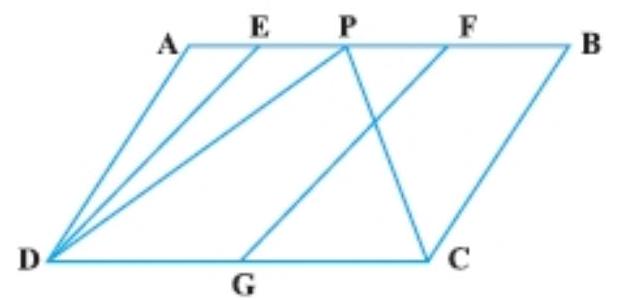
Show Answer
Solution
As triangle DPC and parallelogram ABCD are on same base DC and between the same parallels $AB$ and $DC$. So,
$$ \begin{equation*} area(\triangle D P C)=\dfrac{1}{2} area(A B C D) \tag{I} \end{equation*} $$
Now,
$\dfrac{area(E F G D)}{area(A B C D)}=\dfrac{D G \times h}{D C \times h}=\dfrac{D G}{2 D G}=\dfrac{1}{2}(G$ is the mid-point of $DC)$
Implies that, area $(E F G D)=\dfrac{1}{2} area(A B C D)$
So, area $(D P C)=area(E F G D) \quad[$ From equation $(I)]$
Hence, the given statement is false.
Short Answer Questions
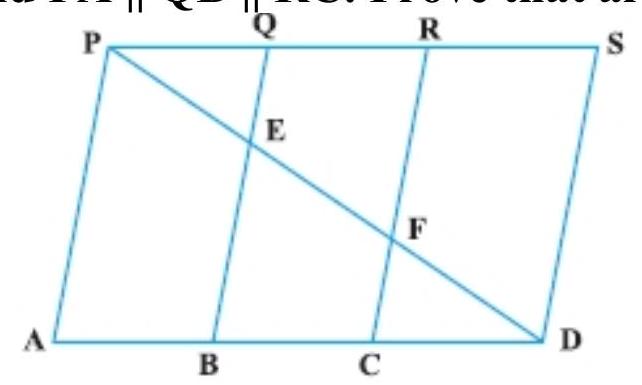
1. In Fig., PSDA is a parallelogram. Points $Q$ and $R$ are taken on PS such that $P Q=Q R=R S$ and $P A||Q B| |R C$. Prove that $ar(P Q E)=ar(C F D)$.
Show Answer
Solution
Given: PSDA is a parallelogram. Points $Q$ and $R$ are taken on $PS$ such that $PQ=QR=RS$ and PA $||$ QB $||$ RC.
To prove that ar $(PQE)=ar(CFD)$.
Proof: $PS=AD \quad$ [opposite angle of a parallelogram]
$\dfrac{1}{3} P S=\dfrac{1}{3} A D$
$PQ=CD$
Similarly, PS $|| AD$ and $QB$ cut them. So,
$\angle P Q E=\angle C B E \quad$ [Alternate angles]…(II)
Again, $QB || RC$ and $AD$ cut them, $\angle Q B D=\angle R C D$ [Corresponding angle]
So, $\angle P Q E=\angle F C D \quad \ldots$ (IV) [From (II) and (III), $\angle C B E$ and $\angle Q B D$ are same and $\angle R C D$ and $\angle F C D$ are same]
Now, in triangle $PQE$ and triangle $CFD$,
$\angle P Q E=\angle C D F \quad$ [Alternate angle]
$PQ=CD \quad$ [From equation (I)]
$\angle Q P E=\angle F C D \quad[$ From equation (IV)]
$\triangle P Q E \cong \triangle C F D \quad$ [By ASA congruence rule]
Hence, $ar(\triangle P Q E)=ar(\triangle C F D)$. [Congruence triangle are equal in area]
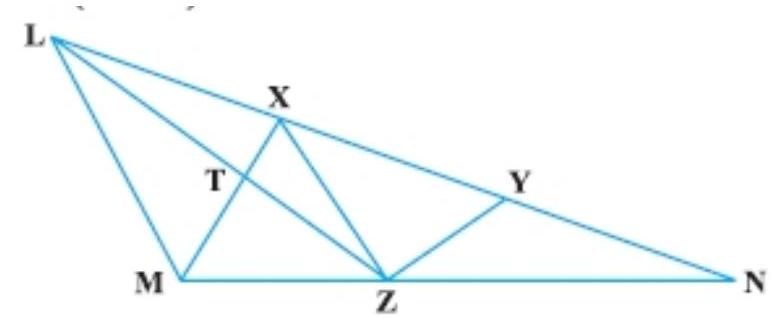
2. $X$ and $Y$ are points on the side $L N$ of the triangle $L M N$ such that $L X=X Y$ $=Y N$. Through $X$, a line is drawn parallel to $LM$ to meet $MN$ at $Z$ (See Fig.). Prove that $ar(L Z Y)=ar(M Z Y X)$
Show Answer
Solution
Prove that ar $(LZY)=ar(MZYX)$
Proof: As $\triangle L X Z$ and $\triangle X M Z$ are on the same base and between the same parallels LM and XZ.
$ar(\triangle L X Z)=ar(\triangle X M Z)$
Now, adding $ar(\triangle X Y Z)$ to both sides of (I), get:
$ \begin{aligned} ar(\triangle L X Z)+ar(\triangle X Y Z) & =ar(\triangle X M Z)+ar(\triangle X Y Z) \\ ar(\triangle L Z Y) & =ar(M Z Y X) \end{aligned} $
3. The area of the parallelogram $ABCD$ is $90 ~cm^{2}$ (see Fig.). Find
(i) ar (ABEF)
(ii) ar (ABD)
(iii) ar (BEF)
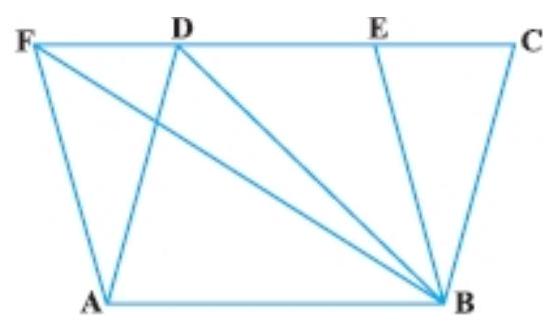
Show Answer
Solution
(i) As we know that parallelogram on the same base and between the same parallels are equal in area.
$ar(A B E F)=ar(A B C D)$
Hence, $ar(A B E F)=ar(A B C D)=90 ~cm^{2}$.
(ii) $\quad ar(\triangle A B D)=\dfrac{1}{2} ar(A B C D)$ [A diagonal of a parallelogram divides the parallelogram in two triangle of equal area]
$=\dfrac{1}{2} \times 90 ~cm^{2}=45 ~cm^{2}$
(iii) $ar(\triangle B E F)=\dfrac{1}{2} ar(A B E F)=\dfrac{1}{2} \times 90 ~cm^{2}=45 ~cm^{2}$
4. In $\triangle A B C$, $D$ is the mid-point of $A B$ and $P$ is any point on $B C$. If $C Q || P D$ meets $A B$ in $Q$
(Fig.), then prove that
$ar(BPQ)=\dfrac{1}{2} ar(ABC)$
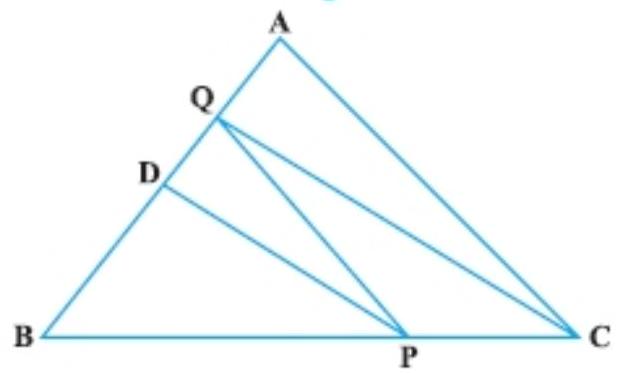
Show Answer
Solution
Given in triangle $ABC, D$ is the mid-point of $AB$ and $P$ is any point on $BC$.
$CQ || PD$ means $AB$ in $Q$.
To prove that $ar(\triangle B P Q)=\dfrac{1}{2} ar(\triangle A B C)$
Construction: Join PQ and CD.
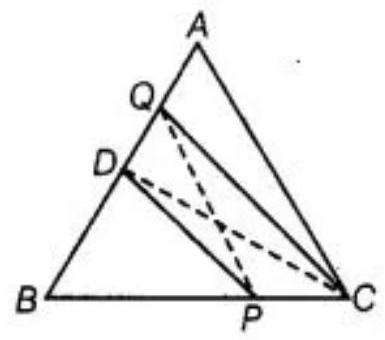
Proof:
As we know that median of a triangle divides it into two triangles of equal area. So,
$ar(\triangle B C D)=\dfrac{1}{2} ar(\triangle A B C)$
Also, we know that triangles on the same base and between the same parallels are equal in area. So,
$ar(\triangle D P Q)=ar(\triangle D P C) \quad[$ Triangle DPQ and DPC are on the same base DP and between the same parallels DP and CQ]
$ar(\triangle D P Q)+ar(\triangle D P B)=ar(\triangle D P C)+ar(D P B)$
Hence, $ar(\triangle B P Q)=ar(\triangle B C D)=\dfrac{1}{2} ar(\triangle A B C)$.
5. $ABCD$ is a square. $E$ and $F$ are respectively the midpoints of $BC$ and $CD$. If $R$ is the mid-point of EF (Fig.), prove that ar $(AER)=ar(AFR)$
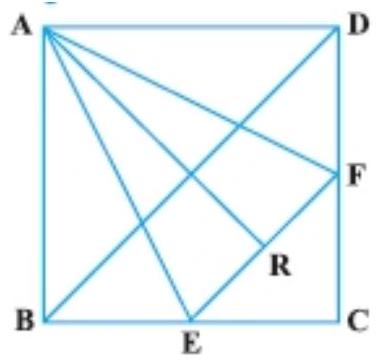
Show Answer
Solution
Given: $ABCD$ is a square. $E$ and $F$ are respectively the midpoints of $BC$ and $CD$. Also, $R$ is the mid-point of EF.
To prove that $ar(\triangle A E R)=ar(\triangle A F R)$
Construction: Draw $AN \perp EF$
Proof:
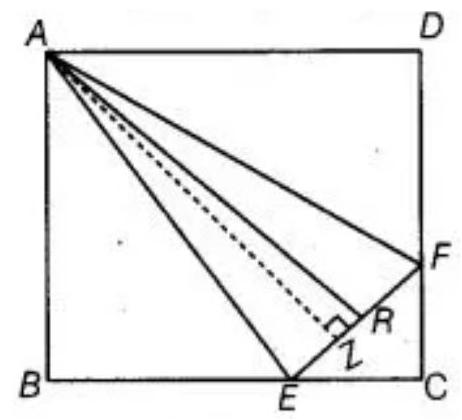
$ar(\triangle A E R)=\dfrac{1}{2} \times$ Base $\times$ Height
$ \begin{aligned} & =\dfrac{1}{2} \times E R \times A N \\ & =\dfrac{1}{2} \times F R \times A N \quad[R \text{ is the mid-point of EF so ER }=FR] \\ & =ar(\triangle A F R) \end{aligned} $
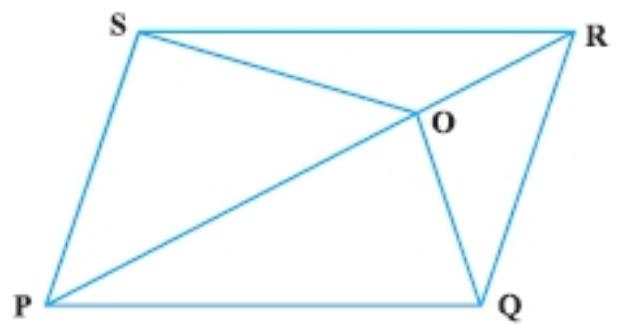
6. $O$ is any point on the diagonal $P R$ of a parallelogram PQRS (Fig.). Prove that
$ar(PSO)=ar(PQO)$.
Show Answer
Solution
Given: $O$ is any point on the diagonal PR of a parallelogram PQRS.
To prove that ar $(PSO)=ar(PQO)$.
Construction: Join SQ which intersects PR at B.
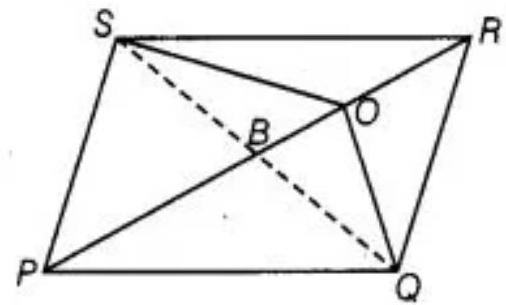
Proof: B is the mid-point of SQ because diagonal of a parallelogram bisect each other.
See the above figure, $PB$ is a median of $\triangle Q P S$ and as we know that a median of a triangle divides it into two triangle of equal area.
$ar(\triangle B P Q)=ar(\triangle B P S)$
Similarly, OB is the median of $\triangle O S Q$.
$ar(\triangle O B Q)=ar(O B S)$
Now, adding equation (I) and (II), get:
$ar(\triangle B P Q)+ar(\triangle O B Q)=ar(\triangle B P S)+ar(\triangle O B S)$
$ar(\triangle P Q O)=ar(\triangle P S O)$
7. $ABCD$ is a parallelogram in which $BC$ is produced to $E$ such that $CE=$ $BC$ (Fig.). $AE$ intersects $CD$ at $F$.
If $ar(DFB)=3 ~cm^{2}$, find the area of the parallelogram $ABCD$.
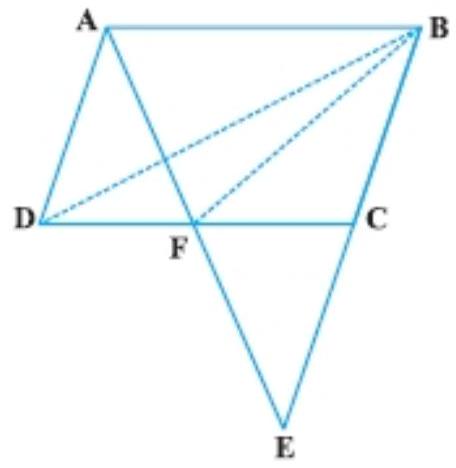
Show Answer
Solution
Given: $ABCD$ is a parallelogram in which $BC$ is produced to $E$ such that $CE=BC . C$ is the mid-point $BE$ and $ar(\triangle D F B)=3 ~cm^{2}$.
In triangle $ADF$ and triangle $EFC$,
$\angle D A F=\angle C E F \quad$ [Alternate interior angle]
$AD=CE \quad[AD=BC=CE]$
$\angle A D F=\angle F C E \quad$ [Alternate interior angle]
So, $\triangle A D F \cong \triangle E C F \quad$ [By SAS rule of congruence]
Now, $\triangle A D F \cong \triangle E C F \quad$ [By SAS rule of congruence] $D F=C F$ $[CPCT]$
$As BF$ is the median of triangle $BCD$.
$ar(\triangle B D F)=\dfrac{1}{2} ar(B C D) \quad \ldots$ (I) [Median divides a triangle into two triangle of equal area]
As we know that a triangle and parallelogram are on the same base and between the same parallels then the area of the triangles is equal to half the area of the parallelogram.
$$ \begin{align*} & ar(\triangle B C D)=\dfrac{1}{2} ar(A B C D) \quad \ldots(II) \tag{II}\\ & ar(\triangle B D F)=\dfrac{1}{2}{\dfrac{1}{2} ar(A B C D)} \quad \text{ [By equation (I)] } \\ & 3 ~cm^{2}=\dfrac{1}{4} ar(A B C D) \\ & ar(A B C D)=12 ~cm^{2} \end{align*} $$
Hence, the area of the parallelogram is $12 ~cm^{2}$.
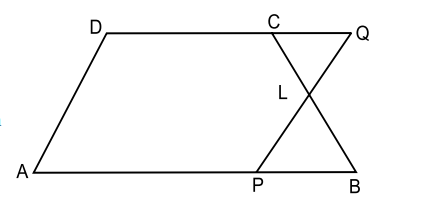
8. In trapezium $A B C D, A B || D C$ and $L$ is the mid-point of $B C$. Through $L$, a line $P Q || A D$ has been drawn which meets $A B$ in $P$ and $D C$ produced in $Q$
(Fig.). Prove that $ar(ABCD)=ar(APQD)$
Show Answer
Solution
To prove that ar $(ABCD)=ar(APQD)$
Proof: $A S A B || D C$ and $A B || D Q$
In triangle CLQ and triangle BLP,
$ \angle Q C L=\angle L B P \quad \text{ [Alternate angles] } $
$CL=LP \quad[L$ is the mid-point og $BC]$
$\angle C L Q=\angle B L P \quad$ [Vertical opposite angles]
$\triangle C L Q \cong \triangle B L P \quad$ [By ASA congruence rule]
So, $ar(\triangle C L Q)=ar(\triangle B L P) \ldots$ (I) [Congruent triangles are equal in area]
Now, adding $ar(A P L C D)$ both side in above equation, get:
$ \begin{aligned} ar(\triangle C L Q)+ar(A P L C D) & =ar(\triangle B L P)+ar(A P L C D) \\ ar(\triangle A P Q D) & =ar(A B C D) \end{aligned} $
Hence, proved.
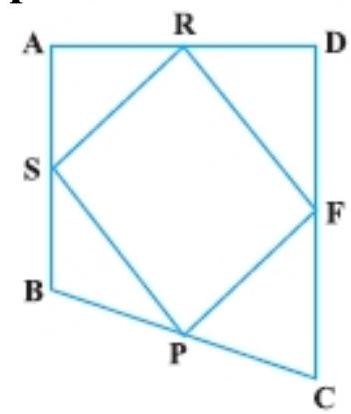
9. If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral (Fig.).
[Hint: Join BD and draw perpendicular from A on BD.]
Show Answer
Solution
According to the question, a quadrilateral $ABCD$ in which the mid-point of the sides of it are joined in order of form parallelogram PQRS.
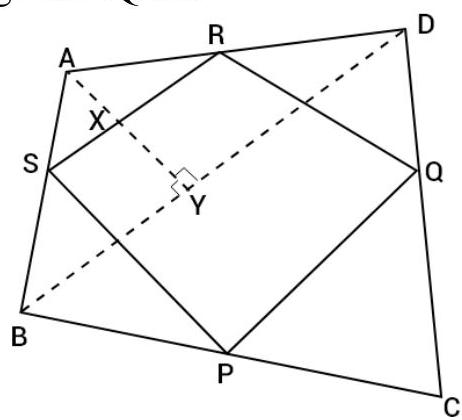
To Prove that $ar(P Q R S)=\dfrac{1}{2} ar(A B C D)$
Construction: Join BD and draw perpendicular from A and BD which interest SR and BD at $X$ and $Y$ respectively.
Proof: In triangle $ABD, S$ and $R$ are the mid-points of sides $AB$ and $AD$ respectively. So, $S R || B D$
And: $A S X || B Y$
See the figure, $x$ is the mid-point of AY. So,
$A X=X Y$
And $S R=\dfrac{1}{2} B D \ldots$ (II)[mid-point theorem]
Now, $ar(\triangle A B D)=\dfrac{1}{2} \times B D \times A Y$ $ar(\triangle A S R)=\dfrac{1}{2} \times S R \times A X$
$ar(\triangle A S R)=\dfrac{1}{2} \times(\dfrac{1}{2} B D) \times(\dfrac{1}{2} A Y) \quad[$ Using equation (I) and (II)]
$ar(\triangle A S R)=\dfrac{1}{4} \times(\dfrac{1}{2} B D \times A Y)$
$ar(\triangle A S R)=\dfrac{1}{4} \times(\triangle A B D)$
Again, $ar(\triangle C P Q)=\dfrac{1}{4} ar(\triangle C B D)$
$ar(\triangle B P S)=\dfrac{1}{4} ar(\triangle B A C)$
$ar(\triangle D R Q)=\dfrac{1}{4} ar(D A C)$
Now, adding equation (III), (IV), (V) and (VI), get:
$ \begin{aligned} & ar(\triangle A S R)+ar(\triangle C P Q)+ar(B P S)+ar(\triangle D R Q) \\ & =\dfrac{1}{4} ar(\triangle A B D)+\dfrac{1}{4} ar(\triangle C B D)+\dfrac{1}{4} ar(\triangle A B C)+\dfrac{1}{4} ar(\triangle D A C) \\ & =\dfrac{1}{4}[ar(\triangle A B D)+ar(\triangle C B D)+ar(\triangle A B C)+ar(\triangle D A C)] \\ & =\dfrac{1}{4}[ar(A B C D)+ar(A B C D)] \\ & =\dfrac{1}{4} \times 2 ar(A B C D) \\ & =\dfrac{1}{2} ar(A B C D) \end{aligned} $
So, $ar(\triangle A S R)+ar(\triangle C P Q)+ar(\triangle B P S)+ar(\triangle D R Q)=\dfrac{1}{2} ar(A B C D)$
$ ar(A B C D)-ar(P Q R S)=\dfrac{1}{2} ar(A B C D) $
Now, $ar(P Q R S)=ar(A B C D)-\dfrac{1}{2} ar(A B C D)$
$ ar(P Q R S)=\dfrac{1}{2} ar(A B C D) $
Hence, proved.
Long Answer Questions
1. A point $E$ is taken on the side $B C$ of a parallelogram $A B C D$. $A E$ and $D C$ are produced to meet at $F$. Prove that $ar(ADF)=ar(ABFC)$
Show Answer
Solution
Given in the question, $A$ point $E$ is taken on the side $BC$ of a parallelogram $ABCD . AE$ and $DC$ are produced to meet at $F$.
Prove that ar $(A D F)=ar(A B F C)$
Proof: $ABCD$ is a parallelogram and $AC$ divides it into two triangle of equal area.
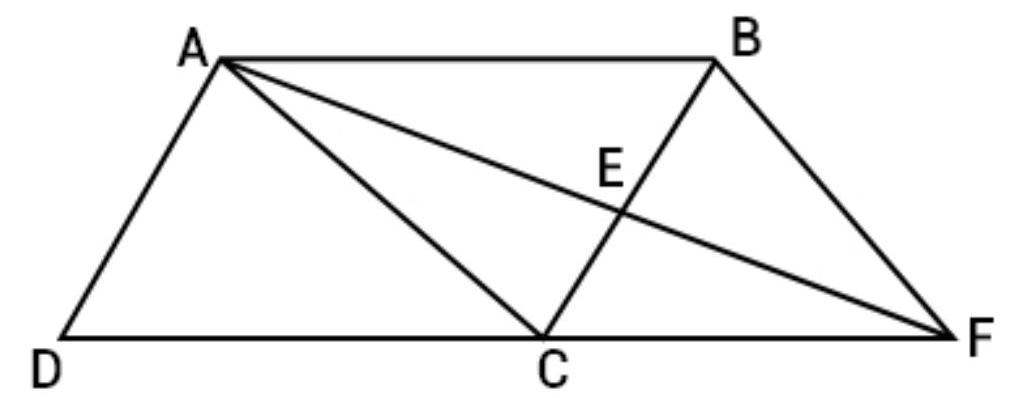
$ar(\triangle A D C)=ar(\triangle A B C)$
So, $DC || AB$ and $CF || AB$
As we know that triangle on the same base and between the same parallels are equal in area. So,
$ar(\triangle A C F)=ar(\triangle B C F)$
Adding equation (I) and (II), get:
$ar(\triangle A D C)+ar(A C F)=ar(\triangle A B C)+ar(\triangle B C F)$
$ar(\triangle A D F)=ar(A B F C)$
Hence, proved.
2. The diagonals of a parallelogram $ABCD$ intersect at a point $O$. Through $O$, a line is drawn to intersect $A D$ at $P$ and $B C$ at $Q$. show that $P Q$ divides the parallelogram into two parts of equal area.
Show Answer
Solution
Given: $ABCD$ is a parallelogram and diagonal interact at $O$, and draw a line PQ which intersects $AD$ and $BC$.
To prove that $PQ$ divides the parallelogram $ABCD$ into two parts of equal area that $ar(A B Q P)=ar(C D P Q)$.
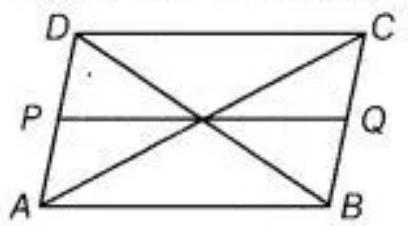
Proof: $A C$ is a diagonal of the parallelogram $A B C D$.
$ar(\triangle \dfrac{1}{2} A C D)=\dfrac{1}{2} ar(A B C D)$
In triangle $AOP$ and triangle $COQ$, $AO=CO$ [Diagonals of a parallelogram bisect each other] $\angle A O P=\angle C O Q$ [Vertical opposite angles] $\angle O A P=\angle O C Q$ [Alternate angles, $AB | CD$ ] $\triangle A O P=\triangle C O Q$ [By ASA congruent rule]
Since, $ar(\triangle A O P)=ar(\triangle C O Q) \quad$ [Congruent area axiom]
Now, adding $ar(A O Q D)$ to both sides of (II), get:
$ar(\triangle A C D)=\dfrac{1}{2} ar(A B C D) \quad$ [From equation (I)]
Hence, $ar(A P Q D)=\dfrac{1}{2} ar(A B C D)$.
3. The medians $BE$ and $CF$ of a triangle $ABC$ intersect at $G$. Prove that the area of $\triangle GBC=$ area of the quidrilateral AFGE
Show Answer
Solution
Given: The medians $BE$ and $CF$ of a triangle $ABC$ intersect at $G$ To prove that $ar(\triangle G B C)=ar(A F G E)$.
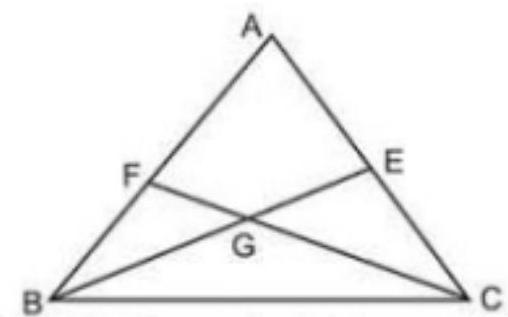
Proof: As median $CF$ divides a triangle into two triangle of equal area. So,
$ar(\triangle B C F)=ar(\triangle A C F)$
$ar(\triangle G B F)+ar(\triangle G B C)=ar(A F G E)+ar(\triangle G C E)$
Now, median $BE$ divides a triangle into two triangle of equal area. So,
$$ \begin{equation*} ar(\triangle G B F)+ar(A F G E)=ar(\triangle G C E)+ar(\triangle G B C) \tag{II} \end{equation*} $$
Now, subtracting (II) from (I), get:
$ \begin{aligned} ar(\triangle G B C)-ar(A F G E) & =ar(\triangle A F G E)-ar(\triangle G B C) \\ ar(\triangle G B C)+ar(\triangle G B C) & =ar(\triangle A F G E)+ar(\triangle A F G E) \\ 2 ar(\triangle G B C) & =2 ar(A F G E) \end{aligned} $
Hence, $ar(\triangle G B C)=ar(A F G E)$.
4. In Fig., $CD || AE$ and $CY || BA$. Prove that $ar(CBX)=ar(AXY)$
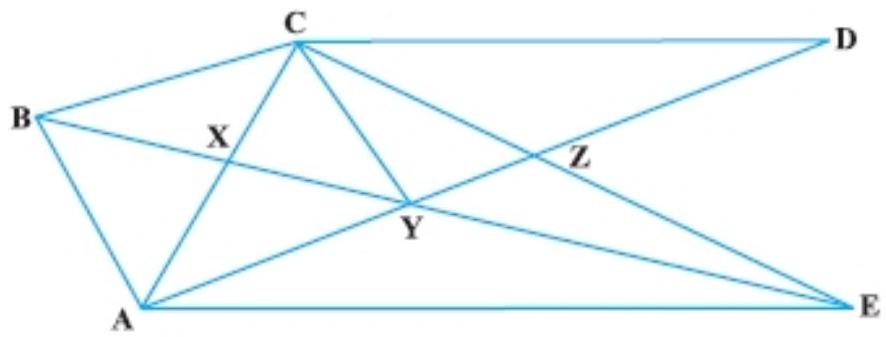
Show Answer
Solution
Given: $CD || AE$ and $CY || BA$
To prove that ar $(C B X)=$ ar $(A X Y)$.
Proof: As we know that triangle on the same base and between the same parallels are equal in area. So,
$ \begin{aligned} ar(\triangle A B C) & =ar(\triangle A B Y) \\ ar(\triangle C B X)+ar(\triangle A B X) & =ar(\triangle A B X)+ar(\triangle A X Y) \end{aligned} $
Hence, $ar(\triangle C B X)=ar(\triangle A X Y)$.
5. $A B C D$ is a trapezium in which $A B || D C, D C=30 ~cm$ and $A B=50 ~cm$. If $X$ and $Y$ are, respectively the mid-points of $A D$ and $B C$, prove that
$ ar(DCYX)=\dfrac{7}{9} ar(XYBA) $
Show Answer
Solution
To prove that $ar(DCYX)=\dfrac{7}{9} ar(XYBA)$
Proof: In triangle MBY and triangle DCY,
$\angle 1=\angle 2 \quad$ [Vertically opposite angles]
$\angle 3=\angle 4 \quad[AB || DC$ and alternate angles are equal $]$
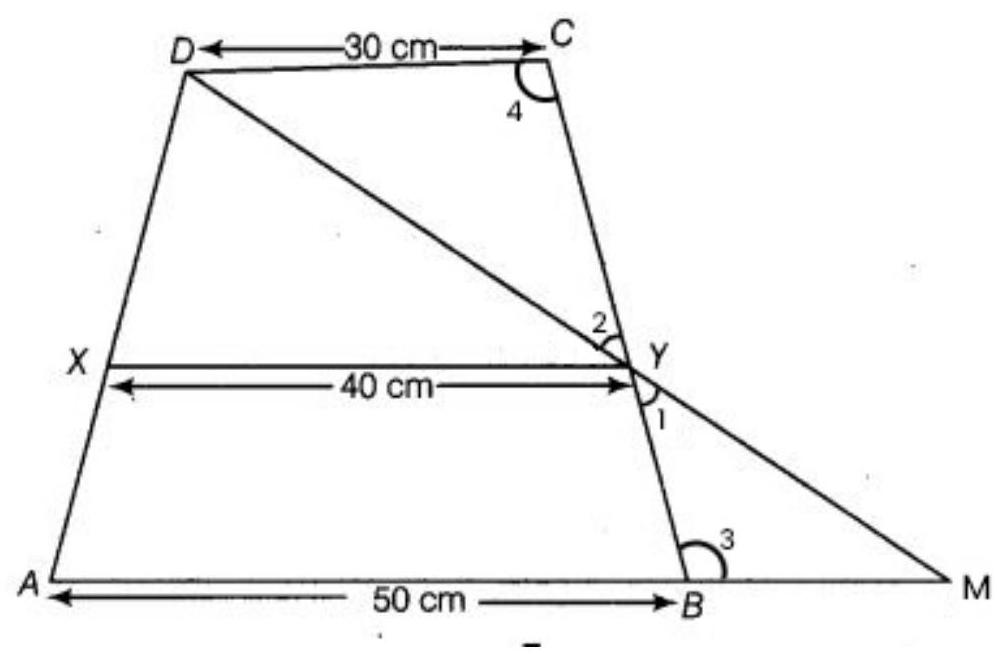
$BY=CY \quad[Y$ is the mid-point of $BC]$
$\triangle M B Y \cong \triangle D C Y \quad$ [By ASA congruent angle]
So, $MB=DC=30 ~cm \quad[CPCT]$
Now, $AM=AB+BM$ $=50 ~cm+30 ~cm$ $=80 ~cm$
In triangle $ADM$,
$X Y=\dfrac{1}{2} A M=\dfrac{1}{2} \times 80 ~cm=40 ~cm$
Now, $AB||XY|| DC$ and $X$ and $Y$ are the mid-points of $AD$ and $BC$, So, height of trapezium DCXY and XYBA are equal and assume the equal height be $h ~cm$.
$\dfrac{ar(D C Y X)}{ar(X Y B A)}=\dfrac{\dfrac{1}{2} \times(30+40) \times h}{\dfrac{1}{2} \times(30+50) \times h}=\dfrac{70}{90}=\dfrac{7}{9}$
Hence, $ar(D C Y X)=\dfrac{7}{9} ar(X Y B A)$.
6. In $\triangle ABC$, if $L$ and $M$ are the points on $AB$ and $AC$, respectively such that LM || BC. Prove that $ar(LOB)=ar(MOC)$
Show Answer
Solution
Given: in triangle $ABC$ and $L$ and $M$ are the points on $AB$ and $AC$, respectively such that $LM$ || BC.
Prove that ar $(LOB)=ar(MOC)$
Proof: As we know that triangle on the same base and between the same parallels are equal in area.
$ar(\triangle L B M)=ar(\triangle L C M)$
[Triangle LBM and triangle L~CM are on the same base LM and between the same parallels LM and $BC]$
$\begin{aligned} ar(\triangle L B M) & =ar(\triangle L C M) \\ ar(\triangle L O M)+ar(\triangle L O B) & =ar(\triangle L O M)+ar(\triangle M O C)\end{aligned}$
Hence, $ar(\triangle L O B)=ar(\triangle M O C)$.
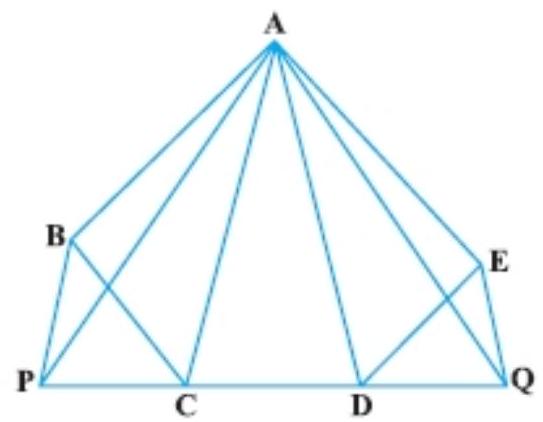
7. In Fig., $ABCDE$ is any pentagon. BP drawn parallel to $AC$ meets $DC$ produced at $P$ and $E Q$ drawn parallel to $A D$ meets $C D$ produced at $Q$. Prove that
$ar(ABCDE)=ar(APQ)$
Show Answer
Solution
Given: $ABCDE$ is any pentagon and $BP || AC$ meets $DC$ produced at $P$ and $EQ || AD$ meets $CD$ produced at $Q$.
Prove that ar $(ABCDE)=ar(APQ)$
Proof: As we know that triangle on the same base and between the same parallels are equal in area.
$ar(\triangle A B C)=ar(\triangle A P C)$
$ar(\triangle A D E)=ar(\triangle A D Q)$
Now, adding equation (I) and (II), get:
$ar(\triangle A B C)+ar(\triangle A D E)=ar(\triangle A P C)+ar(\triangle A D Q)$
Now, adding $ar(\triangle A C D)$ to both side, get:
$ar(\triangle A B C)+ar(\triangle A D E)+ar(A C D)=ar(\triangle A P C)+ar(\triangle A D Q)+ar(A C D)$
Hence, $ar(A B C D E)=ar(\triangle A P Q)$.
8. If the medians of a $\triangle ABC$ intersect at $G$, show that
$ar(AGB)=ar(AGC)=ar(BGC)=\dfrac{1}{3} ar(ABC)$
Show Answer
Solution
Given: The median of a triangle $ABC$ intersect at $G$.
To prove that $ar(AGB)=ar(AGC)=ar(BGC)=\dfrac{1}{3} ar(ABC)$
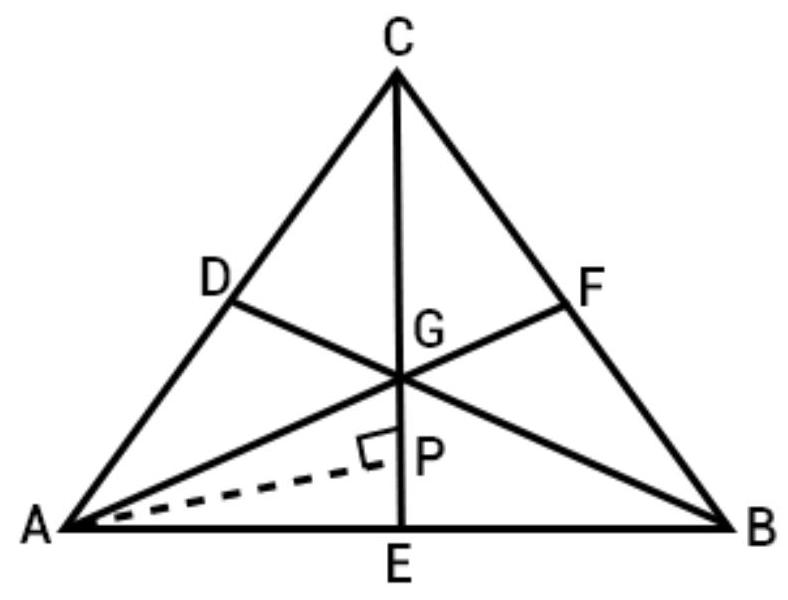
Construction: Draw $BP \perp EG$
Proof: $A G=\dfrac{2}{3} A E \quad$ [Centroid divides the median in the ration 2:1]
Now, $ar(\triangle A G B)=\dfrac{1}{2} \times A G \times B P$
[Median divides a triangle into two triangles equal in area]
$=\dfrac{1}{3} ar(\triangle A B C)$
Again, $ar(\triangle A G C)=ar(\triangle B G C)=\dfrac{1}{3} ar(\triangle A B C)$
So, $ar(\triangle A G B)=ar(\triangle A G C)=ar(\triangle B G C)=\dfrac{1}{3} ar(\triangle A B C)$
Hence, proved.
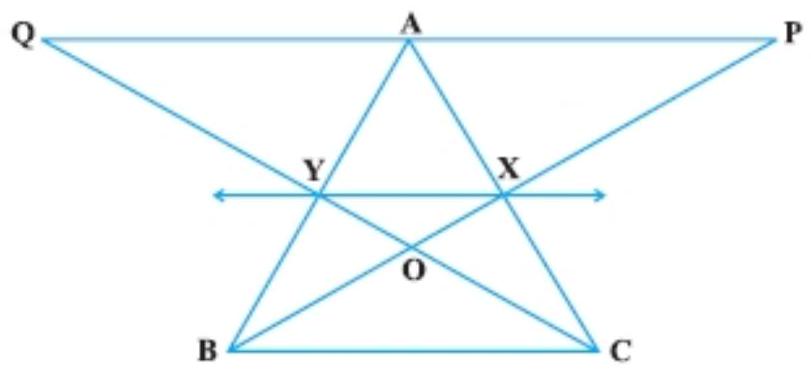
9. In Fig., $X$ and $Y$ are the mid-points of $A C$ and $A B$ respectively, $Q P || B C$ and CYQ and BXP are straight lines. Prove that ar $(A B P)=ar(A C Q)$.
Show Answer
Solution
Given: In triangle $A B C, X$ and $Y$ are the mid-points of $A B$ and $A C$.
To prove that $ar(ABP)=ar(ACQ)$.
Proof: Since, $X Y|| B Y$ [BY mid-point theorem]
As we know that triangle on the same base and between the same parallels lines are equal in area. So,
$ar(\triangle B Y C)=ar(\triangle B X C)$
Now, subtracting $ar(\triangle B O C)$ from both sides in the above, get:
$ar(\triangle B Y C)-ar(\triangle B O C)=ar(\triangle B X C)-ar(\triangle B O C)$
$ar(\triangle B O Y)=ar(\triangle C O X)$
Now, adding $ar(\triangle X O Y)$ to both side in equation (II), get:
$ar(\triangle B O Y)+ar(\triangle X O Y)=ar(\triangle C O X)+ar(\triangle X O Y)$
Again, quadrilaterals XYAP and YXAQ are on the same base XY and between the same parallels $X Y$ and $P Q$. So,
$ar(X Y A P)=ar(X Y Q A)$
Now, adding equation (III) and (IV), get:
$ar(\triangle B X Y)+ar(X Y A P)=ar(\triangle C X Y)+ar(X Y A Q)$
Hence, $ar(\triangle A B P)=ar(\triangle A C Q)$.
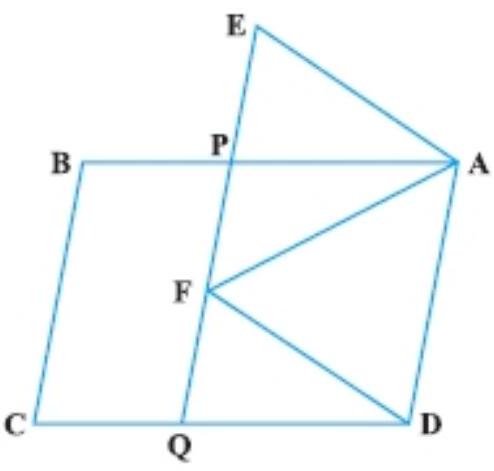
10. In Fig., ABCD and AEFD are two parallelograms. Prove that $ar(PEA)=ar(QFD)$ [Hint: Join PD].
Show Answer
Solution
Given: $ABCD$ and $AEFD$ are two parallelogram.
To prove that $ar(\triangle P E A)=ar(\triangle Q F D)$
Construction: join PD.
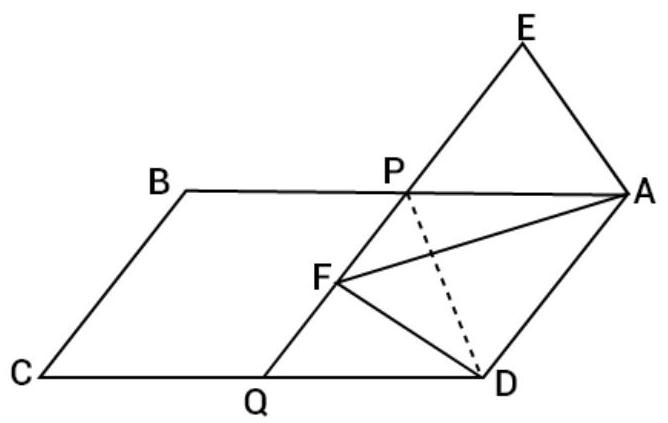
Proof: In triangle PEA and triangle QFD,
$\angle A P E=\angle D Q F \quad$ [Corresponding angles are equal as $AB || CD]$
$\angle A E P=\angle D E Q \quad$ [Corresponding angles are equal as $AE || DF]$
$AE=DF \quad$ [Opposite sides of a parallelogram are equal]
So, $\triangle P E A \cong \triangle Q F D \quad$ [By AAS congruent rule]
Hence, $ar(\triangle P E A)=ar(\triangle Q E D)$.










