Linear Equations in Two Variables
Multiple Choice Questions(MCQs)
1. The linear equation $2 x-5 y=7$ has
(A) A unique solution
(B) Two solutions
(C) Infinitely many solutions
(D) No solution
Show Answer
Solution
The given linear equation $2 x-5 y=7$ has two variable. Since, a linear equation with two variable has infinitely many solution.
Hence, the correct option is (C).
2. The equation $2 x+5 y=7$ has a unique solution, if $x, y$ are:
(A) Natural numbers
(B) Positive real numbers
(C) Real numbers
(D) Rational numbers
Show Answer
Solution
The given equation $2 x+5 y=7$ has a unique solution, if $x, y$ are natural number.
Hence, the correct option is (a).
3. If $(2,0)$ is a solution of the linear equation $2 x+3 y=k$, then the value of $k$ is
(A) 4
(B) 6
(C) 5
(D) 2
Show Answer
Solution
Put $x=2$ and $y=0$ in the linear equation $2 x+3 y=k$.
$2 \times 2+3 \times 0=k$
$k=4$
Hence, the correct option is (A).
4. Any solution of the linear equation $2 x+0 y+9=0$ in two variables is of the form
(A) $(-\dfrac{9}{2}, m)$
(B) $(n,-\dfrac{9}{2})$
(C) $(0,-\dfrac{9}{2})$
(D) $(-9,0)$
Show Answer
Solution
Consider the linear equation:
$2 x+0 y+9=0$
Now,
$2 x=-9$
$x=-\dfrac{9}{2}$
Since, the coefficient of $y$ is 0 in the given equation. So, the solution can be given as $(-\dfrac{9}{2}, m)$.
Hence, the correct option is (A).
5. The graph of the linear equation $2 x+3 y=6$ cuts the $y$-axis at the point
(A) $(2,0)$
(B) $(0, 3)$
(C) $(3,0)$
(D) $(0,2)$
Show Answer
Solution
The graph of the linear equation $2 x+3 y=6$ cuts the $y$-axis at the point where $x$-coordinate is zero.
$ \begin{aligned} & \text{ So, put } x=0 \text{ in } 2 x+3 y=6 \text{, get: } \\ & \begin{aligned} 2 x+3 y & =6 \\ 2 \times 0+3 \times y & =6 \\ 3 y & =6 \\ y & =2 \end{aligned} \end{aligned} $
So, the point is $(0,2)$.
Hence, the correct option is (D).
6. The equation $x=7$, in two variables, can be written as
(A) $1 . x+1 . y=7$
(B) $1 . x+0 . y=7$
(C) $0 . x+1 . y=7$
(D) $0 . x+0 . y=7$
Show Answer
Solution
The equation $x=7$ in two variable can be written as $1 x+0 y=7$.
Hence, the correct option is (B).
7. Any point on the $x$-axis is of the form
(A) $(x, y)$
(B) $(0, y)$
(C) $(x, 0)$
(D) $(x, x)$
Show Answer
Solution
We know that any point on the $x$-axis has its ordinate 0 . Since, the point will be $(x, 0)$.
Hence, the correct option is (C).
8. Any point on the line $y=x$ is of the form
(A) $(a, a)$
(B) $(0, a)$
(C) $(a, 0)$
(D) $(a,-a)$
Show Answer
Solution
Any point on the line $y=x$ is of the form $(a, a)$ because the line $y=x$ will have $x$ and $y$ coordinate same.
Hence, the correct option is (a).
9. The equation of $x$-axis is of the form
(A) $x=0$
(B) $y=0$
(C) $x+y=0$
(D) $x=y$
Show Answer
Solution
The equation of $x$-axis is of the form $y=0$.
Hence, the correct option is (B).
10. The graph of $y=6$ is a line
(A) parallel to $x$-axis at a distance 6 units from the origin
(B) parallel to $y$-axis at a distance 6 units from the origin
(C) making an intercept 6 on the $x$-axis.
(D) making an intercept 6 on both the axes.
Show Answer
Solution
The graph of $y=6$ is a line parallel to $x$-axis because it does not contain $x$.
Hence, the correct option is (A).
11. $x=5, y=2$ is a solution of the linear equation
(A) $x+2 y=7$
(B) $5 x+2 y=7$
(C) $x+y=7$
(D) $5 x+y=7$
Show Answer
Solution
$x=5, y=2$ is a solution of the linear equation $x+y=7$ because $5+2=7$.
Hence, the correct option is (C).
12. If a linear equation has solutions $(-2,2),(0,0)$ and $(2,-2)$, then it is of the form
(A) $y-x=0$
(B) $x+y=0$
(C) $-2 x+y=0$
(D) $-x+2 y=0$
Show Answer
Solution
The point $(-2,2)$ and $(2,-2)$ have $x$ and $y$-coordinate of opposite signs.
Now, the sum of the $x$ and $y$-coordinate is: $x+y=-2+2=0$ i.e., $y=-x$ will have $x$ and $y$ coordinate opposite signs and also satisfies the point $(0,0)$.
Hence, the correct option is (B).
13. The positive solutions of the equation $a x+b y+c=0$ always lie in the
(A) 1 st quadrant
(B) 2nd quadrant
(C) 3rd quadrant
(D) 4th quadrant
Show Answer
Solution
We know that I quadrant has consists of all the point $(x, y)$ positive. So, the positive solution of the equation $a x+b y+c=0$ lie in I quadrant.
Hence, the correct option is (A).
14. The graph of the linear equation $2 x+3 y=6$ is a line which meets the $x$ axis at the point
(A) $(0,2)$
(B) $(2,0)$
(C) $(3,0)$
(D) $(0,3)$
Show Answer
Solution
The graph of the linear equation $2 x+3 y=6$ is a line which meets the $x$-axis at the point where $y=0$. Now, put $y=0$ in the given equation, get:
$ 2 x+3 y=6 $
$2 x+y \times 0=6$
$ 2 x=6 $
$ x=3 $
So, the point is $(3,0)$ which is lies on the line $2 x+3 y=6$.
Hence, the correct option is (C).
15. The graph of the linear equation $y=x$ passes through the point
(A) $(\dfrac{3}{2}, \dfrac{-3}{2})$
(B) $(0, \dfrac{3}{2})$
(C) $(1,1)$
(D) $(\dfrac{-1}{2}, \dfrac{1}{2})$
Show Answer
Solution
The graph of the linear equation $y=x$ passes through the point where $x$ and $y$ coordinate will have same that is $(1,1)$.
Hence, the correct option is (C).
16. If we multiply or divide both sides of a linear equation with a non-zero number, then the solution of the linear equation:
(A) Changes
(B) Remains the same
(C) Changes in case of multiplication only
(D) Changes in case of division only
Show Answer
Solution
If we multiply or divide both sides of a linear equation with a non-zero number, then the solution of the linear equation remains the same.
17. How many linear equations in $x$ and $y$ can be satisfied by $x=1$ and $y=$ 2 ?
(A) Only one
(B) Two
(C) Infinitely many
(D) Three
Show Answer
Solution
There are infinitely linear equations in $x$ and $y$ can be satisfied by $x=1$ and $y=2$. For example: $x+y=3$ or $2 y-x=3$.
Hence, the correct option is $(C)$.
18. The point of the form $(a, a)$ always lies on:
(A) $x$-axis
(B) $y$-axis
(C) On the line $y=x$
(D) On the line $x+y=0$
Show Answer
Solution
The point of the form $(a, a)$ always lies on $y=x$, because $x$ and $y$ coordinate are same. Hence, the correct option is (C).
19. The point of the form $(a,-a)$ always lies on the line
(A) $x=a$
(B) $y=-a$
(C) $y=x$
(D) $x+y=0$
Show Answer
Solution
The point of the form $(a,-a)$ always lies on the line $y=-x$ or $x+y=0$ because $x$ and $y$ coordinate have opposite signs.
Hence, the correct option is (D).
True/False
1. The point $(0,3)$ lies on the graph of the linear equation $3 x+4 y=12$.
Show Answer
Solution
Consider the equation:
$3 x+4 y=12$
Putting $x=0$ and $y=3$ in the equation, get:
$3 \times 0+4 \times 3=12$
$ 12=12 \text{ True } $
So, the point $(0,3)$ satisfies the equation $3 x+4 y=12$.
Hence, the given statement is true.
2. The graph of the linear equation $x+2 y=7$ passes through the point $(0$, 7).
Show Answer
Solution
Consider the linear equation:
$x+2 y=7$
Putting $x=0$ and $y=7$ in the given equation $x+2 y=7$, get:
$ x+2 y=7 $
$0+2 \times 7=7$
$14=7$ Which is False
So, the point $(0,7)$ does not satisfy the equation.
Hence, the given statement is false.
3. The graph given below represents the linear equation $\boldsymbol{{}x}+\boldsymbol{{}y}=\mathbf{0}$.
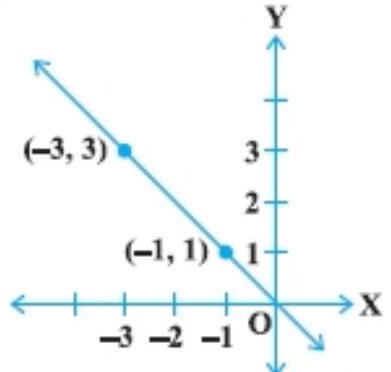
Show Answer
Solution
The given equation is $x+y=0$ that is $y=-x$. Now, any point on the given graph has $x$ and $y$ -coordinate of opposite signs as, the point $(-1,1)$ and $(-3,3)$. So, these points satisfy the given equation.
Hence, the given statement is true.
4. The graph given below represents the linear equation $x=3$ (see Fig. 4.2).
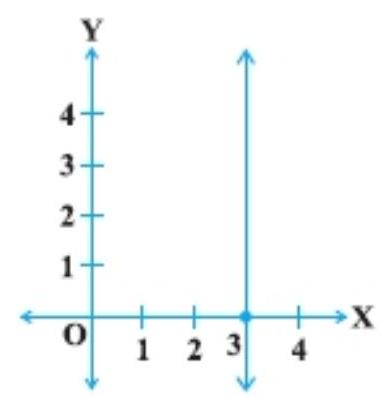
Show Answer
Solution
See the given graph, the equation of the given line is $x=a$ that is $x=3$ parallel to the $y$-axis and to the right of $y$-axis, if $a>0$.
Hence, the given statement is true.
5. The coordinates of points in the table:
$\begin{array}{|l|l|l|l|l|l|} \hline x & 0 & 1 & 2 & 3 & 4 \\ \hline y & 2 & 3 & 4 & -5 & 6 \\ \hline \end{array}$
Represent some of the solutions of the equation
$\boldsymbol{{}x}-\boldsymbol{{}y}+\mathbf{2}=\mathbf{0}$.
Show Answer
Solution
Consider the equation:
$x-y+2=0$.
The point $(0,2),(1,3),(2,4)$ and $(4,6)$ satisfy the given equation then they have solution of it. Now, the point $(3,-5)$ does not satisfy the given equation as $3-(-5)+2=0$, that is $3+5+2=0$ or $10=0$ that is false.
Hence, the given statement is false.
6. Every point on the graph of a linear equation in two variables does not represent a solution of the linear equation.
Show Answer
Solution
Every point on the graph of a linear equation in two variables does represent a solution of the linear equation. So, the given statement is false.
7. The graph of every linear equation in two variables need not be a line.
Show Answer
Solution
The graph of every linear equation in two variables is always a line. So, the given statement is false.
Short Answer Questions
1. Draw the graphs of linear equations $y=x$ and $y=-x$ on the same cartesian plane.
What do you observe?
Show Answer
Solution
The point on the graph $y=x$ will have same signs of $x$ and $y$ coordinate but the point on the graph $y=-x$ will have opposite signs of $x$ and $y$ coordinate.
The graph of the linear equation $y=x$ and $y=-x$ on the same Cartesian plane is show below.
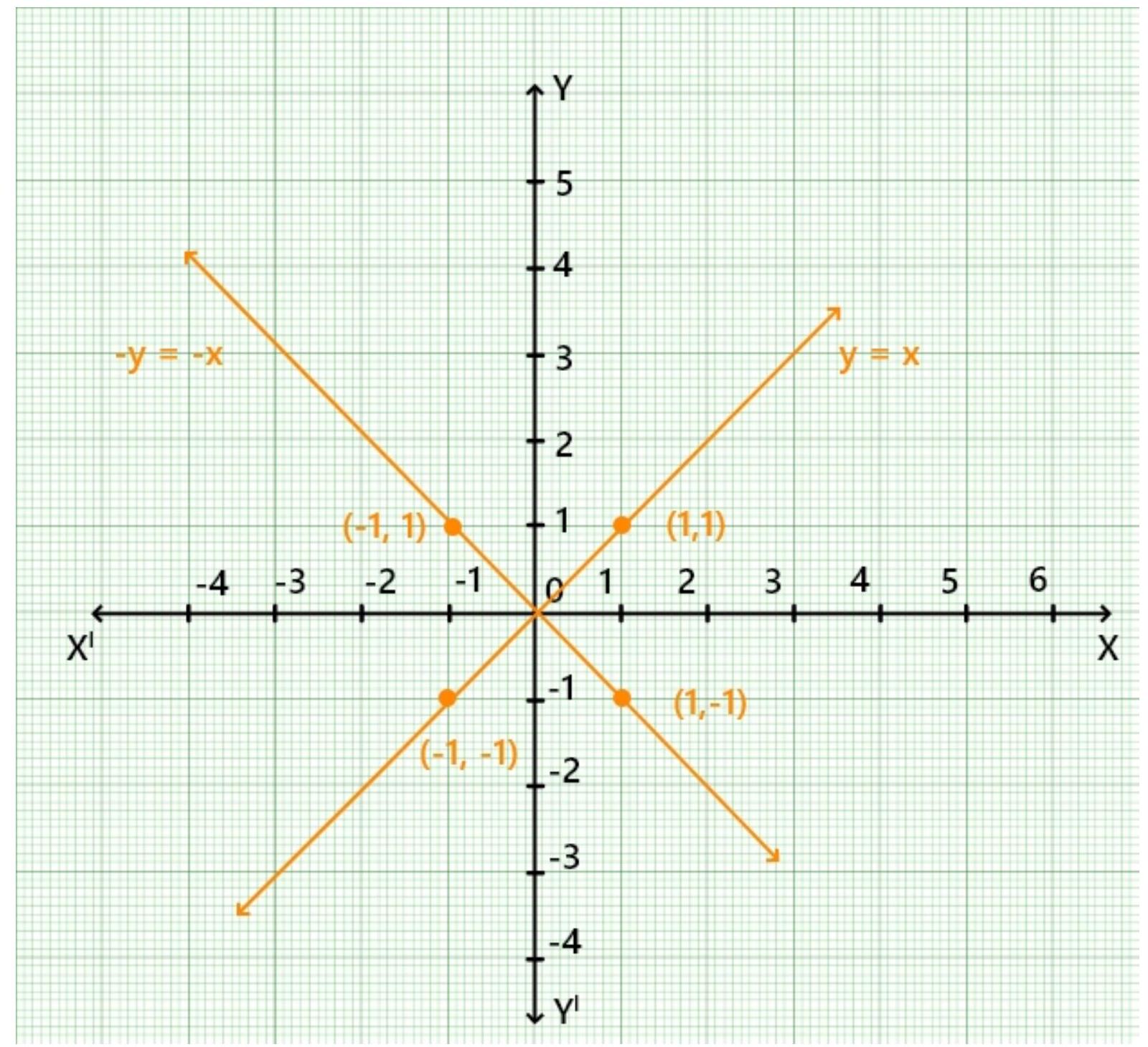
We observed that both graph are passes through the same point $(0,0)$ and they are mirror image of each other about the y-axis.
2. Determine the point on the graph of the linear equation $2 x+5 y=19$, whose ordinate is $1 \dfrac{1}{2}$ times its abscissa.
Show Answer
Solution
Consider the linear equation:
$2 x+5 y=19$
Let the coordinate of the point $(2,3)$.
Putting $x=2$ and $y=3$
$2 x+5 y=2 \times 2+5 \times 3$
$=4+15$
$=19$
Therefore, the point $(2,3)$ is the solution of the given equation.
Now, abscissa of the point is 2 and ordinate is 3 .
Then,
$2 \times 1 \dfrac{1}{2}=2 \times \dfrac{3}{2}=3$
Hence, the ordinate of the point $(2,3)$ is $1 \dfrac{1}{2}$ times its abscissa.
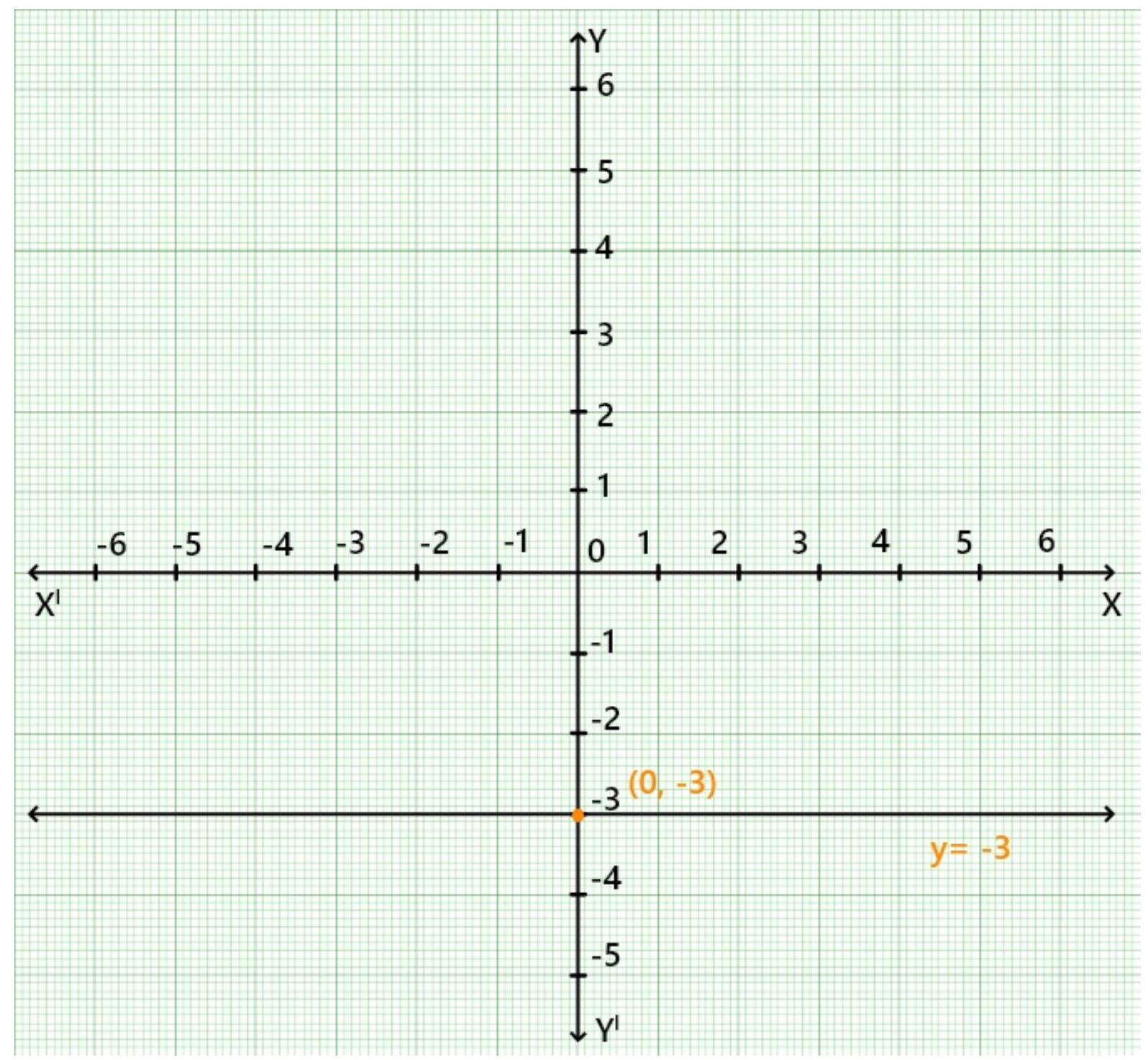
3. Draw the graph of the equation represented by a straight line which is parallel to the $x$-axis and at a distance 3 units below it.
Show Answer
Solution
The graph of the equation $y=-3$ is parallel to the $x$-axis and at a distance 3 units and passing through the point $(0,-3)$ as show in the figure given below.
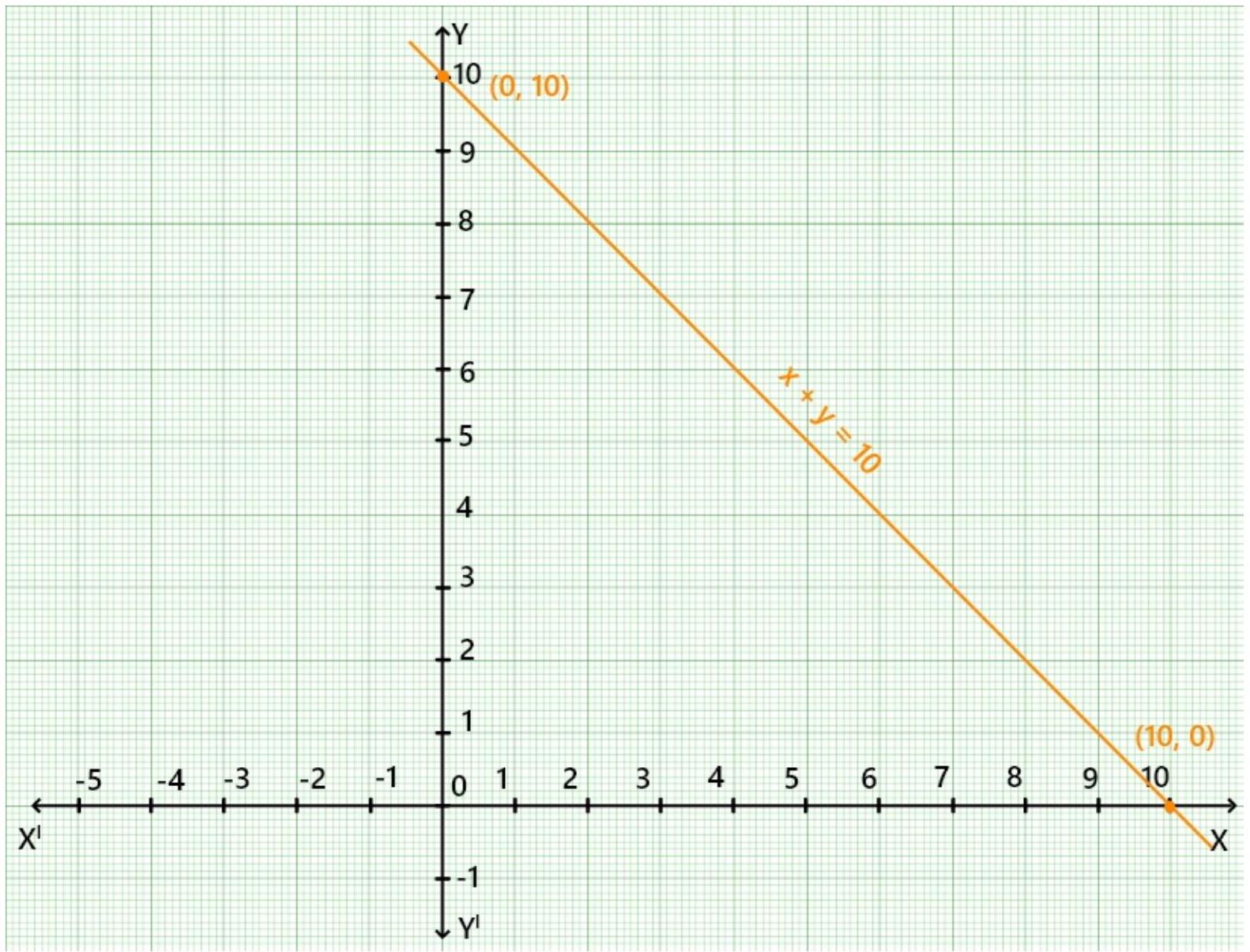
4. Draw the graph of the linear equation whose solutions are represented by the points having the sum of the coordinates as 10 units.
Show Answer
Solution
The graph of the linear equation whose solutions are represented by the points having the sum of the coordinates as 10 units is $x+y=10$.
When $x=0$ then $y=10$ and when $y=0$ then $x=10$.
Now, plot these two point $(0,10)$ and $(10,0)$ on the graph of the paper and joint them to get the straight line.
Hence, the graph of $x+y=10$ is a straight line as show in the figure given below.
5. Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.
Show Answer
Solution
The equation of linear equation such that point on its graph has an ordinate 3 times is $y=3 x$.
6. If the point $(3,4)$ lies on the graph of $3 y=a x+7$, then find the value of $a$.
Show Answer
Solution
Consider the linear equation:
$3 y=ax+7$
The point $(3,4)$ lies on the graph of $3 y=a x+7$. So, this point will be satisfy the given equation, get:
$ 3 y=a x+7 $
$12=3 \times a+7$
$ 12-7=3 a $
$3 a=5$
$ a=\dfrac{5}{3} $
Hence, the value of $a$ is $\dfrac{5}{3}$.
7. How many solution(s) of the equation $2 x+1=x-3$ are there on the:
(i) Number line
(ii) Cartesian plane
Show Answer
Solution
(i) Consider the linear equation:
$2 x+1=x-3$
$2 x-x=-3-1$
$x=-4$
Hence, the $x=-4$ is the solution if the given equation in the number line.
(ii) The given linear equation $2 x+1=x-3$ have infinitely many solution which are lies on the cartesion plane.
8. Find the solution of the linear equation $x+2 y=8$ which represents a point on
(i) $x$-axis
(ii) $y$-axis
Show Answer
Solution
(i) The linear equation which lies on the $x$-axis has its ordinate 0 .
Now, Putting $y=0$ in the equation $x+2 y=8$, get:
$ \begin{aligned} x+2 y & =8 \\ x+2 \times 0 & =8 \\ x & =8 \end{aligned} $
(ii) The linear equation which lies on the y-axis has its abscissa 0 .
Now, Putting $x=0$ in the equation $x+2 y=8$, get:
$x+2 y=8$
$0+2 y=8$
$ \begin{aligned} & y=\dfrac{8}{2} \\ & y=4 \end{aligned} $
9. For what value of $c$, the linear equation $2 x+c y=8$ has equal values of $x$ and $y$ for its solution.
Show Answer
Solution
Consider the linear equation:
$2 x+c y=8$
According to the question, when $x=y$. Putting $y=x$, get: $2 x+c x=8$
$c x=8-2 x$
$c=\dfrac{8-2 x}{x}, x \neq 0$
10. Let $y$ varies directly as $x$. If $y=12$ when $x=4$, then write a linear equation. What is the value of $y$ when $x=5$ ?
Show Answer
Solution
Given:
$y$ varies directly as $x$
$y \propto x$
$y=k x$
Putting $y=12$, when $x=4$, get:
$12=k 4$
$k=\dfrac{12}{4}$
$k=3$
Therefore, the equation is $y=3 x$.
Now, the value of $y$ when $x=5$ is $y=3 \times 5=15$.
Long Answer Questions
1. Show that the points $A(1,2), B(-1,-16)$ and $C(0,-7)$ lie on the graph of the linear equation $y=9 x-7$.
Show Answer
Solution
For $A(1,2)$, we have $2=9(1)-7=9-7=2$
For $B(-1,-16)$, we have $-16=9(-1)-7=-9-7=-16$
For $C(0,-7)$, we have $-7=9(0)-7=0-7=-7$
The line $y=9 x-7$ is satisfied by the point A $(1,2), B(-1,-16)$ and C $(0,-7)$. Hence, the point $A(1,2), B(-1,-16)$ and $C(0,-7)$ are solution of the linear equation $y=9 x-7$.
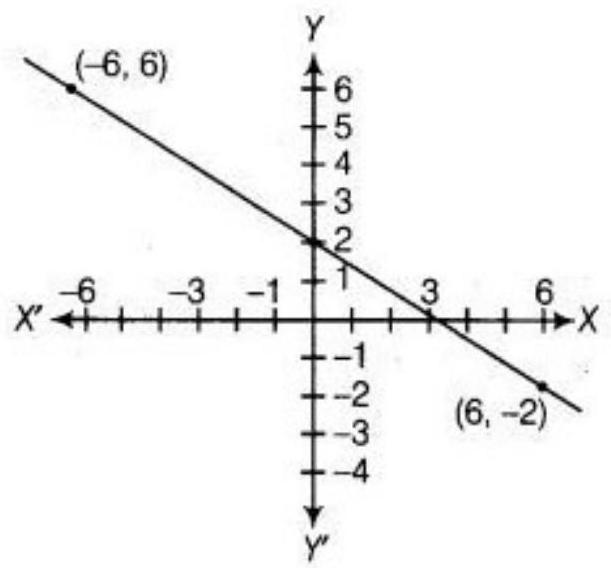
2. The following observed values of $x$ and $y$ are thought to satisfy a linear equation.
Write the linear equation:
$\begin{array}{|l|l|l|l|} \hline x & 6 & -6 \\ \hline y & -2 & 6 \\ \hline \end{array}$
Draw the graph using the values of $x, y$ as given in the above table.
At what points the graph of the linear equation
(i) Cuts the $x$-axis
(ii) Cuts the $y$-axis
Show Answer
Solution
Consider the linear equation:
$3 x+4 y=6$
Both the point $(6,-2)$ and $(-6,6)$ satisfy the linear equation $3 x+4 y=6$. Now, plot the point $(6,-2)$ and $(-6,6)$ on the graph paper and then joint these two points and obtain a line. See the below graph it is cut the $x$-axis at point $(3,0)$ and $y$-axis at $(0,2)$.
3. Draw the graph of the linear equation $3 x+4 y=6$. At what points, the graph cuts the $x$-axis and the $y$-axis.
Show Answer
Solution
Consider the linear equation:
$3 x+4 y=6$
The solution of given(above) linear equation cab be expressed as a table as follows:
$\begin{array}{|l|l|l|l|} \hline x & 2 & -2 & 0 \\ \hline y & 0 & 3 & 1.5 \\ \hline \end{array}$
Now, plot that above point on the graph paper and then join the points, see below:
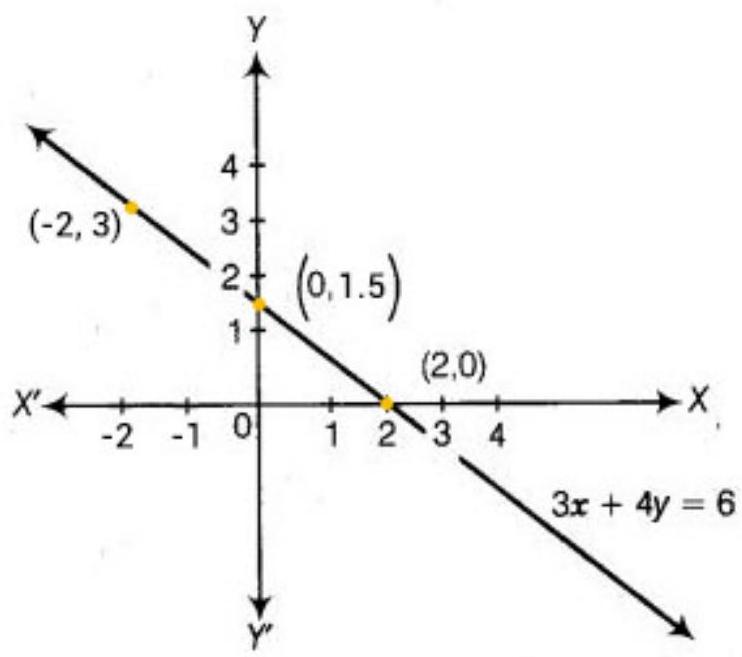
Therefore, the graph cuts the $x$-axis at $(2,0)$ and $y$-axis at $(0,1.5)$.
4. The linear equation that converts Fahrenheit (F) to Celsius (C) is given by the relation
$C=\dfrac{5 F-160}{9}$ (i) If the temperature is $86^{\circ} F$, what is the temperature in Celsius?
(ii) If the temperature is $35^{\circ} C$, what is the temperature in Fahrenheit?
(iii) If the temperature is $0^{\circ} C$ what is the temperature in Fahrenheit and if the temperature is $0^{\circ} F$, what is the temperature in Celsius?
(iv) What is the numerical value of the temperature which is same in both the scales?
Show Answer
Solution
Consider the linear equation:
$C=\dfrac{5 F-160}{9}$
(i) Putting $F=86^{\circ}$, get:
$ \begin{aligned} C & =\dfrac{5 F-160}{9} \\ & =\dfrac{5 \times 86^{\circ}-160}{9} \\ & =\dfrac{430-160}{9} \\ & =\dfrac{270}{9} \\ & =30^{\circ} \end{aligned} $
Hence, the temperature in Celsius is $30^{\circ}$.
(ii) Putting $C=35^{\circ}$, get:
$ \begin{aligned} C & =\dfrac{5 F-160}{9} \\ 35^{\circ} & =\dfrac{5 F-160}{9} \\ 315^{\circ} & =5 F-160 \\ 5 F & =315+160 \\ & =415 \\ F & =\dfrac{475}{5} \\ F & =95^{\circ} \end{aligned} $
Hence, the temperature in Fahrenheit is $95 F$.
(iii) Putting $C=0^{\circ}$, get:
$ \begin{aligned} C & =\dfrac{5 F-160}{9} \\ 0 & =\dfrac{5 F-160}{9} \\ 0 & =5 F-160 \\ 5 F & =160 \\ F & =\dfrac{160}{5} \\ F & =32^{\circ} \end{aligned} $
Now, putting $F=0^{\circ}$, get:
$ \begin{aligned} C & =\dfrac{5 F-160}{9} \\ C & =\dfrac{5 \times 0-160}{9} \\ & =(-\dfrac{160}{9})^{\circ} \end{aligned} $
If the temperature is $0 F$, then the temperature in Fahrenheit is $32^{\circ}$ and if the temperature is $0 F$ then the temperature in Celsius is $(-\dfrac{160}{9})^{\circ} C$.
(iv) Putting $C=F$, get:
$ \begin{aligned} C & =\dfrac{5 F-160}{9} \\ C & =F \\ F & =\dfrac{5 F-160}{9} \\ 9 F-5 F & =-160 \\ 4 F & =-160 \\ F & =\dfrac{-160}{4} \\ F & =-40^{\circ} \end{aligned} $
Therefore, the numerical value of the temperature which is same in both the scales is -40 .
The linear equation that converts kelvin ( $x)$ to Fahrenheit (y) is given by the relation:
$y=\dfrac{9}{5}(x-273)+32$
5. If the temperature of a liquid can be measured in kelvin units as $x^{\circ} K$ or in Fahrenheit units as $y^{\circ} F$. The relation between the two systems of measurement of temperature is given by the linear equation (i) Find the temperature of the liquid in Fahrenheit if the temperature of the body is $313^{\circ} K$.
(ii) If the temperature is $158^{\circ} F$, then find the temperature in Kelvin.
Show Answer
Solution
$y=\dfrac{9}{5}(x-273)+32$
(i) When the temperature of the liquid is $x=313^{\circ} K$.
$ \begin{aligned} y & =\dfrac{9}{5}(313-273)+32 \\ & =\dfrac{9}{5} \times 40+32 \\ & =72^{\circ}+32^{\circ} \\ & =104^{\circ} F \end{aligned} $
(ii) When the temperature of the liquid is $y=158^{\circ} F$.
$ \begin{aligned} 158 & =\dfrac{9}{5}(x-273)+32 \\ & =\dfrac{9}{5}(x-273) \\ & =158-32 \\ x-273 & =126 \times \dfrac{5}{9} \\ & =70 \\ x-273 & =70 \\ x & =273+70 \\ x & =343^{\circ} K \end{aligned} $
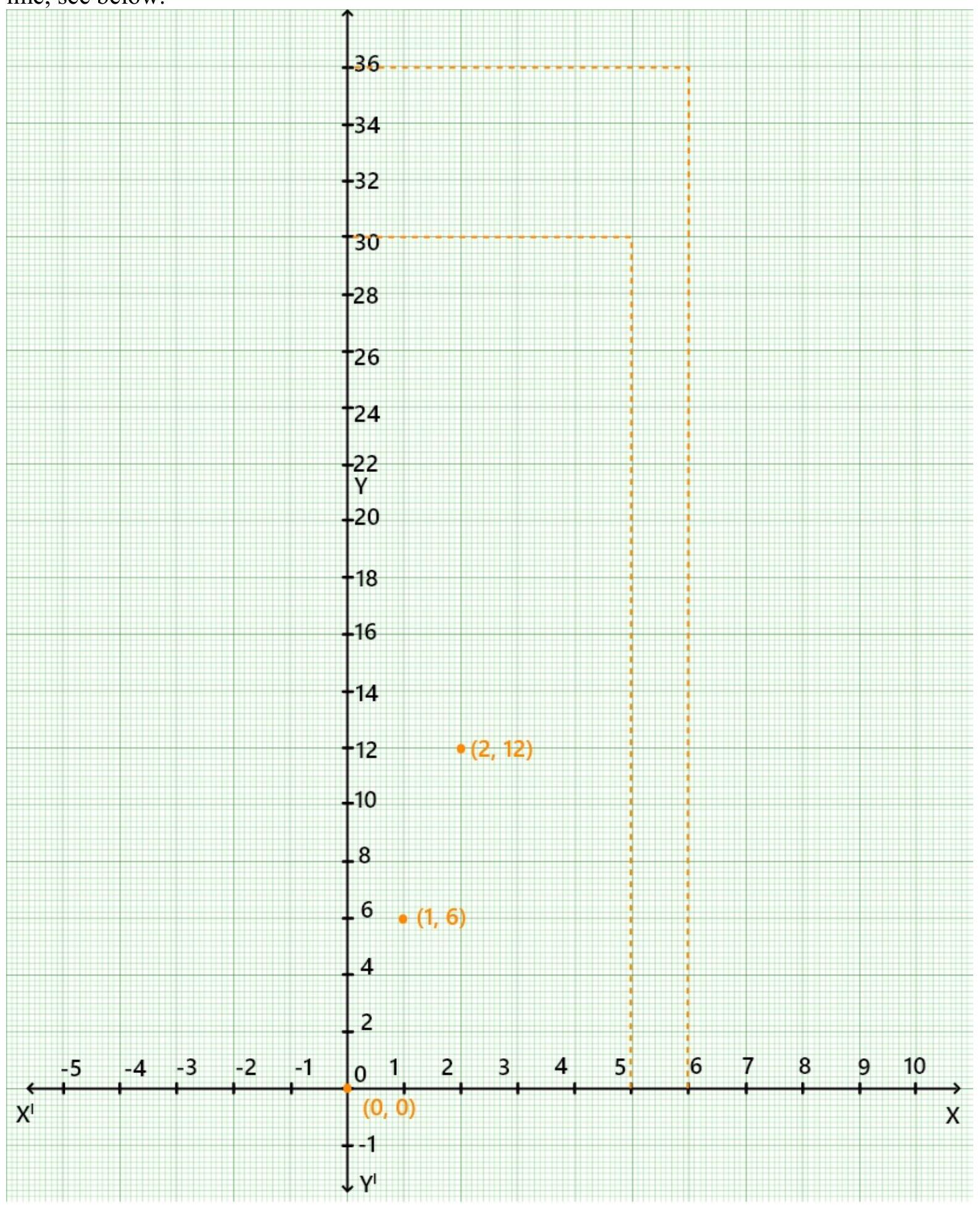
6. The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as a linear equation of two variables and draw the graph of the same by taking the constant mass equal to $6 kg$. Read from the graph, the force required when the acceleration produced is (i) $5 m / s^{2}$, (ii) $6 m / s^{2}$.
Show Answer
Solution
According to the question:
$y \propto x$
$y=m x$
Now, make a table as follows by writing the values of $y$ below the corresponding value of $x$.
$\begin{array}{|l|l|l|l|} \hline x & 0 & 1 & 2 \\ \hline y & 0 & 6 & 12 \\ \hline \end{array}$
Plot the point $(0,0),(1,6)$ and $(2,12)$ on a graph paper. Now, joint all the points and obtain a line, see below.