Coordinate Geometry
Multiple Choice Questions(MCQs)
1. Point $(-3,5)$ lies in the
(A) first quadrant
(B) second quadrant
(C) third quadrant
(D) fourth quadrant
Show Answer
Solution
Given point is $(-3,5)$. In this point, abscissa is negative and ordinate is positive. Hence, it is lies in the second quadrant.
The correct option is (B).
2. Signs of the abscissa and ordinate of a point in the second quadrant are respectively
(A)+,+
(B)-,-
(C)-,+
(D)+,-
Show Answer
Solution
Signs of the abscissa and ordinate of a point in the second quadrant are,-+ respectively.
3. Point $(0,-7)$ lies
(A) on the $x$-axis
(B) in the second quadrant
(C) on the $y$-axis
(D) in the fourth quadrant
Show Answer
Solution
Point $(0,-7)$ lies on y-axis. Therefore, the correct option is (c).
4. Point $(-10,0)$ lies
(A) on the negative direction of the $x$-axis
(B) on the negative direction of the $y$-axis
(C) in the third quadrant
(D) in the fourth quadrant
Show Answer
Solution
Point $(-10,0)$ lies on the negative direction of $x$-axis. Hence, the correct option is (A).
5. Abscissa of all the points on the $x$-axis is
(A) 0
(B) 1
(C) 2
(D) any number
Show Answer
Solution
Abscissa of all the points on the $x$-axis is any number. Hence, the correct option is (D).
6. Ordinate of all points on the $x$-axis is
(A) 0
(B) 1
(C) -1
(D) any number
Show Answer
Solution
Ordinate of all the points on the x-axis is zero. Therefore, the correct option is (a).
7. The point at which the two coordinate axes meet is called the
(A) abscissa
(B) ordinate
(C) origin
(D) quadrant
Show Answer
Solution
The point at which the two coordinate axes meet is called the origin. Hence, the correct option is (C).
8. A point both of whose coordinates are negative will lie in
(A) I quadrant
(B) II quadrant
(C) III quadrant
(D) IV quadrant
Show Answer
Solution
A point whose both of the coordinates are negative will lie in the III quadrant. Hence, the correct option is $(C)$.
9. Points $(1,-1),(2,-2),(4,-5),(-3,-4)$
(A) lie in II quadrant
(B) lie in III quadrant
(C) lie in IV quadrant
(D) do not lie in the same quadrant
Show Answer
Solution
Point $(1,-1),(2,-2),(4,-5),(-3,-4)$ lie in the IV quadrant and $(-3,-4)$ lie in III quadrant. Hence, the correct option is (D).
10. If $y$ coordinate of a point is zero, then this point always lies
(A) in I quadrant
(B) in II quadrant
(C) on $x$ - axis
(D) on $y$ - axis
Show Answer
Solution
We know that if y-coordinate of a point i.e., ordinate is zero, then this point always lies on the $x$-axis.
Hence, the correct option is $(C)$.
11. The points $(-5,2)$ and $(2,-5)$ lie in the
(A) same quadrant
(B) II and III quadrants, respectively
(C) II and IV quadrants, respectively
(D) IV and II quadrants, respectively
Show Answer
Solution
The points $(-5,2)$ and $(2,-5)$ lie in the II and IV quadrants respectively.
Hence, the correct option is (C).
12. If the perpendicular distance of a point $P$ from the $x$-axis is 5 units and the foot of the perpendicular lies on the negative direction of $x$-axis, then the point $P$ has
(A) $x$ coordinate $=-5$
(B) $y$ coordinate $=5$ only
(C) $y$ coordinate $=-5$ only
(D) $y$ coordinate $=5$ or -5
Show Answer
Solution
The point $p$ has $y$-coordinate $=5$ or -5 .
Hence, the correct option is (D).
13. On plotting the points $O(0,0), A(3,0), B(3,4), C(0,4)$ and joining $OA, AB, BC$ and $CO$ which of the following figure is obtained?
(A) Square
(B) Rectangle
(C) Trapezium
(D) Rhombus
Show Answer
Solution
$OABC$ is a rectangle.
Hence, the correct option is (B).
14. If $P(-1,1), Q(3,-4), R(1,-1), S(-2,-3)$ and $T(-4,4)$ are plotted on the graph paper, then the point(s) in the fourth quadrant are
(A) $P$ and $T$
(B) $Q$ and $R$
(C) Only $S$
(D) $P$ and $R$
Show Answer
Solution
In the quadrant IV consists of all points $(x, y)$ for which $x$ is positive and $y$ is negative.
Therefore, the points in the fourth quadrants are $Q(3,-4)$ and $R(1,-1)$.
Hence, the correct option is (B).
15. If the coordinates of the two points are $P(-2,3)$ and $Q(-3,5)$, then (abscissa of $P$ ) - (abscissa of $Q$ ) is
(A) -5
(B) 1
(C) -1
(D) -2
Show Answer
Solution
Abscissa of $P(-2,3)=-2$
Abscissa of $Q(-3,5)=-3$
Therefore, (abscissa of $P)-($ abscissa of $Q)=-2-(-3)=-2+3=1$
Hence, the correct option is (B).
16. If $P(5,1), Q(8,0), R(0,4), S(0,5)$ and $O(0,0)$ are plotted on the graph paper, then the point(s) on the $x$-axis are
(A) $P$ and $R$
(B) $R$ and $S$
(C) Only $Q$
(D) $Q$ and $O$
Show Answer
Solution
If a point lies on the $x$-axis then its ordinate is 0 .
So, the point on the $x$-axis are $Q(8,0)$ and $O(0,0)$.
Hence, the correct option is (D).
17. Abscissa of a point is positive in
(A) I and II quadrants
(B) I and IV quadrants
(C) I quadrant only
(D) II quadrant only
Show Answer
Solution
Abscissa of a point is positive in I and IV quadrants.
Hence, the correct option is (B).
18. The points in which abscissa and ordinate have different signs will lie in
(A) I and II quadrants
(B) II and III quadrants
(C) I and III quadrants
(D) II and IV quadrants
Show Answer
Solution
In II quadrant all $(x, y)$ lie with $x<0$ and $y>0$. In quadrant IV, all $(x, y)$ lie with $x>0$ and $y$ $<0$.
So, the point whose abscissa and ordinate have different signs will lie in II and IV quadrant only.
Hence, the correct option is (D).
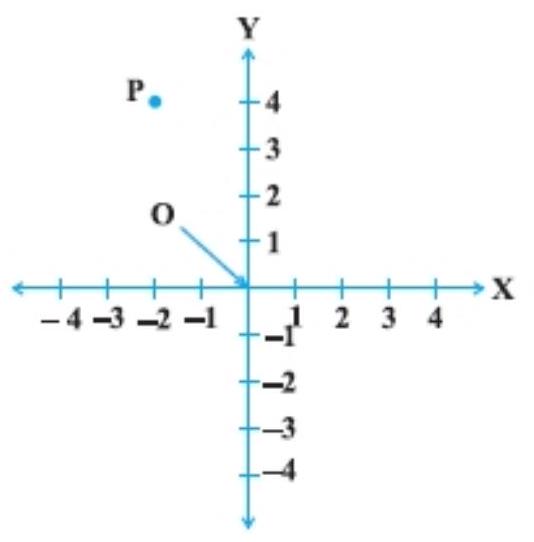
19. In Fig., coordinates of $P$ are
(A) $(-4,2)$
(B) $(-2,4)$
(C) $(4,-2)$
(D) $(2,-4)$
Show Answer
Solution
See the point $P$ given in the figure, it is lies in the second quadrant and its distance from $y$ and $x$-axes are -2 and 4 units respectively. So, its coordinate are $(-2,4)$.
Hence, the correct option is (B).
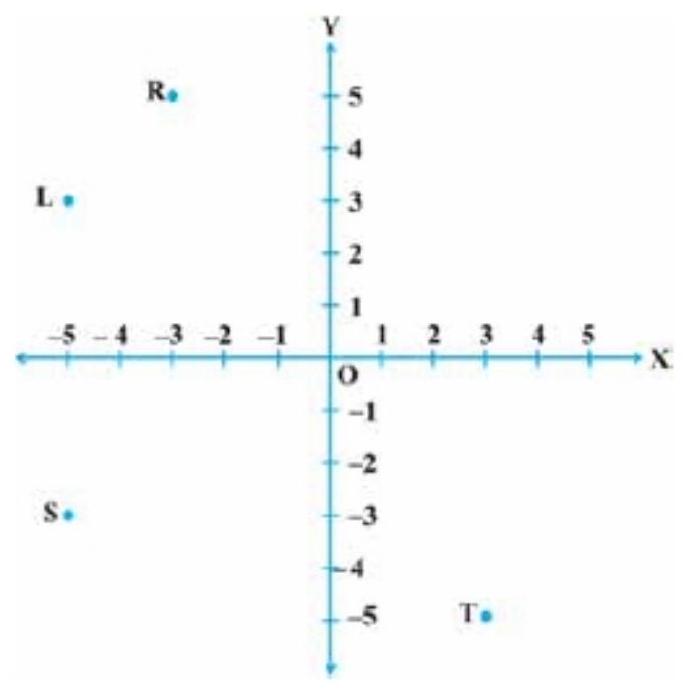
20. In Fig. 3.2, the point identified by the coordinates $(-5,3)$ is
(A) $T$
(B) $R$
(C) $L$
(D) $S$
Show Answer
Solution
See in the question figure, point $T$ lies in the IV quadrant. The distance of $T$ from $y$-axis is 3 units and from $x$-axis is -5 units. So, the point identified by the coordinates $(-5,3)$ is $T$.
Hence, the correct option is (A).
21. The point whose ordinate is 4 and which lies on $y$-axis is
(A) $(4,0)$
(B) $(0,4)$
(C) $(1,4)$
(D) $(4,2)$
Show Answer
Solution
The point on the y-axis has its abscissa 0 . Since, the point whose ordinate is 4 and which lies on y-axis is $(0,4)$.
Hence, the correct option is (B).
22. Which of the points $P(0,3), Q(1,0), R(0,-1), S(-5,0), T(1,2)$ do not lie on the $x$-axis?
(A) P and R only
(B) $Q$ and $S$
(C) P, R and T
(D) $Q, S$ and $T$
Show Answer
Solution
A point which is lies on the $x$-axis has always its ordinate equal to 0 . So, the points which do not lies the $x$-axis are $P(0,3), R(0,-1)$ and $T(1,2)$.
Hence, the correct option is (C).
23. The point which lies on $y$-axis at a distance of 5 units in the negative direction of $y$-axis is
(A) $(0,5)$
(B) $(5,0)$
(C) $(0,-5)$
(D) $(-5,0)$
Show Answer
Solution
The point which are lies on the $y$-axis this show that this $x$-coordinate is zero. Also, the point which lies on $y$-axis at a distance of 5 units in the negative direction of $y$-axis is -5 . Therefore, the required point is $(0,-5)$.
Hence, the correct option is (C).
24. The perpendicular distance of the point $P(3,4)$ from the $y$-axis is
(A) 3
(B) 4
(C) 5
(D) 7
Show Answer
Solution
The perpendicular distance of the any point from the y-axis is abscissa of the point $(3,4)$, which is 3 .
Hence, the correct option is (A).
True/False
1. Point $(3,0)$ lies in the first quadrant.
Show Answer
Solution
Given point is $(3,0)$.
The abscissa is 3 and ordinate is 0 . We know that if ordinate is 0 then the point lies on the $x-$ axis.
Hence, the given statement is false.
2. Points $(1,-1)$ and $(-1,1)$ lie in the same quadrant.
Show Answer
Solution
The given point $(1,-1)$ is lies on the IV quadrant and the point $(-1,1)$ lies in II quadrant.
Hence, the given statement is false.
3. The coordinates of a point whose ordinate is $-\dfrac{1}{2}$ and abscissa is 1 are $(-\dfrac{1}{2}, 1)$.
Show Answer
Solution
The coordinate of a point can be written as (abscissa, ordinate). So, the point will be $(1,-\dfrac{1}{2})$. Hence, the given statement is false.
4. A point lies on $y$-axis at a distance of 2 units from the $x$-axis. Its coordinates are $(2,0)$.
Show Answer
Solution
The point lies on the y-axis is of the from $(0, y)$.
Hence, the correct option is false.
5. $(-1,7)$ is a point in the II quadrant.
Show Answer
Solution
The signs of the point in the II quadrant are,-+ respectively. Since, the given point lies in the II quadrant. Hence, the given statement is true.
Short Answer Questions
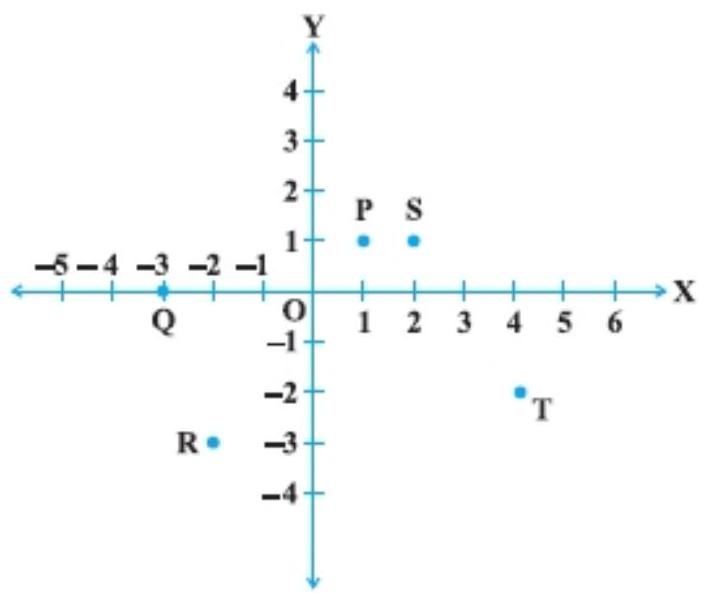
1. Write the coordinates of each of the points $P, Q, R, S, T$ and $O$ from the Fig..
Show Answer
Solution
The coordinates of each of the points $P, Q, R, S, T$ and $O$ are $P(1,1), Q(-3,0), R(-2,-3), S(2$, $1), T(4,-2)$ and $O(0,0)$.
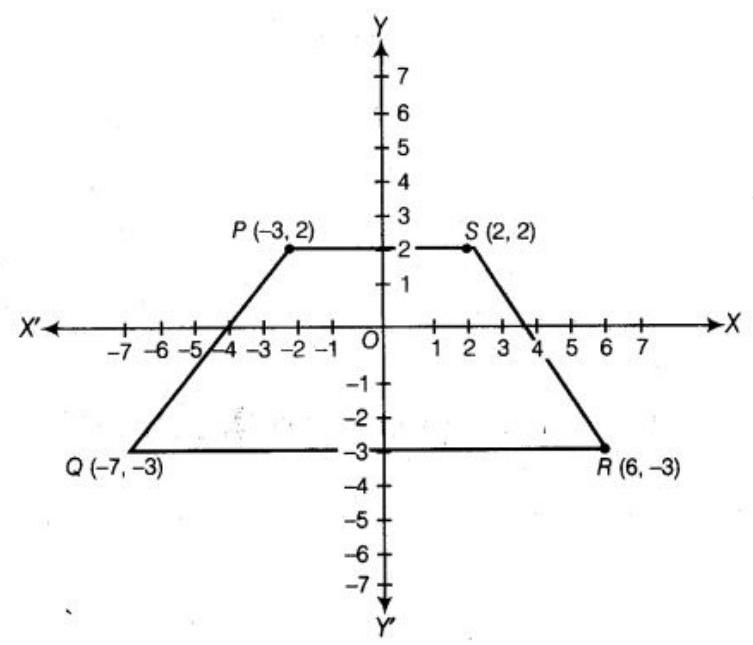
2. Plot the following points and write the name of the figure thus obtained: $P(-3, 2), Q(-7,-3), R(6,-3), S(2, 2)$
Show Answer
Solution
Let $X^{\prime} OX$ is $X$-axis and $Y^{\prime} OY$ is $y$-axis. Then, the given points $P(-3,2), Q(-7,-3), R(6,-$ $3), S(2,2)$ are plated as given below:
3. Plot the points $(x, y)$ given by the following table:
$\begin{array}{|l|l|l|l|l|l|l|} \hline x & 2 & 4 & -3 & -2 & 3 & 0 \\ \hline y & 4 & 2 & 0 & 5 & -3 & 0 \\ \hline \end{array}$
Show Answer
Solution
Let $X^{\prime} OX$ is $x$-axis and $Y^{\prime} OY$ is $y$-axis. Then, the given points are plated as given below:
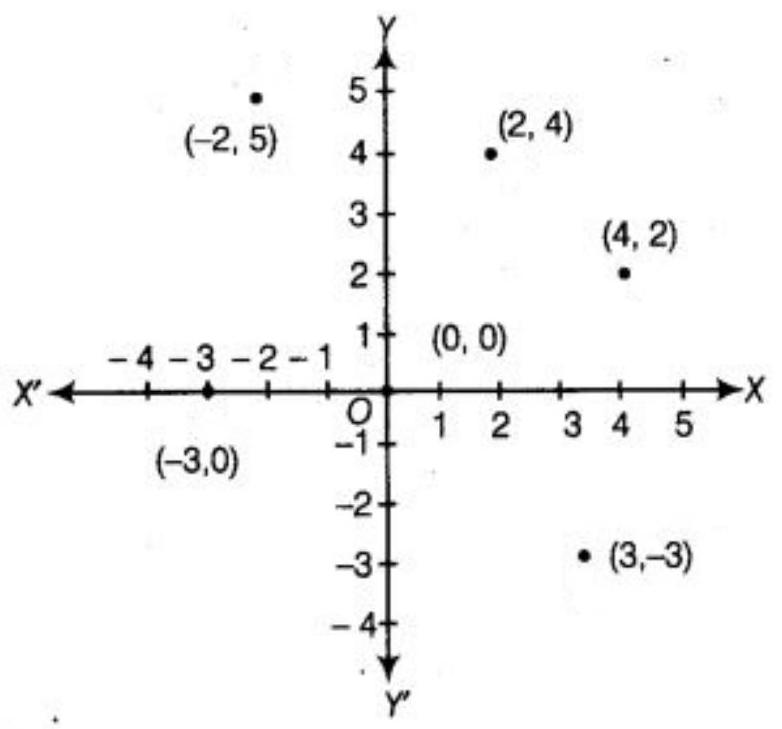
4. Plot the following points and check whether they are collinear or not:
(i) $(1,3),(-1,-1),(-2,-3)$
(ii) $(1,1),(2,-3),(-1,-2)$
(iii) $(0,0),(2,2),(5,5)$
Show Answer
Solution
(i)
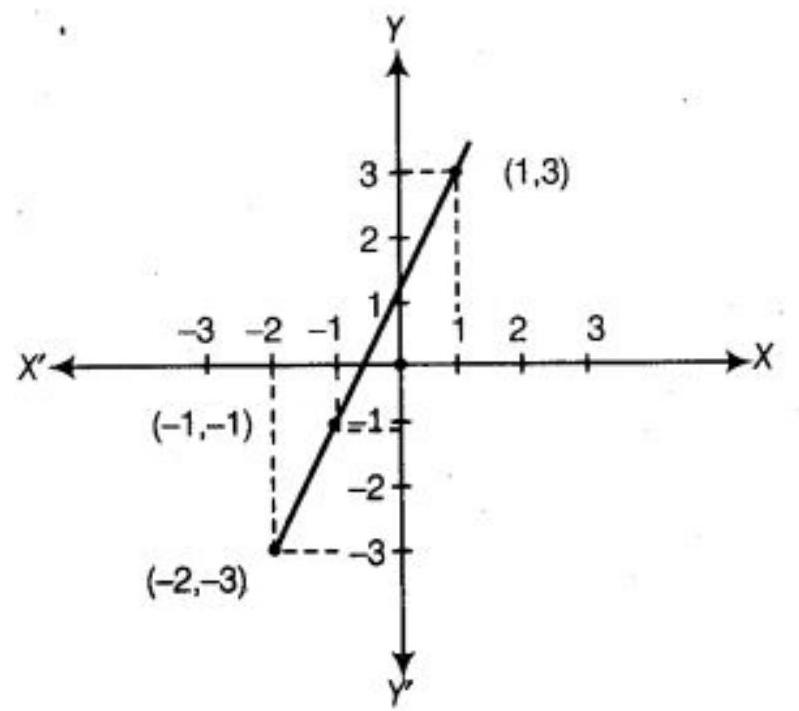
See the above graph, all the three points are lies one the same straight line. Hence, the given points are collinear.
(ii)
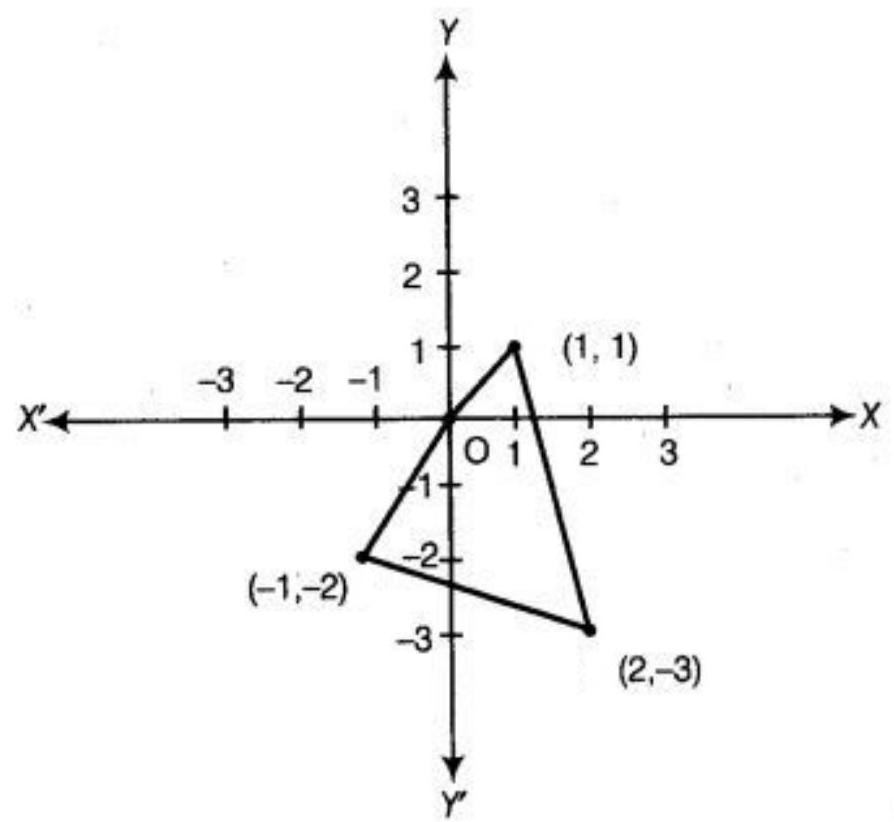
See the above graph, all the three points are not lies one the same straight line. Hence, the given points are not collinear.
(iii)
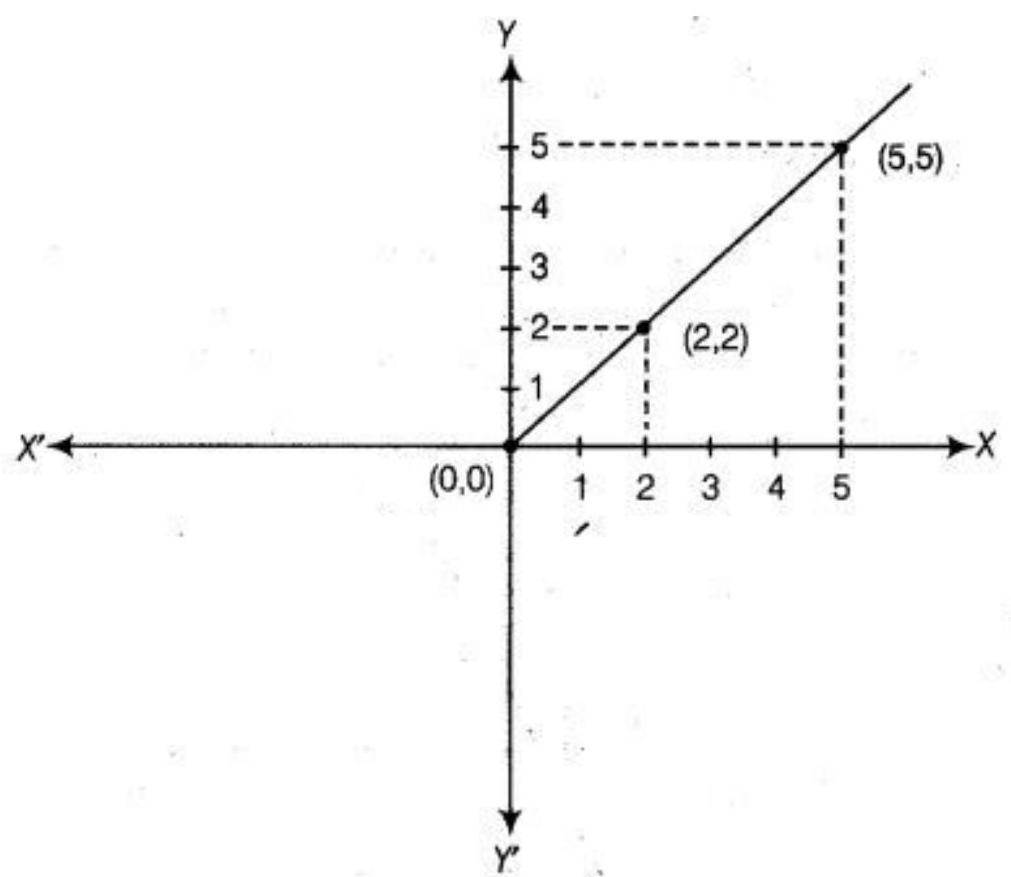
See the above graph, all the three points are lies one the same straight line. Hence, the given points are collinear.
5. Without plotting the points indicate the quadrant in which they will lie, if
(i) Ordinate is 5 and abscissa is -3
(ii) Abscissa is -5 and ordinate is -3
(iii) Abscissa is -5 and ordinate is 3
(iv) Ordinate is 5 and abscissa is 3
Show Answer
Solution
(i) The abscissa is negative and ordinate is positive. So, the given point will be lies in the II quadrant.
(ii) The abscissa is negative and also ordinate is negative. So, the given point will be lies in the III quadrant.
(iii) The abscissa is negative and ordinate is positive. So, the given point will be lies in the II quadrant.
(iv) The abscissa is positive and also ordinate is positive. So, the given point will be lies in the I quadrant.
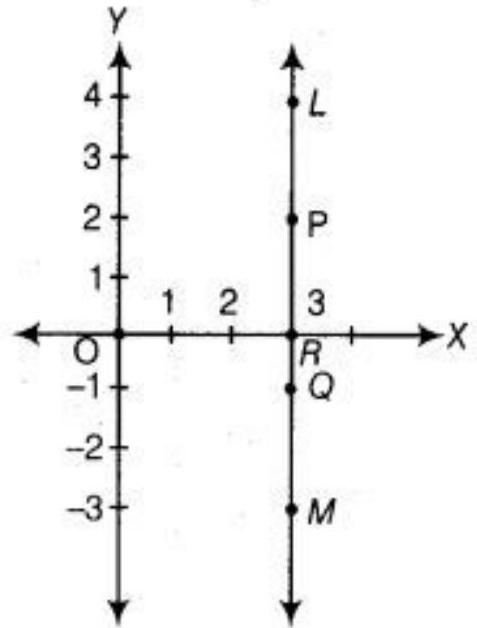
6. In Fig., $LM$ is a line parallel to the $\boldsymbol{{}y}$-axis at a distance of 3 units.
(i) What are the coordinates of the points $P, R$ and $Q$ ?
(ii) What is the difference between the abscissa of the points $L$ and $M$ ?
Show Answer
Solution
(i) See the given figure, the distance from point $P$ at $X$-axis is 2 and distance from $P$ at $Y$ axis is 3 . So, its coordinates is $(3,2)$. Similarly, the distance from point $R$ at $X$-axis is 0 and distance from $P$ at $Y$-axis is 3. So, its coordinates is $(3,0)$. Again, the distance from point $Q$ at $X$-axis is -1 and distance from $P$ at $Y$-axis is 3. So, its coordinates is (3, $-1)$.
(ii) See the given figure, the point $L$ and $M$ are lies on the same straight line. Since, $L$ and $M$ are collinear.
Hence, the difference between the abscissa of the points $L$ and $M$ are 0 .
7. In which quadrant or on which axis each of the following points lie? $(-3,5),(4,-1),(2,0),(2,2),(-3,-6)$
Show Answer
Solution
(i) $(-3,5)$ lies in II quadrant.
(ii) $(4,-1)$ lies in IV quadrant.
(iii) $(2,0)$ lies on $x$-axis.
(iv) $(2,2)$ lies in I quadrant.
(v) $(-3,-6)$ lies in III quadrant.
8. Which of the following points lie on $y$-axis?
A $(1,1)$, B $(1,0)$, C (0, 1), D $(0,0)$, E (0,- 1), F $(-1,0), G(0,5), H(-7,0)$, I $(3,3)$.
Show Answer
Solution
The abscissa is 0 when the point lies on the $y$-axis and its ordinate is the $y$-value and its coordinate are $(0, y)$.
Hence, the points are $C(0,1), E(0,-1), G(0,5)$ are the points which lie on y-axis.
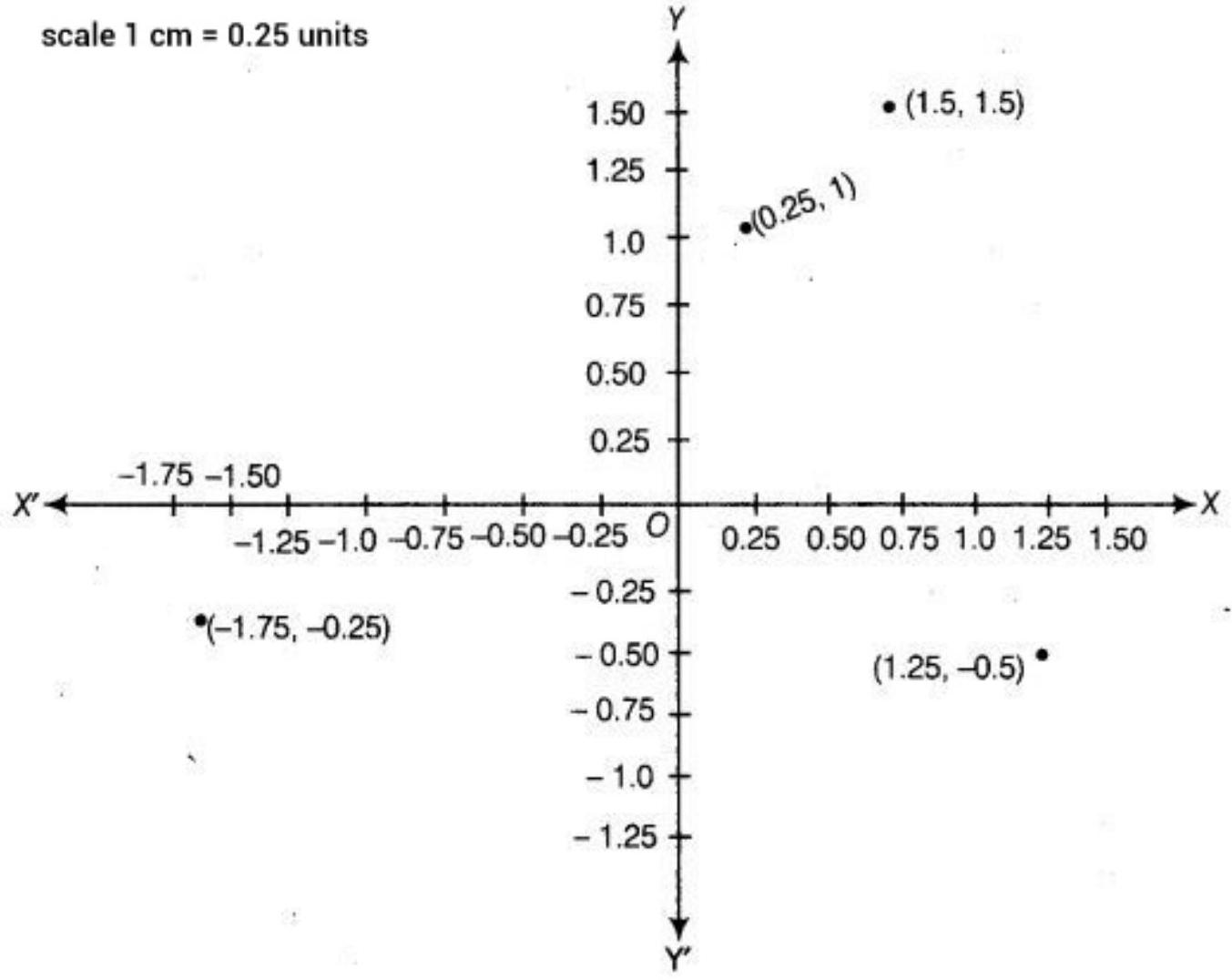
9. Plot the points $(x, y)$ given by the following table.
Use scale $1 cm=0.25$ units
$\begin{array}{|l|l|l|l|l|l|l|} \hline x & 1.25 & 0.25 & 15 & -1.75 \\ \hline y & -0.5 & 1 & 1.5 & -0.25 \\ \hline \end{array}$
Show Answer
Solution
Let $X^{\prime} OX$ is $x$-axis and $Y^{\prime} OY$ is $y$-axis. Then, the given points are plated as given below:
10. A point lies on the $x$-axis at a distance of 7 units from the $y$-axis. What are its coordinates? What will be the coordinates if it lies on $y$-axis at a distance of -7 units from $x$-axis?
Show Answer
Solution
The point lies on the $x$-axis at a distance of 7 units from the $y$-axis and 0 from the x-axis. So, its coordinate are $(7,0)$.
If the point is lies on y-axis, then the distance of it from y-axis is 0 and then of from $x$-axis is 7. Hence, its coordinate are $(0,7)$.
11. Find the coordinates of the point
(i) Which lies on $x$ and $y$ axes both.
(ii) Whose ordinate is -4 and which lies on $y$-axis.
(iii) Whose abscissa is 5 and which lies on $\boldsymbol{{}x}$-axis.
Show Answer
Solution
(i) The point which is lies on the both axis are $(0,0)$.
(ii) The point whose ordinate is -4 and which lies on y-axis are $(0,-4)$.
(iii) The point whose abscissa is 5 which lies on $x$-axis are $(5,0)$.
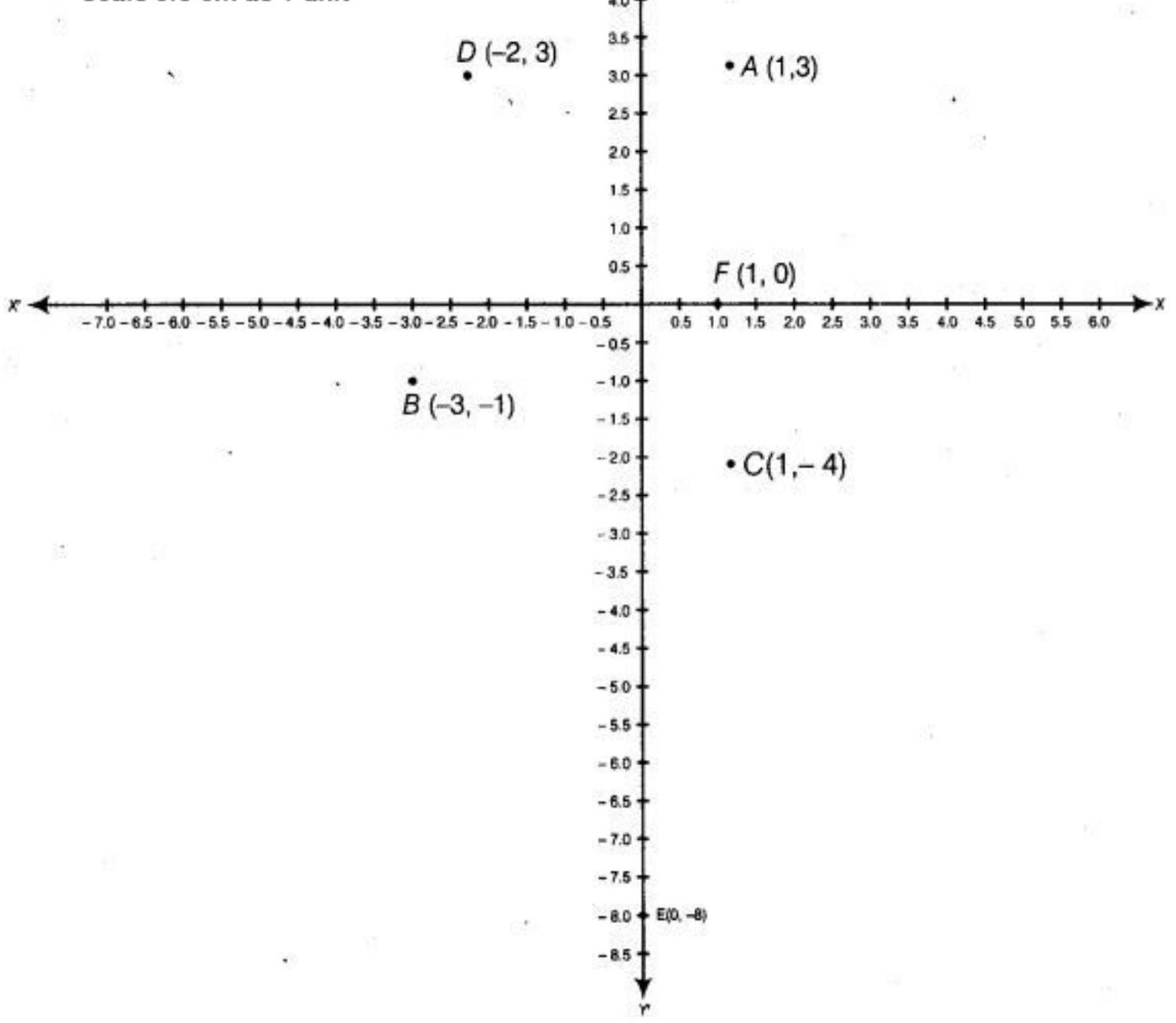
12. Taking $0.5 cm$ as 1 unit, plot the following points on the graph paper: A $(1,3)$, B $(-3,-1), C(1,-4), D(-2,3), E(0,-8)$, F (1, 0$)$
Show Answer
Solution
Let $X^{\prime} OX$ is $x$-axis and $Y^{\prime} OY$ is $y$-axis. Then, the given points are plated as given below:
Scale $0.5 cm$ as 1 unit
Long Answer Questions
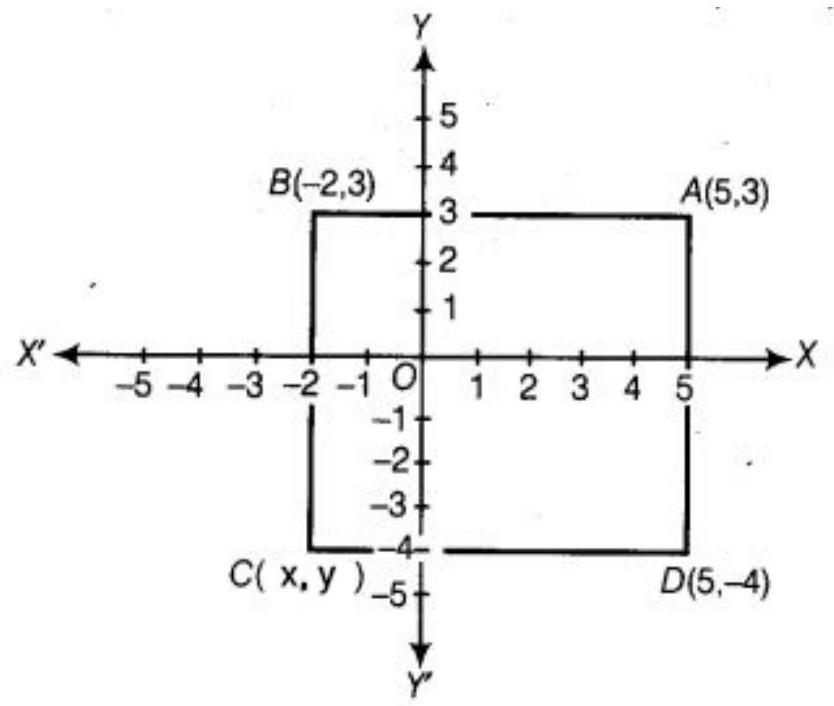
1. Points $A(5,3), B(-2,3)$ and $D(5,-4)$ are three vertices of a square $A B C D$. Plot these points on a graph paper and hence find the coordinates of the vertex $\mathbf{C}$.
Show Answer
Solution
Plot the points $A, B$ and $D$ and join $AB$ and $AD . ABCD$ is a square. So, all the side are equal and each angle is $90^{\circ}$. Now, see the figure the abscissa of the vertex $C$ will be -2 and ordinate is -4 . Therefore, the coordinates of the vertex $C$ are $(-2,-4)$.
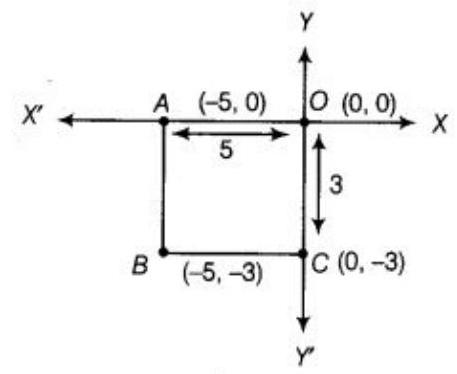
2. Write the coordinates of the vertices of a rectangle whose length and breadth are 5 and 3 units respectively, one vertex at the origin, the longer side lies on the $x$-axis and one of the vertices lies in the third quadrant.
Show Answer
Solution
Given in the question, the length and breadth are 5 and 3units respectively. one vertex at the origin, the longer side lies on the $x$-axis and one of the vertices lies in the third quadrant. Therefore, the coordinate of the vertex of rectangle $OABC$ are $O(0,0), A(-5,0), B(-5,-3)$ and $C(0,-3)$.
3. Plot the points $P(1,0), Q(4,0)$ and $S(1,3)$. Find the coordinates of the point $R$ such that $P Q R S$ is a square.
Show Answer
Solution
Plot the points $P(1,0), Q(4,0)$ and $S(1,3)$ in the cartesian plane. We know the all the sides of square are equal and each angle is $90^{\circ}$. Therefore, the abscissa of the vertex $R$ is 4 and its ordinate is 3 .
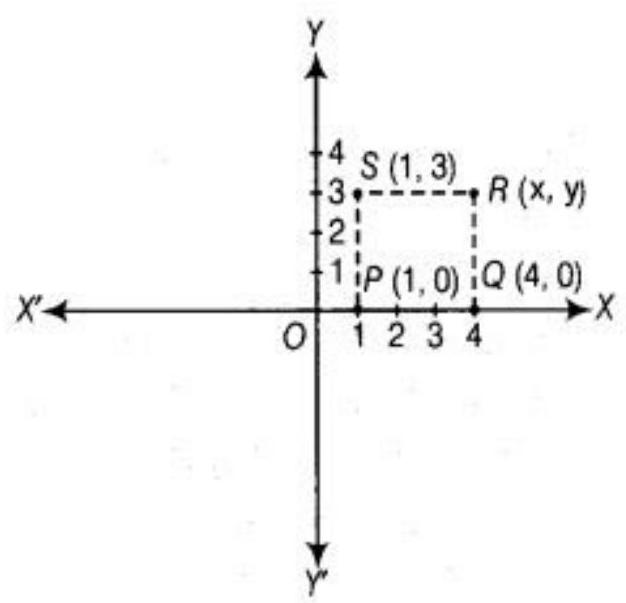
Hence, the coordinate of the point $R$ is $(4,3)$.
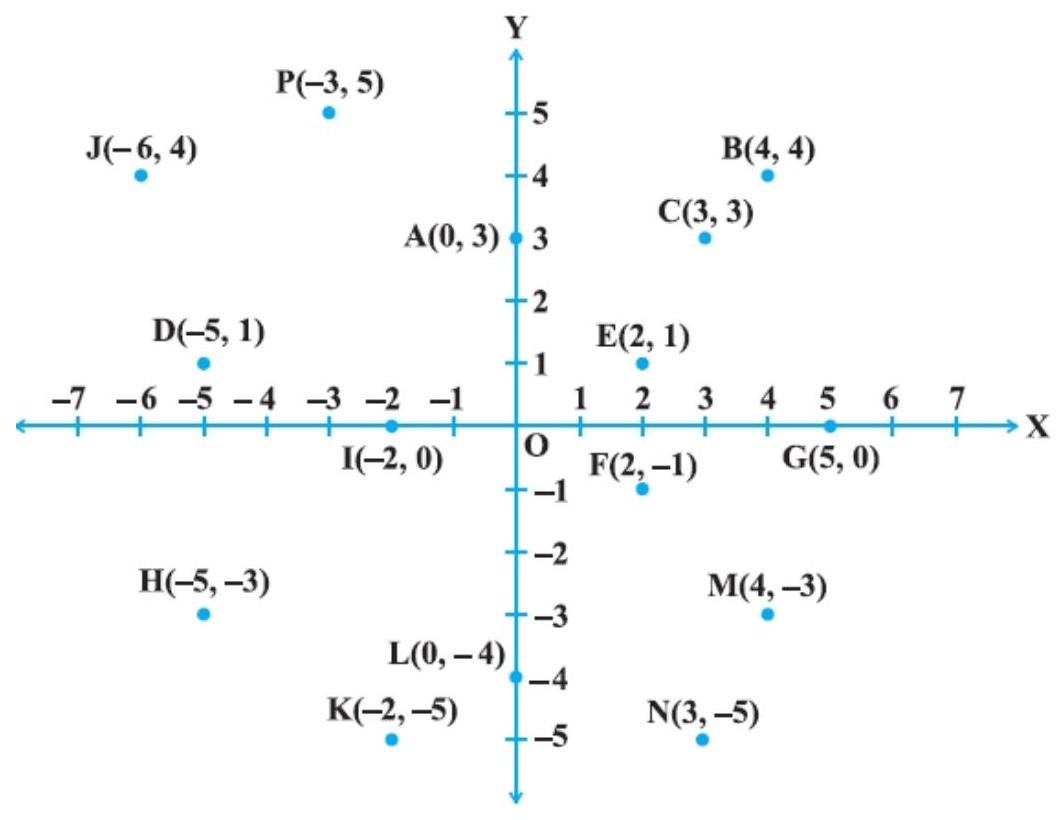
4. From the Fig., answer the following:
(i) Write the points whose abscissa is 0 .
(ii) Write the points whose ordinate is 0 .
(iii) Write the points whose abscissa is -5 .
Show Answer
Solution
(i) From y-axis, the distance of points $A, L$ and $O$ is 0 . $So, A(0,3), L(0,-4)$, and $O(0,0)$ are the points whose abscissa is 0 .
(ii) From y-axis, the distance of points G, I and O is 0 . So, $G(5,0), I(-2,0)$, and $O(0,0)$ are the points whose ordinate is 0 .
(iii) From y-axis, the distance of points $H$ and $D$ is 0 . So, $H(-5,-3)$ and $D(-5,1)$ are the points whose abscissa is -5 .
5. Plot the points $A(1,-1)$ and $B(4,5)$.
(i) Draw a line segment joining these points. Write the coordinates of a point on this line segment between the points $A$ and $B$.
(ii) Extend this line segment and write the coordinates of a point on this line which lies outside the line segment $A B$.
Show Answer
Solution
(i) The point on this line segment between the $A$ and $B$ is $M(2,1)$.
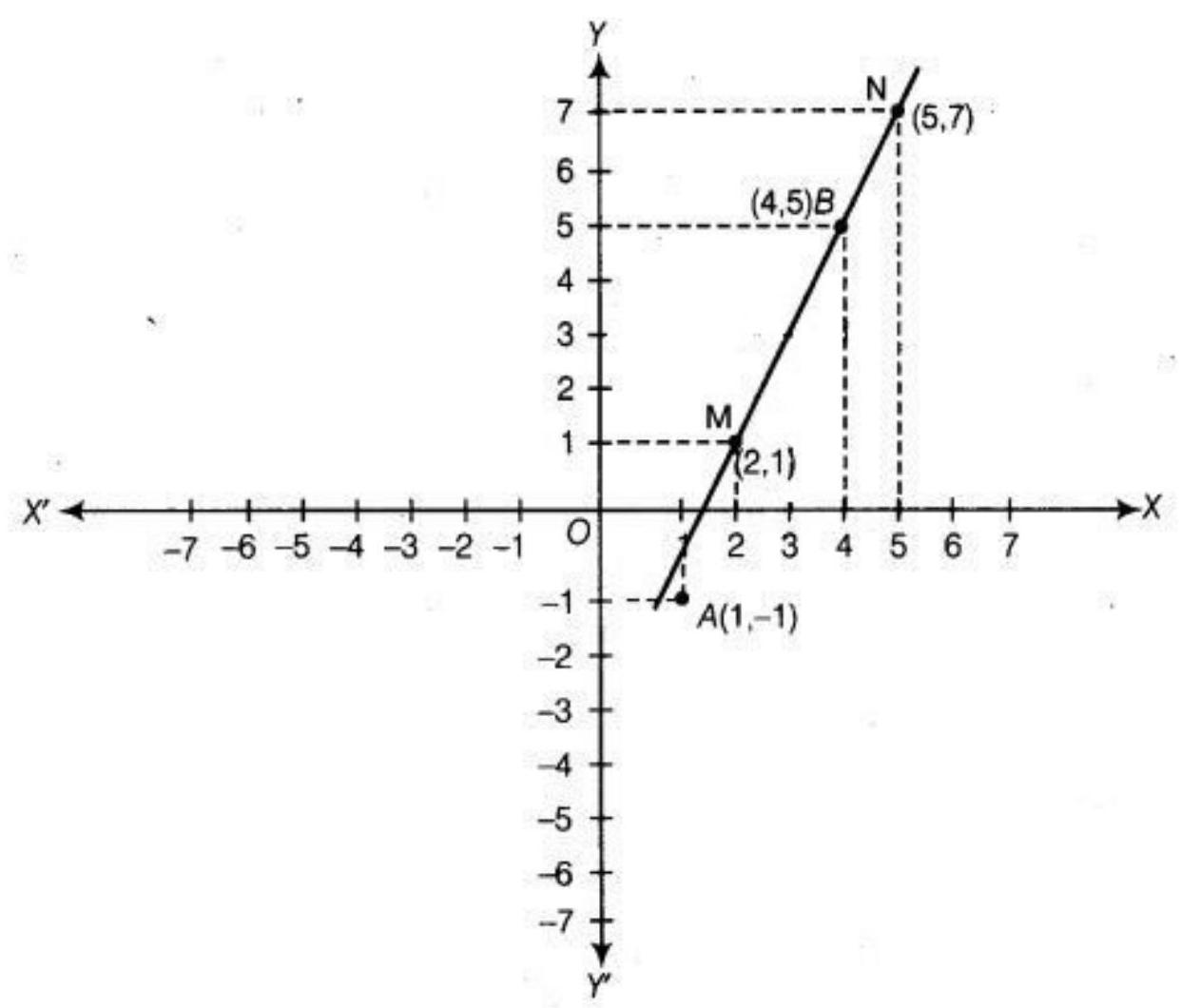
(ii) The point on this line which lies outside the line segment $A B$ is $N(5,7)$.










