Constructions
Multiple Choice Questions(MCQs)
1. With the help of a ruler and a compass it is not possible to construct an angle of:
(A) $37.5^{\circ}$
(B) $40^{\circ}$
(C) $22.5^{\circ}$
(D) $67.5^{\circ}$
Show Answer
Solution
By using the help of a ruler and a compass, that is possible construct the angels, $90^{\circ}, 60^{\circ}$, $45^{\circ}, 22.5^{\circ}, 30^{\circ}$ etc., and its bisector of an angle. So, it is not possible to construct an angle of $40^{\circ}$.
Hence, the correct option is (B).
2. The construction of a triangle $ABC$, given that $BC=6 ~cm , \angle B=45^{\circ}$ is not possible when difference of $A B$ and $A C$ is equal to:
(A) $6.9 ~cm$
(B) $5.2 ~cm$
(C) $5.0 ~cm$
(D) $4.0 ~cm$
Show Answer
Solution
Given: $BC=6 ~cm$ and $\angle B=45^{\circ}$
As, we know that, the construction of a triangle is not possible, if sum of two sides is less than or equal to the third side of the triangle.
So, the difference between other two sides $AB$ and $AC$ should be equal to or greater then $BC$. Hence, the correct option is (A).
3. The construction of a triangle $ABC$, given that $B C=3 ~ ~c m, \angle C=60^{\circ}$ is possible when difference of $A B$ and $A C$ is equal to:
(A) $3.2 ~cm$
(B) $3.1 ~cm$
(C) $3 ~cm$
(D) $2.8 ~cm$
Show Answer
Solution
Given, $BC=3 ~cm$ and $\angle C=60^{\circ}$
As, we know that, the construction of a triangle is possible, if sum of two sides is greater than the third side of the triangle.
So, the difference between other two sides $AB$ and $AC$ should not be equal to or greater than $BC$.
Hence, the correct option is (D).
Short Answer Questions with Reasoning
Write True or False in each of the following. Give reasons for your answer:
1. An angle of $52.5^{\circ}$ can be constructed.
Show Answer
Solution
As, $42.5^{\circ}=\dfrac{1}{4} \times 210^{\circ}$ and an angle of $210^{\circ}=180^{\circ}+30^{\circ}$ cannot be constructed with the help of ruler and compass.
Hence, the given statement is true.
2. An angle of $42.5^{\circ}$ can be constructed.
Show Answer
Solution
As, $42.5^{\circ}=\dfrac{1}{2} \times 85^{\circ}$ and an angle of $85^{\circ}$ cannot be constructed with the help of ruler and compass.
Hence, the given statement is false.
3. A triangle $ABC$ can be constructed in which $A B=5 ~c m, \angle A=45^{\circ}$ and $B C$ $+AC=5 ~cm$.
Show Answer
Solution
As, a triangle can be constructed, if sum of its two sides is greater than third side.
Here, $BC+AC=AB=5 ~cm$
So, triangle $ABC$ cannot be constructed.
Hence, the given statement is false.
4. A triangle $ABC$ can be constructed in which $BC=6 ~cm, \angle C=30^{\circ}$ and $AC$ $-AB=4 ~cm$.
Show Answer
Solution
As, a triangle can be constructed if sum of its two sides is greater than third side.
So, in triangle $ABC, AB+BC>AC$
$BC>AC-AB$
$6>4$, which is true, so triangle $ABC$ with given conditions can be constructed.
Hence, the given statement is true.
5. A triangle $A B C$ can be constructed in which $\angle B=105^{\circ}, \angle C=90^{\circ}$ and $A B$ $+BC+AC=1 0 ~cm$.
Show Answer
Solution
Given: $\angle B=105^{\circ}, \angle C=90^{\circ}$
We know that, sum of angles of a triangle is $180^{\circ}$.
$\angle A+\angle B+\angle C=180^{\circ}$
Here, $\angle B+\angle C=105^{\circ}+90^{\circ}$
$195^{\circ}>180^{\circ}$ which is not true.
Therefore, a triangle $ABC$ with given conditions cannot be constructed.
Hence, the given statement is false.
6. A triangle $ABC$ can be constructed in which $\angle B=60^{\circ}, \angle C=45^{\circ}$ and $AB$ $+BC+AC=12 ~cm$.
Show Answer
Solution
We know that, sum of angles of a triangle is $180^{\circ}$.
$\angle A+\angle B+\angle C=180^{\circ}$
Here, $\angle B+\angle C=60^{\circ}+45^{\circ}=105^{\circ}<180^{\circ}$,
Therefore, a triangle $ABC$ with given conditions can be constructed.
Hence, the given statement is true.
Short Answer Questions
1. Draw an angle of $110^{\circ}$ with the help of a protractor and bisect it. Measure each angle.
Show Answer
Solution
Given: An angle $AXB=110^{\circ}$.
To construct: the bisector of angle AXB as follows:
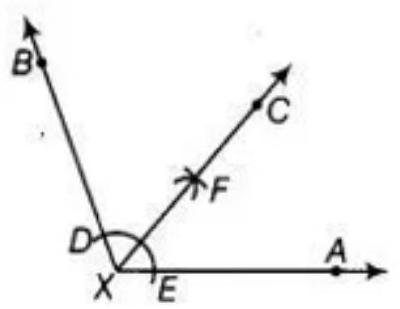
Steps of construction:
1. With $X$ as center and any radius draw an arc to intersect the rays $XA$ and $XB$, say at $E$ and $D$, respectively. 2. With $D$ and $E$ as center’s and with the radius more than $\dfrac{1}{2} DE$, draw arcs to intersect each other, say at $F$. 3. Draw the ray XF.
So, ray XF is the required bisector of the angle BXA. On measuring each angle, get:
$\angle BXC=\angle AXC=55^{\circ} .[As, \angle BXC=\angle AXC=\dfrac{1}{2} \angle BXA=\dfrac{1}{2} \times 110^{\circ}=55^{\circ}]$
2. Draw a line segment $A B$ of $4 ~cm$ in length. Draw a line perpendicular to $A B$ through $A$ and $B$, respectively. Are these lines parallel?
Show Answer
Solution
Given: A line segment $AB$ of length $4 ~cm$.
To construct: To draw a line perpendicular to $AB$ through $A$ and $B$, respectively.
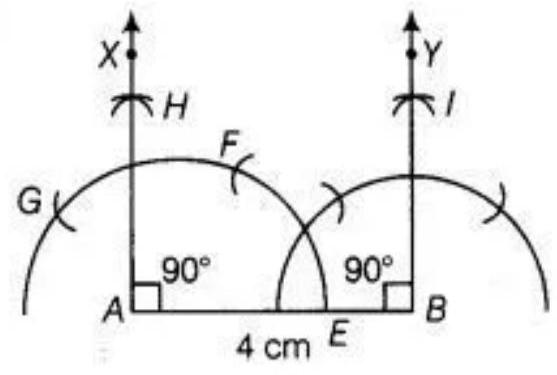
Use the following steps of construction.
1. Draw $AB=4 ~cm$. 2. With 4 as centre and radius more than $\dfrac{1}{2} AB$, draw an arc that is intersect $AB$ at $E$. 3. With $E$ as centre and with same radius as above draw an arc which intersect previous arc at $F$. 4. Again, taking $F$ as centre and with same radius as above draw an arc which intersect previous arc (obtained in step ii) at $G$. 5. With $G$ and $F$ are centres, draw arcs which intersect each other at $H$. 6. Join AH. So, AX is perpendicular to AB at A. Similarly, draw BY $\perp AB$ at B.
Now, we know that if two lines are parallel, then the angle between them will be $0^{\circ}$ or $180^{\circ}$. So,
$\angle XAB=90^{\circ}[XA \perp AB]$
and $\angle YBA=90^{\circ}[YB \perp AB]$
$\angle XAB+\angle YBA=90^{\circ}+90^{\circ}=180^{\circ}$
Hence, the lines XA and YS are parallel. [It sum of interior angle on same side of transversal is $180^{\circ}$, then the two lines are parallel]
3. Draw an angle of $80^{\circ}$ with the help of a protractor. Then construct angles of
(i) $40^{\circ}$
(ii) $160^{\circ}$ and
(iii) $120^{\circ}$.
Show Answer
Solution
Steps of construction:
Given: Draw an angle of $80^{\circ}$ say $\angle QOA=80^{\circ}$ with the help of protractor.
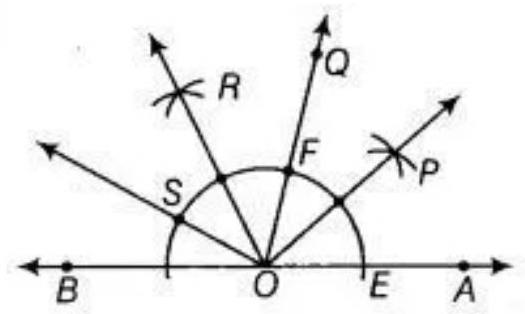
Use the following steps to construct angles of:
1. With $O$ as centre and any radius draw an arc which intersect $OA$ at $E$ and $OO$ at $F$. 2. With $E$ and $F$ as centres and radius more than $\dfrac{1}{2} EF$ draw arcs which intersect each other at $P$. 3. Join OP Since, $\angle POA=40^{\circ}[40^{\circ}=\dfrac{1}{2} \times 80^{\circ}]$ 4. With $F$ as centre and radius equal to $EF$ draw an arc which intersect previous arc obtained in step 2 at $S$. 5. Join OS. Thus, $\angle SOA=160^{\circ}[160^{\circ}=2 \times 80^{\circ}]$ 6. With $S$ and $F$ as centre and radius more than $\dfrac{1}{2} SF$ draw arcs which intersect each other at $R$. 7. Join OR. Thus, $\angle ROA=\angle ROQ=40^{\circ}+80^{\circ}=120^{\circ}$.
4. Construct a triangle whose sides are $3.6 ~cm, 3.0 ~cm$ and $4.8 ~cm$. Bisect the smallest angle and measure each part.
Show Answer
Solution
To construct: a triangle $ABC$ in which $AB=3.6 ~cm, AC=3.0 ~cm$ and $BC=4.8 ~cm$, use the following steps.
1. Draw a line $BC=4.8 ~cm$. 2. From B, point $A$ is at a distance of $3.6 ~cm$. So, having $B$ as centre, draw an arc of radius $3.6 ~cm$. 3. From $C$, point $A$ is at a distance of $3 ~cm$. So, having $C$ as centre, draw an arc of radius $3 ~cm$ which intersect previous arc at $A$. 4. Join $AB$ and $AC$. Therefore, $ABC$ is the required triangle.
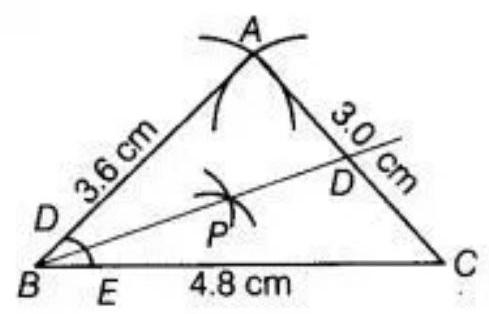
Where, angle B is smallest, as AC is the smallest side.
To direct angle B, we use the following steps.
1. With $B$ as centre, draw an arc intersecting $AB$ and $BC$ at $D$ and $E$, respectively. 2. With $D$ and $E$ as centres and draw arcs intersecting at $P$. 3. Joining BP, we obtain angle bisector of $\angle B$. 4. Here, $\angle ABC=39^{\circ}$
Thus, $\angle ABD=\angle DBC=\dfrac{1}{2} \times 139^{\circ}=19.5^{\circ}$
5. Construct a triangle $ABC$ in which $BC=5 ~cm, \angle B=60^{\circ}$ and $AC+AB=$ $7.5 ~cm$.
Show Answer
Solution
Given, in $\triangle ABC, BC=5 ~cm, \angle B=60^{\circ}$ and $AC+AB=7.5 ~cm$.
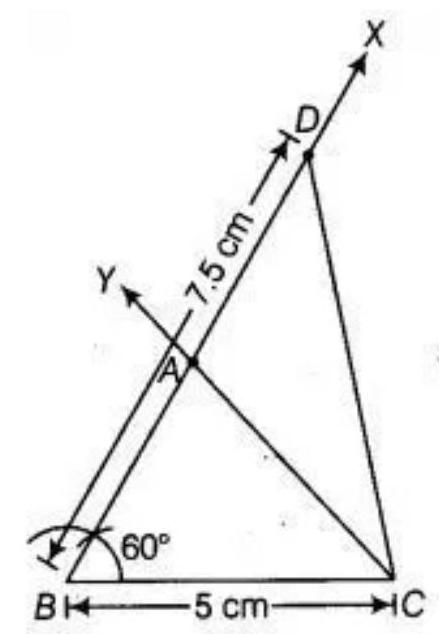
To construct: the triangle $ABC$ use the following steps.
1. Draw the base $BC=5 ~cm$. 2. At the point $B$ make an $\angle XBC=60^{\circ}$. 3. Cut a line segment $BD$ equal to $AB+AC=7.5 ~cm$ from the ray $BX$. 4. Join DC. 5. Make an $\angle DCY=\angle BDC$. 6. Let $CY$ intersect $BX$ at $A$.
Therefore, $ABC$ is the required triangle.
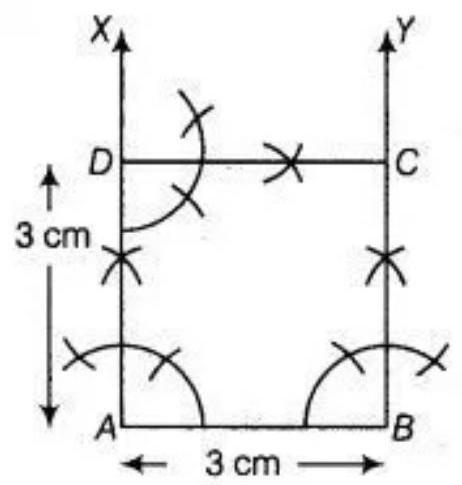
6. Construct a square of side $3 ~cm$.
Show Answer
Solution
As we know that, each angle of a square is right angle that is $90^{\circ}$.
To construct: a square of side $3 ~cm$, use the following steps.
1. Take $AB=3 ~cm$. 2. Now, draw an angle of $90^{\circ}$ at points $A$ and $B$ and plot the parallel lines $AX$ and $BY$ at these points. 3. Cut $AD$ and $SC$ of length $3 ~cm$ from $AX$ and $BY$, respectively. 4. Draw $90^{\circ}$ at any one of the point $C$ or $D$ and join both points by $CD$ of length $3 ~cm$. Therefore, $ABCD$ is the required square of side, $3 ~cm$.
7. Construct a rectangle whose adjacent sides are of lengths $5 ~cm$ and 3.5 ~cm.
Show Answer
Solution
As, we know that, each angle of a rectangle is right angle that is $90^{\circ}$ and its opposite sides are equal and parallel.
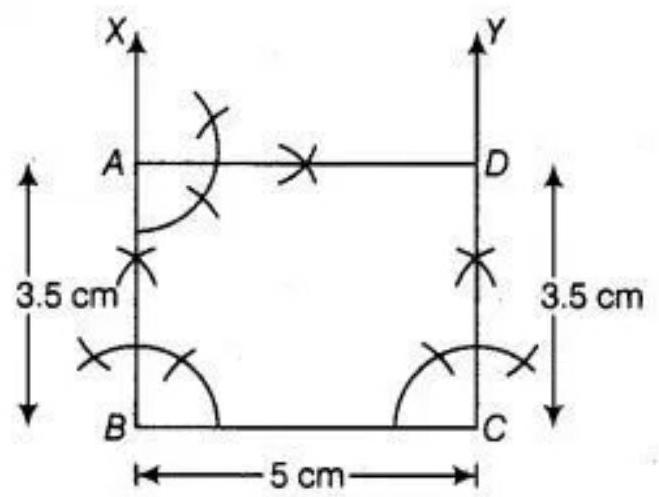
To construct: a rectangle whose adjacent sides are of lengths $5 ~cm$ and $3.5 ~cm$, use the 1 following steps
1. Take $BC=5 ~cm$. 2. Draw $90^{\circ}$ at points $B$ and $C$ of the line segment $BC$ and plot the parallel lines $BX$ and $CY$ at these points. 3. Cut $A B$ and $C D$ of length $3.5 ~cm$ from $B X$ and $C Y$, respectively. 4. Draw an angle $90^{\circ}$ at one of the point $A$ or $D$ and join both points by a line segment $AD$ of length $5 ~cm$.
Therefore, $ABCD$ is the required rectangle with adjacent sides of length $5 ~cm$ and 3.5 $~cm$.
8. Construct a rhombus whose side is of length $3.4 ~cm$ and one of its angles is $45^{\circ}$.
Solution
Show Answer
As, we know that, in rhombus all sides are equal.
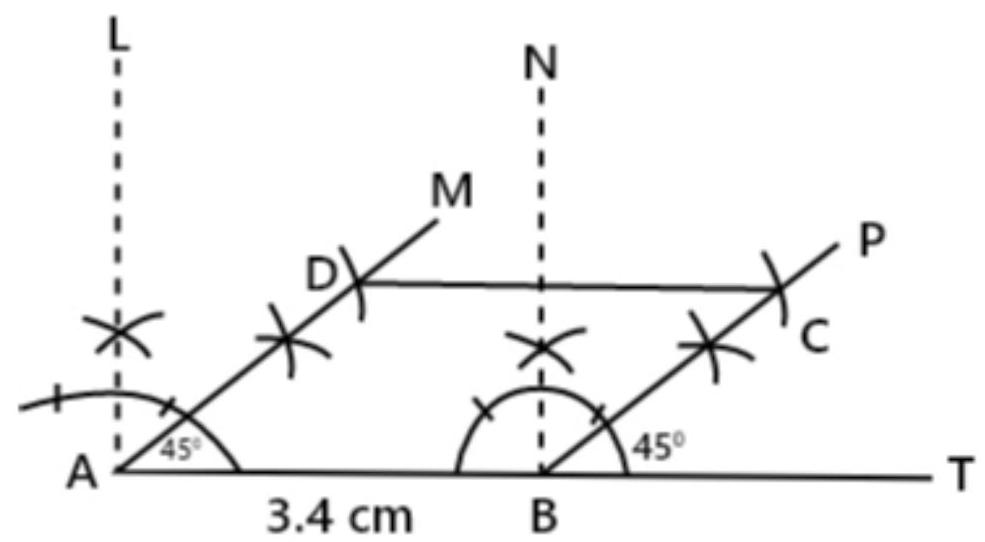
To construct a rhombus whose side is of length $3.4 ~cm$ and one of its angle is $45^{\circ}$.
1. Taking $AB=3.4 ~cm$. 2. AT point $A$ and $B$, construct $\angle B A M=45^{\circ}$ and $\angle T B P=45^{\circ}$, respectively. 3. From $AM$ cut off $AD=3.4 ~cm$ and from $BP$ cut off $BC=3.4 ~cm$. 4. Join $AD, DC$ and $BC . ABCD$ is the required rhombus.
Long Answer Questions
1. A triangle if its perimeter is $10.4 ~cm$ and two angles are $45^{\circ}$ and $120^{\circ}$.
Show Answer
Solution
Let $ABC$ be a triangle.
Given: Perimeter $=10.4 ~cm$ that is, $AB+BC+CA=10.4 ~cm$ and two angles are $45^{\circ}$ and $120^{\circ}$.
So, $\angle B=45^{\circ}$ and $\angle C=120^{\circ}$
Now, to construct the triangle $ABC$ use the following steps.
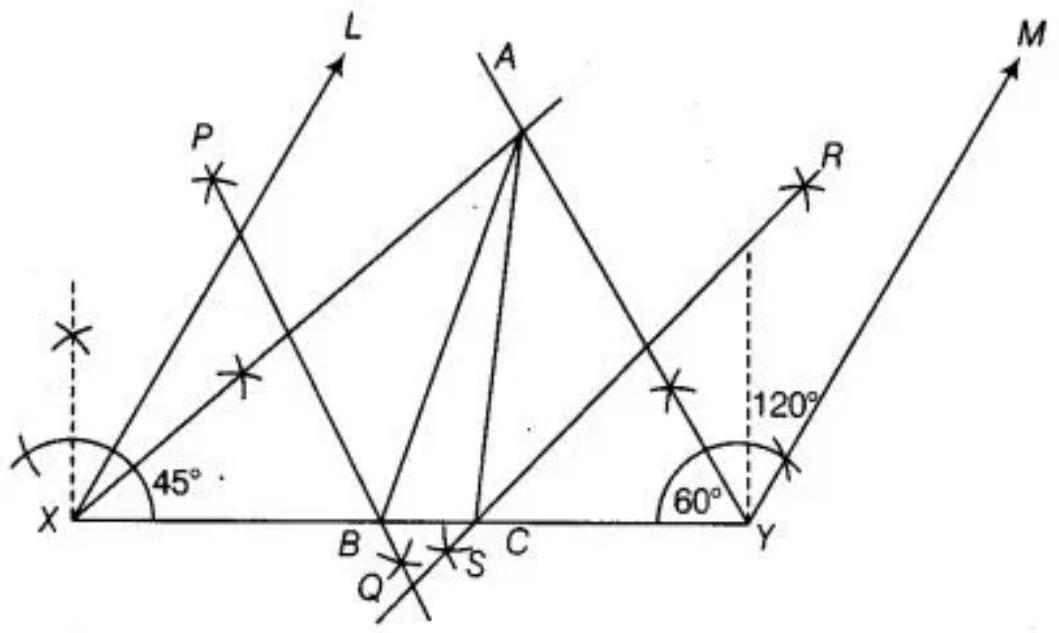
1. Draw $XY$ and equal to perimeter that is, $AB+BC+CA=10.4 ~cm$.
2. Draw $\angle LXY=\angle B=45^{\circ}$ and $\angle MYX=\angle C=120^{\circ}$.
3. Bisect $\angle LXY$ and $\angle MYX$ and let these bisectors intersect at a point $A$.
4. Draw perpendicular bisectors $PQ$ and $RS$ of $AX$ and $AY$, respectively.
5. Let $PQ$ intersect $XY$ at $B$ and $RS$ intersect $XY$ at $C$. Join $AB$ and $AC$. Therefore, $ABC$ is the required triangle.
Justification:
$B$ lies on the perpendicular bisector $PQ$ of $AX$.
Thus, $AB+BC+CA=XB+BC+CY=XY$
Again, $\angle BAX=\angle AXB[As, AB=XB] \ldots(I)$
Also, $\angle ABC=\angle BAX+\angle AXB \quad[\angle ABC$ is an exterior angle of $\triangle AXB]$
$=\angle AXB+\angle AXB[$ From equation $(I)]$ $=2 \angle AXB=\angle LXY[AX$ is a bisector of $\angle LXB]$
Also, $\angle CAY=\angle AYC[$ As, $AC=CY]$
$\angle ACB=\angle CAY+\angle AYC[\angle ACB$ is an exterior angle of triangle $AYC]$
$=\angle CAY+\angle CAY$
$=2 \angle CAY=\angle MYX[AY$ is a bisector of $\angle MYX]$
Therefore, our construction is justified.
2. A triangle $PQR$ given that $QR=3 ~cm, \angle PQR=45^{\circ}$ and $QP-PR=2 ~cm$.
Show Answer
Solution
Given: in triangle $PQR, QR=3 ~cm, \angle PQR=45^{\circ}$ and $QP-PR=2 ~cm$
As, $C$ lies on the perpendicular bisector RS of AY.
To construct: a triangle $PQR$.
Use the following steps of construction.
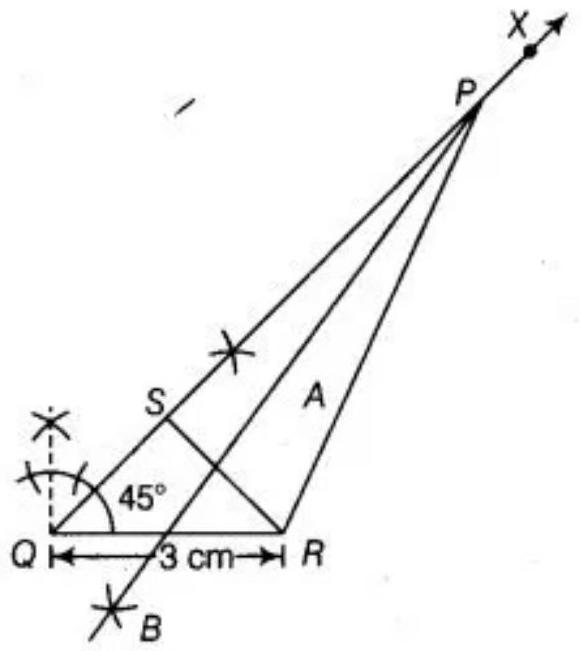
1. Draw $QR=3 ~cm$.
2. Make an angle $XQR=45^{\circ}$ at point $Q$ of base $QR$.
3. Cut the line segment $QS=QP-PR=2 ~cm$ from the ray $QX$.
4. Join SR and draw the perpendicular bisector of SR say AB.
5. Let bisector $AB$ intersect $QX$ at $P$. Join $PR$ Thus, $\triangle PQR$ is the required triangle.
Justification:
Base $QR$ and $\angle PQR$ are drawn as given.
As, the point $P$ lies on the perpendicular bisector of SR.
$PS=PR$
Now, $QS=PQ-PS$
$ =PQ-PR $
Therefore, our construction is justified.
3. A right triangle when one side is $3.5 ~cm$ and sum of other sides and the hypotenuse is $5.5 ~cm$.
Show Answer
Solution
In the right triangle $ABC$, given $BC=3.5 ~cm, \angle B=90^{\circ}$ and sum of other side and hypotenuse be, $AB+AC=5.5 ~cm$.
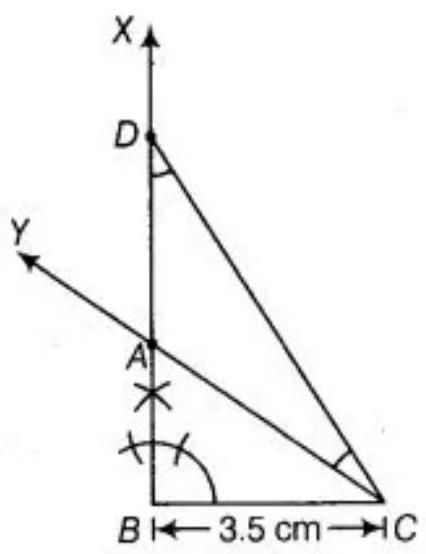
To construct a triangle $ABC$ use the following steps
1. Draw $BC=3.5 ~cm$
2. Make an angle $XBC=90^{\circ}$ at the point $B$ of base $BC$.
3. Cut the line segment $BD$ equal to $AB+AC$ i.e., $5.5 ~cm$ from the ray $XB$.
4. Join $DC$ and make an $\angle DCY$ equal to $\angle BDC$.
5. Let $Y$ intersect $BX$ at $A$.
Therefore, $ABC$ is the required triangle.
Justification:
Base $BC$ and $\angle B$ are drawn as given.
In $\triangle ACD, \angle ACD=\angle ADC$ [by construction]
$AD=AC \ldots$..(I) [sides opposite to equal angles are equal]
Now, $AB=BD-AD=BD-AC[$ From equation $(I)]$
$BD=AB+AC$
Hence, our construction is justified.
4. An equilateral triangle if its altitude is $3.2 ~cm$.
Show Answer
Solution
As, in an equilateral triangle all sides are equal and all angles are equal i.e., each angle is of $60^{\circ}$.
Given: altitude of an equilateral triangle say $ABC$ is $3.2 ~cm$.
To construct the triangle $ABC$ use the following steps.
1. Draw a line PQ.
2. Take a point $D$ on $PQ$ and draw $DE \perp PQ$.
3. Cut $AD$ of length $3.2 ~cm$ from $DE$.
4. Make angles equal to $30^{\circ}$ at $A$ on both sides of $AD$ say $\angle CAD$ and $\angle BAD$, where $B$ and $C$ lie on $PQ$.
5. Cut $DC$ from $PQ$ such that $DC=BD$
Join $AC$
Hence, $ABC$ is the required triangle.
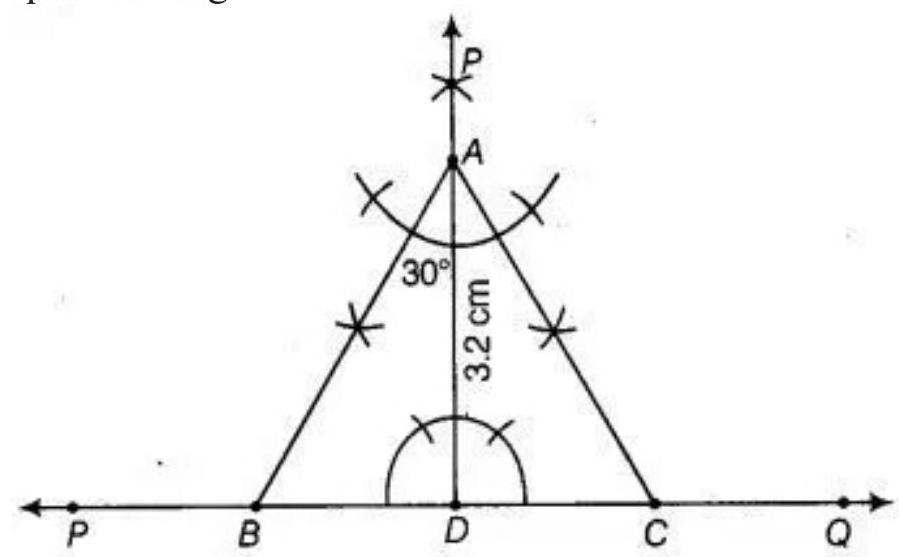
Justification:
Here, $\angle A=\angle BAD+\angle CAD$
$ =30^{\circ}+30^{\circ} $
$ =60^{\circ} \text{. } $
Also, $AD \perp SC$
So, $\angle ADS=90^{\circ}$.
In triangle $ABD, \angle BAD+\angle DBA=180^{\circ}$ [angle sum property]
$30^{\circ}+90^{\circ}+\angle DBA=180^{\circ}[\angle BAD=30^{\circ}.$, by construction $]$
$\angle DBA=60^{\circ}$
Also, $\angle DCA=60^{\circ}$
Therefore, $\angle A=\angle B=\angle C=60^{\circ}$
Hence, $ABC$ is an equilateral triangle.
5. A rhombus whose diagonals are $4 ~cm$ and $6 ~cm$ in lengths.
Show Answer
Solution
As, all sides of a rhombus are equal and the diagonals of a rhombus are perpendicular bisectors of one another. So, to construct a rhombus whose diagonals are $4 ~cm$ and $6 ~cm$. Use the following steps.
1. Draw $AC=4 ~cm$
2. With $A$ and $C$ as centres and radius more than $\dfrac{1}{2} AC$ draw arcs on both sides of $AC$ to intersect each other.
3. Cut both arcs intersect each other at $P$ and $Q$, then join $P Q$.
4. Let $PQ$ intersect $AC$ at the point $O$. So, $PQ$ is perpendicular bisector of $AC$.
5. Cut off $3 ~cm$ lengths from $OP$ and $OQ$, then we get points $B$ and $D$.
6. Join $AB, BC, CD$, and $DA$.
Hence, $ABCD$ is the required rhombus.
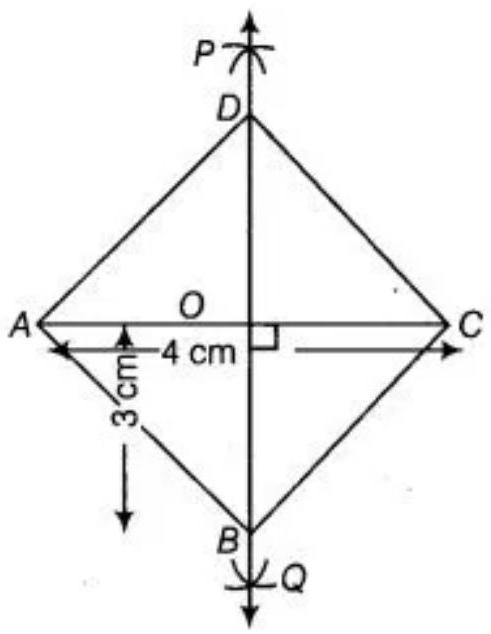
Justification:
$D$ and $B$ lie on perpendicular bisector of $AC$.
$DA=DC$ and $BA=BC \ldots$ (I)
[since, every point on perpendicular bisector of line segment is equidistant from end points of line segment]
Now, $\angle DOC=90^{\circ}$
Also, $OD=OB=3 ~cm$
Thus, $AC$ is perpendicular bisector or $BD$.
$CD=CB \ldots$. (II)
$AB=BC=CD=DA$
Now, from equation (I) and (II):
$ABCD$ is a rhombus.










