Circles
Multiple Choice Questions(MCQs)
1. $A D$ is a diameter of a circle and $A B$ is a chord. If $A D=34 ~cm, A B=30 ~cm$, the distance of $A B$ from the centre of the circle is:
(A) $17 ~cm$
(B) $15 ~cm$
(C) $4 ~cm$
(D) $8 ~cm$
Show Answer
Solution
Construction: Draw $OP \perp AB$.
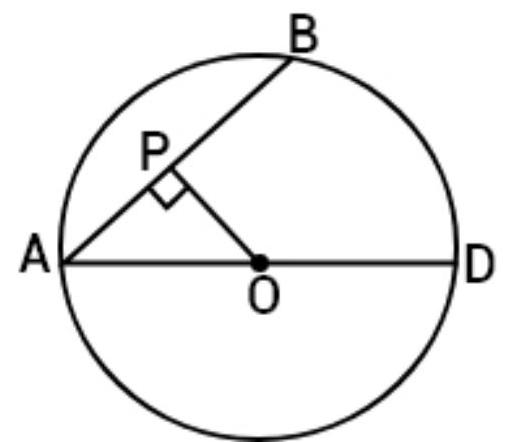
As perpendicular from the center to a chord bisect. So,
$A P=\dfrac{1}{2} \times A B=\dfrac{1}{2} \times 30=15 ~cm$
Radius $=O A=\dfrac{1}{2} \times 34=17 ~cm$
Now, in right triangle OPA,
$ \begin{aligned} O P & =\sqrt{O A^{2}-A P^{2}} \\ & =\sqrt{(17)^{2}-(15)^{2}} \\ & =\sqrt{289-225} \\ & =\sqrt{64} \\ & =8 ~cm \end{aligned} $
Hence, the correct option is (D).
2. In Fig., if $O A=5 ~cm, A B=8 ~cm$ and $O D$ is perpendicular to $A B$, then $C D$ is equal to:
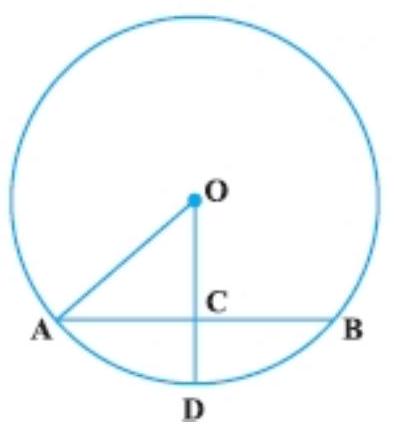
(A) $2 ~cm$
(B) $3 ~cm$
(C) $4 ~cm$
(D) $5 ~cm$
Show Answer
Solution
As the perpendicular from the centre of a circle to a chord bisects the chord.
$AC=CB=\dfrac{1}{2} \times AB=\dfrac{1}{2} \times 8=4 ~cm$
Given $OA=5 ~cm$
$A O^{2}=A C^{2}+O C^{2}$
$(5)^{2}=(4)^{2}+O C^{2}$
$25=16+O C^{2}$
$O C^{2}=25-16$
$=9$
So, $OC=3 ~cm$ [Length is always positive]
$OA=OD$ [same radius of a circle]
$OD=5 ~cm$
$CD=OD-OC$
$=5-3$
$=2 ~cm$
Hence, the correct option is (A).
3. If $A B=12 ~cm, B C=16 ~cm$ and $A B$ is perpendicular to $B C$, then the radius of the circle passing through the points $A, B$ and $C$ is :
(A) $6 ~cm$
(B) $8 ~cm$
(C) $10 ~cm$
(D) $12 ~cm$
Show Answer
Solution
Given in the question, $AB=12 ~cm$ and $BC=16 ~cm$.
In a circle, $B C \perp A B$. So, that means $AC$ will be a diameter of circle.
Now, by using Pythagoras theorem in right angled triangle $ABC$. $A C^{2}=A B^{2}+B C^{2}$
$A C^{2}=(12)^{2}+(16)^{2}$
$A C^{2}=144+256$
$A C^{2}=400$
$A C=20 ~cm$
So, radius of circle $=\dfrac{1}{2} \times A C=\dfrac{1}{2} \times 20=10 ~cm$.
Therefore, the radius of circle is $10 ~cm$.
Hence, the correct option is (C).
4. In Fig., if $\angle ABC=20^{ \circ }$, then $\angle AOC$ is equal to:
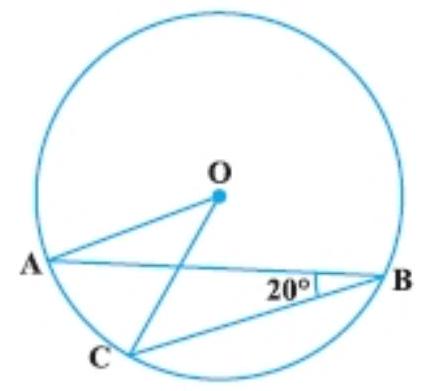
(A) $20^{\circ}$
(B) $40^{\circ}$
(C) $60^{\circ}$
(D) $10^{\circ}$
Show Answer
Solution
Given: $\angle A B C=20^{\circ}$
As angle subtended at the centre by an arc is twice the angle subtended by it at the remaining part of circle. So,
$\angle A O C=2 \angle A B C=2 \times 20^{\circ}=40^{\circ}$.
Hence, the correct option is (B).
5. In Fig., if $A O B$ is a diameter of the circle and $A C=B C$, then $\angle C A B$ is equal to:
(A) $30^{\circ}$
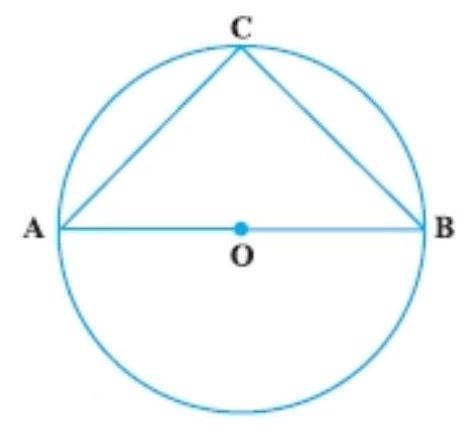
(B) $60^{\circ}$
(C) $90^{\circ}$
(D) $45^{\circ}$
Show Answer
Solution
Given: $AOB$ is a diameter of the circle and $AC=BC$.
So, $\angle C=90^{\circ}$ [Angle on the semicircle is $90^{\circ}$ ]
Now, $AC=BC$
So, $\angle A=\angle B$ [Angles opposite to equal sides of triangle are equal]
Now, by using the sum property of a triangle,
$ \begin{aligned} \angle A+\angle B+\angle C & =180^{\circ} \\ 2 \angle A+90^{\circ} & =180^{\circ} \\ 2 \angle A & =180^{\circ}-90^{\circ} \\ 2 \angle A & =90^{\circ} \\ \angle A & =\dfrac{90^{\circ}}{2} \\ \angle A & =45^{\circ} \end{aligned} $
Hence, the correct option is (D).
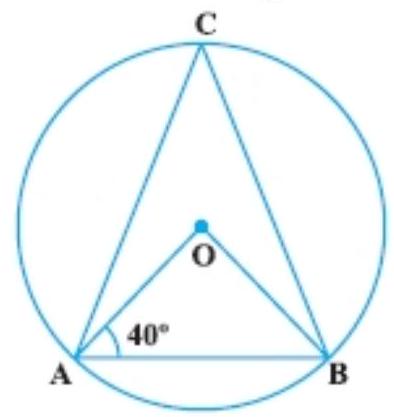
6. In Fig., if $\angle OAB=40^{\circ}$, then $\angle ACB$ is equal to:
(A) $50^{\circ}$
(B) $40^{\circ}$
(C) $60^{\circ}$
(D) $70^{\circ}$
Show Answer
Solution
Given: $\angle OAB=40^{\circ}$
Now, in triangle $OAB$,
$OA=OB[$ Radii of circle $]$
So, $\angle O A B=\angle O B A=40^{\circ} \quad$ [Angle opposite to equal sides are equal]
So,
$ \begin{aligned} \angle A O B & =180^{\circ}-(40^{\circ}+40^{\circ}) \\ & =100^{\circ} \end{aligned} $
As we know that angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle. So,
$\angle A C B=\dfrac{1}{2} \angle A O B=\dfrac{1}{2} \times 100^{\circ}=50^{\circ}$
Hence, the correct option is (A).
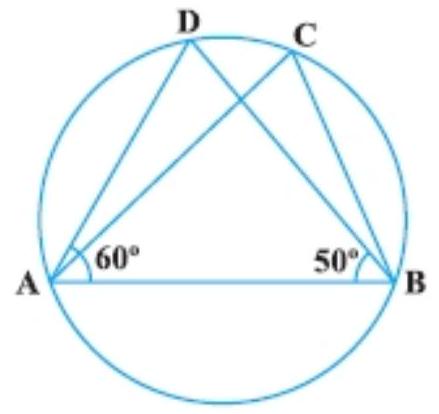
7. In Fig., if $\angle DAB=6 0 ^ { \circ }, \angle ABD=5 0^{\circ}$, then $\angle ACB$ is equal to:
(A) $60^{\circ}$
(B) $50^{\circ}$
(C) $70^{\circ}$
(D) $80^{\circ}$
Show Answer
Solution
In triangle $ABC$,
$ \begin{aligned} \angle A+\angle B+\angle D & =180^{\circ} \quad \text{ [Angle sum property of a triangle] } \\ 60^{\circ}+50^{\circ}+\angle D & =180^{\circ} \\ \angle D & =180^{\circ}-110^{\circ} \\ \angle D & =70^{\circ} \end{aligned} $
That is $\angle A B D=70^{\circ}$
Now, $\angle A C B=\angle A D B=70^{\circ}$ [Angle in the same segment of a circle are equal]
Hence, the correct option is (C).
8. $A B C D$ is a cyclic quadrilateral such that $A B$ is a diameter of the circle circumscribing it and
$\angle ADC=140^{\circ}$, then $\angle BAC$ is equal to:
(A) $80^{\circ}$
(B) $50^{\circ}$
(C) $40^{\circ}$
(D) $30^{\circ}$
Show Answer
Solution
Given: $A B C D$ is a cyclic quadrilateral such that $A B$ is a diameter of the circle circumscribing it and $\angle ADC=140^{\circ}$.
Construction: Join AC.
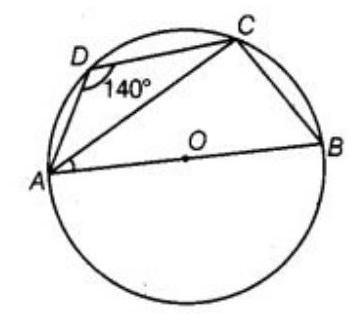
See in the figure, $\angle A D C+\angle A B C=180^{\circ}$ $140^{\circ}+\angle A B C=180^{\circ}$ [Given]
So, $\angle A B C=180^{\circ}-140^{\circ}=40^{\circ}$
Now, $\angle C=90^{\circ} \quad$ [Angle in semicircle is a right angle]
In triangle $ABC$,
$\angle B A C=180^{\circ}-(90^{\circ}+40^{\circ})$
$ =50^{\circ} $
Hence, the correct option is (B).
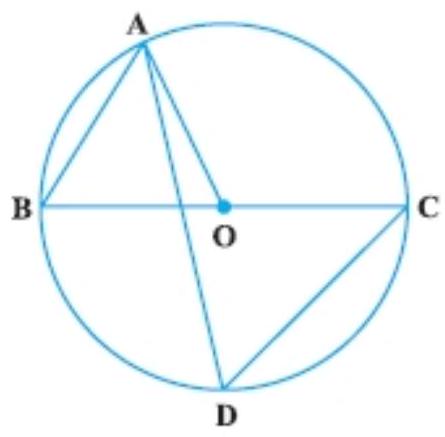
9. In Fig., $BC$ is a diameter of the circle and $\angle BAO=60^{\circ}$. Then $\angle ADC$ is equal to:
(A) $30^{\circ}$
(B) $45^{\circ}$
(C) $60^{\circ}$
(D) $120^{\circ}$
Show Answer
Solution
Given: $BC$ is a diameter of the circle and $\angle BAO=60^{\circ}$.
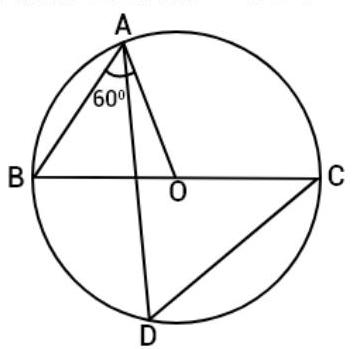
Now, in triangle $OAB$,
$OA=OB[$ Radii of the same circle]
So, $\angle A B O=\angle B A O \quad$ [Angle opposite to equal sides are equal] $\angle A B O=\angle B A O=60^{\circ}$
[Given]
Now, $\angle A D C=\angle A B C=60^{\circ}[\angle A D C$ and $\angle A B C$ are angles in the same segment of a circle are equal]
Therefore, $\angle A D C=60^{\circ}$.
Hence, the correct option is (C).
10. In Fig. 10.9, $\angle A O B=90^{\circ}$ and $\angle A B C=30^{\circ}$, then $\angle C A O$ is equal to:
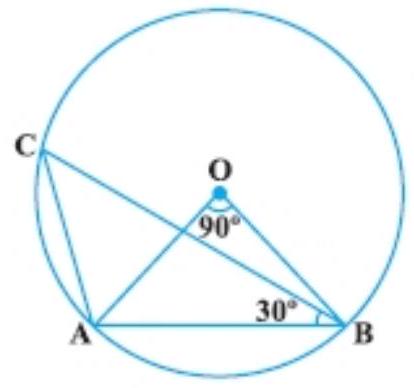
(A) $30^{\circ}$
(B) $45^{\circ}$
(C) $90^{\circ}$
(D) $60^{\circ}$
Show Answer
Solution
In triangle $OAB$,
$OA=OB \quad$ [Radii of the same circle]
So, $\angle O A B=\angle O B A$
Now, in triangle $OAB$,
$\angle O A B+\angle O B A+\angle A O B=180^{\circ}$
So,
$ \begin{aligned} 2 \angle O A B & =180^{\circ}-\angle A O B \\ & =(180^{\circ}-90^{\circ}) \\ & =90^{\circ} \text{ [Sum of angle of triangle is } 180^{\circ}] \end{aligned} $
So, $\angle O A B=\dfrac{1}{2} \times 90^{\circ}=45^{\circ}$
Also, $\angle A C B=\dfrac{1}{2} \angle A O B=\dfrac{1}{2} \times 90^{\circ}=45^{\circ}$
Now, in triangle $CAB$,
$ \begin{aligned} \angle C A B & =180^{\circ}-(\angle A B C+\angle A C B) \\ & =180^{\circ}-(30^{\circ}+45^{\circ})=105^{\circ} \end{aligned} $
Now, $\angle C A O=\angle C A B-\angle O A B$
$\angle C A O=105^{\circ}-45^{\circ}$
Hence, the correct option is (D).
Short Answer Questions with Reasoning
Write True or False and justify your answer in each of the following:
1. Two chords $A B$ and $C D$ of a circle are each at distances $4 ~cm$ from the center. Then $A B=C D$.
Show Answer
Solution
As we know that the chords equidistant from the centre of circle are equal in length.
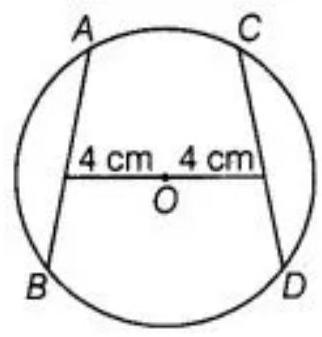
Hence, the given statement is true.
2. Two chords $A B$ and $A C$ of a circle with center $O$ are on the opposite side of $O A$. Then $\angle OAB=\angle OAC$.
Show Answer
Solution
In this question, two chords $AB$ and $AC$ are not given equal.
Hence, the given statement is false because the angles will be equal if $AB=AC$.
3. Two congruent circles with center’s $O$ and $O^{\prime}$ intersect at two points $A$ and B. Then $\angle A O B=\angle A O^{\prime} B$.
Show Answer
Solution
The equal chords of congruent circle subtend equal angles at the respective centers.
Hence, the given statement is true.
4. Through three collinear points a circle can be drawn.
Show Answer
Solution
A circle can pass through only two collinear points but not through three collinear points.
Hence, the given statement is false.
5. A circle of radius $3 ~cm$ can be drawn through two points $A$, B such that $AB=6 ~cm$.
Show Answer
Solution
As we know that radii of circle is half of the diameter. So,
Radii of circle $=\dfrac{6}{2} ~cm=3 ~cm$
Hence, the given statement is true.
6. If $A O B$ is a diameter of a circle and $C$ is a point on the circle, then $AC^{2}+BC^{2}=AB^{2}$.
Show Answer
Solution
Given: $AOB$ is a diameter of a circle and $C$ is a point on the circle.
So, $\angle A C B=90^{\circ} \quad$ [Angle in a semicircle is a right angle]
In right triangle $ABC$,
$AC^{2}+BC^{2}=AB^{2} \quad[$ By Pythagoras theorem $]$
Hence, the correct option is true.
7. $ABCD$ is a cyclic quadrilateral such that $\angle A=90^{\circ}, \angle B=70^{\circ}, \angle C=95^{\circ}$ and $\angle D=105^{\circ}$.
Show Answer
Solution
Given: $ABCD$ is a cyclic quadrilateral such that $\angle A=90^{\circ}, \angle B=70^{\circ}, \angle C=95^{\circ}$ and $\angle D=105^{\circ}$.
Now, sum of the opposite site of angle of quadrilateral is:
$\angle A+\angle C=90^{\circ}+95^{\circ}=185^{\circ}$
And, $\angle B+\angle D=70^{\circ}+105^{\circ}=175^{\circ}$
Since, sum of opposite angles is not equal to $180^{\circ}$. So, $ABCD$ is not a cyclic quadrilateral.
Hence, the given statement is true.
8. If $A, B, C, D$ are four points such that $\angle BAC=30^{\circ}$ and $\angle BDC=60^{\circ}$, then $D$ is the center of the circle through $A, B$ and $C$.
Show Answer
Solution
There can be many points $D$, such that $\angle BDC=60^{\circ}$ and each such point cannot be the centre of the circle through A, B and C.
Hence, the given statement is false.
9. If $A, B, C$ and $D$ are four points such that $\angle BAC=45^{\circ}$ and $\angle BDC=45^{\circ}$, then A, B, C, D are concyclic.
Show Answer
Solution
Given: $\angle B A C=45^{\circ}$ and $\angle B D C=45^{\circ}$
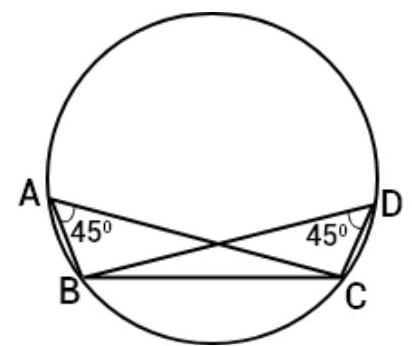
As we know that, angles in the same segment of a circle are equal. Hence, A, B, C and D are concyclic.
Hence, the given statement is true.
10. In Fig., if $A O B$ is a diameter and $\angle A D C=120^{\circ}$, then $\angle CAB=30^{\circ}$.
Show Answer
Solution
See the given figure, $A O B$ is a diameter of circle with center $O$.
$\angle A D C+\angle A B C=180^{\circ} \quad[ABCD$ is a cyclic quadrilateral]
$120^{\circ}+\angle A B C=180^{\circ}$
$\angle ABC=180^\circ - 120^\circ=60^\circ$
In triangle $ABC$,
$\angle A C B=90^{\circ} \quad$ [Angle in a semicircle and $\angle A B C=60^{\circ}$ (proved above)]
So, $\angle C A B=180^{\circ}-(90^{\circ}+60^{\circ})=30^{\circ}$
Hence, the given statement is true.
Short Answer Questions
1. If arcs $A X B$ and $C Y D$ of a circle are congruent, find the ratio of $A B$ and CD.
Show Answer
Solution
As we know that if two arcs of a circle are congruent, then their corresponding arcs are equal. So, we have chord $AB=$ chord $CD$.
Hence, the ratio of $AB$ and $CD$ is $1: 1$.
2. If the perpendicular bisector of a chord $A B$ of a circle $P X A Q B Y$ intersects the circle at $P$ and $Q$, prove that $arcPXA \cong arcPYB$.
Show Answer
Solution
Given: $PQ$ is the perpendicular bisector of $AB$.
To prove that $arcPXA \cong arcPYB$.
Proof: See the above figure,
$AM=BM$
In triangle APM and triangle BPM,
$AM=BM \quad$ [Proved above]
$\angle A M P=\angle B M P \quad[$ Each $=90^{\circ}]$
$PM=PM$ [Common side]
So, $\triangle A P M \cong \triangle B P M$ [By SAS congruence rule]
So, $AP=BP \quad[By CPCT]$
Hence, $arcPXA \cong arcPYB$. [If two chords of a circle are equal, then their corresponding arcs are congruent]
3. $A, B$ and $C$ are three points on a circle. Prove that the perpendicular bisectors of $AB, BC$ and $CA$ are concurrent.
Show Answer
Solution
Given: A, B and C are three points on a circle.
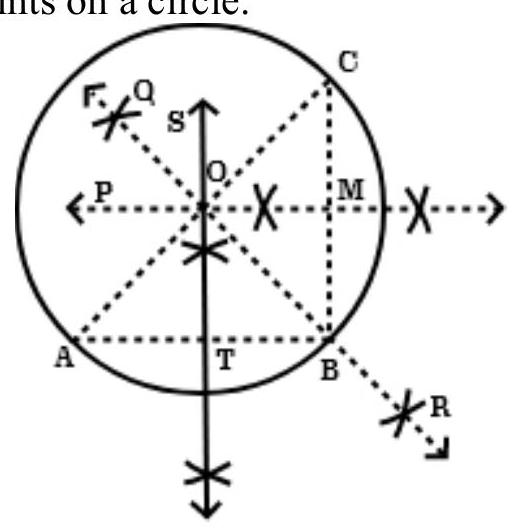
To prove that perpendicular bisector of $AB, BC$ and $CA$.
Construction: Draw perpendicular bisectors $ST$ of $AB, PM$ of $BC$ and $QR$ of $CA$. Join $AB, BC$, and CA.
Proof: $OA=OB \quad \ldots$ (I) [O lies on $ST$, the perpendicular bisector of $AB]$
Again, $OB=OC \ldots$…(II) [O lies on $PM$ the perpendicular bisector of $BC]$
And, $OC=OA \ldots$…III) [O lies on $QR$, the perpendicular bisector of $CA]$
Now, from equation (I), (II), and (III),
$OA=OB=OC=r$
So, draw a circle with center $O$ and radius $r$, that will pass through $A, B$ and $C$.
That means a circle passing through the point A, B and C. Since, ST, PM or QR can cut each other at one and only one point $O$.
Therefore, $O$ is the only one point which is equidistance from $A, B$ and $C$.
Hence, the perpendicular bisector of $AB, BC$ and $CA$ are concurrent.
4. $A B$ and $A C$ are two equal chords of a circle. Prove that the bisector of the angle $B A C$ passes through the center of the circle.
Show Answer
Solution
Given: $AB$ and $AC$ are two equal chords of a circle.
To prove that AM passing through $O$.
Construction: Let AM intersect BC at P. Join BC.
Proof: In triangle BAP and triangle CAP.
$AB=AC \quad[$ Given]
$\angle B A P=\angle C A P \quad[$ Given]
And, $AP=BP[$ Common side $]$
So, $\triangle B A P \cong \triangle C A P \quad[$ By SAS congruency $]$
Again, $\angle B A P=\angle C P A \quad[CPCT]$
And, $CP=PB$
But, $\angle B P A+\angle C P A=180^{\circ} \quad$ [linear pair angles]
Now, $\angle B P A=\angle C P A=90^{\circ}$
Since, AP is perpendicular bisector of the chord $BC$, which will pass through the center $O$ on being produced.
Hence, AM passes through O.
5. If a line segment joining mid-points of two chords of a circle passes through the center of the circle, prove that the two chords are parallel.
Show Answer
Solution
Given: The diameter $P Q$ passes through the center $O$ of the circle. $A B$ and $C D$ are two chords of a circle whose center of $O$, and $PQ$ is a diameter bisecting the chord $AB$ and $CD$ at $L$ and $M$ respectively.
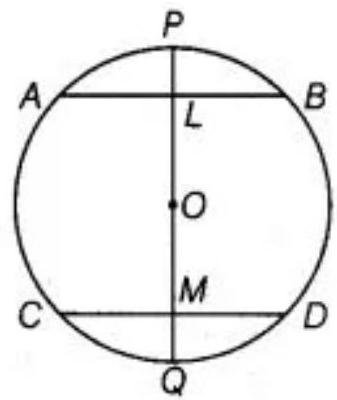
To prove that $AB || CD$
Proof: See the figure, the mid-point of $AB$ is $L$.
$So, OL \perp AB \quad$ [The line joining the center of circle to the mid-point of a chord is perpendicular to the chord]
$\angle A L O=90^{\circ} \quad \ldots$ (I)
Again, $OM \perp CD$
So, $\angle O M D=90^{\circ}$
Now, from equation (I) and (II), get:
$\angle A L O=\angle O M D=90^{\circ}$
Since, there are alternating angles. So,
$AB || CD$
Hence proved.
6. $A B C D$ is such a quadrilateral that $A$ is the centre of the circle passing through B, C and D. Prove that
$\angle CBD+\angle CDB=\dfrac{1}{2} \angle BAD$
Show Answer
Solution
In a circle, $ABCD$ is a quadrilateral having center $A$.
To prove $\angle C B D+\angle C D B=\dfrac{1}{2} \angle B A D$
Construction: join AC.
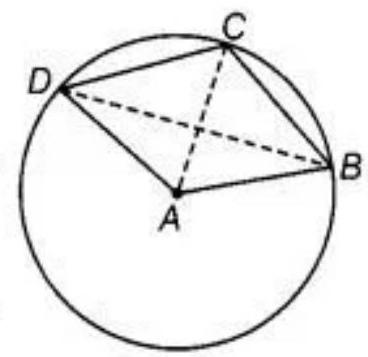
Proof: As we know that angle subtended by an arc at the center is double the angle subtended by it at point on the remaining part of the circle.
So, $\angle C A D=2 \angle C B D \ldots$ (I)
And $\angle B A C=2 \angle C D B \quad$…(II)
Now, adding equation (I) and (II), get:
$\angle C A D+\angle B A C=2(\angle C B D+\angle C D B)$ $\angle B A D=2(\angle C B D+\angle C D B)$
Hence, $\angle C B D+\angle C D B=\dfrac{1}{2} \angle B A D$.
7. $O$ is the circumventer of the triangle $A B C$ and $D$ is the mid-point of the base $B C$. Prove that $\angle \angle B O D=\angle A$
Show Answer
Solution
Given: $O D \perp B C$ and $O$ is the circumcenter of $\triangle A B C$.
To prove that $\angle B O D=\angle A$
Construction: join OD and OC.
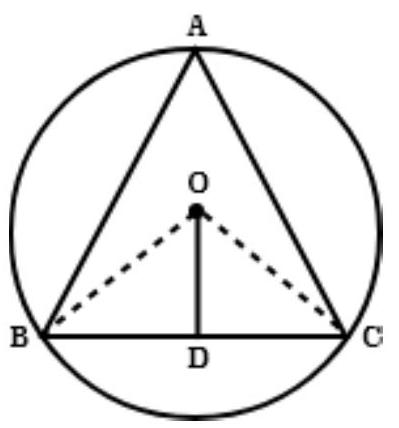
Proof: In triangle OBD and triangle OCD,
$OB=OC$ [Each equal to radius of the circumcircle]
$ \begin{aligned} & \angle O D B=\angle O D C \quad[\text{ Each of } 90^{\circ}] \\ & OD=OD \quad \text{[Common]} \\ & \text{ So, } \angle O B D \cong \angle O C D \quad \text{[By \text{ SAS congruency] }} \\ & \text{ Since, } \angle B O D=\angle C O D \quad \text{[By CPCT]} \\ & \angle B O C=2 \angle B O D=2 \angle C O D \\ & \text{ Therefore, } \angle B O C=2 \angle A \\ & \text{ Now, } 2 \angle B O D=2 \angle A[\angle B O C=2 \angle B O D] \\ & \angle B O D=\angle A \end{aligned} $
Hence, proved.
8. On a common hypotenuse $A B$, two right triangles $A C B$ and $A D B$ are situated on opposite sides. Prove that $\angle BAC=\angle BDC$.
Show Answer
Solution
To prove that $\angle BAC=\angle BDC$.
Proof: In right triangle $ACB$ and $ADB$,
$\angle A C B=90^{\circ}$ and $\angle A D B=90^{\circ}$
So, $\angle A C B+\angle A D B=90^{\circ}+90^{\circ}=180^{\circ}$
As we know that if the sum of any pair of opposite angle of a quadrilateral is $180^{\circ}$, then the quadrilateral is cyclic. So, $ADBC$ is a cyclic quadrilateral.
Join $CD$. Now, angle $\angle B A C$ and $\angle B D C$ are made by arc $BC$ in the same segment $BDAC$.
Hence, $\angle B A C=\angle B D C . \quad$ [Angle in the same segment are equal]
9. Two chords $A B$ and $A C$ of a circle subtends angles equal to $90^{\circ}$ and $150^{\circ}$, respectively at the center. Find $\angle BAC$, if $AB$ and $AC$ lie on the opposite sides of the center.
Show Answer
Solution
In triangle BOA,
$OB=OA[$ Both are the radius of circle]
$\angle O A B=\angle O B A$
.. (I) [Angle opposite to equal sides are equal]
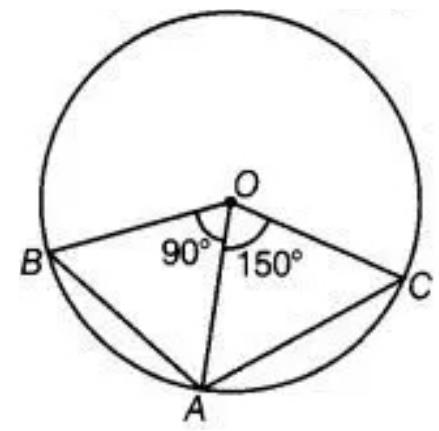
Now, In triangle $OAB$,
$\angle O B A+\angle O A B+\angle A O C=180^{\circ}$
[By angle sum property of a triangle]
$\angle O A B+\angle O A B+90^{\circ}=180^{\circ}$ [From equation (I)]
$2 \angle O A B=180^{\circ}-90^{\circ}$
$2 \angle O A B=90^{\circ}$
$\angle O A B=45^{\circ}$
Again, in triangle AOC,
$AO=OC$ [radii or circle]
$\angle O C A=\angle O A C \quad$…(II)
[Angle opposite to equal sides are equal]
Now, by angle sum property of a triangle:
$\angle A O C+\angle O A C+\angle O C A=180^{\circ}$
$150^{\circ}+2 \angle O A C=180^{\circ} \quad$ [From equation (II)]
$2 \angle O A C=180^{\circ}-150^{\circ}$
$2 \angle O A C=30^{\circ}$
$\angle O A C=15^{\circ}$
$\angle B A C=\angle O A B+\angle O A C=45^{\circ}+15^{\circ}=60^{\circ}$
10. If $B M$ and $C N$ are the perpendiculars drawn on the sides $A C$ and $A B$ of the triangle $ABC$, prove that the points $B, C, M$ and $N$ are concyclic.
Show Answer
Solution
Given: In $\triangle ABC, BM \perp AC$ and $CN \perp AB$.
To prove that points $B, C, M$ and $N$ are con-cyclic.
Construction: Draw a circle passing through the points B, C, M and N.
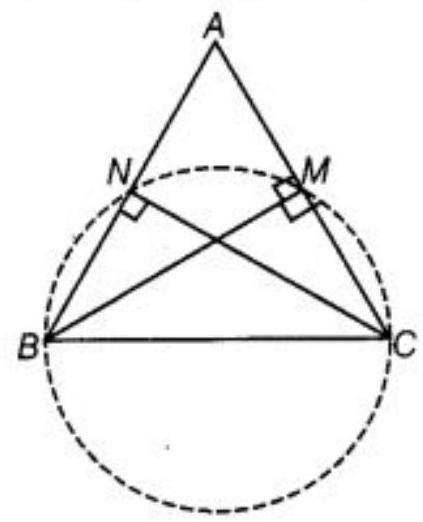
Proof suppose, we consider SC as a diameter of the circle. Also, we know that SC subtends a $90^{\circ}$ to the circle.
So, the points $M$ and $N$ should be on a circle.
Hence, B~CMN form a con-cyclic quadrilateral.
Hence proved.
11. If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
Show Answer
Solution
Given: In triangle $ABC$ is an isosceles triangle such that $AB=AC$ and also $DE || SC$.
To prove that quadrilateral $BCDE$ is a cyclic quadrilateral.
Construction: Draw a circle passes through the point B, C, D and E.
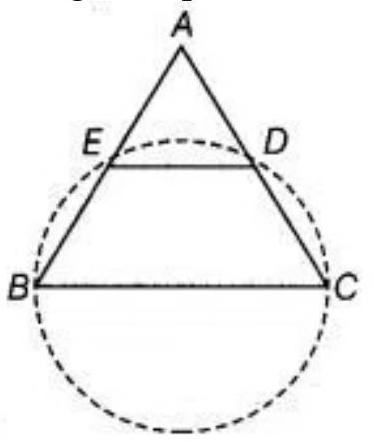
Proof: In triangle $ABC$ :
$AB=AC \quad$ [Equal sides of an isosceles triangle]
$\angle A C B=\angle A B C \quad$…(I) [Angles opposite to the equal sides are equal]
Now, $DE || BC$
$\angle A D E=\angle A C B \quad$ [Corresponding angles]
Now, adding equation (I) and (II), get:
$\angle A D E+\angle E D C=\angle A C B+\angle E D C$
$180^{\circ}=\angle A C B+\angle E D C \quad[\angle A D E$ and $\angle EDC$ from linear pair aniom $]$
$\angle E D C+\angle A C B=180^{\circ} \quad$ [From equation (I)]
Hence, BCDE is a cyclic quadrilateral because sum of the opposite angles is $180^{\circ}$.
12. If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
Show Answer
Solution
Given: let $ABCD$ be a cyclic quadrilateral and $AD=BC$.
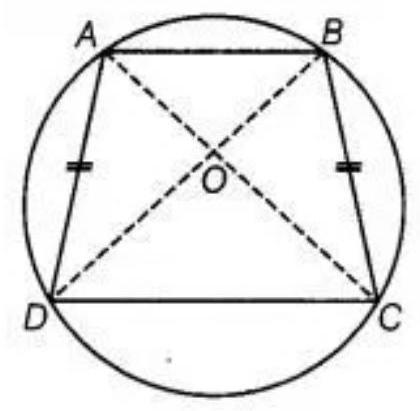
Construction: Join $AC$ and $BD$.
To prove that $AC=BD$
Proof: In triangle AOD and triangle BOC,
$\angle O A D=\angle O B C$ and $\angle ODA=\angle O C B$ [Same segments subtends equal angle to the circle]
$AB=BC \quad[$ Given]
$\triangle A O D=\triangle B O C \quad[$ By ASA congruence rule $]$
Now, adding $\triangle D O C$ on both sides, get:
$\triangle A O D+\triangle D O C \cong \triangle B O C+\triangle D O C$
$ \triangle A D C \cong \triangle B C D $
$AC=BD \quad[By CPCT]$
Hence, proved.
13. The circumcentre of the triangle $ABC$ is $O$. Prove that
$\angle OBC+\angle BAC=90^{\circ}$
Show Answer
Solution
Given: A circle is circumscribed on a triangle $ABC$ having center $O$.
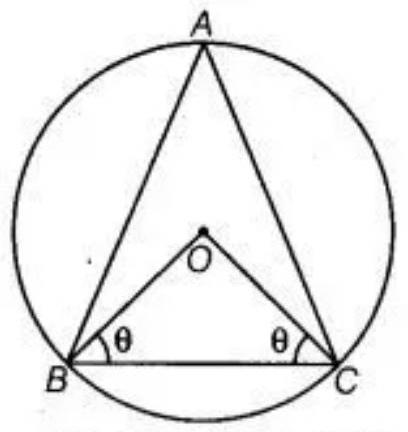
To prove that $\angle O B C+\angle B A C=90^{\circ}$
Construction: Join BO and CO.
Proof: Suppose $\angle O B C=\angle O C B=\theta$
Now, in triangle $OBC, \angle B O C+\angle O C B+\angle C B O=180^{\circ}$ [By angle sum property of a triangle is $180^{\circ}$ ]
$ \begin{aligned} & \angle B O C+\theta+\theta=180^{\circ} \\ & \angle B O C=180^{\circ}-2 \theta \end{aligned} $
As we know that, in a circle, the angle subtended by an arc at the center is twice the angle subtended by it at the remaining part of the circle.
$ \begin{aligned} \angle B O C & =2 \angle B A C \\ \angle B A C & =\dfrac{\angle B O C}{2} \\ & =\dfrac{180^{\circ}-2 \theta}{2} \\ & =90^{\circ}-\theta \end{aligned} $
$ \angle B A C+\theta=90^{\circ} $
$\angle B A C+\angle O B C=90^{\circ}$
Hence, proved.
14. A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
Show Answer
Solution
Given: $AB$ is a chord of a circle, which is equal to the radius of the circle that is:
$AB=BO$
Construction: Join $OA, AC$ and $BC$
As, $OA=OB=$ Radius of circle
So, $OA=AS=BO$
Therefore, triangle $OAB$ is an equilateral triangle,
$\angle A O B=60^{\circ}$ [Each angle of an equilateral triangle is $60^{\circ}$.
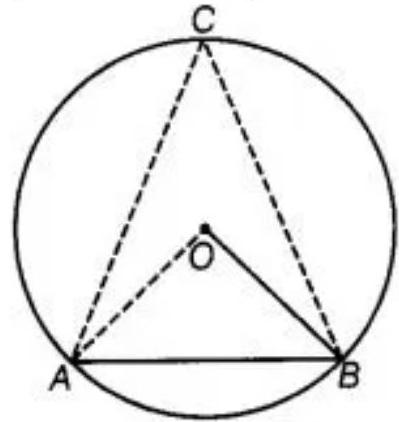
As using the theorem, in a circle, the angle subtended by an arc at the center is twice the angle subtended by it at the remaining part of the circle. So,
$\angle A O B=2 \angle A C B$
$\angle A C B=\dfrac{60^{\circ}}{2}=30^{\circ}$
Hence, the angle subtended by this chord at a point in major segment is $30^{\circ}$.
15. In Fig., $\angle ADC=130^{\circ}$ and chord $BC=$ chord BE. Find $\angle CBE$.
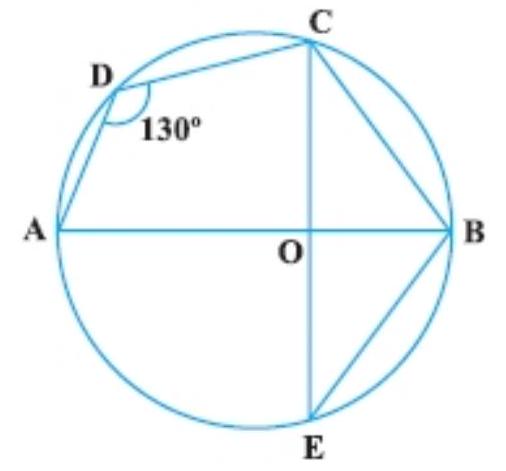
Show Answer
Solution
Given: $\angle ADC=130^{\circ}$ and chord $BC=$ chord $BE$.
Let the points $A, B, C$ and $D$ form a cyclic quadrilateral.
As, the sum of opposite angles of a cyclic quadrilateral $\triangle DCB$ is $180^{\circ}$.
$\angle ADC+\angle OBC=180^{\circ}$
$130^{\circ}+\angle OBC=180^{\circ}$
$\angle OBC=180^{\circ}-130^{\circ}=50^{\circ}$
In triangle $BOC$ and triangle $BOE$,
$BC=BE \quad$ [given equal chord]
$OC=OE \quad$ [both are the radius of the circle]
And $OB=OB$ [common side]
$\triangle BOC \cong \triangle BOE$
$\angle OBC=\angle OBE=50^{\circ}[$ by $CPCT]$
$\angle CBE=\angle CBO+\angle EBO=50^{\circ}+50^{\circ}=100^{\circ}$
Hence, the angle $\angle CBE$ is $100^{\circ}$.
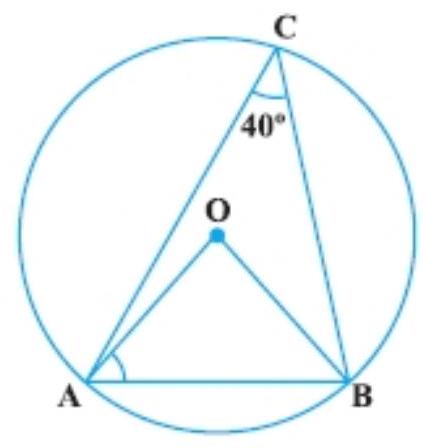
16. In Fig., $\angle ACB=40^{\circ}$. Find $\angle OAB$.
Show Answer
Solution
Given: $\angle A C B=40^{\circ}$
As we know that, a segment subtends an angle to the circle is half the angle subtends to the centre.
$\angle A O B=2 \angle A C B$
Long Answer Questions
1. If two equal chords of a circle intersect, prove that the parts of one chord are separately equal to the parts of the other chord.
Show Answer
Solution
Given: let $AB$ and $CD$ are two equal chords of a circle that are meet at point $E$.
TP prove that:
(1) $AE=CE$
(2) $\quad BE=DE$
Construction: Draw $OM \perp AB$ and $ON \perp CD$ and join $OE$ where $O$ is the center of circle.
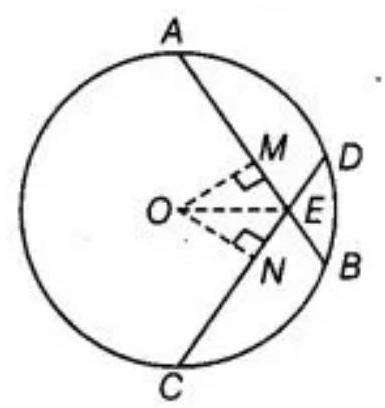
Proof: In triangle OME and triangle ONE,
$OM=ON \quad$ [Equal chords of equidistance from the centre]
$OE=OE \quad[$ Common side $]$
$\angle O M E=\angle O N E \quad[$ Each 90 ${ }^{\circ}]$
So, $\triangle O M E \cong \triangle O N E \quad$ [By RHS congruence rule]
$EM=EN \quad$[By CPCT]
$AB=CD$
Now, dividing both side by 2 in the above equation, get:
$\dfrac{A B}{2}=\dfrac{C D}{2}$
$A M=C N \quad$…(II) [ Perpendicular drawn from centre to chord bisect the chord that is AM
$=MB$ and $CN=ND]$
Now, adding equation (I) and (II), get:
$EM+AM=EN+CN$
$AE=CE \quad \ldots$ (II) $\quad[$ Prove part (1)]
$AB=CD$
Now, subtracting both sides by $AE$, get:
$AB-AE=CD-AE$
$BE=CD-CE \quad$ [From equation (II)] $BE=DE \quad[$ Prove part (2)]
Hence, proved.
2. If non-parallel sides of a trapezium are equal, prove that it is cyclic.
Show Answer
Solution
Given: $ABCD$ is a trapezium which $AD | BC$ and whose non-parallel sides $AD$ and $BC$ are equal that is $AB=DC$
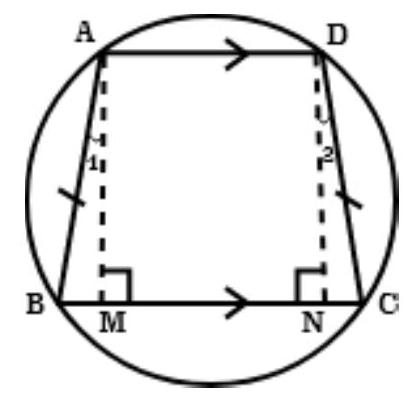
To prove that trapezium $A B C D$ is cyclic.
Construction: Draw $A M \perp B C$ and $D N \perp B C$.
Proof: In right triangle $AMB$ and $DNC$.
$\angle A M B=\angle D N C \quad[$ Each $90^{\circ}]$
$AB=DC \quad$ [Given]
$AM=DN[$ Perpendicular distance between two parallel lines are same]
$\triangle A M B \cong \triangle D N C \quad$ [By RHS congruence rule]
$\angle B=\angle C \quad$[ By CPCT]
Also, $BM=CN \quad\quad$[By CPCT]
Therefore, $\angle 1=\angle 2 \quad$ [Angles opposite to equal sides are equal]
So, $\angle B A D=\angle 1+90^{\circ}$
$\angle B A D=\angle 2+90^{\circ} \quad[\angle 1=\angle 2$ Prove above $]$
$=\angle C D A$
Now, in quadrilateral $A B C D$,
$\angle B+\angle C+\angle C D A+\angle B A D=360^{\circ}$
$\angle B+\angle C+\angle C D A+\angle B A D=360^{\circ} \quad$ [As, $\angle B=\angle C$ and $\angle C D A=\angle B A D$ prove above]
$2(\angle B+\angle C D A)=360^{\circ}$
$\angle B+\angle C D A=180^{\circ}$
As, if the same of any pair of opposite angles of a quadrilateral is $180^{\circ}$ then the quadrilateral is cyclic.
Hence, the trapezium ABCD is cyclic.
3. If $P, Q$ and $R$ are the mid-points of the sides $B C, C A$ and $A B$ of a triangle and $A D$ is the perpendicular from $A$ on $B C$, prove that $P, Q, R$ and $D$ are concyclic.
Show Answer
Solution
To prove that R, D, P and Q are concyclie.
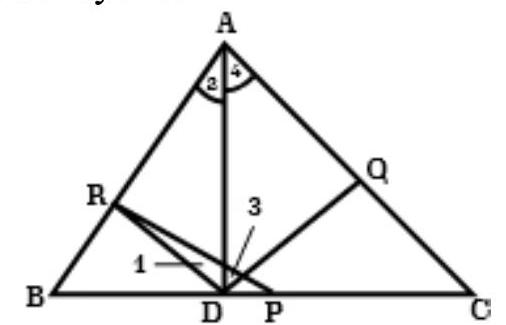
Construction: Join RD, QD, PR and PQ. So, RP join to R and P, the mid-point of AB and BC.
Proof: RP $|| AC$
Also, $PQ || AB$
[Mid-point theorem]
Now, ARPQ is a parallelogram. So,
$\angle R A Q=\angle R P Q \quad$ [opposite angles of a parallelogram]
In triangle $ABD$, angle $D$ is right angle and $DR$ is a median. So,
$RA=DR$ and $\angle 1=\angle 2$
Also, $\angle 3=\angle 4$
Now, adding equation (II) and (III), get:
$\angle 1+\angle 3=\angle 2+\angle 4$
$\angle R D Q=\angle R A Q$
$=\angle R P Q$
Hence, R, D, P and Q are concyclie.
4. $A B C D$ is a parallelogram. A circle through $A, B$ is so drawn that it intersects $A D$ at $P$ and $B C$ at $Q$. Prove that $P, Q, C$ and $D$ are concyclic.
Show Answer
Solution
Given: $ABCD$ is a parallelogram. A circle through $A, B$ is so drawn that it intersects $AD$ at $P$ and $BC$ at $Q$.
A circle through $A, B$ is so drawn that it intersects $A D$ at $P$ and $B C$ at $Q$.
Construction: Join PQ.
Proof:
$\angle 1=\angle A \quad$ [Exterior angle property of cyclic quadrilateral]
Also, $\angle A=\angle C \quad$ [Opposite angles of a parallelogram]
So, $\angle 1=\angle C$
As, $\angle C+\angle D=180^{\circ}$ [sum of cointerior angles on same side is $180^{\circ}$ ]
$\angle 1+\angle D=180^{\circ}$ [from equation (I)]
Since, the quadrilateral QCDP is cyclic.
Therefore, the points P, Q, C and D are con-cyclic.
Hence proved.
5. Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
Show Answer
Solution
Given: In triangle $A B C, 1$ is perpendicular bisector of $B C$.
To prove that angle bisector of $\angle A$ and perpendicular bisector of $BC$ intersect on the circumcircle of triangle $ABC$.
Proof: See the figure, the angle bisector of $\angle A$ intersect circumcircle of triangle $ABC$ at $D$. Join $BP$ and $CP$.
$\angle B A P=\angle B C P \quad$ [Angle in the same segment are equal] $\angle B A P=\angle B C P=\dfrac{1}{2} \angle A$ …(I) $[AP$ is bisector of $\angle A]$
Also,
$\angle P A C=\angle P B C=\dfrac{1}{2} \angle A$
Now, from equation (I) and (II), get:
$\angle B C P=\angle P B C$
$BP=CP \quad[$ If the angles subtended by two chords of a circle at the center are equal, the chords are equal]
As, $P$ is on perpendicular of $BC$.
Hence, angle bisector of $\angle A$ and perpendicular bisector of $BC$ intersect on the circumcircle of triangle $ABC$.
6. If two chords $A B$ and $C D$ of a circle $A Y D Z B W C X$ intersect at right angle (see Fig.), prove that $arc$ CXA $+arc ~D Z B=arc ~A Y D+arc ~B W C=$ semicircle.
Show Answer
Solution
Given: In the given circle AYDZBWCX, two chords $AB$ and $CD$ intersect at right angles. To prove that arc CXA $+arc DZB=arc AYD+arc BWC=$ Semi-circle.
Construction: Draw a diameter EF parallel to CD having centre M.
Proof: As, $CD || EF$
$arc EC=arc PD \ldots$ (I)
arc $ECXA=$ arc EWB [symmetrical about diameter of a circle]
$arc AF=arc BF \ldots$..(I)
Also, know that: arc ECXAYDF $=$ Semi-circle
Arc EA $+arc AF=$ Semi-circle
Arc EC $+arc CXA+arc FB=$ Semi-circle [From equation (II)]
Arc DF $+arc CXA+arc FB=$ Semi-circle [From equation (I)]
Arc DF + arc FB + arc $CXA=$ Semi-circle
Arc DZB $+arc$ CXA $=$ Semi-circle
As we know that, circle divides itself in two semi-circles, therefore the remaining portion of the circle is also equal to the semi-circle.
So, arc AYD + arc BWC $=$ Semi-circle
Hence, proved.
7. If $A B C$ is an equilateral triangle inscribed in a circle and $P$ be any point on the minor arc $B C$ which does not coincide with $B$ or $C$, prove that $P A$ is angle bisector of $\angle BPC$.
Show Answer
Solution
Given $\triangle ABC$ is an equilateral triangle inscribed in a circle and $P$ be any point on the minor arc $BC$ which does not coincide with $B$ or $C$.
To prove that PA is an angle bisector of $\angle BPC$.
Construction: Join PB and PC.
Proof: $ABC$ is an equilateral triangle. So,
$\angle 3=\angle 4=60^{\circ}$
And, $\angle 1=\angle 4=60^{\circ} \quad$ [Angle in the same segment AB]
Now, $\angle 2=\angle 3=60^{\circ}$ [Angle in the same segment AC]
Also, $\angle 1=\angle 2=60^{\circ}$
Therefore, PA is the bisector of triangle BPC.
Hence, prove.
8. In Fig., $A B$ and $C D$ are two chords of a circle intersecting each other at point E. Prove that
$\angle AEC=\dfrac{1}{2}(\begin{matrix} \text{ Angle subtended by arc CXA at centre } \\ + \text{ angle subtended by arc DYB at the centre }\end{matrix} )$
Show Answer
Solution
Given: $AB$ and $CD$ are two chords of a circle intersecting each other at point $E$.
To prove that $\angle A E C=\dfrac{1}{2} \quad$ [Angles subtended by an arc CXA at the centre + angle subtended by arc DYB at the centre]
Construction: Join $AC, BC$ and $BD$.
As we known that, the angles subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle, now arc CXA subtends $\angle A O C$ at the centre and $\angle A B C$ at the remaining part of the circle. So,
$\angle A O C=2 \angle A B C$
Also, $\angle B O D=\angle B C D$
Now, adding equation (I) and (II), get:
$\angle A O C+\angle B O D=2(\angle A B C+\angle B C D)$
As, exterior angle of a triangle is equal to the sum of interior opposite angles. So, in triangle CEB:
$\angle A E C=\angle A B C+\angle B C D$
Now, from equation (III) and (IV), get:
$\angle A O C+\angle B O D=2 \angle A E C$
$\angle A E C=\dfrac{1}{2}(\angle A O C+\angle B O D)$
or
$\angle A E C=\dfrac{1}{2}$ (Angle subtended by an arc CXA at the centre + angle subtended by an arc DYB at the centre)
Hence, proved.
9. If bisectors of opposite angles of a cyclic quadrilateral $A B C D$ intersect the circle, circumscribing it at the points $P$ and $Q$, prove that $P Q$ is a diameter of the circle.
Show Answer
Solution
Given: $ABCD$ is a cyclic quadrilateral.
$DP$ and $QB$ are the bisectors of $\angle D$ and $\angle B$, respectively.
To prove that $PQ$ is the diameter of a circle.
Construction: Join QD and QC.
Proof: As, $ABCD$ is a cyclic quadrilateral. So,
$\angle C D A+\angle C B A=180^{\circ} \quad$ [Sum of opposite angles of cyclic quadrilateral is $180^{\circ}$ ]
Now, dividing the above equation by 2 , get:
$\dfrac{1}{2} \angle C D A+\dfrac{1}{2} \angle C B A=\dfrac{1}{2} \times 180^{\circ}$ $\angle 1+\angle 2=90^{\circ}$
[As, $\angle 1=\dfrac{1}{2} \angle C D A$ and $\angle 2=\dfrac{1}{2} \angle C B A$ ]
$\angle 2=\angle 3 \quad$ [Angles in the same augment $QC$ are equal]
$\angle 1+\angle 3=90^{\circ}$
Now, from equation (I) and (II), get:
$\angle P D Q=90^{\circ}$
Hence, PQ is a diameter of a circle, because diameter of the circle.
10. A circle has radius $\sqrt{2} ~cm$. It is divided into two segments by a chord of length $2 ~cm$. Prove that the angle subtended by the chord at a point in major segment is $45^{\circ}$.
Show Answer
Solution
Draw a circle having centre $O$ and radius $\sqrt{2} ~cm$. let chord $BC, 2 ~cm$ long divides the circle into two segments. And $\angle B A C$ lies in the major segment.
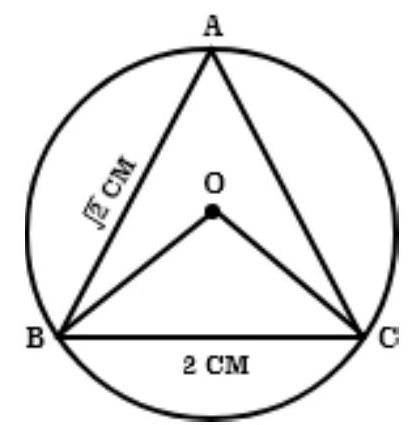
To prove that $\angle B A C=50^{\circ}$
Construction: Join OB and OC.
$B C^{2}=(2)^{2}=4=2+2=(\sqrt{2})^{2}+(\sqrt{2})^{2}$
$B C^{2}=O B^{2}+O C^{2}$
In triangle $BOC$, get:
$B C^{2}=O B^{2}+O C^{2}$
So, $\angle B O C=90^{\circ} \quad$ [By converse of Pythagoras theorem]
Since, arc Bc subtends $\angle B O C$ at the centre $O$ and $\angle B A C$ at the remaining part of the circle. So,
$ \begin{aligned} \angle B A C & =\dfrac{1}{2} \angle B O C \\ & =\dfrac{1}{2} \times 90^{\circ} \\ & =45^{\circ} \end{aligned} $
Hence, proved.
11. Two equal chords $A B$ and $C D$ of a circle when produced intersect at a point $P$. Prove that $P B=P D$.
Show Answer
Solution
Given: Two equal chords $AB$ and $CD$ of a circle when produced intersect at a point $P$.
To prove that $PB=PD$.
Construction: Join $OP$ and draw $OL \perp AB$ and $OM \perp CD$.
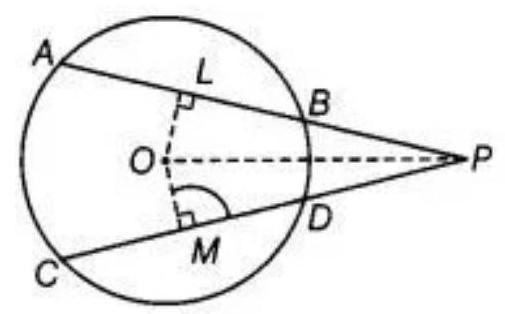
Proof: $AB=CD$
$OL=OM \quad$ [Equal chords are equidistance from the centre]
In triangle OLP and triangle OMP,
$OL=OM \quad$ [above prove]
$\angle O L P=\angle O M P \quad[$ Each 90]
$OP=OP \quad[$ Common side $]$
So, $\triangle O L P \cong \triangle O M P \quad[$ By RHS congruence rule $]$
$LP=MP \quad[By \mathrm{CPCT]}$…
$As, AB=CD$
Now, dividing both side by 2 in the above equation, get:
$\dfrac{1}{2} A B=\dfrac{1}{2} C D$
$BL=DM \quad[$ Perpendicular distance from centre to the circle bisectors the chord that is $AL$ $=LB$ and $~CM=MD]$
Now, subtracting equation (II) from equation (I), get:
$LP-BL=MP-DM$
Or PB $=PD$
Hence, proved.
12. $A B$ and $A C$ are two chords of a circle of radius $r$ such that $A B=2 A C$. If $p$ and $q$ are the distances of $AB$ and $AC$ from the centre, prove that $4 q^{2}=p^{2}+3 r^{2}$.
Show Answer
Solution
Given: In a circle of radius $r$, there are two chords $Ab$ and $AC$ sch that $AB=2 AC$. Also, the distance of $AB$ and $AC$ from the centre are $P$ and $q$, respectively.
To prove that $4 q^{2}=p^{2}+3 r^{2}$
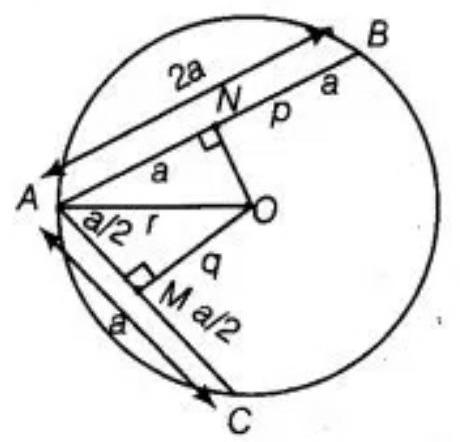
Proof: Suppose $AC=a$, then $AB=2 a$
At centre $O$, perpendicular is drawn to the chords $AC$ and $AB$ at $M$ and $N$, respectively.
$AM=MC=\dfrac{a}{2}$
$AN=NB=a$
In triangle OAM, $A O^{2}=A M^{2}+M O^{2}$ [By Pythagoras theorem] $A O^{2}=(\dfrac{a}{2})^{2}+q^{2}$
In triangle OAN, using Pythagoras throrem:
$ \begin{aligned} & A O^{2}=(A N)^{2}+(N O)^{2} \\ & A O^{2}=(a)^{2}+(p)^{2} \end{aligned} $
From equation (I) and (II), get:
$ \begin{aligned} (\dfrac{a}{2})^{2}+q^{2} & =a^{2}+p^{2} \\ \dfrac{a^{2}}{4}+q^{2} & =a^{2}+p^{2} \\ a^{2}+4 q^{2} & =4 a^{2}+4 p^{2} \\ 4 q^{2} & =3 a^{2}+4 p^{2} \\ 4 q^{2} & =p^{2}+3(a^{2}+p^{2}) \end{aligned} $
$4 q^{2}=p^{2}+3 r^{2} \quad[.$ In right angled triangle OAN, $.r^{2}=a^{2}+p^{2}]$
Hence, proved.
13. In Fig., $O$ is the centre of the circle, $\angle B C O=30^{\circ}$. Find $x$ and $y$.
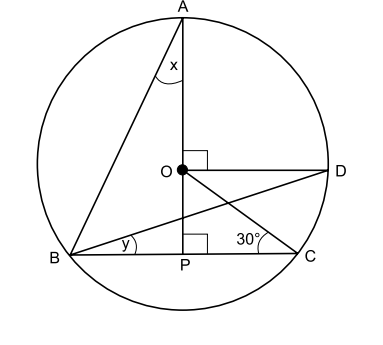
Show Answer
Solution
$\mathrm{O}$ is the centre of the circle and $\angle \mathrm{BCO}=30^{\circ}$. We have to find the values of $x$ and $y$.
In right $\triangle \mathrm{OCP}$, we have
$$ \begin{array}{rlr} \angle \mathrm{POC} & =180^{\circ}-(\angle \mathrm{OPC}+\angle \mathrm{PCO}) \\ \Rightarrow \quad \angle \mathrm{POC} & =180^{\circ}-\left(90^{\circ}+30^{\circ}\right)=60^{\circ} \\ \text { Now, } \quad \angle \mathrm{AOD} & =90^{\circ} \quad \text { [Given] } \\ \angle \mathrm{AOD}+\angle \mathrm{DOP} & =180^{\circ} \quad \\ \therefore \quad & \angle \mathrm{DOP} =180^{\circ}-\angle \mathrm{AOD}\quad \text{[Angles of a linear pair]} \\ &=180^{\circ}-90^{\circ}=90^{\circ} \end{array} $$
Now, $\quad \angle \mathrm{COD}=90^{\circ}-\angle \mathrm{POC}=90^{\circ}-60^{\circ}=30^{\circ}$
Since the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle,
$$ \begin{aligned} & \angle \mathrm{CBD}=\dfrac{1}{2} \angle \mathrm{COD} \Rightarrow y=\dfrac{1}{2} \times 30^{\circ}=15^{\circ} \\ \text{Also,} \quad & \angle \mathrm{ABD}=\dfrac{1}{2} \angle \mathrm{AOD}=\dfrac{1}{2} \times 90^{\circ}=45^{\circ} \end{aligned} $$
Now, in $\triangle \mathrm{ABP}$, we have $x+\left(45^{\circ}+y\right)+90^{\circ}=180^{\circ}$ $$ \begin{aligned} \Rightarrow & x+45^{\circ}+15^{\circ}+90^{\circ} =180^{\circ} \\ \Rightarrow & x =180^{\circ}-150^{\circ}=30^{\circ} \end{aligned} $$
Hence, $x=30^{\circ}$ and $y=15^{\circ}$.
14. In the given figure, $O$ is the centre of the circle, $BD = OD$ and $CD \perp AB$. Find $\angle CAB$ .
Show Answer
Solution
In $\triangle ODB,$ we have
$BD=OD \quad \text{[Given]}$
$\therefore \quad \angle DOB=\angle DBO \quad \text{[$\because$ Angles opp. to equal sides of triangle are equal]}$
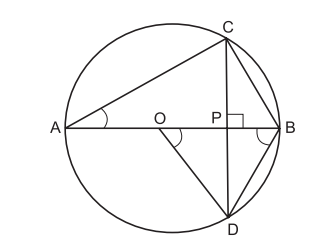
In $\triangle ODP$ and $\triangle BDP,$ we have
$\angle DOP=\angle DBP \quad \text{[$\because \angle DOB=\angle DBO $(Proved above)]}$
$\angle DPO=\angle DPB \quad \text{[Each=$90^{\circ}$]}$
$OD=BD \quad \text{[Given]}$
$\therefore$ $\Delta \mathrm{ODP} \cong \Delta \mathrm{BDP}\quad$ [By AAS congruence rule]
$\therefore$ $\angle \mathrm{ODP}=\angle \mathrm{BDP}\quad$ $\ldots(1)[\mathrm{CPCT}]$
Now, $\quad \mathrm{OD}=\mathrm{OB}\quad$ [Radii of the same circle]
and $\quad \mathrm{OD}=\mathrm{BD}\quad$ [Given]
$\therefore$ $\mathrm{OB}=\mathrm{OD}=\mathrm{BD}, \mathrm{so}$ $\triangle OBD$ is equilateral.
$\therefore \angle \mathrm{ODB}=60^{\circ}\quad$ $[\because$ Each ar }e of an equilateral triangle is $60^{\circ}$ ]
Now, $\angle \mathrm{BDP}=\dfrac{1}{2} \angle \mathrm{ODB}\quad$ [From(1)]
$\angle \mathrm{BDP}=\dfrac{1}{2} \times 60^{\circ}=30^{\circ}$ $\angle CDB=30^{\circ}$
Since angles in the same segment of a circle are equal, so we have
$$ \text{So,} \quad \angle \mathrm{CAB}=\angle \mathrm{CDB}=30^{\circ} $$










