Number Systems
Multiple Choice Questions(MCQs)
1. Every rational number is
(A) a natural number
(B) an integer
(C) a real number
(D) a whole number
Show Answer
Solution
We know that every real number is either an irrational number or rational number. Therefore, every rational number is a real number.
Hence, the correct option is (C).
2. Between two rational numbers
(A) there is no rational number
(B) there is exactly one rational number
(C) there are infinitely many rational numbers
(D) there are only rational numbers and no irrational numbers
Show Answer
Solution
Between two rational numbers there are infinitely many rational numbers.
Hence, the correct option is (C).
3. Decimal representation of a rational number cannot be
(A) terminating
(B) non-terminating
(C) non-terminating repeating
(D) non-terminating non-repeating
Show Answer
Solution
We know that, the decimal representation of a rational number cannot be non-terminating and non-repeating.
Hence, the correct option is (D).
4. The product of any two irrational numbers is
(A) always an irrational number
(B) always a rational number
(C) always an integer
(D) sometimes rational, sometimes irrational
Show Answer
Solution
We know that, the product of any two irrational numbers is sometimes rational and sometimes irrational.
Hence, the correct option is (D).
5. The decimal expansion of the number $\sqrt{2}$ is
(A) a finite decimal
(B) ${1 . 4 1 4 2 1}$
(C) non-terminating recurring
(D) non-terminating non-recurring
Show Answer
Solution
The decimal expansion of the number $\sqrt{2}$ is $1.41421 \ldots$, which is non-terminating and nonrecurring.
Hence, the correct option is (B).
6. Which of the following is irrational?
(A) $\sqrt{\dfrac{4}{9}}$
(B) $\dfrac{\sqrt{12}}{\sqrt{3}}$
(C) $\sqrt{7}$
(D) $\sqrt{81}$
Show Answer
Solution
(A) $\sqrt{\dfrac{4}{9}}=\dfrac{2}{3}$, Which is rational number.
(B) $\dfrac{\sqrt{12}}{\sqrt{3}}=\dfrac{\sqrt{4 \times 3}}{\sqrt{3}}=\dfrac{2 \sqrt{3}}{\sqrt{3}}=2$, Which is rational number.
(C) $\sqrt{7}$ is a irrational number.
(D) $\sqrt{81}=\sqrt{9^{2}}=9$, which is a rational number.
Hence, the correct option is (C).
7. Which of the following is irrational?
(A) 0.14
(B) $0.14 \overline{16}$
(C) $0 . \overline{1416}$
(D) $0.4014001400014 \ldots$
Show Answer
Solution
(A) 0.14 is a terminating decimal. Hence, it can’t be an irrational number.
(B) $0.14 \overline{16}$ is a non-terminating and recurring decimal. Hence, it can’t be an irrational number.
(C) $0 . \overline{1416}$ is a non-terminating and recurring decimal. Hence, it can’t be an irrational number.
(D) $0.4014001400014 \ldots$ is a non-terminating and non-recurring decimal. Hence, it is an irrational number.
Hence, the correct option is (D).
8. A rational number between 2 and 3 is
(A) $\dfrac{\sqrt{2}+\sqrt{3}}{2}$
(B) $\dfrac{\sqrt{2} \cdot \sqrt{3}}{2}$
(C) 1.5
(D) 1.8
Show Answer
Solution
We know that,
$\sqrt{2}=1.4142135$ and $\sqrt{3}=1.732050807$
5 is a rational number which lies between $\sqrt{2}=1.4142135$ and $\sqrt{3}=1.732050807$.
Hence, the correct option is (C).
9. The value of $1.999 . .$. in the form,$\dfrac{p}{q}$ where $\boldsymbol{{}p}$ and $\boldsymbol{{}q}$ are integers and $\boldsymbol{{}q} \neq 0$ , is
(A) $\dfrac{19}{10}$
(B) $\dfrac{1999}{1000}$
(C) 2
(D) $\dfrac{1}{9}$
Show Answer
Solution
Let $x=1.999 \ldots=1 . \overline{9} \quad \ldots$ (I)
Then, $10 x=19.999 \ldots=19 . \overline{9}$
Subtracting (I) and (II), get:
$9 x=18$
$x=2$
Therefore, the value of $1.999 \ldots$ in the form $\dfrac{p}{q}$ is 2 or $\dfrac{2}{1}$.
Hence, the correct option is (C).
10. $2 \sqrt{ } 3+\sqrt{ } 3$ is equal to
(A) $2 \sqrt{ } 6$
(B) 6
(C) $3 \sqrt{ } 3$
(D) $4 \sqrt{ } 6$
Show Answer
Solution
$2 \sqrt{3}+\sqrt{3}=3 \sqrt{3}$
Hence, the correct option is (C).
11. $\sqrt{10} \times \sqrt{15}$ is equal to
(A) $6 \sqrt{5}$
(B) $5 \sqrt{6}$
(C) $\sqrt{25}$
(D) $10 \sqrt{5}$
Show Answer
Solution
$\sqrt{10} \times \sqrt{15}=\sqrt{5 \times 2 \times 5 \times 3}=5 \sqrt{6}$
Hence, the correct option is (B).
12. The number obtained on rationalising the denominator of $\dfrac{1}{\sqrt{7}-2}$ is
(A) $\dfrac{\sqrt{7}+2}{3}$
(B) $\dfrac{\sqrt{7}-2}{3}$
(C) $\dfrac{\sqrt{7}+2}{5}$
(D) $\dfrac{\sqrt{7}+2}{45}$
Show Answer
Solution
Rationalizing the denominator as follows:
$ \begin{aligned} \dfrac{1}{\sqrt{7}-2} & =\dfrac{1}{\sqrt{7}-2} \times \dfrac{\sqrt{7}+2}{\sqrt{7}+2} \\ & =\dfrac{\sqrt{7}+2}{(\sqrt{7})^{2}-2^{2}} \\ & =\dfrac{\sqrt{7}+2}{7-4} \\ & =\dfrac{\sqrt{7}+2}{3} \end{aligned} $
Hence, the correct option is (A).
13. $\dfrac{1}{\sqrt{9}-\sqrt{8}}$ is equal to
(A) $\dfrac{1}{2}(3-2 \sqrt{2})$
(B) $\dfrac{1}{3+2 \sqrt{2}}$
(C) $3-2 \sqrt{2}$
(D) $3+2 \sqrt{2}$
Show Answer
Solution
$ \begin{aligned} \dfrac{1}{\sqrt{9}-\sqrt{8}} & =\dfrac{1}{\sqrt{9}-\sqrt{8}} \times \dfrac{\sqrt{9}+\sqrt{8}}{\sqrt{9}+\sqrt{8}} \\ & =\dfrac{\sqrt{9}+\sqrt{8}}{(\sqrt{9})^{2}-(\sqrt{8})^{2}} \\ & =\dfrac{\sqrt{3^{2}}+\sqrt{2^{3}}}{9-8} \\ & =3+2 \sqrt{2} \end{aligned} $
Hence, the correct option is (D).
14. After rationalizing the denominator of $\dfrac{7}{3 \sqrt{3}-2 \sqrt{2}}$, we get the denominator as
(A) 13
(B) 19
(C) 5
(D) 35
Show Answer
Solution
$ \begin{aligned} \dfrac{7}{3 \sqrt{3}-2 \sqrt{2}} & =\dfrac{7}{3 \sqrt{3}-2 \sqrt{2}} \times \dfrac{3 \sqrt{3}+2 \sqrt{2}}{3 \sqrt{3}+2 \sqrt{2}} \\ & =\dfrac{7(3 \sqrt{3}+2 \sqrt{2})}{(3 \sqrt{3})^{2}-(2 \sqrt{2})^{2}} \\ & =\dfrac{7(3 \sqrt{3}+2 \sqrt{2})}{27-8} \\ & =\dfrac{7(3 \sqrt{3}+2 \sqrt{2})}{19} \end{aligned} $
Hence, the correct option is (B).
15. The value of $\dfrac{\sqrt{32}+\sqrt{48}}{\sqrt{8}+\sqrt{12}}$ is equal to
(A) $\sqrt{2}$
(B) 2
(C) 4
(D) 8
Show Answer
Solution
$ \begin{aligned} \dfrac{\sqrt{32}+\sqrt{48}}{\sqrt{8}+\sqrt{12}} & =\dfrac{\sqrt{16 \times 2}+\sqrt{16 \times 3}}{\sqrt{4 \times 2}+\sqrt{4 \times 3}} \\ & =\dfrac{4 \sqrt{2}+4 \sqrt{3}}{2 \sqrt{2}+2 \sqrt{3}} \\ & =\dfrac{4(\sqrt{2}+\sqrt{3})}{2(\sqrt{2}+\sqrt{3})} \\ & =2 \end{aligned} $
Hence, the correct option is (B).
16. If $\sqrt{2}=1.4142$, then $\sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}$ is equal to
(A) 2.4142
(B) 5.8282
(C) 0.4142
(D) 0.1718
Show Answer
Solution
$ \begin{aligned} \sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}} & =\sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1} \times \dfrac{\sqrt{2}-1}{\sqrt{2}-1}} \\ & =\sqrt{\dfrac{(\sqrt{2}-1)^{2}}{(\sqrt{2})^{2}-1^{2}}} \\ & =\sqrt{\dfrac{(\sqrt{2}-1)^{2}}{2-1}} \\ & =\sqrt{\dfrac{(\sqrt{2}-1)^{2}}{1}} \\ & =1.4142-1 \\ & =0.4142 \end{aligned} $
Hence, the correct option is (C).
17. $\sqrt[4]{\sqrt[3]{2^{2}}}$ equals
(A) $2^{-\dfrac{1}{6}}$
(B) $2^{-6}$
(C) $2^{\dfrac{1}{6}}$
(D) $2^{6}$
Show Answer
Solution
$ \begin{aligned} \sqrt[4]{\sqrt[3]{2^{2}}} & =\sqrt[4]{(2^{2})^{\dfrac{1}{3}}} \\ & =(2^{\dfrac{2}{3}})^{\dfrac{1}{4}} \\ & =2^{\dfrac{2}{3^{3}} \dfrac{1}{4}} \\ & =2^{\dfrac{1}{6}} \end{aligned} $
Hence, the correct option is (C).
18. The product $\sqrt[3]{2} \cdot \sqrt[4]{2} \cdot \sqrt[12]{32}$ equals
(A) $\sqrt{2}$
(B) 2
(C) $\sqrt[12]{2}$
(D) $\sqrt[12]{32}$
Show Answer
Solution
$ \begin{aligned} \sqrt[3]{2} \cdot \sqrt[4]{2} \cdot \sqrt[12]{32} & =2^{\dfrac{1}{2}} \times 2^{\dfrac{1}{4}} \times(2^{5})^{\dfrac{1}{12}} \\ & =2^{\dfrac{1}{3}} \times 2^{\dfrac{1}{4}} \times 2^{\dfrac{5}{12}} \\ & =2^{\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{5}{12}} \\ & =2^{\dfrac{4+3+5}{12}} \\ & =2^{\dfrac{12}{12}} \\ & =2 \end{aligned} $
Hence, the correct option is (B).
19. Value of $\sqrt[4]{(81)^{-2}}$ is
(A) $\dfrac{1}{9}$
(B) $\dfrac{1}{3}$
(C) 9
(D) $\dfrac{1}{81}$
Show Answer
Solution
$ \begin{aligned} \sqrt[4]{(81)^{-2}} & =\sqrt[4]{(\dfrac{1}{81})^{2}} \\ & =(\dfrac{1}{81})^{2 \times \dfrac{1}{4}} \\ & =(\dfrac{1}{81})^{\dfrac{1}{2}} \\ & =\dfrac{1}{9} \end{aligned} $
Hence, the correct option is (A).
20. Value of $(256)^{0.16} \times(256)^{0.09}$ is
(A) 4
(B) 16
(C) 64
(D) 256.25
Show Answer
Solution
$ \begin{aligned} (256)^{0.16} \times(256)^{0.09} & =(256)^{0.16+0.09} \\ & =256^{0.25} 1 \\ & =256^{\dfrac{1}{4}} \\ & =4^{4 \times \dfrac{1}{4}} \\ & =4 \end{aligned} $
Hence, the correct option is (A).
21. Which of the following is equal to $x$ ?
(A) $x^{\dfrac{12}{7}}-x^{\dfrac{5}{7}}$
(B) $\sqrt[12]{(x^{4})^{\dfrac{1}{3}}}$
(C) $(\sqrt{x^{3}})^{\dfrac{2}{3}}$
(D) $x^{\dfrac{12}{7}} \times x^{\dfrac{7}{12}}$
Show Answer
Solution
(A) $x^{\dfrac{12}{7}}-x^{\dfrac{5}{7}} \neq x$
(B)
$ \begin{aligned} \sqrt[12]{(x^{4})^{\dfrac{1}{3}}} & =\sqrt[12]{x^{\dfrac{4}{3}}} \\ & =(x^{\dfrac{4}{3}})^{\dfrac{1}{12}} \\ & =x^{\dfrac{4}{3} \times \dfrac{1}{12}} \\ & =x^{\dfrac{1}{9}} \neq x \end{aligned} $
(C) $(\sqrt{x^{3}})^{\dfrac{2}{3}}=x^{\dfrac{3}{2} \times \dfrac{2}{3}}=x$
(D) $x^{\dfrac{12}{7}} \times x^{\dfrac{7}{12}}=x^{\dfrac{12}{7}+\dfrac{7}{12}}=x^{\dfrac{193}{84}} \neq x$
Hence, the correct option is (C).
Short Answer Questions with Reasoning
1. Let $x$ and $y$ be rational and irrational numbers, respectively. Is $x+y$ necessarily an irrational number? Give an example in support of your answer.
Show Answer
Solution
True, $x+y$ is necessary an irrational number.
Let $x=6$ and $\sqrt{3}$.
Now, $x+y=6+\sqrt{3}=6+1.732 \ldots$ which is non-terminating and non-repeating.
Therefore, $x+y$ is an irrational number.
2. Let $x$ be rational and $y$ be irrational. Is $x y$ necessarily irrational? Justify your answer by an example.
Show Answer
Solution
Let $x=0$ is a rational number and $y=\sqrt{3}$ is a irrational number. $x y=0 \times \sqrt{3}=0$ Which is an irrational number.
Therefore, $x y$ is not necessarily an irrational number.
3. State whether the following statements are true or false? Justify your answer.
(i) $\dfrac{\sqrt{2}}{3}$ is a rational number.
(ii) There are infinitely many integers between any two integers.
(iii) Number of rational numbers between 15 and 18 is finite.
(iv) There are numbers which cannot be written in the form $\dfrac{p}{q}, q \neq 0, p, q$ both are integers.
(v) The square of an irrational number is always rational.
(vi) $\dfrac{\sqrt{12}}{\sqrt{3}}$ is not a rational number as $\sqrt{12}$ and $\sqrt{3}$ are not integers. (vii) $\dfrac{\sqrt{15}}{\sqrt{3}}$ is written in the form $\dfrac{p}{q}, q \neq 0$ and so it is a rational number.
Show Answer
Solution
(i) $\dfrac{\sqrt{2}}{3}$ is a rational number.
(ii) We know that, in between two integer there are infinitely many integer.
(iii) Rational number between 15 and 18 is finite.
(iv) There are number which can be written in the form $\dfrac{p}{q}, q \neq 0, p, q$ both are not integers.
(v) The square of an irrational number is always rational.
(vi) $\dfrac{\sqrt{12}}{\sqrt{3}}$ cab not be a rational number as $\sqrt{12}$ and $\sqrt{3}$ are not integers.
(vii) $\dfrac{\sqrt{15}}{\sqrt{3}}$ can be written in the form $\dfrac{p}{q}$, where $q \neq 0$ so it a rational number.
4. Classify the following numbers as rational or irrational with justification:
(i) $\sqrt{196}$
(ii) $3 \sqrt{18}$
(iii) $\sqrt{\dfrac{9}{27}}$
(iv) $\dfrac{\sqrt{28}}{\sqrt{343}}$
(v) $-\sqrt{0.4}$
(vi) $\dfrac{\sqrt{12}}{\sqrt{75}}$
(vii) 0.5918
(viii) $(1+\sqrt{5})-(4+\sqrt{5})$
(ix) 10.124124
(x) $1.010010001 \ldots$
Show Answer
Solution
(i) $\sqrt{196}=\sqrt{14^{2}}=14$, which is a rational number.
(ii) $3 \sqrt{18}=9 \sqrt{2}$, which is an irrational number.
(iii) $\sqrt{\dfrac{9}{27}}=\dfrac{1}{\sqrt{3}}$, which is an irrational number.
(iv) $\dfrac{\sqrt{28}}{\sqrt{343}}=\dfrac{\sqrt{4}}{\sqrt{49}}=\dfrac{2}{7}$, which is a rational number.
(v) $-\sqrt{0.4}=-\dfrac{2}{\sqrt{10}}$, which is an irrational number.
(vi) $\dfrac{\sqrt{12}}{\sqrt{75}}=\sqrt{\dfrac{4}{25}}=\dfrac{2}{5}$, which is a rational number.
(vii) 0.5918 is terminating decimal, Therefore, it is a rational number.
(viii) $(1+\sqrt{5})-(4+\sqrt{5})=-3$, which is a rational number.
(ix) $10.124124 \ldots$ is a decimal expansion which is non-terminating but recurring. Hence, it is a rational number.
(x) $1.010010001 \ldots$ is a decimal expansion which is non-terminating but recurring. Hence, it is a rational number.
Short Answer Questions
1. Find which of the variables $x, y, z$ and $u$ represent rational numbers and which irrational numbers:
(i) $x^{2}=5$
(ii) $y^{2}=9$
(iii) $z^{2}=0.04$
(iv) $u^{2}=\dfrac{17}{4}$
Show Answer
Solution
(i)
(ii)
$ \begin{aligned} & x^{2}=5 \\ & x= \pm \sqrt{5} \end{aligned} $
Which is an irrational number.
$y^{2}=9$
$y=\sqrt{9}$
$y= \pm 3$
Which is a rational number.
(iii)
$ \begin{aligned} & z^{2}=0.04 \\ & z= \pm \sqrt{0.04} \\ & z= \pm 0.2 \end{aligned} $
Which is a rational number.
(iv)
$u^{2}=\dfrac{17}{4}$
$u= \pm \sqrt{\dfrac{17}{4}}$
$u= \pm \dfrac{\sqrt{17}}{2}$
Where, $\sqrt{17}$ is not an integer. Which is an irrational number.
2. Find three rational numbers between
(i) -1 and -2
(ii) 0.1 and 0.11
(iii) $\dfrac{5}{7}$ and $\dfrac{6}{7}$
(iv) $\dfrac{1}{4}$ and $\dfrac{1}{5}$
Show Answer
Solution
(i) $-1.1,-1,2$ and $-1,3$ are three rational numbers, which are lying between -1 and -2 .
(ii) $0.101,0,102,0.103$ are three rational number which are lying between 0.1 and 0.11 .
(iii) $\dfrac{5}{7}=\dfrac{5}{7} \times \dfrac{10}{10}=\dfrac{50}{70}$ and $\dfrac{6}{7}=\dfrac{6}{7} \times \dfrac{10}{10}=\dfrac{60}{70}$
$\dfrac{51}{70}, \dfrac{52}{70}, \dfrac{53}{70}$ are three rational numbers lying between $\dfrac{50}{70}$ and $\dfrac{60}{70}$. It mean that lying
between $\dfrac{5}{7}$ and $\dfrac{6}{7}$.
(iv)
$\dfrac{1}{4}=\dfrac{1}{4} \times \dfrac{20}{20}=\dfrac{20}{80}$ and $\dfrac{1}{5}=\dfrac{1}{5} \times \dfrac{16}{16}=\dfrac{16}{80}$
Now, $\sqrt{2} \times \sqrt{3} \times \dfrac{18}{80}(=\dfrac{9}{10}), \dfrac{19}{80}$ are three rational numbers lying between $\dfrac{1}{4}$ and $\dfrac{1}{5}$.
3. Insert a rational number and an irrational number between the following:
(i) 2 and 3
(ii) 0 and 0.1
(iii) $\dfrac{1}{3}$ and $\dfrac{1}{2}$
(iv) $\dfrac{-2}{5}$ and $\dfrac{1}{2}$
(v) 0.15 and 0.16
(vi) $\sqrt{2}$ and $\sqrt{3}$
(vii) 2.357 and 3.121
(viii) .0001 and .001
(ix) 3.623623 and 0.484848
Show Answer
Solution
(i) A rational number between 2 and 3 is: $\dfrac{2+3}{2}=\dfrac{5}{2}=2.5$
(ii) 0.04 is rational number which lies between 0 and 0.1 .
(iii)
$\dfrac{1}{3}=\dfrac{1}{3} \times \dfrac{4}{4}=\dfrac{4}{12}$ and $\dfrac{1}{2}=\dfrac{1}{2} \times \dfrac{6}{6}=\dfrac{6}{12}$
$\dfrac{5}{12}$ is a rational number between $\dfrac{4}{12}$ and $\dfrac{6}{12}$. Which is also lying between $\dfrac{1}{3}$ and $\dfrac{1}{2}$.
Now, $\dfrac{1}{3}=0.33333$ and $\dfrac{1}{2}=0.5$.
Now, $0.414114111 \ldots$ is a non-terminating and non-recurring decimal.
Hence, $0.414114111 \ldots$ is an irrational number lying between $\dfrac{1}{3}$ and $\dfrac{1}{2}$.
(iv) $\dfrac{-2}{5}=-0.4$ and $\dfrac{1}{2}=0.5$
0 is rational number between -0.4 and 0.5 i.e., 0 is a rational number between $\dfrac{-2}{5}$ and $\dfrac{1}{2}$
Again, $0.131131113 \ldots$ is a non-terminating and non-recurring decimal which lies between -0.4 and 0.5 .
Hence, $0.131131113 \ldots$ is an irrational number lying between $\dfrac{-2}{5}$ and $\dfrac{1}{2}$.
(v) 0.151 is a rational number between 0.15 and 0.16 . Similarly, $0.153,0.157$, etc, are rational number lying between 0.15 and 0.16 .
0.151151115 is an irrational number between 0.15 and 0.16 .
(vi) $\sqrt{2}=1.4142135 \ldots$ and $\sqrt{3}=1.732050807$
Now, 1.5 which lies between $1.4142135 \ldots$ and $1.732050807 \ldots$
Since, 1.5 is a rational number between $\sqrt{2}$ and $\sqrt{3}$.
Now, $1.5755755557 \ldots$ is an irrational number lying between $\sqrt{2}$ and $\sqrt{3}$.
(vii) 3 is a rational number between 2.357 and 3.121 .
Again, 3.101101110 is an irrational number between 2.357 and 3.121.
(viii) 0.00011 is a rational number between 0.0001 and 0.001
Again, 0.0001131331333 is an irrational number between 0.0001 and 0.001 . (ix) 1 is a rational number between 0.484848 and 3.623623 .
Again, $1.909009000 \ldots$ is an irrational number lying between 0.484848 and 3.623623 .
(x) $\quad 6.3753$ is an rational number between 6.375289 and 6.375738 .
Again, $6.37541411411 \ldots$ is an irrational number lying between 6.375289 and 6.375738 .
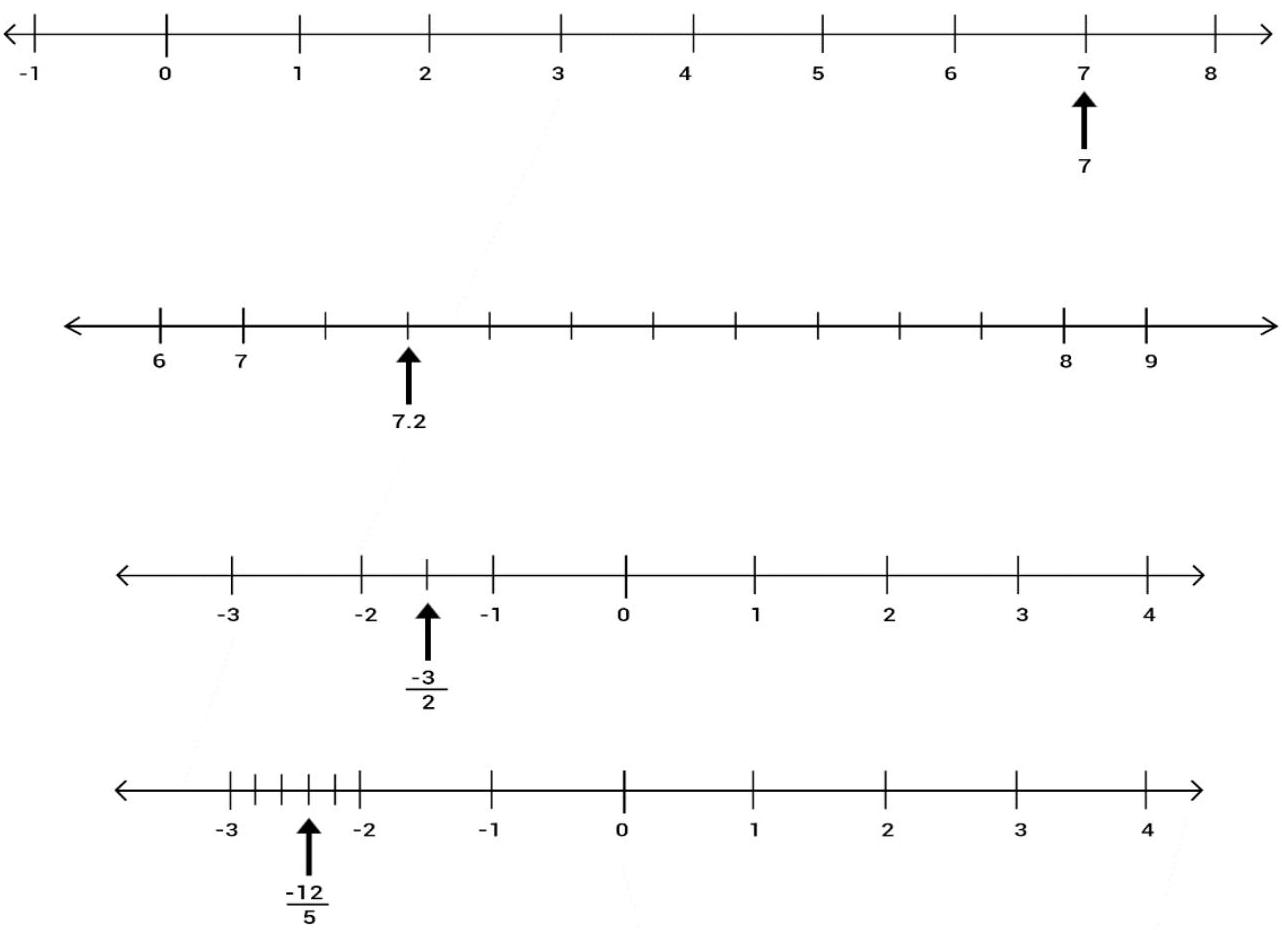
4. Represent geometrically the following numbers on the number line:
$7,7.2, \dfrac{-3}{2}, \dfrac{-12}{5}$
Show Answer
Solution
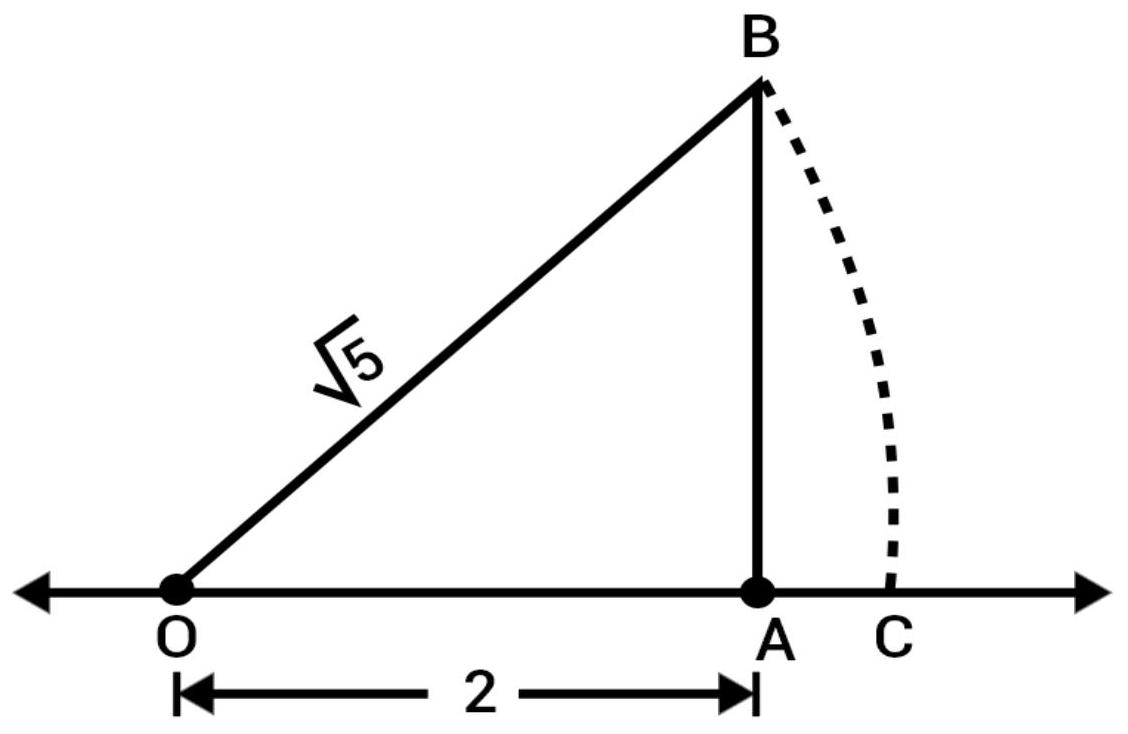
5. Locate $\sqrt{5}, \sqrt{10}$ and $\sqrt{17}$ on the number line.
Show Answer
Solution
Presentation of $\sqrt{5}$ on number line:
We can write 5 as the sum of the square of two natural numbers:
$5=1+4$
$=1^{2}+2^{2}$
On the number line, take $OA=2$ units.
Draw $BA=1$ unit, perpendicular to $OA$ join $OB$.
By Pythagoras theorem, $O B=\sqrt{5}$
Using a compass with center $O$ and radius $OB$, draw an arc which intersects the number line at a point $C$. Then, $C$ corresponds to $\sqrt{5}$.
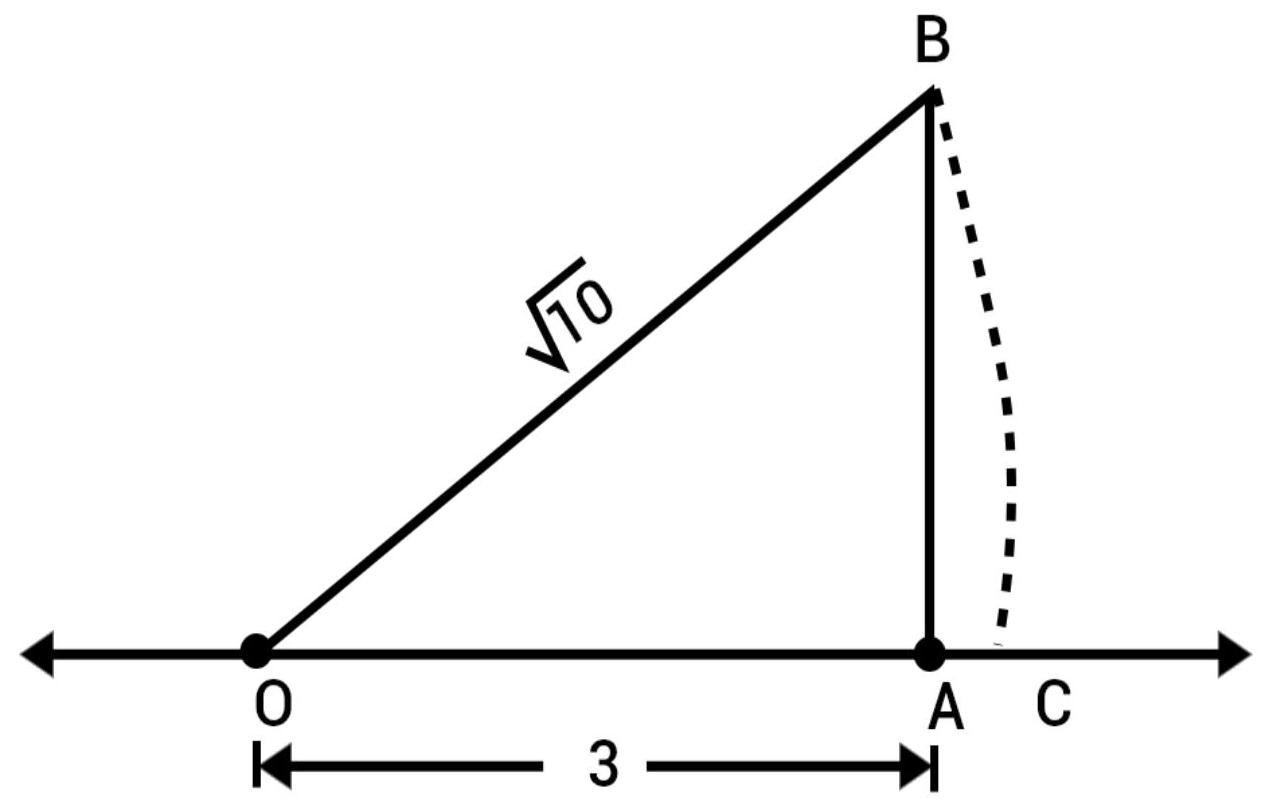
Presentation of $\sqrt{10}$ on number line:
We can write 10 as the sum of the square of two natural numbers:
$10=1+9$
$=1^{2}+3^{2}$
On the number line, take $OA=3$ units.
Draw $BA=1$ unit, perpendicular to $OA$ join $OB$.
By Pythagoras theorem, $O B=\sqrt{10}$
Using a compass with center $O$ and radius $OB$, draw an arc which intersects the number line at a point $C$. Then, $C$ corresponds to $\sqrt{10}$.
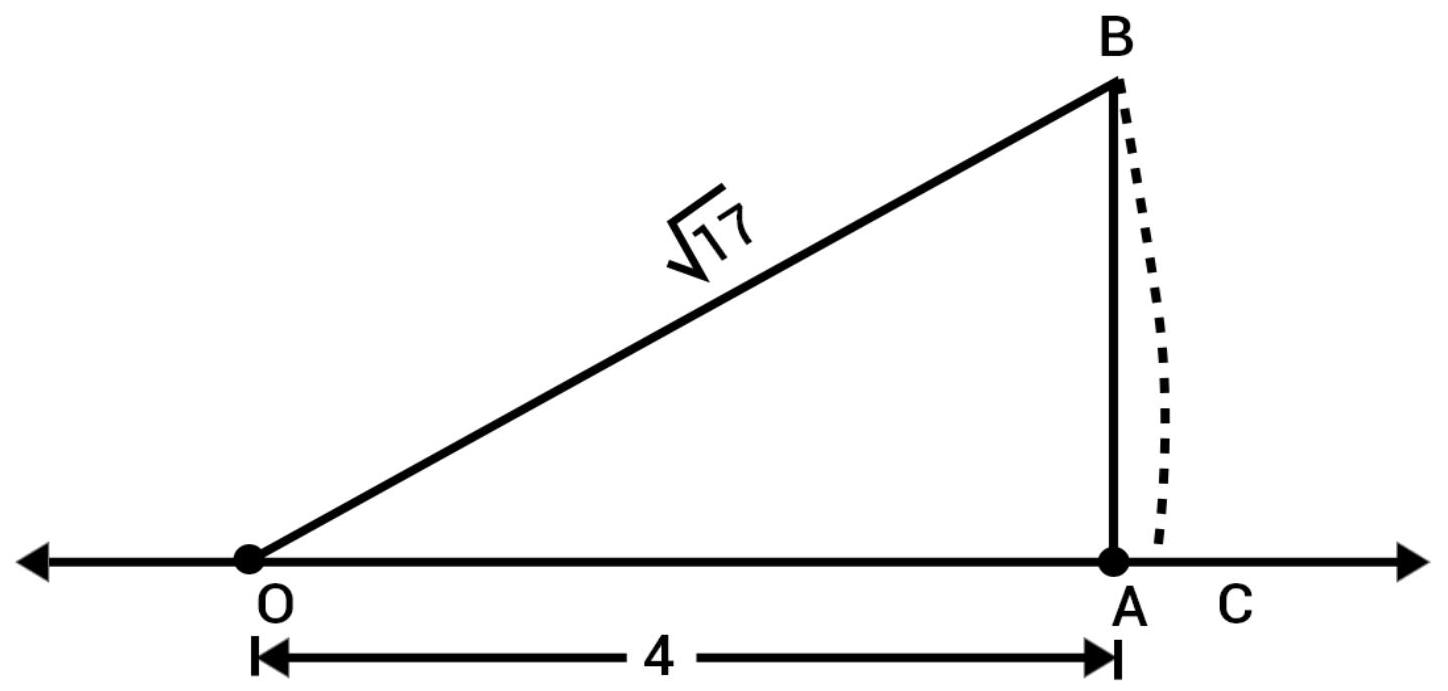
Presentation of $\sqrt{17}$ on number line:
We can write 17 as the sum of the square of two natural numbers:
$10=1+16$
$ =1^{2}+4^{2} $
On the number line, take $OA=4$ units.
Draw $BA=1$ unit, perpendicular to $OA$ join $OB$.
By Pythagoras theorem, $O B=\sqrt{17}$
Using a compass with center $O$ and radius $OB$, draw an arc which intersects the number line at a point $C$. Then, $C$ corresponds to $\sqrt{17}$.
6. Represent geometrically the following numbers on the number line:
(i) $\sqrt{4.5}$
(ii) $\sqrt{5.6}$
(iii) $\sqrt{8.1}$
(iv) $\sqrt{2.3}$
Show Answer
Solution
(i) Presentation of $\sqrt{4.5}$ on number line:
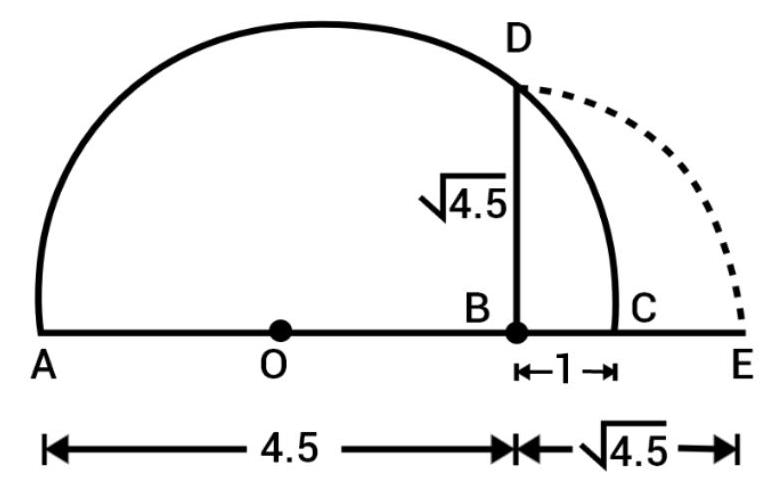
Mark the distance 4.5 units from a fixed point $A$ on a given line to obtain a point $B$ such that $AB=4.5$ units. From $B$, mark a distance of 1 units and mark the new points as $C$.
Find the mid-point of $AC$ and mark that points as $O$. Draw a semicircle with center $O$ and radius $OC$.
Draw a line perpendicular to $AC$ passing through $B$ and intersecting the semicircle at $D$. Then, $BD=\sqrt{4.5}$.
Now, draw an arc with center $B$ and $B$ radius $BD$, which intersects the number line in $E$.
Thus, E represent $\sqrt{4.5}$.
(ii) Presentation of $\sqrt{5.6}$ on number line:
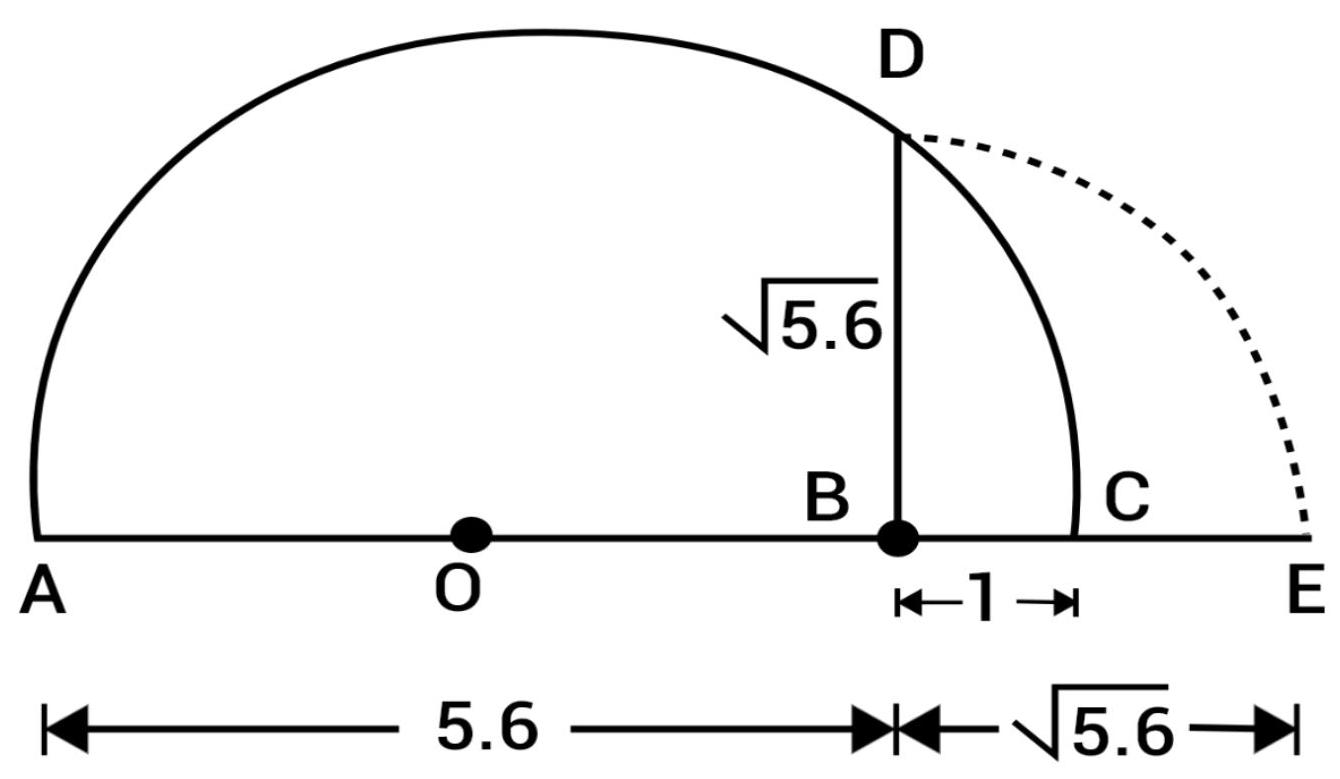
Mark the distance 5.6 units from a fixed point $A$ on a given line to obtain a point $B$ such that $A B=5.6$ units. From B, mark a distance of 1 units and mark the new points as $C$.
Find the mid-point of $AC$ and mark that points as $O$. Draw a semicircle with center $O$ and radius $OC$.
Draw a line perpendicular to $AC$ passing through $B$ and intersecting the semicircle at $D$. Then, $BD=\sqrt{5.6}$.
Now, draw an arc with center B and B radius BD, which intersects the number line in E.
Thus, E represent $\sqrt{5.6}$.
(iii) Presentation of $\sqrt{8.1}$ on number line:
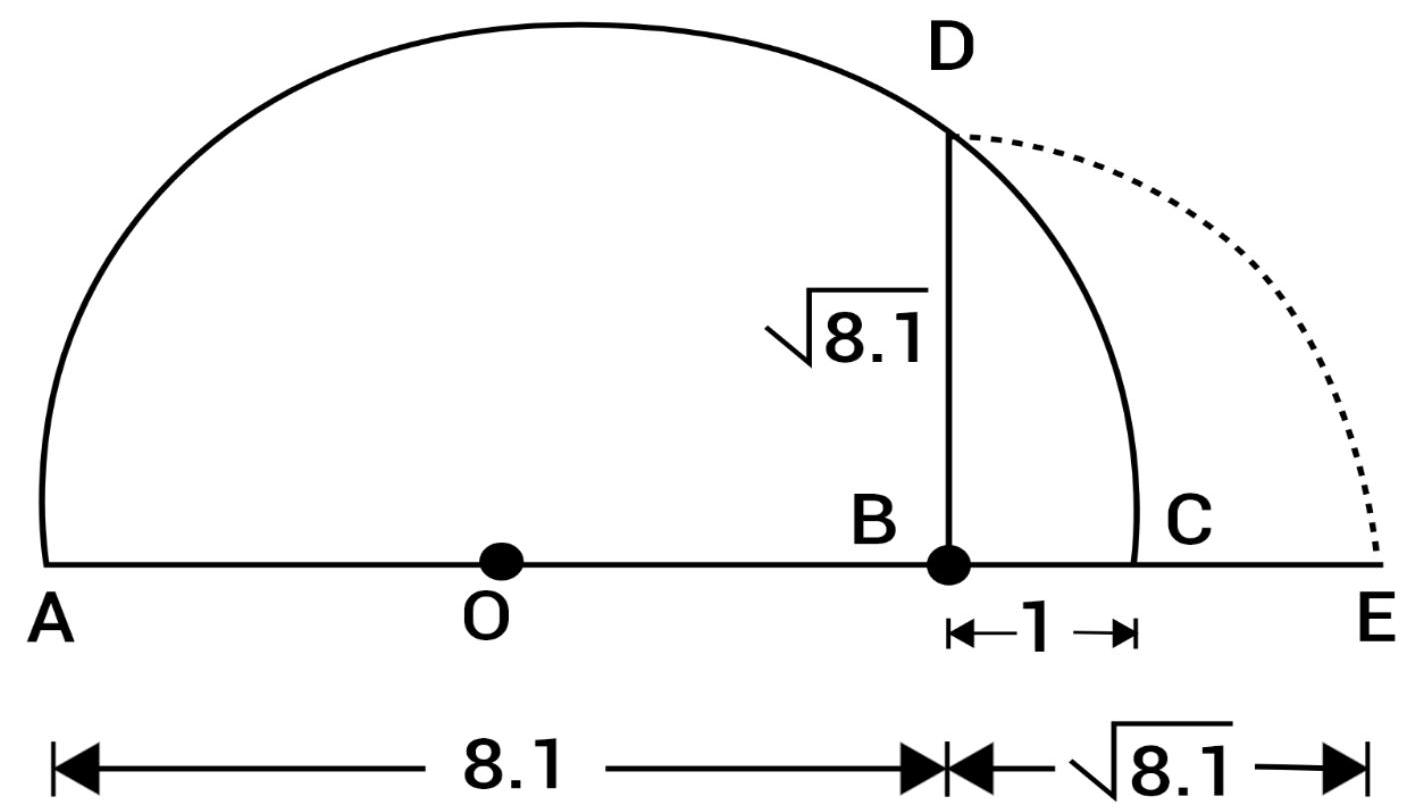
Mark the distance 8.1 units from a fixed point $A$ on a given line to obtain a point $B$ such that $AB=8.1$ units. From B, mark a distance of 1 units and mark the new points as $C$.
Find the mid-point of $AC$ and mark that points as $O$. Draw a semicircle with center $O$ and radius $OC$.
Draw a line perpendicular to $AC$ passing through $B$ and intersecting the semicircle at $D$. Then, $BD=\sqrt{8.1}$.
Now, draw an arc with center B and B radius BD, which intersects the number line in $E$.
Thus, E represent $\sqrt{8.1}$.
(iv) Presentation of $\sqrt{2.3}$ on number line:
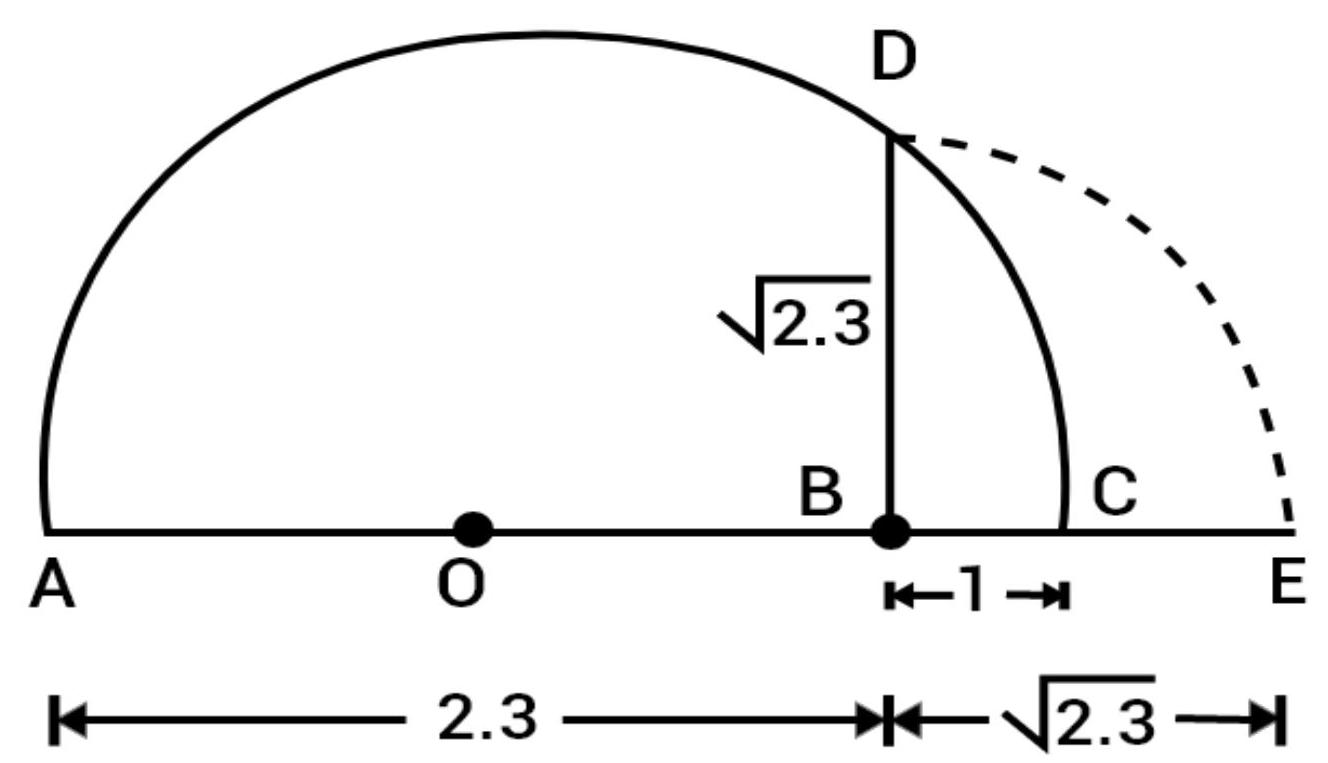
Mark the distance 2.3 units from a fixed point $A$ on a given line to obtain a point $B$ such that $AB=2.3$ units. From B, mark a distance of 1 units and mark the new points as $C$.
Find the mid-point of $AC$ and mark that points as $O$. Draw a semicircle with center $O$ and radius $OC$.
Draw a line perpendicular to $AC$ passing through $B$ and intersecting the semicircle at $D$. Then, $BD=\sqrt{2.3}$.
Now, draw an arc with center B and B radius BD, which intersects the number line in E.
Thus, E represent $\sqrt{2.3}$.
7. Express the following in the form $\dfrac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0:$
(i) 0.2
(ii) $0.888 \ldots$
(iii) $5 . \overline{2}$
(iv) $0 . \overline{001}$
(v) $0.2555 \ldots$
(vi) $0.1 \overline{34}$
(vii) $0.00323232 \ldots$
(viii) $0.404040 \ldots$
Show Answer
Solution
(i) $0.2=\dfrac{2}{10}=\dfrac{1}{5}$
(ii) Let $x=0.888 \ldots=0 . \overline{8}$
$10 x=8 . \overline{8}$
Subtracting (I) from (II), get:
$9 x=8$
Therefore, $x=\dfrac{8}{9}$.
(iii) Let $x=5 . \overline{2}=5.2222 \ldots$
Multiplying both sides by 10 , get:
$10 x=52.222 \ldots=52 . \overline{2}$
Subtracting (I) from (II), get:
$10 x-x=47$
$ 9 x=47 $
$ x=\dfrac{47}{9} $
Hence, $5 . \overline{2}=\dfrac{47}{9}$.
(iv) Let $x=0 . \overline{001}=0.001001$
$1000 x=1.001001 \ldots$
Subtracting (I) from (II), get:
$999 x=1$
Hence, $x=\dfrac{1}{999}$.
(v) Let $x=0.2555 \ldots=0.2 \overline{5}$. So,
$10 x=2 . \overline{5}$
And:
$100 x=25 . \overline{5}$
Subtracting (II) from (III), get:
$90 x=23$
$x=\dfrac{23}{90}$
(vi) Let $x=0.1 \overline{34}=0.1343434$
Multiplying both sides by 100 , get:
$100 x=13.43434=13.4 \overline{34}$
Subtracting (I) from (II), get:
Long Answer Questions
1. Express $0.6+0 . \overline{7}+0.4 \overline{7}$ in the form $\dfrac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Show Answer
Solution
Consider the expression:
$0.6+0 . \overline{7}+0.4 \overline{7}$
We have:
$0.6=\dfrac{6}{10}$
Let
$x=0 . \overline{7}=0.777 \ldots$
And: $10 x=7.77 \ldots$
Subtract equation (I) from equation (II), get:
$9 x=7$
$x=\dfrac{7}{9}$
Similarly: Let $y=0.4 \overline{7}=0.4777 \ldots$
Now, $10 y=4 . \overline{7}$
$100 y=47 . \overline{7}$
Subtract equation (III) from equation (IV), get:
$90 y=43$
$ y=\dfrac{43}{90} $
$0.4 \overline{7}=\dfrac{43}{90}$
Now,
$ \begin{aligned} 0.6+0 . \overline{7}+0.4 \overline{7} & =\dfrac{6}{10}+\dfrac{7}{9}+\dfrac{43}{90} \\ & =\dfrac{54+70+43}{90} \\ & =\dfrac{167}{90} \end{aligned} $
Therefore, $\dfrac{167}{90}$ in the form $\dfrac{p}{q}$ and $q \neq 0$.
2. Simplify:
$ \begin{aligned}\dfrac{7 \sqrt{3}}{\sqrt{10}+\sqrt{3}}-\dfrac{2 \sqrt{5}}{\sqrt{6}+\sqrt{5}}-\dfrac{3 \sqrt{2}}{\sqrt{15}+3 \sqrt{2}}\end{aligned} $
Show Answer
Solution
Consider the expression: $ \begin{aligned}\dfrac{7 \sqrt{3}}{\sqrt{10}+\sqrt{3}}-\dfrac{2 \sqrt{5}}{\sqrt{6}+\sqrt{5}}-\dfrac{3 \sqrt{2}}{\sqrt{15}+3 \sqrt{2}}\end{aligned} $
Simplify the above expression as follows:
$\begin{aligned} \dfrac{7 \sqrt{3}}{\sqrt{10}+\sqrt{3}}-\dfrac{2 \sqrt{5}}{\sqrt{6}+\sqrt{5}}-\dfrac{3 \sqrt{2}}{\sqrt{15}+3 \sqrt{2}} \\ =\dfrac{7 \sqrt{3}}{\sqrt{10}+\sqrt{3}} \times \dfrac{\sqrt{10}-\sqrt{3}}{\sqrt{10}-\sqrt{3}}-\dfrac{2 \sqrt{5}}{\sqrt{6}+\sqrt{5}} \times \dfrac{\sqrt{6}-\sqrt{5}}{\sqrt{6}-\sqrt{5}} \\ - \dfrac{3 \sqrt{2}}{\sqrt{15}+3 \sqrt{2}} \times \dfrac{\sqrt{15}-3 \sqrt{2}}{\sqrt{15}-3 \sqrt{2}} \\ = \dfrac{7 \sqrt{3}(\sqrt{10}-\sqrt{3})}{(\sqrt{10})^{2}-(\sqrt{3})^{2}}-\dfrac{2 \sqrt{5}(\sqrt{6}-\sqrt{5})}{(\sqrt{6})^{2}-(\sqrt{5})^{2}}-\dfrac{3 \sqrt{2}(\sqrt{15}-3 \sqrt{2})}{(\sqrt{15})^{2}-(3 \sqrt{2})^{2}} \\ = \dfrac{7 \sqrt{3}(\sqrt{10}-\sqrt{3})}{10-3}-\dfrac{2 \sqrt{5}(\sqrt{6}-\sqrt{5})}{6-5}-\dfrac{3 \sqrt{2}(\sqrt{15}-3 \sqrt{2})}{15-18} \\ = \dfrac{7 \sqrt{3}(\sqrt{10}-\sqrt{3})}{7}-\dfrac{2 \sqrt{5}(\sqrt{6}-\sqrt{5})}{1}-\dfrac{3 \sqrt{2}(\sqrt{15}-3 \sqrt{2})}{-3} \\ = \sqrt{3}(\sqrt{10}-\sqrt{3})-2 \sqrt{5}(\sqrt{6}-\sqrt{5})+\sqrt{2}(\sqrt{15}-3 \sqrt{2}) \\ = \sqrt{30}-3-2 \sqrt{30}+10+\sqrt{30}-6 \\ =2\sqrt{30}-9-2\sqrt{30}+10=1 \end{aligned}$
3. If $\sqrt{2}=1.414, \sqrt{3}=1.732$, then find the value of $\dfrac{4}{3 \sqrt{3}-2 \sqrt{2}}+\dfrac{3}{3 \sqrt{3}+2 \sqrt{2}}$.
Show Answer
Solution
Consider the expression:
$\dfrac{4}{3 \sqrt{3}-2 \sqrt{2}}+\dfrac{3}{3 \sqrt{3}+2 \sqrt{2}}$
Rationalization the above expression as follows:
$ \begin{aligned} \dfrac{4}{3 \sqrt{3}-2 \sqrt{2}}+\dfrac{3}{3 \sqrt{3}+2 \sqrt{2}} & =\dfrac{4}{3 \sqrt{3}-2 \sqrt{2}} \times \dfrac{3 \sqrt{3}+2 \sqrt{2}}{3 \sqrt{3}+2 \sqrt{2}}+\dfrac{3}{3 \sqrt{3}+2 \sqrt{2}} \\ \times \dfrac{3 \sqrt{3}-2 \sqrt{2}}{3 \sqrt{3}-2 \sqrt{2}} \\ & =\dfrac{4(3 \sqrt{3}+2 \sqrt{2})}{(3 \sqrt{3})^{2}-(2 \sqrt{2})^{2}}+\dfrac{3(3 \sqrt{3}-2 \sqrt{2})}{(3 \sqrt{3})^{2}-(2 \sqrt{2})^{2}} \\ & =\dfrac{4(3 \sqrt{3}+2 \sqrt{2})}{27-8}+\dfrac{3(3 \sqrt{3}-2 \sqrt{2})}{27-8} \\ & =\dfrac{12 \sqrt{3}+8 \sqrt{2}+9 \sqrt{3}-6 \sqrt{2}}{27-8} \\ & =\dfrac{12 \sqrt{3}+8 \sqrt{2}+9 \sqrt{3}-6 \sqrt{2}}{19} \\ & =\dfrac{21 \sqrt{3}+2 \sqrt{2}}{19} \end{aligned} $
Substitute 1.414 for $\sqrt{2}$ and 1.732 for $\sqrt{3}$ in the above expression.
$\dfrac{21 \times 1.732+2 \times 1.414}{19}=2.063$
4. If $a=\dfrac{3+\sqrt{5}}{2}$, then find the value of $a^{2}+\dfrac{1}{a^{2}}$.
Show Answer
Solution
Given:
$a=\dfrac{3+\sqrt{5}}{2}$
The value of $a^{2}$ will be:
$ \begin{aligned} a^{2} & =(\dfrac{3+\sqrt{5}}{2})^{2} \\ & =\dfrac{9+5+6 \sqrt{5}}{4} \\ & =\dfrac{14+6 \sqrt{5}}{4} \\ & =\dfrac{7+3 \sqrt{5}}{2} \end{aligned} $
Now,
$ \begin{aligned} \dfrac{1}{a^{2}} & =\dfrac{2}{7+3 \sqrt{5}} \\ & =\dfrac{2}{7+3 \sqrt{5}} \times \dfrac{7-3 \sqrt{5}}{7-3 \sqrt{5}} \\ & =\dfrac{2(7-3 \sqrt{5})}{7^{2}-(3 \sqrt{5})^{2}} \\ & =\dfrac{2(7-3 \sqrt{5})}{49-45} \\ & =\dfrac{2(7-3 \sqrt{5})}{4} \\ & =\dfrac{7-3 \sqrt{5}}{2} \end{aligned} $
The value of $a^{2}+\dfrac{1}{a^{2}}$ is:
$ \begin{aligned} a^{2}+\dfrac{1}{a^{2}} & =\dfrac{7+3 \sqrt{5}}{2}+\dfrac{7-3 \sqrt{5}}{2} \\ & =\dfrac{7+3 \sqrt{5}+7-3 \sqrt{5}}{2} \\ & =\dfrac{14}{2} \\ & =7 \end{aligned} $
5. If $x=\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$ and $y=\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$, then find the value of $x^{2}+y^{2}$.
Show Answer
Solution
Given:
$ x=\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}} \text{ and } y=\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}} $
Rationalization the $x$ as follows:
$ \begin{aligned} x & =\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}} \times \dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}} \\ & =\dfrac{(\sqrt{3}+\sqrt{2})^{2}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}} \end{aligned} $
$ \begin{aligned} & =\dfrac{(\sqrt{3})^{2}+(\sqrt{2})^{2}+2 \times \sqrt{3} \times \sqrt{2}}{3-2} \\ & =\dfrac{3+2+2 \times \sqrt{6}}{1} \\ & =5+2 \sqrt{6} \end{aligned} $
Similarly: $y=5-2 \sqrt{6}$
Now,
$ \begin{aligned} x+y & =5+2 \sqrt{6}+5-2 \sqrt{6} \\ & =10 \end{aligned} $
And,
$ x y=\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}} \times \dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}} $
$ =1 $
Therefore,
$ \begin{aligned} x+y & =(10)^{2}-(1)^{2} \\ & =100-1 \\ & =99 \end{aligned} $
6. Simplify: $(256)^{-(\dfrac{-3}{4^{2}})}$
Show Answer
Solution
Consider the expression: $(256)^{-(\dfrac{-3}{4^{2}})}$
Now, simplify the above expression as follows:
$ \begin{aligned} (256)^{-(\dfrac{-3}{4^{2}})} & =2^{8-(4^{-\dfrac{3}{2}})} \\ & =2^{8-(2^{2 \times \dfrac{3}{2}})} \\ & =(2^{8})^{-(2^{-3})} \\ & =(2^{8})^{-\dfrac{1}{8}} \\ & =2^{8 \times-\dfrac{1}{8}} \\ & =2^{-1} \\ & =\dfrac{1}{2} \end{aligned} $
7. Find the value of $\dfrac{4}{(216)^{-\dfrac{2}{3}}}+\dfrac{1}{(256)^{-\dfrac{3}{4}}}+\dfrac{2}{(243)^{-\dfrac{1}{5}}}$
Show Answer
Solution
Consider the expression:
$\dfrac{4}{(216)^{-\dfrac{2}{3}}}+\dfrac{1}{(256)^{-\dfrac{3}{4}}}+\dfrac{2}{(243)^{-\dfrac{1}{5}}}$
Simplify the above expression as follows:
$ \begin{aligned} \dfrac{4}{(216)^{-\dfrac{2}{3}}}+\dfrac{1}{(256)^{-\dfrac{3}{4}}}+\dfrac{2}{(243)^{-\dfrac{1}{5}}} & 4 \times(216)^{\dfrac{2}{3}}+(256)^{\dfrac{3}{4}}+2 \times(243)^{\dfrac{1}{5}} \\ & =4 \times(216)^{\dfrac{2}{3}}+(256)^{\dfrac{3}{4}}+2 \times(243)^{\dfrac{1}{5}} \\ & =4 \times 6^{3 \times \dfrac{2}{3}}+4^{4 \times \dfrac{3}{4}}+2 \times 3^{5 \times \dfrac{1}{5}} \\ & =4 \times 6^{2}+4^{3}+2 \times 3 \\ & =144+64+6 \\ & =214 \end{aligned} $










