Chapter 08 Introduction to Trigonometry and Its Applications
Multiple Choice Questions (MCQs)
1 If
(a)
(c)
Show Answer
Thinking Process
(i) First, we use the formula
(ii) Second, we use the formula
Solution
(b) Given,
Hence, the required value of
Show Answer
Thinking Process
(i) First, we use the formula
(ii) Now, we use the trigonometric ratio
Solution
(a) Given,
Hence, the required value of
(a) -1
Show Answer
Thinking Process
We see that, the given trigonometric angle of the ratio are the reciprocal in the sense of sign. Then, use the following formulae
(i)
Solution
(b) Given, expression
Hence, the required value of the given expression is 0 .
(a)
Show Answer
Solution
(c) Given,
(a)
(c)
Show Answer
Solution
(b) Given,
Now,
Hence,
(a) 0
Show Answer
Thinking Process
Use the transformation
Solution
(b)
(a)
Show Answer
Solution
(c) Given,
not in between.
8 If
(a) 0
Show Answer
Solution
(a) We know that, in
(a) 1
Show Answer
Solution
(a) Given,
On squaring both sides, we get
(a)
(c)
Show Answer
Solution
(d) Given,
(a) 3
Show Answer
Solution
(b) Given expression,
12 If
(a)
(c)
Show Answer
Solution
(c) Given,
[divide by
[put the value from Eq. (i)]
13 If
(a) 1
Show Answer
Thinking Process
Firstly, from
Solution
(c) Given,
Now,
(a)
Show Answer
Solution
(b)
(a)
Show Answer
Solution
(a) Let
Now, in
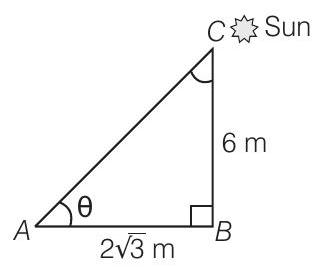
Hence, the Sun’s elevation is
Very Short Answer Type Questions
Write whether True or False and justify your answer.
1.
Show Answer
Solution
True
Show Answer
Solution
False
which may be either positive or negative.
Show Answer
Solution
False
We know that,
[positive]
Show Answer
Solution
True
Show Answer
Solution
True
Show Answer
Solution
False
Show Answer
Solution
False
To understand the fact of this question, consider the following example
I. A tower
II. A same hight of tower casts a shadow
 point, then the Sun's elevation is
point, then the Sun's elevation is 
Hence, we conclude from above two examples that if the length of the shadow of a tower is increasing, then the angle of elevation of the Sun is decreasing.
Alternate Method
False, we know that, if the elevation moves towards the tower, it increases and if its elevation moves away the tower, it decreases. Hence, if the shadow of a tower is increasing, then the angle of elevation of a Sun is not increasing.
Show Answer
Solution
False
From figure, we observe that, a man standing on a platform at point
Now at same point
So, angle of depression is different in the lake from the angle of elevation of the cloud above the surface of a lake.
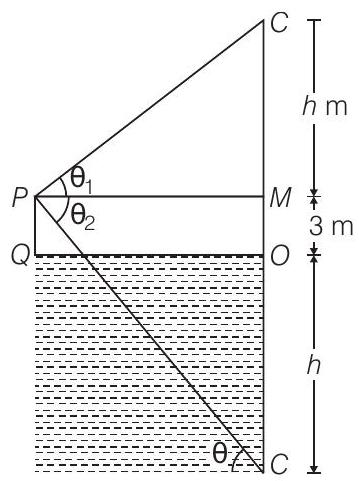
Hence,
Alternate Method
False, we know that, if
Here, the man is standing on a platform
Show Answer
Thinking Process
Use the relation between arithmetic mean and geometric mean i.e., AM > GM.
Solution
False
Given,
[since, AM and GM of two number’s
which is not possible.
Hence, the value of
Show Answer
Solution
False
Given,
Using,
[since, AM and GM of two number
which is not possible.
Hence,
Show Answer
Thinking Process
(i) Firstly, we find relation between
(ii) After that we take double height and taking angle of elevation is
Solution
False
Case I Let the height of the tower is
Case II By condition, the height of the tower is doubled. i.e.,

Hence, the required angle is not doubled.
Show Answer
Solution
True
Case I Let the height of a tower be
In
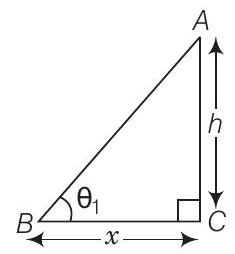
Case II Now, the height of a tower increased by

From Eqs. (i) and (ii),
Hence, the required angle of elevation of its top remains unchanged.
Short Answer Type Questions
Prove the following questions 1 to 7.
1.
Show Answer
Solution
Show Answer
Solution
3 If
Show Answer
Thinking Process
We know that,
Solution
Given,
Let
By Pythagoras theorem,
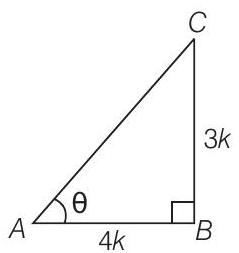
Hence proved.
Show Answer
Solution
Show Answer
Solution
RHS
LHS
Hence proved.
Show Answer
Solution
LHS
Show Answer
Solution
Show Answer
Solution
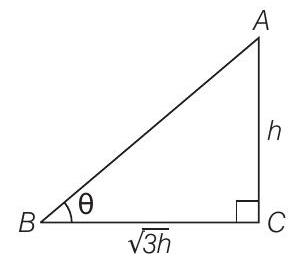
Let the angle of elevation of the Sun is
Given,
Now, in
Hence, the angle of elevation of the Sun is
Show Answer
Thinking Process
From the given equation, get the value of
Solution
Given that,
Now,
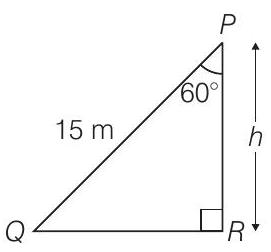
10 A ladder
Show Answer
Solution
Given that, the height of the ladder
Let the height of the vertical wall
and the ladder makes an angle of elevation
Hence, the required height of the wall
Show Answer
Solution
Show Answer
Solution
Given,
Show Answer
Solution
LHS
Show Answer
Solution
Let the angle of elevation of the top of the tower from the eye of the observe is
Given that,
and
Now, in
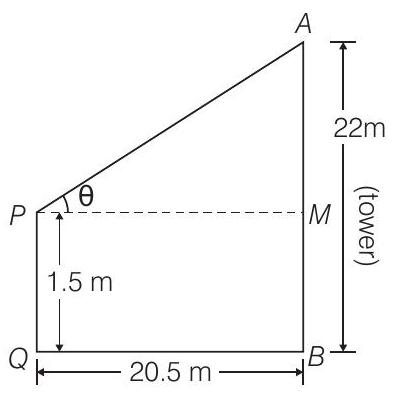
Hence, required angle of elevation of the top of the tower from the eye of the observer is
Show Answer
Solution
LHS
Long Answer Type Questions
1 If
Show Answer
Thinking Process
Reduce the given equation into
Solution
Given,
Using componendo and dividendo rule, we get
Hence proved.
Show Answer
Solution
LHS
Show Answer
Thinking Process
(i) First, we drawn a right angle triangle from the given information in the question.
(ii) Now, apply the suitable trigonometric ratio corresponding to given sides in the triangle and get the required value of which we want.
Solution
Let the height of the tower be
also,
Given that,
and
Now, in
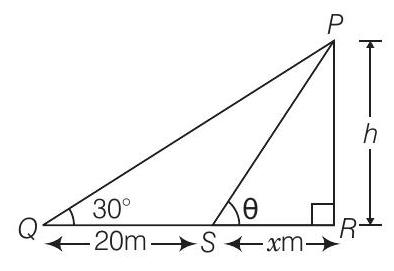
Now, in
Since, after moving
i.e.,
[by rationalisation]
[from Eq. (i)]
Hence, the required height of tower is
Show Answer
Thinking Process
(i) First we reduce the given equation, with the help of trigonometric ratio and identities in the form of
(ii) Now, factorise the quadratic equation in
Solution
Given,
On dividing by
Hence proved.
Show Answer
Thinking Process
Squaring both sides the given equation and use the identity
Solution
Given,
On squaring both sides, we get
Show Answer
Thinking Process
Use the concept of complementary angles in the angle of elevation. i.e., if two anlges are complementary to each other, then the sum of both angles is equal to
Solution
Let the height of the tower is
Given that,
and angle of elevation on both positions are complementary.
i.e.,
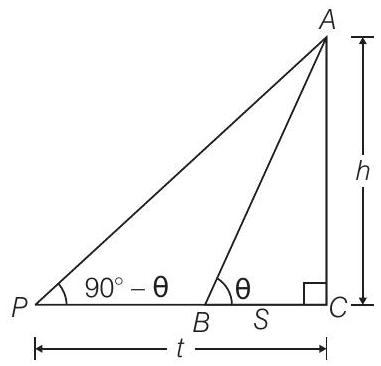
[if two angles are complementary to each other, then the sum of both angles is equal to
Now in
and in
On, multiplying Eqs. (i) and (ii), we get
So, the required height of the tower is
Hence proved.
Show Answer
Thinking Process
Consider the shadow of the tower be
Solution
Let the height of the tower be
Given that,
and
Now, in
and in
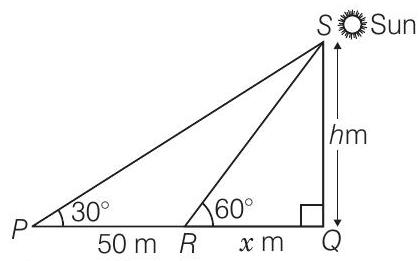
[from Eq. (i)]
Hence, the required height of tower is
Show Answer
Solution
Let the height of the tower be
Given that, height of flag staff
Now, in
and in
From Eqs. (i) and (ii),
Hence the required height of tower is
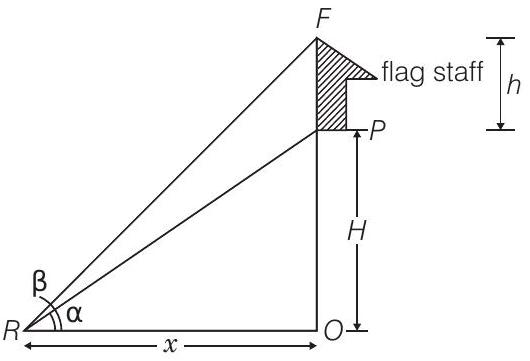
Hence proved.
Show Answer
Thinking Process
Firstly, we find the value of
Solution
Given,
[multiply by (
On adding Eqs. (i) and (ii), we get
Hence proved.
Show Answer
Thinking Process
(i) Firstly we will get the value of
(ii) Now, squaring both sides of the equation
Solution
Given that
and
On squaring both sides, we get
Show Answer
Solution
Given that,
On squaring both sides,
Show Answer
Solution
LHS
Show Answer
Solution
Let distance between the two towers
Given that, height of the tower
Now, in
and in
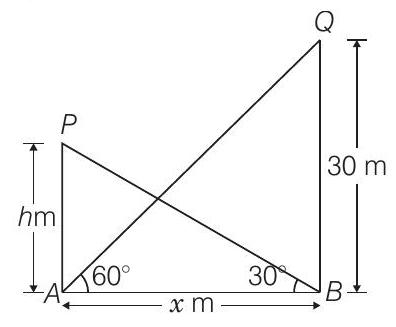
Hence, the required distance and height are
Show Answer
Solution
Let the distance between two objects is
and the height of tower,
Now, in
and in
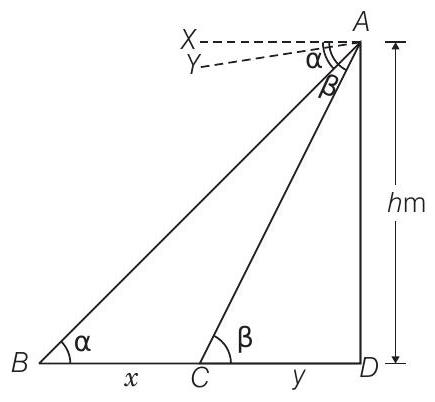
From Eqs. (i) and (ii),
which is the required distance between the two objects.
Show Answer
Thinking Process
(i) First, we draw a figure in which the both positions of ladder are shown. In required figure generate two triangles.
(ii) In first position, when ladder makes an angle of elevation is
(iii) In second position, when ladder makes an angle of elevation is
(iv) Now, we find the value of
Solution
Let
Given that,
Also,
Now, in
Now, in
and
Eq. (v) divided by Eq. (vi), we get
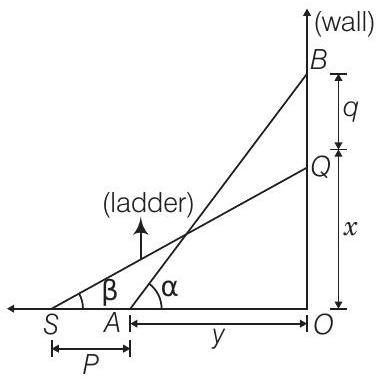
Hence proved.
Show Answer
Solution
Let the height the vertical tower,
Given that,
and
Now, in
and in
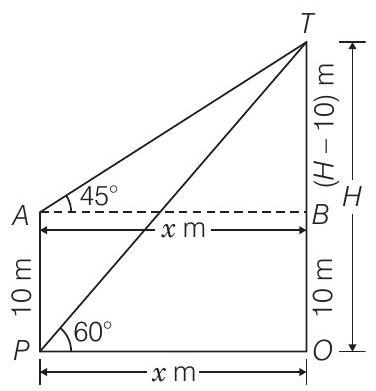
[from Eq. (i)]
[by rationalisation]
Hence, the required height of the tower is
Show Answer
Solution
Let the height of the other house
Given that, height of the first house
[alternate angle]
Now, in
And in
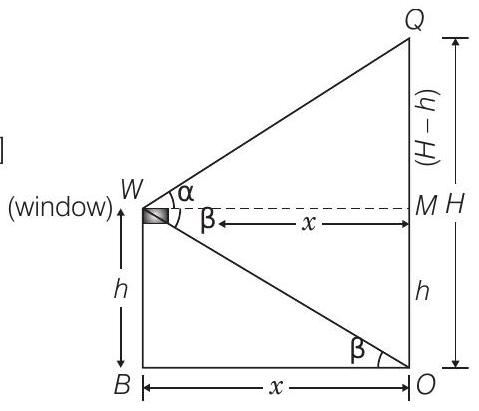
From Eqs. (i) and (ii),
Hence, the required height of the other house is
Hence proved.
Show Answer
Solution
Let the height of the balloon from above the ground is
Given that, height of lower window from above the ground
Height of upper window from above the lower window
and
Now, in
and in
From Eqs. (i) and (ii),
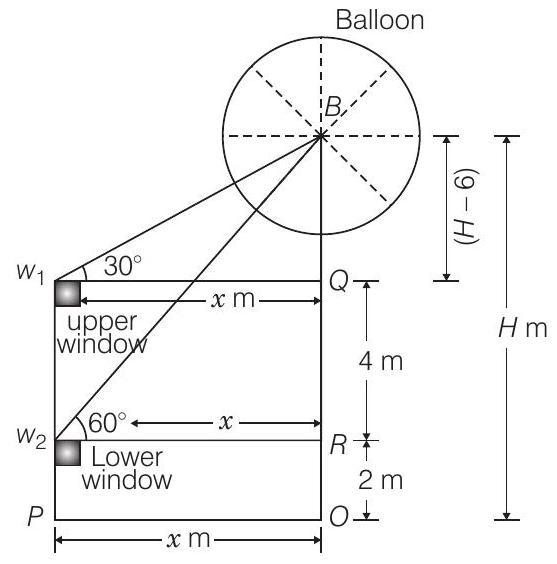
So, the required height is
Hence, the required height of the ballon from above the ground is










