Chapter 07 Coordinate Geometry
Multiple Choice Questions (MCQs)
1 The distance of the point
(a) 2
Show Answer
Solution
(b) We know that, if
Then,
and

Distance of the point
(a) 6
Show Answer
Thinking Process
The distance between two points
Solution
(b)
Here,
(a) 8
Show Answer
Thinking Process
Coordinate of origin is
Solution
(c)
Here,
(a) 5
Show Answer
Solution
(b)
(a) 5
Show Answer
Solution
(c)

Now, length of the diagonal
Here,
Hence, the required length of its diagonal is
(a) 5
Show Answer
Thinking Process
(i) Firstly, plot the given points on a graph paper and join them to get a triangle.
(ii) Secondly, determine the length of the each sides by using the distance formula,
(iii) Further, adding all the distance of a triangle to get the perimeter of a triangle.
Solution
(b) We plot the vertices of a triangle i.e.,

Now, perimeter of
Hence, the required perimeter of triangle is 12 .
(a) 14
Show Answer
Thinking Process
The area of triangle, whose vertices are
Solution
(c) Area of
Here,
Hence, the required area of
(a) right angled triangle
(c) equilateral triangle
Show Answer
Solution
(b) Let
Now, distance between
Distance between
Distance between
Hence,
(a) I quadrant
(c) III quadrant
Show Answer
Solution
(d) If
Given that,
So,
[since, in IV quadrant,
(a)
Show Answer
Solution
(a) We know that, the perpendicular bisector of the any line segment divides the line segment into two equal parts i.e., the perpendicular bisector of the line segment always passes through the mid-point of the line segment.
since, mid-point of any line segment which passes through the points
Hence,
(a)
Show Answer
Thinking Process
(i) Firstly, consider the fourth vertex of a parallelogram be
(ii) Secondly, determine the mid point of
(iii) Further, equating both points and get the required coordinate of fourth vertex.
Solution
(b) Let the fourth vertex of parallelogram,
Then,
since, mid - point of a line segment having points
and

Since,
Hence, the fourth vertex of parallelogram is
(a)
(c)
Show Answer
Solution
(d) Given that, the point

Now, distance between
Distance between
Distance between
Hence, required condition is
(a) -4
Show Answer
Solution
(b) Given that,

since, mid-point of line segment having points
But mid-point
On comparing the coordinates, we get
Hence, the required value of
(a)
Show Answer
Solution
(a) Firstly, we plot the points of the line segment on the paper and join them.

We know that, the perpendicular bisector of the line segment
Now, we draw a straight line on paper passes through the mid-point
Hence, the required point is
Alternate Method
We know that, the equation of line which passes through the points
Here,
So, the equation of line segment joining the points
If two lines are perpendicular to each other, then the relation between its slopes is
where,
and
Also, we know that the perpendicular bisector of the line segment is perpendicular on the line segment.
Let slope of line segment is
From Eq. (iii),
Also we know that the perpendicular bisector is passes through the mid-point of line segment.
Equation of perpendicular bisector, which has slope (-3) and passes through the point
[since, equation of line passes through the point
If the perpendicular bisector cuts the
So, the required point is
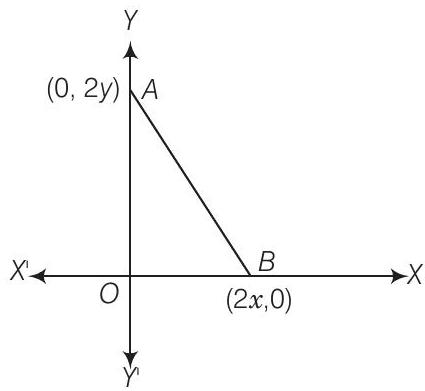
(a)
(c)
Show Answer
Thinking Process
(i) Firstly consider the new point be
(ii) Secondly, determine the distance
(iii) Further, solving two-two terms at a time and solving them to get required point.
Solution
(a) Let the coordinate of the point which is equidistant from the three vertices
Then,
By distance formula,
Taking first two equations, we get
Taking first and third equations, we get
(a)
(c)
Show Answer
Solution
(d) It is given that, centre of circle in
A point lie outside on or inside the circles of the distance of it from the centre of the circle is greater than equal to or less than radius of the circle.
Now, to get the correct option we have to check the option one by one.
(a) Distance between
So, the point
(b) Distance between
So, the point
(c) Distance between
So, the point
(d) Distance between
So, the point
(a)
(c)
Show Answer
Solution
(d) Let the coordinates of
So, the mid-point of
But it is given that, mid-point of

So, the coordinates of
(a)
Show Answer
Solution
(b) Let the vertices of a triangle are,
Hence, the required area of triangle is 0 .
(a) 4 only
Show Answer
Solution
(b) According to the question, the distance between the points
On squaring both the sides, we get
(a)
Show Answer
Solution
(c) Let the given points are
Since, the points
i.e.,
area of
Hence, the required relation is
Very Short Answer Type Questions
Write whether True or False and justify your answer
1.
Show Answer
Solution
True
Similarly, distance between
Distance between
Distance between
Now,
Here, we see that sides of 
Hence, both the triangles are similar.
Show Answer
Solution
True
We plot all the points

From the figure, point
Show Answer
Solution
False
Here,
If the area of triangle formed by the points
Hence, the points are non-collinear.
Show Answer
Solution
False
We know that, the points lies on perpendicular bisector of the line segment joining the two points is equidistant from these two points.
So, the point
Alternate Method
Slope of the line segment joining the points
Since, the perpendicular bisector is perpendicular to the line segment, so its slope,
[by perpendicularity condition,
Also, the perpendicular bisector passing through the mid-point of the line segment joining the points
[since, mid-point of the line segment joining the points
Now, equation of perpendicular bisector have slope
[since, the equation of line is
If the perpendicular bisector cuts the
Hence, the required intersection point is
Show Answer
Solution
True
Let
and
Hence, the points
Show Answer
Solution
False
Now, distance between
Distance between
Distance between
Distance between
In parallelogram, opposite sides are equal. Here, we see that all sides
Hence, given vertices are not the vertices of a parallelogram.
Show Answer
Thinking Process
Firstly, we find the distance between
Solution
True
First, we draw a circle and a point from the given information.

Now, distance between origin i.e.,
and
We know that, if the distance of any point from the centre is less than/equal to/ more than the radius, then the point is inside/on/outside the circle, respectively.
Here, we see that,
Hence, it is true that point
Show Answer
Solution
False
If
So,
Alternate Method
If the point
Now, we find the equation of perpendicular bisector. For this, we find the slope of perpendicular bisector.
[since, perpendicular bisector is perpendicular to the line segment, so its slopes have the condition,
Since, the perpendicular bisector passes through the mid-point of the line segment joining the points
So, the equation of perpendicular bisector having slope
Now, check whether the point
Hence, the point
Show Answer
Solution
True
Let
By section formula, the coordinate of point
So the point
Hence, point
Show Answer
Solution
True
If the area of triangle formed by the points
Here,
So, given points are collinear.
Now, distance between
Distance between
which is the required relation.
Show Answer
Solution
False
If the distance between the centre and any point is equal to the radius, then we say that point lie on the circle.
Now, distance between
which is not equal to the radius of the circle.
Hence, the point
Show Answer
Solution
True
Distance between
Distance between
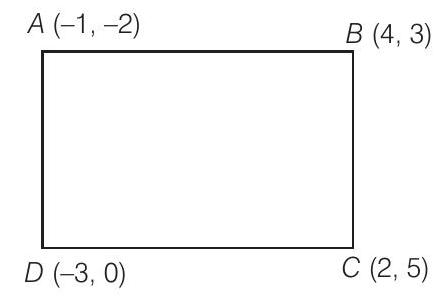
Distance between
and distance between
We know that, in a rectangle, opposite sides and equal diagonals are equal and bisect each other.
Since,
Also, distance between
Since, diagonals
Hence, the points
Short Answer Type Questions
1 Name the type of triangle formed by the points
Show Answer
Thinking Process
(i) Firstly, determine the distances
(ii) Secondly, check the condition for types of a triangles
(a) If any two sides are equal, then it is an isosceles triangle.
(b) If sides of a triangle satisfy the phythagoras theorem, then it is a right angled triangle.
(c) If all three sides of a triangle are equal, then it is an equilateral triangle.
(d) If none of the side of a triangle are equal, then it is an scalene triangle.
Solution
To find the type of triangle, first we determine the length of all three sides and see whatever condition of triangle is satisfy by these sides.
Now, using distance formula between two points,
and
We see that,
and not hold the condition of Pythagoras in a
i.e.,
Hence, the required triangle is scalene because all of its sides are not equal i.e., different to each other.
Show Answer
Solution
We know that, every point on the
Hence, there are two points lies on the axis, which are
Show Answer
Thinking Process
(i) Firstly, determine the distances
(ii) Secondly, check the condition for types of a quadrilaterals
(a) If all four sides and also diagonals are equal, then quadrilateral is a square.
(b) If all four sides are equal but diagonal are not equal, then quadrilateral is a rhombus.
(c) If opposite sides of a quadrilateral are equal and diagonals are also equal then quadrilateral is a rectangle.
Solution
To find the type of quadrilateral, we find the length of all four sides as well as two diagonals and see whatever condition of quadrilateral is satisfy by these sides as well as diagonals. Now, using distance formula between two points,
since, distance between two points
and
and
Here, we see that the sides
Also, diagonals are equal i.e.,
which shows the quadrilateral is a rectangle.
Show Answer
Solution
According to the question,
Distance between
On squaring both the sides, we get
Hence, the required value of
Show Answer
Solution
Let
At point (-3, 5), from Eq. (i),
So, the mid-point of
Replacing
Show Answer
Solution
Firstly, we plot the points of the line segment on the paper and join them.

We know that, the perpendicular bisector of the line segment
Now, we draw a straight line on paper passes through the mid-point
Hence, the required coordinates of
Alternate Method
(i) To find the coordinates of the point of
Now, slope of line segment
Let
Let the slope of perpendicular bisector of line segment is
Since, perpendicular bisector is perpendicular to the line segment
By perpendicularity condition of two lines,
Also, we know that, the perpendicular bisector is always passes through the mid-point of the line segment.
To find the equation of perpendicular bisector of line segment, we find the slope and a point through which perpendicular bisector is pass.
Now, equation of perpendicular bisector having slope
So, the coordinates of the point
To know the type of triangle formed by the points
Now, using distance formula between two points,
and
We see that,

which shows that the triangle formed by the points
Show Answer
Thinking Process
(i) First, using the condition of collinearity
(ii) Simplify it and get the result.
Solution
Let
Hence, the required value of
Show Answer
Solution
According to the question,
i.e.,
On squaring both the sides, we get
If
If
Now, distance between
Again, distance between
Hence, the values of
Show Answer
Solution
Given that, the vertices of triangles
Let
and
We know that, the area of triangle with vertices
Hence, the required area of triangle is 0 .
Show Answer
Thinking Process
(i) Firstly, determine the ratio by using the formula
(ii) Further, put the y coordinate of above formula is zero and get the value of
(iii) Finally, put the value of
Solution
Let the required ratio be
Here,
i.e.,
But according to the question, line segment joining
So, the required ratio is
i.e.,
Hence, the required point of division is
Show Answer
Solution
Let
Using the section formula, we get
On equating, we get
Hence, the required ratio is
Show Answer
Solution
Let
By section formula,
and
and
and
and
Hence, the required values of
Show Answer
Solution
Since,
since, mid-point of a line segment having points
Now, equating coordinates on both sides, we get
Hence, the required value of
Now, distance between
Hence, the required distance of
Show Answer
Thinking Process
(i) Firstly, determine the distance between centre and point on a circle by using the distance Formula
(ii) Further, using the given condition and simply it.
Solution
By given condition,

Distance between the centre
Given that,
Put this value in Eq. (i), we get
Squaring on both sides, we get
Hence, the required values of
Show Answer
Solution
Given that, the line segment joining the points
But the point
[given]
Hence, the required value of
Show Answer
Thinking Process
(i) Firstly, consider the vertices of of
(ii) With the help of mid-point formula form the equations in terms of
(iii) Further, determine the area of triangle by using the formula,
Solution
Let
Gives,
Since,
since, mid-point of a line segment having points
and
and
Also,
On adding Eqs. (i), (iii) and (v), we get
On subtracting Eqs. (i), (iii) and (v) from Eq. (vii) respectively, we get
On adding Eqs. (ii), (iv) and (vi), we get
On subtracting Eqs. (ii), (iv) and (vi) from Eq. (viii) respectively, we get
Hence, the vertices of
Show Answer
Solution
Given that, the points
Now, by distance formula,
and
Put the values of
Here,
So,
Now, the coordinate of
Hence, the required area of
Show Answer
Solution
According to the question,

Suppose,
Hence, the required coordinates of the point
Show Answer
Solution
We know that, if three points are collinear, then the area of triangle formed by these points is zero.
Since, the points
Then, area of
Show Answer
Thinking Process
(i) Firstly, consider the given line divides the line segment
Then, coordinate of
(ii) Substitute the coordinate in the given equation of line and get the value of
(iii) Further, substitute the value of
Solution
Let the line
But
So, the point
Hence, the required point of division is
Long Answer Type Questions
1 If
Show Answer
Solution
Let the third vertex of an equilateral triangle be
Now, taking first two parts
Now, taking first and third parts,
On subtracting Eq. (ii) from Eq. (iii), we get
Now, put the value of
So, the points of third vertex are
But given that, the origin lies in the interior of the
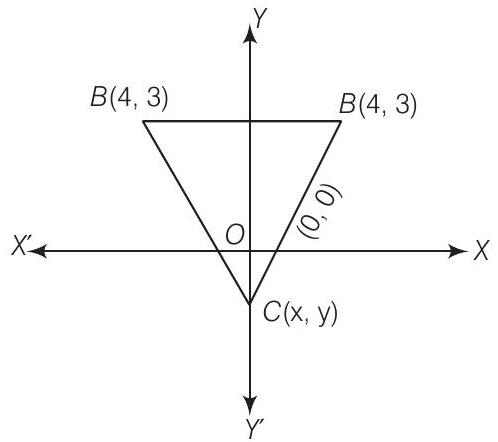
Hence, the required coordinate of third vertex,
2.
Show Answer
Thinking Process
(i) Firstly, consider the fourth vertex of a parallelogram be
(ii) Using the concept that mid-point of both diagonals are coincide, determine the coordinate of fourth vertex.
(iii) Also, determine the coordinate of E by using mid point formula,
(iv) Further, determine the required area of triangle by using the formula,
and simplify it to get the result.
Solution
Given that,
Let the fourth vertex of parallelogram be
We know that, the diagonals of a parallelogram bisect each other.

So, fourth vertex of a parallelogram is
Now,
Hence, the required area of
(i) The median from
(ii) Find the coordinates of the point
(iii) Find the coordinates of points
(iv) What are the coordinates of the centroid of the
Show Answer
Solution
Given that, the points
(i) We know that, the median bisect the line segment into two equal parts i.e., here
(ii) Let the coordinates of a point
Given that, the point

(iii) Let the coordinates of a point

Given that, the point
since,
So, the required coordinate of point
Now, let the coordinates of a point
since,
So, the required coordinate of point
(iv) Coordinate of the centroid of the
Show Answer
Solution
In parallelogram, we know that, diagonals are bisects each other i.e., mid-point of

since, mid-point of a line segment having points
So, the required value of
Given that,
Let the slope of
Since,
By condition of perpendicularity,
Now, Eq. of
On adding Eqs. (i) and (ii), then we get the intersection point
Put the value of
Put the value of
So, length of the height of a parallelogram,
Hence, the required length of height of a parallelogram is
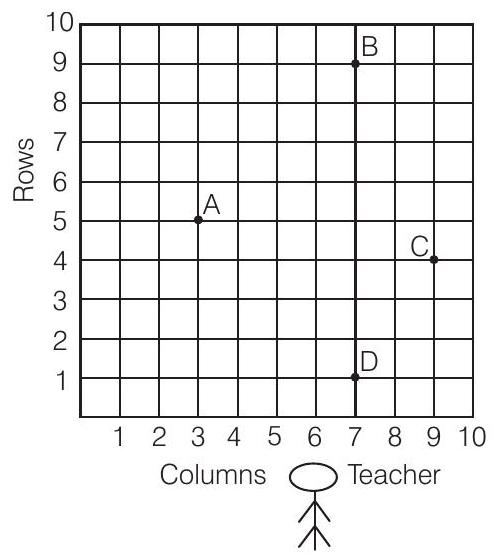
Show Answer
Solution
Yes, from the figure we observe that the positions of four students
Now,

by distance formula,
and
We see that,
Now, we find length of both diagonals.
and
Here,
Since,
Which represent a square. Also known the diagonals of a square bisect each other. So,
since, mid-point of a line segment having points
Hence, the required position of Jaspal is
Show Answer
Solution
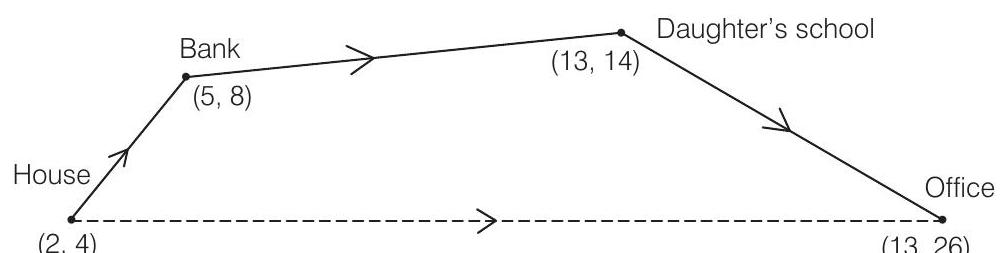
By given condition, we drawn a figure in which every place are indicated with his coordinates and direction also.
We know that,
distance between two points
Now, distance between house and bank
Distance between bank and daughter’s school
Distance between daughter’s school and office
Total distance (House + Bank + School + Office) travelled
Distance between house to offices
So, extra distance travelled by Ayush in reaching his office











