Chapter 06 Triangles
Multiple Choice Questions (MCQs)
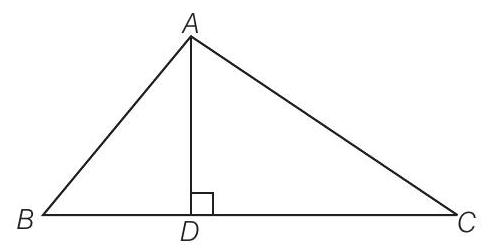
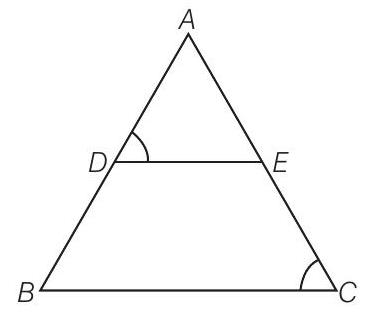
1 In figure, if
(a)
Show Answer
Solution
(c) In

(a)
Show Answer
Solution
(b) We know that, the diagonals of a rhombus are perpendicular bisector of each other.
Given,
and
In right angled

(a)
(c)
Show Answer
Solution
(c) Given,

Taking first two terms, we get
So, option (d) is true.
Taking last two terms, we get
So, option (a) is also true.
Taking first and last terms, we get
Hence, option (b) is true.
(a)
(c)
Show Answer
Solution
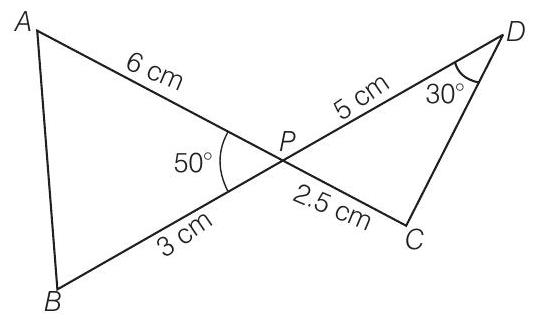
(a) Given, in two
which shows that sides of one triangle are proportional to the side of the other triangle, then their corresponding angles are also equal, so by SSS similarity, triangles are similar.
i.e.,

(a)
Show Answer
Solution
(d) In
[vertically opposite angles]
and
From Eqs. (i) and (ii)
(a)
(c)
Show Answer
Solution
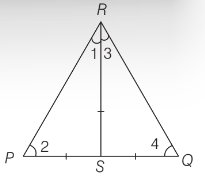
(b) Given, in 
(a) congruent but not similar
(c) neither congruent nor similar
Show Answer
Solution
(b) In 
We know that, if in two triangles corresponding two angles are same, then they are similar by AAA similarity criterion. Also,
(a) 9
(c)
Show Answer
Thinking Process
Use the property of area of similar triangle.
Solution
(a) Given,
We know that, the ratio of the areas of two similar triangles is equal to square of the ratio of their corresponding sides.
(a)
(c)
Show Answer
Solution
(b) Given, 
(a)
(c)
Show Answer
Solution
(c) Given, in

By converse of basic proportionality theorem,
Then,
and
(a)
Show Answer
Solution
(a) Given, 
We know that, the ratio of area of two similar triangles is equal to the ratio of square of their corresponding sides.
(a)
(c)
Show Answer
Solution
(c) Given, in
[using Eqs. (ii) and (iii)]
Similarly, in
[corresponding angles of equal sides are equal] Now, in
In
Very Short Answer Type Questions
Write whether True or False and justify your answer.
1 Is the triangle with sides
Show Answer
Solution
False
Let
Now,
Hence, given sides do not make a right triangle because it does not satisfy the property of Pythagoras theorem.
Show Answer
Solution
False
We know that, if two triangles are similar, then their corresponding angles are equal.
Show Answer
Solution
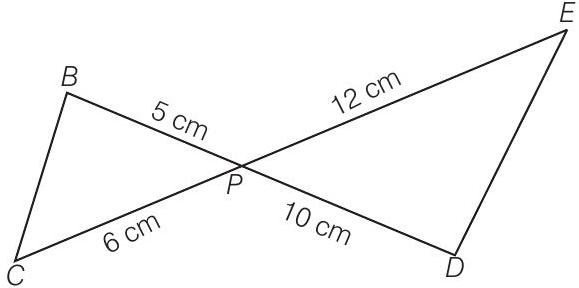
False
Given,

Then,
Now,
and
From Eqs. (i) and (ii),
By converse of basic proportionality theorem,
Show Answer
Solution
True
In
| [vertically opposite angles] | |||
|---|---|---|---|
| Now, | |||
| and | |||
| From Eqs. (i) and (ii), |
Since, one angle of
Hence,
Show Answer
Solution
False
We know that, the sum of three angles of a triangle is

In
and
Hence,
Show Answer
Solution
False
Two quadrilaterals are similar, if their corresponding angles are equal and corresponding sides must also be proportional.
Show Answer
Solution
True
Here, the corresponding two sides and the perimeters of two triangles are proportional, then third side of both triangles will also in proportion.
Show Answer
Solution
True
Let two right angled triangles be 
In which
and
Then, by AAA similarity criterion,
Show Answer
Solution
False
By the property of area of two similar triangles,
So, given statement is not correct.
Show Answer
Solution
False
In
[common side]
[each

Here, no other sides or angles are equal, so we can say that
But, if
[each equal to
Show Answer
Solution
True
In
Show Answer
Solution
False
Because, according to SAS similarity criterion, if one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
Here, one angle and two sides of two triangles are equal but these sides not including equal angle, so given statement is not correct.
Short Answer Type Questions
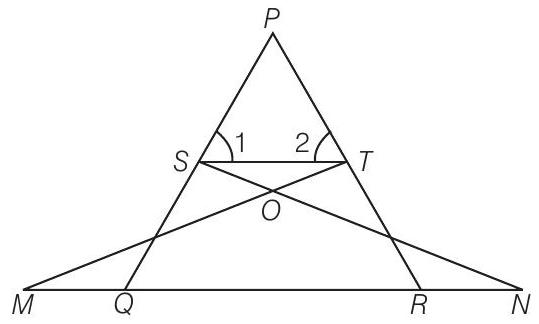
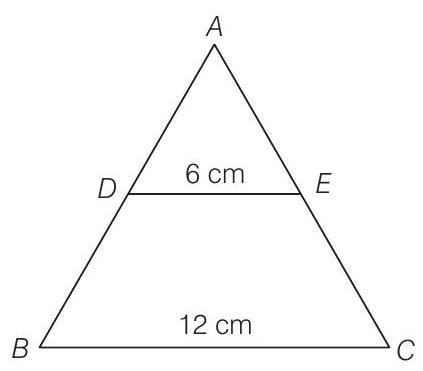
1 In a
Show Answer
Solution
Given

So,
In
Now, using property of area of similar triangles, we get
Thinking Process
Use the basic proportionality theorem to get required value of
Show Answer
Solution
Given,
[by basic proportionality theorem]

Hence, the required value of
Show Answer
Thinking Process
Firstly, show that
Solution
Given
To prove
Proof Since,
So,
Also,
From Eqs. (i) and (ii),
[since, sides opposite to equal angles are also equal]
and
In
[by AAA similarity criterion]
Hence proved.
Show Answer
Thinking Process
Firstly, show that
Solution
Given

In
By property of area of similar triangle,
Hence, the required ratio is
Show Answer
Solution
Given
To prove
Proof
[since,
Then,
Hence proved.
Show Answer
Solution
Let
Draw altitude
Hence, altitude of an equilateral triangle is

Show Answer
Solution
Given
Also,
On taking first two terms, we get
Now,
Show Answer
Solution
Given,
In
and
Then,
[corresponding angle] [corresponding angle]
[common side]
[by AAA similarity criterion]
Let
Now, ar
Show Answer
Solution
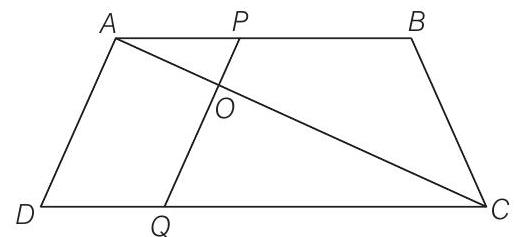
Given, a trapezium

Join
In
By basic proportionality theorem,
Show Answer
Thinking Process
Use the property area of similar triangle to get required area.
Solution
Given, ratio of corresponding sides of two similar triangles
Area of smaller triangle
By the property of area of two similar triangle,
Ratio of area of both riangles
Show Answer
Thinking Process
Firstly, show that
Solution
Given
and

To prove
Proof We have,
In
and
Then,
i.e.,
On adding both sides, we get
We know that, sum of angles of a triangle
In
Show Answer
Solution
Given, area of smaller triangle
Also, length of a side of the larger triangle
Let length of the corresponding side of the smaller triangle
By property of area of similar triangle,
Hence, the length of corresponding side of the smaller triangle is
Show Answer
Solution
Given,
From figure,

In right angled
In
[each
[each equal to
Then,
Show Answer
Thinking Process
Firstly, draw the figure according to given conditions, then show that both triangles are similar by AAA similarity criterion and then use ratio of sides of both triangles to get required length.
Solution
Let 
In
[by AAA similarity criterion]
Then,
Hence, the height of the telephone pole is
Thinking Process
Firstly, draw the figure according to given conditions and then apply Pythagoras theorem to get required height.
Show Answer
Solution
Let
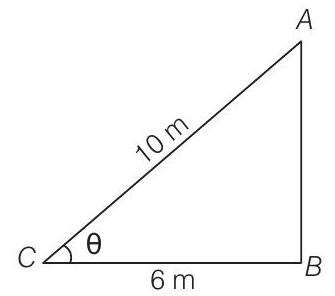
In right angled
Hence, the height of the point on the wall where the top of the ladder reaches is
Long Answer Type Questions
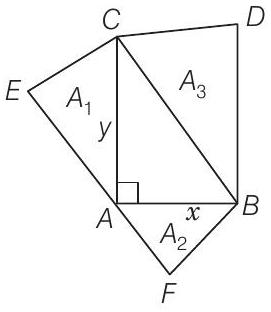
1 In given figure, if
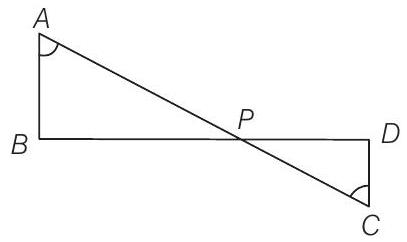
Show Answer
Solution
Given,
[by Pythagoras theorem]
Triangles
On taking first two terms, we get
On taking first and last term, we get
Hence, length of
Show Answer
Thinking Process
Use the property of similar triangles i.e., the corresponding sides are in the same ratio and then simplify.
Solution
Given,

Also,
On putting these values in Eq. (i), we get
On taking first and second terms, we get
On taking first and third terms, we get
Hence, lengths of the remaining sides of the triangles are
Show Answer
Solution
Let a
To prove
i.e.,

Construction Join
Proof Here,
similarly,
Now, since,
So,
From Eqs. (i), (ii) and (iii),
Hence proved.
Show Answer
Solution
Given

To prove
Proof in
Then,
[common angle] [corresponding angles] [by AAA similarity criterion]
In
[since,
From Eqs. (i) and (ii),
On subtracting from both sides, we get
By converse of basic proportionality theorem,
Hence proved.
Show Answer
Solution
Let

Hence, the top of the ladder would slide upwards on the wall at distance
Show Answer
Thinking Process
Firstly draw the figure according to the given conditions and use Pythagoras theorem to find the value of
Solution
Given,
On drawing the figure, we get the right angled
Now, In

Since, distance cannot be negative.
The distance covered to reach city
Distance covered to reach city
Hence, the required saved distance is
Show Answer
Solution
Let

Show Answer
Thinking Process
Firstly, draw the figure according to the question and get two triangles. Then, show both triangles are similar by AAA similarity criterion and then calculate the required distance.
Solution
Let

Here, woman and pole both are standing vertically.
So,
In
Then,
[common angle] [each equal to
Hence, she is at the distance of
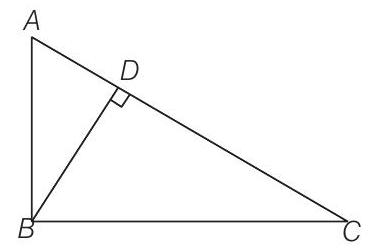
Show Answer
Solution
Given,
Also,
In
and
Then,
In right angled
Again,
Hence,
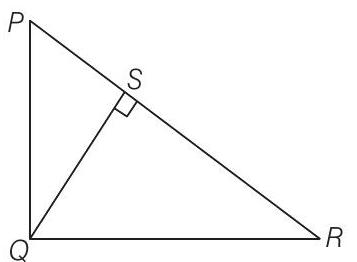
Show Answer
Solution
Given,
Then,
In
In right angled
On putting the value of
Show Answer
Thinking Process
Apply the Pythagoras theorem in both
Solution
Given In
To prove
Proof In right angled

From Eqs. (i) and (ii),
Show Answer
Thinking Process
Firstly, produce
Solution
Given Quadrilateral
Construct Produce
Also, join
Proof
Then, by Pythagoras theorem,
In

On adding both equations, we get
In
and in
On adding both equations, we get
From Eqs. (i) and (ii),
Hence proved.
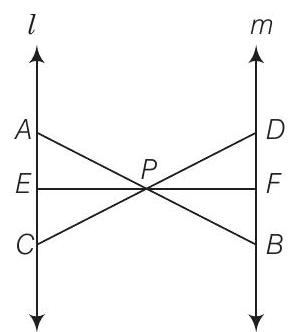
Show Answer
Solution
Given
To prove
Proof
Then,
In
Then,
In
from Eqs. (i), (ii) and (iii),
Hence proved.
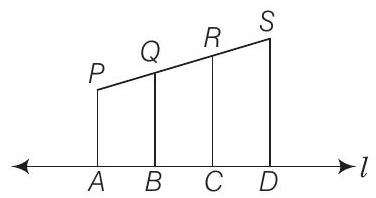
Show Answer
Solution
Given,
By basic proportionality theorem,
Let
Since, length of
Now,
15
Show Answer
Solution
Given
To prove

Proof In
Then,
Now, in
In
From Eqs. (iii) and (iv),
Adding 1 on both sides, we get
[from Eqs. (i) and (ii)] [from Eq. (ii)] Hence proved.
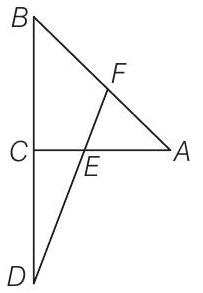
Show Answer
Solution
Given
To prove
Construction Take a point
Proof Since,
In
So,
Now, in

Show Answer
Thinking Process
Firstly, draw these semi-circles on three sides of right triangle taking each side as diameter. Then, find area of each semi-circle by using formula area of semi-circle
Solution
Let
Three semi-circles are drawn on the sides
Again, let area of circles with diameters
To prove
Proof
We know that, area of a semi-circle with radius,
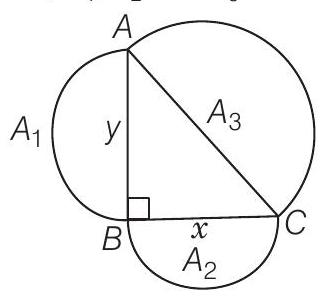
Now, area of semi-circle drawn on
and area of semi-circle drawn on
On adding Eqs. (ii) and (iii), we get
18 Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangle drawn on the other two sides of the triangle.
Show Answer
Thinking Process
Firstly draw equilateral triangles on each side of right angled
Solution
Let a right triangle
Three equilateral triangles
Again let area of triangles made on
To prove
Proof In
We know that, area of an equilateral triangle
and area of equilateral










