Chapter 04 Quadratic Equations
Multiple Choice Questions (MCQs)
1 Which of the following is a quadratic equation?
(a)
(b)
(c)
(d)
Show Answer
Thinking Process
An equation which is of the form
Solution
(d)
(a) Given that,
which is not of the form
(b) Given that,
(c) Given that,
which is also not a quadratic equation.
(d)
(a)
(c)
Show Answer
Solution
(d)
(a)
which represents a quadratic equation because it has the quadratic form
(b)
which also represents a quadratic equation because it has the quadratic form
(c)
which also represents a quadratic equation because it has the quadratic form
(d) Given that,
which is not of the form
(a)
(c)
Show Answer
Thinking Process
If
Solution
(c)
(a) Substituting
So,
(b) Substituting
So,
(c) Substituting
So,
(d) Substituting
So,
(a) 2
Show Answer
Thinking Process
Since,
Solution
(a) Since,
(a)
(c)
Show Answer
Thinking Process
If
Solution
(b)
(a) Given that,
On comparing with
So, sum of the roots of the quadratic equation
(b) Given that,
On compare with
So, sum of the roots of the quadratic equation
(c) Given that,
On comparing with
So, sum of the roots of the quadratic equation
(d) Given that,
On comparing with
So, sum of the roots of the quadratic equation
Show Answer
Thinking Process
If any quadratic equation i.e.,
Solution
(d) Given equation is
On comparing with
For equal roots, the discriminant must be zero.
i.e.,
Hence, the required values of
(a)
(b)
(c)
(d)
Show Answer
Solution
(b) Given equation is
On putting
Thus,
8 The quadratic equation
(a) two distinct real roots
(b) two equal real roots
(c) no real roots
(d) more than 2 real roots
Show Answer
Thinking Process
If a quadratic equation is in the from of
(i) If D
(ii) If D
(iii) If
Any quadratic equation must have only two roots.
Solution
(c) Given equation is
On comparing with
Since, discriminant is negative, therefore quadratic equation
(a)
(c)
Show Answer
Solution
(b) The given equation is
On comparing with
The discriminant of
So,
(a) Given equation is,
On comparing with
Now,
Thus, the equation has real and equal roots.
(c) Given equation is
On comparing with
Now,
(d) Given equation is,
On comparing with
Now,
Hence, roots of the equation are not real.
(a)
(c)
Show Answer
Solution
(a)
(a) The given equation is
On comparing with
The discriminant of
(b) The given equation is
On comparing the equation with
Then,
Hence, the equation has real roots.
(c) Given equation is
On comparing the equation with
Then,
Hence, the equation has real roots.
(d) Given equation is
On comparing the equation with
Then,
Hence, the equation has real roots.
Hence,
(a) four real roots
Show Answer
Solution
(c) Given equation is
Very Short Answer Type Questions
1 State whether the following quadratic equations have two distinct real roots. Justify your answer.
(i)
(iii)
(v)
(vii)
(ix)
Show Answer
Thinking Process
If
(i)
(ii)
(iii)
Solution
(i) Given equation is
On comparing with
Hence, the equation
(ii) Given equation is,
On comparing with
Hence, the equation
(iii) Given equation is
On comparing with
Hence, the equation
On comparing with
Hence, the equation
(v) Given equation is
On comparing with
Hence, the equation
(vi) Given equation is
On comparing with
Hence, the equation
(vii) Given, equation is
On comparing with
Hence, the equation
(viii) Given equation is
On comparing with
Hence, the equation
(ix) Given equation is
On comparing the equation with
Hence, equation has two distinct real roots.
(x) Given equation is
On comparing with
Hence, the equation
(i) Every quadratic equation has exactly one root.
(ii) Every quadratic equation has atleast one real root.
(iii) Every quadratic equation has atleast two roots.
(iv) Every quadratic equation has atmost two roots.
(v) If the coefficient of
(vi) If the coefficient of
Show Answer
Solution
(i) False, since a quadratic equation has two and only two roots.
(ii) False, for example
(iii) False, since a quadratic equation has two and only two roots.
(iv) True, because every quadratic polynomial has atmost two roots.
(v) True, since in this case discriminant is always positive, so it has always real roots, i.e., ac
(vi) True, since in this case discriminant is always negative, so it has no real roots i.e., if
Show Answer
Solution
No, consider the quadratic equation
Show Answer
Solution
Yes, consider the quadratic equation
Show Answer
Solution
Yes, consider the quadratic equation with all distinct irrationals coefficients i.e.,
Show Answer
Solution
No, since 0.2 does not satisfy the quadratic equation i.e.,
Show Answer
Solution
Given that,
Put
Short Answer Type Questions
1 Find the roots of the quadratic equations by using the quadratic formula in each of the following
(i)
Show Answer
Thinking Process
Compare the given quadratic equation with
i.e.,
Solution
(i) Given equation is
On comparing with
By quadratic formula,
So,
(ii) Given equation is
On comparing with
By quadratic formula,
(iii) Given equation is
On comparing with
By quadratic formula,
So,
(iv) Given equation is
On comparing with
By quadratic formula,
So, 2 and 5 are two roots of the given equation.
(v) Given equation is
On comparing with
By quadratic formula,
So,
(vi) Given equation is
On comparing with
By quadratic formula,
So,
(vii) Given equation is
On comparing with
So,
(i)
(iii)
(v)
Show Answer
Thinking Process
If any coefficient of the quadratic equation of the form
Solution
(i) Given equation is
On multiplying by 3 on both sides, we get
Hence, the roots of the equation
On multiplying by 5 on both sides, we get
Hence, the roots of the equation
(iii) Given equation is
Hence, the roots of the equation
(iv) Given equation is
Hence, the roots of the equation
(v) Given equation is
On multiplying by 21 on both sides, we get
Hence, the roots of the equation
Long Answer Type Questions
1 Find whether the following equations have real roots. If real roots exist, find them
(i)
(iii)
(v)
Show Answer
Thinking Process
(i) Firstly we will check the quadratic equation has real roots or not for this, is discriminant,
(ii) If roots are real, we may factorise the equation or use the quadratic formula to obtain the roots of the equation.
Solution
(i) Given equation is
On comparing with
Therefore, the equation
Roots
(ii) Given equation is
On comparing with
Therefore, the equation
(iii) Given equation is
On comparing with
Therefore, the equation
(iv) Given equation is
On comparing with
Therefore, the equation
(v) Given equation is
On comparing with
Therefore, the equation
Show Answer
Thinking Process
Firstly, we make a quadratic equation by using the given condition after that we solve the equation by factorisation equation. Finally, method to obtain the desired number.
Solution
Let
Square of a natural number diminished by
and thrice of 8 more than the natural number
Now, by given condition,
Hence, the required natural number is 12 .
Show Answer
Solution
Let the natural number be
According to the question,
On multiplying by
[by factorisation method]
Now,
Hence, the required natural number is 8 .
Show Answer
Solution
Let the original speed of the train
Then, the increased speed of the train
According to the question,
Show Answer
Solution
Let the actual age of Zeba
Herage when she was 5 yr younger
Now, by given condition,
Square of her age
[here,
Show Answer
Solution
Let Nisha’s present age be
Then, Asha’s present age
[by given condition]
Now, when Nisha grows to her mother’s present age i.e., after
Asha’s age also increased by
Again by given condition,
Age of Asha
Hence, required age of Nisha
and required age of Asha
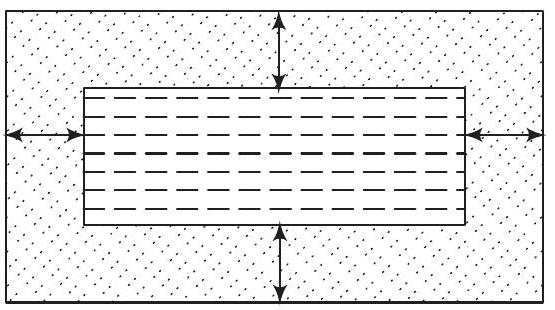
Show Answer
Solution
Given that a rectangular pond has to be constructed in the centre of a rectangular lawn of dimensions

Now, length of rectangular lawn
and breadth of rectangular lawn
and breadth of rectangular pond
Also, area of the grass surrounding the pond
show
Show Answer
Solution
We know that, the time between
Given that, at
Hence, the required value of










