SATHEE: Chapter 03 Pair of Linear Equations in Two Variables

Chapter 03 Pair of Linear Equations in Two Variables

Multiple Choice Questions (MCQs)

1 Graphically, the pair of equations

$\begin{matrix} 6 x - 3 y + 10 = 0 \\ 2 x - y + 9 = 0 \end{matrix}$

represents two lines which are

(a) intersecting at exactly one point

(b) intersecting exactly two points

(d) parallel

Show Answer

Solution

(d) The given equations are

and table for $2 x - y + 9 = 0$ ,

$x$	0	$- \frac{9}{2}$
$y = 2 x + 9$	9	0
Points	$\underset{―}{C}$	$\underset{―}{D}$

Hence, the pair of equations represents two parallel lines.

2 The pair of equations

x + 2 y + 5 = 0

and

- 3 x - 6 y + 1 = 0

has (a) a unique Solution

(b) exactly two Solutions

(d) no Solution

Show Answer

Solution

(d) Given, equations are $x + 2 y + 5 = 0$ and $- 3 x - 6 y + 1 = 0$

Here, $a_{1} = 1, b_{1} = 2, c_{1} = 5$ and $a_{2} = - 3, b_{2} = - 6, c_{2} = 1$

$\begin{aligned} \frac{c_{1}}{c_{2}} = \frac{5}{1} \\ ∴ & \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \end{aligned}$

$∴ \frac{a_{1}}{a_{2}} = - \frac{1}{3}, \frac{b_{1}}{b_{2}} = - \frac{2}{6} = - \frac{1}{3}$

Hence, the pair of equations has no Solution.

3 If a pair of linear equations is consistent, then the lines will be

(a) parallel

(b) always coincident

(d) always intersecting

Show Answer

Solution

and

$\begin{aligned} \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} [intersecting lines having unique Solution] \\ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} [coincident or dependent] \end{aligned}$

4 The pair of equations

y = 0

and

y = - 7

has (a) one Solution (b) two Solutions (c) infinitely many Solutions (d) no Solutiontion

Show Answer

Solution

(d) The given pair of equations are $y = 0$ and $y = - 7$ .

By graphically, both lines are parallel and having no Solution.

5 The pair of equations

x = a

and

y = b

graphically represents lines which are

(a) parallel

(b) intersecting at $(b, a)$

(d) intersecting at $(a, b)$

Show Answer

Solution

(d) By graphically in every condition, if $a, b > 0; a, b < 0, a > 0, b < 0; a < 0, b > 0$ but $a = b \neq 0$ .

The pair of equations $x = a$ and $y = b$ graphically represents lines which are intersecting at $(a, b)$ . If $a, b > 0$

Similarly, in all cases two lines intersect at $(a, b)$ .

6 For what value of

k

, do the equations

3 x - y + 8 = 0

and

6 x - k y = - 16

represent coincident lines?

(a) $\frac{1}{2}$

(b) $- \frac{1}{2}$

(d) -2

Show Answer

Solution

Given lines,

and

$\begin{aligned} (i) & \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} & = \frac{c_{1}}{c_{2}} \\ 3 x - y + 8 & = 0 \\ 6 x - k y + 16 & = 0 \end{aligned}$

Here,

and

From Eq. (i),

$\begin{matrix} \Rightarrow & 6 \\ \frac{1}{k} & = \frac{1}{2} \end{matrix}$

$\begin{aligned} a_{1} = 3, b_{1} & = - 1, c_{1} = 8 \\ a_{2} = 6, b_{2} & = - k, c_{2} = 16 \\ \frac{3}{6} & = \frac{- 1}{- k} = \frac{8}{16} \\ \frac{1}{k} & = \frac{1}{2} \\ k & = 2 \end{aligned}$

7 If the lines given by

3 x + 2 k y = 2

and

2 x + 5 y = 1

are parallel, then the value of

k

(a) $- \frac{5}{4}$

(b) $\frac{2}{5}$

(d) $\frac{3}{2}$

	$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$
Given lines, and	$3 x + 2 k y - 2 = 0$ $2 x + 5 y - 1 = 0$
Here, and	$a_{1} = 3, b_{1} = 2 k, c_{1} = - 2$ $a_{2} = 2, b_{2} = 5, c_{2} = - 1$
From Eq. (i),	$\frac{3}{2} = \frac{2 k}{5}$
$∴$	$k = \frac{15}{4}$

Show Answer

Solution

8 The value of

c

for which the pair of equations

c x - y = 2

and

6 x - 2 y = 3

will have infinitely many Solutions is

(a) 3

(b) -3

(d) no value

Show Answer

Solution

(d) Condition for infinitely many Solutions

$\begin{matrix} (i) & \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \end{matrix}$

The given lines are $c x - y = 2$ and $6 x - 2 y = 3$

Here,

$a_{1} = c, b_{1} = - 1, c_{1} = - 2$

and

$a_{2} = 6, b_{2} = - 2, c_{2} = - 3$

From Eq. (i),

$\frac{c}{6} = \frac{- 1}{- 2} = \frac{- 2}{- 3}$

Here,

$\frac{c}{6} = \frac{1}{2} and \frac{c}{6} = \frac{2}{3}$

$\Rightarrow c = 3 and c = 4$

Since, $c$ has different values.

Hence, for no value of $c$ the pair of equations will have infinitely many Solutions.

9 One equation of a pair of dependent linear equations is

- 5 x + 7 y - 2 = 0

. The second equation can be

(a) $10 x + 14 y + 4 = 0$

(b) $- 10 x - 14 y + 4 = 0$

(d) $10 x - 14 y + 4 = 0$

Show Answer

Solution

(d) Condition for dependent linear equations

$\begin{matrix} (i) & \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} = \frac{1}{k} \end{matrix}$

Given equation of line is, $- 5 x + 7 y - 2 = 0$

Here,

$\begin{aligned} a_{1} & = - 5, b_{1} = 7, c_{1} = - 2 \\ (say) & - \frac{5}{a_{2}} & = \frac{7}{b_{2}} = - \frac{2}{c_{2}} = \frac{1}{k} \\ a_{2} & = - 5 k, b_{2} = 7 k, c_{2} = - 2 k \end{aligned}$

From Eq. (i),

$\Rightarrow$

where, $k$ is any arbitrary constant. Putting $k = 2$ , then and $a_{2} = - 10, b_{2} = 14$ $c_{2} = - 4$

$∴$ The required equation of line becomes

$\begin{array}{lrl} a_{2} x + b_{2} y + c_{2} = 0 \\ \Rightarrow & - 10 x + 14 y - 4 = 0 \\ \Rightarrow & 10 x - 14 y + 4 = 0 \end{array}$

10 A pair of linear equations which has a unique Solution

x = 2

and

y = - 3

(a) $x + y = 1$ and $2 x - 3 y = - 5$

(b) $2 x + 5 y = - 11$ and $4 x + 10 y = - 22$

(d) $x - 4 y - 14 = 0$ and $5 x - y - 13 = 0$

Show Answer

Solution

(b) If $x = 2, y = - 3$ is a unique Solution of any pair of equation, then these values must satisfy that pair of equations.

From option (b),

$\begin{aligned} L H S = 2 x + 5 y = 2 (2) + 5 (- 3) = 4 - 15 = - 11 = R H S \\ L H S = 4 x + 10 y = 4 (2) + 10 (- 3) = 8 - 30 = - 22 = R H S \end{aligned}$

$and$

11 If

x = a

and

y = b

is the Solution of the equations

x - y = 2

and

x + y = 4

, then the values of

a

and

b

are, respectively (a) 3 and 5 (b) 5 and 3 (c) 3 and 1 (d) -1 and -3

Show Answer

Solution

(c) Since, $x = a$ and $y = b$ is the Solution of the equations $x - y = 2$ and $x + y = 4$ , then these values will satisfy that equations

and

$\begin{aligned} (i) & a - b = 2 \\ (ii) & a + b = 4 \end{aligned}$

On adding Eqs. (i) and (ii), we get

$2 a = 6$

$∴ a = 3 and b = 1$

12 Aruna has only

₹ 1

and

₹ 2

coins with her. If the total number of coins that she has is 50 and the amount of money with her is

₹ 75

, then the number of

₹ 1

and

₹ 2

coins are, respectively (a) 35 and 15 (b) 35 and 20 (c) 15 and 35 (d) 25 and 25

Show Answer

Solution

(d) Let number of $₹ 1$ coins $= x$

and number of $₹ 2$ coins $= y$

Now, by given conditions $x + y = 50$

Also, $x \times 1 + y \times 2 = 75$

$\Rightarrow x + 2 y = 75$

On subtracting Eq. (i) from Eq. (ii), we get

$\Rightarrow y = 25$

When $y = 25$ , then $x = 25$

$(x + 2 y) - (x + y) = 75 - 50$

13 The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. The present ages (in year) of the son and the father are, respectively (a) 4 and 24 (b) 5 and 30 (c) 6 and 36 (d) 3 and 24

Show Answer

Solution

Four years hence, it has relation by given condition,

		$(x + 4)$	$= 4 (y + 4)$
	and	$x - 4 y$	$= 12$
	$x$	$= 6 y$

On putting the value of $x$ from Eq. (ii) in Eq. (i), we get

$\begin{matrix} \Rightarrow & 2 y = 12 \\ \Rightarrow & y = 6 \end{matrix}$

When $y = 6$ , then $x = 36$

Hence, present age of father is $36 y r$ and age of son is $6 y r$ .

Very Short Answer Type Questions

1 Do the following pair of linear equations have no Solution? Justify your answer.

(i) $2 x + 4 y = 3$ and $12 y + 6 x = 6$

(ii) $x = 2 y$ and $y = 2 x$

(iii) $3 x + y - 3 = 0$ and $2 x + \frac{2}{3} y = 2$

Show Answer

Solution

Condition for no Solution $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$

(i) Yes, given pair of equations,

$\begin{aligned} 2 x + 4 y = 3 and 12 y + 6 x = 6 \\ Here, a_{1} = 2, b_{1} = 4, c_{1} = - 3, \\ a_{2} = 6, b_{2} = 12, c_{2} = - 6 \\ ∴ \frac{a_{1}}{a_{2}} = \frac{2}{6} = \frac{1}{3}, \frac{b_{1}}{b_{2}} = \frac{4}{12} = \frac{1}{3} \\ \frac{c_{1}}{c_{2}} = \frac{- 3}{- 6} = \frac{1}{2} \\ ∴ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \end{aligned}$

Hence, the given pair of linear equations has no Solution.

(ii) No, given pair of equations,

$x = 2 y and y = 2 x$

$x - 2 y = 0 and 2 x - y = 0$

Here,

$\begin{aligned} a_{1} = 1, b_{1} = - 2, c_{1} = 0 \\ a_{2} = 2, b_{2} = - 1, c_{2} = 0 \end{aligned}$

$\begin{matrix} ∴ & \frac{a_{1}}{a_{2}} = \frac{1}{2} and \frac{b_{1}}{b_{2}} = \frac{2}{1} \\ ∵ & \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \end{matrix}$

Hence, the given pair of linear equations has unique Solution.

(iii) No, given pair of equations,

$3 x + y - 3 = 0 and 2 x + \frac{2}{3} y - 2 = 0$

Here,

$\begin{aligned} a_{1} = 3, b_{1} = 1, c_{1} = - 3, \\ a_{2} = 2, b_{2} = \frac{2}{3}, c_{2} = - 2 \\ \frac{a_{1}}{a_{2}} = \frac{3}{2}, \frac{b_{1}}{b_{2}} = \frac{1}{2 / 3} = \frac{3}{2} \\ \frac{c_{1}}{c_{2}} = \frac{- 3}{- 2} = \frac{3}{2} \end{aligned}$

$\begin{matrix} ∴ & \frac{a_{1}}{a_{2}} = \frac{3}{2}, \frac{b_{1}}{b_{2}} = \frac{1}{2 / 3} = \frac{3}{2} \\ ∵ & \frac{c_{1}}{c_{2}} = \frac{- 3}{- 2} = \frac{3}{2} \\ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} = \frac{3}{2} \end{matrix}$

Hence, the given pair of linear equations is coincident and having infinitely many Solutions.

2 Do the following equations represent a pair of coincident lines? Justify your answer.

(i) $3 x + \frac{1}{7} y = 3$ and $7 x + 3 y = 7$

(ii) $- 2 x - 3 y = 1$ and $6 y + 4 x = - 2$

(iii) $\frac{x}{2} + y + \frac{2}{5} = 0$ and $4 x + 8 y + \frac{5}{16} = 0$

Show Answer

Solution

Condition for coincident lines,

$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$

(i) No, given pair of linear equations

and

$3 x + \frac{y}{7} - 3 = 0$

where,

$\begin{matrix} 7 x + 3 y - 7 = 0, \\ a_{1} = 3, b_{1} = \frac{1}{7}, c_{1} = - 3; \\ a_{2} = 7, b_{2} = 3, c_{2} = - 7 \end{matrix}$

$Now, \frac{a_{1}}{a_{2}} = \frac{3}{7}, \frac{b_{1}}{b_{2}} = \frac{1}{21}, \frac{c_{1}}{c_{2}} = \frac{3}{7}$

Hence, the given pair of linear equations has unique Solution. (ii) Yes, given pair of linear equations

$\begin{aligned} - 2 x - 3 y - 1 = 0 and 6 y + 4 x + 2 = 0 \\ where, a_{1} = - 2, b_{1} = - 3, c_{1} = - 1; \\ a_{2} = 4, b_{2} = 6, c_{2} = 2 \\ \frac{a_{1}}{a_{2}} = - \frac{2}{4} = - \frac{1}{2} \\ \frac{b_{1}}{b_{2}} = - \frac{3}{6} = - \frac{1}{2}, \frac{c_{1}}{c_{2}} = - \frac{1}{2} \\ ∵ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} = - \frac{1}{2} \end{aligned}$

Hence, the given pair of linear equations is coincident.

(iii) No, the given pair of linear equations are

Here,

$\frac{x}{2} + y + \frac{2}{5} = 0 and 4 x + 8 y + \frac{5}{16} = 0$

$a_{1} = \frac{1}{2}, b_{1} = 1, c_{1} = \frac{2}{5}$

$a_{2} = 4, b_{2} = 8, c_{2} = \frac{5}{16}$

Now,

$\begin{aligned} \frac{a_{1}}{a_{2}} = \frac{1}{8}, \frac{b_{1}}{b_{2}} = \frac{1}{8}, \frac{c_{1}}{c_{2}} = \frac{32}{25} \\ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \end{aligned}$

Hence, the given pair of linear equations has no Solution.

3 Are the following pair of linear equations consistent? Justify your answer.

(i) $- 3 x - 4 y = 12$ and $4 y + 3 x = 12$

(ii) $\frac{3}{5} x - y = \frac{1}{2}$ and $\frac{1}{5} x - 3 y = \frac{1}{6}$

(iii) $2 a x + b y = a$ and $4 a x + 2 b y - 2 a = 0; a, b \neq 0$

(iv) $x + 3 y = 11$ and $2 (2 x + 6 y) = 22$

Show Answer

Solution

Conditions for pair of linear equations are consistent

and

$\begin{aligned} \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} & [unique Solution] \\ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} & [infinitely many Solutions] \end{aligned}$

(i) No, the given pair of linear equations

$\begin{aligned} - 3 x - 4 y = 12 and 3 x + 4 y = 12 \\ Here, & a_{1} = - 3, b_{1} = - 4, c_{1} = - 12 \\ a_{2} = 3, b_{2} = 4, c_{2} = - 12 \\ Now, & \frac{a_{1}}{a_{2}} = - \frac{3}{3} = - 1, \frac{b_{1}}{b_{2}} = - \frac{4}{4} = - 1, \frac{c_{1}}{c_{2}} = \frac{- 12}{- 12} = 1 \\ ∵ & \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \end{aligned}$

Hence, the pair of linear equations has no Solution, i.e., inconsistent. (ii) Yes, the given pair of linear equations

$\begin{aligned} \frac{3}{5} x - y = \frac{1}{2} and \frac{1}{5} x - 3 y = \frac{1}{6} \\ Here, \begin{aligned} a_{1} & = \frac{3}{5}, b_{1} = - 1, c_{1} = - \frac{1}{2} \\ a_{2} & = \frac{1}{5}, b_{2} = - 3, c_{2} = - \frac{1}{6} \\ and \frac{a_{1}}{a_{2}} & = \frac{3}{1}, \frac{b_{1}}{b_{2}} = \frac{- 1}{- 3} = \frac{1}{3}, \frac{c_{1}}{c_{2}} = \frac{3}{1} & ∵ \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \end{aligned} \end{aligned}$

Hence, the given pair of linear equations has unique Solution, i.e., consistent.

(iii) Yes, the given pair of linear equations

$\begin{aligned} 2 a x + b y - a = 0 \\ and 4 a x + 2 b y - 2 a = 0; a, b \neq 0 \\ \begin{aligned} Here, a_{1} & = 2 a, b_{1} = b, c_{1} = - a; \\ a_{2} & = 4 a, b_{2} = 2 b, c_{2} = - 2 a \\ Now, \frac{a_{1}}{a_{2}} & = \frac{2 a}{4 a} = \frac{1}{2}, \frac{b_{1}}{b_{2}} = \frac{b}{2 b} = \frac{1}{2}, \frac{c_{1}}{c_{2}} = \frac{- a}{- 2 a} = \frac{1}{2} \\ ∵ \frac{a_{1}}{a_{2}} & = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} = \frac{1}{2} \end{aligned} \end{aligned}$

Hence, the given pair of linear equations has infinitely many Solutions, i.e., consistent or dependent.

(iv) No, the given pair of linear equations

$\begin{aligned} x + 3 y = 11 and 2 x + 6 y = 11 \\ a_{1} = 1, b_{1} = 3, c_{1} = - 11 \\ a_{2} = 2, b_{2} = 6, c_{2} = - 11 \\ Now, \frac{a_{1}}{a_{2}} & = \frac{1}{2}, \frac{b_{1}}{b_{2}} = \frac{3}{6} = \frac{1}{2}, \frac{c_{1}}{c_{2}} = \frac{- 11}{- 11} = 1 \\ ∴ & \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \end{aligned}$

Hence, the pair of linear equation have no Solution i.e., inconsistent.

4 For the pair of equations

λ x + 3 y + 7 = 0

and

2 x + 6 y - 14 = 0

. To have infinitely many Solutions, the value of

λ

should be 1 . Is the statement true? Give reasons.

Show Answer

Solution

No, the given pair of linear equations

$λ x + 3 y + 7 = 0 and 2 x + 6 y - 14 = 0$

$Here, a_{1} = λ, b_{1} = 3, c_{1} = 7; a_{2} = 2, b_{2} = 6, c_{2} = - 14$

If $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$ , then system has infinitely many Solutions.

$\begin{matrix} \Rightarrow & \frac{λ}{2} = \frac{3}{6} = - \frac{7}{14} \\ ∵ & \frac{λ}{2} = \frac{3}{6} \Rightarrow λ = 1 \\ and & \frac{λ}{2} = - \frac{7}{14} \Rightarrow λ = - 1 \end{matrix}$

Hence, $λ = - 1$ does not have a unique value.

So, for no value of $λ$ the given pair of linear equations has infinitely many Solutions.

5 For all real values of

c

, the pair of equations

x - 2 y = 8

and

5 x - 10 y = c

have a unique Solution. Justify whether it is true or false.

Show Answer

Solution

False, the given pair of linear equations

and

$\begin{aligned} x - 2 y - 8 & = 0 \\ 5 x - 10 y - c & = 0 \\ a_{1} & = 1, b_{1} = - 2, c_{1} = - 8 \\ a_{2} & = 5, b_{2} = - 10, c_{2} = - c \\ \frac{a_{1}}{a_{2}} & = \frac{1}{5}, \frac{b_{1}}{b_{2}} = \frac{- 2}{- 10} = \frac{1}{5} \\ \frac{c_{1}}{c_{2}} & = \frac{- 8}{- c} = \frac{8}{c} \end{aligned}$

Here,

Now,

But if $c = 40$ (real value), then the ratio $\frac{c_{1}}{c_{2}}$ becomes $\frac{1}{5}$ and then the system of linear equations has an infinitely many Solutions.

Hence, at $c = 40$ , the system of linear equations does not have a unique Solution.

6 The line represented by

x = 7

is parallel to the

X

-axis, justify whether the statement is true or not.

Show Answer

Solution

Not true, by graphically, we observe that $x = 7$ line is parallel to $Y$ -axis and perpendicular to $X$ -axis.

Short Answer Type Questions

1 For which value(s) of $λ$ , do the pair of linear equations $λ x + y = λ^{2}$ and $x + λ y = 1$ have

(i) no Solution? (ii) infinitely many Solutions?

(iii) a unique Solution?

Show Answer

Solution

The given pair of linear equations is

$λ x + y = λ^{2} and x + λ y = 1$

Here,

$\begin{aligned} a_{1} = λ, b_{1} = 1, c_{1} = - λ^{2} \\ a_{2} = 1, b_{2} = λ, c_{2} = - 1 \end{aligned}$

(i) For no Solution,

$\begin{aligned} \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \\ \Rightarrow & \frac{λ}{1} = \frac{1}{λ} \neq \frac{- λ^{2}}{- 1} \end{aligned}$

$\begin{aligned} \Rightarrow & \frac{λ}{1} = \frac{λ^{2}}{1} \\ \Rightarrow & λ (λ - 1) = 0 \end{aligned}$

When $λ \neq 0$ , then $λ = 1$

Here, we take only $λ = - 1$ because at $λ = 1$ the system of linear equations has infinitely many Solutions.

(ii) For infinitely many Solutions,

$\begin{aligned} \frac{a_{1}}{a_{2}} & = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \\ \Rightarrow & \frac{λ}{1} & = \frac{1}{λ} = \frac{λ^{2}}{1} \\ \Rightarrow & \frac{λ}{1} & = \frac{λ^{2}}{1} \\ \Rightarrow & λ (λ - 1) & = 0 \end{aligned}$

When $λ \neq 0$ , then $λ = 1$

(iii) For a unique Solution,

$\begin{aligned} \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \\ \Rightarrow \frac{λ}{1} \neq \frac{1}{λ} \\ \Rightarrow & λ^{2} \neq 1 \\ \Rightarrow & λ \neq \pm 1 \end{aligned}$

$\begin{array}{lll} \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \Rightarrow \frac{λ}{1} \neq \frac{1}{λ} \\ \Rightarrow & λ^{2} \neq 1 \\ \Rightarrow & λ \neq \pm 1 \end{array}$

So, all real values of $λ$ except $\pm 1$

2 For which value (s) of

k

will the pair of equations

$\begin{aligned} k x + 3 y & = k - 3 \\ 12 x + k y & = k \end{aligned}$

has no Solution?

Show Answer

Solution

Given pair of linear equations is

and

$\begin{matrix} (i) & k x + 3 y = k - 3 \end{matrix}$

$\begin{matrix} (ii) & 12 x + k y = k \end{matrix}$

On comparing with $a x + b y + c = 0$ , we get

$\begin{aligned} a_{1} = k, b_{1} = 3 and c_{1} = - (k - 3) \\ a_{2} = 12, b_{2} = k and c_{2} = - k \end{aligned}$

For no Solution of the pair of linear equations,

[from Eq. (i)] [from Eq. (ii)]

$\begin{matrix} Taking first two parts, we get \\ \Rightarrow & \frac{k}{12} = \frac{3}{k} \\ \Rightarrow & k^{2} = 36 \\ \Rightarrow & k = \pm 6 \end{matrix}$

$\begin{aligned} \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \\ \frac{k}{12} = \frac{3}{k} \neq \frac{- (k - 3)}{- k} \end{aligned}$

Taking last two parts, we get

$\begin{array}{lr} \frac{3}{k} \neq \frac{k - 3}{k} \\ \Rightarrow & 3 k \neq k (k - 3) \\ \Rightarrow & 3 k - k (k - 3) \neq 0 \\ \Rightarrow & k (3 - k + 3) \neq 0 \\ \Rightarrow & k (6 - k) \neq 0 \\ \Rightarrow & k \neq 0 and k \neq 6 \end{array}$

Hence, required value of $k$ for which the given pair of linear equations has no Solution is -6 .

3 For which values of

a

and

b

will the following pair of linear equations has infinitely many Solutions?

$\begin{matrix} x + 2 y = 1 \\ (a - b) x + (a + b) y = a + b - 2 \end{matrix}$

Show Answer

Solution

Given pair of linear equations are

$x + 2 y$	$= 1$	(i)
and $(a - b) x + (a + b) y$	$= a + b - 2$	$\dots$ (ii)
On comparing with $a x + b y + c$	$= 0$ , we get	[from Eq. (i)]
$a_{1}$	$= 1, b_{1} = 2$ and $c_{1} = - 1$	[from Eq. (ii)]
$a_{2}$	$= (a - b), b_{2} = (a + b)$

For infinitely many Solutions of the the pairs of linear equations,

$\begin{aligned} \frac{a_{1}}{a_{2}} & = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \\ \Rightarrow \frac{1}{a - b} & = \frac{2}{a + b} = \frac{- 1}{- (a + b - 2)} \end{aligned}$

Taking first two parts,

$\begin{matrix} (iii) & \begin{array}{lr} \frac{1}{a - b} & = \frac{2}{a + b} \\ \Rightarrow & a + b = 2 a - 2 b \\ \Rightarrow & 2 a - a = 2 b + b \\ \Rightarrow & a = 3 b \end{array} \end{matrix}$

$\begin{array}{lll} \frac{1}{a - b} & = \frac{2}{a + b} \\ \Rightarrow & a + b & = 2 a - 2 b \\ \Rightarrow & 2 a - a & = 2 b + b \\ \Rightarrow & a & = 3 b \end{array}$

Taking last two parts,

$\begin{aligned} \frac{2}{a + b} & = \frac{1}{(a + b - 2)} \\ \Rightarrow & 2 a + 2 b - 4 & = a + b \\ (iv) & \Rightarrow & a + b & = 4 \end{aligned}$

Now, put the value of a from Eq. (iii) in Eq. (iv), we get

$3 b + b = 4$

$\begin{matrix} \Rightarrow & 4 b & = 4 \\ \Rightarrow & b & = 1 \end{matrix}$

Put the value of $b$ in Eq. (iii), we get

$\Rightarrow a = 3$

So, the values $(a, b) = (3, 1)$ satisfies all the parts. Hence, required values of $a$ and $b$ are 3 and 1 respectively for which the given pair of linear equations has infinitely many Solutions.

4 Find the values of

p

in (i) to (iv) and

p

and

q

in (v) for the following pair of equations

(i) $3 x - y - 5 = 0$ and $6 x - 2 y - p = 0$ , if the lines represented by these equations are parallel.

(ii) $- x + p y = 1$ and $p x - y = 1$ , if the pair of equations has no Solution.

(iii) $- 3 x + 5 y = 7$ and $2 p x - 3 y = 1$ ,

if the lines represented by these equations are intersecting at a unique point.

(iv) $2 x + 3 y - 5 = 0$ and $p x - 6 y - 8 = 0$ ,

if the pair of equations has a unique Solution.

(v) $2 x + 3 y = 7$ and $2 p x + p y = 28 - q y$ ,

if the pair of equations has infinitely many Solutions.

Show Answer

Solution

(i) Given pair of linear equations is $3 x - y - 5 = 0$ $6 x - 2 y - p = 0$ and On comparing with $a x + b y + c = 0$ , we get and

$\begin{aligned} a_{1} = 3, b_{1} = - 1 \\ c_{1} = - 5 \\ a_{2} = 6, b_{2} = - 2 \end{aligned}$

$c_{2} = - p$

and [from Eq. (ii)]

Since, the lines represented by these equations are parallel, then

$\begin{matrix} \frac{a_{1}}{a_{2}} & = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \\ \frac{3}{6} & = \frac{- 1}{- 2} \neq \frac{- 5}{- p} \\ Taking last two parts, we get & \frac{- 1}{- 2} \neq \frac{- 5}{- p} \\ \Rightarrow & \frac{1}{2} \neq \frac{5}{p} \\ \Rightarrow & p \neq 10 \end{matrix}$

Hence, the given pair of linear equations are parallel for all real values of $p$ except 10 i.e., $p \in R - 10$ .

(ii) Given pair of linear equations is

$\begin{aligned} - x + p y - 1 = 0 \\ and p x - y - 1 = 0 \\ On comparing with a x + b y + c = 0, we get \\ \begin{array}{c} a_{1} = - 1, b_{1} = p and c_{1} = - 1 \\ a_{2} = p, b_{2} = - 1 and c_{2} = - 1 \end{array} \end{aligned}$

Since, the pair of linear equations has no Solution i.e., both lines are parallel to each other.

$∴ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \Rightarrow \frac{- 1}{p} = \frac{p}{- 1} \neq \frac{- 1}{- 1}$

Taking last two parts, we get

$\begin{aligned} \frac{p}{- 1} \neq \frac{- 1}{- 1} \\ \Rightarrow p \neq - 1 \end{aligned}$

Taking first two parts, we get

$\begin{array}{ll} \frac{- 1}{p} = \frac{p}{- 1} \\ \Rightarrow & p^{2} = 1 \\ \Rightarrow & p = \pm 1 \\ but & p \neq - 1 \\ ∴ & p = 1 \end{array}$

Hence, the given pair of linear equations has no Solution for $p = 1$ .

(iii) Given, pair of linear equations is

$- 3 x + 5 y - 7 = 0$ $\dots$ (i)
and $2 p x - 3 y - 1 = 0$ $\dots$ (ii)

On comparing with $a x + b y + c = 0$ , we get

$a_{1} = - 3, b_{1} = 5$

and $c_{1} = - 7$ [from Eq. (i)]

$a_{2} = 2 p, b_{2} = - 3$

and $c_{1} = - 1$ [from Eq. (ii)]

Since, the lines are intersecting at a unique point i.e., it has a unique Solution.

$\begin{matrix} ∴ & \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \\ \Rightarrow & \frac{- 3}{2 p} \neq \frac{5}{- 3} \\ \Rightarrow & 9 \neq 10 p \\ \Rightarrow & p \neq \frac{9}{10} . \end{matrix}$

Hence, the lines represented by these equations are intersecting at a unique point for all real values of $p$ except $\frac{9}{10}$

(iv) Given pair of linear equations is

$\begin{aligned} 2 x + 3 y - 5 = 0 \\ p x - 6 y - 8 = 0 \\ a_{1} = 2, b_{1} = 3 \\ c_{1} = - 5 \\ a_{2} = p, b_{2} = - 6 \\ c_{2} = - 8 \end{aligned}$

Since, the pair of linear equations has a unique Solution.

$\begin{matrix} ∴ & \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \\ \Rightarrow & \frac{2}{p} \neq \frac{3}{- 6} \\ \Rightarrow & p \neq - 4 \end{matrix}$

Hence, the pair of linear equations has a unique Solution for all values of $p$ except -4 i.e.,

$p \in R - - 4, .$

(v) Given pair of linear equations is

$\begin{aligned} (i) & 2 x + 3 y & = 7 \\ and & 2 p x + p y & = 28 - q y \\ (ii) & \Rightarrow & 2 p x + (p + q) y & = 28 \end{aligned}$

On comparing with $a x + b y + c = 0$ , we get

$\begin{aligned} a_{1} = 2, b_{1} = 3 \\ c_{1} = - 7 \\ a_{2} = 2 p, b_{2} = (p + q) \end{aligned}$

$\begin{matrix} and & c_{1} = - 7 \\ a_{2} = 2 p, b \\ and & c_{2} = - 28 \end{matrix}$

Since, the pair of equations has infinitely many Solutions i.e., both lines are coincident.

$\begin{matrix} ∴ & \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \\ \Rightarrow & \frac{2}{2 p} = \frac{3}{(p + q)} = \frac{- 7}{- 28} \end{matrix}$

Taking first and third parts, we get

$\begin{aligned} \frac{2}{2 p} & = \frac{- 7}{- 28} \\ \Rightarrow & \frac{1}{p} & = \frac{1}{4} \\ \Rightarrow & p & = 4 \end{aligned}$

Again, taking last two parts, we get

$\begin{aligned} \frac{3}{p + q} = \frac{- 7}{- 28} \Rightarrow \frac{3}{p + q} = \frac{1}{4} \\ \Rightarrow p + q = 12 \\ \Rightarrow 4 + q = 12 [∵ p = 4] \\ ∴ q = 8 \end{aligned}$

Here, we see that the values of $p = 4$ and $q = 8$ satisfies all three parts.

Hence, the pair of equations has infinitely many Solutions for the values of $p = 4$ and $q = 8$

5 Two straight paths are represented by the equations

x - 3 y = 2

and

- 2 x + 6 y = 5

. Check whether the paths cross each other or not.

Show Answer

Solution

Given linear equations are

$x - 3 y - 2 = 0$

$\begin{matrix} (i) & - 2 x + 6 y - 5 = 0 \end{matrix}$

On comparing both the equations with $a x + b y + c = 0$ , we get

and $a_{1} = 1, b_{1} = - 3$

$c_{1} = - 2 [from Eq. (i)]$

and $a_{2} = - 2, b_{2} = 6$

$c_{2} = - 5$ [from Eq. (ii)]

Here, $\frac{a_{1}}{a_{2}} = \frac{1}{- 2}$

$\frac{b_{1}}{b_{2}} = \frac{- 3}{6} = - \frac{1}{2}$ and $\frac{c_{1}}{c_{2}} = \frac{- 2}{- 5} = \frac{2}{5}$

i.e., $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$ [parallel lines]

i.e.,

Hence, two straight paths represented by the given equations never cross each other, because they are parallel to each other.

6 Write a pair of linear equations which has the unique Solution

x = - 1

and

y = 3

. How many such pairs can you write?

Show Answer

Solution

Condition for the pair of system to have unique Solution

$\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}$

Let the equations are,

and

$\begin{matrix} a_{1} x + b_{1} y + c_{1} = 0 \\ a_{2} x + b_{2} y + c_{2} = 0 \end{matrix}$

Since, $x = - 1$ and $y = 3$ is the unique Solution of these two equations, then

$\begin{matrix} (ii) & \begin{matrix} \Rightarrow & a_{1} (- 1) + b_{1} (3) + c_{1} = 0 \\ and & - a_{1} + 3 b_{1} + c_{1} = 0 \\ \Rightarrow & a_{2} (- 1) + b_{2} (3) + c_{2} = 0 \\ - a_{2} + 3 b_{2} + c_{2} = 0 \end{matrix} \end{matrix}$

So, the different values of $a_{1}, a_{2}, b_{1}, b_{2}, c_{1}$ and $c_{2}$ satisfy the Eqs. (i) and (ii).

Hence, infinitely many pairs of linear equations are possible.

7 If

2 x + y = 23

and

4 x - y = 19

, then find the values of

5 y - 2 x

and

\frac{y}{x} - 2

Show Answer

Solution

Given equations are

and | $2 x + y = 23$ | | —: | | $4 x - y = 19$ |

On adding both equations, we get

$\begin{matrix} (ii) & 6 x = 42 \Rightarrow x = 7 \end{matrix}$

Put the value of $x$ in Eq. (i), we get

$\begin{array}{lrlrl} \Rightarrow & 14 + y & = 23 \\ \Rightarrow & y & = 23 - 14 \\ \Rightarrow & y & = 9 \\ We have, & 5 y - 2 x & = 5 \times 9 - 2 \times 7 \\ = 45 - 14 = 31 \\ and & \frac{y}{x} - 2 = \frac{4}{x} - 2 & = \frac{9}{7} - 2 = \frac{9 - 14}{7} = - \frac{5}{7} \end{array}$

We have,

Hence, the values of $(5 y - 2 x)$ and $(\frac{y}{x} - 2)$ are 31 and $\frac{- 5}{7}$ , respectively.

8 Find the values of

x

and

y

in the following rectangle

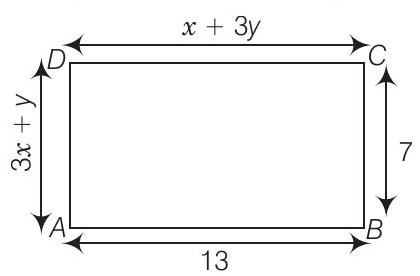
Show Answer

Solution

By property of rectangle,

Lengths are equal, i.e.,

$\Rightarrow$

$\begin{aligned} C D & = A B \\ (i) & x + 3 y & = 13 \\ A D & = B C \\ (ii) & 3 x + y & = 7 \end{aligned}$

On multiplying Eq. (ii) by 3 and then subtracting Eq. (i), we get

$\begin{matrix} 9 x + 3 y = 21 \\ x + 3 y = 13 \\ 8 x = 8 \\ x = 1 \end{matrix}$

On putting $x = 1$ in Eq. (i), we get

$3 y = 12 \Rightarrow y = 4$

Hence, the required values of $x$ and $y$ are 1 and 4, respectively.

9 Solve the following pairs of equations

(i) $x + y = 3.3$ , $\frac{0.6}{3 x - 2 y} = - 1, 3 x - 2 y \neq 0$

(ii) $\frac{x}{3} + \frac{y}{4} = 4$ , $\frac{5 x}{6} - \frac{y}{8} = 4$

(iii) $4 x + \frac{6}{y} = 15$ , $6 x - \frac{8}{y} = 14, y \neq 0$

(iv) $\frac{1}{2 x} - \frac{1}{y} = - 1$ $\frac{1}{x} + \frac{1}{2 y} = 8, x, y \neq 0$

(v) $43 x + 67 y = - 24$ , $67 x + 43 y = 24$

(vi) $\frac{x}{a} + \frac{y}{b} = a + b$ , $\frac{x}{a^{2}} + \frac{y}{b^{2}} = 2, a, b \neq 0$

(vii) $\frac{2 x y}{x + y} = \frac{3}{2^{'}}$ $\frac{x y}{2 x - y} = \frac{- 3}{10}, x + y \neq 0, 2 x - y \neq 0$

Show Answer

Solution

(i) Given pair of linear equations are is

$\begin{matrix} (i) & \begin{matrix} + y & = 3.3 \\ \frac{0.6}{3 x - 2 y} & = - 1 \end{matrix} \end{matrix}$

$\begin{matrix} (ii) & \begin{array}{rrr} \Rightarrow & 0.6 = - 3 x + 2 y \\ \Rightarrow & 3 x - 2 y = - 0.6 \end{array} \end{matrix}$

Now, multiplying Eq. (i) by 2 and then adding with Eq. (ii), we get

$\begin{aligned} \Rightarrow & 2 x + 2 y & = 6.6 \\ \Rightarrow & 3 x - 2 y & = - 0.6 \\ 5 x & = 6 \Rightarrow x = \frac{6}{5} = 1.2 \end{aligned}$

Now, put the value of $x$ in Eq. (i), we get

$\begin{aligned} 1.2 + y = 3.3 \\ \Rightarrow & y = 3.3 - 1.2 \\ \Rightarrow & y = 2.1 \end{aligned}$

Hence, the required values of $x$ and $y$ are 1.2 and 2.1, respectively.

(ii) Given, pair of linear equations is $\frac{x}{3} + \frac{y}{4} = 4$

On multiplying both sides by $LCM (3, 4) = 12$ , we get $4 x + 3 y = 48$

$\frac{5 x}{6} - \frac{y}{8} = 4$

On multiplying both sides by $L C M (6, 8) = 24$ , we get

$\begin{matrix} (ii) & 20 x - 3 y = 96 \end{matrix}$

Now, adding Eqs. (i) and (ii), we get

$24 x = 144$

$\Rightarrow x = 6$

Now, put the value of $x$ in Eq. (i), we get

$\begin{aligned} 4 \times 6 + 3 y & = 48 \\ \Rightarrow & 3 y & = 48 - 24 \\ \Rightarrow & 3 y & = 24 \Rightarrow y = 8 \end{aligned}$

Hence, the required values of $x$ and $y$ are 6 and 8 , respectively.

(iii) Given pair of linear equations are

$\begin{aligned} (i) & 4 x + \frac{6}{y} = 15 \\ (ii) & 6 x - \frac{8}{y} = 14, y \neq 0 \end{aligned}$

and

Let $u = \frac{1}{y}$ , then above equation becomes

$\begin{aligned} (iii) & 4 x + 6 u = 15 \\ (iv) & 6 x - 8 u = 14 \end{aligned}$

On multiplying Eq. (iii) by 8 and Eq. (iv) by 6 and then adding both of them, we get

$\begin{aligned} 32 x + 48 u & = 120 \\ 36 x - 48 u & = 84 \Rightarrow 68 x = 204 \\ x & = 3 \end{aligned}$

$\Rightarrow$

Now, put the value of $x$ in Eq. (iii), we get

$\begin{aligned} \Rightarrow & 4 \times 3 + 6 u & = 15 \\ \Rightarrow & 6 u & = 15 - 12 \Rightarrow 6 u = 3 \\ \Rightarrow & u & = \frac{1}{2} \Rightarrow \frac{1}{y} = \frac{1}{2} \\ \Rightarrow & y & = 2 \end{aligned}$

$\Rightarrow u = \frac{1}{2} \Rightarrow \frac{1}{y} = \frac{1}{2} ∵ u = \frac{1}{y}$

Hence, the required values of $x$ and $y$ are 3 and 2, respectively.

(iv) Given pair of linear equations is

and

$\begin{aligned} (i) & \frac{1}{2 x} - \frac{1}{y} = - 1 \\ (ii) & \frac{1}{x} + \frac{1}{2 y} = 8, x, y \neq 0 \end{aligned}$

Let $u = \frac{1}{x}$ and $v = \frac{1}{y}$ , then the above equations becomes

$\begin{array}{lc} \frac{u}{2} - v = - 1 \\ \Rightarrow & u - 2 v = - 2 \\ and & u + \frac{v}{2} = 8 \\ \Rightarrow & 2 u + v = 16 \end{array}$

On, multiplying Eq. (iv) by 2 and then adding with Eq. (iii), we get

$\begin{aligned} 4 u + 2 v & = 32 \\ u - 2 v & = - 2 \\ 5 u & = 30 \\ \Rightarrow u & = 6 \end{aligned}$

Now, put the value of $u$ in Eq. (iv), we get

$2 \times 6 + v = 16$

$\begin{matrix} \Rightarrow & v = 16 - 12 = 4 \\ \Rightarrow & v = 4 \\ ∴ & x = \frac{1}{u} = \frac{1}{6} and y = \frac{1}{v} = \frac{1}{4} \end{matrix}$

Hence, the required values of $x$ and $y$ are $\frac{1}{6}$ and $\frac{1}{4}$ , respectively.

(v) Given pair of linear equations is

$\begin{aligned} (i) & 43 x + 67 y = - 24 \\ (ii) & 67 x + 43 y = 24 \end{aligned}$

and

On multiplying Eq. (i) by 43 and Eq. (ii) by 67 and then subtracting both of them, we get

$\begin{aligned} (67)^{2} x + 43 \times 67 y = 24 \times 67 \\ (43)^{2} x + 43 \times 67 y = - 24 \times 43 \\ (67)^{2} - (43)^{2} x = 24 (67 + 43) \end{aligned}$

$\begin{aligned} \Rightarrow (67 + 43) (67 - 43) x = 24 \times 110 [∵ (a^{2} - b^{2}) = (a - b) (a + b)] \\ \Rightarrow 110 \times 24 x = 24 \times 110 \\ \Rightarrow x = 1 \end{aligned}$

Now, put the value of $x$ in Eq. (i), we get

$\begin{aligned} 43 \times 1 + 67 y & = - 24 \\ 67 y & = - 24 - 43 \end{aligned}$

$\begin{matrix} \Rightarrow & 67 y = - 24 \\ \Rightarrow & 67 y = - 67 \\ \Rightarrow & y = - 1 \end{matrix}$

Hence, the required values of $x$ and $y$ are 1 and -1 , respectively. (vi) Given pair of linear equations is

and

$\begin{aligned} (i) & \frac{x}{a} + \frac{y}{b} & = a + b \\ (ii) & \frac{x}{a^{2}} + \frac{y}{b^{2}} & = 2, a, b \neq 0 \end{aligned}$

On multiplying Eq. (i) by $\frac{1}{a}$ and then subtracting from Eq. (ii), we get

$\begin{aligned} \frac{x}{a^{2}} + \frac{y}{b^{2}} & = 2 \\ \frac{x}{a^{2}} + \frac{y}{a b} & = 1 + \frac{b}{a} \\ \frac{- 1}{y \frac{1}{b^{2}} - \frac{1}{a b}} & = 2 - 1 - \frac{b}{a} \\ \Rightarrow y \frac{a - b}{a b^{2}} & = 1 - \frac{b}{a} = \frac{a - b}{a} \\ \Rightarrow y & = \frac{a b^{2}}{a} \Rightarrow y = b^{2} \end{aligned}$

Now, put the value of $y$ in Eq. (ii), we get

$\begin{matrix} \Rightarrow & \frac{x}{a^{2}} + \frac{b^{2}}{b^{2}} & = 2 \\ \Rightarrow & \frac{x}{a^{2}} & = 2 - 1 = 1 \\ x & = a^{2} \end{matrix}$

Hence, the required values of $x$ and $y$ are $a^{2}$ and $b^{2}$ , respectively.

(vii) Given pair of equations is

$\begin{matrix} \Rightarrow & \frac{2 x y}{x + y} = \frac{3}{2}, where x + y \neq 0 \\ \Rightarrow & \frac{x + y}{2 x y} = \frac{2}{3} \\ \Rightarrow & \frac{x}{x y} + \frac{y}{x y} = \frac{4}{3} \\ and & \frac{1}{y} + \frac{1}{x} = \frac{4}{3} \\ \Rightarrow & \frac{x y}{2 x - y} = \frac{- 3}{10}, where 2 x - y \neq 0 \\ \Rightarrow & \frac{2 x - y}{x y} = \frac{- 10}{3} \\ \Rightarrow & \frac{2 x}{x y} - \frac{y}{x y} = \frac{- 10}{3} \\ \Rightarrow & \frac{2}{y} - \frac{1}{x} = \frac{- 10}{3} \end{matrix}$

Now, put $\frac{1}{x} = u$ and $\frac{1}{y} = v$ , then the pair of equations becomes

and

$\begin{aligned} (iii) & v + u & = \frac{4}{3} \\ (iv) & 2 v - u & = \frac{- 10}{3} \end{aligned}$

On adding both equations, we get

$\begin{aligned} \Rightarrow & 3 v & = \frac{4}{3} - \frac{10}{3} = \frac{- 6}{3} \\ \Rightarrow & 3 v & = - 2 \\ v & = \frac{- 2}{3} \end{aligned}$

Now, put the value of $v$ in Eq. (iii), we get

$\begin{aligned} \frac{- 2}{3} + u & = \frac{4}{3} \\ u & = \frac{4}{3} + \frac{2}{3} = \frac{6}{3} = 2 \\ x & = \frac{1}{u} = \frac{1}{2} \\ and & y & = \frac{1}{v} = \frac{1}{(- 2 / 3)} = \frac{- 3}{2} \end{aligned}$

Hence, the required values of $x$ and $y$ are $\frac{1}{2}$ and $\frac{- 3}{2}$ , respectively.

10 Find the Solution of the pair of equations

\frac{x}{10} + \frac{y}{5} - 1 = 0

and

\frac{x}{8} + \frac{y}{6} = 15

and find

λ

, if

y = λ x + 5

Show Answer

Solution

Given pair of equations is

and

$\begin{aligned} (i) & \frac{x}{10} + \frac{y}{5} - 1 & = 0 \\ (ii) & \frac{x}{8} + \frac{y}{6} & = 15 \end{aligned}$

Now, multiplying both sides of Eq. (i) by $L C M (10, 5) = 10$ , we get

$x + 2 y - 10 = 0$

$\begin{matrix} (iii) & \Rightarrow x + 2 y = 10 \end{matrix}$

Again, multiplying both sides of Eq. (iv) by $L C M (8, 6) = 24$ , we get

$\begin{matrix} (iv) & 3 x + 4 y = 360 \end{matrix}$

On, multiplying Eq. (iii) by 2 and then subtracting from Eq. (iv), we get

$\begin{matrix} 3 x + 4 y = 360 \\ 2 x + 4 y = 20 \\ - - \\ x = 340 \end{matrix}$

Put the value of $x$ in Eq. (iii), we get

$\begin{aligned} 340 + 2 y & = 10 \\ \Rightarrow & 2 y & = 10 - 340 = - 330 \\ \Rightarrow & y & = - 165 \end{aligned}$

Given that, the linear relation between $x, y$ and $λ$ is

$y = λ x + 5$

Now, put the values of $x$ and $y$ in above relation, we get

$\begin{aligned} \Rightarrow & 340 λ & = - 170 \\ \Rightarrow & λ & = - \frac{1}{2} \end{aligned}$

Hence, the Solution of the pair of equations is $x = 340, y = - 165$ and the required value of $λ$ is $- \frac{1}{2}$ .

11 By the graphical method, find whether the following pair of equations are consistent or not. If consistent, solve them.

(i) $3 x + y + 4 = 0, 6 x - 2 y + 4 = 0$

(ii) $x - 2 y = 6, 3 x - 6 y = 0$

(iii) $x + y = 3, 3 x + 3 y = 9$

Show Answer

Solution

(i) Given pair of equations is

$\begin{aligned} 3 x + y + 4 = 0 \\ \begin{array}{c} and 6 x - 2 y + 4 = 0 \\ On comparing with a x + b y + c = 0, we get \end{array} \\ a_{1} = 3, b_{1} = 1 \\ c_{1} = 4 \\ a_{2} = 6, b_{2} = - 2 \\ and \\ c_{2} = 4 \\ \frac{a_{1}}{a_{2}} = \frac{3}{6} = \frac{1}{2}; \frac{b_{1}}{b_{2}} = \frac{1}{- 2} \\ \frac{c_{1}}{c_{2}} = \frac{4}{4} = \frac{1}{1} \\ \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \end{aligned}$

So, the given pair of linear equations are intersecting at one point, therefore these lines have unique Solution.

Hence, given pair of linear equations is consistent.

We have,

$\begin{matrix} 3 x + y + 4 = 0 \\ y = - 4 - 3 x \end{matrix}$

$\Rightarrow$

When $x = 0$ , then $y = - 4$

When $x = - 1$ , then $y = - 1$

When $x = - 2$ , then $y = 2$

$x$	0	-1	-2
$y$	-4	-1	2
Points	$B$	$C$	$A$

and

$6 x - 2 y + 4 = 0$

$\Rightarrow$

$2 y = 6 x + 4$

$\Rightarrow$

$y = 3 x + 2$

When $x = 0$ , then $y = 2$

When $x = - 1$ , then $y = - 1$

When $x = 1$ , then $y = 5$

$x$	-1	0	1
$y$	-1	2	5
Points	$C$	$Q$	$P$

Plotting the points $B (0, - 4)$ and $A (- 2, 2)$ , we get the straight tine $A B$ . Plotting the points $Q (0, 2)$ and $P (1, 5)$ , we get the straight line $P Q$ . The lines $A B$ and $P Q$ intersect at $C$ $(- 1, - 1)$ .

(ii) Given pair of equations is

$\begin{matrix} (ii) & \begin{matrix} x - 2 y = 6 \\ 3 x - 6 y = 0 \end{matrix} \end{matrix}$

and

On comparing with $a x + b y + c = 0$ , we get

$\begin{aligned} (i) & a_{1} = 1, b_{1} = - 2 and c_{1} = - 6 \\ a_{2} = 3, b_{2} = - 6 and c_{2} = 0 \end{aligned}$

Here,

$\frac{a_{1}}{a_{2}} = \frac{1}{3}, \frac{b_{1}}{b_{2}} \frac{- 2}{- 6} = \frac{1}{3} and \frac{c_{1}}{c_{2}} = \frac{- 6}{0}$

$∴ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$

Hence, the lines represented by the given equations are parallel. Therefore, it has no Solution. So, the given pair of lines is inconsistent.

(iii) Given pair of equations is $x + y = 3$

and

$\begin{matrix} (i) & 3 x + 3 y = 9 \end{matrix}$

On comparing with $a x + b y + c = 0$ , we get

$\begin{aligned} a_{1} = 1, b_{1} = 1 and c_{1} = - 3 \\ (ii) & a_{2} = 3, b_{2} = 3 and c_{2} = - 9 \\ \frac{a_{1}}{a_{2}} = \frac{1}{3}, \frac{b_{1}}{b_{2}} = \frac{1}{3} and \frac{c_{1}}{c_{2}} = \frac{- 3}{- 9} = \frac{1}{3} \\ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \end{aligned}$

Here,

$\Rightarrow$

coincident. Therefore, these lines have infinitely many

Now, $x + y = 3 \Rightarrow y = 3 - x$

If $x = 0$ , then $y = 3$ , If $x = 3$ , then $y = 0$

$x$	0	3
$y$	3	0
Points	A	B

and

$\begin{aligned} 3 x + 3 y & = 9 \Rightarrow 3 y = 9 - 3 x \\ y & = \frac{9 - 3 x}{3} \end{aligned}$

Plotting the points $A (0, 3)$ and $B (3, 0)$ , we get the line $A B$ . Again, plotting the points $C (0, 3) D (1, 2)$ and $E (3, 0)$ , we get the line $C D E$ .

We observe that the lines represented by Eqs. (i) and (ii) are coincident.

12 Draw the graph of the pair of equations

2 x + y = 4

and

2 x - y = 4

. Write the vertices of the triangle formed by these lines and the

Y

-axis, find the area of this triangle?

Show Answer

Solution

The given pair of linear equations

Table for line $2 x + y = 4$ ,

$x$	0	2
$y = 4 - 2 x$	4	0
Points	$A$	$B$

and table for line $2 x - y = 4$ ,

$x$	0	2
$y = 2 x - 4$	-4	0
Points	$C$	$B$

Graphical representation of both lines. Here, both lines and $Y$ -axis form a $△ A B C$ .

Hence, the vertices of a $△ A B C$ are $A (0, 4) B (2, 0)$ and $C (0, - 4)$ .

$\begin{aligned} ∴ Required area of △ A B C & = 2 \times Area of △ A O B \\ = 2 \times \frac{1}{2} \times 4 \times 2 = 8 sq units \end{aligned}$

Hence, the required area of the triangle is 8 sq units.

13 Write an equation of a line passing through the point representing Solution of the pair of linear equations

x + y = 2

and

2 x - y = 1

, How many such lines can we find?

Show Answer

Solution

Given pair of linear equations is and

$\begin{aligned} (i) & x + y - 2 = 0 \\ (ii) & 2 x - y - 1 = 0 \end{aligned}$

On comparing with $a x + b y + c = 0$ , we get

$\begin{matrix} (i) & \begin{matrix} a_{1} = 1, b_{1} = 1 and c_{1} = - 2 & [from Eq. (i)] \\ a_{2} = 2, b_{2} = - 1 and c_{2} = - 1 & [from Eq. (ii)] \\ \frac{a_{1}}{a_{2}} = \frac{1}{2}, \frac{b_{1}}{b_{2}} = \frac{1}{- 1} \\ \frac{c_{1}}{c_{2}} = \frac{- 2}{- 1} = \frac{2}{1} \Rightarrow \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \end{matrix} \end{matrix}$

Here,

and

So, both lines intersect at a point. Therefore, the pair of equations has a unique Solution. Hence, these equations are consistent.

Now,

$x + y = 2 \Rightarrow y = 2 - x$

If $x = 0$ , then $y = 2$ and if $x = 2$ , then $y = 0$

and

$x$	0	2
$y$	2	0
Points	$A$	$B$
$2 x - y - 1 = 0 \Rightarrow y = 2 x - 1$

If $x = 0$ , then $y = - 1$ ; if $x = \frac{1}{2}$ , then $y = 0$ and if $x = 1$ , then $y = 1$

Plotting the points $A (2, 0)$ and $B (0, 2)$ , we get the straight line $A B$ . Plotting the points $C$ $(0, - 1)$ and $D (1 / 2, 0)$ , we get the straight line $C D$ . The lines $A B$ and $C D$ intersect at $E (1, 1)$ . Hence, infinite lines can pass through the intersection point of linear equations $x + y = 2$ and $2 x - y = 1$ i.e., $E (1, 1)$ like as $y = x, 2 x + y = 3, x + 2 y = 3$ . so on.

14 If

(x + 1)

is a factor of

2 x^{3} + a x^{2} + 2 b x + 1

, then find the value of

a

and

b

given that

2 a - 3 b = 4

Show Answer

Solution

Given that, $(x + 1)$ is a factor of $f (x) = 2 x^{s} + a x^{2} + 2 b x + 1$ , then $f (- 1) = 0$ .

$[if (x + α) is a factor of f (x) = a x^{2} + b x + c, then f (-) = 0]$

$\begin{matrix} (i) & \begin{matrix} \Rightarrow & 2 (- 1)^{3} + a (- 1)^{2} + 2 b (- 1) + 1 & = 0 \\ \Rightarrow & - 2 + a - 2 b + 1 & = 0 \\ \Rightarrow & a - 2 b - 1 & = 0 \\ Also, & 2 a - 3 b & = 4 \\ \Rightarrow & 3 b & = 2 a - 4 \\ \Rightarrow & b & = \frac{2 a - 4}{3} \end{matrix} \end{matrix}$

Now, put the value of $b$ in Eq. (i), we get

$\begin{matrix} \Rightarrow & 3 a - 2 (2 a - 4) - 3 = 0 \\ \Rightarrow & 3 a - 4 a + 8 - 3 = 0 \\ \Rightarrow & - a + 5 = 0 \\ \Rightarrow & a = 5 \end{matrix}$

Now, put the value of a in Eq. (i), we get

$\begin{aligned} \Rightarrow & 5 - 2 b - 1 & = 0 \\ \Rightarrow & 2 b & = 4 \\ \Rightarrow & b & = 2 \end{aligned}$

Hence, the required values of $a$ and $b$ are 5 and 2 , respectively.

15 If the angles of a triangle are

x, y

and

40^{\circ}

and the difference between

the two angles $x$ and $y$ is $30^{\circ}$ . Then, find the value of $x$ and $y$ .

Show Answer

Solution

Given that, $x, y$ and $40^{\circ}$ are the angles of a triangle.

$∴$

$\Rightarrow$

Also,

On adding Eqs. (i) and (ii), we get

$x + y + 40^{\circ} = 180^{\circ}$

[since, the sum of all the angles of a triangle is $180^{\circ}$ ]

$\begin{matrix} (i) & x + y = 140^{\circ} \end{matrix}$

$\begin{matrix} (ii) & x - y = 30^{\circ} \end{matrix}$

$\begin{matrix} 2 x & = 170^{\circ} \\ \Rightarrow & x & = 85^{\circ} \end{matrix}$

On putting $x = 85^{\circ}$ in Eq. (i), we get

$\begin{aligned} 85^{\circ} + y & = 140^{\circ} \\ = 55^{\circ} \end{aligned}$

$\Rightarrow y = 55^{\circ}$

Hence, the required values of $x$ and $y$ are $85^{\circ}$ and $55^{\circ}$ , respectively.

16 Two years ago, Salim was thrice as old as his daughter and six years later, he will be four year older than twice her age. How old are they now?

Show Answer

Solution

Let Salim and his daughter’s age be $x$ and yyr respectively.

Now, by first condition

Two years ago, Salim was thrice as old as his daughter.

$\begin{aligned} i.e., x - 2 = 3 (y - 2) \Rightarrow x - 2 = 3 y - 6 \\ (i) & \Rightarrow x - 3 y = - 4 \end{aligned}$

and by second condition, six years later. Salim will be four years older than twice her age.

$\begin{matrix} (ii) & \begin{matrix} \Rightarrow & x + 6 = 2 (y + 6) + 4 \\ \Rightarrow & x + 6 = 2 y + 12 + 4 \\ \Rightarrow & x - 2 y = 16 - 6 \\ \Rightarrow & - 2 y = 10 \end{matrix} \end{matrix}$

On subtracting Eq. (i) from Eq. (ii), we get

$\begin{array}{lr} x - 2 y = 10 \\ \underline{x} - \underset{+}{3 y} = \underset{+}{- 4} \\ y = 14 \end{array}$

Put the value of $y$ in Eq. (ii), we get $\begin{aligned} x - 2 \times 14 = 10 \\ \Rightarrow & x = 10 + 28 \Rightarrow x = 38 \end{aligned}$

Hence, Salim and his daughter’s age are $38 y r$ and $14 y r$ , respectively.

17. The age of the father is twice the sum of the ages of his two children. After

20 y r

, his age will be equal to the sum of the ages of his children. Find the age of the father.

Show Answer

Solution

Let the present age (in year) of father and his two children be $x$ , $y$ and $z y r$ , respectively. Now by given condition, and after $20 y r$ ,

$\begin{aligned} x & = 2 (y + z) \\ (x + 20) & = (y + 20) + (z + 20) \\ y + z + 40 & = x + 20 \end{aligned}$

$\begin{aligned} \Rightarrow y + z + 40 = x + 20 \\ \Rightarrow y + z = x - 20 \\ On putting the value of (y + z) in Eq. (i) and get the present age of father \\ ∴ x = 2 (x - 20) \\ ∴ x = 2 x - 40 = 40 \end{aligned}$

Hence, the father’s age is $40 y r$ .

18 Two numbers are in the ratio

5 : 6

. If 8 is subtracted from each of the numbers, the ratio becomes

4 : 5

, then find the numbers.

Show Answer

Solution

Let the two numbers be $x$ and $y$ .

Then, by first condition, ratio of these two numbers $= 5 : 6$

$\Rightarrow \begin{aligned} x : y & = 5 : 6 \\ (i) & \frac{x}{y} & = \frac{5}{6} \Rightarrow y = \frac{6 x}{5} \end{aligned}$

and by second condition, then, 8 is subtracted from each of the numbers, then ratio becomes $4 : 5$ .

$\begin{aligned} \frac{x - 8}{y - 8} & = \frac{4}{5} \\ \Rightarrow & 5 x - 40 & = 4 y - 32 \\ \Rightarrow & 5 x - 4 y & = 8 \end{aligned}$

Now, put the value of $y$ in Eq. (ii), we get

$\begin{aligned} 5 x - 4 (\frac{6 x}{5}) = 8 \\ \Rightarrow 25 x - 24 x = 40 \\ \Rightarrow x = 40 \\ y = \frac{6}{5} \times 40 \\ = 6 \times 8 = 48 \end{aligned}$

Hence, the required numbers are 40 and 48.

19 There are some students in the two examination halls A and B. To make the number of students equal in each hall, 10 students are sent from

A

B

but, if 20 students are sent from

B

A

, the number of students in

A

becomes double the number of students in

B

, then find the number of students in the both halls.

Show Answer

Solution

Let the number of students in halls $A$ and $B$ are $x$ and $y$ , respectively.

Now, by given condition,

$\begin{aligned} x - 10 & = y + 10 \\ (i) & x - y & = 20 \\ (x + 20) & = 2 (y - 20) \\ (ii) & x - 2 y & = - 60 \end{aligned}$

$\begin{aligned} \Rightarrow \\ and \\ \Rightarrow \end{aligned}$

On subtracting Eq. (ii) from Eq. (i), we get

$\begin{aligned} (x - y) - (x - 2 y) & = 20 + 60 \\ x - y - x + 2 y & = 80 \Rightarrow y = 80 \end{aligned}$

On putting $y = 80$ in Eq. (i), we get

$x - 80 = 20 \Rightarrow x = 100$

$and y = 80$

Hence, 100 students are in hall $A$ and 80 students are in hall $B$ .

20 A shopkeeper gives books on rent for reading. She takes a fixed charge for the first two days and an additional charge for each day thereafter. Latika paid ₹ 22 for a book kept for six days, while Anand paid ₹ 16 for the book kept for four days. Find the fixed charges and the charge for each extra day.

Show Answer

Solution

Let Latika takes a fixed charge for the first two day is $₹ x$ and additional charge for each day thereafter is ₹ $y$ .

Now by first condition.

Latika paid ₹ 22 for a book kept for six days i.e.,

$\begin{matrix} (i) & x + 4 y = 22 \end{matrix}$

and by second condition,

Anand paid ₹ 16 for a book kept for four days i.e.,

$\begin{matrix} (ii) & x + 2 y = 16 \end{matrix}$

Now, subtracting Eq. (ii) from Eq. (i), we get

$2 y = 6 \Rightarrow y = 3$

On putting the value of $y$ in Eq. (ii), we get

$x + 2 \times 3 = 16$

$∴ x = 16 - 6 = 10$

Hence, the fixed charge $= ₹ 10$

and the charge for each extra day $= ₹ 3$

21 In a competitive examination, 1 mark is awarded for each correct answer while

1 / 2

mark is deducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly?

Show Answer

Solution

Let $x$ be the number of correct answers of the questions in a competitive examination, then $(120 - x)$ be the number of wrong answers of the questions.

Then, by given condition,

$\begin{aligned} x \times 1 - (120 - x) \times \frac{1}{2} & = 90 \\ \Rightarrow & x - 60 + \frac{x}{2} & = 90 \\ \Rightarrow & \frac{3 x}{2} & = 150 \\ ∴ & x & = \frac{150 \times 2}{3} = 50 \times 2 = 100 \end{aligned}$

Hence, Jayanti answered correctly 100 questions.

22 The angles of a cyclic quadrilateral

A B C D

are

∠ A = (6 x + 10)^{\circ}

∠ B = (5 x)^{\circ}, ∠ C = (x + y)^{\circ}

and

∠ D = (3 y - 10)^{\circ}

. Find

x

and

y

and hence the values of the four angles.

Show Answer

Solution

We know that, by property of cyclic quadrilateral,

Sum of opposite angles $= 180^{\circ}$

$∠ A + ∠ C = (6 x + 10)^{\circ} + (x + y)^{\circ} = 180^{\circ}$

$\Rightarrow$

$7 x + y = 170$

and

$\begin{matrix} (i) & ∠ B + ∠ D = (5 x)^{\circ} + (3 y - 10)^{\circ} = 180^{\circ} \end{matrix}$

$[∵ ∠ B = (5 x)^{\circ}, ∠ D = (3 y - 10)^{\circ} .$ , given $]$

$\Rightarrow 5 x + 3 y = 190^{\circ}$

On multiplying Eq. (i) by 3 and then subtracting, we get

$\begin{aligned} (ii) & 3 \times (7 x + y) - (5 x + 3 y) & = 510^{\circ} - 190^{\circ} \\ \Rightarrow & 21 x + 3 y - 5 x - 3 y & = 320^{\circ} \\ \Rightarrow & 16 x & = 320^{\circ} \\ ∴ & x & = 20^{\circ} \end{aligned}$

On putting $x = 20^{\circ}$ in Eq. (i), we get

$\begin{aligned} \Rightarrow 7 \times 20 + y & = 170^{\circ} \\ ∴ y & = 170^{\circ} - 140^{\circ} \Rightarrow y = 30^{\circ} \\ ∴ ∠ A & = (6 x + 10)^{\circ} = 6 \times 20^{\circ} + 10^{\circ} \\ = 120^{\circ} + 10^{\circ} = 130^{\circ} \\ ∠ B & = (5 x)^{\circ} = 5 \times 20^{\circ} = 100^{\circ} \\ ∠ C & = (x + y)^{\circ} = 20^{\circ} + 30^{\circ} = 50^{\circ} \\ ∠ D & = (3 y - 10)^{\circ} = 3 \times 30^{\circ} - 10^{\circ} \\ = 90^{\circ} - 10^{\circ} = 80^{\circ} \end{aligned}$

Hence, the required values of $x$ and $y$ are $20^{\circ}$ and $30^{\circ}$ respectively and the values of the four angles i.e., $∠ A, ∠ B, ∠ C$ and $∠ D$ are $130^{\circ}, 100^{\circ}, 50^{\circ}$ and $80^{\circ}$ , respectively.

Long Answer Type Questions

1 Graphically, solve the following pair of equations

$2 x + y = 6 and 2 x - y + 2 = 0$

Find the ratio of the areas of the two triangles formed by the lines representing these equations with the $X$ -axis and the lines with the $Y$ -axis.

Show Answer

Solution

Given equations are $2 x + y = 6$ and $2 x - y + 2 = 0$

Table for equation $2 x + y = 6$ ,

$x$	0	3
$y$	6	0
Points	B	A

Table for equation $2 x - y + 2 = 0$ ,

$x$	0	-1
$y$	2	0
Points	$D$	$C$

Let $A_{1}$ and $A_{2}$ represent the areas of $△ A C E$ and $△ B D E$ , respectively.

Now,

and

$\begin{aligned} A_{1} = Area of △ A C E & = \frac{1}{2} \times A C \times P E \\ = \frac{1}{2} \times 4 \times 4 = 8 \end{aligned}$

$A_{2} =$ Area of $△ B D E = \frac{1}{2} \times B D \times Q E$

$= \frac{1}{2} \times 4 \times 1 = 2$

$∴ A_{1} : A_{2} = 8 : 2 = 4 : 1$

Hence, the pair of equations intersect graphically at point $E (1, 4)$ , i.e., $x = 1$ and $y = 4$ .

2 Determine graphically, the vertices of the triangle formed by the lines

$y = x, 3 y = x and x + y = 8$

Show Answer

Solution

Given linear equations are

For equation

$x + y = 8 \Rightarrow y = 8 - x$

If $x = 0$ , then $y = 8$ ; if $x = 8$ , then $y = 0$ and if $x = 4$ , then $y = 4$

Table for line $x + y = 8$ .

$x$	0	4	8
$y$	8	4	0
Points	$P$	$Q$	$R$

Plotting the points $A (1, 1)$ and $B (2, 2)$ , we get the straight line $A B$ . Plotting the points $C (3, 1)$ and $D (6, 2)$ , we get the straight line $C D$ . Plotting the points $P (0, 8), Q (4, 4)$ and $R (8, 0)$ , we get the straight line $P Q R$ . We see that lines $A B$ and $C D$ intersecting the line $P R$ on $Q$ and $D$ , respectively.

So, $△ O Q D$ is formed by these lines. Hence, the vertices of the $△ O Q D$ formed by the given lines are $O (0, 0), Q (4, 4)$ and $D (6, 2)$ .

3 Draw the graphs of the equations

x = 3, x = 5

and

2 x - y - 4 = 0

. Also find the area of the quadrilateral formed by the lines and the

X

-axis.

Show Answer

Solution

Given equation of lines $2 x - y - 4 = 0, x = 3$ and $x = 5$

Table for line $2 x - y - 4 = 0$ ,

$x$	0	2
$y = 2 x - 4$	-4	0
Points	$P$	$Q$

Draw the points $P (0, - 4)$ and $Q (2, 0)$ and join these points and form a line $P Q$ also draw the lines $x = 3$ and $x = 5$ .

$∴$ Area of quadrilateral $A B C D = \frac{1}{2} \times$ distance between parallel lines $(A B) \times (A D + B C)$

$= \frac{1}{2} \times 2 \times (6 + 2)$

[since, quadrilateral $A B C D$ is a trapezium]

$B C = 6]$

$∵ A B = O B - O A = 5 - 3 = 2, A D = 2$

$= 8 s q units$

Hence, the required area of the quadrilateral formed by the lines and the $X$ -axis is 8 sq units.

4 The cost of 4 pens and 4 pencils boxes is ₹ 100 . Three times the cost of a pen is

₹ 15

more than the cost of a pencil box. Form the pair of linear equations for the above situation. Find the cost of a pen and a pencil box.

Show Answer

Solution

Let the cost of a pen be ₹ $x$ and the cost of a pencil box be ₹ $y$ .

Then, by given condition,

and

$\begin{aligned} (i) & 4 x + 4 y & = 100 \Rightarrow x + y = 25 \\ 3 x & = y + 15 \end{aligned}$

$\Rightarrow 3 x - y = 15$

On adding Eqs. (i) and (ii), we get

$\begin{matrix} 4 x & = 40 \\ \Rightarrow & x & = 10 \end{matrix}$

By substituting $x = 10$ , in Eq. (i) we get

$y = 25 - 10 = 15$

Hence, the cost of a pen and a pencil box are ₹ 10 and ₹ 15 , respectively.

5 Determine, algebraically, the vertices of the triangle formed by the lines

and

$\begin{matrix} (iii) & \begin{matrix} 3 x - y = 3 \\ 2 x - 3 y = 2 \\ x + 2 y = 8 \\ 3 x - y = 3 \\ 2 x - 3 y = 2 \\ x + 2 y = 8 \end{matrix} \end{matrix}$

and

$△ A B C$ i.e., $A B, B C$ and $C A$ , respectively.

On solving lines (i) and (ii), we will get the intersecting point $B$ .

On multiplying Eq. (i) by 3 in Eq. (i) and then subtracting, we get

$\begin{matrix} 9 x - 3 y = 9 \\ 2 x - 3 y = 2 \\ - + \\ 7 x = 7 \Rightarrow x = 1 \end{matrix}$

On putting the value of $x$ in Eq. (i), we get

$\begin{matrix} 3 \times 1 - y = 3 \\ y = 0 \end{matrix}$

So, the coordinate of point or vertex $B$ is $(1, 0)$ .

On solving lines (ii) and (iii), we will get the intersecting point $C$ .

On multiplying Eq. (iii) by 2 and then subtracting, we get

$\begin{matrix} 2 x + 4 y = 16 \\ 2 x - 3 y = 2 \\ + = \\ 7 y = 14 \\ y = 2 \end{matrix}$

$\Rightarrow$

On putting the value of $y$ in Eq. (iii), we gat

$\begin{aligned} x + 2 \times 2 & = 8 \\ \Rightarrow & x & = 8 - 4 \\ \Rightarrow & x & = 4 \end{aligned}$

Hence, the coordinate of point or vertex $C$ is $(4, 2)$ .

Show Answer

Solution

ing lines (iii) and (i), we will get the intersecting point $A$ .

On multiplying in Eq. (i) by 2 and then adding Eq. (iii), we get

$\begin{matrix} 6 x - 2 y = 6 \\ x + 2 y = 8 \\ 7 x = 14 \end{matrix}$

$\Rightarrow x = 2$

On putting the value of $x$ in Eq. (i), we get

$\begin{aligned} 3 \times 2 - y & = 3 \\ \Rightarrow & y & = 6 - 3 \\ \Rightarrow & y & = 3 \end{aligned}$

So, the coordinate of point or vertex $A$ is $(2, 3)$ .

Hence, the vertices of the $△ A B C$ formed by the given lines are $A (2, 3), B (1, 0)$ and $C (4, 2)$ .

6 Ankita travels

14 k m

to her home partly by rickshaw and partly by bus. She takes half an hour, if she travels

2 k m

by rickshaw and the remaining distance by bus. On the other hand, if she travels

4 k m

by rickshaw and the remaining distance by bus, she takes 9 min longer. Find the speed of the rickshaw and of the bus.

Show Answer

Solution

Let the speed of the rickshaw and the bus are $x$ and $y k m / h$ , respectively.

Now, she has taken time to travel $2 k m$ by rickshaw , $t_{1} = \frac{2}{x} h . ∵$ speed $= \frac{distance}{time}$

and she has taken time to travel remaining distance i.e., $(14 - 2) = 12 k m$ by bus $= t_{2} = \frac{12}{y} h$ .

By first condition, $t_{1} + t_{2} = \frac{1}{2} \Rightarrow \frac{2}{x} + \frac{12}{y} = \frac{1}{2}$

Now, she has taken time to travel $4 k m$ by rickshaw, $t_{3} = \frac{4}{x} h$

and she has taken time to travel remaining distance i.e., $(14 - 4) = 10 k m$ by bus $= t_{4} = \frac{10}{y} h$ .

By second condition, $t_{3} + t_{4} = \frac{1}{2} + \frac{9}{60} = \frac{1}{2} + \frac{3}{20}$

$\Rightarrow \frac{4}{x} + \frac{10}{y} = \frac{13}{20}$

Let $\frac{1}{x} = u$ and $\frac{1}{y} = v$ , then Eqs. (i) and (ii) becomes

and

$\begin{aligned} (iii) & 2 u + 12 v = \frac{1}{2} \\ (iv) & 4 u + 10 v = \frac{13}{20} \end{aligned}$

On multiplying in Eq. (iii) by 2 and then subtracting, we get

$\begin{aligned} 4 u + 24 v = 1 \\ 4 u + 10 v = \frac{13}{20} \\ - - \underset{―}{- 13} \\ 14 v = 1 - \frac{7}{20} = \frac{7}{20} \\ 2 v = \frac{1}{20} \Rightarrow v = \frac{1}{40} \end{aligned}$

Now, put the value of $v$ in Eq. (iii), we get

$\begin{matrix} \Rightarrow & 2 u + 12 \frac{1}{40} = \frac{1}{2} \\ \Rightarrow & 2 u = \frac{1}{2} - \frac{3}{10} = \frac{5 - 3}{10} \\ ∴ & 2 u = \frac{2}{10} \Rightarrow u = \frac{1}{10} \\ \Rightarrow & \frac{1}{x} = u \\ and & \frac{1}{x} = \frac{1}{10} \Rightarrow x = 10 k m / h \\ \Rightarrow & \frac{1}{y} = v \Rightarrow \frac{1}{y} = \frac{1}{40} \\ y = 40 k m / h \end{matrix}$

Hence, the speed of rickshaw and the bus are $10 k m / h$ and $40 k m / h$ , respectively.

7 A person, rowing at the rate of

5 k m / h

in still water, takes thrice as much time in going

40 k m

upstream as in going

40 k m

downstream. Find the speed of the stream.

Show Answer

Solution

Let the speed of the stream be $v k m / h$ .

Given that, a person rowing in still water $= 5 k m / h$

The speed of a person rowing in downstream $= (5 + v) k m / h$

and the speed of a person has rowing in upstream $= (5 - v) k m / h$

Now, the person taken time to cover $40 k m$ downstream,

$t_{1} = \frac{40}{5 + v} h ∵ speed = \frac{distance}{time}$

and the person has taken time to cover $40 k m$ upstream,

$t_{2} = \frac{4 U}{5 - v} h .$

By condition,

$\Rightarrow t_{2} = t_{1} \times 3 \frac{40}{5 - v} = \frac{40}{5 + v} \times 3$

$\Rightarrow \frac{1}{5 - v} = \frac{3}{5 + v}$

$5 + v = 15 - 3 v \Rightarrow 4 v = 10$

$∴ v = \frac{10}{4} = 2.5 km / h$

Hence, the speed of the stream is $2.5 k m / h$ .

8 A motorboat can travel

30 k m

upstream and

28 k m

downstream in

7 h

. It can travel

21 k m

upstream and return in

5 h

. Find the speed of the boat in still water and the speed of the stream.

Show Answer

Solution

Let the speed of the motorboat in still water and the speed of the stream are $u k m / h$ and $v k m / h$ , respectively.

Then, a motorboat speed in downstream $= (u + v) k m / h$

and a motorboat speed in upstream $= (u - v) k m / h$ .

Motorboat has taken time to travel $30 k m$ upstream,

$t_{1} = \frac{30}{u - v} h$

and motorboat has taken time to travel $28 k m$ downstream,

$t_{2} = \frac{28}{u + v} h$

By first condition, a motorboat can travel $30 k m$ upstream and $28 k m$ downstream in $7 h$

$\begin{aligned} i.e., t_{1} + t_{2} = 7 h \\ \Rightarrow \\ \frac{30}{u - v} + \frac{28}{u + v} = 7 \end{aligned}$

Now, motorboat has taken time to travel $21 k m$ upstream and return i.e., $t_{3} = \frac{21}{u - v}$ .

and

$t_{4} = \frac{21}{u + v}$

[for upstream]

By second condition,

$t_{4} + t_{3} = 5 h$

$\begin{matrix} (ii) & \Rightarrow \frac{21}{u + v} + \frac{21}{u - v} = 5 \end{matrix}$

[for downstream]

Let

Eqs. (i) and (ii) becomes

and

$\Rightarrow$

$\begin{matrix} x = \frac{1}{u + v} and y = \frac{1}{u - v} \\ (iii) & 30 x + 28 y = 7 \\ 21 x + 21 y = 5 \\ (iv) & x + y = \frac{5}{21} \end{matrix}$

Now, multiplying in Eq. (iv) by 28 and then subtracting from Eq. (iii), we get

$\begin{aligned} 30 x + 28 y = 7 \\ 28 x + 28 y = \frac{140}{21} \\ - - - \end{aligned}$

$\Rightarrow 2 x = \frac{1}{3} \Rightarrow x = \frac{1}{6}$

On putting the value of $x$ in Eq. (iv), we get

$\begin{matrix} (v) & \begin{matrix} \Rightarrow & \frac{1}{6} + y & = \frac{5}{21} \\ y = \frac{5}{21} - \frac{1}{6} = \frac{10 - 7}{42} = \frac{3}{42} \Rightarrow y = \frac{1}{14} \\ and & x & = \frac{1}{u + v} = \frac{1}{6} \Rightarrow u + v = 6 \end{matrix} \end{matrix}$

$\Rightarrow u - v = 14$

Now, adding Eqs. (v) and (vi), we get

$2 u = 20 \Rightarrow u = 10$

On putting the value of $u$ in Eq. (v), we get

$\begin{aligned} 10 + v = 6 \\ \Rightarrow & v = - 4 \end{aligned}$

Hence, the speed of the motorboat in still water is $10 k m / h$ and the speed of the stream $4 k m / h$ .

9 A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3 . Find the number.

Show Answer

Solution

Let the two-digit number $= 10 x + y$

Case I Multiplying the sum of the digits by 8 and then subtracting $5 =$ two-digit number

$\begin{matrix} (i) & \begin{matrix} \Rightarrow & 8 \times (x + y) - 5 = 10 x + y \\ \Rightarrow & 8 x + 8 y - 5 = 10 x + y \\ \Rightarrow & 2 x - 7 y = - 5 \end{matrix} \end{matrix}$

Case II Multiplying the difference of the digits by 16 and then adding $3 =$ two-digit number

$\begin{matrix} (ii) & \begin{matrix} \Rightarrow & 16 \times (x - y) + 3 = 10 x + y \\ \Rightarrow & 16 x - 16 y + 3 = 10 x + y \\ \Rightarrow & 6 x - 17 y = - 3 \end{matrix} \end{matrix}$

Now, multiplying in Eq. (i) by 3 and then subtracting from Eq. (ii), we get

$\begin{array}{lr} 6 x - 17 y = - 3 \\ 6 x - 21 y = - 15 \\ 4 y = 12 \Rightarrow y = 3 \end{array}$

Now, put the value of $y$ in Eq. (i), we get

$2 x - 7 x \times 3 = - 5 \Rightarrow 2 x = 21 - 5 = 16 \Rightarrow x = 8$

Hence, the required two-digit number

$\begin{aligned} = 10 x + y \\ = 10 \times 8 + 3 = 80 + 3 = 83 \end{aligned}$

10 A railway half ticket cost half the full fare but the reservation charges are the same on a half ticket as on a full ticket. One reserved first class ticket from the stations

A

B

costs ₹ 2530 . Also, one reserved first class ticket and one reserved first class half ticket from stations

A

B

costs ₹ 3810. Find the full first class fare from stations

A

B

and also the reservation charges for a ticket.

Show Answer

Solution

Let the cost of full and half first class fare be $₹ x$ and $₹ \frac{x}{2}$ , respectively and reservation charges be ₹ y per ticket.

Case I The cost of one reserved first class ticket from the stations $A$ to $B$

$\begin{aligned} = ₹ 2530 \\ (i) & x + y & = 2530 \end{aligned}$

$\Rightarrow$

Case II The cost of one reserved first class ticket and one reserved first class half ticket from stations $A$ to $B = ₹ 3810$

$\begin{matrix} (ii) & \begin{matrix} \Rightarrow & x + y + \frac{x}{2} + y & = 3810 \\ \Rightarrow & \frac{3 x}{2} + 2 y & = 3810 \\ \Rightarrow & 3 x + 4 y & = 7620 \end{matrix} \end{matrix}$

Now, multiplying Eq. (i) by 4 and then subtracting from Eq. (ii), we get

$\begin{aligned} 3 x + 4 y = 7620 \\ 4 x + 4 y = 10120 \\ - \\ - x = - 2500 \end{aligned}$

$\Rightarrow x = 2500$

On putting the value of $x$ in Eq. (i), we get

$\begin{aligned} 2500 + y & = 2530 \\ \Rightarrow & y & = 2530 - 2500 \\ \Rightarrow & y & = 30 \end{aligned}$

Hence, full first class fare from stations $A$ to $B$ is ₹ 2500 and the reservation for a ticket is ₹ 30 .

11 A shopkeeper sells a saree at

8

profit and a sweater at

10

discount, thereby, getting a sum

₹ 1008

. If she had sold the saree at

10

profit and the sweater at

8

discount, she would have got ₹ 1028 then find the cost of the saree and the list price (price before discount) of the sweater.

Show Answer

Solution

Let the cost price of the saree and the list price of the sweater be $₹ x$ and $₹ y$ , respectively. Case I Sells a saree at $8$ profit + Sells a sweater at $10$ discount $= ₹ 1008$

$\begin{matrix} (i) & \begin{matrix} \Rightarrow & (100 + 8) % of x + (100 - 10) % of y & = 1008 \\ \Rightarrow & 108 % of x + 90 % of y & = 1008 \\ \Rightarrow & 1.08 x + 0.9 y & = 1008 \end{matrix} \end{matrix}$

Case II Sold the saree at $10 %$ profit + Sold the sweater at $8 %$ discount $= ₹ 1028$

$\begin{matrix} (ii) & \begin{matrix} \Rightarrow & (100 + 10) % of x + (100 - 8) % of y = 1028 \\ \Rightarrow & 110 % of x + 92 % of y = 1028 \\ \Rightarrow & 1.1 x + 0.92 y = 1028 \end{matrix} \end{matrix}$

On putting the value of $y$ from Eq. (i) into Eq. (ii), we get

$\begin{matrix} 1.1 x + 0.92 \frac{1008 - 1.08 x}{0.9} & = 1028 \\ \Rightarrow & 1.1 \times 0.9 x + 927.36 - 0.9936 x & = 1028 \times 0.9 \\ \Rightarrow & 0.99 x - 0.9936 x & = 925.2 - 927.36 \\ \Rightarrow & - 0.0036 x & = - 2.16 \\ ∴ & x & = \frac{2.16}{0.0036} = 600 \end{matrix}$

On putting the value of $x$ in Eq. (i), we get

$1.08 \times 600 + 0.9 y = 1008$

$\begin{aligned} \Rightarrow & 108 \times 6 + 0.9 y & = 1008 \\ \Rightarrow & 0.9 y & = 1008 - 648 \\ \Rightarrow & 0.9 y & = 360 \\ \Rightarrow & y & = \frac{360}{0.9} = 400 \end{aligned}$

Hence, the cost price of the saree and the list price (price before discount) of the sweater are ₹ 600 and ₹ 400 , respectively.

12 Susan invested certain amount of money in two schemes

A

and

B

, which offer interest at the rate of

8

per annum and

9

per annum, respectively. She received ₹ 1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received ₹ 20 more as annual interest. How much money did she invest in each scheme?

Show Answer

Solution

Let the amount of investments in schemes $A$ and $B$ be $₹ x$ and $₹ y$ , respectively.

Case I Interest at the rate of $8$ per annum on scheme $A +$ Interest at the rate of $9$ per annum on scheme $B =$ Total amount received

$\begin{matrix} (i) & \begin{matrix} \Rightarrow & \frac{x \times 8 \times 1}{100} + \frac{y \times 9 \times 1}{100} & = ₹ 1860 ∵ simple interest = \frac{principal \times rate \times time}{100} \\ \Rightarrow 8 x + 9 y & = 186000 \end{matrix} \end{matrix}$

Case II Interest at the rate of $9$ per annum on scheme $A +$ Interest at the rate of $8$ per annum on scheme $B = ₹ 20$ more as annual interest

$\begin{aligned} \Rightarrow \frac{x \times 9 \times 1}{100} + \frac{y \times 8 \times 1}{100} = ₹ 20 + ₹ 1860 \\ \Rightarrow \frac{9 x}{100} + \frac{8 y}{100} = 1880 \\ \Rightarrow 9 x + 8 y = 188000 \end{aligned}$

On multiplying Eq. (i) by 9 and Eq. (ii) by 8 and then subtracting them, we get

$\begin{aligned} 72 x + 81 y & = 9 \times 186000 \\ 72 x + 64 y & = 8 \times 188000 \\ - \\ 17 y & = 1000 [(9 \times 186) - (8 \times 188)] \\ = 1000 (1674 - 1504) = 1000 \times 170 \\ 17 y & = 170000 \Rightarrow y = 10000 \end{aligned}$

$\Rightarrow$

On putting the value of $y$ in Eq. (i), we get

$\begin{aligned} 8 x + 9 \times 10000 & = 186000 \\ \Rightarrow & 8 x & = 186000 - 90000 \\ \Rightarrow & 8 x & = 96000 \\ \Rightarrow & x & = 12000 \end{aligned}$

Hence, she invested ₹ 12000 and ₹ 10000 in two schemes A and B, respectively.

13. Vijay had some bananas and he divided them into two lots A and B. He sold the first lot at the rate of ₹ 2 for 3 bananas and the second lot at the rate of ₹ 1 per banana and got a total of ₹ 400 . If he had sold the first lot at the rate of ₹ 1 per banana and the second lot at the rate of ₹ 4 for 5 bananas, his total collection would have been ₹ 460 . Find the total number of bananas he had.

Show Answer

Solution

Let the number of bananas in lots $A$ and $B$ be $x$ and $y$ , respectively

Case I Cost of the first lot at the rate of ₹ 2 for 3 bananas + Cost of the second lot at the rate of $₹ 1$ per banana $=$ Amount received

$\begin{matrix} (i) & \begin{matrix} \Rightarrow & \frac{2}{3} x + y = 400 \\ \Rightarrow & 2 x + 3 y = 1200 \end{matrix} \end{matrix}$

Case II Cost of the first lot at the rate of $₹ 1$ per banana + Cost of the second lot at the rate of $₹ 4$ for 5 bananas $=$ Amount received

$\begin{matrix} (ii) & \begin{matrix} \Rightarrow & x + \frac{4}{5} y = 460 \\ \Rightarrow & 5 x + 4 y = 2300 \end{matrix} \end{matrix}$

On multiplying in Eq. (i) by 4 and Eq. (ii) by 3 and then subtracting them, we get

$\begin{aligned} 8 x + 12 y & = 4800 \\ 15 x + 12 y & = 6900 \\ - 7 x & = - 2100 \\ x & = 300 \end{aligned}$

$\Rightarrow$

Now, put the value of $x$ in Eq. (i), we get

$\begin{matrix} 2 \times 300 + 3 y & = 1200 \\ \Rightarrow & 600 + 3 y & = 1200 \\ \Rightarrow & 3 y & = 1200 - 600 \\ \Rightarrow & 3 y & = 600 \\ \Rightarrow & y & = 200 \end{matrix}$

$∴$ Total number of bananas $=$ Number of bana nas in lot $A +$ Number of bananas in lot $B$ $= x + y$

$= 300 + 200 = 500$

Hence, he had 500 bananas.

Mathematics 10

Chapter 03 Pair of Linear Equations in Two Variables

Multiple Choice Questions (MCQs)

Very Short Answer Type Questions

Short Answer Type Questions

Long Answer Type Questions

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Mentorship

NCERT Exercise Video Solution

Mathematics 10

Chapter 03 Pair of Linear Equations in Two Variables

Multiple Choice Questions (MCQs)

Very Short Answer Type Questions

Short Answer Type Questions

Long Answer Type Questions

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Mentorship

NCERT Exercise Video Solution

Menu