Chapter 02 Polynomials
Multiple Choice Questions (MCQs)
1 If one of the zeroes of the quadratic polynomial
(a)
(b)
(c)
(d)
Show Answer
Thinking Process
If
Solution
(a) Given that, one of the zeroes of the quadratic polynomial say
(a)
(b)
(c)
(d)
Show Answer
Solution
(c) Let
Then, sum of zeroes
and
product of zeroes
From Eqs. (i) and (ii),
We know that, if we multiply/divide any polynomial by any constant, then the zeroes of polynomial do not change.
Alternate Method
Let the zeroes of a quadratic polynomial are
Then, sum of zeroes
and product of zeroes
(a)
(b)
(c)
(d)
Show Answer
Solution
(d) Let
Given that, 2 and -3 are the zeroes of the quadratic polynomial
On adding Eqs. (i) and (ii), we get
Put the value of
So, the required values are
(a) 1
(b) 2
(c) 3
(d) more than 3
Show Answer
Solution
(d) Let
and
From Eqs. (i) and (ii),
But we know that, if we multiply/divide any polynomial by any arbitrary constant. Then, the zeroes of polynomial never change.
Hence, the required number of polynomials are infinite i.e., more than 3.
Show Answer
Thinking Process
Firstly, we find the sum of product of two zeroes at a time and put the value of one of the zeroes i.e.,zero, we get the required product of the other two zeroes.
Solution
(b) Let
Given that, one of the zeroes of the cubic polynomial
Let
We know that,
Sum of product of two zeroes at a time
Hence, product of other two zeroes
Show Answer
Thinking Process
Firstly, we find the value of constant term ’
Solution
(a) Let
Let
| and |
[given]
We know that,
Product of all zeroes
Hence, product of the other two roots is
Alternate Method
Since, -1 is one of the zeroes of the cubic polynomial
Now, using division algorithm,
Let
Product of zeroes
Hence, the required product of other two roots is
Show Answer
Solution
(b) Let given quadratic polynomial be
On comparing
We know that,
[by quadratic formula]
Hence, both zeroes of the given quadratic polynomial
Alternate Method
We know that,
In quadratic polynomial, if
In given polynomial, we see that
which satisfy the above condition.
So, both zeroes of the given quadratic polynomial are negative.
(a) cannot both be positive (b) cannot both be negative
(c) are always unequal (d) are always equal
Show Answer
Solution
Let
On comparing

Here, we see that
Now, we know that
In quadratic polynomial
So, both zeroes are of opposite sign.
So, both zeroes are negative.
Hence, in any case zeroes of the given quadratic polynomial cannot both be positive.
(a) c and a have opposite signs
(b)
(c)
(d)
Show Answer
Solution
(c) The zeroes of the given quadratic polynomial
Alternate Method
Given that, the zeroes of the quadratic polynomial
which is only possible when
(a) has no linear term and the constant term is negative
(b) has no linear term and the constant term is positive
(c) can have a linear term but the constant term is negative
(d) can have a linear term but the constant term is positive
Show Answer
Solution
(a) Let
Now,
Let
Given that, one of the zeroes of a quadratic polynomial
[from Eq. (i)]
Hence,
Put
Alternate Method
Let
and by given condition the zeroes are
and product of zeroes
which is possible when,
Hence, it has no linear term and the constant term is negative.
(a)
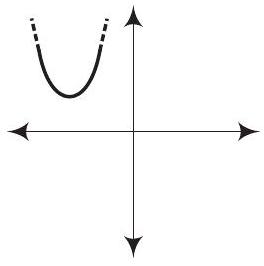
(C)
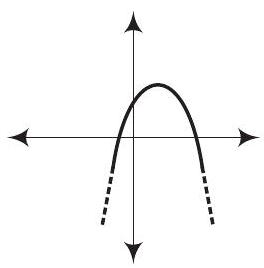
(b)
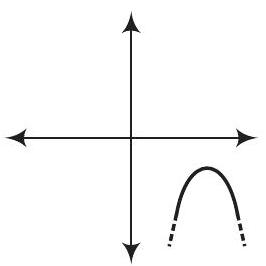
(d)
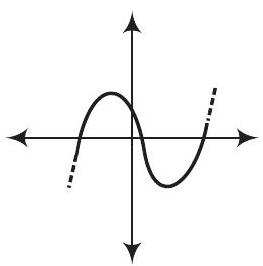
Show Answer
Solution
(d) For any quadratic polynomial
Also, the curve of a quadratic polynomial crosses the
Very Short Answer Type Questions
1 Answer the following and justify.
(i) Can
(ii) What will the quotient and remainder be on division of
(iii) If on division of a polynomial
(iv) If on division of a non-zero polynomial
(v) Can the quadratic polynomial
Show Answer
Solution
(i) No, because whenever we divide a polynomial
and
By division algorithm for polynomials,
Dividend
[in division algorithm, degree of divisor
But dividend
So, division algorithm is not satisfied.
Hence,
(ii) Given that, Divisor
and dividend
We see that,
Degree of divisor
So, by division algorithm,
quotient
If degree of dividend
(iii) If division of a polynomial
(iv) If division of a non-zero polynomial
On comparing
So, the quadratic polynomial
(i) If the zeroes of a quadratic polynomial
(ii) If the graph of a polynomial intersects the
(iii) If the graph of a polynomial intersects the
(iv) If two of the zeroes of a cubic polynomial are zero, then it does not have linear and constant terms.
(v) If all the zeroes of a cubic polynomial are negative, then all the coefficients and the constant term of the polynomial have the same sign.
(vi) If all three zeroes of a cubic polynomial
(vii) The only value of
Show Answer
Solution
(i) False, if the zeroes of a quadratic polynomial
where
(ii) True, if the graph of a polynomial intersects the
(iii) True, if the graph of a polynomial intersects the
which does not have linear and constant terms.
(v) True, if
(vi) False, let
Then,
Given that, all three zeroes are positive. So, the product of all three zeroes is also positive i.e.,
[from Eq. (i)]
Now, sum of the zeroes
But
Thus, its sum is also positive.
So,
and sum of the product of two zeroes at a time
So, the cubic polynomial
(vii) False, let
For equal roots. Its discriminant should be zero i.e.,
So, for two values of
Short Answer Type Questions
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
(i)
Show Answer
Thinking Process
Firstly, we use the factorisation method i.e., splitting the middle term of quadratic polynomial and find its zeroes. After that use the formula of sum of zeroes and product of zeroes for verification.
Solution
Let
So, the value of
So, the zeroes of
and
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Show Answer
Solution
Let
So, the value of
and
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Show Answer
Solution
Let
So, the value of
i.e.,
So, the zeroes of
and
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Show Answer
Solution
Let
So, the value of
i.e.,
So, the zeroes of
Sum of product of two zeroes at a time
and product of zeroes
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Show Answer
Solution
Let
So, the value of
i.e.,
So, the zeroes of
And
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Show Answer
Solution
Let
So, the value of
i.e.,
So, the zeroes of
and
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Show Answer
Solution
Let
So, the value of
i.e.,
So, the zeroes of
and product of zeroes
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Show Answer
Solution
Let
So, the value of
i.e.,
So, the zeroes of
and
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Show Answer
Solution
Let
So, the value of
So, the zeroes of
And product of zeroes
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Show Answer
Solution
Let
So, the value of
i.e.,
So, the zeroes of
and product of zeroes
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Long Answer Type Questions
1 For each of the following, find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also, find the zeroes of these polynomials by factorisation.
(i)
(ii)
(iii)
(iv)
Show Answer
Thinking Process
(i) Firstly we use the concept or method of formation a quadratic equation, i.e.,
(ii) After making a quadratic polynomial we factorise it by splitting the middle term and get the required zeroes.
Solution
(i) Given that, sum of zeroes
and product of zeroes
Using factorisation method,
Hence, the zeroes of
(ii) Given that,
Using factorisation method
Hence, the zeroes of
(iii) Given that,
Hence, the zeroes of
(iv) Given that,
Using factorisation method,
Hence, the zeroes of
Show Answer
Thinking Process
Using the following relations related to a cubic polynomial.
(i) Sum of the zeroes
(ii) Sum of product of two zeroes at a time
Solution
Let
Given that,
Using factorisation method,
[using Eq. (i)]
Hence, the required values of
Show Answer
Thinking Process
Use division algorithm and get a quadratic polynomial. Further factorize the quadratic polynomial by factorisation method and get the other two required roots.
Solution
Let
Now, using division algorithm,

So, its other zeroes are
Show Answer
Solution
Given that,

Since,
So, when we apply division algorithm remainder should be zero.
Here, if we take
Thus, the required value of
Using factorisation method,
Hence, the zeroes of
Show Answer
Solution
Let

Hence, all the zeroes of polynomial are
Show Answer
Thinking Process
(i) Firstly, we use the division algorithm to get the remainder. Since,
(ii) Now, equating the like terms of
(iii) Finally, we get two more zeroes, which are not the zeroes of
Solution
Given that the zeroes of
If
On comparing the coefficient of
For
Hence, the zeroes of










