Solution

(d) We know that, to divide a line segment $A B$ in the ratio $m: n$, first draw a ray $A X$ which makes an acute angle $\angle B A X$, then marked $m+n$ points at equal distance.

Here,

$ m=5, n=7 $

So, minimum number of these points $=m+n=5+7=12$.

Solution

(b) Here, minimum $4+7=11$ points are located at equal distances on the ray $A X$, and then $B$ is joined to last point is $A _{11}$.

Solution

(a) Given, a line segment $A B$ and we have to divide it in the ratio $5: 6$.

Steps of construction

1. Draw a ray $A X$ making an acute $\angle B A X$.

2. Draw a ray $B Y$ parallel to $A X$ by making $\angle A B Y$ equal to $\angle B A X$.

3. Now, locate the points $A_1, A_2, A_3, A_4$ and $A_5(m=5)$ on $A X$ and $B_1, B_2, B_3, B_4, B_5$ and $B_6(n=6)$ such that all the points are at equal distance from each other.

4. Join $B_6 A_5$. Let it intersect $A B$ at a point $C$.

Then, $A C: B C=5: 6$

Solution

(c) Here, we locate points $B_1, B_2, B_3, B_4, B_5, B_6$ and $B_7$ on $B X$ at equal distance and in next step join the last points is $B_7$ to $C$.

Solution

(b) To construct a triangle similar to a given triangle, with its sides $\dfrac{m}{n}$ of the corresponding sides of given triangle the minimum number of points to be located at equal distance is equal to the greater of $m$ and $n$ in $\dfrac{m}{n}$.

Here,

$ \dfrac{m}{n}=\dfrac{8}{5} $

So, the minimum number of point to be located at equal distance on ray $B X$ is 8 .

Solution

(d) The angle between them should be $120^{\circ}$ because in that case the figure formed by the intersection point of pair of tangent, the two end points of those two radii (at which tangents are drawn) and the centre of the circle is a quadrilateral.

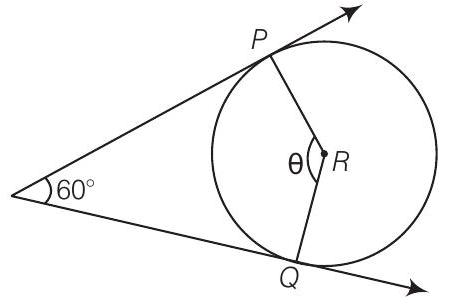
From figure it is quadrilateral,

$ \begin{aligned} \angle P O Q+\angle P R Q = 180^{\circ} \quad[\because \text{ sum of opposite angles are } 180^{\circ}] \\ 60^{\circ}+\theta = 180^{\circ} \\ \theta = 120 \end{aligned} $

Hence, the required angle between them is $120^{\circ}$.

Solution

True

Given,

$ \text{ ratio }=\sqrt{3}: \dfrac{1}{\sqrt{3}} $

$\therefore \quad$ Required ratio $=3: 1 \quad$ [multiply $\sqrt{3}$ in each term]

So, $\sqrt{3}: \dfrac{1}{\sqrt{3}}$ can be simplified as $3: 1$ and 3 as well as 1 both are positive integer.

Hence, the geometrical construction is possible to divide a line segment in the ratio $3: 1$.

Solution

False

Steps of construction

1. Draw a line segment $B C$ with suitable length.

2. Taking $B$ and $C$ as centres draw two arcs of suitable radii intersecting each other at $A$.

3. Join $B A$ and $C A . \triangle A B C$ is the required triangle.

4. From $B$ draw any ray $B X$ downwards making an acute angle $C B X$.

5. Locate seven points $B_1, B_2, B_3, \ldots, B_7$ on $B X$, such that $B B_1=B_1 B_2=B_2 B_3=B_3 B_4=B_4 B_5$ $=B_5 B_6=B_6 B_7$.

6. Join $B_3 C$ and from $B_7$ draw a line $B_7 C^{\prime} | B_3 C$ intersecting the extended line segment $B C$ at $C^{\prime}$.

7. From point $C^{\prime}$ draw $C^{\prime} A^{\prime} | C A$ intersecting the extended line segment $B A$ at $A^{\prime}$.

Then, $\triangle A^{\prime} B C^{\prime}$ is the required triangle whose sides are $\dfrac{7}{3}$ of the corresponding sides of $\triangle A B C$.

Given that, segment $B_6 C^{\prime}$ is drawn parallel to $B_3 C$. But from our construction is never possible that segment $B_6 C^{\prime}$ is parallel to $B_3 C$ because the similar triangle $A^{\prime} B C^{\prime}$ has its sides $\dfrac{7}{3}$ of the corresponding sides of triangle $A B C$. So, $B_7 C^{\prime}$ is parallel to $B_3 C$.

Solution

False

Since, the radius of the circle is $3.5 cm$ i.e., $r=3.5 cm$ and a point $P$ situated at a distance of $3 cm$ from the centre i.e., $d=3 cm$

We see that, $\quad r>d$

i.e., a point $P$ lies inside the circle. So, no tangent can be drawn to a circle from a point lying inside it.

Thinking Process

If the angle between pair of tangents is greater than $180^{\circ}$, then a pair of tangent never constructed to a circle.

Solution

True

If the angle between the pair of tangents is always greater than 0 or less than $180^{\circ}$, then we can construct a pair of tangents to a circle.

Hence, we can drawn a pair of tangents to a circle inclined at an angle of $170^{\circ}$.

Solution

Steps of construction

1. Draw a line segment $A B=7 cm$.

2. Draw a ray $A X$, making an acute $\angle B A X$.

3. Along $A X$, mark $3+5=8$ points

$A_1, A_2, A_3, A_4, A_5, A_6, A_7, A_8$ such that

$A A_1=A_1 A_2=A_2 A_3=A_3 A_4=A_4 A_5=A_5 A_6=A_6 A_7=A_7 A_8$

4. Join $A_8 B$.
5. From $A_3$, draw $A_3 C | A_8 B$ meeting $A B$ at $C$.

[by making an angle equal to $\angle B A_8 A$ at $A_3$ ]

Then, $C$ is the point on $A B$ which divides it in the ratio $3: 5$.

Thus, $A C: C B=3: 5$

Justification

Let $\quad A A_1=A_1 A_2=A_2 A_3=A_3 A_4=\ldots=A_7 A_8=x$

In $\triangle A B A_8$, we have

$ \begin{aligned} & \therefore \quad \dfrac{A C}{A_3 C | A_8 B} \\ & \text{ Hence, } \quad \dfrac{A A_3}{A_3 A_8}=\dfrac{3 x}{5 x}=\dfrac{3}{5} \\ & \quad A C: C B=3: 5 \end{aligned} $

Thinking Process

Here, Scale factor $\dfrac{m}{n}=\dfrac{2}{3}$ i.e., $m<n$, then the triangle to be constructed is smaller than the given triangle. Use this concept and then construct the required triangle.

Solution

Steps of construction

1. Draw a line segment $B C=12 cm$.

2. From $B$ draw a line $A B=5 cm$ which makes right angle at $B$.

3. Join $A C, \triangle A B C$ is the given right triangle.
4. From $B$ draw an acute $\angle C B Y$ downwards.
5. On ray $B Y$, mark three points $B_1, B_2$ and $B_3$, such that $B B_1=B_1 B_2=B_2 B_3$.
6. Join $B_3 C$.
7. From point $B_2$ draw $B_2 N | B_3 C$ intersect $B C$ at $N$.
8. From point $N$ draw $N M | C A$ intersect $B A$ at $M . \triangle M B N$ is the required triangle. $\triangle M B N$ is also a right angled triangle at $B$.

Thinking Process

Here, scale factor $\dfrac{m}{n}=\dfrac{5}{3}$ i.e., $m>n$, then the triangle to be constructed is larger than the given triangle. Use this concept and then constant the required triangle.

Solution

Steps of construction

1. Draw a line segment $B C=6 cm$.

2. Taking $B$ and $C$ as centres, draw two arcs of radii $4 cm$ and $5 cm$ intersecting each other at $A$.

3. Join $B A$ and $C A . \triangle A B C$ is the required triangle.

4. From $B$, draw any ray $B X$ downwards making at acute angle.

5. Mark five points $B_1, B_2, B_3, B_4$ and $B_5$ on $B X$, such that $B B_1=B_1 B_2=B_2 B_3=B_3 B_4=B_4 B_5$.

6. Join $B_3 C$ and from $B_5$ draw $B_5 M | B_3 C$ intersecting the extended line segment $B C$ at $M$.

7. From point $M$ draw $M N | C A$ intersecting the extended line segment $B A$ at $N$.

Then, $\triangle N B M$ is the required triangle whose sides is equal to $\dfrac{5}{3}$ of the corresponding sides of the $\triangle A B C$.

Hence, $\triangle$ NBM is the required triangle.

Thinking Process

(i) Firstly taking the perpendicular bisector of the distance from the centre to the external point. After that taking one half of bisector as radius and draw a circle.

(ii) Drawing circle intersect the given circle at two points. Now, meet these intersecting points to an external point and get the required tangents.

Solution

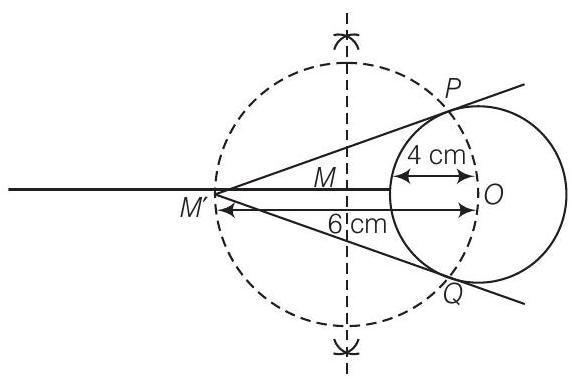
Given, a point $M^{\prime}$ is at a distance of $6 cm$ from the centre of a circle of radius $4 cm$.

Steps of construction

1. Draw a circle of radius $4 cm$. Let centre of this circle is $O$.

2. Join $O M^{\prime}$ and bisect it. Let $M$ be mid-point of $O M^{\prime}$.

3. Taking $M$ as centre and $M O$ as radius draw a circle to intersect circle $(0,4)$ at two points, $P$ and $Q$.

4. Join $P M^{\prime}$ and $Q M^{\prime}$. $P M^{\prime}$ and $Q M^{\prime}$ are the required tangents from $M^{\prime}$ to circle

Thinking Process

(i) Firstly we find the ratio of $A B$ in which $P$ divides it with the help of the relation $A=\dfrac{3}{4} A B$.

(ii) Secondly we find the ratio of $A C$ in which $Q$ divides it with the help of the relation $A Q=\dfrac{1}{4} A C$.

(iii) Now, construct the line segment $A B$ and $A C$ in which $P$ and $Q$ respectively divides it in the ratio from step (i) and (ii), respectively.

(iv) Finally get the point P and Q. After that join PQ and get the required measurement of $P Q$.

Solution

Given that, $A B=5 cm$ and $A C=7 cm$

Also,

$$ \begin{equation*} A P=\dfrac{3}{4} A B \text{ and } A Q=\dfrac{1}{4} A C \tag{i} \end{equation*} $$

From Eq. (i),

$ A P=\dfrac{3}{4} \cdot A B=\dfrac{3}{4} \times 5=\dfrac{15}{4} cm $

Then, $\quad P B=A B-A P=5-\dfrac{15}{4}=\dfrac{20-15}{4}=\dfrac{5}{4} cm \quad[\because P$ is any point on the $A B]$

$ \therefore \quad A P: P B=\dfrac{15}{4}: \dfrac{5}{4} \Rightarrow A P: P B=3: 1 $

i.e., scale factor of line segment $A B$ is $\dfrac{3}{1}$.

Again from Eq. (i), $\quad A Q=\dfrac{1}{4} A C=\dfrac{1}{4} \times 7=\dfrac{7}{4} cm$

Then, $\quad Q C=A C-A Q=7-\dfrac{7}{4}$

$ =\dfrac{28-7}{4}=\dfrac{21}{4} cm $

$[\because Q$ is any point on the $A C]$

$\therefore \quad A Q: Q C=\dfrac{7}{4}: \dfrac{21}{4}=1: 3$

$\Rightarrow \quad A Q: Q C=1: 3$

i.e., scale factor of line segment $A Q$ is $\dfrac{1}{3}$.

Steps of construction

1. Draw a line segment $A B=5 cm$.

2. Now draw a ray $A Z$ making an acute $\angle B A Z=60^{\circ}$.

3. With $A$ as centre and radius equal to $7 cm$ draw an arc cutting the line $A Z$ at $C$.

4. Draw a ray $A X$, making an acute $\angle B A X$.

5. Along $A X$, mark $1+3=4$ points $A_1, A_2, A_3$, and $A_4$ Such that $A A_1=A_1 A_2=A_2 A_3=A_3 A_4$

6. Join $A_4 B$

7. From $A_3$ draw $A_3 P | A_4 B$ meeting $A B$ at $P$. [by making an angle equal to $\angle A A_4 B$ ] Then, $P$ is the point on $A B$ which divides it in the ratio $3: 1$.

So,

$A P: P B=3: 1$

8. Draw a ray $A Y$, making an acute $\angle C A Y$.

9. Along $A Y$, mark $3+1=4$ points $B_1, B_2, B_3$ and $B_4$.

Such that $A B_1=B_1 B_2=B_2 B_3=B_3 B_4$

10. Join $B_4 C$.
11. From $B_1$ draw $B_1 Q | B_4 C$ meeting $A C$ at $Q$. [by making an angle equal to $\angle A B_4 C$ ] Then, $Q$ is the point on $A C$ which divides it in the ratio $1: 3$.

So,

$A Q: Q C=1: 3$

12. Finally, join $P Q$ and its measurment is $3.25 cm$.

Thinking Process

(i) Firstly we draw a line segment, then either of one end of the line segment with length $50 cm$ and making an angle $60^{\circ}$ with this end. We know that in parallelogram both opposite sides are equal and parallel, then again draw a line with $50 cm$ making an angle with $60^{\circ}$ from other end of line segment. Now, join both parallel line by a line segment whose measurement is $3 cm$, we get a parallelogram. After that we draw a diagonal and get a triangle BOC.

(ii) Now, we construct the triangle $B D^{\prime} C^{\prime}$ similar to $\triangle B D C$ with scale factor $\dfrac{4}{3}$.

(iii) Now, draw the line segment $D$ ’ $A$ ’ parallel to $D A$.

(iv) Finaly, we get the required parallelogram $A^{\prime} B C^{\prime} D$.

Solution

Steps of construction

1. Draw a line segment $A B=3 cm$.

2. Now, draw a ray $B Y$ making an acute $\angle A B Y=60^{\circ}$.

3. With $B$ as centre and radius equal to $5 cm$ draw an arc cut the point $C$ on $B Y$.

4. Again draw a ray $A Z$ making an acute $\angle Z A X^{\prime}=60^{\circ} . \quad[\because B Y | A Z, \therefore \angle Y B X^{\prime}=Z A X^{\prime}=60^{\circ}]$

5. With $A$ as centre and radius equal to $5 cm$ draw an arc cut the point $D$ on $A Z$.

6. Now, join $C D$ and finally make a parallelogram $A B C D$.

7. Join $B D$, which is a diagonal of parallelogram $A B C D$.

8. From $B$ draw any ray $B X$ downwards making an acute $\angle C B X$.

9. Locate 4 points $B_1, B_2, B_3, B_4$ on $B X$, such that $B B_1=B_1 B_2=B_2 B_3=B_3 B_4$.

10. Join $B_4 C$ and from $B_3 C$ draw a line $B_4 C^{\prime} | B_3 C$ intersecting the extended line segment $B C$ at $C^{\prime}$.

11. From point $C^{\prime}$ draw $C^{\prime} D^{\prime} | C D$ intersecting the extended line segment $B D$ at $D^{\prime}$. Then, $\triangle D^{\prime} B C^{\prime}$ is the required triangle whose sides are $\dfrac{4}{3}$ of the corresponding sides of $\triangle D B C$.

12. Now draw a line segment $D^{\prime} A^{\prime}$ parallel to $D A$, where $A^{\prime}$ lies on extended side $B A$ i.e., a ray $B X^{\prime}$.

13. Finally, we observe that $A^{\prime} B C^{\prime} D^{\prime}$ is a parallelogram in which $A^{\prime} D^{\prime}=6.5 cm A^{\prime} B=4 cm$ and $\angle A^{\prime} B D^{\prime}=60^{\circ}$ divide it into triangles $B C^{\prime} D^{\prime}$ and $A^{\prime} B D^{\prime}$ by the diagonal $B D^{\prime}$.

Solution

Given, two concentric circles of radii $3 cm$ and $5 cm$ with centre $O$. We have to draw pair of tangents from point $P$ on outer circle to the other.

Steps of construction

1. Draw two concentric circles with centre $O$ and radii $3 cm$ and $5 cm$.

2. Taking any point $P$ on outer circle. Join $O P$.

3. Bisect $O P$, let $M^{\prime}$ be the mid-point of $O P$.

Taking $M^{\prime}$ as centre and $O M^{\prime}$ as radius draw a circle dotted which cuts the inner circle at $M$ and $P^{\prime}$.

4. Join $P M$ and $P P^{\prime}$. Thus, $P M$ and $P P^{\prime}$ are the required tangents.

5. On measuring $P M$ and $P P^{\prime}$, we find that $P M=P P^{\prime}=4 cm$.

Actual calculation

In right angle $\triangle O M P$,

$ \begin{aligned} \therefore & \angle P M O = 90^{\circ} \\ \Rightarrow & P M^{2} = O P^{2}-O M^{2} \end{aligned} $

[by Pythagoras theorem i.e. (hypotenuse $)^{2}=(\text{ base })^{2}+(\text{ perpendicular })^{2}$ ]

$\Rightarrow$ $P M^{2}=(5)^{2}-(3)^{2}=25-9=16$

Hence, the length of both tangents is $4 cm$.

Thinking Process

(i) Here, for making two similar triangles with one vertex is same of base. We assume that,

In $\triangle A B C$ and $\triangle P Q R ;$ vertex $B=$ vertex $Q$

So, we get the required scale factor.

(ii) Now, construct a $\triangle A B C$ and then a $\triangle P B R$, similar to $\triangle A B C$ whose sides are $\dfrac{P Q}{A B}$ of the corresponding sides of the $\triangle A B C$.

Solution

Let $\triangle P Q R$ and $\triangle A B C$ are similar triangles, then its scale factor between the corresponding sides is $\dfrac{P Q}{A B}=\dfrac{8}{6}=\dfrac{4}{3}$.

Steps of construction

1. Draw a line segment $B C=5 cm$.

2. Construct $O Q$ the perpendicular bisector of line segment $B C$ meeting $B C$ at $P^{\prime}$.

3. Taking $B$ and $C$ as centres draw two arcs of equal radius $6 cm$ intersecting each other at $A$.

4. Join $B A$ and $C A$. So, $\triangle A B C$ is the required isosceles triangle.

5. From $B$, draw any ray $B X$ making an acute $\angle C B X$.

6. Locate four points $B_1, B_2, B_3$ and $B_4$ on $B X$ such that $B B_1=B_1 B_2=B_2 B_3=B_3 B_4$

7. Join $B_3 C$ and from $B_4$ draw a line $B_4 R | B_3 C$ intersecting the extended line segment $B C$ at $R$.

8. From point $R$, draw $R P | C A$ meeting $B A$ produced at $P$.

Then, $\triangle P B R$ is the required triangle.

Justification

$$ \begin{array}{llrl} \because & & B_4 R | B_3 C \\ \\ \therefore & & \dfrac{B C}{C R} & =\dfrac{3}{1} \\ \\ \text { Now, } & & \dfrac{B R}{B C} & =\dfrac{B C+C R}{B C} \\ \\ & & =1+\dfrac{C R}{B C}=1+\dfrac{1}{3}=\dfrac{4}{3} \end{array} $$

$$ RP || CA $$

$$ \triangle A B C \sim \triangle P B R $$

$$ \dfrac{P B}{A B}=\dfrac{R P}{C A}=\dfrac{B R}{B C}=\dfrac{4}{3} $$

Hence, the new triangle is similar to the given triangle whose sides are $\dfrac{4}{3}$ times of the corresponding sides of the isosceles $\triangle A B C$.

Solution

Steps of construction

1. Draw a line segment $A B=5 cm$.

2. From point $B$, draw $\angle A B Y=60^{\circ}$ on which take $B C=6 cm$.

3. Join $A C, \triangle A B C$ is the required triangle.

4. From $A$, draw any ray $A X$ downwards making an acute angle.

5. Mark 7 points $B_1, B_2, B_3, B_4, B_5, B_6$ and $B_7$ on $A X$, such that $A B_1=B_1 B_2=B_2 B_3$

$ =B_3 B_4=B_4 B_5=B_5 B_6=B_6 B_7 $

6. Join $B_7 B$ and from $B_5$ draw $B_5 M | B_7 B$ intersecting $A B$ at $M$.

7. From point $M$ draw $M N | B C$ intersecting $A C$ at $N$. Then, $\triangle A M N$ is the required triangle whose sides are equal to $\dfrac{5}{7}$ of the corresponding sides of the $\triangle A B C$.

Justification

Here,

$B_5 M | B_7 B \quad$ (by construction)

$\therefore \quad \dfrac{A M}{M B}=\dfrac{5}{2}$

Now, $\quad \dfrac{A B}{A M}=\dfrac{A M+M B}{A M}$

$ =1+\dfrac{M B}{A M}=1+\dfrac{2}{5}=\dfrac{7}{5} $

Also,

$M N | B C$

$\therefore$ $ \triangle A M N \sim \triangle A B C $

Therefore,

$ \dfrac{A M}{A B}=\dfrac{A N}{A C}=\dfrac{N M}{B C}=\dfrac{5}{7} $

Solution

In order to draw the pair of tangents, we follow the following steps

Steps of construction

1. Take a point $O$ on the plane of the paper and draw a circle of radius $O A=4 cm$.

2. Produce $O A$ to $B$ such that $O A=A B=4 cm$.

3. Taking $A$ as the centre draw a circle of radius $A O=A B=4 cm$.

Suppose it cuts the circle drawn in step 1 at $P$ and $Q$.

4. Join $B P$ and $B Q$ to get desired tangents.

Justification In $\triangle O A P$, we have

Also,

$$ \begin{align*} & O A=O P=4 cm \\ & A P=4 cm \end{align*} $$

$\therefore \quad \triangle O A P$ is equilateral

$ \begin{aligned} & \angle P A O=60^{\circ} \\ & \angle B A P=120^{\circ} \end{aligned} $

$ \Rightarrow $

In $\triangle B A P$, we have

$ \begin{aligned} & B A=A P \text{ and } \angle B A P=120^{\circ} \\ & \therefore \quad \angle A B P=\angle A P B=30^{\circ} \\ & \Rightarrow \quad \angle P B Q=60^{\circ} \end{aligned} $

Alternate Method

Steps of construction

1. Take a point $O$ on the plane of the paper and draw a circle with centre $O$ and radius $O A=4 cm$

2. At $O$ construct radii $O A$ and $O B$ such that to $\angle A O B$ equal $120^{\circ}$ i.e., supplement of the angle between the tangents.

3. Draw perpendiculars to $O A$ and $O B$ at $A$ and $B$, respectively. Suppose these perpendiculars intersect at $P$. Then, $P A$ and $P B$ are required tangents.

Justification

In quadrilateral $O A P B$, we have

$ \begin{matrix} & \angle O A P = \angle O B P=90^{\circ} \\ \text{ and } & \angle A O B = 120^{\circ} \\ \therefore & \angle O A P+\angle O B P+\angle A O B+\angle A P B = 360^{\circ} \\ \Rightarrow & 90^{\circ}+90^{\circ}+120^{\circ}+\angle A P B = 360^{\circ} \\ \therefore & \angle A P B = 360^{\circ}-(90^{\circ}+90^{\circ}+120^{\circ}) \\ & = 360^{\circ}-300^{\circ}=60^{\circ} \end{matrix} $

Thinking Process

Triangles are congruent when all corresponding sides and interior angles are congruent. The triangles will have the same shape and size, but one may be a mirror image of the other.

So, first we construct a triangle similar to $\triangle A B C$ with scale factor $3 / 2$ and use the above concept to check the triangles are congruent or not.

Solution

Steps of construction

1. Draw a line segment $B C=6 cm$.

2. Taking $B$ and $C$ as centres, draw two arcs of radii $4 cm$ and $9 cm$ intersecting each other at $A$.

3. Join $B A$ and $C A . \triangle A B C$ is the required triangle.

4. From $B$, draw any ray $B X$ downwards making an acute angle.

5. Mark three points $B_1, B_2, B_3$ on $B X$, such that $B B_1=B_1 B_2=B_2 B_3$.

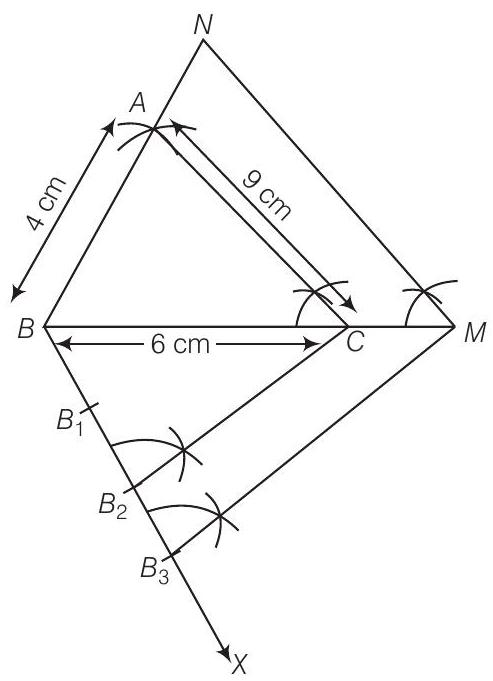
6. Join $B_2 C$ and from $B_3$ draw $B_3 M | B_2 C$ intersecting the extended line segment $B C$ at $M$.

7. From point $M$, draw $M N | C A$ intersecting the extended line segment $B A$ to $N$.

Then, $\triangle$ NBM is the required triangle whose sides are equal to $\dfrac{3}{2}$ of the corresponding sides of the $\triangle A B C$.

Justification

Here,

$B_3 M | B_2 C$

$\therefore$ $\dfrac{B C}{C M}=\dfrac{2}{1}$

$\dfrac{B M}{B C}=\dfrac{B C+C M}{B C}$

$=1+\dfrac{C M}{B C}=1+\dfrac{1}{2}=\dfrac{3}{2}$

Also,

$M N | C A$

$\therefore$ $\triangle ABC \sim \triangle NBM$

Therefore,

$ \dfrac{N B}{A B}=\dfrac{N M}{A C}=\dfrac{B M}{B C}=\dfrac{3}{2} $

The two triangles are not congruent because, if two triangles are congruent, then they have same shape and same size. Here, all the three angles are same but three sides are not same i.e., one side is different.