Unit 6 General Principles And Processes Of Isolation Of Elements-Deleted
A few elements like carbon, sulphur, gold and noble gases, occur in free state while others in combined forms in the earth’s crust. The extraction and isolation of an element from its combined form involves various principles of chemistry. A particular element may occur in a variety of compounds. The process of metallurgy and isolation should be such that it is chemically feasible and commercially viable. Still, some general principles are common to all the extraction processes of metals. For obtaining a particular metal, first we look for minerals which are naturally occurring chemical substances in the earth’s crust obtainable by mining. Out of many minerals in which a metal may be found, only a few are viable to be used as sources of that metal. Such minerals are known as ores.
Rarely, an ore contains only a desired substance. It is usually contaminated with earthly or undesired materials known as gangue. The extraction and isolation of metals from ores involve the following major steps:
- Concentration of the ore,
- Isolation of the metal from its concentrated ore, and
- Purification of the metal.
The entire scientific and technological process used for isolation of the metal from its ores is known as metallurgy.
6.1 Occurrence of Metals
In the present Unit, first we shall describe various steps for effective concentration of ores. After that we shall discuss the principles of some of the common metallurgical processes. Those principles shall include the thermodynamic and electrochemical aspects involved in the effective reduction of the concentrated ore to the metal.
Elements vary in abundance. Among metals, aluminium is the most abundant. It is the third most abundant element in earth’s crust (
The principal ores of aluminium, iron, copper and zinc have been given in Table 6.1.
Table 6.1: Principal Ores of Some Important Metals
| Metal | Composition | |
|---|---|---|
| Aluminium | Bauxite | |
| Iron | ||
| Kaolinite (a form of clay) | ||
| Haematite | ||
| Magnetite | ||
| Iron pyrites | ||
| Copper pyrites | ||
| Malachite | ||
| Cuprite | ||
| Copper glance | ||
| Zinc blende or Sphalerite | ||
| Calamine | ||
| Zincite |
For the purpose of extraction, bauxite is chosen for aluminium. For iron, usually the oxide ores which are abundant and do not produce polluting gases (like
Removal of the unwanted materials (e.g., sand, clays, etc.) from the ore is known as concentration, dressing or benefaction. It involves several steps and selection of these steps depends upon the differences in physical properties of the compound of the metal present and that of the gangue. The type of the metal, the available facilities and the environmental factors are also taken into consideration. Some of the important procedures are described below.
6.2 Concentration of Ores
Removal of the unwanted materials (e.g., sand, clays, etc.) from the ore is known as concentration, dressing or benefaction. Before proceeding for concentration, ores are graded and crushed to reasonable size. Concentration of ores involves several steps and selection of these steps depends upon the differences in physical properties of the compound of the metal present and that of the gangue. The type of the metal, the available facilities and the environmental factors are also taken into consideration. Some of the important procedures for concentration of ore are described below.
6.2.1 Hydraulic Washing
This is based on the difference between specific gravities of the ore and the gangue particles. It is therefore a type of gravity separation. In one such process, an upward stream of running water is used to wash the powdered ore. The lighter gangue particles are washed away and the heavier ore particles are left behind.
6.2.2 Magnetic Separation
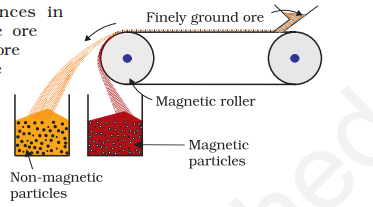
This is based on differences in magnetic properties of the ore components. If either the ore or the gangue is attracted towards magnetic field, then the separation is carried out by this method. For example iron ores are attracted towards magnet, hence, non–magnetic impurities can be separted from them using magnetic separation. The powdered ore is dropped over a conveyer belt which moves over a magnetic roller (Fig.6.1) Magnetic substance remains attracted towards the belt and falls close to it.
6.2.3 Froth Floatation Method
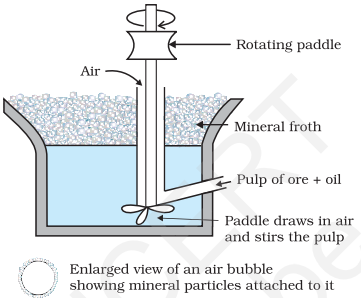
This method is used for removing gangue from sulphide ores. In this process, a suspension of the powdered ore is made with water. Collectors and froth stabilisers are added to it. Collectors (e.g., pine oils, fatty acids, xanthates, etc.) enhance nonwettability of the mineral particles and froth stabilisers (e.g., cresols, aniline) stabilise the froth.
The mineral particles become wet by oils while the gangue particles by water. A rotating paddle agitates the mixture and draws air in it. As a result, froth is formed which carries the mineral particles. The froth is light and is skimmed off. It is then dried for recovery of the ore particles.
Sometimes, it is possible to separate two sulphide ores by adjusting proportion of oil to water or by using ‘depressants’. For example, in the case of an ore containing ZnS and PbS, the depressant used is NaCN. It selectively prevents ZnS from coming to the froth but allows PbS to come with the froth.
The Innovative Washerwoman
One can do wonders if he or she has a scientific temperament and is attentive to observations. A washerwoman had an innovative mind too. While washing a miner’s overalls, she noticed that sand and similar dirt fell to the bottom of the washtub. What was peculiar, the copper bearing compounds that had come to the clothes from the mines, were caught in the soapsuds and so they came to the top. One of her clients, Mrs. Carrie Everson was a chemist. The washerwoman told her experience to Mrs. Everson. The latter thought that the idea could be used for separating copper compounds from rocky and earth materials on large scale. This way an invention came up. At that time only those ores were used for extraction of copper, which contained large amounts of the metal. Invention of the Froth Floatation Method made copper mining profitable even from the lowgrade ores. World production of copper soared and the metal became cheaper.
6.2.4 Leaching
Leaching is often used if the ore is soluble in some suitable solvent. Following examples illustrate the procedure:
(a) Leaching of alumina from bauxite
The principal ore of aluminium, bauxite, usually contains
The aluminate in solution is neutralised by passing
The sodium silicate remains in the solution and hydrated alumina is filtered, dried and heated to give back pure
(b) Other examples
In the metallurgy of silver and that of gold, the respective metal is leached with a dilute solution of
6.3 Extraction of Crude Metal from Concentrated Ore
To extract metal from concentrated ore, it must be converted to a form which is suitable for reduction to metal. Usually sulphide ores are converted to oxide before reduction because oxides are easier to reduce. Thus isolation of metals from concentrated ore involves two major steps viz.,
(a) conversion to oxide, and (b) reduction of the oxide to metal.
( a ) Conversion to oxide
(i) Calcination: Calcinaton involves heating. It removes the volatile matter which escapes leaving behind the metal oxide:
(ii) Roasting: In roasting, the ore is heated in a regular supply of air in a furnace at a temperature below the melting point of the metal. Some of the reactions involving sulphide ores are:
The sulphide ores of copper are heated in reverberatory furnace [Fig. 6.3]. If the ore contains iron, it is mixed with silica before heating. Iron oxide ‘slags of ’* as iron silicate and copper is produced in the form of copper matte which contains Cu2S and FeS.
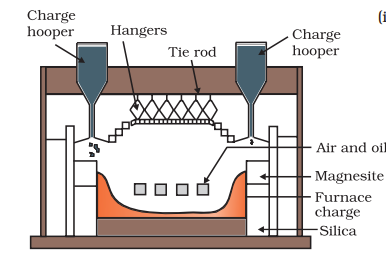
The SO2 produced is utilised for manufacturing H2SO4 .
(b) Reduction of oxide to the metal
Reduction of the metal oxide usually involves heating it with some other substance acting as a reducing agent (
Some metal oxides get reduced easily while others are very difficult to be reduced (reduction means electron gain by the metal ion). In any case, heating is required.
6.4 Thermodynamic Principles of Metallurgy
Some basic concepts of thermodynamics help us in understanding the theory of metallurgical transformations. Gibbs energy is the most significant term here.The change in Gibbs energy,
where,
where,
1. When the value of
2. If reactants and products of two reactions are put together in a system and the net
Ellingham Diagram
The graphical representation of Gibbs energy was first used by H.J.T.Ellingham. This provides a sound basis for considering the choice of reducing agent in the reduction of oxides. This is known as Ellingham Diagram. Such diagrams help us in predicting the feasibility of thermal reduction of an ore. The criterion of feasibility is that at a given temperature, Gibbs energy of the reaction must be negative.
(a) Ellingham diagram normally consists of plots of
In this reaction, the gaseous amount (hence molecular randomness) is decreasing from left to right due to the consumption of gases leading to a -ve value of
(b) Each plot is a straight line except when some change in phase (
(c) There is a point in a curve below which
(d) In an Ellingham diagram, the plots of
(e) Similar diagrams are also constructed for sulfides and halides and it becomes clear why reductions of
Limitations of Ellingham Diagram
1. The graph simply indicates whether a reaction is possible or not, i.e., the tendency of reduction with a reducing agent is indicated. This is so because it is based only on the thermodynamic concepts. It does not explain the kinetics of the reduction process. It cannot answer questions like how fast reduction can proceed? However, it explains why the reactions are sluggish when every species is in solid state and smooth when the ore melts down. It is interesting to note here that DH (enthalpy change) and the DS (entropy change) values for any chemical reaction remain nearly constant even on varying temperature. So the only dominant variable in equation(6.14) becomes T. However, DS depends much on the physical state of the compound. Since entropy depends on disorder or randomness in the system, it will increase if a compound melts (s® l) or vapourises (l® g) since molecular randomness increases on changing the phase from solid to liquid or from liquid to gas.
2. The interpretation of
This is not always true because the reactant/product may be solid. In commercial processes reactants and products are in contact for a short time.
6.4.1 Applications
(a) Extraction of iron from its oxides
Oxide ores of iron, after concentration through calcination/roasting (to remove water, to decompose carbonates and to oxidise sulphides) are mixed with limestone and coke and fed into a Blast furnace from its top. Here, the oxide is reduced to the metal. Thermodynamics helps us to understand how coke reduces the oxide and why this furnace is chosen. One of the main reduction steps in this process is:
It can be seen as a couple of two simpler reactions. In one, the reduction of
When both the reactions take place to yield the equation (6.24), the net Gibbs energy change becomes:
Naturally, the resultant reaction will take place when the right hand side in equation 6.27 is negative. In
(C,CO) goes downward. At temperatures above 1073K (approx.), the
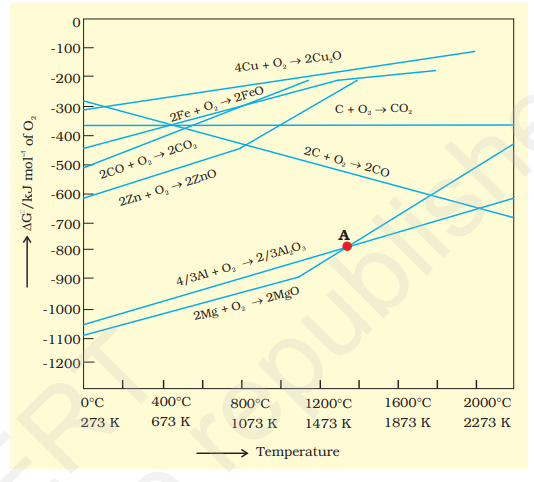
In the Blast furnace, reduction of iron oxides takes place in different temperature ranges. Hot air is blown from the bottom of the furnace and coke is burnt to give temperature upto about
At 500 -
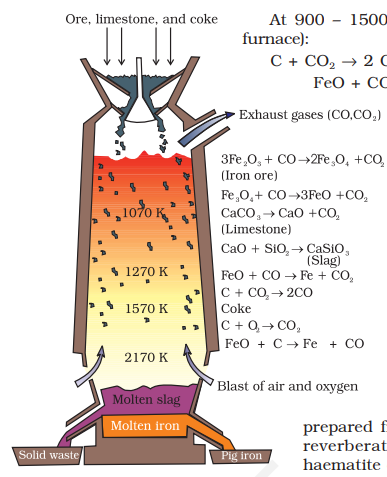
Limestone is also decomposed to
The iron obtained from Blast furnace contains about
Further Reductions
Wrought iron or malleable iron is the purest form of commercial iron and is prepared from cast iron by oxidising impurities in a reverberatory furnace lined with haematite. The haematite oxidises carbon to carbon monoxide:
Limestone is added as a flux and sulphur, silicon and phosphorus are oxidised and passed into the slag. The metal is removed and freed from the slag by passing through rollers.
(b) Extraction of copper from cuprous oxide [copper(I) oxide]
In the graph of
The oxide can then be easily reduced to metallic copper using coke:
In actual process, the ore is heated in a reverberatory furnace after mixing with silica. In the furnace, iron oxide ‘slags of as iron silicate and copper is produced in the form of copper matte. This contains
Copper matte is then charged into silica lined convertor. Some silica is also added and hot air blast is blown to convert the remaining
FeS,
The solidified copper obtained has blistered appearance due to the evolution of SO2 and so it is called blister copper.
(c) Extraction of zinc from zinc oxide The reduction of zinc oxide is done using coke. The temperature in this case is higher than that in the case of copper. For the purpose of heating, the oxide is made into brickettes with coke and clay.
The metal is distilled off and collected by rapid chilling.
6.5 Electrochemical Principles of Metallurgy
We have seen how principles of thermodyamics are applied to pyrometallurgy. Similar principles are effective in the reductions of metal ions in solution or molten state. Here they are reduced by electrolysis or by adding some reducing element.
In the reduction of a molten metal salt, electrolysis is done. Such methods are based on electrochemical principles which could be understood through the equation,
here
In simple electrolysis, the
Aluminium
In the metallurgy of aluminium, purified
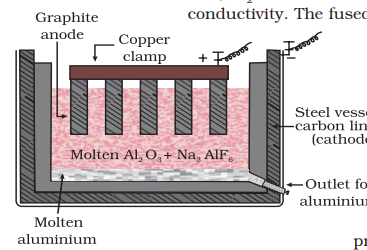
This process of electrolysis is widely known as Hall-Heroult process.
Thus electrolysis of the molten mass is carried out in an electrolytic cell using carbon electrodes. The oxygen liberated at anode reacts with the carbon of anode
Anode:
6.6 Oxidation Reduction
Besides reductions, some extractions are based on oxidation particularly for non-metals. A very common example of extraction based on oxidation is the extraction of chlorine from brine (chlorine is abundant in sea water as common salt) .
The
As studied earlier, extraction of gold and silver involves leaching the metal with
6.7 Refining
A metal extracted by any method is usually contaminated with some impurity. For obtaining metals of high purity, several techniques are used depending upon the differences in properties of the metal and the impurity. Some of them are listed below.
(a) Distillation (b) Liquation (c) Electrolysis (d) Zone refining (e) Vapour phase refining (f ) Chromatographic methods
These are described in detail here.
(a) Distillation
This is very useful for low boiling metals like zinc and mercury. The impure metal is evaporated to obtain the pure metal as distillate.
(b) Liquation
In this method a low melting metal like tin can be made to flow on a sloping surface. In this way it is separated from higher melting impurities.
(c) Electrolytic refining
In this method, the impure metal is made to act as anode. A strip of the same metal in pure form is used as cathode. They are put in a suitable electrolytic bath containing soluble salt of the same metal. The more basic metal remains in the solution and the less basic ones go to the anode mud. This process is also explained using the concept of electrode potential, over potential, and Gibbs energy which you have seen in previous sections. The reactions are:
Anode:
Cathode:
Copper is refined using an electrolytic method. Anodes are of impure copper and pure copper strips are taken as cathode. The electrolyte is acidified solution of copper sulphate and the net result of electrolysis is the transfer of copper in pure form from the anode to the cathode:
Anode:
Cathode:
Impurities from the blister copper deposit as anode mud which contains antimony, selenium, tellurium, silver, gold and platinum; recovery of these elements may meet the cost of refining. Zinc may also be refined this way.
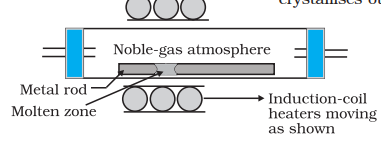
(d) Zone refining : This method is based on the principle that the impurities are more soluble in the melt than in the solid state of the metal. A mobile heater surrounding the rod of impure metal is fixed at its one end (Fig. 6.7). The molten zone moves along with the heater which is moved forward. As the heater moves forward, the pure metal crystallises out of the melt left behind and the impurities pass on into the adjacent new molten zone created by movement of heaters. The process is repeated several times and the heater is moved in the same direction again and again. Impurities get concentrated at one end. This end is cut off. This method is very useful for producing semiconductor and other metals of very high purity, e.g., germanium, silicon, boron, gallium and indium.
(e) Vapour phase refining In this method, the metal is converted into its volatile compound which is collected and decomposed to give pure metal. So, the two requirements are:
(i) the metal should form a volatile compound with an available reagent,
(ii) the volatile compound should be easily decomposable, so that the recovery is easy.
Following examples will illustrate this technique.
Mond Process for Refining Nickel: In this process, nickel is heated in a stream of carbon monoxide forming a volatile complex named as nickel tetracarbonyl. This compex is decomposed at higher temperature to obtain pure metal.
The carbonyl is subjected to higher temperature so that it is decomposed giving the pure metal:
van Arkel Method for Refining Zirconium or Titanium: This method is very useful for removing all the oxygen and nitrogen present in the form of impurity in certain metals like Zr and Ti. The crude metal is heated in an evacuated vessel with iodine. The metal iodide being more covalent, volatilises:
The metal iodide is decomposed on a tungsten filament, electrically heated to about
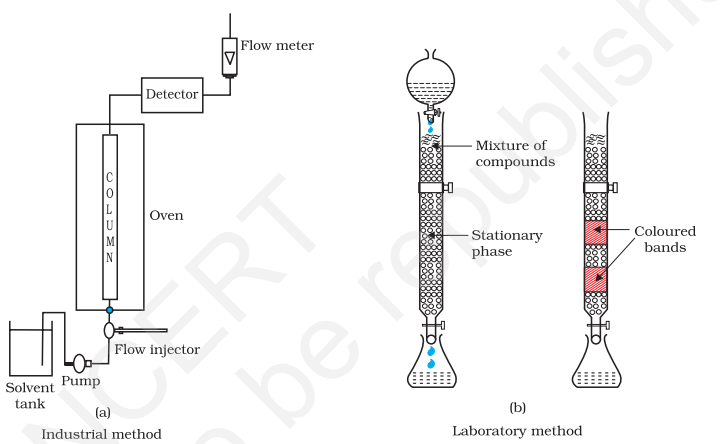
(f) Chromatographic methods : You have learnt about chromatographic technique of purification of substances in Class XI (Unit–12).
Column chromatography is very useful for purification of the elements which are available in minute quantities and the impurities are not very different in chemical properties from the element to be purified.
6.8 Uses of Aluminium, Copper, Zinc and Iron
Aluminium foils are used as wrappers for food materials. The fine dust of the metal is used in paints and lacquers. Aluminium, being highly reactive, is also used in the extraction of chromium and manganese from their oxides. Wires of aluminium are used as electricity conductors. Alloys containing aluminium, being light, are very useful.
Copper is used for making wires used in electrical industry and for water and steam pipes. It is also used in several alloys that are rather tougher than the metal itself, e.g., brass (with zinc), bronze (with tin) and coinage alloy (with nickel).
Zinc is used for galvanising iron. It is also used in large quantities in batteries, as a constituent of many alloys, e.g., brass, (Cu 60\%, Zn
Cast iron, which is the most important form of iron, is used for casting stoves, railway sleepers, gutter pipes , toys, etc. It is used in the manufacture of wrought iron and steel. Wrought iron is used in making anchors, wires, bolts, chains and agricultural implements. Steel finds a number of uses. Alloy steel is obtained when other metals are added to it. Nickel steel is used for making cables, automobiles and aeroplane parts, pendulum, measuring tapes. Chrome steel is used for cutting tools and crushing machines, and stainless steel is used for cycles, automobiles, utensils, pens, etc.
Summary
Although modern metallurgy had exponential growth after Industrial Revolution, many modern concepts in metallurgy have their roots in ancient practices that predated the Industrial Revolution. For over 7000 years, India has had high tradition of metallurigical skills. Ancient Indian metallurgists have made major contributions which deserve their place in metallurgical history of the world. In the case of zinc and high–carbon steel, ancient India contributed significantly for the developemnt of base for the modern metallurgical advancements which induced metallurgical study leading to Industrial Revolution.
Metals are required for a variety of purposes. For this, we need their extraction from the minerals in which they are present and from which their extraction is commercially feasible.These minerals are known as ores. Ores of the metal are associated with many impurities. Removal of these impurities to certain extent is achieved in concentration steps. The concentrated ore is then treated chemically for obtaining the metal. Usually the metal compounds (e.g., oxides, sulphides) are reduced to the metal. The reducing agents used are carbon, CO or even some metals.
In these reduction processes, the thermodynamic and electrochemical concepts are given due consideration. The metal oxide reacts with a reducing agent; the oxide is reduced to the metal and the reducing agent is oxidised. In the two reactions, the net Gibbs energy change is negative, which becomes more negative on raising the temperature. Conversion of the physical states from solid to liquid or to gas, and formation of gaseous states favours decrease in the Gibbs energy for the entire system. This concept is graphically displayed in plots of DG0 vs T (Ellingham diagram) for such oxidation/reduction reactions at different temperatures. The concept of electrode potential is useful in the isolation of metals (e.g., Al, Ag, Au) where the sum of the two redox couples is positive so that the Gibbs energy change is negative. The metals obtained by usual methods still contain minor impurities. Getting pure metals requires refining. Refining process depends upon the differences in properties of the metal and the impurities. Extraction of aluminium is usually carried out from its bauxite ore by leaching it with NaOH. Sodium aluminate, thus formed, is separated and then neutralised to give back the hydrated oxide, which is then electrolysed using cryolite as a flux. Extraction of iron is done by reduction of its oxide ore in blast furnace. Copper is extracted by smelting and heating in a reverberatory furnace. Extraction of zinc from zinc oxides is done using coke. Several methods are employed in refining the metal. Metals, in general, are very widely used and have contributed significantly in the development of a variety of industries.






