Solution

The given function is $f(x)=\frac{\log x}{x}$.

$ f^{\prime}(x)=\frac{x(\frac{1}{x})-\log x}{x^{2}}=\frac{1-\log x}{x^{2}} $

Now, $f^{\prime}(x)=0$

$\Rightarrow 1-\log x=0$ $\Rightarrow \log x=1$

$\Rightarrow \log x=\log e$

$\Rightarrow x=e$

Now, $f^{\prime \prime}(x)=\frac{x^{2}(-\frac{1}{x})-(1-\log x)(2 x)}{x^{4}}$

$ \begin{aligned} & =\frac{-x-2 x(1-\log x)}{x^{4}} \\ & =\frac{-3+2 \log x}{x^{3}} \end{aligned} $

Now, $f^{\prime \prime}(e)=\frac{-3+2 \log e}{e^{3}}=\frac{-3+2}{e^{3}}=\frac{-1}{e^{3}}<0$

Therefore, by second derivative test, $f$ is the maximum at $x=e$.

Solution

Let $\triangle A B C$ be isosceles where $B C$ is the base of fixed length $b$.

Let the length of the two equal sides of $\triangle A B C$ be $a$.

Draw AD $\square BC$.

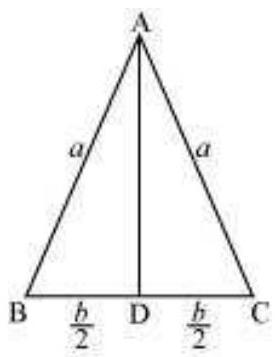
Now, in $\triangle A D C$, by applying the Pythagoras theorem, we have:

$AD=\sqrt{a^{2}-\frac{b^{2}}{4}}$

Area of triangle

$ (A)=\frac{1}{2} b \sqrt{a^{2}-\frac{b^{2}}{4}} $

The rate of change of the area with respect to time $(t)$ is given by,

$\frac{d A}{d t}=\frac{1}{2} b \cdot \frac{2 a}{2 \sqrt{a^{2}-\frac{b^{2}}{4}}} \frac{d a}{d t}=\frac{a b}{\sqrt{4 a^{2}-b^{2}}} \frac{d a}{d t}$

It is given that the two equal sides of the triangle are decreasing at the rate of $3 cm$ per second.

$ \begin{aligned} & \\ & \square \frac{d a}{d t}=-3 cm / s \\ & \therefore \frac{d A}{d t}=\frac{-3 a b}{\sqrt{4 a^{2}-b^{2}}} \end{aligned} $

Then, when $a=b$, we have:

$\frac{d A}{d t}=\frac{-3 b^{2}}{\sqrt{4 b^{2}-b^{2}}}=\frac{-3 b^{2}}{\sqrt{3 b^{2}}}=-\sqrt{3} b$

Hence, if the two equal sides are equal to the base, then the area of the triangle is decreasing at the rate of $\sqrt{3} bm cm^{2} / s$.

Solution

$f(x)=\frac{4 \sin x-2 x-x \cos x}{2+\cos x}$

$\therefore f^{\prime}(x)=\frac{(2+\cos x)(4 \cos x-2-\cos x+x \sin x)-(4 \sin x-2 x-x \cos x)(-\sin x)}{(2+\cos x)^{2}}$

$=\frac{(2+\cos x)(3 \cos x-2+x \sin x)+\sin x(4 \sin x-2 x-x \cos x)}{(2+\cos x)^{2}}$

$=\frac{6 \cos x-4+2 x \sin x+3 \cos ^{2} x-2 \cos x+x \sin x \cos x+4 \sin ^{2} x-2 x \sin x-x \sin x \cos x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-4+3 \cos ^{2} x+4 \sin ^{2} x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-4+3 \cos ^{2} x+4-4 \cos ^{2} x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-\cos ^{2} x}{(2+\cos x)^{2}}=\frac{\cos x(4-\cos x)}{(2+\cos x)^{2}}$

Now, $f^{\prime}(x)=0$

$\Rightarrow \cos x=0$ or $\cos x=4$

But, $\cos x \neq 4$

$\square \cos x=0$

$\Rightarrow x=\frac{\pi}{2}, \frac{3 \pi}{2}$

Now, $x=\frac{\pi}{2}$ and $x=\frac{3 \pi}{2}$ divides $(0,2 \pi)$ into three disjoint intervals i.e.,

$(0, \frac{\pi}{2}),(\frac{\pi}{2}, \frac{3 \pi}{2})$, and $(\frac{3 \pi}{2}, 2 \pi)$.

In intervals $(0, \frac{\pi}{2})$ and $(\frac{3 \pi}{2}, 2 \pi), f^{\prime}(x)>0$.

Thus, $f(x)$ is increasing for $0<x<\frac{x}{2}$ and $\frac{3 \pi}{2}<x<2 \pi$.

In the interval $(\frac{\pi}{2}, \frac{3 \pi}{2}), f^{\prime}(x)<0$.

Thus, $f(x)$ is decreasing for $\frac{\pi}{2}<x<\frac{3 \pi}{2}$.

Solution

$f(x)=x^{3}+\frac{1}{x^{3}}$

$\therefore f^{\prime}(x)=3 x^{2}-\frac{3}{x^{4}}=\frac{3 x^{6}-3}{x^{4}}$

Then, $f^{\prime}(x)=0 \Rightarrow 3 x^{6}-3=0 \Rightarrow x^{6}=1 \Rightarrow x= \pm 1$

Now, the points $x=1$ and $x=-1$ divide the real line into three disjoint intervals

i.e., $(-\infty,-1),(-1,1)$, and $(1, \infty)$.

In intervals $(-\infty,-1)$ and $(1, \infty)$ i.e., when $x<-1$ and $x>1, f^{\prime}(x)>0$.

Thus, when $x<-1$ and $x>1, f$ is increasing.

In interval $(-1,1)$ i.e., when $-1<x<1, f^{\prime}(x)<0$.

Thus, when $-1<x<1, f$ is decreasing.

Solution

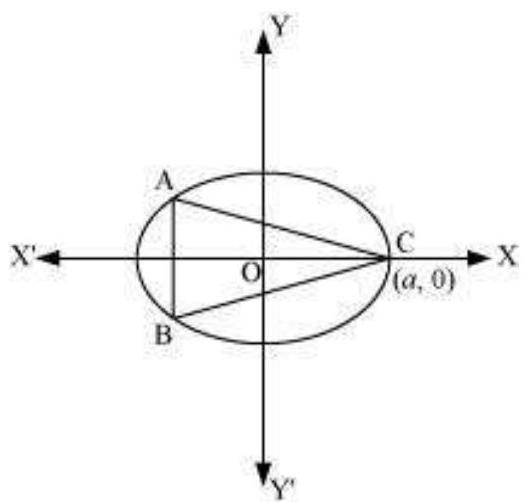
The given ellipse is $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$.

Let the major axis be along the $x$-axis.

Let $A B C$ be the triangle inscribed in the ellipse where vertex $C$ is at $(a, 0)$.

Since the ellipse is symmetrical with respect to the $x$-axis and $y$-axis, we can assume the coordinates of $A$ to be $(-x_1, y_1)$ and the coordinates of $B$ to be $(-x_1,-y_1)$.

Now, we have $y_1= \pm \frac{b}{a} \sqrt{a^{2}-x_1^{2}}$.

$\square$ Coordinates of $A$ are $(-x_1, \frac{b}{a} \sqrt{a^{2}-x_1^{2}})$ and the coordinates of $B$ are $(x_1,-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})$.

As the point $(x_1, y_1)$ lies on the ellipse, the area of triangle $ABC(A)$ is given by,

$ \begin{aligned} & A=\frac{1}{2}|a(\frac{2 b}{a} \sqrt{a^{2}-x_1^{2}})+(-x_1)(-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})+(-x_1)(-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})| \\ & \Rightarrow A=b \sqrt{a^{2}-x_1^{2}}+x_1 \frac{b}{a} \sqrt{a^{2}-x_1^{2}} \\ & \therefore \frac{d A}{d x_1}=\frac{-2 x_1 b}{2 \sqrt{a^{2}-x_1^{2}}}+\frac{b}{a} \sqrt{a^{2}-x_1^{2}}-\frac{2 b x_1^{2}}{a 2 \sqrt{a^{2}-x_1^{2}}} \\ & =\frac{b}{a \sqrt{a^{2}-x_1^{2}}}[-x_1 a+(a^{2}-x_1^{2})-x_1^{2}] \\ & =\frac{b(-2 x_1^{2}-x_1 a+a^{2})}{a \sqrt{a^{2}-x_1^{2}}} \end{aligned} $

Now, $\frac{d A}{d x_1}=0$

$\Rightarrow-2 x_1^{2}-x_1 a+a^{2}=0$

$\Rightarrow x_1=\frac{a \pm \sqrt{a^{2}-4(-2)(a^{2})}}{2(-2)}$

$=\frac{a \pm \sqrt{9 a^{2}}}{-4}$

$=\frac{a \pm 3 a}{-4}$

$\Rightarrow x_1=-a, \frac{a}{2}$

But, $x_1$ cannot be equal to $a$. $\therefore x_1=\frac{a}{2} \Rightarrow y_1=\frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}}=\frac{b a}{2 a} \sqrt{3}=\frac{\sqrt{3} b}{2}$

Now, $\frac{d^{2} A}{d x_1^{2}}=\frac{b}{a}{\frac{\sqrt{a^{2}-x_1^{2}}(-4 x_1-a)-(-2 x_1^{2}-x_1 a+a^{2}) \frac{(-2 x_1)}{2 \sqrt{a^{2}-x_1^{2}}}}{a^{2}-x_1^{2}}}$

$ =\frac{b}{a}{\frac{(a^{2}-x_1^{2})(-4 x_1-a)+x_1(-2 x_1^{2}-x_1 a+a^{2})}{(a^{2}-x_1^{2})^{\frac{3}{2}}}} $

$ =\frac{b}{a}{\frac{2 x^{3}-3 a^{2} x-a^{3}}{(a^{2}-x_1^{2})^{\frac{3}{2}}}} $

Also, when $x_1=\frac{a}{2}$, then

$ \begin{aligned} \frac{d^{2} A}{d x_1^{2}} & =\frac{b}{a}{\frac{2 \frac{a^{3}}{8}-3 \frac{a^{3}}{2}-a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}}=\frac{b}{a}{\frac{\frac{a^{3}}{4}-\frac{3}{2} a^{3}-a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}} \\ & =-\frac{b}{a}{\frac{\frac{9}{4} a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}}<0 \end{aligned} $

Thus, the area is the maximum when $x_1=\frac{a}{2}$.

$\square$ Maximum area of the triangle is given by,

$ \begin{aligned} A & =b \sqrt{a^{2}-\frac{a^{2}}{4}}+(\frac{a}{2}) \frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}} \\ & =a b \frac{\sqrt{3}}{2}+(\frac{a}{2}) \frac{b}{a} \times \frac{a \sqrt{3}}{2} \\ & =\frac{a b \sqrt{3}}{2}+\frac{a b \sqrt{3}}{4}=\frac{3 \sqrt{3}}{4} a b \end{aligned} $

Solution

Let $l, b$, and $h$ represent the length, breadth, and height of the tank respectively.

Then, we have height $(h)=2 m$

Volume of the tank $=8 m^{3}$

Volume of the tank $=l \times b \times h$

$\square 8=l \times b \times 2$

$\Rightarrow l b=4 \Rightarrow b=\frac{4}{l}$

Now, area of the base $=I b=4$

Area of the 4 walls $(A)=2 h(I+b)$

$\therefore A=4(l+\frac{4}{l})$

$\Rightarrow \frac{d A}{d l}=4(1-\frac{4}{l^{2}})$

Now, $\frac{d A}{d l}=0$

$\Rightarrow 1-\frac{4}{l^{2}}=0$

$\Rightarrow l^{2}=4$

$\Rightarrow l= \pm 2$

However, the length cannot be negative.

Therefore, we have $I=4$.

$\therefore b=\frac{4}{l}=\frac{4}{2}=2$

Now, $\frac{d^{2} A}{d l^{2}}=\frac{32}{l^{3}}$

When $l=2, \frac{d^{2} A}{d l^{2}}=\frac{32}{8}=4>0$.

Thus, by second derivative test, the area is the minimum when $I=2$.

We have $I=b=h=2$.

$\square$ Cost of building the base $=Rs 70 \times(I b)=Rs 70(4)=Rs 280$

Cost of building the walls $=Rs 2 h(I+b) \times 45=Rs 90(2)(2+2)$

$=Rs 8(90)=Rs 720$

Required total cost $=Rs(280+720)=Rs 1000$

Hence, the total cost of the tank will be Rs 1000.

Solution

Let $r$ be the radius of the circle and $a$ be the side of the square.

Then, we have:

$2 \pi r+4 a=k$ (where $k$ is constant)

$\Rightarrow a=\frac{k-2 \pi r}{4}$

The sum of the areas of the circle and the square $(A)$ is given by,

$A=\pi r^{2}+a^{2}=\pi r^{2}+\frac{(k-2 \pi r)^{2}}{16}$

$\therefore \frac{d A}{d r}=2 \pi r+\frac{2(k-2 \pi r)(-2 \pi)}{16}=2 \pi r-\frac{\pi(k-2 \pi r)}{4}$

Now, $\frac{d A}{d r}=0$

$\Rightarrow 2 \pi r=\frac{\pi(k-2 \pi r)}{4}$

$8 r=k-2 \pi r$

$\Rightarrow(8+2 \pi) r=k$

$\Rightarrow r=\frac{k}{8+2 \pi}=\frac{k}{2(4+\pi)}$

Now, $\frac{d^{2} A}{d r^{2}}=2 \pi+\frac{\pi^{2}}{2}>0$

$\therefore$ When $r=\frac{k}{2(4 \pi)}, \frac{d^{2} A}{d r^{2}}>0$.

When $r=\frac{k}{2(4 \pi)}, a=\frac{k-2 \pi[\frac{k}{2(4 \pi)}]}{4}=\frac{k(4 \pi) \pi k}{4(\pi)}=\frac{4 k}{4(\pi)}=\frac{k}{\pi}=2 r$.

Hence, it has been proved that the sum of their areas is least when the side of the square is double the radius of the circle.

Solution

Let $x$ and $y$ be the length and breadth of the rectangular window.

Radius of the semicircular opening $=\frac{x}{2}$

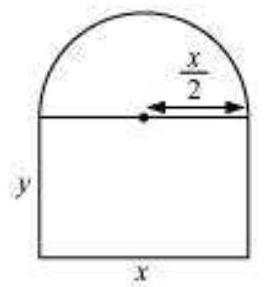
It is given that the perimeter of the window is $10 m$.

$\therefore x+2 y+\frac{\pi x}{2}=10$

$\Rightarrow x(1+\frac{\pi}{2})+2 y=10$

$\Rightarrow 2 y=10-x(1+\frac{\pi}{2})$

$\Rightarrow y=5-x(\frac{1 \pi}{2}+\frac{-}{4})$

$\square$ Area of the window $(A)$ is given by,

$ \begin{aligned} A & =x y+\frac{\pi}{2}(\frac{x}{2})^{2} \\ & =x[5-x(\frac{1 \pi}{2}+\frac{\pi}{4})]+\frac{x^{2}}{8} \\ & =5 x-x^{2}(\frac{1 \pi}{2}+\frac{\pi}{4})+\frac{\pi}{8} x^{2} \\ \therefore & \frac{d A}{d x}=5-2 x(\frac{1 \pi}{2}+\frac{\pi}{4})+\frac{\pi}{4} x \\ & =5-x(1+\frac{\pi}{2})+\frac{\pi}{4} x \\ \therefore & \frac{d^{2} A}{d x^{2}}=-(1+\frac{\pi}{2})+\frac{\pi}{4}=-1-\frac{\pi}{4} \end{aligned} $

Now, $\frac{d A}{d x}=0$

$\Rightarrow 5-x(1+\frac{\pi}{2})+\frac{\pi}{4} x=0$

$\Rightarrow 5-x-\frac{\pi}{4} x=0$

$\Rightarrow x(1+\frac{\pi}{4})=5$

$\Rightarrow x=\frac{5}{(1+\frac{\pi}{4})}=\frac{20}{\pi+4}$

Thus, when $x=\frac{20}{\pi+4}$ then $\frac{d^{2} A}{d x^{2}}<0$.

Therefore, by second derivative test, the area is the maximum when length $x=\frac{20}{\pi+4} m$. Now,

$y=5-\frac{20}{\pi+4}(\frac{2+\pi}{4})=5-\frac{5(2+\pi)}{\pi+4}=\frac{10}{\pi+4} m$

Hence, the required dimensions of the window to admit maximum light is given

by length $=\frac{20}{\pi+4} m$ and breadth $=\frac{10}{\pi+4} m$.

Solution

Let $\triangle A B C$ be right-angled at $B$. Let $A B=x$ and $B C=y$.

Let $P$ be a point on the hypotenuse of the triangle such that $P$ is at a distance of $a$ and $b$ from the sides $A B$ and $B C$ respectively.

Let $\square C=\theta$.

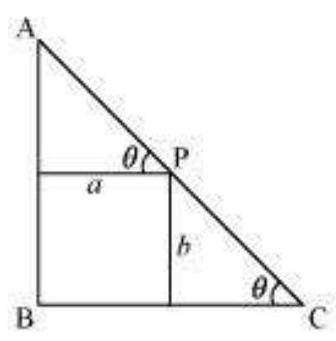
We have,

$AC=\sqrt{x^{2}+y^{2}}$

Now,

$PC=b cosec \theta$

And, $AP=a \sec \theta$

$\square AC=AP+PC$

$\square AC=b cosec \theta+a \sec \theta \ldots$ (1)

$\therefore \frac{d(AC)}{d \theta}=-b cosec \theta \cot \theta+a \sec \theta \tan \theta$

$\therefore \frac{d(AC)}{d \theta}=0$

$\Rightarrow a \sec \theta \tan \theta=b cosec \theta \cot \theta$

$\Rightarrow \frac{a}{\cos \theta} \cdot \frac{\sin \theta}{\cos \theta}=\frac{b}{\sin \theta} \frac{\cos \theta}{\sin \theta}$

$\Rightarrow a \sin ^{3} \theta=b \cos ^{3} \theta$

$\Rightarrow(a)^{\frac{1}{3}} \sin \theta=(b)^{\frac{1}{3}} \cos \theta$

$\Rightarrow \tan \theta=(\frac{b}{a})^{\frac{1}{3}}$

$\therefore \sin \theta=\frac{(b)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$ and $\cos \theta=\frac{(a)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$

It can be clearly shown that $\frac{d^{2}(AC)}{d \theta^{2}}<0$ when $\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$.

Therefore, by second derivative test, the length of the hypotenuse is the maximum when

$\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$.

Now, when $\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$, we have:

$ \begin{aligned} AC & =\frac{b \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{b^{\frac{1}{3}}}+\frac{a \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{a^{\frac{1}{3}}} \\ & =\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}(b^{\frac{2}{3}}+a^{\frac{2}{3}}) \\ & =(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}} \end{aligned} $

Hence, the maximum length of the hypotenuses is $(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}}$.

Solution

The given function is $f(x)=(x-2)^{4}(x+1)^{3}$.

$ \begin{aligned} \therefore f^{\prime}(x) & =4(x-2)^{3}(x+1)^{3}+3(x+1)^{2}(x-2)^{4} \\ & =(x-2)^{3}(x+1)^{2}[4(x+1)+3(x-2)] \\ & =(x-2)^{3}(x+1)^{2}(7 x-2) \end{aligned} $

Now, $f^{\prime}(x)=0 \Rightarrow x=-1$ and $x=\frac{2}{7}$ or $x=2$

Now, for values of $x$ close to $\frac{2}{7}$ and to the left of $\frac{2}{7}, f^{\prime}(x)>0$. Also, for values of $x$ close to $\frac{2}{7}$ and to the right of $\frac{2}{7}, f^{\prime}(x)<0$.

Thus, $x=\frac{2}{7}$ is the point of local maxima.

Now, for values of $x$ close to 2 and to the left of $2, f^{\prime}(x)<0$. Also, for values of $x$ close to 2 and to the right of $2, f^{\prime}(x)>0$.

Thus, $x=2$ is the point of local minima.

Now, as the value of $x$ varies through $-1, f^{\prime}(x)$ does not changes its sign.

Thus, $x=-1$ is the point of inflexion.

Solution

$ \begin{aligned} f(x) & =\cos ^{2} x+\sin x \\ f^{\prime}(x) & =2 \cos x(-\sin x)+\cos x \\ & =-2 \sin x \cos x+\cos x \end{aligned} $

Now, $f^{\prime}(x)=0$

$\Rightarrow 2 \sin x \cos x=\cos x \Rightarrow \cos x(2 \sin x-1)=0$

$\Rightarrow \sin x=\frac{1}{2}$ or $\cos x=0$

$\Rightarrow x=\frac{\pi}{6}$, or $\frac{\pi}{2}$ as $x \in[0, \pi]$

Now, evaluating the value of $f$ at critical points $x=\frac{\pi}{2}$ and $x=\frac{\pi}{6}$ and at the end points of

the interval $[0, \pi]$ (i.e., at $x=0$ and $x=\pi$ ), we have: $f(\frac{\pi}{6})=\cos ^{2} \frac{\pi}{6}+\sin \frac{\pi}{6}=(\frac{\sqrt{3}}{2})^{2}+\frac{1}{2}=\frac{5}{4}$

$f(0)=\cos ^{2} 0+\sin 0=1+0=1$

$f(\pi)=\cos ^{2} \pi+\sin \pi=(-1)^{2}+0=1$

$f(\frac{\pi}{2})=\cos ^{2} \frac{\pi}{2}+\sin \frac{\pi}{2}=0+1=1$

Hence, the absolute maximum value of $f$ is $\frac{5}{4}$ occurring at $x=\frac{\pi}{6}$ and the absolute minimum value of $f$ is 1 occurring at $x=0, \frac{\pi}{2}$, and $\pi$.

Solution

A sphere of fixed radius $(r)$ is given.

Let $R$ and $h$ be the radius and the height of the cone respectively.

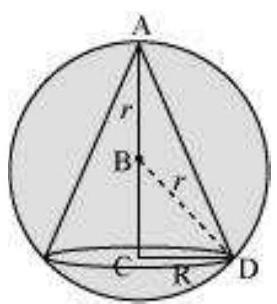
The volume $(V)$ of the cone is given by,

$V=\frac{1}{3} \pi R^{2} h$

Now, from the right triangle $B C D$, we have:

$BC=\sqrt{r^{2}-R^{2}}$

$\square h=r+\sqrt{r^{2}-R^{2}}$

$ \begin{aligned} & \therefore V=\frac{1}{3} \pi R^{2}(r+\sqrt{r^{2}-R^{2}})=\frac{1}{3} \pi R^{2} r+\frac{1}{3} \pi R^{2} \sqrt{r^{2}-R^{2}} \\ & \begin{aligned} \therefore \frac{d V}{d R} & =\frac{2}{3} \pi R r+\frac{2 \pi}{3} \pi R \sqrt{r^{2}-R^{2}}+\frac{R^{2}}{3} \cdot \frac{(-2 R)}{2 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi}{3} \pi R \sqrt{r^{2}-R^{2}}-\frac{R^{3}}{3 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi R(r^{2}-R^{2})-\pi R^{3}}{3 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi R r^{2}-3 \pi R^{3}}{3 \sqrt{r^{2}-R^{2}}} \end{aligned} \end{aligned} $

Now, $\frac{d V}{d R^{2}}=0$

$\Rightarrow \frac{2 \pi r R}{3}=\frac{3 \pi R^{3}-2 \pi R r^{2}}{3 \sqrt{r^{2}-R^{2}}}$

$\Rightarrow 2 r \sqrt{r^{2}-R^{2}}=3 R^{2}-2 r^{2}$

$\Rightarrow 4 r^{2}(r^{2}-R^{2})=(3 R^{2}-2 r^{2})^{2}$

$\Rightarrow 4 r^{4}-4 r^{2} R^{2}=9 R^{4}+4 r^{4}-12 R^{2} r^{2}$

$\Rightarrow 9 R^{4}-8 r^{2} R^{2}=0$

$\Rightarrow 9 R^{2}=8 r^{2}$

$\Rightarrow R^{2}=\frac{8 r^{2}}{9}$

Now, $\frac{d^{2} V}{d R^{2}}=\frac{2 \pi r}{3}+\frac{3 \sqrt{r^{2}-R^{2}}(2 \pi r^{2}-9 \pi R^{2})-(2 \pi R r^{2}-3 \pi R^{3})(-6 R) \frac{1}{2 \sqrt{r^{2}-R^{2}}}}{9(r^{2}-R^{2})}$

$ =\frac{2 \pi r}{3}+\frac{3 \sqrt{r^{2}-R^{2}}(2 \pi r^{2}-9 \pi R^{2})+(2 \pi R r^{2}-3 \pi R^{3})(3 R) \frac{1}{2 \sqrt{r^{2}-R^{2}}}}{9(r^{2}-R^{2})} $

Now, when $R^{2}=\frac{8 r^{2}}{9}$, it can be shown that $\frac{d^{2} V}{d R^{2}}<0$.

$\square$ The volume is the maximum when

$ R^{2}=\frac{8 r^{2}}{9} $

When $R^{2}=\frac{8 r^{2}}{9}$, height of the cone $=r+\sqrt{r^{2}-\frac{8 r^{2}}{9}}=r+\sqrt{\frac{r^{2}}{9}}=r+\frac{r}{3}=\frac{4 r}{3}$.

Hence, it can be seen that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius $r$ is $\frac{4 r}{3}$.

Solution

Let us take any 2 points $\mathrm{c}_1$ and $\mathrm{c}_2$ such that

${\mathrm{c} _1, \mathrm{c} _2} \in(\mathrm{a}, \mathrm{b})$ and

$\mathrm{c} _2=\mathrm{c} _1+\mathrm{h}$,

where $\mathrm{h} \rightarrow \mathrm{O}$

Now, $f^{\prime}\left(c _1\right)=\lim _{h \rightarrow 0} \frac{f\left(c _1+h\right)-f\left(c _1\right)}{h}=\frac{f\left(c _2\right)-f\left(c _1\right)}{c _2-c _1}$

Now, it is given that $\mathrm{f}^{\prime}(\mathrm{x})>0 \quad \forall \mathrm{x} \in(\mathrm{a}, \mathrm{b})$. Therefore, $\mathrm{f}^{\prime}\left(\mathrm{c}_1\right)>0$

$\Rightarrow \frac{\mathrm{f}\left(\mathrm{c}_2\right)-\mathrm{f}\left(\mathrm{c}_1\right)}{\mathrm{c}_2-\mathrm{c}_1}>\mathrm{O}$

From the above fraction, we can conclude that:

1. For $\mathrm{c}_2>\mathrm{c}_1, \mathrm{f}\left(\mathrm{c}_2\right)>\mathrm{f}\left(\mathrm{c}_1\right)$

2. For $c_1>c_2, f\left(c_1\right)>f\left(c_2\right)$

Hence, $\mathrm{f}(\mathrm{x})$ is an increasing function in $(\mathrm{a}, \mathrm{b})$.

Solution

A sphere of fixed radius $(R)$ is given.

Let $r$ and $h$ be the radius and the height of the cylinder respectively.

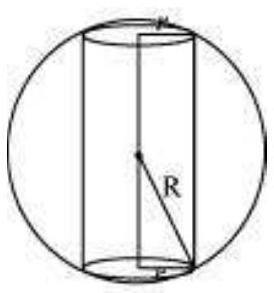
From the given figure, we have $h=2 \sqrt{R^{2}-r^{2}}$.

The volume $(V)$ of the cylinder is given by,

$ \begin{aligned} & V=\pi r^{2} h=2 \pi r^{2} \sqrt{R^{2}-r^{2}} \\ & \begin{aligned} \therefore \frac{d V}{d r} & =4 \pi r \sqrt{R^{2}-r^{2}}+\frac{2 \pi r^{2}(-2 r)}{2 \sqrt{R^{2}-r^{2}}} \\ & =4 \pi r \sqrt{R^{2}-r^{2}}-\frac{2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{4 \pi r(R^{2}-r^{2})-2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{4 \pi r R^{2}-6 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \end{aligned} \end{aligned} $

Now, $\frac{d V}{d r}=0 \Rightarrow 4 \pi r R^{2}-6 \pi r^{3}=0$

$\Rightarrow r^{2}=\frac{2 R^{2}}{3}$

Now, $\frac{d^{2} V}{d r^{2}}=\frac{\sqrt{R^{2}-r^{2}}(4 \pi R^{2}-18 \pi r^{2})-(4 \pi r R^{2}-6 \pi r^{3}) \frac{(-2 r)}{2 \sqrt{R^{2}-r^{2}}}}{(R^{2}-r^{2})}$

$ \begin{aligned} & =\frac{(R^{2}-r^{2})(4 \pi R^{2}-18 \pi r^{2})+r(4 \pi r R^{2}-6 \pi r^{3})}{(R^{2}-r^{2})^{\frac{3}{2}}} \\ & =\frac{4 \pi R^{4}-22 \pi r^{2} R^{2}+12 \pi r^{4}+4 \pi r^{2} R^{2}}{(R^{2}-r^{2})^{\frac{3}{2}}} \end{aligned} $

Now, it can be observed that at $r^{2}=\frac{2 R^{2}}{3}, \frac{d^{2} V}{d r^{2}}<0$.

$\square$ The volume is the maximum when $r^{2}=\frac{2 R^{2}}{3}$.

When $r^{2}=\frac{2 R^{2}}{3}$, the height of the cylinder is $2 \sqrt{R^{2}-\frac{2 R^{2}}{3}}=2 \sqrt{\frac{R^{2}}{3}}=\frac{2 R}{\sqrt{3}}$.

Hence, the volume of the cylinder is the maximum when the height of the cylinder is $\frac{2 R}{\sqrt{3}}$.

Solution

The given right circular cone of fixed height $(h)$ and semi-vertical angle ( $a$ ) can be drawn as:

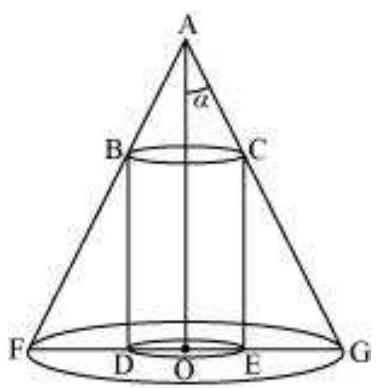
Here, a cylinder of radius $R$ and height $H$ is inscribed in the cone.

Then, $\square GAO=a, OG=r, OA=h, OE=R$, and $CE=H$.

We have,

$r=h \tan a$

Now, since $\triangle AOG$ is similar to $\triangle CEG$, we have:

$\frac{AO}{OG}=\frac{CE}{EG}$

$\Rightarrow \frac{h}{r}=\frac{H}{r-R} \quad[EG=OG-OE]$

$\Rightarrow H=\frac{h}{r}(r-R)=\frac{h}{h \tan \alpha}(h \tan \alpha-R)=\frac{1}{\tan \alpha}(h \tan \alpha-R)$

Now, the volume $(V)$ of the cylinder is given by,

$V=\pi R^{2} H=\frac{\pi R^{2}}{\tan \alpha}(h \tan \alpha-R)=\pi R^{2} h-\frac{\pi R^{3}}{\tan \alpha}$

$\therefore \frac{d V}{d R}=2 \pi R h-\frac{3 \pi R^{2}}{\tan \alpha}$

Now, $\frac{d V}{d R}=0$

$\Rightarrow 2 \pi R h=\frac{3 \pi R^{2}}{\tan \alpha}$

$\Rightarrow 2 h \tan \alpha=3 R$

$\Rightarrow R=\frac{2 h}{3} \tan \alpha$

Now, $\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi R}{\tan \alpha}$

And, for $R=\frac{2 h}{3} \tan \alpha$, we have:

$\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi}{\tan \alpha}(\frac{2 h}{3} \tan \alpha)=2 \pi h-4 \pi h=-2 \pi h<0$

$\square$ By second derivative test, the volume of the cylinder is the greatest when

$R=\frac{2 h}{3} \tan \alpha$.

When $R=\frac{2 h}{3} \tan \alpha, H=\frac{1}{\tan \alpha}(h \tan \alpha-\frac{2 h}{3} \tan \alpha)=\frac{1}{\tan \alpha}(\frac{h \tan \alpha}{3})=\frac{h}{3}$.

Thus, the height of the cylinder is one-third the height of the cone when the volume of the cylinder is the greatest.

Now, the maximum volume of the cylinder can be obtained as:

$\pi(\frac{2 h}{3} \tan \alpha)^{2}(\frac{h}{3})=\pi(\frac{4 h^{2}}{9} \tan ^{2} \alpha)(\frac{h}{3})=\frac{4}{27} \pi h^{3} \tan ^{2} \alpha$

Hence, the given result is proved.

Solution

Let $r$ be the radius of the cylinder.

Then, volume $(V)$ of the cylinder is given by,

$V=\pi(\text{ radius })^{2} \times$ height

$ \begin{matrix} =\pi(10)^{2} h & (\text{ radius }=10 m) \\ =100 \pi h \end{matrix} $

Differentiating with respect to time $t$, we have:

$\frac{d V}{d t}=100 \pi \frac{d h}{d t}$

The tank is being filled with wheat at the rate of 314 cubic metres per hour.

$ \square \frac{d V}{d t}=314 m^{3} / h $

Thus, we have:

$ \begin{aligned} & 314=100 \pi \frac{d h}{d t} \\ & \Rightarrow \frac{d h}{d t}=\frac{314}{100(3.14)}=\frac{314}{314}=1 \end{aligned} $

Hence, the depth of wheat is increasing at the rate of $1 m / h$.

The correct answer is $A$.