Chapter 10 Vector Algebra EXERCISE 10.2
EXERCISE 10.2
1. Compute the magnitude of the following vectors:
$$ \vec{a}=\hat{i}+\hat{j}+k ; \quad \vec{b}=2 \hat{i}-7 \hat{j}-3 \hat{k} ; \quad \vec{c}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}-\frac{1}{\sqrt{3}} \hat{k} $$
Show Answer
Solution
The given vectors are:
$ \begin{aligned} \vec{a} & =\hat{i}+\hat{j}+\hat{k} ; \quad \vec{b}=2 \hat{i}-7 \hat{j}-3 \hat{k} ; \quad \vec{c}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}-\frac{1}{\sqrt{3}} \hat{k} \\ |\vec{a}| & =\sqrt{(1)^{2}+(1)^{2}+(1)^{2}}=\sqrt{3} \\ |\vec{b}| & =\sqrt{(2)^{2}+(-7)^{2}+(-3)^{2}} \\ & =\sqrt{4+49+9} \\ & =\sqrt{62} \\ |\vec{c}| & =\sqrt{(\frac{1}{\sqrt{3}})^{2}+(\frac{1}{\sqrt{3}})^{2}+(-\frac{1}{\sqrt{3}})^{2}} \\ & =\sqrt{\frac{1}{3}+\frac{1}{3}+\frac{1}{3}}=1 \end{aligned} $
2. Write two different vectors having same magnitude.
Show Answer
Solution
Consider $\vec{a}=(\hat{i}-2 \hat{j}+3 \hat{k})$ and $\vec{b}=(2 \hat{i}+\hat{j}-3 \hat{k})$.
It can be observed that $|\vec{a}|=\sqrt{1^{2}+(-2)^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14}$ and $|\vec{b}|=\sqrt{2^{2}+1^{2}+(-3)^{2}}=\sqrt{4+1+9}=\sqrt{14}$.
Hence, $\vec{a}$ and $\vec{b}$ are two different vectors having the same magnitude. The vectors are different because they have different directions.
3. Write two different vectors having same direction.
Show Answer
Solution
Consider $\vec{p}=(\hat{i}+\hat{j}+\hat{k})$ and $\vec{q}=(2 \hat{i}+2 \hat{j}+2 \hat{k})$.
The direction cosines of $\vec{p}$ are given by,
$l=\frac{1}{\sqrt{1^{2}+1^{2}+1^{2}}}=\frac{1}{\sqrt{3}}, m=\frac{1}{\sqrt{1^{2}+1^{2}+1^{2}}}=\frac{1}{\sqrt{3}}$, and $n=\frac{1}{\sqrt{1^{2}+1^{2}+1^{2}}}=\frac{1}{\sqrt{3}}$.
The direction cosines of $\vec{q}$ are given by
$l=\frac{2}{\sqrt{2^{2}+2^{2}+2^{2}}}=\frac{2}{2 \sqrt{3}}=\frac{1}{\sqrt{3}}, m=\frac{2}{\sqrt{2^{2}+2^{2}+2^{2}}}=\frac{2}{2 \sqrt{3}}=\frac{1}{\sqrt{3}}$,
and $n=\frac{2}{\sqrt{2^{2}+2^{2}+2^{2}}}=\frac{2}{2 \sqrt{3}}=\frac{1}{\sqrt{3}}$.
The direction cosines of $\vec{p}$ and $\vec{q}$ are the same. Hence, the two vectors have the same direction.
4. Find the values of $x$ and $y$ so that the vectors $2 \hat{i}+3 \hat{j}$ and $x \hat{i}+y \hat{j}$ are equal.
Show Answer
Solution
The two vectors $2 \hat{i}+3 \hat{j}$ and $x \hat{i}+y \hat{j}$ will be equal if their corresponding components are equal.
Hence, the required values of $x$ and $y$ are 2 and 3 respectively.
5. Find the scalar and vector components of the vector with initial point $(2,1)$ and terminal point $(-5,7)$.
Show Answer
Solution
The vector with the initial point $P(2,1)$ and terminal point $Q(-5,7)$ can be given by, $\overrightarrow{{}PQ}=(-5-2) \hat{i}+(7-1) \hat{j}$
$\Rightarrow \overrightarrow{{}PQ}=-7 \hat{i}+6 \hat{j}$
Hence, the required scalar components are -7 and 6 while the vector components are $-7 \hat{i}$ and $6 \hat{j}$.
6. Find the sum of the vectors $\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k}$ and $\vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}$.
Show Answer
Solution
The given vectors are $\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k}$ and $\vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}$.
$ \begin{aligned} \therefore \vec{a}+\vec{b}+\vec{c} & =(1-2+1) \hat{i}+(-2+4-6) \hat{j}+(1+5-7) \hat{k} \\ & =0 \cdot \hat{i}-4 \hat{j}-1 \cdot \hat{k} \\ & =-4 \hat{j}-\hat{k} \end{aligned} $
7. Find the unit vector in the direction of the vector $\vec{a}=\hat{i}+\hat{j}+2 \hat{k}$.
Show Answer
Solution
The unit vector $\hat{a}$ in the direction of vector $\vec{a}=\hat{i}+\hat{j}+2 \hat{k}$ is given by $\hat{a}=\frac{\vec{a}}{|a|}$.
$|\vec{a}|=\sqrt{1^{2}+1^{2}+2^{2}}=\sqrt{1+1+4}=\sqrt{6}$
$\therefore \hat{a}=\frac{\vec{a}}{|\vec{a}|}=\frac{\hat{i}+\hat{j}+2 \hat{k}}{\sqrt{6}}=\frac{1}{\sqrt{6}} \hat{i}+\frac{1}{\sqrt{6}} \hat{j}+\frac{2}{\sqrt{6}} \hat{k}$
8. Find the unit vector in the direction of vector $\overrightarrow{{}PQ}$, where $P$ and $Q$ are the points $(1,2,3)$ and $(4,5,6)$, respectively.
Show Answer
Solution
The given points are $P(1,2,3)$ and $Q(4,5,6)$.
$ \begin{aligned} & \therefore \overrightarrow{{}PQ}=(4-1) \hat{i}+(5-2) \hat{j}+(6-3) \hat{k}=3 \hat{i}+3 \hat{j}+3 \hat{k} \\ & |\overrightarrow{{}PQ}|=\sqrt{3^{2}+3^{2}+3^{2}}=\sqrt{9+9+9}=\sqrt{27}=3 \sqrt{3} \end{aligned} $
Hence, the unit vector in the direction of $\overrightarrow{{}PQ}$ is
$ \frac{\overrightarrow{{}PQ}}{|\overrightarrow{{}PQ}|}=\frac{3 \hat{i}+3 \hat{j}+3 \hat{k}}{3 \sqrt{3}}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}+\frac{1}{\sqrt{3}} \hat{k} $
9. For given vectors, $\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$ and $\vec{b}=-\hat{i}+\hat{j}-\hat{k}$, find the unit vector in the direction of the vector $\vec{a}+\vec{b}$.
Show Answer
Solution
The given vectors are $\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$ and $\vec{b}=-\hat{i}+\hat{j}-\hat{k}$.
$\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$
$\vec{b}=-\hat{i}+\hat{j}-\hat{k}$
$\therefore \vec{a}+\vec{b}=(2-1) \hat{i}+(-1+1) \hat{j}+(2-1) \hat{k}=1 \hat{i}+0 \hat{j}+1 \hat{k}=\hat{i}+\hat{k}$
$|\vec{a}+\vec{b}|=\sqrt{1^{2}+1^{2}}=\sqrt{2}$
Hence, the unit vector in the direction of $(\vec{a}+\vec{b})$ is
$\frac{(\vec{a}+\vec{b})}{|\vec{a}+\vec{b}|}=\frac{\hat{i}+\hat{k}}{\sqrt{2}}=\frac{1}{\sqrt{2}} \hat{i}+\frac{1}{\sqrt{2}} \hat{k}$
10. Find a vector in the direction of vector $5 \hat{i}-\hat{j}+2 \hat{k}$ which has magnitude 8 units.
Show Answer
Solution
Let $\vec{a}=5 \hat{i}-\hat{j}+2 \hat{k}$.
$\therefore|\vec{a}|=\sqrt{5^{2}+(-1)^{2}+2^{2}}=\sqrt{25+1+4}=\sqrt{30}$
$\therefore \hat{a}=\frac{\vec{a}}{|\vec{a}|}=\frac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}}$
Hence, the vector in the direction of vector $5 \hat{i}-\hat{j}+2 \hat{k}$ which has magnitude 8 units is given by,
$8 \hat{a}=8(\frac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}})=\frac{40}{\sqrt{30}} \hat{i}-\frac{8}{\sqrt{30}} \hat{j}+\frac{16}{\sqrt{30}} \hat{k}$
$ \begin{aligned} & =8(\frac{5 \vec{i}-\vec{j}+2 \vec{k}}{\sqrt{30}}) \\ & =\frac{40}{\sqrt{30}} \vec{i}-\frac{8}{\sqrt{30}} \vec{j}+\frac{16}{\sqrt{30}} \vec{k} \end{aligned} $
11. Show that the vectors $2 \hat{i}-3 \hat{j}+4 \hat{k}$ and $-4 \hat{i}+6 \hat{j}-8 \hat{k}$ are collinear.
Show Answer
Solution
Let $\vec{a}=2 \hat{i}-3 \hat{j}+4 \hat{k}$ and $\vec{b}=-4 \hat{i}+6 \hat{j}-8 \hat{k}$.
It is observed that $\vec{b}=-4 \hat{i}+6 \hat{j}-8 \hat{k}=-2(2 \hat{i}-3 \hat{j}+4 \hat{k})=-2 \vec{a}$
$\therefore \vec{b}=\lambda \vec{a}$
where,
$\lambda=-2$
Hence, the given vectors are collinear.
12. Find the direction cosines of the vector $\hat{i}+2 \hat{j}+3 \hat{k}$.
Show Answer
Solution
Let $\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}$.
$\therefore|\vec{a}|=\sqrt{1^{2}+2^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14}$
Hence, the direction cosines of $\vec{a}$ are $(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}})$.
13. Find the direction cosines of the vector joining the points $A(1,2,-3)$ and $B(-1,-2,1)$, directed from $A$ to $B$.
Show Answer
Solution
The given points are $A(1,2,-3)$ and $B(-1,-2,1)$. $\therefore \overrightarrow{{}AB}=(-1-1) \hat{i}+(-2-2) \hat{j}+{1-(-3)} \hat{k}$
$\Rightarrow \overrightarrow{{}AB}=-2 \hat{i}-4 \hat{j}+4 \hat{k}$
$\therefore|\overrightarrow{{}AB}|=\sqrt{(-2)^{2}+(-4)^{2}+4^{2}}=\sqrt{4+16+16}=\sqrt{36}=6$
Hence, the direction cosines of $\overrightarrow{{}AB}$ are $(-\frac{2}{6},-\frac{4}{6}, \frac{4}{6})=(-\frac{1}{3},-\frac{2}{3}, \frac{2}{3})$.
14. Show that the vector $\hat{i}+\hat{j}+\hat{k}$ is equally inclined to the axes OX, OY and OZ.
Show Answer
Solution
Let $\vec{a}=\hat{i}+\hat{j}+\hat{k}$.
Then,
$|\vec{a}|=\sqrt{1^{2}+1^{2}+1^{2}}=\sqrt{3}$
Therefore, the direction cosines of $\vec{a}$ are $(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})$.
Now, let $a, \beta$, and $y$ be the angles formed by $\vec{a}$ with the positive directions of $x, y$, and $z$ axes.
Then, we have $\cos \alpha=\frac{1}{\sqrt{3}}, \cos \beta=\frac{1}{\sqrt{3}}, \cos \gamma=\frac{1}{\sqrt{3}}$.
Hence, the given vector is equally inclined to axes OX, OY, and OZ.
15. Find the position vector of a point $R$ which divides the line joining two points $P$ and $Q$ whose position vectors are $\hat{i}+2 \hat{j}-\hat{k}$ and $-\hat{i}+\hat{j}+\hat{k}$ respectively, in the ratio $2: 1$
(i) internally
(ii) externally
Show Answer
Solution
The position vector of point $R$ dividing the line segment joining two points $P$ and $Q$ in the ratio $m: n$ is given by:
i. Internally: $\frac{m \vec{b}+n \vec{a}}{m+n}$
ii. Externally:
$\frac{m \vec{b}-n \vec{a}}{m-n}$
Position vectors of $P$ and $Q$ are given as:
$\overrightarrow{{}OP}=\hat{i}+2 \hat{j}-\hat{k}$ and $\overrightarrow{{}OQ}=-\hat{i}+\hat{j}+\hat{k}$
(i) The position vector of point $R$ which divides the line joining two points $P$ and $Q$ internally in the ratio $2: 1$ is given by,
$ \begin{aligned} \overrightarrow{{}OR} & =\frac{2(-\hat{i}+\hat{j}+\hat{k})+1(\hat{i}+2 \hat{j}-\hat{k})}{2+1}=\frac{(-2 \hat{i}+2 \hat{j}+2 \hat{k})+(\hat{i}+2 \hat{j}-\hat{k})}{3} \\ & =\frac{-\hat{i}+4 \hat{j}+\hat{k}}{3}=-\frac{1}{3} \hat{i}+\frac{4}{3} \hat{j}+\frac{1}{3} \hat{k} \end{aligned} $
(ii) The position vector of point $R$ which divides the line joining two points $P$ and $Q$ externally in the ratio $2: 1$ is given by,
$ \begin{aligned} \overrightarrow{{}OR} & =\frac{2(-\hat{i}+\hat{j}+\hat{k})-1(\hat{i}+2 \hat{j}-\hat{k})}{2-1}=(-2 \hat{i}+2 \hat{j}+2 \hat{k})-(\hat{i}+2 \hat{j}-\hat{k}) \\ & =-3 \hat{i}+3 \hat{k} \end{aligned} $
16. Find the position vector of the mid point of the vector joining the points $P(2,3,4)$ and $Q(4,1,-2)$.
Show Answer
Solution
The position vector of mid-point $R$ of the vector joining points $P(2,3,4)$ and $Q(4,1$, 2) is given by,
$ \begin{aligned} \overrightarrow{{}OR} & =\frac{(2 \hat{i}+3 \hat{j}+4 \hat{k})+(4 \hat{i}+\hat{j}-2 \hat{k})}{2}=\frac{(2+4) \hat{i}+(3+1) \hat{j}+(4-2) \hat{k}}{2} \\ & =\frac{6 \hat{i}+4 \hat{j}+2 \hat{k}}{2}=3 \hat{i}+2 \hat{j}+\hat{k} \end{aligned} $
17. Show that the points $A, B$ and $C$ with position vectors, $\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}$, $\vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ and $\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}$, respectively form the vertices of a right angled triangle.
Show Answer
Solution
Position vectors of points $A, B$, and $C$ are respectively given as:
$\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}, \vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ and $\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}$
$\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}, \vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ and $\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}$
$\therefore \overrightarrow{{}AB}=\vec{b}-\vec{a}=(2-3) \hat{i}+(-1+4) \hat{j}+(1+4) \hat{k}=-\hat{i}+3 \hat{j}+5 \hat{k}$
$\overrightarrow{{}BC}=\vec{c}-\vec{b}=(1-2) \hat{i}+(-3+1) \hat{j}+(-5-1) \hat{k}=-\hat{i}-2 \hat{j}-6 \hat{k}$
$\overrightarrow{{}CA}=\vec{a}-\vec{c}=(3-1) \hat{i}+(-4+3) \hat{j}+(-4+5) \hat{k}=2 \hat{i}-\hat{j}+\hat{k}$
$\therefore|\overrightarrow{{}AB}|^{2}=(-1)^{2}+3^{2}+5^{2}=1+9+25=35$
$|\overrightarrow{{}BC}|^{2}=(-1)^{2}+(-2)^{2}+(-6)^{2}=1+4+36=41$
$|\overrightarrow{{}CA}|^{2}=2^{2}+(-1)^{2}+1^{2}=4+1+1=6$
$\therefore|\overrightarrow{{}AB}|^{2}+|\overrightarrow{{}CA}|^{2}=36+6=41=|\overrightarrow{{}BC}|^{2}$
Hence, $A B C$ is a right-angled triangle.
18. In triangle $ABC$ (Fig 10.18), which of the following is not true:
$\quad\quad$(A) $\overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}0}$
$\quad\quad$(B) $\overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}AC}=\overrightarrow{{}0}$
$\quad\quad$(C) $\overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}AC}=\overrightarrow{{}0}$
$\quad\quad$(D) $\overrightarrow{{}AB}-\overrightarrow{{}CB}+\overrightarrow{{}CA}=\overrightarrow{{}0}$
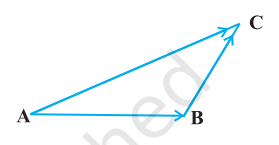
Fig 10.18
Show Answer
Solution

On applying the triangle law of addition in the given triangle, we have:
$$ \begin{align*} & \overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}AC} \tag{1}\\ & \Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}=-\overrightarrow{{}CA} \\ & \Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}0} \tag{2} \end{align*} $$
$\therefore$ The equation given in alternative $A$ is true.
$\overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}AC}$
$\Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}AC}=\overrightarrow{{}0}$
$\therefore$ The equation given in alternative $B$ is true.
From equation (2), we have:
$\overrightarrow{{}AB}-\overrightarrow{{}CB}+\overrightarrow{{}CA}=\overrightarrow{{}0}$
$\therefore$ The equation given in alternative $D$ is true.
Now, consider the equation given in alternative $C$ :
$\overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}CA}=\overrightarrow{{}0}$
$\Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}CA}$
From equations (1) and (3), we have:
$ \overrightarrow{{}AC}=\overrightarrow{{}CA} $
$\Rightarrow \overrightarrow{{}AC}=-\overrightarrow{{}AC}$
$\Rightarrow \overrightarrow{{}AC}+\overrightarrow{{}AC}=\overrightarrow{{}0}$
$\Rightarrow 2 \overrightarrow{{}AC}=\overrightarrow{{}0}$
$\Rightarrow \overrightarrow{{}AC}=\overrightarrow{{}0}$, which is not true.
Hence, the equation given in alternative $C$ is incorrect.
The correct answer is $\mathbf{C}$.
19. If $\vec{a}$ and $\vec{b}$ are two collinear vectors, then which of the following are incorrect:
(A) $\vec{b}=\lambda \vec{a}$, for some scalar $\lambda$
(B) $\vec{a}= \pm \vec{b}$
(C) the respective components of $\vec{a}$ and $\vec{b}$ are not proportional
(D) both the vectors $\vec{a}$ and $\vec{b}$ have same direction, but different magnitudes.
Show Answer
Solution
If $\vec{a}$ and $\vec{b}$ are two collinear vectors, then they are parallel.
Therefore, we have:
$\vec{b}=\lambda \vec{a}$ (For some scalar $\lambda$ )
If $\lambda= \pm 1$, then $\vec{a}= \pm \vec{b}$.
If $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ and $\vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, then
$\vec{b}=\lambda \vec{a}$.
$\Rightarrow b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=\lambda(a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k})$
$\Rightarrow b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=(\lambda a_1) \hat{i}+(\lambda a_2) \hat{j}+(\lambda a_3) \hat{k}$
$\Rightarrow b_1=\lambda a_1, b_2=\lambda a_2, b_3=\lambda a_3$
$\Rightarrow \frac{b_1}{a_1}=\frac{b_2}{a_2}=\frac{b_3}{a_3}=\lambda$
Thus, the respective components of $\vec{a}$ and $\vec{b}$ are proportional.
However, vectors $\vec{a}$ and $\vec{b}$ can have different directions.
Hence, the statement given in $\mathbf{D}$ is incorrect.
The correct answer is $\mathbf{D}$.










