Answer :

(i) The given equation is $x+7 y=0$.

It can be written as

$y=-\dfrac{1}{7} x+0$

This equation is of the form $y=m x+c$, where

$ m=-\dfrac{1}{7} \text{ and } c=0 $

Therefore, equation (1) is in the slope-intercept form, where the slope and the $y$-intercept are $-\dfrac{1}{7}$ and 0 respectively.

(ii) The given equation is $6 x+3 y -5=0$.

It can be written as

$y=\dfrac{1}{3}(-6 x+5)$

$y=-2 x+\dfrac{5}{3}$

This equation is of the form $y=m x+c$, where $m=-2$ and $c=\dfrac{5}{3}$.

Therefore, equation (2) is in the slope-intercept form, where the slope and the $y$-intercept are- 2 and $\dfrac{5}{3}$ respectively.

(iii) The given equation is $y=0$.

It can be written as

$y=0 . x+0$

This equation is of the form $y=m x+c$, where $m=0$ and $c=0$.

Therefore, equation (3) is in the slope-intercept form, where the slope and the $y$-intercept are 0 and 0 respectively.

Answer :

(i) The given equation is $3 x+2 y$ - $12=0$.

It can be written as

$3 x+2 y=12$

$\dfrac{3 x}{12}+\dfrac{2 y}{12}=1$ i.e., $\dfrac{x}{4}+\dfrac{y}{6}=1$

This equation is of the form $\dfrac{x}{a}+\dfrac{y}{b}=1$, where $a=4$ and $b=6$.

Therefore, equation (1) is in the intercept form, where the intercepts on the $x$ and $y$ axes are 4 and 6 respectively.

(ii) The given equation is $4 x - 3 y=6$.

It can be written as

$\dfrac{4 x}{6}-\dfrac{3 y}{6}=1$

$\dfrac{2 x}{3}-\dfrac{y}{2}=1$

i.e., $\dfrac{x}{(\dfrac{3}{2})}+\dfrac{y}{(-2)}=1$

This equation is of the form $\dfrac{x}{a}+\dfrac{y}{b}=1$, where $a=\dfrac{3}{2}$ and $b=-$2 .

Therefore, equation (2) is in the intercept form, where the intercepts on the $x$ and $y$ axes are $\dfrac{3}{2}$ and -2 respectively.

(iii) The given equation is $3 y+2=0$.

It can be written as

$3 y=-2$

i.e., $\dfrac{y}{(-\dfrac{2}{3})}=1$

This equation is of the form $\dfrac{x}{a}+\dfrac{y}{b}=1$, where $a=0$ and $b=-\dfrac{2}{3}$.

Therefore, equation (3) is in the intercept form, where the intercept on the $y$-axis is $-\dfrac{2}{3}$ and it has no intercept on the $x$-axis.

Answer :

The given equation of the line is $12(x+6)=5(y - 2)$.

$\Rightarrow 12 x+72=5 y$ 10

$\Rightarrow 12 x - 5 y+82=0$..

On comparing equation (1) with general equation of line $A x+B y+C=0$, we obtain $A=12, B=$ - 5 , and $C=82$.

It is known that the perpendicular distance ( $d$ ) of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by

$d=\dfrac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}$.

The given point is $(x_1, y_1)=(- 1,1)$.

Therefore, the distance of point $( - 1,1 )$ from the given line

$=\dfrac{|12(-1)+(-5)(1)+82|}{\sqrt{(12)^{2}+(-5)^{2}}}$ units $=\dfrac{|-12-5+82|}{\sqrt{169}}$ units $=\dfrac{|65|}{13}$ units $=5$ units

Answer :

The given equation of line is

$\dfrac{x}{3}+\dfrac{y}{4}=1$

or, $4 x+3 y-12=0$

On comparing equation (1) with general equation of line $A x+B y+C=0$, we obtain $A=4, B=3$, and $C=$ - 12 .

Let $(a, 0)$ be the point on the $x$-axis whose distance from the given line is 4 units.

It is known that the perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by

$d=\dfrac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}$.

Therefore,

$4=\dfrac{|4 a+3 \times 0-12|}{\sqrt{4^{2}+3^{2}}}$

$\Rightarrow 4=\dfrac{|4 a-12|}{5}$

$\Rightarrow|4 a-12|=20$

$\Rightarrow \pm(4 a-12)=20$

$\Rightarrow(4 a-12)=20$ or $-(4 a-12)=20$

$\Rightarrow 4 a=20+12$ or $4 a=-20+12$

$\Rightarrow a=8$ or -2

Thus, the required points on the $x$-axis are (-2,0) and $(8,0)$.

Answer :

It is known that the distance (d) between parallel lines $A x+B y+C_1=0$ and $A x+B y+C_2=0$ is given by $d=\dfrac{|C_1-C_2|}{\sqrt{A^{2}+B^{2}}}$

(i) The given parallel lines are $15 x+8 y - 34=0$ and $15 x+8 y+31=0$.

Here, $A=15, B=8, C_1=$ - 34 , and $C_2=31$.

Therefore, the distance between the parallel lines is $d=\dfrac{|C_1-C_2|}{\sqrt{A^{2}+B^{2}}}=\dfrac{|-34-31|}{\sqrt{(15)^{2}+(8)^{2}}}$ units $=\dfrac{|-65|}{17}$ units $=\dfrac{65}{17}$ units

(ii) The given parallel lines are $l(x+y)+p=0$ and $l(x+y) - r=0$.

$l x+l y+p=0$ and $l x+l y - r=0$

Here, $A=l, B=l, C_1=p$, and $C_2=- r$.

Therefore, the distance between the parallel lines is

$d=\dfrac{|C_1-C_2|}{\sqrt{A^{2}+B^{2}}}=\dfrac{|p+r|}{\sqrt{l^{2}+l^{2}}}$ units $=\dfrac{|p+r|}{\sqrt{2 l^{2}}}$ units $=\dfrac{|p+r|}{l \sqrt{2}}$ units $=\dfrac{1}{\sqrt{2}}|\dfrac{p+r}{l}|$ units

Answer :

The equation of the given line is

$3 x-4 y+2=0$

or $y=\dfrac{3 x}{4}+\dfrac{2}{4}$

or $y=\dfrac{3}{4} x+\dfrac{1}{2}$, which is of the form $y=m x+c$

$\therefore$ Slope of the given line

$ =\dfrac{3}{4} $

It is known that parallel lines have the same slope.

$\therefore$ Slope of the other line $=$

$ m=\dfrac{3}{4} $

Now, the equation of the line that has a slope of $\dfrac{3}{4}$ and passes through the point $(-$ $2,3)$ is

$ \begin{aligned} & (y-3)=\dfrac{3}{4}\{x-(-2)\} \\ & 4 y-12=3 x+6 \\ & \text{ i.e., } 3 x-4 y+18=0 \end{aligned} $

Answer :

The given equation of line is $x-7 y+5=0$.

Or, $y=\dfrac{1}{7} x+\dfrac{5}{7}$, which is of the form $y=m x+c$

$\therefore$ Slope of the given line

$ =\dfrac{1}{7} $

The slope of the line perpendicular to the line having a slope of $\dfrac{1}{7}$ is $m=-\dfrac{1}{(\dfrac{1}{7})}=-7$

The equation of the line with slope $- 7$ and $x$-intercept 3 is given by

$y=m(x - d)$

$\Rightarrow y=- 7(x - 3)$

$\Rightarrow y=- 7 x+21$

$\Rightarrow 7 x+y=21$

Answer :

The given lines are $\sqrt{3} x+y=1$ and $x+\sqrt{3} y=1$.

$y=-\sqrt{3} x+1 \quad \ldots(1) \quad$ and $y=-\dfrac{1}{\sqrt{3}} x+\dfrac{1}{\sqrt{3}}$

The slope of line (1) is $m_1=-\sqrt{3}$, while the slope of line (2) is $m_2=-\dfrac{1}{\sqrt{3}}$.

The acute angle i.e., $\theta$ between the two lines is given by $\tan \theta=|\dfrac{m_1-m_2}{1+m_1 m_2}|$

$\tan \theta=|\dfrac{-\sqrt{3}+\dfrac{1}{\sqrt{3}}}{1+(-\sqrt{3})(-\dfrac{1}{\sqrt{3}})}|$

$\tan \theta=|\dfrac{\dfrac{-3+1}{\sqrt{3}}}{1+1}|=|\dfrac{-2}{2 \times \sqrt{3}}|$

$\tan \theta=\dfrac{1}{\sqrt{3}}$

$\theta=30^{\circ}$

Thus, the angle between the given lines is either $30^{\circ}$ or $180^{\circ} - 30^{\circ}=150^{\circ}$.

Answer :

The slope of the line passing through points $(h, 3)$ and $(4,1)$ is

$m_1=\dfrac{1-3}{4-h}=\dfrac{-2}{4-h}$

The slope of line $7 x$ - $9 y$ - $19=0$ or $y=\dfrac{7}{9} x-\dfrac{19}{9} \quad m_2=\dfrac{7}{9}$.

It is given that the two lines are perpendicular.

$\therefore m_1 \times m_2=-1$

$\Rightarrow(\dfrac{-2}{4-h}) \times(\dfrac{7}{9})=-1$

$\Rightarrow \dfrac{-14}{36-9 h}=-1$

$\Rightarrow 14=36-9 h$

$\Rightarrow 9 h=36-14$

$\Rightarrow h=\dfrac{22}{9}$

Thus, the value of $h$ is $\dfrac{22}{9}$.

Answer :

The slope of line $A x+B y+C=0$ or $y=(\dfrac{-A}{B}) x+(\dfrac{-C}{B})$ is $\quad m=-\dfrac{A}{B}$

It is known that parallel lines have the same slope.

$\therefore$ Slope of the other line $=m=-\dfrac{A}{B}$

The equation of the line passing through point $(x_1, y_1)$ and having a slope $m=-\dfrac{A}{B}$ is

$y-y_1=m(x-x_1)$

$y-y_1=-\dfrac{A}{B}(x-x_1)$

$B(y-y_1)=-A(x-x_1)$

$A(x-x_1)+B(y-y_1)=0$

Hence, the line through point $(x_1, y_1)$ and parallel to line $A x+B y+C=0$ is

$A(x - x_1)+B(y - y_1)=0$

Answer :

It is given that the slope of the first line, $m_1=2$.

Let the slope of the other line be $m_2$.

The angle between the two lines is $60^{\circ}$. $\therefore \tan 60^{\circ}=|\dfrac{m_1-m_2}{1+m_1 m_2}|$

$\Rightarrow \sqrt{3}=|\dfrac{2-m_2}{1+2 m_2}|$

$\Rightarrow \sqrt{3}= \pm(\dfrac{2-m_2}{1+2 m_2})$

$\Rightarrow \sqrt{3}=\dfrac{2-m_2}{1+2 m_2}$ or $\sqrt{3}=-(\dfrac{2-m_2}{1+2 m_2})$

$\Rightarrow \sqrt{3}(1+2 m_2)=2-m_2$ or $\sqrt{3}(1+2 m_2)=-(2-m_2)$

$\Rightarrow \sqrt{3}+2 \sqrt{3} m_2+m_2=2$ or $\sqrt{3}+2 \sqrt{3} m_2-m_2=-2$

$\Rightarrow \sqrt{3}+(2 \sqrt{3}+1) m_2=2$ or $\sqrt{3}+(2 \sqrt{3}-1) m_2=-2$

$\Rightarrow m_2=\dfrac{2-\sqrt{3}}{(2 \sqrt{3}+1)}$ or $m_2=\dfrac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}$

Case I: $\quad m_2=(\dfrac{2-\sqrt{3}}{2 \sqrt{3}+1})$

The equation of the line passing through point $(2,3)$ and having a slope of $\dfrac{(2-\sqrt{3})}{(2 \sqrt{3}+1)}$ is

$(y-3)=\dfrac{2-\sqrt{3}}{2 \sqrt{3}+1}(x-2)$

$(2 \sqrt{3}+1) y-3(2 \sqrt{3}+1)=(2-\sqrt{3}) x-2(2-\sqrt{3})$

$(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-4+2 \sqrt{3}+6 \sqrt{3}+3$

$(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$

In this case, the equation of the other line is $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$.

Case II : $\quad m_2=\dfrac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}$

The equation of the line passing through point $(2,3)$ and having a slope of $\dfrac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}$ is

$ \begin{aligned} & (y-3)=\dfrac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}(x-2) \\ & (2 \sqrt{3}-1) y-3(2 \sqrt{3}-1)=-(2+\sqrt{3}) x+2(2+\sqrt{3}) \\ & (2 \sqrt{3}-1) y+(2+\sqrt{3}) x=4+2 \sqrt{3}+6 \sqrt{3}-3 \\ & (2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3} \end{aligned} $

In this case, the equation of the other line is $(2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}$.

Thus, the required equation of the other line is $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$

or $(2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}$

Answer :

The right bisector of a line segment bisects the line segment at $90^{\circ}$.

The end-points of the line segment are given as A $(3,4)$ and $B(-{ } 1,2)$.

Accordingly, mid-point of $A B$

$ =(\dfrac{3-1}{2}, \dfrac{4+2}{2})=(1,3) $

Slope of $A B=\dfrac{2-4}{-1-3}=\dfrac{-2}{-4}=\dfrac{1}{2}$

$\therefore$ Slope of the line perpendicular to $A B=$

$ =-\dfrac{1}{(\dfrac{1}{2})}=-2 $

The equation of the line passing through $(1,3)$ and having a slope of - 2 is

(y - 3$)=$ -2 (x - 1)

$y $ - $3=- 2 x+2$

$2 x+y=5$

Thus, the required equation of the line is $2 x+y=5$.

Answer :

Let $(a, b)$ be the coordinates of the foot of the perpendicular from the point $(- 1,3)$ to the line $3 x - 4 y - 16=0$.

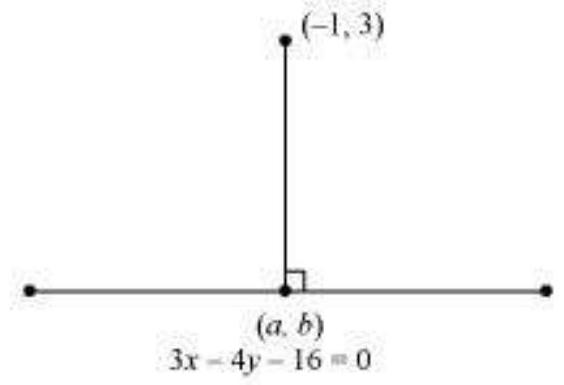
Slope of the line joining $( - 1,3) \text{ and } (a, b), m_1=\dfrac{b-3}{a+1}$

Slope of the line $3 x$- $4 y$- $16=0$ or $y=\dfrac{3}{4} x-4, m_2=\dfrac{3}{4}$

Since these two lines are perpendicular, $m_1 m_2=$ - 1

$\therefore(\dfrac{b-3}{a+1}) \times(\dfrac{3}{4})=-1$

$\Rightarrow \dfrac{3 b-9}{4 a+4}=-1$

$\Rightarrow 3 b-9=-4 a-4$

$\Rightarrow 4 a+3 b=5$

Point $(a, b)$ lies on line $3 x$ - $4 y=16$.

$\therefore 3 a$ - $4 b=16$

On solving equations (1) and (2), we obtain

$a=\dfrac{68}{25}$ and $b=-\dfrac{49}{25}$

Thus, the required coordinates of the foot of the perpendicular are $(\dfrac{68}{25},-\dfrac{49}{25})$

Answer :

The given equation of line is $y=m x+c$.

It is given that the perpendicular from the origin meets the given line at (-1,2).

Therefore, the line joining the points $(0,0)$ and $(- 1,2)$ is perpendicular to the given line.

$\therefore$ Slope of the line joining $(0,0)$ and $( - 1,2)$

$ =\dfrac{2}{-1}=-2 $

The slope of the given line is $m$.

$\therefore m \times -2=-1$

[The two lines are perpendicular]

$\Rightarrow m=\dfrac{1}{2}$

Since point $( - 1,2)$ lies on the given line, it satisfies the equation $y=m x+c$.

$\therefore 2=m(-1)+c$

$\Rightarrow 2=\dfrac{1}{2}(-1)+c$

$\Rightarrow c=2+\dfrac{1}{2}=\dfrac{5}{2}$

Thus, the respective values of $m$ and $c$ are $\dfrac{1}{2}$ and $\dfrac{5}{2}$.

Answer :

The equations of given lines are

$x \cos \theta - y \sin \theta=k \cos 2 \theta \ldots$ (1)

$x \sec \theta+y cosec \theta=k$.

The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by

$$ \begin{equation*} d=\dfrac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}} . \tag{2} \end{equation*} $$

On comparing equation (1) to the general equation of line i.e., $A x+B y+C=0$, we obtain $A=\cos \theta, B=$ -sin $\theta$, and $C=- k \cos 2 \theta$.

It is given that $p$ is the length of the perpendicular from $(0,0)$ to line (1). $\therefore p=\dfrac{|A(0)+B(0)+C|}{\sqrt{A^{2}+B^{2}}}=\dfrac{|C|}{\sqrt{A^{2}+B^{2}}}=\dfrac{|-k \cos 2 \theta|}{\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}}=|-k \cos 2 \theta|$

On comparing equation (2) to the general equation of line i.e., $A x+B y+C=0$, we obtain $A=\sec \theta, B=cosec \theta$, and $C=$ -k.

It is given that $q$ is the length of the perpendicular from $(0,0)$ to line (2).

$\therefore q=\dfrac{|A(0)+B(0)+C|}{\sqrt{A^{2}+B^{2}}}=\dfrac{|C|}{\sqrt{A^{2}+B^{2}}}=\dfrac{|-k|}{\sqrt{\sec ^{2} \theta+cosec^{2} \theta}}$

From (3) and (4), we have

$ \begin{aligned} & p^{2}+4 q^{2}=(\mid-k \cos 2 \theta)^{2}+4(\dfrac{|-k|}{\sqrt{\sec ^{2} \theta+cosec^{2} \theta}})^{2} \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{(\sec ^{2} \theta+cosec^{2} \theta)} \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{(\dfrac{1}{\cos ^{2} \theta}+\dfrac{1}{\sin ^{2} \theta})} \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{(\dfrac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin ^{2} \theta \cos ^{2} \theta})} \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{(\dfrac{1}{\sin ^{2} \theta \cos ^{2} \theta})} \\ & =k^{2} \cos ^{2} 2 \theta+4 k^{2} \sin ^{2} \theta \cos ^{2} \theta \\ & =k^{2} \cos ^{2} 2 \theta+k^{2}(2 \sin ^{2} \theta \cos ^{2} \theta. \\ & =k^{2} \cos ^{2} 2 \theta+k^{2} \sin ^{2} 2 \theta \\ & =k^{2}(\cos ^{2} 2 \theta+\sin ^{2} 2 \theta) \\ & =k^{2} \end{aligned} $

Hence, we proved that $p^{2}+4 q^{2}=k^{2}$.

Answer :

Let $A D$ be the altitude of triangle $A B C$ from vertex $A$.

Accordingly, $A D \perp B C$

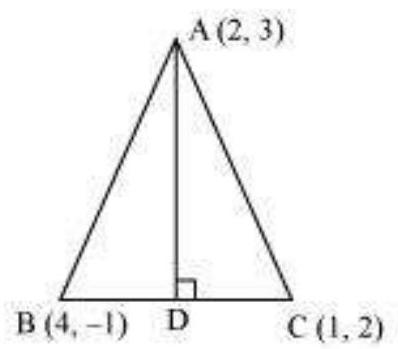
The equation of the line passing through point $(2,3)$ and having a slope of 1 is

$(y - 3)=1(x -2 )$

$\Rightarrow x - y+1=0$

$\Rightarrow y $ - $x=1$

Therefore, equation of the altitude from vertex $A=y $ - $x=1$.

Length of $A D=$ Length of the perpendicular from $A(2,3)$ to $B C$

The equation of $B C$ is

$(y+1)=\dfrac{2+1}{1-4}(x-4)$

$\Rightarrow(y+1)=-1(x-4)$

$\Rightarrow y+1=-x+4$

$\Rightarrow x+y-3=0$

The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by $\sqrt{A^{2}+B^{2}}$.

On comparing equation (1) to the general equation of line $A x+B y+C=0$, we obtain $A=1, B=1$, and $C=$ - 3 .

$\therefore$ Length of $A D$

$ =\dfrac{|1 \times 2+1 \times 3-3|}{\sqrt{1^{2}+1^{2}}} \text{ units }=\dfrac{|2|}{\sqrt{2}} \text{ units }=\dfrac{2}{\sqrt{2}} \text{ units }=\sqrt{2} \text{ units } $

Thus, the equation and the length of the altitude from vertex $A$ are $y -$ $x=1$ and $\sqrt{2}$ units respectively.

Answer :

It is known that the equation of a line whose intercepts on the axes are $a$ and $b$ is

$$ \begin{align*} & \dfrac{x}{a}+\dfrac{y}{b}=1 \\ & \text{ or } b x+a y=a b \\ & \text{ or } b x+a y-a b=0 \tag{1} \end{align*} $$

The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by

$ d=\dfrac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}} $

On comparing equation (1) to the general equation of line $A x+B y+C=0$, we obtain $A=b, B=a$, and $C=a -a b$.

Therefore, if $p$ is the length of the perpendicular from point $(x_1, y_1)=(0,0)$ to line (1), we obtain

$p=\dfrac{|A(0)+B(0)-a b|}{\sqrt{b^{2}+a^{2}}}$

$\Rightarrow p=\dfrac{|-a b|}{\sqrt{a^{2}+b^{2}}}$

On squaring both sides, we obtain

$p^{2}=\dfrac{(-a b)^{2}}{a^{2}+b^{2}}$

$\Rightarrow p^{2}(a^{2}+b^{2})=a^{2} b^{2}$

$\Rightarrow \dfrac{a^{2}+b^{2}}{a^{2} b^{2}}=\dfrac{1}{p^{2}}$

$\Rightarrow \dfrac{1}{p^{2}}=\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}$

Hence, we showed that $\dfrac{1}{p^{2}}=\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}$.