Chapter 06 Thermodynamics
Multiple Choice Questions (MCQs)
1. Thermodynamics is not concerned about
(a) energy changes involved in a chemical reaction
(b) the extent to which a chemical reaction proceeds
(c) the rate at which a reaction proceeds
(d) the feasibility of a chemical reaction
Answer (c) Thermodynamics is not concerned with the rate at which a reaction proceeds. Thermodynamics deals with the energy change, feasibility and extent of a reaction, but not with the rate and mechanism of a process.Show Answer
(a) The presence of reacting species in a covered beaker is an example of open system.
(b) There is an exchange of energy as well as matter between the system and the surroundings in a closed system.
(c) The presence of reactants in a closed vessel made up of copper is an example of a closed system.
(d) The presence of reactants in a thermos flask or any other closed insulated vessel is an example of a closed system.
Answer (c) For a closed vessel made of copper, no matter can exchange between the system and the surroundings but energy exchange can occur through its walls. Presence of reaction species in a covered beaker-closed system and exchange of matter as well as energy-open-system. Presence of reactant in a closed vessel closed system and presence of reactant in thermos flask-isolated system.Show Answer
(a) pressure, volume, temperature
(b) temperature, amount, pressure
(c) amount, volume, temperature
(d) pressure, volume, temperature, amount
Answer (d) The state of a gas can be described by quoting the relationship between pressure, volume, temperature and amount. The ideal gas equation is $$
p V=n R T
$$ Thus, $p, V, T$ and $n$ describe the state of the system.Show Answer
(a) reduce to half
(b) be doubled
(c) remain constant
(d) increase four times
Answer (c) The volume of gas is reduced to half from its original volume. The specific heat will be remain constant. Specific heat is an intensive property depending only on the nature of the gas.Show Answer
(a) $2 C_{4} H_{10}(~g)+13 O_{2}(~g) \rightarrow 8 CO_{2}(~g)+10 H_{2} O(l) ; \Delta_{C} H=-2658.0 ~kJ ~mol^{-1}$
(b) $C_{4} H_{10}(~g)+\frac{13}{2} O_{2}(~g) \rightarrow 4 CO_{2}(~g)+5 H_{2} O(l) ; \Delta_{C} H=-1329.0 ~kJ ~mol^{-1}$
(c) $C_{4} H_{10}(~g)+\frac{13}{2} O_{2}(~g) \rightarrow 4 CO_{2}(~g)+5 H_{2} O(l) ; \Delta_{C} H=-2658.0 ~kJ ~mol^{-1}$
(d) $C_{4} H_{10}(~g)+\frac{13}{2} O_{2}(~g) \rightarrow 4 CO_{2}(~g)+5 H_{2} O(l) ; \Delta_{C} H=+2658.0 ~kJ ~mol^{-1}$
Answer (c) Given that, the complete combustion of one mole of butane is represented by thermochemical reaction as $$
C_{4} H_{10}(g)+\frac{13}{2} O_{2}(g) \rightarrow 4 CO_{2}(g)+5 H_{2} O(l)
$$ We have to take the combustion of one mole of $C_{4} H_{10}$ and $\Delta_{C} H$ should be negative and have a value of $2658 ~kJ ~mol^{-1}$.Show Answer
(a) zero
(b) $<\Delta_{f} U^{s}$
(c) $>\Delta_{f} U^{s}$
(d) equal to $\Delta_{f} U^{\text {s }}$
Answer (b) The reaction is $CH_{4}(g)+2 O_{2}(g) \rightarrow CO_{2}(g)+2 H_{2} O(l)$ $$
\Delta n_{g} =\left(n_{p}-n_{r}\right)_{g}=1-3=-2 $$ $$ \Delta_{f} H^{-s} =\Delta_{f} U^{s}+\Delta n_{g} R T $$ $$\text { As } \quad \Delta_{g} =-2 $$ $$\therefore \quad\Delta_{f} H^{s} <\Delta_{f} U^{s}
$$Show Answer
(a) $q=0, \Delta T \neq 0, W=0$
(b) $q \neq 0, \Delta T=0, W=0$
(c) $q=0, \Delta T=0, W=0$
(d) $q=0, \Delta T<0, W \neq 0$
Answer (c) Free expansion, $W=0$ Adiabatic process, $q=0$ $\Delta U=q+W=0$, this means that internal energy remains constant. Therefore, $\Delta T=0 \mathrm{ln}$ ideal gas there is no intermolecular attraction. Hence, when such a gas expands under adiabatic conditions into a vacuum, no heat is absorbed or evolved since no external work is done to separate the molecules.Show Answer
(a) $W$ (reversible) $=W$ (irreversible)
(b) $W$ (reversible) $<W$ (irreversible)
(c) $W$ (reversible) $=W$ (irreversible)
(d) $W$ (reversible) $=W$ (irreversible) $+p_{\mathrm{ex}} \cdot \Delta V$
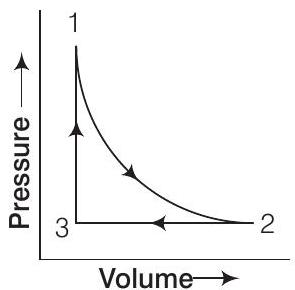
Answer (b) The correct option is W (reversible) $<W$ (irreversible). This is because area under the curve is always more in irreversible compression as can be seen from given figure. $p V$-plot when pressure is not constant and changes in finite steps during compression from initial volume, $V_{i}$ to final volume, $V_{f}$. Work done on the gas is represented by the shaded area. $P V$-plot when pressure is not constant and changes in infinite steps (reversible conditions) during compression from initial volume, $V_{i}$ to final volume, $V_{f}$. Work done on the gas is represented by the shaded area.Show Answer


(a) $\Delta S$ (system) decreases but $\Delta S$ (surroundings) remains the same
(b) $\Delta S$ (system) increases but $\Delta S$ (surroundings) decreases
(c) $\Delta S$ (system) decreases but $\Delta S$ (surroundings) increases
(d) $\Delta S$ (system) decreases but $\Delta S$ (surroundings) also decreases
Answer (c) The entropy change can be calculated by using the expression $$
\Delta S=\frac{q_{\mathrm{rev}}}{T}
$$ When water freezes in a glass beaker, $\Delta S$ (system) decreases because molecules in solid ice are less random than in liquid water. However, when water freezes to ice, heat is released which is absorbed by the surroundings. Hence, entropy of the surrounding increases.Show Answer
- $C$ (graphite) $+O_{2}(g) \rightarrow CO_{2}(g) ; \Delta_{r} H=x ~kJ ~mol^{-1}$
- $C$ (graphite) $+\frac{1}{2} O_{2}(g) \rightarrow CO(g) ; \Delta_{r} H=y ~kJ ~mol^{-1}$
- $CO(g)+\frac{1}{2} O_{2}(g) \rightarrow CO_{2}(g) ; \Delta_{r} H=z ~kJ ~mol^{-1}$
(a) $z=x+y$
(b) $x=y-z$
(c) $x=y+z$
(d) $y=2 z-x$
Answer (c) The algebraic relationships of the given reaction is equation (a) -equation (b) = equation (c) (a) $C$ (graphite) $+O_{2}(g) \rightarrow CO_{2}(g) ; \Delta_{r} H=x ~kJ ~mol^{-1}$ (b) $C$ (graphite) $+\frac{1}{2} O_{2}(g) \rightarrow CO(g) ; \Delta_{r} H=y ~kJ ~mol^{-1}$ $CO(g)+\frac{1}{2} O_{2}(g) \rightarrow CO_{2}(g) ; \Delta_{r} H=z ~kJ ~mol^{-1}$ Hence, $x-y=z$ or $x=y+z$Show Answer
- $C(g)+4 H(g) \rightarrow CH_{4}(g) ; \Delta_{r} H=x ~kJ ~mol^{-1}$
- $C$ (graphite) $+2 H_{2}(g) \rightarrow CH_{4}(g) ; \Delta_{r} H=y ~kJ ~mol^{-1}$
(a) $x=y$
(b) $x=2 y$
(c) $x>y$
(d) $x<y$
Answer (c) Same bonds are formed in reaction (1) and (2) but no bonds are broken in reaction (1) whereas bonds in the reactant molecules are broken in reaction (2). As energy is absorbed when bonds are broken, energy released in reaction (1) is greater than that in reaction (2) hence, $x>y$Show Answer
(a) is always negative
(b) is always positive
(c) may be positive or negative
(d) is never negative
Answer (c) Combustion of elements to form a compound can be exothermic or endothermic. e.g., $C+O_{2} \rightarrow CO_{2}$ is exothermic. whereas, $\mathrm{C}+2 \mathrm{~S} \rightarrow \mathrm{CS}_{2}$ is endothermic. Hence, enthalpy of formation can be positive or negative.Show Answer
(a) enthalpy of fusion + enthalpy of vaporisation
(b) enthalpy of fusion
(c) enthalpy of vaporisation
(d) twice the enthalpy of vaporisation
Answer (a) Enthalpy of sublimation of a substance is equal to enthalpy of fusion + enthalpy of vaporisation. Sublimation is, direct conversion of solid to vapour. solid $\rightarrow$ vapour Writing in two steps, we have solid $\rightarrow$ liquid $\rightarrow$ vapour, solid $\rightarrow$ liquid requires enthalpy of fusion liquid $\rightarrow$ vapour requires enthalpy of vaporisationShow Answer
(a) $\Delta \mathrm{G}$ is zero for a reversible reaction.
(b) $\Delta \mathrm{G}$ is positive for a spontaneous reaction.
(c) $\Delta G$ is negative for a spontaneous reaction.
(d) $\Delta \mathrm{G}$ is positive for a non-spontaneous reaction.
Show Answer
Answer
(b) $\Delta G$ gives a criteria for spontaneity at constant pressure and temperature.
(i) If $\Delta G$ is negative $(<0)$, the process is spontaneous.
(ii) If $\Delta G$ is positive ( $>0$ ), the process is non-spontaneous.
(iii) If $\Delta G$ is zero then reaction is equilibrium.
###Multiple Choice Questions (More Than One Options)
15. Thermodynamics mainly deals with
(a) interrelation of various forms of energy and their transformation from one form to another.
(b) energy changes in the processes which depend only on initial and final states of the microscopic systems containing a few molecules.
(c) how and at what rate these energy transformations are carried out.
(d) the system in equilibrium state or moving from one equilibrium state to another equilibrium state.
Answer $(a, d)$ Thermodynamics deals with interrelation of various forms of energy and their transformation into each other. It also deals with thermal or mechanical equilibrium. However, it does not tell anything about the rate of reaction.Show Answer
(a) $q_{p}$ will be negative
(b) $\Delta_{r} H$ will be negative
(c) $q_{p}$ will be positive
(d) $\Delta_{r} H$ will be positive
Answer $(a, b)$ Exothermic reactions are those reactions which are accompanied by the evolution of heat. e.g., $$
\begin{aligned}
& C(s)+O_{2}(g) \rightarrow CO_{2}(g)+393.5 ~kJ \\
& H_{2}(g)+\frac{1}{2} O_{2}(g) \rightarrow H_{2} O(l)+285.8 ~kJ
\end{aligned}
$$ $q_{p}$ and $\Delta_{r} H$ are negative for exothermic reaction.Show Answer
(a) flow of heat from colder to warmer body
(b) gas in a container contracting into one corner
(c) gas expanding to fill the available volume
(d) burning carbon in oxygen to give carbon dioxide
Answer (c, $d)$ Options (a) and (b) can neither occur by themselves nor by initiation, (c) can occur by itself, (d) occur on initiation. Flowing of heat from warmer to colder body, expanding of gas and burning of carbon to give carbon dioxide, all are spontaneous process.Show Answer
A sample containing $1.0 \mathrm{~mol}$ of an ideal gas is expanded isothermally and reversible to ten times of its original volume, in two separate experiments. The expansion is carried out at $300 \mathrm{~K}$ and at $600 \mathrm{~K}$ respectively. Choose the correct option.
(a) Work done at $600 \mathrm{~K}$ is 20 times the work done at $300 \mathrm{~K}$
(b) Work done at $300 \mathrm{~K}$ is twice the work done at $600 \mathrm{~K}$
(c) Work done at $600 \mathrm{~K}$ is twice the work done at $300 \mathrm{~K}$
(d) $\Delta U=0$ in both cases
Answer $(c, d)$ Given that, the work of reversible expansion under isothernal condition can be calculated by using the expression $$
\begin{aligned}
W & =-n R T \ln \frac{V_{f}}{V_{i}} \\
V_{f} & =10 V_{i} \\
T_{2} & =600 \mathrm{~K} \\
T_{1} & =300 \mathrm{~K}
\end{aligned}
$$ Putting these values in above expression $$
\begin{aligned}
& W_{600 \mathrm{~K}}=1 \times R \times 600 \mathrm{~K} \ln \frac{10}{1} \\
& W_{300 \mathrm{~K}}=1 \times R \times 300 \mathrm{~K} \ln \frac{10}{1} \\
& \text { Ratio }=\frac{W_{600 \mathrm{~K}}}{W_{300 \mathrm{~K}}}=\frac{1 \times R \times 600 \mathrm{~K} \ln \frac{10}{1}}{1 \times R \times 300 \mathrm{~K} \ln \frac{10}{1}}=\frac{600}{300}=2
\end{aligned}
$$ For isothermal expansion of ideal gases, $\Delta U=0$. Since, temperature is constant this means there is no channe in internal enernv Therefore $\Lambda / /=0$Show Answer
$$ 2 \mathrm{Zn}(s)+\mathrm{O}_{2}(g) \rightarrow 2 \mathrm{ZnO}(s) ; \Delta H=-693.8 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
(a) The enthalpy of two moles of $\mathrm{ZnO}$ is less than the total enthalpy of two moles of $\mathrm{Zn}$ and one mole of oxygen by $693.8 \mathrm{~kJ}$
(b) The enthalpy of two moles of $\mathrm{ZnO}$ is more than the total enthalpy of two moles of $\mathrm{Zn}$ and one mole of oxygen by $693.8 \mathrm{~kJ}$
(c) $693.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ energy is evolved in the reaction
(d) $693.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ energy is absorbed in the reaction
Show Answer
Answer
$(a, c)$
For the reaction,
$$ 2 \mathrm{Zn}(s)+\mathrm{O}_{2}(g) \rightarrow 2 \mathrm{ZnO}(\mathrm{s}) ; \Delta H=-693.8 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
As we know that,
$$ \Delta H=H_{p}-H_{R} $$
A negative value of $\Delta H$ shows that $H_{R}>H_{P}$ or $H_{P}<H_{R}$, i.e., enthalpy of two moles of $\mathrm{ZnO}$ is less than the enthalpy of two moles of zinc and one mole of oxygen by 693.8kJ. As $H_{R}>H_{P}$, $693.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ of energy is evolved in the reaction.
Short Answer Type Questions
20. $18.0 ~g$ of water completely vaporises at $100^{\circ} C$ and 1 bar pressure and the enthalpy change in the process is $40.79 ~kJ ~mol^{-1}$. What will be the enthalpy change for vaporising two moles of water under the same conditions? What is the standard enthalpy of vaporisation for water?
Answer Given that, quantity of water $=18.0 \mathrm{~g}$, pressure $=1$ bar As we know that, $18.0 gH_{2} O=1$ mole $H_{2} O$ Enthalpy change for vaporising 1 mole of $\mathrm{H}_{2} \mathrm{O}=40.79 \mathrm{~kJ} \mathrm{~mol}^{-1}$ $\therefore$ Enthalpy change for vaporising 2 moles of $\mathrm{H}_{2} \mathrm{O}=2 \times 40.79 \mathrm{~kJ}=81.358 \mathrm{~kJ}$ Standard enthalpy of vaporisation at $100^{\circ} \mathrm{C}$ and 1 bar pressure, $\Delta_{\text {vap }} H^{\circ}=+40.79 \mathrm{~kJ} \mathrm{~mol}^{-1}$Show Answer
Answer One mole of acetone requires less heat to vaporise than 1 mole of water. Hence, acetone has less enthalpy of vaporisation and water has higher enthalpy of vaporisation. It can be represented as $\left(\Delta H_{V}\right)$ water $>\left(\Delta H_{V}\right)$ acetone.Show Answer
$$ CaO(s)+CO_{2}(g) \rightarrow CaCO_{3}(s) ; \Delta_{f} H^{s}=-178.3 ~kJ ~mol^{-1} $$
Answer No, the $\Delta_{r} H^{\mathrm{s}}$ for the given reaction is not same as $\Delta_{r} H^{\mathrm{s}}$. The standard enthalpy change for the formation of one mole of a compound from its elements in their most stable states (reference states) is called standard molar enthalpy of formation, $\Delta_{f} H^{\mathrm{s}}$. $$
Ca(s)+C(s)+\frac{3}{2} O_{2}(g) \rightarrow CaCO_{3}(~s) ; \Delta_{f} H^{s}
$$ This reaction is different from the given reaction. Hence, $\Delta_{r} H^{\circ} \neq \Delta_{f} H^{\circ}$Show Answer
$$ 2 NH_{3}(g) \rightarrow N_{2}(g)+3 H_{2}(g) $$
Answer Given, $\frac{1}{2} ~N_{2}(g)+\frac{3}{2} H_{2}(g) \rightarrow NH_{3}(g) ; \Delta_{f} H^{s}=-91.8 ~kJ ~mol^{-1}$ $\left(\Delta_{f} H^{s}\right.$ means enthalpy of formation of 1 mole of $\left.\mathrm{NH}_{3}\right)$ $\therefore \quad$ Enthalpy change for the formation of 2 moles of $\mathrm{NH}_{3}$ $$
N_{2}(g)+3 H_{2}(g) \rightarrow 2 NH_{3}(g) ; \Delta_{f} H^{s}=2 \times-91.8=-183.6 ~kJ ~mol^{-1}
$$ And for the reverse reaction, $$
2 NH_{3}(g) \rightarrow N_{2}(g)+3 H_{2}(g) ; \Delta_{f} H^{s}=+183.6 ~kJ ~mol^{-1}
$$ Hence, the value of $\Delta_{f} H^{\mathrm{s}}$ for $\mathrm{NH}_{3}$ is $+183.6 \mathrm{~kJ} \mathrm{~mol}^{-1}$Show Answer
Answer In general, if enthalpy of an overall reaction $A \rightarrow B$ along one route is $\Delta_{r} H$ and $\Delta_{r} H_{1}, \Delta_{r} H_{2}, \Delta_{r} H_{3} \ldots$ representing enthalpies of reaction leading to same product $B$ along another route, then we have $$
\Delta_{r} H=\Delta_{r} H_{1}+\Delta_{r} H_{2}+\Delta_{r} H_{3}+\ldots
$$ Note For a general reaction Hess’s law of constant heat summation can be represented asShow Answer

Thinking Process To solve this problem, keep in mind that in methane all the four $\mathrm{C}-\mathrm{H}$ bonds are identical in bond length and energy. However, the energies required to break the individual $\mathrm{C}-\mathrm{H}$ bonds in each successive step differ. In such cases, we use mean bond enthalpy of $\mathrm{C}-\mathrm{H}$ bond i.e., $\Delta_{\mathrm{C}-H} H^{\mathrm{s}}=\frac{1}{4}\left(\Delta_{\mathrm{a}} H^{\mathrm{s}}\right)$ Answer In $CH_{4}$, there are four $C-H$ bonds. The enthalpy of atomisation of 1 mole of $CH_{4}$ means dissociation of four moles of $C-H$ bond. $$
\begin{aligned}
\therefore \quad \mathrm{C}-\mathrm{H} \text { bond energy per } \mathrm{mol} & =\frac{1665 \mathrm{~kJ}}{4 \mathrm{~mol}} \\
& =416.25 \mathrm{~kJ} \mathrm{~mol}^{-1}
\end{aligned}
$$Show Answer
Thinking Process This question is based upon the concept of Born-Haber cycle as well as Hess’s law. Following steps are used to solve this problem. (i) $\mathrm{Na}(\mathrm{s}) \rightarrow \mathrm{Na}(g) ; \Delta_{\text {sub }} H^{\mathrm{s}}$ (ii) $\mathrm{Na}(g) \rightarrow \mathrm{Na}^{+}(g)+\mathrm{e}^{-}(g)$; $I E$ (iii) $\frac{1}{2} Br_{2}(g) \rightarrow Br(g) ; \Delta_{\text {diss }} H^{s}$ (iv) $\mathrm{Br}(g)+\mathrm{e}^{-}(g) \rightarrow \mathrm{Br}^{-}(g) ; \Delta_{\mathrm{eg}} H^{\mathrm{s}}$ (v) Applying Hess’s law $\Delta_{f} H^{\mathrm{s}}=\Delta_{\text {sub }} H^{\mathrm{s}}+I \mathrm{E}+\Delta_{\text {diss }} H^{\mathrm{s}}+\Delta_{\text {eg }} H^{\mathrm{s}}+U$ Answer Given that, $\Delta_{\text {sub }} H^{\mathrm{s}}$ for $\mathrm{Na}$ metal $=108.4 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}$ IE of $\mathrm{Na}=496 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}, \Delta_{\text {eg }} H^{\mathrm{s}}$ of $\mathrm{Br}=-325 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}, \Delta_{\text {diss }} H^{\mathrm{s}}$ of $\mathrm{Br}=192 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}, \Delta_{f} H^{\mathrm{s}}$ for $\mathrm{NaBr}=-360.1 \mathrm{~kJ} \mathrm{~mol}^{-1}$ Born-Haber cycle for the formation of $\mathrm{NaBr}$ is as By applying Hess’s law, $$
\begin{aligned}
\Delta_{f} H^{\mathrm{s}} & =\Delta_{\text {sub }} H^{\mathrm{s}}+I E+\Delta_{\text {diss }} H^{\mathrm{s}}+\Delta_{\mathrm{eg}} H^{\mathrm{s}}+U \\
-360.1 & =108.4+496+96+(-325)-U \\
U & =+735.5 \mathrm{~kJ} \mathrm{~mol}^{-1}
\end{aligned}
$$Show Answer

Answer The mixing of two gases have $\Delta H$ equal to zero. Therefore, it is spontaneous process because energy factor has no role to play but randomness increases i.e., randomness factor favours the process.Show Answer
Answer Heat has randomising influence on a system and temperature is the measure of average chaotic motion of particles in the system. The mathematical relation which relates these three parameters is $$
\Delta S=\frac{q_{\text {rev }}}{T}
$$ Here, $\Delta S=$ change in entropy $q_{\text {rev }}=$ heat of reversible reaction $T=$ temperatureShow Answer
Answer Yes, the temperature of system and surroundings be the same when they are in thermal equilibrium. Note Thermal equilibrium is defined as when two physical systems are brought into a connection that does not allow transfer of matter between them, and does not allow transfer of energy between them, such a connection is said to permit transfer of energy as heat, and is called diathermal. If a diathermal connection is made between two physical systems and the making of the connection is followed by no change of state of either, then the two systems are said to be in relation of thermal equilibrium. It obeys zeroth law of thermodynamics.Show Answer
Answer For the reaction, $N_{2} O_{4}(g) \rightleftharpoons 2 NO_{2}(g), K_{p}=0.98$ As we know that $\quad \Delta_{r} \mathrm{G}^{\mathrm{s}}=-2.303 \mathrm{RT} \log K_{p}$ Here, $K_{p}=0.98$ i.e., $K_{p}<1$ therefore, $\Delta_{r} G^{\circ}$ is positive, hence the reaction is non-spontaneous.Show Answer
Answer The net enthalpy change, $\Delta H$ for a cyclic process is zero as enthalpy change is a state function, i.e., $\Delta H($ cycle $)=0$Show Answer
Answer The standard molar entropy of $H_{2} O(l)$ is $70 JK^{-1} ~mol^{-1}$. The solid form of $H_{2} O$ is ice. In ice, molecules of $H_{2} O$ are less random than in liquid water. Thus, molar entropy of $H_{2} O(s)<$ molar entropy of $H_{2} O(l)$. The standard molar entropy of $H_{2} O(s)$ is less than $70 ~J ~K^{-1} ~mol^{-1}$.Show Answer
Answer State functions are those values which depend only on the state of the system and not on how it is reached e.g., enthalpy, entropy, temperature and free energy. Path functions are those values which depend on the path of the system. e. $g$, heat and work.Show Answer
Answer Amount of heat required to vaporise one mole of a liquid at constant temperature and under standard pressure ( 1 bar ) is called its molar enthalpy of vaporisation $\Delta_{\text {vap }} H^{s}$. Molar enthalpy of vaporisation of water is more than that of acetone because there is strong hydrogen bonding in $\mathrm{H}_{2} \mathrm{O}$ molecule.Show Answer
Answer Gibbs energy for a reaction in which all reactants and products are in standard state. $\Delta_{r} G^{s}$ is related to the equilibrium constant of the reaction as follows $$
\Delta_{r} G=\Delta_{r} G^{\mathrm{s}}+R T \ln K
$$ $$
\begin{aligned}
\text{At equilibrium} \quad 0 & =\Delta_{r} G^{\circ}+R T \ln K \quad (\therefore \Delta_r G= 0)\\
\ \text{or} \quad \Delta_{r} G^{\mathrm{s}} & =-R T \ln K \\
\Delta_{r} G^{\mathrm{s}} & =0 \text { when } K=1
\end{aligned}
$$ For all other values of $K, \Delta_{r} G^{s}$ will be non-zero.Show Answer
Answer For isolated system there is no transfer of energy as heat, i.e., $q=0$ and there is no transfer of energy as work. i.e., $W=0$. According to the first law of thermodynamics $$
\begin{aligned}
& \Delta U=q+W \\
& \Delta U=0+0=0
\end{aligned}
$$Show Answer
Answer The two conditions under which heat becomes independent of path are (i) when volume remains constant (ii) when pressure remains constant Explanation (i) At constant volume By first law of thermodynamics, $\Delta U=q+W$ or $q=\Delta U-W$. But $W=-p \Delta V$ Hence, $q=\Delta U+p \Delta V$. But as volume remains constant $\Delta V=0$ $\therefore q_{V}=\Delta V$ but $\Delta U$ is a state function. Hence, $q_{v}$ is a state function. (ii) At constant pressure As we know, $q_{p}=\Delta U+p \Delta V$. But $\Delta U+p \Delta V=\Delta H$. $\therefore q_{p}=\Delta H$. As $\Delta H$ is a state function therefore, $q_{p}$ is a state function.Show Answer
Answer Work done of a gas in vacuum, $W=-p_{\text {ext }}\left(V_{2}-V_{1}\right)$. As $p_{\text {ext }}=0$ so $W=-0(5-1)=0$ As internal energy of an ideal gas depends only on temperature, therefore, for isothermal expansion of an ideal gas, internal energy remains constant, i.e., $$
\Delta U=0 .
$$ It is to be remember that as $H=U+p V, \Delta H=\Delta(U+p V)=\Delta U+p \Delta V=\Delta U+n R(\Delta T)$. For isothermal process, $\Delta T=0$ and also $\Delta U=0$, as stated above, therefore, $\Delta H=0$.Show Answer
Answer For water, molar heat capacity, $C_{p}=18 \times$ Specific heat, $c$ $$
\begin{aligned}
C_{p} & =18 \times c \text { Specific heat } \\
c & =4.18 \mathrm{Jg}^{-1} \mathrm{~K}^{-1} \quad \text{(for work)}\\
\text { Heat capacity, } \quad C_{p} & =18 \times 4.18 \mathrm{JK}^{-1} \mathrm{~mol}^{-1} \\
& =75.3 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}
\end{aligned}
$$Show Answer
Answer Given that, $C_{v}=$ heat capacity at constant volume, $C_{p}=$ heat capacity at constant pressure Difference between $C_{p}$ and $C_{v}$ is equal to gas constant $(R)$. $$
\begin{aligned}
\therefore \quad C_{p}-C_{v} & =n R \quad \text { (where, } n=\text { no. of moles) } \\
& =10 \times 4.184 \mathrm{~J} \\
& =41.84 \mathrm{~J}
\end{aligned}
$$Show Answer
Answer Given that, enthalpy of combustion of $1 \mathrm{~g}$ graphite $=20.7 \mathrm{~kJ}$ Molar enthalpy change for the combustion of graphite, $\Delta H=$ enthalpy of combustion of $1 \mathrm{~g}$ graphite $\times$ molar mass $$
\begin{aligned}
& \Delta H=-20.7 \mathrm{kJg}^{-1} \times 12 \mathrm{~g} \mathrm{~mol}^{-1} \\
& \Delta H=-2.48 \times 10^{2} \mathrm{~kJ} \mathrm{~mol}^{-1}
\end{aligned}
$$ Negative sign in the value of $\Delta H$ indicates that the reaction is exothermic.Show Answer
Thinking Process To, calculate the enthalpy change, use the following formula when the reactants, and products are in gas phase as $$
\Delta_{r} H^{\mathrm{s}}=\Sigma \text { bond energy (reactants) }-\Sigma \text { bond energy (products) }
$$ Answer Given that, bond energy of $\mathrm{H}_{2}=435 \mathrm{~kJ} \mathrm{~mol}^{-1}$ bond energy of $\mathrm{Br}_{2}=192 \mathrm{~kJ} \mathrm{~mol}^{-1}$ bond energy of $\mathrm{HBr}=368 \mathrm{~kJ} \mathrm{~mol}^{-1}$ For the reaction $$
\begin{aligned}
& H_{2}(g)+Br_{2}(g) \rightarrow 2 HBr(g) \\
& \Delta_{r} H^{s}=\Sigma BE(\operatorname{Reactants})-\Sigma BE(\text { Products }) \\
&=BE\left(H_{2}\right)+BE\left(Br_{2}\right)-2 BE(HBr) \\
&=435+192-(2 \times 368) kJ mol^{-1} \\
&=-109 ~kJ ~mol^{-1}
\end{aligned}
$$Show Answer
Answer Given that, $1 \text{mol of} \quad CCl_{4}=154 ~g$ $$
\begin{aligned}
& \Delta_{\text {vap }} H \text { for } 154 ~g CCl_{4}=30.5 ~kJ \\
\therefore \quad & \Delta_{\text {vap }} H \text { for } 284 ~g CCl_{4}=\frac{30.5 \times 284}{154} ~kJ=56.25 ~kJ
\end{aligned}
$$Show Answer
$$ 2 H_{2}(g)+O_{2}(g) \rightarrow 2 H_{2} O(l) \text { is } \Delta_{r} H^{s}=-572 ~kJ ~mol^{-1} $$
What will be standard enthalpy of formation of $\mathrm{H}_{2} \mathrm{O}(l)$ ?
Answer Given that, $$
2 H_{2}(g)+O_{2}(g) \rightarrow 2 H_{2} O(l), \Delta_{r} H^{\circ}=-572 ~kJ ~mol^{-1}
$$ Enthalpy of formation is the enthalpy change of the reaction when 1 mole of the compound is formed from its elements then $$
H_{2}(g)+\frac{1}{2} O_{2}(g) \rightarrow H_{2} O(l), \Delta_{r} H^{\circ}=?
$$ This can be obtained by dividing the given equation by 2 . Therefore, $$
\Delta_{f} H^{\circ}\left(\mathrm{H}_{2} \mathrm{O}\right)=-\frac{572 \mathrm{kJmol}^{-1}}{2}=-286 \mathrm{~kJ} \mathrm{~mol}^{-1}
$$Show Answer
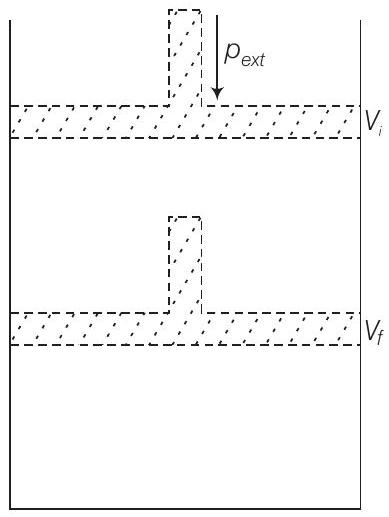
Answer Suppose total volume of the gas is $V_{i}$ and pressure of the gas inside cylinder is $p$. After compression by constant external pressure, $\left(p_{\text {ext }}\right)$ in a single step, final volume of the gas becomes $V_{f}$. Then volume change, $\Delta v=\left(V_{f}-V_{i}\right)$ If $W$ is the work done on the system by movement of the piston, then $$
\begin{aligned}
& W=p_{\text {ext }}(-\Delta V) \\
& W=-p_{\text {ext }}\left(V_{f}-V_{i}\right)
\end{aligned}
$$ This can be calculated from $p-V$ graph as shown in the figure. Work done is equal to the shaded area $A B V_{f} V_{i}$ The negative sign in this expression is required to obtain conventional sign for $W$ which will be positive. Because in case of compression work is done on the system, so $\Delta V$ will be negative.Show Answer

Answer When compression is carried out in infinite steps with change in pressure, it is a reversible process. The work done can be calculated from $p-V$ plot as shown in the given figure. Shaded area under the curve represents the work done on the gas.Show Answer

(a) Throwing a stone from the ground to roof.
(b) $\frac{1}{2} H_{2}(g)+\frac{1}{2} Cl_{2}(g) \rightleftharpoons HCl(g) \Delta_{r} H^{s}=-92.32 ~kJ ~mol^{-1}$
In which of the processes potential energy/enthalpy change is contributing factor to the spontaneity?
Answer Representation of potential energy/enthalpy change in the following processes (a) Throwing a stone from the ground to roof. (b) $\frac{1}{2} H_{2}(g)+\frac{1}{2} Cl_{2}(g) \rightleftharpoons HCl(g) ; \Delta_{r} H^{s}=-92.32 ~kJ ~mol^{-1}$ Energy increases in (a) and it decreases in (b) process. Hence, in process (b), enthalpy change is the contributing factor to the spontaneity.Show Answer


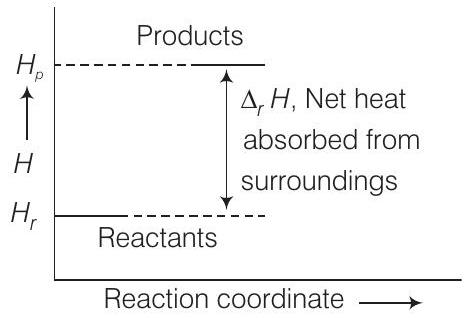
Answer No, enthalpy is one of the contributing factors in deciding spontaneity but it is not the only factor. Another contributory factor, entropy factor has also to be taken into consideration.Show Answer
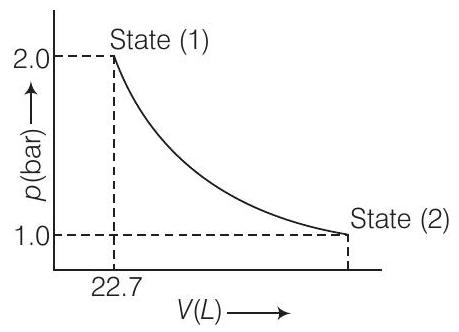
Answer The given diagram represent that the process is carried out in infinite steps, hence it is isothermal reversible expansion of the ideal gas from pressure $2.0 \mathrm{~atm}$ to $1.0 \mathrm{~atm} 298 \mathrm{~K}$. $$
\begin{aligned}
& W=-2.303 n R T \log \frac{p_{1}}{p_{2}} \\
& W=-2.303 \times 1 \mathrm{~mol} \times 8.314 \mathrm{JK}^{-1} \mathrm{~mol}^{-1} \times 298 \mathrm{Klog} 2 \quad\left(\because \frac{p_{1}}{p_{2}}=\frac{2}{1}\right) \\
& W=-2.303 \times 1 \times 8.314 \times 298 \times 0.3010 \mathrm{~J} \\
& W=-1717.46 \mathrm{~J}
\end{aligned}
$$Show Answer
(Given that, $1 \mathrm{~L}$ bar $=100 \mathrm{~J}$ )
Show Answer
Answer
In the first case, as the expansion is against constant external pressure
$$ \begin{aligned} W & =-p_{\text {ext }}\left(V_{2}-V_{1}\right)=-2 \operatorname{bar} \times(50-10) \mathrm{L} \\ & =-80 \mathrm{~L} \text { bar } \quad \quad (1L bar = 100 J)\\ & =-80 \times 100 \mathrm{~J} \\ & =-8 \mathrm{~kJ} \end{aligned} $$
If the given expansion was carried out reversibly, the internal pressure of the gas should be greater than the external pressure at every stage. Hence, the work done will be more.
Matching the Columns
51. Match the following.
| List I | List II | ||
|---|---|---|---|
| A. | Adiabatic process | 1. | Heat |
| B. | Isolated system | 2. | At constant volume |
| C. | Isothermal change | 3. | First law of thermodynamics |
| D. | Path function | 4. | No exchange of energy and matter |
| E. | State function | 5. | No transfer of heat |
| F. | $\Delta U=q$ | 6. | Constant temperature |
| G. | Law of conservation of energy | 7. | Internal energy |
| H. | Reversible process | 8. | Pext = 0 |
| I. | Free expansion | 9. | At constant pressure |
| J. | $\Delta H=q$ | 10. | Infinitely slow process which |
| proceeds through a series of | |||
| K. | Intensive property | 11. | Entropy |
| L. | Extensive property | 12. | Pressure |
| 13. | Specific heat |
Answer A. $\rightarrow(5)$ B. $\rightarrow(4)$ C. $\rightarrow(6)$ D. $\rightarrow(1)$ E. $\rightarrow(7,11,12)$ F. $\rightarrow(2)$ G. $\rightarrow(3)$ H. $\rightarrow(10)$ I. $\rightarrow(8)$ J. $\rightarrow(9)$ K. $\rightarrow(1,12,13)$ L. $\rightarrow(7,11)$ Correct Matching can be done asShow Answer
A.
Adiabatic process
No transfer of heat
B.
Isolated system
No exchange of energy and matter
C.
Isothermal change
Constant temperature
D.
Path function
Heat
E.
State function
Internal energy
Entropy
Pressure
F.
$\Delta U=q$
At constant volume
G.
Law of conservation of energy
First law of thermodynamics
H.
Reversible process
Infinitely slow process which
proceeds through a series of
I.
Free expansion
equilibrium states
J.
$\Delta H=q$
Pext $=0$
K.
Intensive property
At constant pressure
Heat
Pressure
L.
Extensive property
Specific heat
| Reaction | Entropy change | ||
|---|---|---|---|
| A. | A liquid vaporises | 1. | $\Delta S=0$ |
| B. | Reaction is non-spontaneous at all temperatures and $\Delta H$ is positive |
2. | $\Delta S=$ positive |
| C. | Reversible expansion of an ideal gas | 3. | $\Delta S=$ negative |
Answer A. $\rightarrow(2) \quad$ B. $\rightarrow(3) \quad$ C. $\rightarrow(1)$ A. When a liquid vaporises, i.e., liquid $\rightarrow$ vapour, entropy increase i.e., $\Delta S=$ positive B. When $\Delta H=$ positive, i.e., energy factor opposes. The process is non-spontaneous at all temperatures if entropy factor also opposes the process, i.e., $\Delta S=$ negative C. In the reversible expansion of an ideal gas, the system remains in equilibrium at every stage. Hence, $\Delta S=0$Show Answer
| $\Delta$ (Parameters) $\Delta_{r} \boldsymbol{H}^{\mathrm{S}} \Delta_{r} S^{\mathrm{S}} \Delta_{r} G^{\mathrm{S}}$ |
Description | |
|---|---|---|
| A. | +-+ | 1. Non-spontaneous at high temperature |
| B. | –+ at high $T$ | 2. Spontaneous at all temperatures |
| C. | -+- | 3. Non-spontaneous at all temperatures |
Answer A. $\rightarrow(3)$ B. $\rightarrow(1)$ C. $\rightarrow(2)$ A. When $\Delta_{r} G^{s}$ is positive, reaction is non-spontaneous at all temperatures B. When $\Delta_{r} G^{s}$ is positive at high temperature means the reaction is non-spontaneous at high temperature. C. When $\Delta_{r} H^{\mathrm{s}}=$ negative means it favours, $\Delta_{r} S^{\mathrm{s}}=$ positive means it also favours. $\Delta_{r} G^{\circ}=$ negative means reaction is spontaneous at all temperatures.Show Answer
| A. | Entropy of vaporisation | 1. | decreases |
|---|---|---|---|
| B. | $K$ for spontaneous process | 2. | is always positive |
| C. | Crystalline solid state | 3. | lowest entropy |
| D. | $\Delta U$ in adiabatic expansion of ideal gas | 4. | $\frac{\Delta H_{\text {vap }}}{T_{b}}$ |
Answer A. $\rightarrow(2,4)$ B. $\rightarrow(2)$ C. $\rightarrow(3)$ D. $\rightarrow(1)$ A. Entropy of vaporisation is always positive. It is equal to $\Delta H_{\text {vap }} / T_{b}$ B. $\Delta_{r} G^{\circ}=-R T \ln K$ If $K$ is positive, $\Delta_{r} G^{\circ}=$ negative and reaction is spontaneous. C. Crystalline solid state has lowest entropy. D. During adiabatic expansion of an ideal gas, $q=0$. Hence, $\Delta U=q+W$ gives $\Delta U=W$, i.e., work done is at the cost of internal energy which decreases. In the following questions a statement of assertion (A) followed by a statement of reason $(\mathrm{R})$ is given. Choose the correct option out of the choices given below in each question.Show Answer
Assertion and Reason
Reason (R) The enthalpies of all elements in their standard state are zero.
(a) Both $A$ and $R$ are true and $R$ is the correct explanation of $A$
(b) Both $\mathrm{A}$ and $\mathrm{R}$ are true but $\mathrm{R}$ is not the correct explanation of $\mathrm{A}$
(c) $A$ is true but $R$ is false
(d) $A$ is false but $R$ is true
Answer (b) Both assertion and reason are true but reason is not the correct explanation of assertion. Correct explanation In a combustion reaction, sum of enthalpies of reactants is greater than the sum of the enthalpies of products.Show Answer
Reason (R) Decrease in enthalpy is a contributory factor for spontaneity.
(a) Both $A$ and $R$ are true and $R$ is the correct explanation of $A$
(b) Both $A$ and $R$ are true but $R$ is not the correct explanation of $A$
(c) $A$ is true but $R$ is false
(d) $A$ is false but $R$ is true
Answer (b) Both assertion and reason are true but reason is not the correct explanation of assertion. Spontaneous processes are accompanied by decrease in energy and increase in randomness.Show Answer
Reason (R) In crystals, molecules organise in an ordered manner.
(a) Both $A$ and $R$ are true and $R$ is the correct explanation of $A$
(b) Both $\mathrm{A}$ and $\mathrm{R}$ are true but $\mathrm{R}$ is not the correct explanation of $\mathrm{A}$
(c) $A$ is true but $R$ is false
(d) $A$ is false but $R$ is true
Show Answer
Answer
(a) Both assertion and reason are true and reason is the correct explanation of assertion. When a liquid crystallises, entropy decreases because in crystalline form the molecules are more ordered as compared to the liquid.
Long Answer Type Questions
58. Derive the relationship between $\Delta H$ and $\Delta U$ for an ideal gas. Explain each term involved in the equation.
Answer From the first law of thermodynamics, $\quad q=\Delta U+p \Delta V$ If the process carried out at constant volume, $\Delta V=0$ Hence, $ \quad\quad $[Here, $q_v=$ Heat absorbed at constant volume, $\Delta U=$ change in internal energy]
$$q_v=\Delta U$$ Similarly, Here, $q_p=$ heat absorbed at constant pressure $\Delta H=$ enthalpy change of the system. Enthalpy change of a system is equal to the heat absorbed or evolved by the system at constant pressure. As we know that at constant pressure, $\Delta H=\Delta U+p \Delta V$ where, $\Delta V$ is the change in volume. This equation can be rewritten as $\Delta H=\Delta U+p\left(V_f-V_i\right)=\Delta U+\left(p V_f-p V_i\right)$ where, $V_i=$ initial volume of the system $V_f=$ final volume of the system But for the ideal gases,
$$
\begin{aligned}
& p V=n R T
\end{aligned}
$$ So that
$$ V_1=n_1 R T$$ and
$$p V_2=n_2 R T$$ where, $n_1=$ number of moles of the gaseous reactants
$n_2=$ number of moles of the gaseous products. Substituting these values in Eq. (i), we get $$
\begin{aligned}
& \Delta H=\Delta U+\left(n_{2} R T-n_{1} R T\right) \\
& \Delta H=\Delta U+\left(n_{2}-n_{1}\right) R T \\
or & \quad \Delta H=\Delta U+\Delta n_{g} R T
\end{aligned}
$$ where, $\Delta n_{g}=n_{2}-n_{1}$ is the difference between the number of moles of the gaseous products and gaseous reactants. Putting the values of $\Delta H$ and $\Delta U$ we get $$
q_{p}=q_{v}+\Delta n_{g} R T
$$ Note Conditions under which $q_{p}=q_{v}$ or $\Delta H=\Delta U$ (i) When reaction is carried out in a closed vessel so that volume remains constant i.e., $\Delta V=0$ (ii) When reaction involves only solids or liquids or solutions but no gaseous reactant or product. This is because the volume changes of the solids and liquids during a chemical reaction are negligible. (iii) When reaction involves gaseous reactants and products but their number of moles are equal (i.e., $n_{p}=n_{r}$ ) e.g., $$
\begin{array}{r}
H_{2}(~g)+Cl_{2}(~g) \longrightarrow 2 HCl(g) \\
C(s)+O_{2}(~g) \longrightarrow CO_{2}(~g)
\end{array}
$$ Since, $a_{p}$ is different from $q_{v}$ only in those reactions which involves gaseous reactants and products and $\left(n_{p}\right)$ gaseous $\neq\left(n_{r}\right)$ gaseous.Show Answer
Mass, internal energy, pressure, heat capacity, molar heat capacity, density, mole fraction, specific heat, temperature and molarity.
Answer Extensive properties Those properties whose value depends on the quantity or size of matter present in the system is known as extensive properties. e.g., mass, internal energy, heat capacity. Intensive properties Those properties which do not depend on the quantity or size of matter present are known as intensive properties. e.g., pressure, molar heat capacity, density, mole fraction, specific heat, temperature and molarity. Mole fraction or molarity of a solution is same whether we take a small amount of the solution or large amount of the solution. Ratio of two extensive properties is always intensive. $$
\frac{\text { Extensive }}{\text { Extensive }}=\text { Intensive }
$$ So, mole fraction and molarity are intensive properties. $$
\begin{gathered}
\text { e.g, \quad mole fraction }=\frac{\text { Moles of the component }}{\text { Total no. of moles }}=\frac{\text { Extensive }}{\text { Extensive }} \\
\text {and \quad molarity }=\frac{\text { Mole }}{\text { Volume }}=\frac{\text { Extensive }}{\text { Extensive }}
\end{gathered}
$$Show Answer
Answer The lattice enthalpy of an ionic compound is the enthalpy change which occurs when one mole of an ionic compound dissociates into its ions in gaseous state. For the reaction $$
\mathrm{Na}^{+} \mathrm{Cl}^{-}(s) \rightarrow \mathrm{Na}^{+}(g)+\mathrm{Cl}^{-}(g) ; \Delta_{\text {lattice }} H^{\mathrm{s}}=+788 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}
$$ Since, it is impossible to determine lattice enthalpies directly by experiment, we use an indirect method where we construct an enthalpy diagram called a Born-Haber cycle. Let us now calculate the lattice enthalpy of $\mathrm{Na}^{+} \mathrm{Cl}^{-}$(s) by following steps given below (i) $\mathrm{Na}^{+}(\mathrm{s}) \rightarrow \mathrm{Na}(g)$; Sublimation of sodium metal, $\Delta_{\text {sub }} H^{\mathrm{s}}=108.4 \mathrm{~kJ} \mathrm{~mol}^{-1}$ (ii) $\mathrm{Na}(g) \rightarrow \mathrm{Na}^{+}(g)+e^{-}(g)$; The ionisation of sodium atoms, ionisation enthalpy $\Delta_{i} H^{\mathrm{s}}=496 \mathrm{~kJ} \mathrm{~mol}^{-1}$ (iii) $\frac{1}{2} Cl_{2}(g) \rightarrow Cl(g)$; The dissociation of chlorine, the reaction enthalpy is half the bond dissociation enthalpy $\frac{1}{2} \Delta_{\text {bond }} H^{s}=121 ~kJ ~mol^{-1} $ (iv) $\mathrm{Cl}(g)+e^{-}(g) \rightarrow \mathrm{Cl}^{-}(g)$; electron gained by chlorine atoms. The electron gain enthalpy, $\Delta_{\text {eg }} H^{\mathrm{S}}=-348.6 \mathrm{~kJ} \mathrm{~mol}^{-1}$ Enthalply diagram for lattice enthalpy of $\mathrm{NaCl}$ (v) $\mathrm{Na}^{+}(g)+\mathrm{Cl}^{-}(g) \longrightarrow \mathrm{Na}^{+} \mathrm{Cl}^{-}(s)$ The sequence of steps is shown in given figure and is known as Born-Haber cycle. The importance of the cycle is that, the sum of the enthalpy changes round a cycle is zero. Applying Hess’s law, we get $$
\Delta_{\text {lattice }} H^{\mathrm{S}}=411.2+108.4+121+496-348.6
$$ $\Delta_{\text {latitice }} H^{\mathrm{s}}=+788 \mathrm{~kJ}$Show Answer

Answer Gibbs free energy is that thermodynamic quantity of a system, the decrease in whose value during a process is equal to the maximum possible useful work that can be obtained from the system. Mathematically, this results may be derived as follows The relationship between heat absorbed by a system $q$, the change in its internal energy, $\Delta U$ and the work done by the system is given by the equation of the first law of thermodynamics, therefore, $$
q=\Delta U+W_{\text {expansion }}+W_{\text {non-expansion }} \quad …(i)
$$ Under constant pressure condition, the expansion work is given by $p \Delta V$. $$
\begin{array}{rlr}
\therefore \quad & q =\Delta U+p \Delta V+W_{\text {nonexpansion }} \quad (\because \Delta U+p \Delta V=\Delta H) \\
& =\Delta H+W_{\text {non-expansion }} \quad …(ii)&
\end{array}
$$ For a reversible change taking place at constant temperature, $$
\Delta S=\frac{q_{\text {rev }}}{T} \text { or } q_{\text {rev }}=T \Delta S \quad …(iii)
$$ Substituting the value of $q$ from Eq. (iii) in Eq. (ii), we get $$
\begin{aligned}
T \Delta S & =\Delta H+W_{\text {non-expansion }} \\
or \quad \Delta H-T \Delta S & =-W_{\text {non expansion }} \quad …(iv)
\end{aligned}
$$ For a change taking place under conditions of constant temperature and pressure, $$
\Delta G=\Delta H-T \Delta S
$$ Substituting this value in equation (iv), we get $$
\Delta G=-W_{\text {non-expansion }} \quad …(v)
$$ Thus, free energy change can be taken as a measure of work other than the work of expansion. For most changes, the work of expansion can not be converted to other useful work, whereas the non-expansion work is convertible to useful work. Rearranging equation $(\mathrm{v})$, it may write as $$
-\Delta G=W_{\text {non-expansion }}=W_{\text {useful }}
$$ As $-\Delta G=W_{\text {useful }}$ therefore, $\Delta G$ has the same units as those of work i.e., joule $$
\Delta G=\Delta H-T \Delta S .
$$ If $\Delta H=$ positive and $\Delta S=$ positive, then $\Delta G$ will be negative i.e., process will be spontaneous only when $T \Delta S>\Delta H$ in magnitude, which will be so when temperature is high.Show Answer
Show Answer
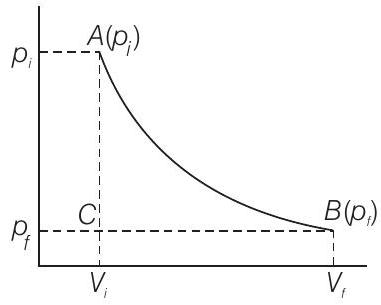
Answer
(i) Total work done in an expansion when the state of an ideal gas is changed reversibly and isothermally from $\left(p_{i}, V_{i}\right)$ to $\left(p_{f}, V_{f}\right)$. Reversible work is represented by the combined areas $A B C$ and $B C V_{i} V_{f}$.
(ii) Work against constant pressure, $p_{f}$ is represented by the area $B C V_{i} V_{f}$. Work (i) $>$ work (ii)