Chapter 04 Chemical Bonding and Moleuclar Structure
“Scientists are constantly discovering new compounds, orderly arranging the facts about them, trying to explain with the existing knowledge, organising to modify the earlier views or evolve theories for explaining the newly observed facts.”
Matter is made up of one or different type of elements. Under normal conditions no other element exists as an independent atom in nature, except noble gases. However, a group of atoms is found to exist together as one species having characteristic properties. Such a group of atoms is called a molecule. Obviously there must be some force which holds these constituent atoms together in the molecules. The attractive force which holds various constituents (atoms, ions, etc.) together in different chemical species is called a chemical bond. Since the formation of chemical compounds takes place as a result of combination of atoms of various elements in different ways, it raises many questions. Why do atoms combine? Why are only certain combinations possible? Why do some atoms combine while certain others do not? Why do molecules possess definite shapes? To answer such questions different theories and concepts have been put forward from time to time. These are Kössel-Lewis approach, Valence Shell Electron Pair Repulsion (VSEPR) Theory, Valence Bond (VB) Theory and Molecular Orbital (MO) Theory. The evolution of various theories of valence and the interpretation of the nature of chemical bonds have closely been related to the developments in the understanding of the structure of atom, the electronic configuration of elements and the periodic table. Every system tends to be more stable and bonding is nature’s way of lowering the energy of the system to attain stability.
4.1 KÖSSEL-LEWIS APPROACH TO CHEMICAL BONDING
In order to explain the formation of chemical bond in terms of electrons, a number of attempts were made, but it was only in 1916 when Kössel and Lewis succeeded independently in giving a satisfactory explanation. They were the first to provide some logical explanation of valence which was based on the inertness of noble gases.
Lewis pictured the atom in terms of a positively charged ‘Kernel’ (the nucleus plus the inner electrons) and the outer shell that could accommodate a maximum of eight electrons. He, further assumed that these eight electrons occupy the corners of a cube which surround the ‘Kernel’. Thus the single outer shell electron of sodium would occupy one corner of the cube, while in the case of a noble gas all the eight corners would be occupied. This octet of electrons, represents a particularly stable electronic arrangement. Lewis postulated that atoms achieve the stable octet when they are linked by chemical bonds. In the case of sodium and chlorine, this can happen by the transfer of an electron from sodium to chlorine thereby giving the $\mathrm{Na}^+$ and $\mathrm{Cl}^{-}$ ions. In the case of other molecules like $ \mathrm{Cl}_2, \mathrm{H}_2, \mathrm{~F}_2 $ , etc., the bond is formed by the sharing of a pair of electrons between the atoms. In the process each atom attains a stable outer octet of electrons.
Lewis Symbols: In the formation of a molecule, only the outer shell electrons take part in chemical combination and they are known as valence electrons. The inner shell electrons are well protected and are generally not involved in the combination process. G.N. Lewis, an American chemist introduced simple notations to represent valence electrons in an atom. These notations are called Lewis symbols. For example, the Lewis symbols for the elements of second period are as under:

Significance of Lewis Symbols : The number of dots around the symbol represents the number of valence electrons. This number of valence electrons helps to calculate the common or group valence of the element. The group valence of the elements is generally either equal to the number of dots in Lewis symbols or 8 minus the number of dots or valence electrons.
Kössel, in relation to chemical bonding, drew attention to the following facts:
- In the periodic table, the highly electronegative halogens and the highly electropositive alkali metals are separated by the noble gases;
- The formation of a negative ion from a halogen atom and a positive ion from an alkali metal atom is associated with the gain and loss of an electron by the respective atoms;
- The negative and positive ions thus formed attain stable noble gas electronic configurations. The noble gases (with the exception of helium which has a duplet of electrons) have a particularly stable outer shell configuration of eight (octet) electrons, $n s^{2} n p^{6}$.
- The negative and positive ions are stabilized by electrostatic attraction.
For example, the formation of $\mathrm{NaCl}$ from sodium and chlorine, according to the above scheme, can be explained as:
| $\mathrm{Na}$ | $\rightarrow$ | $\mathrm{Na}^{+}+\mathrm{e}^{-}$ |
| $[\mathrm{Ne}] 3 \mathrm{~s}^{1}$ | $[\mathrm{Ne}]$ | |
| $\mathrm{Cl}+\mathrm{e}^{-}$ | $\rightarrow$ | $\mathrm{Cl}^{-}$ |
| $[\mathrm{Ne}] 3 s^{2} 3 p^{5}$ | $[\mathrm{Ne}] 3 s^{2} 3 p^{6}$ or $[\mathrm{Ar}]$ | |
| $\mathrm{Na}^{+}+\mathrm{Cl}^{-}$ | $\rightarrow$ | $\mathrm{NaCl}$ or $\mathrm{Na}^{+} \mathrm{Cl}^{-}$ |
Similarly the formation of $\mathrm{CaF}_{2}$ may be shown as:
| $\mathrm{Ca}$ | $\rightarrow$ | $\mathrm{Ca}^{2+}+2 \mathrm{e}^{-}$ |
| $[\mathrm{Ar}] 4 s^{2}$ | $[\mathrm{Ar}]$ | |
| $\mathrm{F}+\mathrm{e}^{-}$ | $\rightarrow$ | $\mathrm{F}^{-}$ |
| $[\mathrm{He}] 2 s^{2} 2 p^{5}$ | $[\mathrm{He}] 2 s^{2} 2 p^{6}$ or $[\mathrm{Ne}]$ | |
| $\mathrm{Ca}^{2+}+2 \mathrm{~F}^{-}$ | $\rightarrow$ | $\mathrm{CaF}_2$ or $\mathrm{Ca}^{2+}\left(\mathrm{F}^{-}\right)_2$ |
The bond formed, as a result of the electrostatic attraction between the positive and negative ions was termed as the electrovalent bond. The electrovalence is thus equal to the number of unit charge(s) on the ion. Thus, calcium is assigned a positive electrovalence of two, while chlorine a negative electrovalence of one.
Kössel’s postulations provide the basis for the modern concepts regarding ion-formation by electron transfer and the formation of ionic crystalline compounds. His views have proved to be of great value in the understanding and systematisation of the ionic compounds. At the same time he did recognise the fact that a large number of compounds did not fit into these concepts.
4.1.1 Octet Rule
Kössel and Lewis in 1916 developed an important theory of chemical combination between atoms known as electronic theory of chemical bonding. According to this, atoms can combine either by transfer of valence electrons from one atom to another (gaining or losing) or by sharing of valence electrons in order to have an octet in their valence shells. This is known as octet rule.
4.1.2 Covalent Bond
Langmuir (1919) refined the Lewis postulations by abandoning the idea of the stationary cubical arrangement of the octet, and by introducing the term covalent bond. The Lewis-Langmuir theory can be understood by considering the formation of the chlorine molecule, $\mathrm{Cl}_2$. The $\mathrm{Cl}$ atom with electronic configuration, $[\mathrm{Ne}] 3 s^2 3 p^5$, is one electron short of the argon configuration. The formation of the $\mathrm{Cl}_2$ molecule can be understood in terms of the sharing of a pair of electrons between the two chlorine atoms, each chlorine atom contributing one electron to the shared pair. In the process both chlorine atoms attain the outer shell octet of the nearest noble gas (i.e., argon).

Covalent bond between two Cl atoms
The dots represent electrons. Such structures are referred to as Lewis dot structures.
The Lewis dot structures can be written for other molecules also, in which the combining atoms may be identical or different. The important conditions being that:
- Each bond is formed as a result of sharing of an electron pair between the atoms.
- Each combining atom contributes at least one electron to the shared pair.
- The combining atoms attain the outershell noble gas configurations as a result of the sharing of electrons.
- Thus in water and carbon tetrachloride molecules, formation of covalent bonds can be represented as:

Thus, when two atoms share one electron pair they are said to be joined by a single covalent bond. In many compounds we have multiple bonds between atoms. The formation of multiple bonds envisages sharing of more than one electron pair between two atoms. If two atoms share two pairs of electrons, the covalent bond between them is called a double bond. For example, in the carbon dioxide molecule, we have two double bonds between the carbon and oxygen atoms. Similarly in ethene molecule the two carbon atoms are joined by a double bond..

$\mathrm{C} _{2} \mathrm{H} _{4}$ Molecule
When combining atoms share three electron pairs as in the case of two nitrogen atoms in the $N_{2}$ molecule and the two carbon atoms in the ethyne molecule, a triple bond is formed.
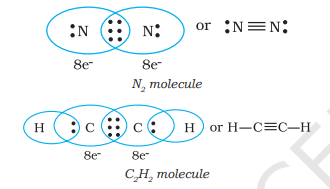
4.1.3 Lewis Representation of Simple Molecules (the Lewis Structures)
The Lewis dot structures provide a picture of bonding in molecules and ions in terms of the shared pairs of electrons and the octet rule. While such a picture may not explain the bonding and behaviour of a molecule completely, it does help in understanding the formation and properties of a molecule to a large extent. Writing of Lewis dot structures of molecules is, therefore, very useful. The Lewis dot structures can be written by adopting the following steps:
- The total number of electrons required for writing the structures are obtained by adding the valence electrons of the combining atoms. For example, in the $\mathrm{CH}_{4}$ molecule there are eight valence electrons available for bonding ( 4 from carbon and 4 from the four hydrogen atoms).
- For anions, each negative charge would mean addition of one electron. For cations, each positive charge would result in subtraction of one electron from the total number of valence electrons. For example, for the $CO_3^{2-}$ ion, the two negative charges indicate that there are two additional electrons than those provided by the neutral atoms. For $\mathrm{NH}_{4}^{+}$ ion, one positive charge indicates the loss of one electron from the group of neutral atoms.
- Knowing the chemical symbols of the combining atoms and having knowledge of the skeletal structure of the compound (known or guessed intelligently), it is easy to distribute the total number of electrons as bonding shared pairs between the atoms in proportion to the total bonds.
- In general the least electronegative atom occupies the central position in the molecule/ion. For example in the $\mathrm{NF}_3$ and $CO_3^{2-}$, nitrogen and carbon are the central atoms whereas fluorine and oxygen occupy the terminal positions.
- After accounting for the shared pairs of electrons for single bonds, the remaining electron pairs are either utilized for multiple bonding or remain as the lone pairs. The basic requirement being that each bonded atom gets an octet of electrons.
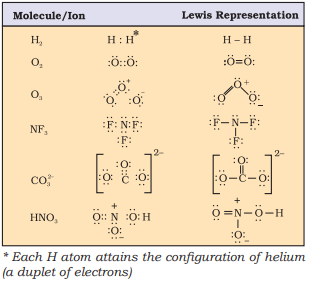
Lewis representations of a few molecules/ ions are given in Table 4.1.
Table 4.1 The Lewis Representation of Some Molecules
Problem 4.1
Write the Lewis dot structure of $\mathrm{CO}$ molecule.
Solution
Step 1. Count the total number of valence electrons of carbon and oxygen atoms. The outer (valence) shell configurations of carbon and oxygen atoms are: $2 s^{2} 2 p^{2}$ and $2 s^{2} 2 p^{4}$, respectively. The valence electrons available are $4+6=10$.
Step 2. The skeletal structure of $\mathrm{CO}$ is written as: C O
Step 3. Draw a single bond (one shared electron pair) between $\mathrm{C}$ and $\mathrm{O}$ and complete the octet on $\mathrm{O}$, the remaining two electrons are the lone pair on $\mathrm{C}$.
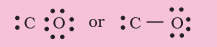
This does not complete the octet on carbon and hence we have to resort to multiple bonding (in this case a triple bond) between $\mathrm{C}$ and $\mathrm{O}$ atoms. This satisfies the octet rule condition for both atoms.
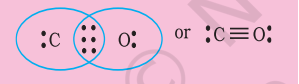
Problem 4.2
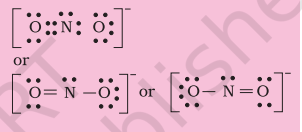
Write the Lewis structure of the nitrite ion, $\mathrm{NO}_{2}^{-}$.
Solution
Step 1. Count the total number of valence electrons of the nitrogen atom, the oxygen atoms and the additional one negative charge (equal to one electron).
$$ \begin{aligned} & \mathrm{N}\left(2 s^{2} 2 p^{3}\right), \mathrm{O}\left(2 s^{2} 2 p^{4}\right) \\ & 5+(2 \times 6)+ = 17 \text { electrons } \end{aligned} $$
Total number of electrons when one electron is deposited for unit negative charge = 17+1 = 18
Step 2. The skeletal structure of $\mathrm{NO}_{2}^{-}$is written as: $\mathrm{O} \quad \mathrm{N} \mathrm{O}$
Step 3. Draw a single bond (one shared electron pair) between the nitrogen and each of the oxygen atoms completing the octets on oxygen atoms. This, however, does not complete the octet on nitrogen if the remaining two electrons constitute lone pair on it.

Hence we have to resort to multiple bonding between nitrogen and one of the oxygen atoms (in this case a double bond). This leads to the following Lewis dot structures.
4.1.4 Formal Charge
Lewis dot structures, in general, do not represent the actual shapes of the molecules. In case of polyatomic ions, the net charge is possessed by the ion as a whole and not by a particular atom. It is, however, feasible to assign a formal charge on each atom. The formal charge of an atom in a polyatomic molecule or ion may be defined as the difference between the number of valence electrons of that atom in an isolated or free state and the number of electrons assigned to that atom in the Lewis structure. It is expressed as :

The counting is based on the assumption that the atom in the molecule owns one electron of each shared pair and both the electrons of a lone pair.
Let us consider the ozone molecule $\left(\mathrm{O}_3\right)$. The Lewis structure of $\mathrm{O}_3$ may be drawn as:
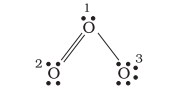
The atoms have been numbered as 1,2 and 3. The formal charge on:
- The central $\mathrm{O}$ atom marked 1 $=6-2-\frac{1}{2}(6)=+1$
- The end $\mathrm{O}$ atom marked 2 $=6-4-\frac{1}{2}(4)=0$
- The end $\mathrm{O}$ atom marked 3 $=6-6-\frac{1}{2}(2)=-1$
Hence, we represent $\mathrm{O}_{3}$ along with the formal charges as follows:
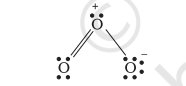
We must understand that formal charges do not indicate real charge separation within the molecule. Indicating the charges on the atoms in the Lewis structure only helps in keeping track of the valence electrons in the molecule. Formal charges help in the selection of the lowest energy structure from a number of possible Lewis structures for a given species. Generally the lowest energy structure is the one with the smallest formal charges on the atoms. The formal charge is a factor based on a pure covalent view of bonding in which electron pairs are shared equally by neighbouring atoms.
4.1.5 Limitations of the Octet Rule
The octet rule, though useful, is not universal. It is quite useful for understanding the structures of most of the organic compounds and it applies mainly to the second period elements of the periodic table. There are three types of exceptions to the octet rule.
The incomplete octet of the central atom
In some compounds, the number of electrons surrounding the central atom is less than eight. This is especially the case with elements having less than four valence electrons. Examples are $\mathrm{LiCl}, \mathrm{BeH}_2$ and $\mathrm{BCl}_3$.
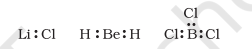
$\mathrm{Li}$, Be and B have 1, 2 and 3 valence electrons only. Some other such compounds are $\mathrm{AlCl}_3$ and $\mathrm{BF}_3$.
Odd-electron molecules
In molecules with an odd number of electrons like nitric oxide, $\mathrm{NO}$ and nitrogen dioxide, $\mathrm{NO}_2$, the octet rule is not satisfied for all the atoms
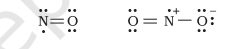
The expanded octet
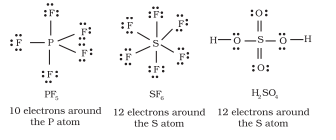
Elements in and beyond the third period of the periodic table have, apart from $3 s$ and $3 p$ orbitals, $3 d$ orbitals also available for bonding. In a number of compounds of these elements there are more than eight valence electrons around the central atom. This is termed as the expanded octet. Obviously the octet rule does not apply in such cases.
Some of the examples of such compounds are: $\mathrm{PF}_5, \mathrm{SF}_6, \mathrm{H}_2 \mathrm{SO}_4$ and a number of coordination compounds.
Interestingly, sulphur also forms many compounds in which the octet rule is obeyed. In sulphur dichloride, the $\mathrm{S}$ atom has an octet of electrons around it.
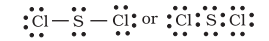
Other drawbacks of the octet theory
- It is clear that octet rule is based upon the chemical inertness of noble gases. However, some noble gases (for example xenon and krypton) also combine with oxygen and fluorine to form a number of compounds like $\mathrm{XeF}_2, \mathrm{KrF}_2, \mathrm{XeOF}_2$ etc.
- This theory does not account for the shape of molecules.
- It does not explain the relative stability of the molecules being totally silent about the energy of a molecule.
4.2 IONIC OR ELECTROVALENT BOND
From the Kössel and Lewis treatment of the formation of an ionic bond, it follows that the formation of ionic compounds would primarily depend upon:
- The ease of formation of the positive and negative ions from the respective neutral atoms;
- The arrangement of the positive and negative ions in the solid, that is, the lattice of the crystalline compound.
The formation of a positive ion involves ionization, i.e., removal of electron(s) from the neutral atom and that of the negative ion involves the addition of electron(s) to the neutral atom.
| $\mathrm{M}(\mathrm{g}) $ | $\rightarrow$ | $\mathrm{M}^{+}(\mathrm{g})+\mathrm{e}^{-} ;$ | |
| Ionization enthalpy | |||
| $\mathrm{X}(\mathrm{g})+\mathrm{e}^{-}$ | $\rightarrow$ | $\mathrm{X}^{-}(\mathrm{g}) ;$ | |
| Electron gain enthalpy | |||
| $\mathrm{M}^{+}(\mathrm{g})+\mathrm{X}^{-}(\mathrm{g}) \rightarrow$ | $\mathrm{MX}(\mathrm{s})$ |
The electron gain enthalpy, $\Delta_{e g} \boldsymbol{H}$, is the enthalpy change (Unit 3), when a gas phase atom in its ground state gains an electron. The electron gain process may be exothermic or endothermic. The ionization, on the other hand, is always endothermic. Electron affinity, is the negative of the energy change accompanying electron gain.
Obviously ionic bonds will be formed more easily between elements with comparatively low ionization enthalpies and elements with comparatively high negative value of electron gain enthalpy.
Most ionic compounds have cations derived from metallic elements and anions from non-metallic elements. The ammonium ion, $\mathrm{NH}_{4}^{+}$(made up of two non-metallic elements) is an exception. It forms the cation of a number of ionic compounds.
Ionic compounds in the crystalline state consist of orderly three-dimensional arrangements of cations and anions held together by coulombic interaction energies. These compounds crystallise in different crystal structures determined by the size of the ions, their packing arrangements and other factors. The crystal structure of sodium chloride, $\mathrm{NaCl}$ (rock salt), for example is shown below.
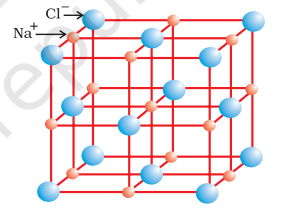
Rock salt structure
In ionic solids, the sum of the electron gain enthalpy and the ionization enthalpy may be positive but still the crystal structure gets stabilized due to the energy released in the formation of the crystal lattice. For example: the ionization enthalpy for $\mathrm{Na}^{+}(\mathrm{g})$ formation from $\mathrm{Na}(\mathrm{g})$ is $495.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$; while the electron gain enthalpy for the change $\mathrm{Cl}(\mathrm{g})+\mathrm{e}^{-} \rightarrow$ $\mathrm{Cl}^{-}(\mathrm{g})$ is, $-348.7 \mathrm{~kJ} \mathrm{~mol}^{-1}$ only. The sum of the two, $147.1 \mathrm{~kJ} \mathrm{~mol}^{-1}$ is more than compensated for by the enthalpy of lattice formation of $\mathrm{NaCl}(\mathrm{s})\left(-788 \mathrm{~kJ} \mathrm{~mol}^{-1}\right)$. Therefore, the energy released in the processes is more than the energy absorbed. Thus a qualitative measure of the stability of an ionic compound is provided by its enthalpy of lattice formation and not simply by achieving octet of electrons around the ionic species in gaseous state.
Since lattice enthalpy plays a key role in the formation of ionic compounds, it is important that we learn more about it.
4.2.1 Lattice Enthalpy
The Lattice Enthalpy of an ionic solid is defined as the energy required to completely separate one mole of a solid ionic compound into gaseous constituent ions. For example, the lattice enthalpy of $\mathrm{NaCl}$ is $788 \mathrm{~kJ} \mathrm{~mol}^{-1}$. This means that 788 $\mathrm{kJ}$ of energy is required to separate one mole of solid $\mathrm{NaCl}$ into one mole of $\mathrm{Na}^{+}(\mathrm{g})$ and one mole of $\mathrm{Cl}^{-}(\mathrm{g})$ to an infinite distance.
This process involves both the attractive forces between ions of opposite charges and the repulsive forces between ions of like charge. The solid crystal being threedimensional; it is not possible to calculate lattice enthalpy directly from the interaction of forces of attraction and repulsion only. Factors associated with the crystal geometry have to be included.
4.3 BOND PARAMETERS
4.3.1 Bond Length
Bond length is defined as the equilibrium distance between the nuclei of two bonded atoms in a molecule. Bond lengths are measured by spectroscopic, X-ray diffraction and electron-diffraction techniques about which you will learn in higher classes. Each atom of the bonded pair contributes to the bond length (Fig. 4.1). In the case of a covalent bond, the contribution from each atom is called the covalent radius of that atom.
The covalent radius is measured approximately as the radius of an atom’s core which is in contact with the core of an adjacent atom in a bonded situation. The covalent radius is half of the distance between two similar atoms joined by a covalent bond in the same molecule.
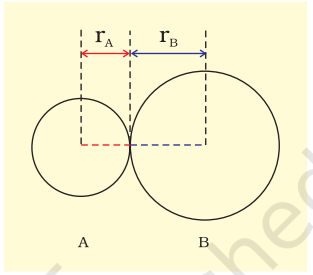
Fig. 4.1 The bond length in a covalent molecule AB. R = rA + rB (R is the bond length and rA and rB are the covalent radii of atoms A and B respectively)
The van der Waals radius represents the overall size of the atom which includes its valence shell in a nonbonded situation. Further, the van der Waals radius is half of the distance between two similar atoms in separate molecules in a solid. Covalent and van der Waals radii of chlorine are depicted in Fig. 4.2.
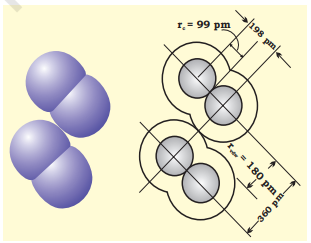
Fig. 4.2 Covalent and van der Waals radii in a chlorine molecule. The inner circles correspond to the size of the chlorine atom (rvdw and rc are van der Waals and covalent radii respectively).
Some typical average bond lengths for single, double and triple bonds are shown in Table 4.2. Bond lengths for some common molecules are given in Table 4.3.
The covalent radii of some common elements are listed in Table 4.4.
4.3.2 Bond Angle
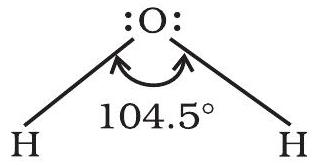
It is defined as the angle between the orbitals containing bonding electron pairs around the central atom in a molecule/complex ion. Bond angle is expressed in degree which can be experimentally determined by spectroscopic methods. It gives some idea regarding the distribution of orbitals around the central atom in a molecule/complex ion and hence it helps us in determining its shape. For example $\mathrm{H}-\mathrm{O}-\mathrm{H}$ bond angle in water can be represented as under :
4.3.3 Bond Enthalpy
It is defined as the amount of energy required to break one mole of bonds of a particular type between two atoms in a gaseous state. The unit of bond enthalpy is $\mathrm{kJ} \mathrm{mol}^{-1}$. For example, the $\mathrm{H}-\mathrm{H}$ bond enthalpy in hydrogen molecule is $435.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$.
$\mathrm{H}_2 (\mathrm{~g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{H}(\mathrm{g})$;
$\Delta_{\mathrm{a}} H^\ominus =435.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$
Similarly the bond enthalpy for molecules containing multiple bonds, for example $\mathrm{O}_2$ and $\mathrm{N}_2$ will be as under :
$\mathrm{O}_{2}(\mathrm{O}=\mathrm{O})(\mathrm{g}) \rightarrow \mathrm{O}(\mathrm{g})+\mathrm{O}(\mathrm{g}) ;$
$$ \Delta_{\mathrm{a}} H^{\ominus}=498 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
$\mathrm{N}_{2}(\mathrm{~N} \equiv \mathrm{N})(\mathrm{g}) \rightarrow \mathrm{N}(\mathrm{g})+\mathrm{N}(\mathrm{g}) ;$
$$ \Delta_{\mathrm{a}} H^{\ominus}=946.0 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
It is important that larger the bond dissociation enthalpy, stronger will be the bond in the molecule. For a heteronuclear diatomic molecules like $\mathrm{HCl}$, we have
$$ \mathrm{HCl}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{Cl}(\mathrm{g}) ; \Delta_{\mathrm{a}} \mathrm{H}^{\ominus}=431.0 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
In case of polyatomic molecules, the measurement of bond strength is more complicated. For example in case of $\mathrm{H}_{2} \mathrm{O}$ molecule, the enthalpy needed to break the two $\mathrm{O}-\mathrm{H}$ bonds is not the same.
Table 4.2 Average Bond Lengths for Some Single, Double and Triple Bonds
| Bond Type | Covalent Bond Length (pm) |
|---|---|
| $\mathrm{O}-\mathrm{H}$ | 96 |
| $\mathrm{C}-\mathrm{H}$ | 107 |
| $\mathrm{~N}-\mathrm{O}$ | 136 |
| $\mathrm{C}-\mathrm{O}$ | 143 |
| $\mathrm{C}-\mathrm{N}$ | 143 |
| $\mathrm{C}-\mathrm{C}$ | 154 |
| $\mathrm{C}=\mathrm{O}$ | 121 |
| $\mathrm{~N}=\mathrm{O}$ | 122 |
| $\mathrm{C}=\mathrm{C}$ | 133 |
| $\mathrm{C}=\mathrm{N}$ | 138 |
| $\mathrm{C} \equiv \mathrm{N}$ | 116 |
| $\mathrm{C} \equiv \mathrm{C}$ | 120 |
Table 4.3 Bond Lengths in Some Common Molecules
| Molecule | Bond Length (pm) |
|---|---|
| $\mathrm{H}_{2}(\mathrm{H}-\mathrm{H})$ | 74 |
| $\mathrm{~F}_{2}(\mathrm{~F}-\mathrm{F})$ | 144 |
| $\mathrm{Cl}_{2}(\mathrm{Cl}-\mathrm{Cl})$ | 199 |
| $\mathrm{Br}_{2}(\mathrm{Br}-\mathrm{Br})$ | 228 |
| $\mathrm{I}_{2}(\mathrm{I}-\mathrm{I})$ | 267 |
| $\mathrm{~N}_{2}(\mathrm{~N} \equiv \mathrm{N})$ | 109 |
| $\mathrm{O}_{2}(\mathrm{O}=\mathrm{O})$ | 121 |
| $\mathrm{HF}(\mathrm{H}-\mathrm{F})$ | 92 |
| $\mathrm{HCl}(\mathrm{H}-\mathrm{Cl})$ | 127 |
| $\mathrm{HBr}(\mathrm{H}-\mathrm{Br})$ | 141 |
| $\mathrm{HI}(\mathrm{H}-\mathrm{I})$ | 160 |
Table 4.4 Covalent Radii, $ \mathbf{r}_{\text {cov }} /(\mathrm{pm})$
| $\mathrm{H}$ | 37 | ||||||
|---|---|---|---|---|---|---|---|
| $\mathrm{C}$ | $77(1)$ | $\mathrm{N}$ | $74(1)$ | $\mathrm{O}$ | $66(1)$ | $\mathrm{F}$ | 64 |
| $67(2)$ | $65(2)$ | $57(2)$ | $\mathrm{Cl}$ | 99 | |||
| $60(3)$ | $55(3)$ | ||||||
| $\mathrm{P}$ | 110 | $\mathrm{~S}$ | $104(1)$ | $\mathrm{Br}$ | 114 | ||
| $95(2)$ | |||||||
| $\mathrm{As}$ | 121 | $\mathrm{Se}$ | 104 | $\mathrm{I}$ | 133 | ||
| $\mathrm{Sb}$ | 141 | $\mathrm{Te}$ | 137 |
- The values cited are for single bonds, except where otherwise indicated in parenthesis. (See also Unit 3 for periodic trends).
$\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{OH}(\mathrm{g}) ; \Delta_a H_1^\ominus=502 \mathrm{~kJ} \mathrm{~mol}^{-1}$
$\mathrm{OH}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{O}(\mathrm{g}) ; \Delta_{\mathrm{a}} H_{2}^{\ominus}=427 \mathrm{~kJ} \mathrm{~mol}^{-1}$
The difference in the $\Delta_{\mathrm{a}} H^{\ominus}$ value shows that the second $\mathrm{O}-\mathrm{H}$ bond undergoes some change because of changed chemical environment. This is the reason for some difference in energy of the same $\mathrm{O}-\mathrm{H}$ bond in different molecules like $\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}$ (ethanol) and water. Therefore in polyatomic molecules the term mean or average bond enthalpy is used. It is obtained by dividing total bond dissociation enthalpy by the number of bonds broken as explained below in case of water molecule,
$ \text { Average bond enthalpy } =\frac{502+427}{2} $
$$ =464.5 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
4.3.4 Bond Order
In the Lewis description of covalent bond, the Bond Order is given by the number of bonds between the two atoms in a molecule. The bond order, for example in $\mathrm{H}_2$ (with a single shared electron pair), in $\mathrm{O}_2$ (with two shared electron pairs) and in $\mathrm{N}_2$ (with three shared electron pairs) is $1,2,3$ respectively. Similarly in CO (three shared electron pairs between $\mathrm{C}$ and $\mathrm{O}$) the bond order is 3 . For $\mathrm{N}_2$, bond order is 3 and its $\Delta_a H^\ominus$ is $946 \mathrm{~kJ} \mathrm{~mol}^{-1}$; being one of the highest for a diatomic molecule.
Isoelectronic molecules and ions have identical bond orders; for example, $F_2$ and $\mathrm{O}_{2}^{2-}$ have bond order 1. $\mathrm{N}_2, \mathrm{CO}$ and $\mathrm{NO}^{+}$ have bond order 3.
A general correlation useful for understanding the stablities of molecules is that: with increase in bond order, bond enthalpy increases and bond length decreases.
4.3.5 Resonance Structures
It is often observed that a single Lewis structure is inadequate for the representation of a molecule in conformity with its experimentally determined parameters. For example, the ozone, $\mathrm{O}_{3}$ molecule can be equally represented by the structures I and II shown below:
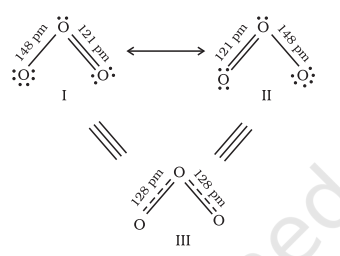
Fig. 4.3 Resonance in the O3 molecule
(structures I and II represent the two canonical forms while the structure III is the resonance hybrid)
In both structures we have a $\mathrm{O}-\mathrm{O}$ single bond and a $\mathrm{O}=\mathrm{O}$ double bond. The normal $\mathrm{O}-\mathrm{O}$ and $\mathrm{O}=\mathrm{O}$ bond lengths are $148 \mathrm{pm}$ and $121 \mathrm{pm}$ respectively. Experimentally determined oxygen-oxygen bond lengths in the $\mathrm{O}_3$ molecule are same ( $\left.128 \mathrm{pm}\right)$. Thus the oxygen-oxygen bonds in the $\mathrm{O}_3$ molecule are intermediate between a double and a single bond. Obviously, this cannot be represented by either of the two Lewis structures shown above.
The concept of resonance was introduced to deal with the type of difficulty experienced in the depiction of accurate structures of molecules like $\mathrm{O}_3$. According to the concept of resonance, whenever a single Lewis structure cannot describe a molecule accurately, a number of structures with similar energy, positions of nuclei, bonding and non-bonding pairs of electrons are taken as the canonical structures of the hybrid which describes the molecule accurately. Thus for $\mathrm{O}_3$, the two structures shown above constitute the canonical structures or resonance structures and their hybrid i.e., the III structure represents the structure of $\mathrm{O}_3$ more accurately. This is also called resonance hybrid. Resonance is represented by a double headed arrow.
Some of the other examples of resonance structures are provided by the carbonate ion and the carbon dioxide molecule.
Problem 4.3
Explain the structure of $\mathrm{CO}_{3}^{2-}$ ion in terms of resonance.
Solution
The single Lewis structure based on the presence of two single bonds and one double bond between carbon and oxygen atoms is inadequate to represent the molecule accurately as it represents unequal bonds. According to the experimental findings, all carbon to oxygen bonds in $\mathrm{CO}_{3}^{2-}$ are equivalent. Therefore the carbonate ion is best described as a resonance hybrid of the canonical forms I, II, and III shown below.
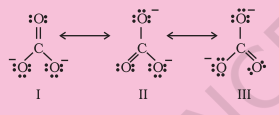
Fig. 4.4 Resonance in $\mathrm{CO}_{3}^{2-}, \mathrm{I}$, II and III represent the three canonical forms.
Problem 4.4
Explain the structure of $\mathrm{CO}_{2}$ molecule.
Solution
The experimentally determined carbon to oxygen bond length in $\mathrm{CO}_2$ is $115 \mathrm{pm}$. The lengths of a normal carbon to oxygen double bond $(\mathrm{C}=\mathrm{O})$ and carbon to oxygen triple bond $(\mathrm{C} \equiv \mathrm{O})$ are $121 \mathrm{pm}$ and $110 \mathrm{pm}$ respectively. The carbon-oxygen bond lengths in $\mathrm{CO}_2(115 \mathrm{pm})$ lie between the values for $\mathrm{C}=\mathrm{O}$ and $\mathrm{C} \equiv \mathrm{O}$. Obviously, a single Lewis structure cannot depict this position and it becomes necessary to write more than one Lewis structures and to consider that the structure of $\mathrm{CO}_2$ is best described as a hybrid of the canonical or resonance forms I, II and III.

Fig. 4.5 Resonance in $\mathrm{CO}_{2}$ molecule, I, II and III represent the three canonical forms.
In general, it may be stated that
- Resonance stabilizes the molecule as the energy of the resonance hybrid is less than the energy of any single cannonical structure; and,
- Resonance averages the bond characteristics as a whole.
Thus the energy of the $\mathrm{O}_{3}$ resonance hybrid is lower than either of the two cannonical froms I and II (Fig. 4.3).
Many misconceptions are associated with resonance and the same need to be dispelled. You should remember that:
- The cannonical forms have no real existence.
- The molecule does not exist for a certain fraction of time in one cannonical form and for other fractions of time in other cannonical forms.
- There is no such equilibrium between the cannonical forms as we have between tautomeric forms (keto and enol) in tautomerism.
- The molecule as such has a single structure which is the resonance hybrid of the cannonical forms and which cannot as such be depicted by a single Lewis structure.
4.3.6 Polarity of Bonds
The existence of a hundred percent ionic or covalent bond represents an ideal situation. In reality no bond or a compound is either completely covalent or ionic. Even in case of covalent bond between two hydrogen atoms, there is some ionic character.
When covalent bond is formed between two similar atoms, for example in $\mathrm{H}_2, \mathrm{O}_2$, $\mathrm{Cl}_2, \mathrm{~N}_2$ or $\mathrm{F}_2$, the shared pair of electrons is equally attracted by the two atoms. As a result electron pair is situated exactly between the two identical nuclei. The bond so formed is called nonpolar covalent bond. Contrary to this in case of a heteronuclear molecule like $\mathrm{HF}$, the shared electron pair between the two atoms gets displaced more towards fluorine since the electronegativity of fluorine (Unit 3) is far greater than that of hydrogen. The resultant covalent bond is a polar covalent bond.
As a result of polarisation, the molecule possesses the dipole moment (depicted below) which can be defined as the product of the magnitude of the charge and the distance between the centres of positive and negative charge. It is usually designated by a Greek letter ’ $\mu$ ‘. Mathematically, it is expressed as follows :
Dipole moment $(\mu)=$ charge $(Q) \times$ distance of separation ( $\mathrm{r}$ )
Dipole moment is usually expressed in Debye units (D). The conversion factor is
$$ 1 \mathrm{D}=3.33564 \times 10^{-30} \mathrm{C} \mathrm{m} $$
where $\mathrm{C}$ is coulomb and $\mathrm{m}$ is meter.
Further dipole moment is a vector quantity and by convention it is depicted by a small arrow with tail on the negative centre and head pointing towards the positive centre. But in chemistry presence of dipole moment is represented by the crossed arrow $(\rightarrow)$ put on Lewis structure of the molecule. The cross is on positive end and arrow head is on negative end. For example the dipole moment of HF may be represented as :
$$ \stackrel{+}{\mathrm{H} \longrightarrow} \underset{\because}{*}: $$
This arrow symbolises the direction of the shift of electron density in the molecule. Note that the direction of crossed arrow is opposite to the conventional direction of dipole moment vector
Peter Debye, the Dutch chemist received Nobel prize in 1936 for his work on X-ray diffraction and dipole moments. The magnitude of the dipole moment is given in Debye units in order to honour him.

In case of polyatomic molecules the dipole moment not only depend upon the individual dipole moments of bonds known as bond dipoles but also on the spatial arrangement of various bonds in the molecule. In such case, the dipole moment of a molecule is the vector sum of the dipole moments of various bonds. For example in $\mathrm{H}_{2} \mathrm{O}$ molecule, which has a bent structure, the two $\mathrm{O}-\mathrm{H}$ bonds are oriented at an angle of $104.5^{\circ}$. Net dipole moment of $6.17 \times 10^{-30} \mathrm{C} \mathrm{m} \mathrm{(1D} \mathrm{=} 3.33564$ $\times 10^{-30} \mathrm{C} \mathrm{m}$ ) is the resultant of the dipole moments of two $\mathrm{O}-\mathrm{H}$ bonds.
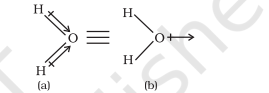
Net Dipole moment, $\mu=1.85 \mathrm{D}$
$=1.85 \times 3.33564 \times 10^{-30} \mathrm{C} \mathrm{m}=6.17 \times 10^{-30} \mathrm{C} \mathrm{m}$
The dipole moment in case of $\mathrm{BeF}_{2}$ is zero. This is because the two equal bond dipoles point in opposite directions and cancel the effect of each other.

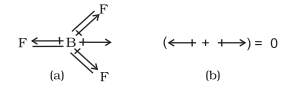
In tetra-atomic molecule, for example in $\mathrm{BF}_{3}$, the dipole moment is zero although the $\mathrm{B}-\mathrm{F}$ bonds are oriented at an angle of $120^{\circ}$ to one another, the three bond moments give a net sum of zero as the resultant of any two is equal and opposite to the third.
$\mathrm{BF}_3$ molecule; representation of (a) bond dipoles and (b) total dipole moment
Let us study an interesting case of $\mathrm{NH}_3$ and $\mathrm{NF}_3$ molecule. Both the molecules have pyramidal shape with a lone pair of electrons on nitrogen atom. Although fluorine is more electronegative than nitrogen, the resultant dipole moment of $\mathrm{NH}_3\left(4.90 \times 10^{-30} \mathrm{C} \mathrm{m}\right)$ is greater than that of $\mathrm{NF}_3\left(0.8 \times 10^{-30} \mathrm{C} \mathrm{m}\right)$. This is because, in case of $\mathrm{NH}_3$ the orbital dipole due to lone pair is in the same direction as the resultant dipole moment of the $\mathrm{N}-\mathrm{H}$ bonds, whereas in $\mathrm{NF}_3$ the orbital dipole is in the direction opposite to the resultant dipole moment of the three N-F bonds. The orbital dipole because of lone pair decreases the effect of the resultant $\mathrm{N}-\mathrm{F}$ bond moments, which results in the low dipole moment of $\mathrm{NF}_3$ as represented below :

Dipole moments of some molecules are shown in Table 4.5.
Just as all the covalent bonds have some partial ionic character, the ionic bonds also have partial covalent character. The partial covalent character of ionic bonds was discussed by Fajans in terms of the following rules:
- The smaller the size of the cation and the larger the size of the anion, the greater the covalent character of an ionic bond.
- The greater the charge on the cation, the greater the covalent character of the ionic bond.
- For cations of the same size and charge, the one, with electronic configuration $(n-1) d^{n} n s^{\circ}$, typical of transition metals, is more polarising than the one with a noble gas configuration, $n s^{2} n p^{6}$, typical of alkali and alkaline earth metal cations.
The cation polarises the anion, pulling the electronic charge toward itself and thereby increasing the electronic charge between the two. This is precisely what happens in a covalent bond, i.e., buildup of electron charge density between the nuclei. The polarising power of the cation, the polarisability of the anion and the extent of distortion (polarisation) of anion are the factors, which determine the per cent covalent character of the ionic bond.
4.4 THE VALENCE SHELL ELECTRON PAIR REPULSION (VSEPR) THEORY
As already explained, Lewis concept is unable to explain the shapes of molecules. This theory provides a simple procedure to predict the shapes of covalent molecules. Sidgwick and Powell in 1940, proposed a simple theory based on the repulsive interactions of the electron pairs in the valence shell of the atoms. It was further developed and redefined by Nyholm and Gillespie (1957).
Table 4.5 Dipole Moments of Selected Molecules
| Type of Molecule | Example | Dipole Moment, $\boldsymbol{\mu}(\mathbf{D})$ |
Geometry |
|---|---|---|---|
| Molecule $(\mathbf{A B})$ | $\mathrm{HF}$ | 1.78 | linear |
| $\mathrm{HCl}$ | 1.07 | linear | |
| $\mathrm{HBr}$ | 0.79 | linear | |
| $\mathrm{Hl}$ | 0.38 | linear | |
| $\mathrm{H}_{2}$ | 0 | linear | |
| Molecule $\left(\mathbf{A B}_{\mathbf{2}}\right)$ | $\mathrm{H}_{2} \mathrm{O}$ | 1.85 | bent |
| $\mathrm{H}_{2} \mathrm{~S}$ | 0.95 | bent | |
| $\mathrm{CO}_{2}$ | 0 | linear | |
| Molecule $\left(\mathbf{A B}_{3}\right)$ | $\mathrm{NH}_{3}$ | 1.47 | trigonal-pyramidal |
| $\mathrm{NF}_{3}$ | 0.23 | trigonal-pyramidal | |
| $\mathrm{BF}_{3}$ | 0 | trigonal-planar | |
| Molecule $\left(\mathbf{A B}_{\mathbf{4}}\right)$ | $\mathrm{CH}_{4}$ | 0 | tetrahedral |
| $\mathrm{CHCl}_{3}$ | 1.04 | tetrahedral | |
| $\mathrm{CCl}_{4}$ | 0 | tetrahedral |
The main postulates of VSEPR theory are as follows:
- The shape of a molecule depends upon the number of valence shell electron pairs (bonded or nonbonded) around the central atom.
- Pairs of electrons in the valence shell repel one another since their electron clouds are negatively charged.
- These pairs of electrons tend to occupy such positions in space that minimise repulsion and thus maximise distance between them.
- The valence shell is taken as a sphere with the electron pairs localising on the spherical surface at maximum distance from one another.
- A multiple bond is treated as if it is a single electron pair and the two or three electron pairs of a multiple bond are treated as a single super pair.
- Where two or more resonance structures can represent a molecule, the VSEPR model is applicable to any such structure.
The repulsive interaction of electron pairs decrease in the order:
Lone pair (lp) - Lone pair (lp) > Lone pair (lp) - Bond pair (bp) > Bond pair (bp) Bond pair (bp)
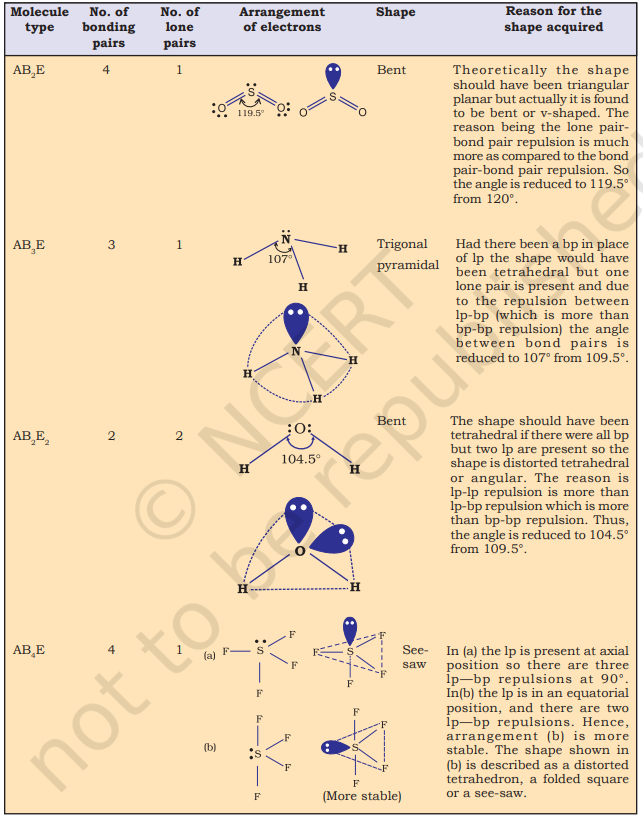
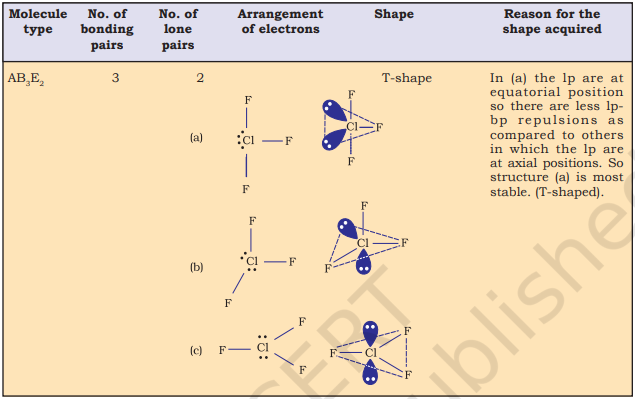
Nyholm and Gillespie (1957) refined the VSEPR model by explaining the important difference between the lone pairs and bonding pairs of electrons. While the lone pairs are localised on the central atom, each bonded pair is shared between two atoms. As a result, the lone pair electrons in a molecule occupy more space as compared to the bonding pairs of electrons. This results in greater repulsion between lone pairs of electrons as compared to the lone pair - bond pair and bond pair bond pair repulsions. These repulsion effects result in deviations from idealised shapes and alterations in bond angles in molecules.
For the prediction of geometrical shapes of molecules with the help of VSEPR theory, it is convenient to divide molecules into two categories as (i) molecules in which the central atom has no lone pair and (ii) molecules in which the central atom has one or more lone pairs.
Table 4.6 (page114) shows the arrangement of electron pairs about a central atom A (without any lone pairs) and geometries of some molecules/ions of the type AB. Table 4.7 (page 115) shows shapes of some simple molecules and ions in which the central atom has one or more lone pairs. Table 4.8 (page 116) explains the reasons for the distortions in the geometry of the molecule.
As depicted in Table 4.6, in the compounds of $\mathrm{AB}_2, \mathrm{AB}_3, \mathrm{AB}_4, \mathrm{AB}_5$ and $\mathrm{AB}_6$, the arrangement of electron pairs and the $\mathrm{B}$ atoms around the central atom A are : linear, trigonal planar, tetrahedral, trigonal-bipyramidal and octahedral, respectively. Such arrangement can be seen in the molecules like $\mathrm{BF}_3\left(\mathrm{AB}_3\right), \mathrm{CH}_4\left(\mathrm{AB}_4\right)$ and $\mathrm{PCl}_5\left(\mathrm{AB}_5\right)$ as depicted below by their ball and stick models.
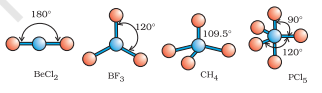
Fig. 4.8 The shapes of molecules in which central atom has no lone pair
The VSEPR Theory is able to predict geometry of a large number of molecules, especially the compounds of $p$-block elements accurately. It is also quite successful in determining the geometry quite-accurately even when the energy difference between possible structures is very small. The theoretical basis of the VSEPR theory regarding the effects of electron pair repulsions on molecular shapes is not clear and continues to be a subject of doubt and discussion.
Table 4.6 Geometry of Molecules in which the Central Atom has No Lone Pair of Electrons
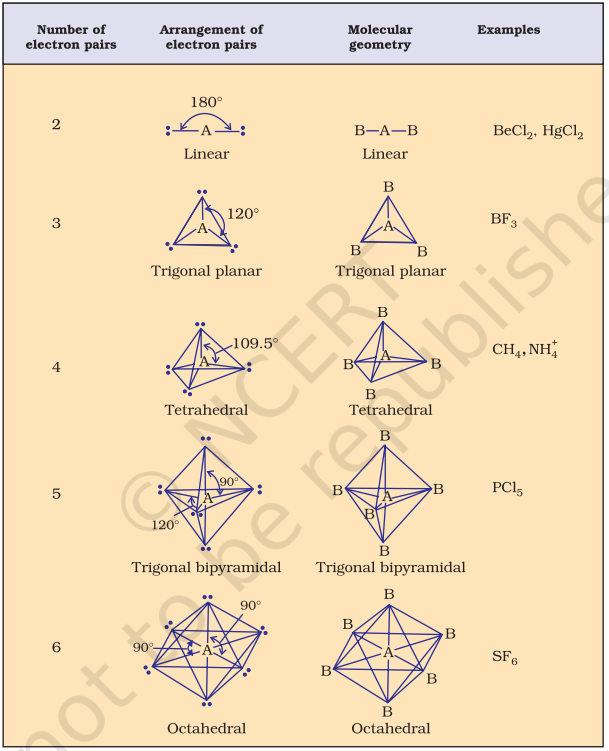
Table 4.7 Shape (geometry) of Some Simple Molecules/Ions with Central Ions having One or More Lone Pairs of Electrons(E)
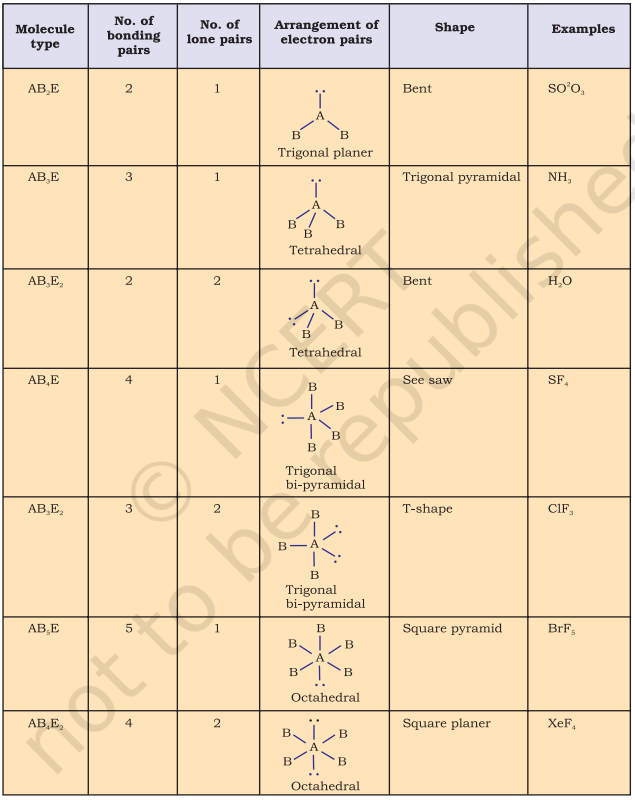
Table 4.8 Shapes of Molecules containing Bond Pair and Lone Pair
4.5 VALENCE BOND THEORY
As we know that Lewis approach helps in writing the structure of molecules but it fails to explain the formation of chemical bond. It also does not give any reason for the difference in bond dissociation enthalpies and bond lengths in molecules like $\mathrm{H}_2(435.8 \mathrm{~kJ}$ $\left.\mathrm{mol}^{-1}, 74 \mathrm{pm}\right)$ and $\mathrm{F}_2\left(155 \mathrm{~kJ} \mathrm{~mol}^{-1}, 144 \mathrm{pm}\right)$, although in both the cases a single covalent bond is formed by the sharing of an electron pair between the respective atoms. It also gives no idea about the shapes of polyatomic molecules.
Similarly the VSEPR theory gives the geometry of simple molecules but theoretically, it does not explain them and also it has limited applications. To overcome these limitations the two important theories based on quantum mechanical principles are introduced. These are valence bond (VB) theory and molecular orbital (MO) theory.
Valence bond theory was introduced by Heitler and London (1927) and developed further by Pauling and others. A discussion of the valence bond theory is based on the knowledge of atomic orbitals, electronic configurations of elements (Units 2), the overlap criteria of atomic orbitals, the hybridization of atomic orbitals and the principles of variation and superposition. A rigorous treatment of the VB theory in terms of these aspects is beyond the scope of this book. Therefore, for the sake of convenience, valence bond theory has been discussed in terms of qualitative and non-mathematical treatment only. To start with, let us consider the formation of hydrogen molecule which is the simplest of all molecules.
Consider two hydrogen atoms A and B approaching each other having nuclei $\mathrm{N}_{\mathrm{A}}$ and $N_B$ and electrons present in them are represented by $e_A$ and $e_B$. When the two atoms are at large distance from each other, there is no interaction between them. As these two atoms approach each other, new attractive and repulsive forces begin to operate.
Attractive forces arise between:
(i) nucleus of one atom and its own electron that is $N_{A}-e_{A}$ and $N_{B}-e_{B}$.
(ii) nucleus of one atom and electron of other atom i.e., $N_{A}-e_{B}, N_{B}-e_{A}$.
Similarly repulsive forces arise between
(i) electrons of two atoms like $e_{A}-e_{B}$,
(ii) nuclei of two atoms $N_{A}-N_{B}$.
Attractive forces tend to bring the two atoms close to each other whereas repulsive forces tend to push them apart (Fig. 4.7).

Fig. 4.7 Forces of attraction and repulsion during the formation of H2 molecule
Experimentally it has been found that the magnitude of new attractive force is more than the new repulsive forces. As a result, two atoms approach each other and potential energy decreases. Ultimately a stage is reached where the net force of attraction balances the force of repulsion and system acquires minimum energy. At this stage two hydrogen atoms are said to be bonded together to form a stable molecule having the bond length of $74 \mathrm{pm}$.
Since the energy gets released when the bond is formed between two hydrogen atoms, the hydrogen molecule is more stable than that of isolated hydrogen atoms. The energy so released is called as bond enthalpy, which is corresponding to minimum in the curve depicted in Fig. 4.8. Conversely, $435.8 \mathrm{~kJ}$ of energy is required to dissociate one mole of $\mathrm{H}_{2}$ molecule.
$\mathrm{H}_{2}(\mathrm{~g})+435.8 \mathrm{~kJ} \mathrm{~mol}^{-1} \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{H}(\mathrm{g})$

Fig. 4.8 The potential energy curve for the formation of H2 molecule as a function of internuclear distance of the H atoms. The minimum in the curve corresponds to the most stable state of $H_2$.
4.5.1 Orbital Overlap Concept
In the formation of hydrogen molecule, there is a minimum energy state when two hydrogen atoms are so near that their atomic orbitals undergo partial interpenetration. This partial merging of atomic orbitals is called overlapping of atomic orbitals which results in the pairing of electrons. The extent of overlap decides the strength of a covalent bond. In general, greater the overlap the stronger is the bond formed between two atoms. Therefore, according to orbital overlap concept, the formation of a covalent bond between two atoms results by pairing of electrons present in the valence shell having opposite spins.
4.5.2 Directional Properties of Bonds
As we have already seen, the covalent bond is formed by overlapping of atomic orbitals. The molecule of hydrogen is formed due to the overlap of $1 s$-orbitals of two $\mathrm{H}$ atoms.
In case of polyatomic molecules like $\mathrm{CH}_4$, $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$, the geometry of the molecules is also important in addition to the bond formation. For example why is it so that $\mathrm{CH}_4$ molecule has tetrahedral shape and $\mathrm{HCH}$ bond angles are $109.5^{\circ}$ ? Why is the shape of $\mathrm{NH}_3$ molecule pyramidal ?
The valence bond theory explains the shape, the formation and directional properties of bonds in polyatomic molecules like $\mathrm{CH}_4$, $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$, etc. in terms of overlap and hybridisation of atomic orbitals.
4.5.3 Overlapping of Atomic Orbitals
When orbitals of two atoms come close to form bond, their overlap may be positive, negative or zero depending upon the sign (phase) and direction of orientation of amplitude of orbital wave function in space (Fig. 4.9). Positive and negative sign on boundary surface diagrams in the Fig. 4.9 show the sign (phase) of orbital wave function and are not related to charge. Orbitals forming bond should have same sign (phase) and orientation in space. This is called positive overlap. Various overlaps of $s$ and $p$ orbitals are depicted in Fig. 4.9.
The criterion of overlap, as the main factor for the formation of covalent bonds applies uniformly to the homonuclear/heteronuclear diatomic molecules and polyatomic molecules. We know that the shapes of $\mathrm{CH}_4, \mathrm{NH}_3$, and $\mathrm{H}_2 \mathrm{O}$ molecules are tetrahedral, pyramidal and bent respectively. It would be therefore interesting to use VB theory to find out if these geometrical shapes can be explained in terms of the orbital overlaps.
Let us first consider the $CH_4$ (methane) molecule. The electronic configuration of carbon in its ground state is $[\mathrm{He}] 2 s^2 2 p^2$ which in the excited state becomes $[\mathrm{He}] 2 s^1 2 p_{\mathrm{x}}^1$ $2 p_{\mathrm{y}}^1$ $2 p_z^1$. The energy required for this excitation is compensated by the release of energy due to overlap between the orbitals of carbon and the hydrogen.
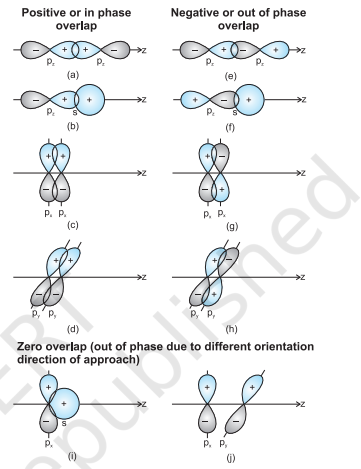
Fig.4.9 Positive, negative and zero overlaps of s and p atomic orbitals
The four atomic orbitals of carbon, each with an unpaired electron can overlap with the $1 \mathrm{~s}$ orbitals of the four $\mathrm{H}$ atoms which are also singly occupied. This will result in the formation of four $\mathrm{C}-\mathrm{H}$ bonds. It will, however, be observed that while the three $\mathrm{p}$ orbitals of carbon are at $90^{\circ}$ to one another, the $\mathrm{HCH}$ angle for these will also be $90^{\circ}$. That is three $\mathrm{C}-\mathrm{H}$ bonds will be oriented at $90^{\circ}$ to one another. The $2 \mathrm{~s}$ orbital of carbon and the $1 \mathrm{~s}$ orbital of $\mathrm{H}$ are spherically symmetrical and they can overlap in any direction. Therefore the direction of the fourth $\mathrm{C}-\mathrm{H}$ bond cannot be ascertained. This description does not fit in with the tetrahedral $\mathrm{HCH}$ angles of $109.5^{\circ}$. Clearly, it follows that simple atomic orbital overlap does not account for the directional characteristics of bonds in $\mathrm{CH}_4$. Using similar procedure and arguments, it can be seen that in the case of $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ molecules, the $\mathrm{HNH}$ and $\mathrm{HOH}$ angles should be $90^{\circ}$. This is in disagreement with the actual bond angles of $107^{\circ}$ and $104.5^{\circ}$ in the $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ molecules respectively.
4.5.4 Types of Overlapping and Nature of Covalent Bonds
The covalent bond may be classified into two types depending upon the types of overlapping:
(i) Sigma( $\sigma$ ) bond, and (ii) pi( $\pi$ ) bond
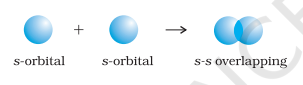
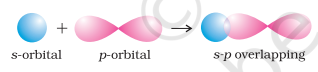
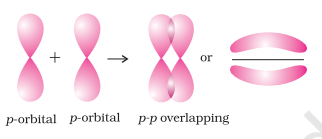
(i) Sigma( $\sigma$ ) bond : This type of covalent bond is formed by the end to end (headon) overlap of bonding orbitals along the internuclear axis. This is called as head on overlap or axial overlap. This can be formed by any one of the following types of combinations of atomic orbitals.
- s-s overlapping : In this case, there is overlap of two half filled s-orbitals along the internuclear axis as shown below :
- s-p overlapping: This type of overlap occurs between half filled $s$-orbitals of one atom and half filled $p$-orbitals of another atom.
- $\boldsymbol{p}-\boldsymbol{p}$ overlapping : This type of overlap takes place between half filled $p$-orbitals of the two approaching atoms.

(ii) pi( $\pi$ ) bond : In the formation of $\pi$ bond the atomic orbitals overlap in such a way that their axes remain parallel to each other and perpendicular to the internuclear axis. The orbitals formed due to sidewise overlapping consists of two saucer type charged clouds above and below the plane of the participating atoms.
4.5.5 Strength of Sigma and pi Bonds
Basically the strength of a bond depends upon the extent of overlapping. In case of sigma bond, the overlapping of orbitals takes place to a larger extent. Hence, it is stronger as compared to the pi bond where the extent of overlapping occurs to a smaller extent. Further, it is important to note that in the formation of multiple bonds between two atoms of a molecule, pi bond(s) is formed in addition to a sigma bond.
4.6 HYBRIDISATION
In order to explain the characteristic geometrical shapes of polyatomic molecules like $\mathrm{CH}_4, \mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ etc., Pauling introduced the concept of hybridisation. According to him the atomic orbitals combine to form new set of equivalent orbitals known as hybrid orbitals. Unlike pure orbitals, the hybrid orbitals are used in bond formation. The phenomenon is known as hybridisation which can be defined as the process of intermixing of the orbitals of slightly different energies so as to redistribute their energies, resulting in the formation of new set of orbitals of equivalent energies and shape. For example when one $2 s$ and three $2 p$-orbitals of carbon hybridise, there is the formation of four new $s p^{3}$ hybrid orbitals.
Salient features of hybridisation: The main features of hybridisation are as under :
1. The number of hybrid orbitals is equal to the number of the atomic orbitals that get hybridised.
2. The hybridised orbitals are always equivalent in energy and shape.
3. The hybrid orbitals are more effective in forming stable bonds than the pure atomic orbitals.
4. These hybrid orbitals are directed in space in some preferred direction to have minimum repulsion between electron pairs and thus a stable arrangement. Therefore, the type of hybridisation indicates the geometry of the molecules.
Important conditions for hybridisation
(i) The orbitals present in the valence shell of the atom are hybridised.
(ii) The orbitals undergoing hybridisation should have almost equal energy.
(iii) Promotion of electron is not essential condition prior to hybridisation.
(iv) It is not necessary that only half filled orbitals participate in hybridisation. In some cases, even filled orbitals of valence shell take part in hybridisation.
4.6.1 Types of Hybridisation
There are various types of hybridisation involving $s, p$ and $d$ orbitals. The different types of hybridisation are as under:
(I) sp hybridisation: This type of hybridisation involves the mixing of one $s$ and one $p$ orbital resulting in the formation of two equivalent $s p$ hybrid orbitals. The suitable orbitals for $s p$ hybridisation are $s$ and $p_{z}$, if the hybrid orbitals are to lie along the $z$-axis. Each $s p$ hybrid orbitals has $50 %$ s-character and $50 % p$-character. Such a molecule in which the central atom is $s p$-hybridised and linked directly to two other central atoms possesses linear geometry. This type of hybridisation is also known as diagonal hybridisation.
The two $s p$ hybrids point in the opposite direction along the $z$-axis with projecting positive lobes and very small negative lobes, which provides more effective overlapping resulting in the formation of stronger bonds.
Example of molecule having $s p$ hybridisation
$\mathbf{B e C l}_{2}$ : The ground state electronic configuration of Be is $1 s^{2} 2 s^{2}$. In the exited state one of the $2 \mathrm{~s}$-electrons is promoted to vacant $2 p$ orbital to account for its bivalency. One $2 s$ and one $2 p$-orbital gets hybridised to form two $s p$ hybridised orbitals. These two $s p$ hybrid orbitals are oriented in opposite direction forming an angle of $180^{\circ}$. Each of the $s p$ hybridised orbital overlaps with the $2 p$-orbital of chlorine axially and form two Be$\mathrm{Cl}$ sigma bonds. This is shown in Fig. 4.10.
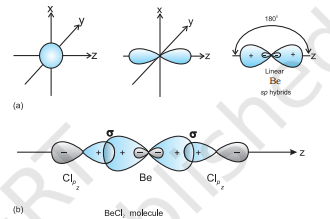
Fig.4.10 (a) Formation of sp hybrids from s and p orbitals; (b) Formation of the linear $BeCl_2$ molecule
(II) $\boldsymbol{s p}^{2}$ hybridisation : In this hybridisation there is involvement of one $s$ and two $p$-orbitals in order to form three equivalent $s p^{2}$ hybridised orbitals. For example, in $\mathrm{BCl} _{3}$ molecule, the ground state electronic configuration of central boron atom is $1 s^{2} 2 s^{2} 2 p^{1}$. In the excited state, one of the $2 s$ electrons is promoted to vacant $2 p$ orbital as a result boron has three unpaired electrons. These three orbitals (one $2 s$ and two $2 p$ ) hybridise to form three $s p^{2}$ hybrid orbitals. The three hybrid orbitals so formed are oriented in a trigonal planar arrangement and overlap with $2 p$ orbitals of chlorine to form three $\mathrm{B}-\mathrm{Cl}$ bonds. Therefore, in $\mathrm{BCl} _{3}$ (Fig. 4.11), the geometry is trigonal planar with $\mathrm{ClBCl}$ bond angle of $120^{\circ}$.
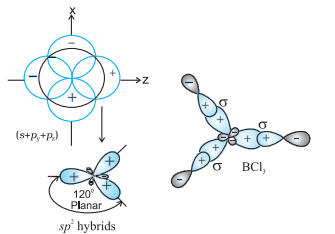
Fig.4.11 Formation of $sp_2$ hybrids and the $BCl_3$ molecule
(III) $\boldsymbol{s p}^{3}$ hybridisation: This type of hybridisation can be explained by taking the example of $\mathrm{CH}_{4}$ molecule in which there is mixing of one s-orbital and three $p$-orbitals of the valence shell to form four $s p^{3}$ hybrid orbital of equivalent energies and shape. There is $25 % s$-character and $75 % p$-character in each $s p^{3}$ hybrid orbital. The four $s p^{3}$ hybrid orbitals so formed are directed towards the four corners of the tetrahedron. The angle between $s p^{3}$ hybrid orbital is $109.5^{\circ}$ as shown in Fig. 4.12.
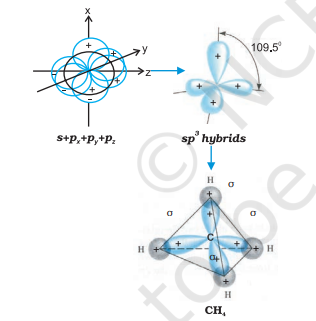
Fig.4.12 Formation of sp3 hybrids by the combination of s, $p_x$, $p_y$ and $p_z$ atomic orbitals of carbon and the formation of $CH_4$ molecule
The structure of $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ molecules can also be explained with the help of $s p^{3}$ hybridisation. In $\mathrm{NH}_3$, the valence shell (outer) electronic configuration of nitrogen in the ground state is $2 S^{2} 2 p_x^{1} 2 p_y^{1} 2 p_z^{1}$ having three unpaired electrons in the $s p^{3}$ hybrid orbitals and a lone pair of electrons is present in the fourth one. These three hybrid orbitals overlap with $1 \mathrm{~s}$ orbitals of hydrogen atoms to form three $\mathrm{N}-\mathrm{H}$ sigma bonds. We know that the force of repulsion between a lone pair and a bond pair is more than the force of repulsion between two bond pairs of electrons. The molecule thus gets distorted and the bond angle is reduced to $107^{\circ}$ from $109.5^{\circ}$. The geometry of such a molecule will be pyramidal as shown in Fig. 4.13.
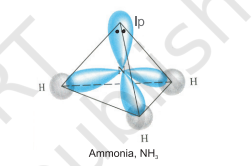
Fig.4.13 Formation of $NH_3$ molecule
In case of $\mathrm{H}_{2} \mathrm{O}$ molecule, the four oxygen orbitals (one $2 s$ and three $2 p$ ) undergo $s p^{3}$ hybridisation forming four $s p^{3}$ hybrid orbitals out of which two contain one electron each and the other two contain a pair of electrons. These four $s p^{3}$ hybrid orbitals acquire a tetrahedral geometry, with two corners occupied by hydrogen atoms while the other two by the lone pairs. The bond angle in this case is reduced to $104.5^{\circ}$ from $109.5^{\circ}$ (Fig. 4.14) and the molecule thus acquires a V-shape or angular geometry.
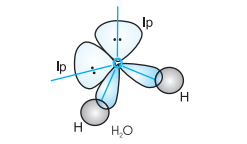
Fig.4.14 Formation of $H_2 O$ molecule
4.6.2 Other Examples of $s p^{3}, s p^{2}$ and $s p$ Hybridisation
sp $^{3}$ Hybridisation in $\mathrm{C}_2 \mathrm{H}_6$ molecule: In ethane molecule both the carbon atoms assume $s p^{3}$ hybrid state. One of the four $s p^{3}$ hybrid orbitals of carbon atom overlaps axially with similar orbitals of other atom to form $s p^{3}-s p^{3}$ sigma bond while the other three hybrid orbitals of each carbon atom are used in forming $s p^{3}-s$ sigma bonds with hydrogen atoms as discussed in section 4.6.1(iii). Therefore in ethane $\mathrm{C}-\mathrm{C}$ bond length is 154 $\mathrm{pm}$ and each $\mathrm{C}-\mathrm{H}$ bond length is $109 \mathrm{pm}$.
$\boldsymbol{s p}^{2}$ Hybridisation in $\mathbf{C}_2 \boldsymbol{H}_4$ : In the formation of ethene molecule, one of the $s p^2$ hybrid orbitals of carbon atom overlaps axially with $s p^2$ hybridised orbital of another carbon atom to form $\mathrm{C}-\mathrm{C}$ sigma bond. While the other two $s p^{2}$ hybrid orbitals of each carbon atom are used for making $s p^2-s$ sigma bond with two hydrogen atoms. The unhybridised orbital ($2 p_x$ or $2 p_y$ ) of one carbon atom overlaps sidewise with the similar orbital of the other carbon atom to form weak $\pi$ bond, which consists of two equal electron clouds distributed above and below the plane of carbon and hydrogen atoms.
Thus, in ethene molecule, the carboncarbon bond consists of one $s p^{2}-s p^{2}$ sigma bond and one pi $(\pi)$ bond between $p$ orbitals which are not used in the hybridisation and are perpendicular to the plane of molecule; the bond length $134 \mathrm{pm}$. The $\mathrm{C}-\mathrm{H}$ bond is $s p^{2}-\mathrm{s}$ sigma with bond length $108 \mathrm{pm}$. The $\mathrm{H}-\mathrm{C}-\mathrm{H}$ bond angle is $117.6^{\circ}$ while the $\mathrm{H}-\mathrm{C}-\mathrm{C}$ angle is $121^{\circ}$. The formation of sigma and pi bonds in ethene is shown in Fig. 4.15.
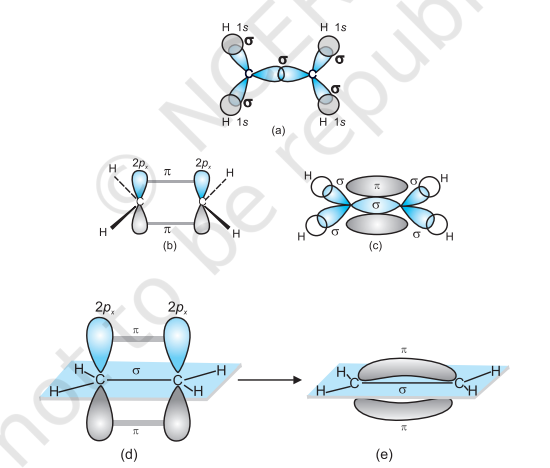
Fig. 4.15 Formation of sigma and pi bonds in ethene
sp Hybridisation in $\mathbf{C}_2 \mathbf{H}_2$ : In the formation of ethyne molecule, both the carbon atoms undergo $s p$-hybridisation having two unhybridised orbital i.e., $2 p_y$ and $2 p_x$.
One $s p$ hybrid orbital of one carbon atom overlaps axially with $s p$ hybrid orbital of the other carbon atom to form $\mathrm{C}-\mathrm{C}$ sigma bond, while the other hybridised orbital of each carbon atom overlaps axially with the half filled $s$ orbital of hydrogen atoms forming $\sigma$ bonds. Each of the two unhybridised $p$ orbitals of both the carbon atoms overlaps sidewise to form two $\pi$ bonds between the carbon atoms. So the triple bond between the two carbon atoms is made up of one sigma and two pi bonds as shown in Fig. 4.16.

Fig.4.16 Formation of sigma and pi bonds in ethyne
4.6.3 Hybridisation of Elements involving d Orbitals
The elements present in the third period contain $d$ orbitals in addition to $s$ and $p$ orbitals. The energy of the $3 d$ orbitals are comparable to the energy of the $3 s$ and $3 p$ orbitals. The energy of $3 d$ orbitals are also comparable to those of $4 s$ and $4 p$ orbitals. As a consequence the hybridisation involving either $3 s, 3 p$ and $3 d$ or $3 d, 4 s$ and $4 p$ is possible. However, since the difference in energies of $3 p$ and $4 s$ orbitals is significant, no hybridisation involving $3 p, 3 d$ and $4 s$ orbitals is possible.
The important hybridisation schemes involving $s, p$ and $d$ orbitals are summarised below:
(i) Formation of $\mathrm{PCl}_{5}\left(\mathrm{sp}^{3} \mathrm{~d}\right.$ hybridisation): The ground state and the excited state outer electronic configurations of phosphorus $(Z=15)$ are represented below.
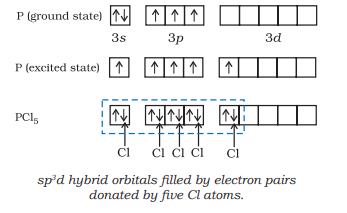
Now the five orbitals (i.e., one $s$, three $p$ and one $d$ orbitals) are available for hybridisation to yield a set of five $s p^{3} d$ hybrid orbitals which are directed towards the five corners of a trigonal bipyramidal as depicted in the Fig. 4.17.
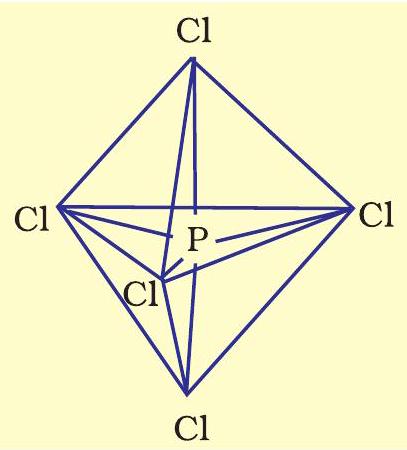
Fig. 4.17 Trigonal bipyramidal geometry of $PCl_5$ molecule
It should be noted that all the bond angles in trigonal bipyramidal geometry are not equivalent. In $\mathrm{PCl}_5$ the five $s p^{3} d$ orbitals of phosphorus overlap with the singly occupied $p$ orbitals of chlorine atoms to form five $\mathrm{P}-\mathrm{Cl}$ sigma bonds. Three $\mathrm{P}-\mathrm{Cl}$ bond lie in one plane and make an angle of $120^{\circ}$ with each other; these bonds are termed as equatorial bonds. The remaining two $\mathrm{P}-\mathrm{Cl}$ bonds-one lying above and the other lying below the equatorial plane, make an angle of $90^{\circ}$ with the plane. These bonds are called axial bonds. As the axial bond pairs suffer more repulsive interaction from the equatorial bond pairs, therefore axial bonds have been found to be slightly longer and hence slightly weaker than the equatorial bonds; which makes $\mathrm{PCl}_5$ molecule more reactive.
(ii) Formation of $\mathbf{S F}_6\left(\mathrm{sp}^{3} d^{2}\right.$ hybridisation): In $\mathrm{SF}_6$ the central sulphur atom has the ground state outer electronic configuration $3 s^{2} 3 p^{4}$. In the exited state the available six orbitals i.e., one s, three $p$ and two $d$ are singly occupied by electrons. These orbitals hybridise to form six new $s p^{3} d^{2}$ hybrid orbitals, which are projected towards the six corners of a regular octahedron in $\mathrm{SF}_6$. These six $s p^{3} d^{2}$ hybrid orbitals overlap with singly occupied orbitals of fluorine atoms to form six $\mathrm{S}-\mathrm{F}$ sigma bonds. Thus $\mathrm{SF}_6$ molecule has a regular octahedral geometry as shown in Fig. 4.18.
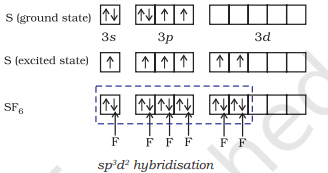
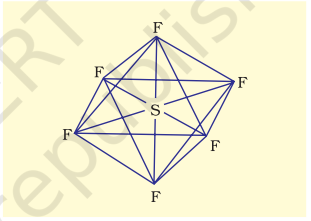
Fig. 4.18 Octahedral geometry of SF6 molecule
4.7 MOLECULAR ORBITAL THEORY
Molecular orbital (MO) theory was developed by F. Hund and R.S. Mulliken in 1932. The salient features of this theory are :
(i) The electrons in a molecule are present in the various molecular orbitals as the electrons of atoms are present in the various atomic orbitals.
(ii) The atomic orbitals of comparable energies and proper symmetry combine to form molecular orbitals.
(iii) While an electron in an atomic orbital is influenced by one nucleus, in a molecular orbital it is influenced by two or more nuclei depending upon the number of atoms in the molecule. Thus, an atomic orbital is monocentric while a molecular orbital is polycentric.
(iv) The number of molecular orbital formed is equal to the number of combining atomic orbitals. When two atomic orbitals combine, two molecular orbitals are formed. One is known as bonding molecular orbital while the other is called antibonding molecular orbital.
(v) The bonding molecular orbital has lower energy and hence greater stability than the corresponding antibonding molecular orbital.
(vi) Just as the electron probability distribution around a nucleus in an atom is given by an atomic orbital, the electron probability distribution around a group of nuclei in a molecule is given by a molecular orbital.
(vii) The molecular orbitals like atomic orbitals are filled in accordance with the aufbau principle obeying the Pauli’s exclusion principle and the Hund’s rule.
4.7.1 Formation of Molecular Orbitals Linear Combination of Atomic Orbitals (LCAO)
According to wave mechanics, the atomic orbitals can be expressed by wave functions ( $\psi$ ’s) which represent the amplitude of the electron waves. These are obtained from the solution of Schrödinger wave equation. However, since it cannot be solved for any system containing more than one electron, molecular orbitals which are one electron wave functions for molecules are difficult to obtain directly from the solution of Schrödinger wave equation. To overcome this problem, an approximate method known as linear combination of atomic orbitals (LCAO) has been adopted.
Let us apply this method to the homonuclear diatomic hydrogen molecule. Consider the hydrogen molecule consisting of two atoms A and B. Each hydrogen atom in the ground state has one electron in $1 \mathrm{~s}$ orbital. The atomic orbitals of these atoms may be represented by the wave functions $\psi_{\mathrm{A}}$ and $\psi_{\mathrm{B}}$. Mathematically, the formation of molecular orbitals may be described by the linear combination of atomic orbitals that can take place by addition and by subtraction of wave functions of individual atomic orbitals as shown below :
$$ \psi_{\mathrm{MO}}=\psi_{\mathrm{A}} \pm \psi_{\mathrm{B}} $$
Therefore, the two molecular orbitals $\sigma$ and $\sigma^{*}$ are formed as :
$$ \begin{aligned} & \sigma=\psi_{\mathrm{A}}+\psi_{\mathrm{B}} \\ & \sigma^{*}=\psi_{\mathrm{A}}-\psi_{\mathrm{B}} \end{aligned} $$
The molecular orbital $\sigma$ formed by the addition of atomic orbitals is called the bonding molecular orbital while the molecular orbital $\sigma^{*}$ formed by the subtraction of atomic orbital is called antibonding molecular orbital as depicted in Fig. 4.19.
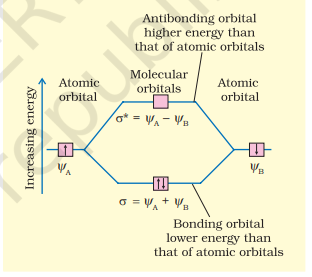
Fig.4.19 Formation of bonding (σ) and antibonding (σ*) molecular orbitals by the linear combination of atomic orbitals ψA and ψB centered on two atoms A and B respectively.
Qualitatively, the formation of molecular orbitals can be understood in terms of the constructive or destructive interference of the electron waves of the combining atoms. In the formation of bonding molecular orbital, the two electron waves of the bonding atoms reinforce each other due to constructive interference while in the formation of antibonding molecular orbital, the electron waves cancel each other due to destructive interference. As a result, the electron density in a bonding molecular orbital is located between the nuclei of the bonded atoms because of which the repulsion between the nuclei is very less while in case of an antibonding molecular orbital, most of the electron density is located away from the space between the nuclei. Infact, there is a nodal plane (on which the electron density is zero) between the nuclei and hence the repulsion between the nuclei is high. Electrons placed in a bonding molecular orbital tend to hold the nuclei together and stabilise a molecule. Therefore, a bonding molecular orbital always possesses lower energy than either of the atomic orbitals that have combined to form it. In contrast, the electrons placed in the antibonding molecular orbital destabilise the molecule. This is because the mutual repulsion of the electrons in this orbital is more than the attraction between the electrons and the nuclei, which causes a net increase in energy.
It may be noted that the energy of the antibonding orbital is raised above the energy of the parent atomic orbitals that have combined and the energy of the bonding orbital has been lowered than the parent orbitals. The total energy of two molecular orbitals, however, remains the same as that of two original atomic orbitals.
4.7.2 Conditions for the Combination of Atomic Orbitals
The linear combination of atomic orbitals to form molecular orbitals takes place only if the following conditions are satisfied:
1. The combining atomic orbitals must have the same or nearly the same energy. This means that $1 \mathrm{~s}$ orbital can combine with another $1 s$ orbital but not with $2 s$ orbital because the energy of $2 s$ orbital is appreciably higher than that of $1 \mathrm{~s}$ orbital. This is not true if the atoms are very different.
2. The combining atomic orbitals must have the same symmetry about the molecular axis. By convention $z$-axis is taken as the molecular axis. It is important to note that atomic orbitals having same or nearly the same energy will not combine if they do not have the same symmetry. For example, $2 p_{z}$ orbital of one atom can combine with $2 p_{z}$ orbital of the other atom but not with the $2 p_{x}$ or $2 p_{y}$ orbitals because of their different symmetries.
3. The combining atomic orbitals must overlap to the maximum extent. Greater the extent of overlap, the greater will be the electron-density between the nuclei of a molecular orbital.
4.7.3 Types of Molecular Orbitals
Molecular orbitals of diatomic molecules are designated as $\sigma$ (sigma), $\pi$ (pi), $\delta$ (delta), etc. In this nomenclature, the sigma $(\sigma)$ molecular orbitals are symmetrical around the bond-axis while pi $(\pi)$ molecular orbitals are not symmetrical. For example, the linear combination of $1 \mathrm{~s}$ orbitals centered on two nuclei produces two molecular orbitals which are symmetrical around the bond-axis. Such molecular orbitals are of the $\sigma$ type and are designated as $\sigma 1 \mathrm{~s}$ and $\sigma^* 1 \mathrm{~s}$ [Fig. 4.20(a), page 124]. If internuclear axis is taken to be in the $\mathrm{z}$ -direction, it can be seen that a linear combination of $2 p_z$ - orbitals of two atoms also produces two sigma molecular orbitals designated as $\boldsymbol{\sigma} \boldsymbol{p}_z$ and $\sigma^{\boldsymbol{*}} \boldsymbol{2}_z$. [Fig. 4.20(b)]
Molecular orbitals obtained from $2 p_{\mathrm{x}}$ and $2 p$ orbitals are not symmetrical around the bond axis because of the presence of positive lobes above and negative lobes below the molecular plane. Such molecular orbitals, are labelled as $\pi$ and $=\pi^{*}$ [Fig. 4.20(c)]. A $\pi$ bonding MO has larger electron density above and below the inter-nuclear axis. The $\pi^{\star}$ antibonding MO has a node between the nuclei.
4.7.4 Energy Level Diagram for Molecular Orbitals
We have seen that $1 \mathrm{~s}$ atomic orbitals on two atoms form two molecular orbitals designated as $\sigma 1 \mathrm{~s}$ and $\sigma^{*} 1 \mathrm{~s}$. In the same manner, the $2 \mathrm{~s}$ and $2 p$ atomic orbitals (eight atomic orbitals on two atoms) give rise to the following eight molecular orbitals:
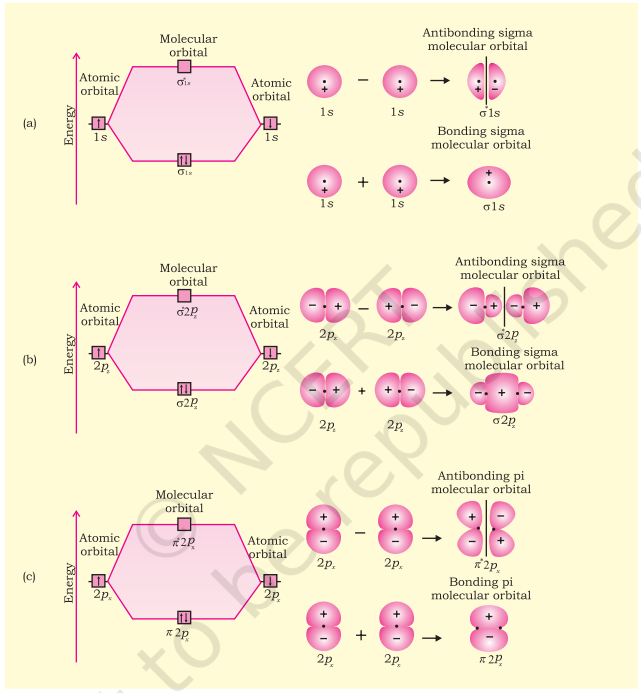
Fig. 4.20 Contours and energies of bonding and antibonding molecular orbitals formed through combinations of (a) 1s atomic orbitals; (b) $2p_z$ atomic orbitals and (c) $2p_x$ atomic orbitals.
$\begin{array}{llllll} \text{Antibonding } & \mathrm{MOs} & \sigma^* 2 s & \sigma^* 2 p_z & \pi^* 2 p_x & \pi^* 2 p_y \\ \text { Bonding } & \mathrm{MOs} & \sigma 2 \mathrm{~s} & \sigma 2 p_{z} & \pi 2 p_{x} & \pi 2 p_{y}\end{array}$
The energy levels of these molecular orbitals have been determined experimentally from spectroscopic data for homonuclear diatomic molecules of second row elements of the periodic table. The increasing order of energies of various molecular orbitals for $\mathrm{O}_2$ and $\mathrm{F}_2$ is given below:
$\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\sigma 2 p_z < \left(\pi 2 p_x = \pi 2 p_y\right) $
$<\left(\pi^* 2 p_x=\pi^* 2 p_y\right) < \sigma^* 2 p_z$
However, this sequence of energy levels of molecular orbitals is not correct for the remaining molecules $\mathrm{Li}_2, \mathrm{Be}_2, \mathrm{~B}_2, \mathrm{C}_2, \mathrm{~N}_2$. For instance, it has been observed experimentally that for molecules such as $\mathrm{B}_2, \mathrm{C}_2, \mathrm{~N}_2$, etc. the increasing order of energies of various molecular orbitals is
$\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\left(\pi 2 p_x=\pi 2 p_y\right)$
$<\sigma 2 p_z<\left(\pi^* 2 p_x=\pi^* 2 p_y\right)<\sigma^* 2 p_z$
The important characteristic feature of this order is that the energy of $\boldsymbol{\sigma 2} \boldsymbol{p}_z$ molecular orbital is higher than that of $\pi 2 p_x$ and $\pi 2 p_y$ molecular orbitals.
4.7.5 Electronic Configuration and Molecular Behaviour
The distribution of electrons among various molecular orbitals is called the electronic configuration of the molecule. From the electronic configuration of the molecule, it is possible to get important information about the molecule as discussed below.
Stability of Molecules: If $\mathrm{N}_b$ is the number of electrons occupying bonding orbitals and $\mathrm{N}_a$ the number occupying the antibonding orbitals, then
(i) the molecule is stable if $\mathrm{N}_b$ is greater than $\mathrm{N}_a$, and
(ii) the molecule is unstable if $\mathrm{N}_b$ is less than $\mathrm{N}_a$.
In (i) more bonding orbitals are occupied and so the bonding influence is stronger and a stable molecule results. In (ii) the antibonding influence is stronger and therefore the molecule is unstable.
Bond order
Bond order (b.o.) is defined as one half the difference between the number of electrons present in the bonding and the antibonding orbitals i.e.,
Bond order (b.o.) $=1 / 2\left(\mathrm{~N}_b-\mathrm{N}_a\right)$
The rules discussed above regarding the stability of the molecule can be restated in terms of bond order as follows: A positive bond order (i.e., $\mathrm{N}_b>\mathrm{N}_a$ ) means a stable molecule while a negative (i.e., $\mathrm{N}_b < \mathrm{N}_a$ ) or zero (i.e., $\mathrm{N}_b=\mathrm{N}_a$ ) bond order means an unstable molecule.
Nature of the bond
Integral bond order values of 1,2 or 3 correspond to single, double or triple bonds respectively as studied in the classical concept.
Bond-length
The bond order between two atoms in a molecule may be taken as an approximate measure of the bond length. The bond length decreases as bond order increases.
Magnetic nature
If all the molecular orbitals in a molecule are doubly occupied, the substance is diamagnetic (repelled by magnetic field). However if one or more molecular orbitals are singly occupied it is paramagnetic (attracted by magnetic field), e.g., $\mathrm{O}_{2}$ molecule.
4.8 BONDING IN SOME HOMONUCLEAR DIATOMIC MOLECULES
In this section we shall discuss bonding in some homonuclear diatomic molecules.
1. Hydrogen molecule $\left(\boldsymbol{H}_{2}\right)$ : It is formed by the combination of two hydrogen atoms. Each hydrogen atom has one electron in 1 s orbital. Therefore, in all there are two electrons in hydrogen molecule which are present in $\sigma 1 \mathrm{~s}$ molecular orbital. So electronic configuration of hydrogen molecule is
$$ \mathrm{H}_{2}:(\sigma 1 s)^{2} $$
The bond order of $\mathrm{H}_{2}$ molecule can be calculated as given below:
$$ \text { Bond order }=\frac{\mathrm{N}_b-\mathrm{N}_a}{2}=\frac{2-0}{2}=1 $$
This means that the two hydrogen atoms are bonded together by a single covalent bond. The bond dissociation energy of hydrogen molecule has been found to be $438 \mathrm{~kJ} \mathrm{~mol}^{-1}$ and bond length equal to $74 \mathrm{pm}$. Since no unpaired electron is present in hydrogen molecule, therefore, it is diamagnetic.
2. Helium molecule $\left(\mathbf{H e}_2\right)$ : The electronic configuration of helium atom is $1 s^2$. Each helium atom contains 2 electrons, therefore, in $\mathrm{He}_2$ molecule there would be 4 electrons. These electrons will be accommodated in $\sigma 1 s$ and $\sigma^{*} 1 s$ molecular orbitals leading to electronic configuration:
$\mathrm{He}_{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}$
Bond order of $\mathrm{He}_{2}$ is $1 / 2(2-2)=0$
$\mathrm{He}_{2}$ molecule is therefore unstable and does not exist.
Similarly, it can be shown that $\mathrm{Be}_2$ molecule $(\sigma 1 s)^2\left(\sigma^* 1 s\right)^2(\sigma 2 s)^2\left(\sigma^* 2 s\right)^2$ also does not exist.
3. Lithium molecule $\left(\mathbf{L i}_2\right)$ : The electronic configuration of lithium is $1 s^2, 2 s^1$. There are six electrons in $\mathrm{Li}_2$. The electronic configuration of $\mathrm{Li}_2$ molecule, therefore, is
$$ \operatorname{Li}_{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}(\sigma 2 s)^{2} $$
The above configuration is also written as $\mathrm{KK}(\sigma 2 \mathrm{~s})^{2}$ where $\mathrm{KK}$ represents the closed $K$ shell structure $(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}$.
From the electronic configuration of $\mathrm{Li}_2$ molecule it is clear that there are four electrons present in bonding molecular orbitals and two electrons present in antibonding molecular orbitals. Its bond order, therefore, is $1 / 2$ (42) $=1$. It means that $\mathrm{Li}_2$ molecule is stable and since it has no unpaired electrons it should be diamagnetic. Indeed diamagnetic $\mathrm{Li}_2$ molecules are known to exist in the vapour phase.
4. Carbon molecule $\left(\boldsymbol{C}_2\right)$ : The electronic configuration of carbon is $1 s^{2} 2 s^{2} 2 p^{2}$. There are twelve electrons in $\mathrm{C}_2$. The electronic configuration of $\mathrm{C}_2$ molecule, therefore, is
$\mathrm{C}_2:(\sigma 1 \mathrm{~s})^{2}\left(\sigma^{*} 1 \mathrm{~s}\right)^{2}(\sigma * 2 \mathrm{~s})^{2}\left(\pi 2 \mathrm{p}_x^{2}=\pi 2 \mathrm{p}_y^{2}\right)$
or $K K(\sigma 2 s)^{2}(\sigma * 2 s)^{2}\left(\pi 2 \mathrm{p}_x^{2}=\pi 2 \mathrm{p}_y^{2}\right)$
The bond order of $\mathrm{C}_2$ is $1 / 2(8-4)=2$ and $\mathrm{C}_2$ should be diamagnetic. Diamagnetic $\mathrm{C}_2$ molecules have indeed been detected in vapour phase. It is important to note that double bond in $\mathrm{C}_2$ consists of both pi bonds because of the presence of four electrons in two pi molecular orbitals. In most of the other molecules a double bond is made up of a sigma bond and a pi bond. In a similar fashion the bonding in $\mathrm{N}_2$ molecule can be discussed.
5. Oxygen molecule $\left(\mathrm{O}_2\right)$ : The electronic configuration of oxygen atom is $1 s^{2} 2 s^{2} 2 p^{4}$. Each oxygen atom has 8 electrons, hence, in $\mathrm{O}_2$ molecule there are 16 electrons. The electronic configuration of $\mathrm{O}_2$ molecule, therefore, is
$\mathrm{O}_{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}(\sigma 2 s)^{2}(\sigma * 2 s)^{2}\left(\sigma 2 \mathrm{p}_z\right)^{2}$
$\left(\pi 2 p_x{ }^{2} \equiv \pi 2 p_y{ }^{2}\right)\left(\pi^{*} 2 p^{1}{ }_x \equiv \pi * 2 p_y{ }^{1}\right)$
or $\mathrm{O}^{2}:\left[\begin{array}{c}\mathrm{KK}(\sigma 2 \mathrm{~s})^{2}\left(\sigma 2 p_S\right)^{2}\left(\sigma 2 p_z\right)^{2} \\ \left(\pi 2 p_x^{2} \equiv \pi 2 p_y^{2}\right),\left(\pi * 2 \mathrm{p}_x^{1} \equiv \pi * 2_y^{1}\right)\end{array}\right]$
From the electronic configuration of $\mathrm{O}_{2}$ molecule it is clear that ten electrons are present in bonding molecular orbitals and six electrons are present in antibonding molecular orbitals. Its bond order, therefore, is
Bond order $=\frac{1}{2}\left[N_{b}-N_{a}\right]=\frac{1}{2}[10-6]=2$
So in oxygen molecule, atoms are held by a double bond. Moreover, it may be noted that it contains two unpaired electrons in $\pi^* 2 p_x$ and $\pi^* 2 p_y$ molecular orbitals, therefore, $\mathrm{O}_2$ molecule should be paramagnetic, a prediction that corresponds to experimental observation. In this way, the theory successfully explains the paramagnetic nature of oxygen.
Similarly, the electronic configurations of other homonuclear diatomic molecules of the second row of the periodic table can be written. In Fig. 4.21 are given the molecular orbital occupancy and molecular properties for $\mathrm{B}_2$ through $\mathrm{Ne}_2$. The sequence of MOs and their electron population are shown. The bond energy, bond length, bond order, magnetic properties and valence electron configuration appear below the orbital diagrams.
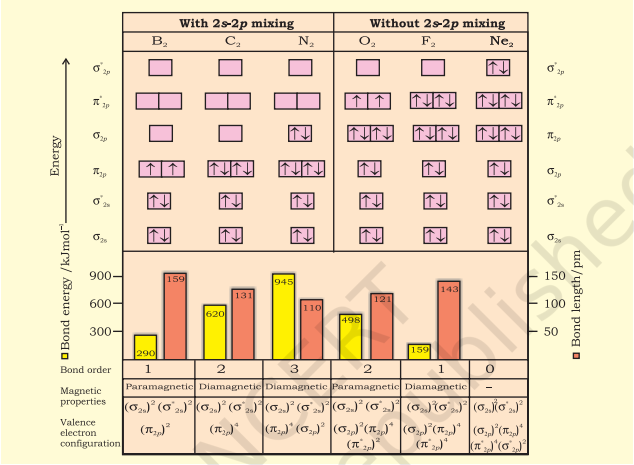
Fig.4.21 MO occupancy and molecular properties for $B_2$ through $Ne_2$.
4.9 HYDROGEN BONDING
Nitrogen, oxygen and fluorine are the highly electronegative elements. When they are attached to a hydrogen atom to form covalent bond, the electrons of the covalent bond are shifted towards the more electronegative atom. This partially positively charged hydrogen atom forms a bond with the other more electronegative atom. This bond is known as hydrogen bond and is weaker than the covalent bond. For example, in HF molecule, the hydrogen bond exists between hydrogen atom of one molecule and fluorine atom of another molecule as depicted below :
$\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}$
Here, hydrogen bond acts as a bridge between two atoms which holds one atom by covalent bond and the other by hydrogen bond. Hydrogen bond is represented by a dotted line ($\text{ - - - }$) while a solid line represents the covalent bond. Thus, hydrogen bond can be defined as the attractive force which binds hydrogen atom of one molecule with the electronegative atom ( $\mathrm{F}, \mathrm{O}$ or $\mathrm{N}$ ) of another molecule.
4.9.1 Cause of Formation of Hydrogen Bond
When hydrogen is bonded to strongly electronegative element ’ $\mathrm{X}$ ‘, the electron pair shared between the two atoms moves far away from hydrogen atom. As a result the hydrogen atom becomes highly electropositive with respect to the other atom ’ $X$ ‘. Since there is displacement of electrons towards $\mathrm{X}$, the hydrogen acquires fractional positive charge $\left(\delta^{+}\right)$while ’ $\mathrm{X}$ ’ attain fractional negative charge $\left(\delta^{-}\right)$. This results in the formation of a polar molecule having electrostatic force of attraction which can be represented as:
$\mathrm{H}^{\delta+}-\mathrm{X}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{X}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{X}^{\delta-}$
The magnitude of $\mathrm{H}$-bonding depends on the physical state of the compound. It is maximum in the solid state and minimum in the gaseous state. Thus, the hydrogen bonds have strong influence on the structure and properties of the compounds.
4.9.2 Types of $H$-Bonds
There are two types of $\mathrm{H}$-bonds
(i) Intermolecular hydrogen bond
(ii) Intramolecular hydrogen bond
(1) Intermolecular hydrogen bond: It is formed between two different molecules of the same or different compounds. For example, $\mathrm{H}$-bond in case of HF molecule, alcohol or water molecules, etc.
(2) Intramolecular hydrogen bond : It is formed when hydrogen atom is in between the two highly electronegative $(\mathrm{F}, \mathrm{O}, \mathrm{N})$ atoms present within the same molecule. For example, in o-nitrophenol the hydrogen is in between the two oxygen atoms.
Fig. 4.22 Intramolecular hydrogen
Summary
Kössel’s first insight into the mechanism of formation of electropositive and electronegative ions related the process to the attainment of noble gas configurations by the respective ions. Electrostatic attraction between ions is the cause for their stability. This gives the concept of electrovalency.
The first description of covalent bonding was provided by Lewis in terms of the sharing of electron pairs between atoms and he related the process to the attainment of noble gas configurations by reacting atoms as a result of sharing of electrons. The Lewis dot symbols show the number of valence electrons of the atoms of a given element and Lewis dot structures show pictorial representations of bonding in molecules.
An ionic compound is pictured as a three-dimensional aggregation of positive and negative ions in an ordered arrangement called the crystal lattice. In a crystalline solid there is a charge balance between the positive and negative ions. The crystal lattice is stabilized by the enthalpy of lattice formation.
While a single covalent bond is formed by sharing of an electron pair between two atoms, multiple bonds result from the sharing of two or three electron pairs. Some bonded atoms have additional pairs of electrons not involved in bonding. These are called lone-pairs of electrons. A Lewis dot structure shows the arrangement of bonded pairs and lone pairs around each atom in a molecule. Important parameters, associated with chemical bonds, like: bond length, bond angle, bond enthalpy, bond order and bond polarity have significant effect on the properties of compounds.
A number of molecules and polyatomic ions cannot be described accurately by a single Lewis structure and a number of descriptions (representations) based on the same skeletal structure are written and these taken together represent the molecule or ion. This is a very important and extremely useful concept called resonance. The contributing structures or canonical forms taken together constitute the resonance hybrid which represents the molecule or ion.
The VSEPR model used for predicting the geometrical shapes of molecules is based on the assumption that electron pairs repel each other and, therefore, tend to remain as far apart as possible. According to this model, molecular geometry is determined by repulsions between lone pairs and lone pairs; lone pairs and bonding pairs and bonding pairs and bonding pairs. The order of these repulsions being : lp-lp $>1 \mathrm{p}-\mathrm{bp}>\mathrm{bp}-\mathrm{bp}$
The valence bond (VB) approach to covalent bonding is basically concerned with the energetics of covalent bond formation about which the Lewis and VSEPR models are silent. Basically the VB theory discusses bond formation in terms of overlap of orbitals. For example the formation of the $\mathrm{H}_{2}$ molecule from two hydrogen atoms involves the overlap of the $1 \mathrm{~s}$ orbitals of the two $\mathrm{H}$ atoms which are singly occupied. It is seen that the potential energy of the system gets lowered as the two $\mathrm{H}$ atoms come near to each other. At the equilibrium inter-nuclear distance (bond distance) the energy touches a minimum. Any attempt to bring the nuclei still closer results in a sudden increase in energy and consequent destabilization of the molecule. Because of orbital overlap the electron density between the nuclei increases which helps in bringing them closer. It is however seen that the actual bond enthalpy and bond length values are not obtained by overlap alone and other variables have to be taken into account.
For explaining the characteristic shapes of polyatomic molecules Pauling introduced the concept of hybridisation of atomic orbitals. $s p, s p^{2}, s p^{3}$ hybridizations of atomic orbitals of $\mathrm{Be}, \mathrm{B}, \mathrm{C}, \mathrm{N}$ and $\mathrm{O}$ are used to explain the formation and geometrical shapes of molecules like $\mathrm{BeCl}_2, \mathrm{BCl}_3, \mathrm{CH}_4, \mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$. They also explain the formation of multiple bonds in molecules like $\mathrm{C}_2 \mathrm{H}_2$ and $\mathrm{C}_2 \mathrm{H}_4$.
The molecular orbital (MO) theory describes bonding in terms of the combination and arrangment of atomic orbitals to form molecular orbitals that are associated with the molecule as a whole. The number of molecular orbitals are always equal to the number of atomic orbitals from which they are formed. Bonding molecular orbitals increase electron density between the nuclei and are lower in energy than the individual atomic orbitals. Antibonding molecular orbitals have a region of zero electron density between the nuclei and have more energy than the individual atomic orbitals.
The electronic configuration of the molecules is written by filling electrons in the molecular orbitals in the order of increasing energy levels. As in the case of atoms, the Pauli exclusion principle and Hund’s rule are applicable for the filling of molecular orbitals. Molecules are said to be stable if the number of elctrons in bonding molecular orbitals is greater than that in antibonding molecular orbitals.
Hydrogen bond is formed when a hydrogen atom finds itself between two highly electronegative atoms such as F, O and N. It may be intermolecular (existing between two or more molecules of the same or different substances) or intramolecular (present within the same molecule). Hydrogen bonds have a powerful effect on the structure and properties of many compounds.
Exercise
4.1 Explain the formation of a chemical bond.
Show Answer
Answer A chemical bond is defined as an attractive force that holds the constituents (atoms, ions etc.) together in a chemical species.
Various theories have been suggested for the formation of chemical bonds such as the electronic theory, valence shell electron pair repulsion theory, valence bond theory, and molecular orbital theory.
A chemical bond formation is attributed to the tendency of a system to attain stability. It was observed that the inertness of noble gases was because of their fully filled outermost orbitals. Hence, it was postulated that the elements having incomplete outermost shells are unstable (reactive). Atoms, therefore, combine with each other and complete their respective octets or duplets to attain the stable configuration of the nearest noble gases. This combination can occur either by sharing of electrons or by transferring one or more electrons from one atom to another. The chemical bond formed as a result of sharing of electrons between atoms is called a covalent bond. An ionic bond is formed as a result of the transference of electrons from one atom to another.
4.2 Write Lewis dot symbols for atoms of the following elements : Mg, Na, B, O, N, Br.
Show Answer
Answer
Mg: There are two valence electrons in Mg atom. Hence, the Lewis dot symbol for Mg is: $\ddot{M} g$
Na: There is only one valence electron in an atom of sodium. Hence, the Lewis dot structure is: Na*
B: There are 3 valence electrons in Boron atom. Hence, the Lewis dot structure is: ${ }^{B} \cdot$
O.: There are six valence electrons in an atom of oxygen. Hence, the Lewis dot structure is: $: \ddot{0}$ :
$\underline{N}$ : There are five valence electrons in an atom of nitrogen. Hence, the Lewis dot structure is: $: \ddot{N}^{*}$
Br: There are seven valence electrons in bromine. Hence, the Lewis dot structure is: $: \ddot{Br}$ :
4.3 Write Lewis symbols for the following atoms and ions: $\mathrm{S}$ and $\mathrm{S}^{2-} ; \mathrm{Al}$ and $\mathrm{Al}^{3+} ; \mathrm{H}$ and $\mathrm{H}^{-}$
Show Answer
Answer
(i) $S$ and $S^{2}$
The number of valence electrons in sulphur is 6 .
The Lewis dot symbol of sulphur ( $S$ ) is $: \ddot{s}$ :
The dinegative charge infers that there will be two electrons more in addition to the six valence electrons. Hence, the Lewis dot symbol of $S^{2 \cdot}$ is
(ii) $Al$ and $Al^{3+}$
The number of valence electrons in aluminium is 3 .
The Lewis dot symbol of aluminium (Al) is $\ddot{Al}$.
The tripositive charge on a species infers that it has donated its three electrons. Hence, the Lewis dot symbol is $[Al]^{3+}$.
(iii) $H$ and $H$
The number of valence electrons in hydrogen is 1.
The Lewis dot symbol of hydrogen $(H)$ is $H$ :
The uninegative charge infers that there will be one electron more in addition to the one valence electron. Hence, the Lewis dot symbol is $[\ddot{H}]^{-}$.
4.4 Draw the Lewis structures for the following molecules and ions :
$\mathrm{H}_2 \mathrm{~S}, \mathrm{SiCl}_4, \mathrm{BeF}_2, \mathrm{CO}_3^{2-}$, $\mathrm{HCOOH}$
Show Answer
Answer $H_2 S$
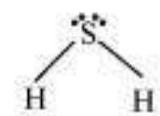
$SiCl_4$
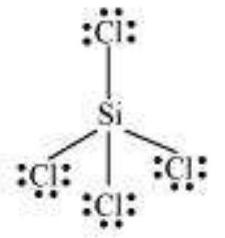
$BeF_2$
$ \ddot{:} F-Be-\ddot{F} $
$CO_3^{2-}$
4.5 Define octet rule. Write its significance and limitations.
Show Answer
Answer
The octet rule or the electronic theory of chemical bonding was developed by Kossel and Lewis. According to this rule, atoms can combine either by transfer of valence electrons from one atom to another or by sharing their valence electrons in order to attain the nearest noble gas configuration by having an octet in their valence shell.
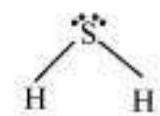
The octet rule successfully explained the formation of chemical bonds depending upon the nature of the element.
Limitations of the octet theory:
The following are the limitations of the octet rule:
(a) The rule failed to predict the shape and relative stability of molecules.
(b) It is based upon the inert nature of noble gases. However, some noble gases like xenon and krypton form compounds such as $XeF_2, KrF_2$ etc.
(c) The octet rule cannot be applied to the elements in and beyond the third period of the periodic table. The elements present in these periods have more than eight valence electrons around the central atom. For example: $PF_5, SF_6$, etc.
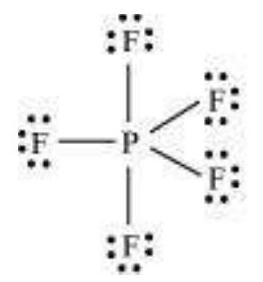
(d) The octet rule is not satisfied for all atoms in a molecule having an odd number of electrons. For example, NO and $NO_2$ do not satisfy the octet rule.
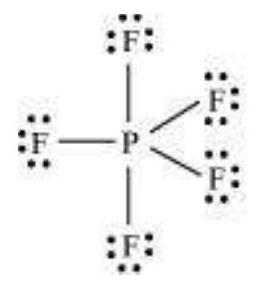
(e) This rule cannot be applied to those compounds in which the number of electrons surrounding the central atom is less than eight. For example, $LiCl, BeH_2, AlCl_3$ etc. do not obey the octet rule. $Li: Cl$ $Cl: . Al: Cl$ ci $H: Be: H$
4.6 Write the favourable factors for the formation of ionic bond.
Show Answer
Answer
An ionic bond is formed by the transfer of one or more electrons from one atom to another. Hence, the formation of ionic bonds depends upon the ease with which neutral atoms can lose or gain electrons. Bond formation also depends upon the lattice energy of the compound formed.
Hence, favourable factors for ionic bond formation are as follows:
(i) Low ionization enthalpy of metal atom.
(ii) High electron gain enthalpy $(\Delta _{e g} H)$ of a non-metal atom.
(iii) High lattice energy of the compound formed.
4.7 Discuss the shape of the following molecules using the VSEPR model:
$\mathrm{BeCl}_2, \mathrm{BCl}_3, \mathrm{SiCl}_4, \mathrm{AsF}_5, \mathrm{H}_2 \mathrm{~S}, \mathrm{PH}_3$
Show Answer
Answer
$\underline{BeCl_2}$
$Cl: Be: Cl$
The central atom has no lone pair and there are two bond pairs. i.e., $BeCl_2$ is of the type $AB_2$. Hence, it has a linear shape.
$BCl_3$
$\stackrel{Cl}{: B}: Cl$
The central atom has no lone pair and there are three bond pairs. Hence, it is of the type $AB_3$. Hence, it is trigonal planar.
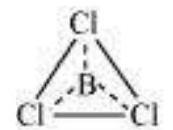
$\underline{SiCl_4}$
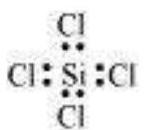
The central atom has no lone pair and there are four bond pairs. Hence, the shape of $SiCl_4$ is tetrahedral being the $AB_4$ type molecule.
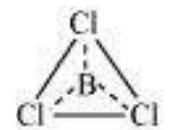
The central atom has no lone pair and there are five bond pairs. Hence, $AsF_5$ is of the type $AB_5$. Therefore, the shape istrigonal bipyramidal.
$H_2 S$ :
н: $\ddot{s}: H$
The central atom has one lone pair and there are two bond pairs. Hence, $H_2 S$ is of the type $AB_2 E$. The shape is Bent.
$PH_3:$
$H: \underset{H}{\ddot{P}}: H$
The central atom has one lone pair and there are three bond pairs. Hence, $PH_3$ is of the $AB_3 E$ type. Therefore, the shape is trigonal pyramidal.
4.8 Although geometries of $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ molecules are distorted tetrahedral, bond angle in water is less than that of ammonia. Discuss.
Show Answer
Answer
The molecular geometry of $NH_3$ and $H_2 O$ can be shown as:

The central atom $(N)$ in $NH_3$ has one lone pair and there are three bond pairs. In $H_2 O$, there are two lone pairs and two bond pairs.
The two lone pairs present in the oxygen atom of $H_2 O$ molecule repels the two bond pairs. This repulsion is stronger than the repulsion between the lone pair and the three bond pairs on the nitrogen atom.
Since the repulsions on the bond pairs in $H_2 O$ molecule are greater than that in $NH_3$, the bond angle in water is less than that of ammonia.
4.9 How do you express the bond strength in terms of bond order ?
Show Answer
Answer
Bond strength represents the extent of bonding between two atoms forming a molecule. The larger the bond energy, the stronger is the bond and the greater is the bond order.
4.10 Define the bond length.
Show Answer
Answer
Bond length is defined as the equilibrium distance between the nuclei of two bonded atoms in a molecule.
Bond lengths are expressed in terms of Angstrom $(10^{-10} m)$ or picometer
$(10^{-12} m)$ and are measured by spectroscopic X-ray diffractions and electron-diffraction techniques.
In an ionic compound, the bond length is the sum of the ionic radii of the constituting atoms $(d=r _{+}+r _{\text{. }}.$. In a covalent compound, it is the sum of their covalent radii $(d=r_A+r_B)$.

4.11 Explain the important aspects of resonance with reference to the $\mathrm{CO}_{3}^{2-}$ ion.
Show Answer
Answer
According to experimental findings, all carbon to oxygen bonds in $CO_3^{2-}$ are equivalent. Hence, it is inadequate to represent $CO_3^{2-}$ ion by a single Lewis structure having two single bonds and one double bond.
Therefore, carbonate ion is described as a resonance hybrid of the following structures:
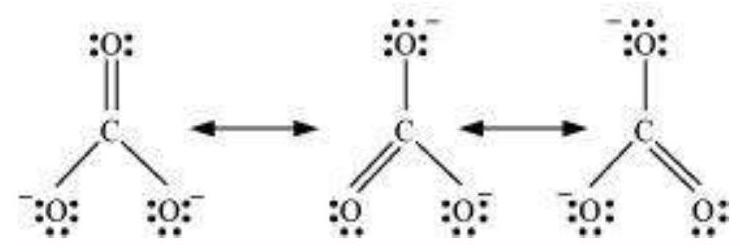
4.12 $ \mathrm{H}_3 \mathrm{PO}_3$ can be represented by structures 1 and 2 shown below. Can these two structures be taken as the canonical forms of the resonance hybrid representing $\mathrm{H}_3 \mathrm{PO}_3$ ? If not, give reasons for the same.

Show Answer
Answer
The given structures cannot be taken as the canonical forms of the resonance hybrid of $H_3 PO_3$ because the positions of the atoms have changed.
4.13 Write the resonance structures for $\mathrm{SO}_3, \mathrm{NO}_2$ and $\mathrm{NO}_3^{-}$.
Show Answer
Answer
The resonance structures are:
(a) $SO_3$ :
(b) $NO_2$ :
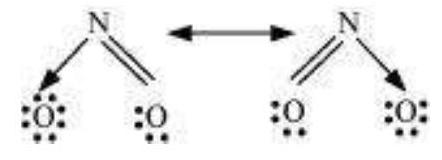
(c) $NO_3^{-}$:
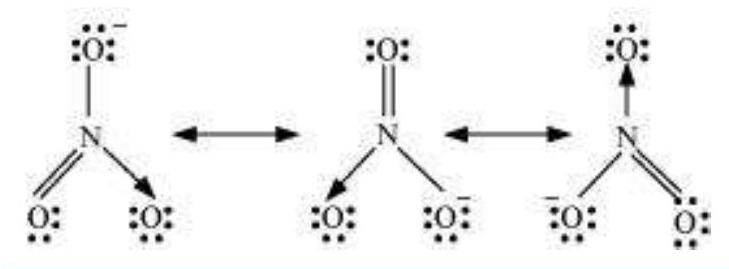
4.14 Use Lewis symbols to show electron transfer between the following atoms to form cations and anions : (a) $\mathrm{K}$ and $\mathrm{S}$ (b) $\mathrm{Ca}$ and $\mathrm{O}$ (c) $\mathrm{Al}$ and $\mathrm{N}$.
Show Answer
Answer
(a) $K$ and $S$ :
The electronic configurations of $K$ and $S$ are as follows:
K: 2, 8, 8, 1
S: $2,8,6$
K$\cdot$
$ \text{ : } $
Sulphur (S) requires 2 more electrons to complete its octet. Potassium (K) requires one electron more than the nearest noble gas i.e., Argon. Hence, the electron transfer can be shown as:
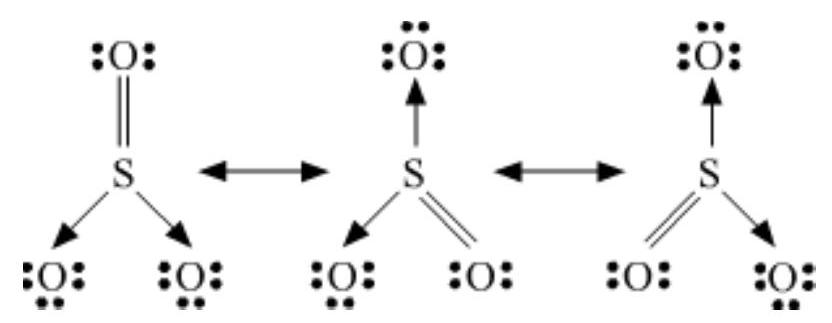
(b) Ca and O:
The electronic configurations of $Ca$ and $O$ are as follows:
Ca: $2,8,8,2$
O: 2,6
Oxygen requires two electrons more to complete its octet, whereas calcium has two electrons more than the nearest noble gas i.e., Argon. Hence, the electron transfer takes place as:

(c) Al and $N$ :
The electronic configurations of $Al$ and $N$ are as follows:
Al: 2, 8, 3
$N: 2,5$
Nitrogen is three electrons short of the nearest noble gas (Neon), whereas aluminium has three electrons more than Neon. Hence, the electron transference can be shown as:

4.15 Although both $\mathrm{CO}_2$ and $\mathrm{H}_2 \mathrm{O}$ are triatomic molecules, the shape of $\mathrm{H}_2 \mathrm{O}$ molecule is bent while that of $\mathrm{CO}_2$ is linear. Explain this on the basis of dipole moment.
Show Answer
Answer
According to experimental results, the dipole moment of carbon dioxide is zero. This is possible only if the molecule is linear so that the dipole moments of $C$-O bonds are equal and opposite to nullify each other.
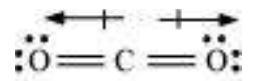
Resultant $\mu=0$ D
$H_2 O$, on the other hand, has a dipole moment value of $1.84 D$ (though it is a triatomic molecule as $CO_2$ ). The value of the dipole moment suggests that the structure of $H_2 O$ molecule is bent where the dipole moment of $O-H$ bonds are unequal.

4.16 Write the significance/applications of dipole moment.
Show Answer
Answer
In heteronuclear molecules, polarization arises due to a difference in the electronegativities of the constituents of atoms. As a result, one end of the molecule acquires a positive charge while the other end becomes negative. Hence, a molecule is said to possess a dipole.
The product of the magnitude of the charge and the distance between the centres of positive-negative charges is called the dipole moment $ \mu $ of the molecule. It is a vector quantity and is represented by an \to with its tail at the positive centre and head pointing towards a negative centre.
Dipole moment $(\mu)=$ charge $(Q) \times$ distance of separation $(r)$
The SI unit of a dipole moment is ’esu'.
1 esu $=3.335 \times 10^{-30} cm$
Dipole moment is the measure of the polarity of a bond. It is used to differentiate between polar and non-polar bonds since all non-polar molecules (e.g. $H_2, O_2$ ) have zero dipole moments. It is also helpful in calculating the percentage ionic character of a molecule.
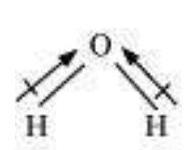
$ \begin{gathered} \stackrel{+}{+}=C=O \\ \mu=0 \end{gathered} $
$ \mu=1.84 D $
4.17 Define electronegativity. How does it differ from electron gain enthalpy?
Show Answer
Answer
Electronegativity is the ability of an atom in a chemical compound to attract a bond pair of electrons towards itself.
Electronegativity of any given element is not constant. It varies according to the element to which it is bound. It is not a measurable quantity. It is only a relative number.
On the other hand, electron gain enthalpy is the enthalpy change that takes place when an electron is added to a neutral gaseous atom to form an anion. It can be negative or positive depending upon whether the electron is added or removed. An element has a constant value of the electron gain enthalpy that can be measured experimentally.
4.18 Explain with the help of suitable example polar covalent bond.
Show Answer
Answer
When two dissimilar atoms having different electronegativities combine to form a covalent bond, the bond pair of electrons is not shared equally. The bond pair shifts towards the nucleus of the atom having greater electronegativity. As a result, electron distribution gets distorted and the electron cloud is displaced towards the electronegative atom.
As a result, the electronegative atom becomes slightly negatively charged while the other atom becomes slightly positively charged. Thus, opposite poles are developed in the molecule and this type of a bond is called a polar covalent bond.
$HCl$, for example, contains a polar covalent bond. Chlorine atom is more electronegative than hydrogen atom. Hence, the bond pair lies towards chlorine and therefore, it acquires a partial negative charge.
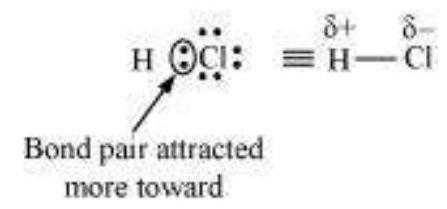
4.19 Arrange the bonds in order of increasing ionic character in the molecules: $\mathrm{LiF}, \mathrm{K}_2 \mathrm{O}$, $\mathrm{N}_2, \mathrm{SO}_2$ and $\mathrm{ClF}_3$.
Show Answer
Answer
The ionic character in a molecule is dependent upon the electronegativity difference between the constituting atoms. The greater the difference, the greater will be the ionic character of the molecule.
On this basis, the order of increasing ionic character in the given molecules is
$N_2<SO_2<ClF_3<K_2 O<LiF$.
4.20 The skeletal structure of $\mathrm{CH}_{3} \mathrm{COOH}$ as shown below is correct, but some of the bonds are shown incorrectly. Write the correct Lewis structure for acetic acid.

Show Answer
Answer
The correct Lewis structure for acetic acid is as follows:
4.21 Apart from tetrahedral geometry, another possible geometry for $\mathrm{CH_4}$ is square planar with the four $\mathrm{H}$ atoms at the corners of the square and the $\mathrm{C}$ atom at its centre. Explain why $\mathrm{CH_4}$ is not square planar?
Show Answer
Answer
Electronic configuration of carbon atom:
$ _6 C: 1 s^{2} 2 s^{2} 2 p^{2}$
In the excited state, the orbital picture of carbon can be represented as:
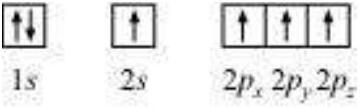
Hence, carbon atom undergoes $s p^{3}$ hybridization in $CH_4$ molecule and takes a tetrahedral shape.
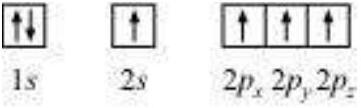
For a square planar shape, the hybridization of the central atom has to be $d s p^{2}$. However, an atom of carbon does not have $d$-orbitalsto undergo $d s p^{2}$ hybridization. Hence, the structure of $CH_4$ cannot be square planar.
Moreover, with a bond angle of $90^{\circ}$ in square planar, the stability of $CH_4$ will be very less because of the repulsion existing between the bond pairs. Hence, VSEPR theory also supports a tetrahedral structure for $CH_4$.
4.22 Explain why $\mathrm{BeH_2}$ molecule has a zero dipole moment although the $\mathrm{Be}-\mathrm{H}$ bonds are polar.
Show Answer
Answer
The Lewis structure for $BeH_2$ is as follows:
$H: Be: H$
There is no lone pair at the central atom (Be) and there are two bond pairs. Hence, $BeH_2$ is of the type $AB_2$. It has a linear structure.
$H \xrightarrow{\longrightarrow} \xrightarrow{+} H$
Dipole moments of each $H$-Be bond are equal and are in opposite directions. Therefore, they nullify each other. Hence, $BeH_2$ molecule has zero dipole moment.
4.23 Which out of $\mathrm{NH_3}$ and $\mathrm{NF_3}$ has higher dipole moment and why ?
Show Answer
Answer
In both molecules i.e., $NH_3$ and $NF_3$, the central atom $(N)$ has a lone pair electron and there are three bond pairs. Hence, both molecules have a pyramidal shape. Since fluorine is more electronegative than hydrogen, it is expected that the net dipole moment of $NF_3$ is greater than $NH_3$. However, the net dipole moment of $NH_3(1.46 D)$ is greater than that of $NF_3(0.24 D)$.
This can be explained on the basis of the directions of the dipole moments of each individual bond in $NF_3$ and $NH_3$. These directions can be shown as:
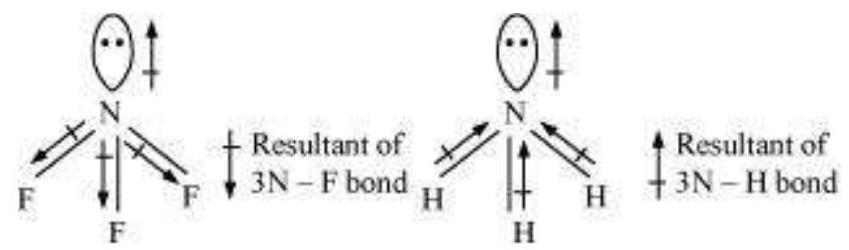
Thus, the resultant moment of the $N-H$ bonds add up to the bond moment of the lone pair (the two being in the same direction), whereas that of the three $N-F$ bonds partly cancels the moment of the lone pair.
Hence, the net dipole moment of $NF_3$ is less than that of $NH_3$.
4.24 What is meant by hybridisation of atomic orbitals? Describe the shapes of $s p, s p^{2}$, $s p^{3}$ hybrid orbitals.
Show Answer
Answer
Hybridization is defined as an intermixing of a set of atomic orbitals of slightly different energies, thereby forming a new set of orbitals having equivalent energies and shapes.
For example, one $2 s$-orbital hybridizes with two $2 p$-orbitals of carbon to form three new $s p^{2}$ hybrid orbitals.
These hybrid orbitals have minimum repulsion between their electron pairs and thus, are more stable. Hybridization helps indicate the geometry of the molecule.
Shape of $s p$ hybrid orbitals: $s p$ hybrid orbitals have a linear shape. They are formed by the intermixing of $s$ and porbitals as:
$s$-orbital
$p_z$-orbital
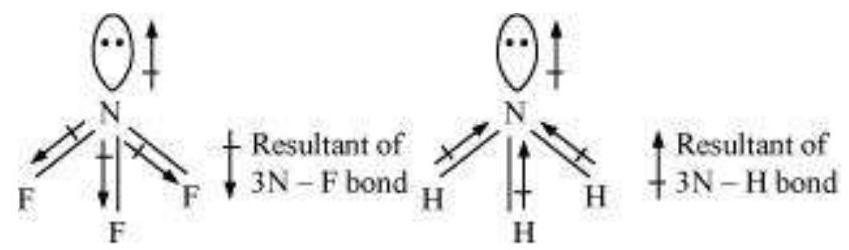
$s p$-hybrids
Shape of $s p^{2}$ hybrid orbitals: $s p^{2}$ hybrid orbitals are formed as a result of the intermixing of one s-orbital and two $2 p$-orbitals. The hybrid orbitals are oriented in a trigonal planar arrangement as:
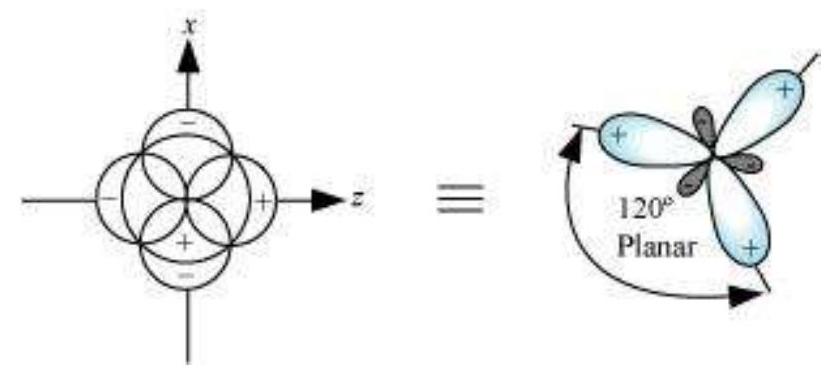
Shape of $s p^{3}$ hybrid orbitals:
Four $s p^{3}$ hybrid orbitals are formed by intermixing one s-orbital with three $p$-orbitals. The four $s p^{3}$ hybrid orbitals are arranged in the form of a tetrahedron as:
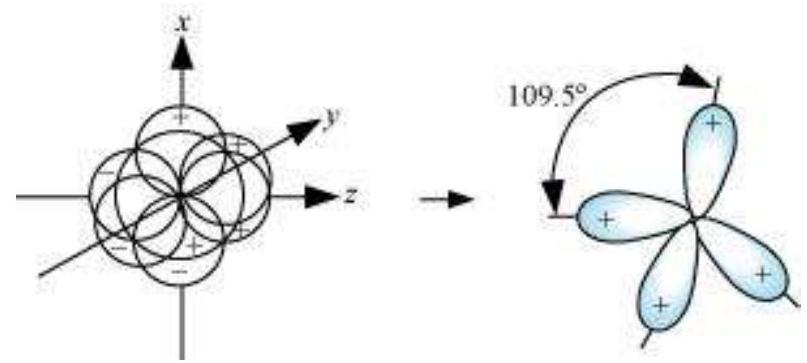
4.25 Describe the change in hybridisation (if any) of the Al atom in the following reaction.
$\mathrm{AlCl_3}+\mathrm{Cl}^{-} \rightarrow \mathrm{AlCl_4}^{-}$
Show Answer
Answer
The valence orbital picture of aluminium in the ground state can be represented as:
$\uparrow$
The orbital picture of aluminium in the excited state can be represented as:
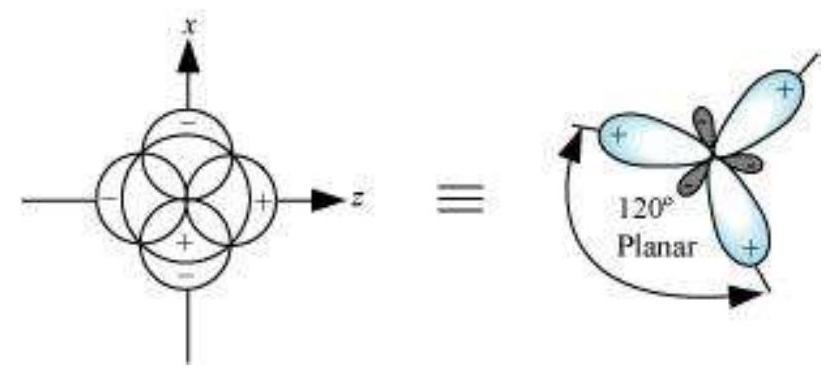
| $\uparrow$ | $\uparrow$ |
|---|
3s $\quad 3 p_x 3 p_y 3 p_z$
Hence, it undergoes $s p^{2}$ hybridization to give a trigonal planar arrangement (in $AlCl_3$ ).
To form $AlCl_4^{-}$, the empty $3 p_z$ orbital also gets involved and the hybridization changes from $s p^{2}$ to $s p^{3}$. As a result, the shape gets changed to tetrahedral.
4.26 Is there any change in the hybridisation of $\mathrm{B}$ and $\mathrm{N}$ atoms as a result of the following reaction?
$\mathrm{BF_3}+\mathrm{NH_3} \rightarrow \mathrm{F_3} \mathrm{~B} \cdot \mathrm{NH_3}$
Show Answer
Answer
Boron atom in $BF_3$ is $s p^{2}$ hybridized. The orbital picture of boron in the excited state can be shown as:
$ \underset{2s}{\boxed{\uparrow}} \quad\quad\quad \underset{2p_x}{\boxed{\uparrow}} \underset{2p_y}{\boxed{\uparrow}}\underset{2p_z}{\Large \boxed{ }}$
Nitrogen atom in $NH_3$ is $s p^{3}$ hybridized. The orbital picture of nitrogen can be represented as:
$ \underset{2s}{\boxed{\uparrow}} \quad\quad\quad \underset{2p_x}{\boxed{\uparrow}} \underset{2p_y}{\boxed{\uparrow}}\underset{2p_z}{\Large \boxed{ }}$
After the reaction has occurred, an adduct $F_3 BA \phi^{\prime \prime}{ }^{\prime \prime}{ }^{\prime} NH_3$ is formed as hybridization of ‘B’ changes to $s p^{3}$. However, the hybridization of ’ $N$ ’ remains intact.
4.27 Draw diagrams showing the formation of a double bond and a triple bond between carbon atoms in $\mathrm{C_2} \mathrm{H_4}$ and $\mathrm{C_2} \mathrm{H_2}$ molecules.
Show Answer
Answer
$C_2 H_4$ :
The electronic configuration of $C$-atom in the excited state is:
$ _6 C=1 s^{2} 2 s^{1} 2 p_x^{1} 2 p_y^{1} 2 p_z^{1}$
In the formation of an ethane molecule $(C_2 H_4)$, one $s p^{2}$ hybrid orbital of carbon overlaps a $s p^{2}$ hybridized orbital of another carbon atom, thereby forming a $C-C$ sigma bond.
The remaining two $s p^{2}$ orbitals of each carbon atom form a $s p^{2}-s$ sigma bond with two hydrogen atoms. The unhybridized orbital of one carbon atom undergoes sidewise overlap with the orbital of a similar kind present on another carbon atom to form a weak $\pi$-bond.
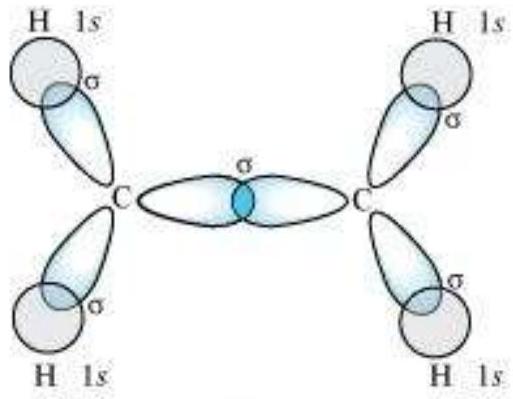
(a)
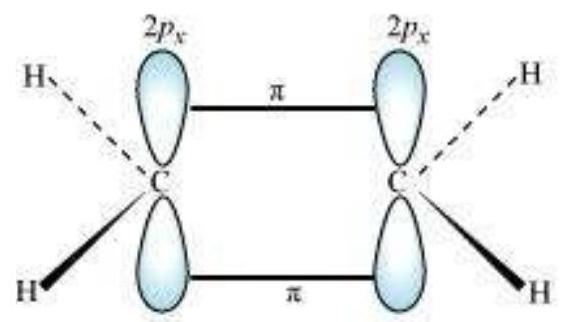
(b)
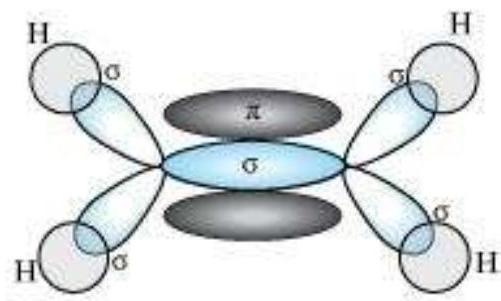
(c)
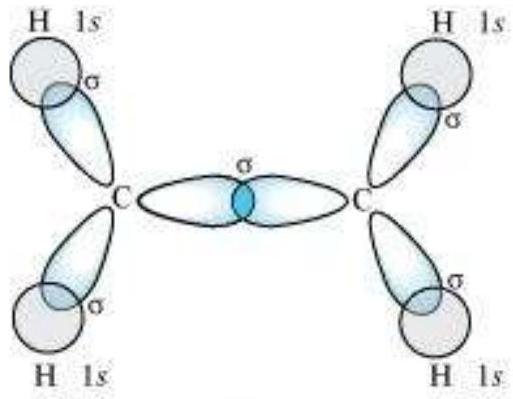
(d)
$\Large C_2 H_2$ :
In the formation of $C_2 H_2$ molecule, each C-atom is $s p$ hybridized with two $2 p$-orbitals in an unhybridized state.
One $s p$ orbital of each carbon atom overlaps with the other along the internuclear axis forming a C- $C$ sigma bond. The second $s p$ orbital of each C-atom overlaps a half-filled $1 s$-orbital to form a $ \sigma $ bond.
The two unhybridized $2 p$-orbitals of the first carbon undergo sidewise overlap with the $2 p$ orbital of another carbon atom, thereby forming two pi ( $\pi$ ) bonds between carbon atoms. Hence, the triple bond between two carbon atoms is made up of one sigma and two $\pi$-bonds.
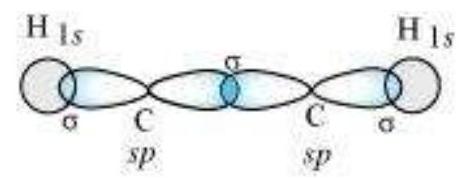
(a)
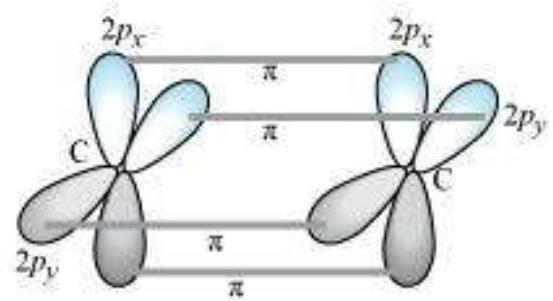
(b)
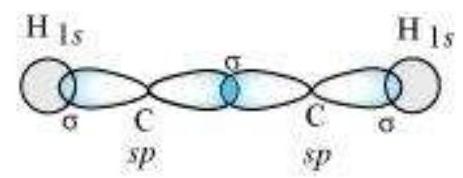
4.28 What is the total number of sigma and pi bonds in the following molecules?
(a) $\mathrm{C_2} \mathrm{H_2}$ (b) $\mathrm{C_2} \mathrm{H_4}$
Show Answer
Answer
A single bond is a result of the axial overlap of bonding orbitals. Hence, it contributes a sigma bond. A multiple bond (double or triple bond) is always formed as a result of the sidewise overlap of orbitals. A pi-bond is always present in it. A triple bond is a combination of two pi-bonds and one sigma bond.
Structure of $C_2 H_2$ can be represented as:
$H-\frac{\sigma}{\frac{\pi}{\sigma}} C \stackrel{\sigma}{-} H$
Hence, there are three sigma and two pi-bonds in $C_2 H_2$.
The structure of $C_2 H_4$ can be represented as:
Hence, there are five sigma bonds and one pi-bond in $C_2 H_4$.
4.29 Considering $x$-axis as the internuclear axis which out of the following will not form a sigma bond and why? (a) $1 \mathrm{~s}$ and $1 \mathrm{~s}$ (b) $1 \mathrm{~s}$ and $2 p_{\mathrm{x}}$; (c) $2 p_{\mathrm{y}}$ and $2 p_{\mathrm{y}}$ (d) $1 s$ and $2 s$.
Show Answer
Answer
$2 p_y$ and $2 p_y$ orbitals will not a form a sigma bond. Taking $x$-axis as the internuclear axis, $2 p_y$ and $2 p_y$ orbitals will undergo lateral overlapping, thereby forming a pi ( $\pi$ ) bond.
4.30 Which hybrid orbitals are used by carbon atoms in the following molecules? $\mathrm{CH_3}-\mathrm{CH_3}$; (b) $\mathrm{CH_3}-\mathrm{CH}=\mathrm{CH_2}$; (c) $\mathrm{CH_3}-\mathrm{CH_2}-\mathrm{OH}$; (d) $\mathrm{CH_3}-\mathrm{CHO}$ (e) $\mathrm{CH_3} \mathrm{COOH}$
Show Answer
Answer
(a)
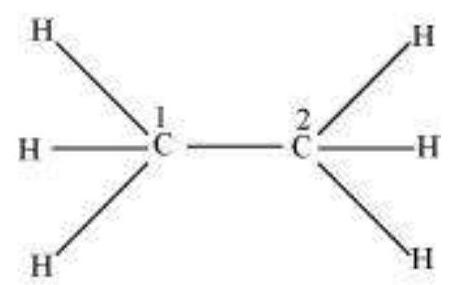
Both $C_1$ and $C_2$ are $s p^{3}$ hybridized.
(b)
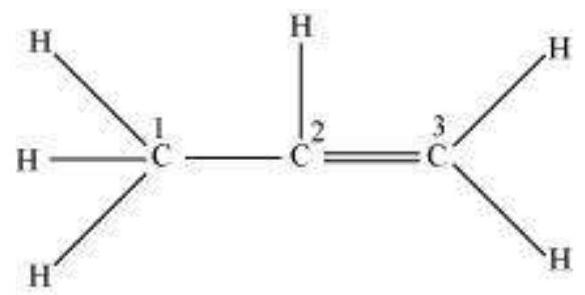
$C_1$ is $s p^{3}$ hybridized, while $C_2$ and $C_3$ are $s p^{2}$ hybridized.
(c)

Both $C_1$ and $C_2$ are $s p^{3}$ hybridized.
(d)
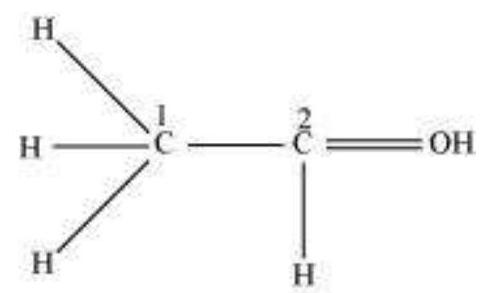
$C_1$ is $s p^{3}$ hybridized and $C_2$ is $s p^{2}$ hybridized.
(e)
 >
>
$C_1$ is $s p^{3}$ hybridized and $C_2$ is $s p^{2}$ hybridized.
4.31 What do you understand by bond pairs and lone pairs of electrons? Illustrate by giving one exmaple of each type.
Show Answer
Answer
When two atoms combine by sharing their one or more valence electrons, a covalent bond is formed between them.
The shared pairs of electrons present between the bonded atoms are called bond pairs. All valence electrons may not participate in bonding. The electron pairs that do not participate in bonding are called lone pairs of electrons.
For example, in $C_2 H_6$ (ethane), there are seven bond pairs but no lone pair present.
$\underset{\Large\mathrm{H}}{\Large\mathrm{C}}$
In $H_2 O$, there are two bond pairs and two lone pairs on the central atom (oxygen).
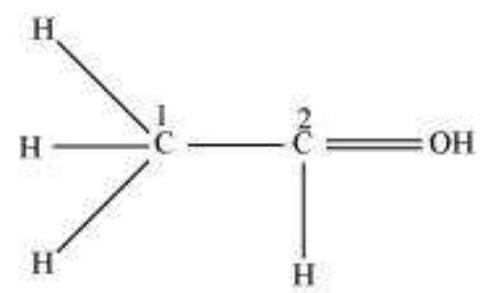
4.32 Distinguish between a sigma and a pi bond.
Show Answer
Answer
The following are the differences between sigma and pi-bonds:
| Sigma ( $ \sigma $) Bond | Pi $(\pi)$ Bond |
|---|---|
| (a) It is formed by the end to end overlap of orbitals. | It is formed by the lateral overlap of orbitals. |
| (b) The orbitals involved in the overlapping are $s -s, s- $p$, or $p - $p$. |
These bonds are formed by the overlap of $p - p$ orbitals only. |
| (c) It is a strong bond. | It is weak bond. |
| (d) The electron cloud is symmetrical about the line joining the two nuclei. |
The electron cloud is not symmetrical. |
| (e) It consists of one electron cloud, which is symmetrical about the internuclear axis. |
There are two electron clouds lying above and below the plane of the atomic nuclei. |
| (f) Free rotation about $\sigma $ bonds is possible. | Rotation is restricted in case of pi-bonds. |
4.33 Explain the formation of $\mathrm{H_2}$ molecule on the basis of valence bond theory.
Show Answer
Answer
Let us assume that two hydrogen atoms ( $A$ and $B$ ) with nuclei $(N_A.$ and $.N_B)$ and electrons $(e_A.$ and $.e_B)$ are taken to undergo a reaction to form a hydrogen molecule.
When $A$ and $B$ are at a large distance, there is no interaction between them. As they begin to approach each other, the attractive and repulsive forces start operating.
Attractive force arises between:
(a) Nucleus of one atom and its own electron i.e., $N_A-e_A$ and $N_B-e_B$.
(b) Nucleus of one atom and electron of another atom i.e., $N_A-e_B$ and $N_B-e_A$
Repulsive force arises between:
(a) Electrons of two atoms i.e., $e_A-e_B$
(b) Nuclei of two atoms i.e., $N_A-N_B$.
The force of attraction brings the two atoms together, whereas the force of repulsion tends to push them apart.
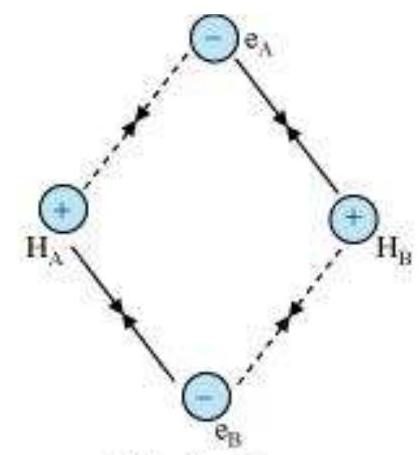
Attractive Forces
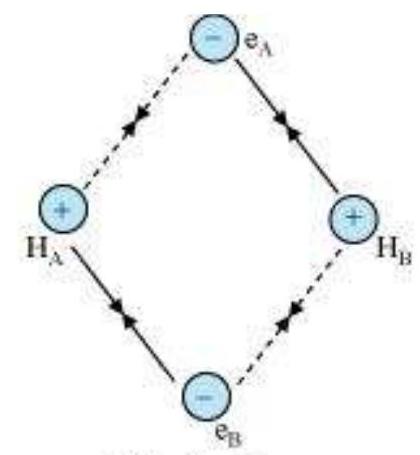
Repulsive Forces
The magnitude of the attractive forces is more than that of the repulsive forces. Hence, the two atoms approach each other. As a result, the potential energy decreases. Finally, a state is reached when the attractive forces balance the repulsive forces and the system acquires minimum energy. This leads to the formation of a dihydrogen molecule.
4.34 Write the important conditions required for the linear combination of atomic orbitals to form molecular orbitals.
Show Answer
Answer
The given conditions should be satisfied by atomic orbitals to form molecular orbitals:
(a) The combining atomic orbitals must have the same or nearly the same energy. This means that in a homonuclear molecule, the 1s-atomic orbital of an atom can combine with the $1 s$-atomic orbital of another atom, and not with the 2s-orbital.
(b) The combining atomic orbitals must have proper orientations to ensure that the overlap is maximum.
(c) The extent of overlapping should be large.
4.35 Use molecular orbital theory to explain why the $\mathrm{Be_2}$ molecule does not exist.
Show Answer
Answer
The electronic configuration of Beryllium is $1 s^{2} 2 s^{2}$.
The molecular orbital electronic configuration for $Be_2$ molecule can be written as:
$\begin{matrix} \sigma_1^{2} & \sigma _{1 s}^{* 2} & \sigma_2^{2} & \sigma _{2 s}^{* 2}\end{matrix} $
Hence, the bond order for $Be_2$ is $\frac{1}{2}(N_b-N_a)$.
Where,
$N_b=$ Number of electrons in bonding orbitals
$N_a=$ Number of electrons in anti-bonding orbitals
$\therefore$ Bond order of $Be_2=\frac{1}{2}(4-4)=0$
A negative or zero bond order means that the molecule is unstable. Hence, $Be_2$ molecule does not exist.
4.36 Compare the relative stability of the following species and indicate their magnetic properties;
$\mathrm{O_2}, \mathrm{O}_2^{+}, \mathrm{O}_2^{-}$(superoxide), $\mathrm{O}_2^{2-}$ (peroxide)
Show Answer
Answer
There are 16 electrons in a molecule of dioxygen, 8 from each oxygen atom. The electronic configuration of oxygen molecule can be written as:
$ [\sigma - (1s)]^2 [\sigma^*(is)]^2 [\sigma (2s)]^2[\sigma (1p_z)]^2[\pi (2p_x)]_2[\pi (2p_y)]^2 [\pi(2p_x)]^1 [\pi (2p_y)]^1 $ Since the $1 s$ orbital of each oxygen atom is not involved in boding, the number of bonding electrons $=8=N_b$ and the number of anti-bonding orbitals $=4=N _{\text{a }}$.
Bond order $=\frac{1}{2}(N_b-N_a)$
$=\frac{1}{2}(8-4)$
$=2$
Similarly, the electronic configuration of $O_2^{+}$can be written as:
$KK[\sigma(2 s)]^{2}[\sigma(2 s)]^{2}[\sigma(2 p_z)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{2}[\pi (2 p_x)]^{1}$
$N_b=8$
$N_a=3$
Bond order of $O_2^{+}=\frac{1}{2}(8-3)$ $=2.5$
Electronic configuration of $O_2^{-}$ion will be:
$KK[\sigma(2 s)]^{2}[\sigma(2 s)]^{2}[\sigma(2 p_z)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{1}$
$N_b=8$
$N_a=5$
Bond order of $O_2^{-}=\frac{1}{2}(8-5)$
$=1.5$
Electronic configuration of $O_2^{2-}$ ion will be:
$KK[\sigma(2 s)]^{2}[\sigma(2 s)]^{2}[\sigma(2 p_z)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{2}$
$N_b=8$
$N_a=6$
Bond order of $O_2^{2-}=\frac{1}{2}(8-6)$
$=1$
Bond dissociation energy is directly proportional to bond order. Thus, the higher the bond order, the greater will be the stability. On this basis, the order of stability is $O_2^{+}>O_2>O_2^{-}>O_2^{2-}$.
4.37 Write the significance of a plus and a minus sign shown in representing the orbitals.
Show Answer
Answer
Molecular orbitals are represented by wave functions. A plus sign in an orbital indicates a positive wave function while a minus sign in an orbital represents a negative wave function.
4.38 Describe the hybridisation in case of $\mathrm{PCl_5}$. Why are the axial bonds longer as compared to equatorial bonds?
Show Answer
Answer
The ground state and excited state outer electronic configurations of phosphorus $(Z=15)$ are:
Ground state:
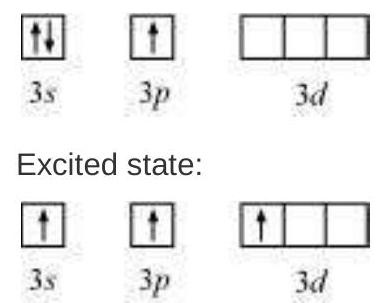
Phosphorus atom is $s p^{3} d$ hybridized in the excited state. These orbitals are filled by the electron pairs donated by five $Cl$ atoms as:
$PCl_5$
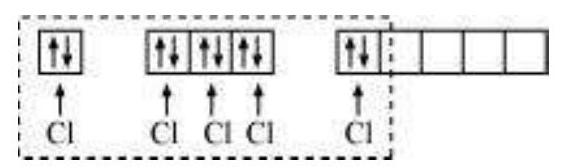
The five $s p^{3} d$ hybrid orbitals are directed towards the five corners of the trigonal bipyramidals. Hence, the geometry of $PCl_5$ can be represented as:
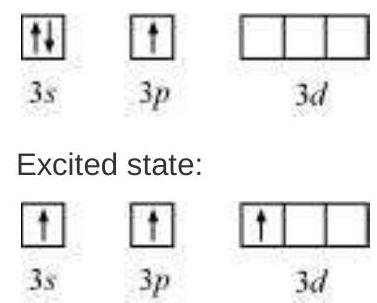
There are five $P-Cl$ sigma bonds in $PCl_5$. Three $P-Cl$ bonds lie in one plane and make an angle of $120^{\circ}$ with each other. These bonds are called equatorial bonds.
The remaining two $P-Cl$ bonds lie above and below the equatorial plane and make an angle of $90^{\circ}$ with the plane. These bonds are called axial bonds.
As the axial bond pairs suffer more repulsion from the equatorial bond pairs, axial bonds are slightly longer than equatorial bonds.
4.39 Define hydrogen bond. Is it weaker or stronger than the van der Waals forces?
Show Answer
Answer
A hydrogen bond is defined as an attractive force acting between the hydrogen attached to an electronegative atom of one molecule and an electronegative atom of a different molecule (may be of the same kind).
Due to a difference between electronegativities, the bond pair between hydrogen and the electronegative atom gets drifted far away from the hydrogen atom. As a result, a hydrogen atom becomes electropositive with respect to the other atom and acquires a positive charge. $4^{\delta}-X^{\delta-} \ldots \ldots . . H^{\delta+}-X^{\delta-} \ldots \ldots . . H^{\delta+}-X^{\delta-}$
The magnitude of $H$-bonding is maximum in the solid state and minimum in the gaseous state.
There are two types of $H$-bonds:
(i) Intermolecular $H$-bond e.g., $HF, H_2 O$ etc.
(ii) Intramolecular H-bond e.g., o-nitrophenol
Hydrogen bonds are stronger than Van der Walls forces since hydrogen bonds are regarded as an extreme form of dipole-dipole interaction.
4.40 What is meant by the term bond order? Calculate the bond order of : $\mathrm{N_2}, \mathrm{O_2}, \mathrm{O_2}^{+}$ and $\mathrm{O_2}^{-}$.
Show Answer
Answer
Bond order is defined as one half of the difference between the number of electrons present in the bonding and antibonding orbitals of a molecule.
If $N_a$ is equal to the number of electrons in an anti-bonding orbital, then $N_b$ is equal to the number of electrons in a bonding orbital.
Bond order $=\frac{1}{2}(N_b-N_a)$
If $N_b>N_a$, then the molecule is said be stable. However, if $N_b \leq N_a$, then the molecule is considered to be unstable.
Bond order of $N_2$ can be calculated from its electronic configuration as:
$\sigma(1s)^2 \sigma*(1s)2 \sigma(2s)^2 \sigma*(2s)2 \pi(2p_x)^2 \pi(2p_y)^2 \sigma(2p_z)^2$
Number of bonding electrons, $N_b=10$
Number of anti-bonding electrons, $N_a=4$
Bond order of nitrogen molecule $=\frac{1}{2}(10-4)$
$=3$
There are 16 electrons in a dioxygen molecule, 8 from each oxygen atom. The electronic configuration of oxygen molecule can be written as:
$ [ \sigma(1s)^2 \sigma*(1s)2 \sigma(2s)^2 \sigma*(2s)2 \sigma(1p_z)^2 \pi(2p_x)^2 \pi(2p_y)^2 \pi*(2p_x)1 \pi*(2p_y)1 ] $
Since the $1 s$ orbital of each oxygen atom is not involved in boding, the number of bonding electrons $=8=N_b$ and the number of anti-bonding electrons $=4=N _{\text{a }}$.
Bond order $=\frac{1}{2}(N_b-N_a)$
$=\frac{1}{2}(8-4)$
$=2$
Hence, the bond order of oxygen molecule is 2 .
Similarly, the electronic configuration of $O_2^{+}$can be written as:
$[ \sigma(2s)^2 \sigma*(2s)2 \sigma(2p_z)^2 \pi(2p_x)^2 \pi(2p_y)^2 \pi*(2p_x)1 ]$
$N_b=8$
$N_a=3$
Bond order of $O_2^{+}=\frac{1}{2}(8-3)$
$=2.5$
Thus, the bond order of $O_2^{+}$is 2.5.
The electronic configuration of $O_2^{-}$ion will be:
$ [ \sigma(2s)^2 \sigma*(2s)2 \sigma(2p_z)^2 \pi(2p_x)^2 \pi(2p_y)^2 \pi*(2p_x)2 \pi*(2p_y)1 ] $
$N_b=8$
$N_a=5$
Bond order of $O_2^{-}=\frac{1}{2}(8-5)$
$=1.5$
Thus, the bond order of $O_2^{-}$ion is 1.5.










