Answer

(a) When $1 \Omega$ and $10^{6} \Omega$ are connected in parallel:

Let $R$ be the equivalent resistance.

$ \begin{aligned} & \therefore \dfrac{1}{R}=\dfrac{1}{1}+\dfrac{1}{10^{6}} \\ & R=\dfrac{10^{6}}{1+10^{6}} \approx \dfrac{10^{6}}{10^{6}}=1 \Omega \end{aligned} $

Therefore, equivalent resistance $\approx 1 \Omega$

(b) When $1 \Omega, 103 \Omega$ and $106 \Omega$ are connected in parallel:

Let $R$ be the equivalent resistance.

$ \begin{aligned} & \dfrac{1}{R}=\dfrac{1}{1}+\dfrac{1}{10^{3}}+\dfrac{1}{10^{6}} \dfrac{10^{6}+10^{3}+1}{10^{6}} \\ & R=\dfrac{1000000}{1001001}=0.999 \Omega \end{aligned} $

Therefore, equivalent resistance $=0.999 \Omega$

Answer

Resistance of electric lamp, $R_1=100 \Omega$

Resistance of toaster, $R_2=50 \Omega$

Resistance of water filter, $R_3=500 \Omega$

Potential difference of the source, $V=220 V$

These are connected in parallel, as shown in the following figure. $R_1=100 \Omega$

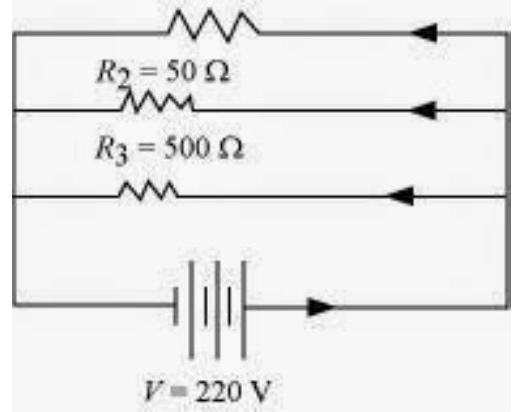
Let $R$ be the equivalent resistance of the circuit. $\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{100}+\dfrac{1}{50}+\dfrac{1}{500}$

According to Ohm’s law,

$V=I R$

$I=\dfrac{V}{R}$

Where,

Current flowing through the circuit $=I$

$I=\dfrac{220}{\dfrac{500}{16}}=\dfrac{220 / 16}{50}=7.04 A$

7.04 A of current is drawn by all the three given appliances.

Therefore, current drawn by an electric iron connected to the same source of potential $220 V=7.04 A$

Let $R^{\prime}$ be the resistance of the electric iron. According to Ohm’s law,

$V=I R^{\prime}$

$R^{\prime}=\dfrac{V}{I}=\dfrac{220}{7.04}=31.25 \Omega$

Therefore, the resistance of the electric iron is $31.25 \Omega$ and the current flowing through it is $7.04 A$.

Answer

There is no division of voltage among the appliances when connected in parallel. The potential difference across each appliance is equal to the supplied voltage.

The total effective resistance of the circuit can be reduced by connecting electrical appliances in parallel.

Answer

There are three resistors of resistances $2 \Omega, 3 \Omega$, and $6 \Omega$ respectively.

(a) The following circuit diagram shows the connection of the three resistors.

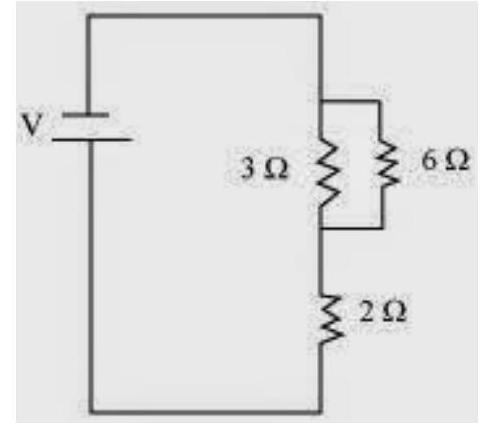
Here, $6 \Omega$ and $3 \Omega$ resistors are connected in parallel.

Therefore, their equivalent resistance will be given by

$ \dfrac{1}{\dfrac{1}{6}+\dfrac{1}{3}}=\dfrac{6 \times 3}{6+3}=2 \Omega $

This equivalent resistor of resistance $2 \Omega$ is connected to a $2 \Omega$ resistor in series.

Therefore, the equivalent resistance of the circuit $=2 \Omega+2 \Omega=4 \Omega$

Hence the total resistance of the circuit is $4 \Omega$.

(b) The following circuit diagram shows the connection of the three resistors.

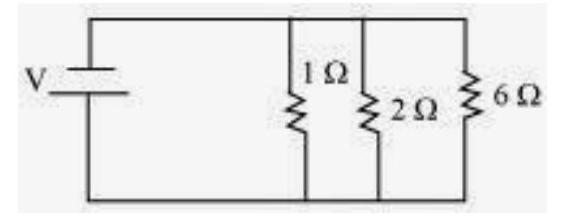
All the resistors are connected in series. Therefore, their equivalent resistance will be given as

$ \dfrac{1}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}}=\dfrac{1}{\dfrac{3+2+1}{6}}=\dfrac{6}{6}=1 \Omega $

Therefore, the total resistance of the circuit is $1 \Omega$.

Answer

There are four coils of resistances $4 \Omega, 8 \Omega, 12 \Omega$ and $24 \Omega$ respectively.

(a) If these coils are connected in series, then the equivalent resistance will be the highest, given by the sum $4+8+12+24=48 \Omega$

(b) If these coils are connected in parallel, then the equivalent resistance will be the lowest, given by

$ \dfrac{1}{\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{12}+\dfrac{1}{24}}=\dfrac{1}{\dfrac{6+3+2+1}{24}}=\dfrac{24}{12}=2 \Omega $

Therefore, $2 \Omega$ is the lowest total resistance.