Chapter 09 Light – Reflection and Refraction
We see a variety of objects in the world around us. However, we are unable to see anything in a dark room. On lighting up the room, things become visible. What makes things become visible. What makes things visible? During the day, the sunlight helps us to see objects. An object reflects light that falls on it. This reflected light, when received by our eyes, enables us to see things. We are able to see through a transparent medium as light is transmitted through it. There are a number of common wonderful phenomena associated with light such as image formation by mirrors, the twinkling of stars, the beautiful colours of a rainbow, bending of light by a medium and so on. A study of the properties of light helps us to explore them.
By observing the common optical phenomena around us, we may conclude that light seems to travel in straight lines. The fact that a small source of light casts a sharp shadow of an opaque object points to this straight-line path of light, usually indicated as a ray of light.
More to Know!
If an opaque object on the path of light becomes very small, light has a tendency to bend around it and not walk in a straight line - an effect known as the diffraction of light. Then the straight-line treatment of optics using rays fails. To explain phenomena such as diffraction, light is thought of as a wave, the details of which you will study in higher classes. Again, at the beginning of the
century, it became known that the wave theory of light often becomes inadequate for treatment of the interaction of light with matter, and light often behaves somewhat like a stream of particles. This confusion about the true nature of light continued for some years till a modern quantum theory of light emerged in which light is neither a ‘wave’ nor a ‘particle’ - the new theory reconciles the particle properties of light with the wave nature.
In this Chapter, we shall study the phenomena of reflection and refraction of light using the straight-line propagation of light. These basic concepts will help us in the study of some of the optical phenomena in nature. We shall try to understand in this Chapter the reflection of light by spherical mirrors and refraction of light and their application in real life situations.
9.1 REFLECTION OF LIGHT
A highly polished surface, such as a mirror, reflects most of the light falling on it. You are already familiar with the laws of reflection of light.
Let us recall these laws -
(i) The angle of incidence is equal to the angle of reflection, and
(ii) The incident ray, the normal to the mirror at the point of incidence and the reflected ray, all lie in the same plane.
These laws of reflection are applicable to all types of reflecting surfaces including spherical surfaces. You are familiar with the formation of image by a plane mirror. What are the properties of the image? Image formed by a plane mirror is always virtual and erect. The size of the image is equal to that of the object. The image formed is as far behind the mirror as the object is in front of it. Further, the image is laterally inverted. How would the images be when the reflecting surfaces are curved? Let us explore.
Activity 9.1
- Take a large shining spoon. Try to view your face in its curved surface.
- Do you get the image? Is it smaller or larger?
- Move the spoon slowly away from your face. Observe the image. How does it change?
- Reverse the spoon and repeat the Activity. How does the image look like now?
- Compare the characteristics of the image on the two surfaces.
The curved surface of a shining spoon could be considered as a curved mirror. The most commonly used type of curved mirror is the spherical mirror. The reflecting surface of such mirrors can be considered to form a part of the surface of a sphere. Such mirrors, whose reflecting surfaces are spherical, are called spherical mirrors. We shall now study about spherical mirrors in some detail.
9.2 SPHERICAL MIRRORS
The reflecting surface of a spherical mirror may be curved inwards or outwards. A spherical mirror, whose reflecting surface is curved inwards, that is, faces towards the centre of the sphere, is called a concave mirror. A spherical mirror whose reflecting surface is curved outwards, is called a convex mirror. The schematic representation of these mirrors is shown in Fig. 9.1. You may note in these diagrams that the back of the mirror is shaded.
You may now understand that the surface of the spoon curved inwards can be approximated to a concave mirror and the surface of the spoon bulged outwards can be approximated to a convex mirror.
Before we move further on spherical mirrors, we need to recognise and understand the meaning of a few terms. These terms are commonly used in discussions about spherical mirrors. The centre of the reflecting surface of a spherical mirror is a point called the pole. It lies on the surface of the mirror. The pole is usually represented by the letter

Figure 9.1 Schematic representation of spherical mirrors; the shaded side is non-reflecting.
The reflecting surface of a spherical mirror forms a part of a sphere. This sphere has a centre. This point is called the centre of curvature of the spherical mirror. It is represented by the letter
Activity 9.2
CAUTION: Do not look at the Sun directly or even into a mirror reflecting sunlight. It may damage your eyes.
- Hold a concave mirror in your hand and direct its reflecting surface towards the Sun.
- Direct the light reflected by the mirror on to a sheet of paper held close to the mirror.
- Move the sheet of paper back and forth gradually until you find on the paper sheet a bright, sharp spot of light.
- Hold the mirror and the paper in the same position for a few minutes. What do you observe? Why?
The paper at first begins to burn producing smoke. Eventually it may even catch fire. Why does it burn? The light from the Sun is converged at a point, as a sharp, bright spot by the mirror. In fact, this spot of light is the image of the Sun on the sheet of paper. This point is the focus of the concave mirror. The heat produced due to the concentration of sunlight ignites the paper. The distance of this image from the position of the mirror gives the approximate value of focal length of the mirror.
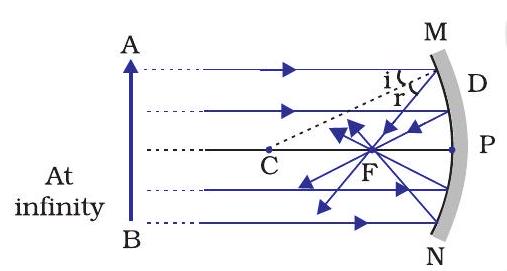
(a)
(b)
Figure 9.2 (a) Concave mirror (b) Convex mirror
Let us try to understand this observation with the help of a ray diagram.
Observe Fig.9.2 (a) closely. A number of rays parallel to the principal axis are falling on a concave mirror. Observe the reflected rays. They are all meeting/intersecting at a point on the principal axis of the mirror. This point is called the principal focus of the concave mirror. Similarly, observe Fig. 9.2 (b). How are the rays parallel to the principal axis, reflected by a convex mirror? The reflected rays appear to come from a point on the principal axis. This point is called the principal focus of the convex mirror. The principal focus is represented by the letter
The reflecting surface of a spherical mirror is by-and-large spherical. The surface, then, has a circular outline. The diameter of the reflecting surface of spherical mirror is called its aperture. In Fig.9.2, distance MN represents the aperture. We shall consider in our discussion only such spherical mirrors whose aperture is much smaller than its radius of curvature.
Is there a relationship between the radius of curvature
9.2.1 Image Formation by Spherical Mirrors
You have studied about the image formation by plane mirrors. You also know the nature, position and relative size of the images formed by them. How about the images formed by spherical mirrors? How can we locate the image formed by a concave mirror for different positions of the object? Are the images real or virtual? Are they enlarged, diminished or have the same size? We shall explore this with an Activity.
Activity 9.3
- You have already learnt a way of determining the focal length of a concave mirror. In Activity 9.2, you have seen that the sharp bright spot of light you got on the paper is, in fact, the image of the Sun. It was a tiny, real, inverted image. You got the approximate focal length of the concave mirror by measuring the distance of the image from the mirror.
- Take a concave mirror. Find out its approximate focal length in the way described above. Note down the value of focal length. (You can also find it out by obtaining image of a distant object on a sheet of paper.)
- Mark a line on a Table with a chalk. Place the concave mirror on a stand. Place the stand over the line such that its pole lies over the line.
- Draw with a chalk two more lines parallel to the previous line such that the distance between any two successive lines is equal to the focal length of the mirror. These lines will now correspond to the positions of the points
and , respectively. Remember For a spherical mirror of small aperture, the principal focus lies mid-way between the pole and the centre of curvature . - Keep a bright object, say a burning candle, at a position far beyond C. Place a paper screen and move it in front of the mirror till you obtain a sharp bright image of the candle flame on it.
- Observe the image carefully. Note down its nature, position and relative size with respect to the object size.
- Repeat the activity by placing the candle - (a) just beyond C, (b) at
, (c) between and , (d) at , and (e) between and . - In one of the cases, you may not get the image on the screen. Identify the position of the object in such a case. Then, look for its virtual image in the mirror itself.
- Note down and tabulate your observations.
You will see in the above Activity that the nature, position and size of the image formed by a concave mirror depends on the position of the object in relation to points
Table 9.1 Image formation by a concave mirror for different positions of the object
| Position of the object | Position of the image | Size of the image Highly diminished, point-sized | Nature of the image |
|---|---|---|---|
| At infinity | At the focus F | Diminished | Real and inverted |
| Beyond C | Between F and C | Same size | Real and inverted |
| At C | At C | Enlarged | Real and inverted |
| Between C and F | Beyond C | Highly enlarged | Real and inverted |
| At F | At infinity | Enlarged | Virtual and erect |
| Between P and F | Behind the mirror |
9.2.2 Representation of Images Formed by Spherical Mirrors Using Ray Diagrams
We can also study the formation of images by spherical mirrors by drawing ray diagrams. Consider an extended object, of finite size, placed in front of a spherical mirror. Each small portion of the extended object acts like a point source. An infinite number of rays originate from each of these points. To construct the ray diagrams, in order to locate the image of an object, an arbitrarily large number of rays emanating from a point could be considered. However, it is more convenient to consider only two rays, for the sake of clarity of the ray diagram. These rays are so chosen that it is easy to know their directions after reflection from the mirror.
The intersection of at least two reflected rays give the position of image of the point object. Any two of the following rays can be considered for locating the image.
(i) A ray parallel to the principal axis, after reflection, will pass through the principal focus in case of a concave mirror or appear to diverge from the principal focus in case of a convex mirror. This is illustrated in Fig.9.3 (a) and (b).

Figure 9.3
(ii) A ray passing through the principal focus of a concave mirror or a ray which is directed towards the principal focus of a convex mirror, after reflection, will emerge parallel to the principal axis. This is illustrated in Fig. 9.4 (a) and (b).

Figure 9.4
(iii) A ray passing through the centre of curvature of a concave mirror or directed in the direction of the centre of curvature of a convex mirror, after reflection, is reflected back along the same path. This is illustrated in Fig. 9.5 (a) and (b). The light rays come back along the same path because the incident rays fall on the mirror along the normal to the reflecting surface.

Figure 9.5
(iv) A ray incident obliquely to the principal axis, towards a point

Figure 9.6
Remember that in all the above cases the laws of reflection are followed. At the point of incidence, the incident ray is reflected in such a way that the angle of reflection equals the angle of incidence.
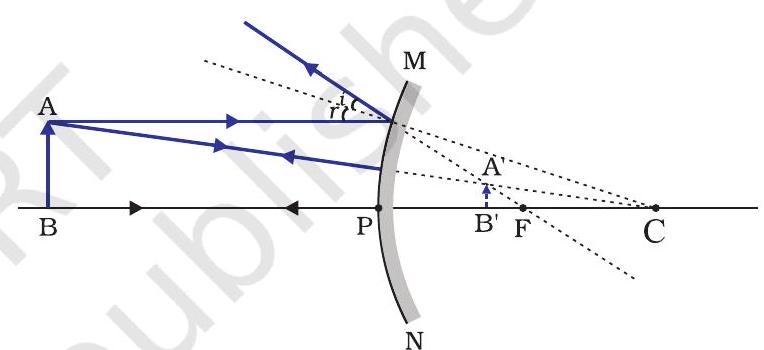
(a) Image formation by Concave Mirror
Figure 9.7 illustrates the ray diagrams for the formation of image by a concave mirror for various positions of the object.

Figure 9.7 Ray diagrams for the image formation by a concave mirror
Activity 9.4
- Draw neat ray diagrams for each position of the object shown in Table 9.1.
- You may take any two of the rays mentioned in the previous section for locating the image.
- Compare your diagram with those given in Fig. 9.7.
- Describe the nature, position and relative size of the image formed in each case.
- Tabulate the results in a convenient format.
Uses of concave mirrors
Concave mirrors are commonly used in torches, search-lights and vehicles headlights to get powerful parallel beams of light. They are often used as shaving mirrors to see a larger image of the face. The dentists use concave mirrors to see large images of the teeth of patients. Large concave mirrors are used to concentrate sunlight to produce heat in solar furnaces.
(b) Image formation by a Convex Mirror
We studied the image formation by a concave mirror. Now we shall study the formation of image by a convex mirror.
Activity 9.5
- Take a convex mirror. Hold it in one hand.
- Hold a pencil in the upright position in the other hand.
- Observe the image of the pencil in the mirror. Is the image erect or inverted? Is it diminished or enlarged?
- Move the pencil away from the mirror slowly. Does the image become smaller or larger?
- Repeat this Activity carefully. State whether the image will move closer to or farther away from the focus as the object is moved away from the mirror?
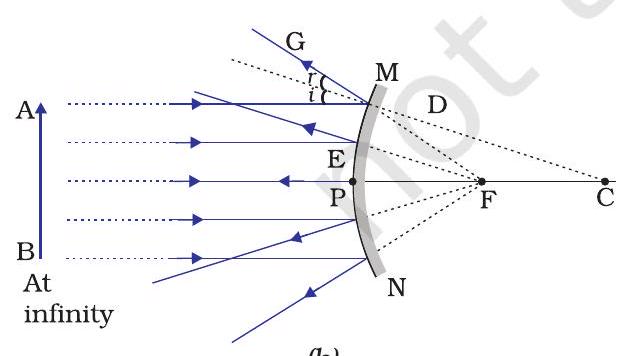
We consider two positions of the object for studying the image formed by a convex mirror. First is when the object is at infinity and the second position is when the object is at a finite distance from the mirror. The ray diagrams for the formation of image by a convex mirror for these two positions of the object are shown in Fig. 9.8 (a) and (b), respectively. The results are summarised in Table 9.2.
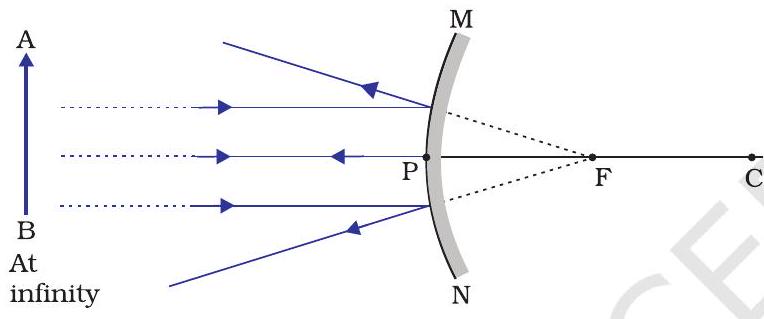
(a)
(b)
Figure 9.8 Formation of image by a convex mirror
Table 9.2 Nature, position and relative size of the image formed by a convex mirror
| Position of the object | Position of the image | Size of the image | Nature of the image |
|---|---|---|---|
| At infinity | At the focus F, behind the mirror | Highly diminished, point-sized | Virtual and erect |
| Between infinity and the pole P of the mirror | Between P and F, behind the mirror | Diminished | Virtual and erect |
You have so far studied the image formation by a plane mirror, a concave mirror and a convex mirror. Which of these mirrors will give the full image of a large object? Let us explore through an Activity.
Activity 9.6
- Observe the image of a distant object, say a distant tree, in a plane mirror.
- Could you see a full-length image?
- Try with plane mirrors of different sizes. Did you see the entire object in the image?
- Repeat this Activity with a concave mirror. Did the mirror show full length image of the object?
- Now try using a convex mirror. Did you succeed? Explain your observations with reason.
You can see a full-length image of a tall building/tree in a small convex mirror. One such mirror is fitted in a wall of Agra Fort facing Taj Mahal. If you visit the Agra Fort, try to observe the full image of Taj Mahal. To view distinctly, you should stand suitably at the terrace adjoining the wall.
Uses of convex mirrors
Convex mirrors are commonly used as rear-view (wing) mirrors in vehicles. These mirrors are fitted on the sides of the vehicle, enabling the driver to see traffic behind him/her to facilitate safe driving. Convex mirrors are preferred because they always give an erect, though diminished, image. Also, they have a wider field of view as they are curved outwards. Thus, convex mirrors enable the driver to view much larger area than would be possible with a plane mirror.
Questions
1. Define the principal focus of a concave mirror.
Show Answer
Answer
Light rays that are parallel to the principal axis of a concave mirror converge at a specific point on its principal axis after reflecting from the mirror. This point is known as the principal focus of the concave mirror.
2. The radius of curvature of a spherical mirror is 20 cm. What is its focal length?
Show Answer
Answer
Radius of curvature,
Radius of curvature of a spherical mirror
Hence, the focal length of the given spherical mirror is
3. Name a mirror that can give an erect and enlarged image of an object.
Show Answer
Answer
When an object is placed between the pole and the principal focus of a concave mirror, the image formed is virtual, erect, and enlarged.
4. Why do we prefer a convex mirror as a rear-view mirror in vehicles?
Show Answer
Answer
Convex mirrors give a virtual, erect, and diminished image of the objects placed in front of them. They are preferred as a rear-view mirror in vehicles because they give a wider field of view, which allows the driver to see most of the traffic behind him.
9.2.3 Sign Convention for Reflection by Spherical Mirrors
While dealing with the reflection of light by spherical mirrors, we shall follow a set of sign conventions called the New Cartesian Sign Convention. In this convention, the pole (P) of the mirror is taken as the origin (Fig. 9.9). The principal axis of the mirror is taken as the
(i) The object is always placed to the left of the mirror. This implies that the light from the object falls on the mirror from the left-hand side.
(ii) All distances parallel to the principal axis are measured from the pole of the mirror.
(iii) All the distances measured to the right of the origin (along
(iv) Distances measured perpendicular to and above the principal axis (along
(v) Distances measured perpendicular to and below the principal axis (along
The New Cartesian Sign Convention described above is illustrated in Fig.9.9 for your reference. These sign conventions are applied to obtain the mirror formula and solve related numerical problems.
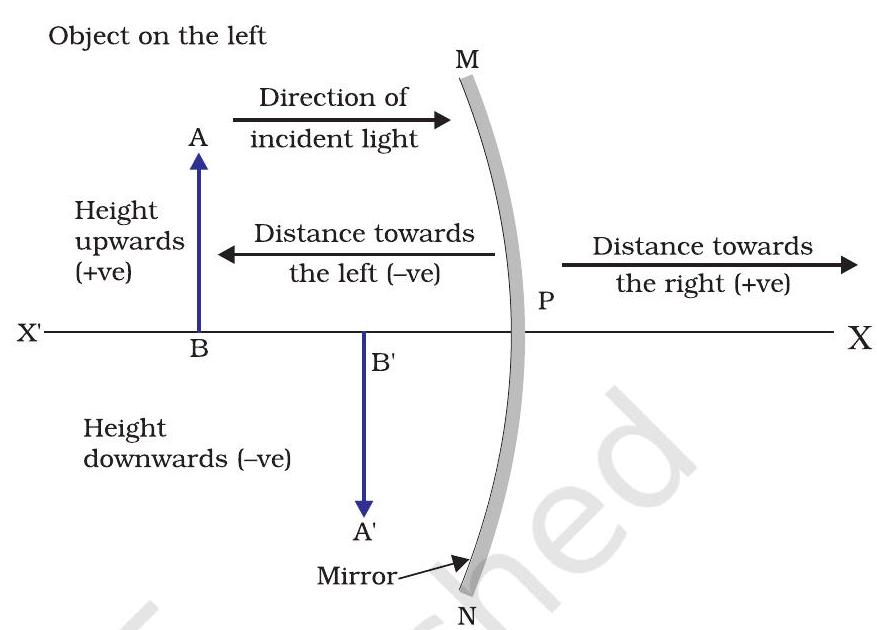
Figure 9.9 The New Cartesian Sign Convention for spherical mirrors
9.2.4 Mirror Formula and Magnification
In a spherical mirror, the distance of the object from its pole is called the object distance
This formula is valid in all situations for all spherical mirrors for all positions of the object. You must use the New Cartesian Sign Convention while substituting numerical values for
Magnification
Magnification produced by a spherical mirror gives the relative extent to which the image of an object is magnified with respect to the object size. It is expressed as the ratio of the height of the image to the height of the object. It is usually represented by the letter
If
The magnification
You may note that the height of the object is taken to be positive as the object is usually placed above the principal axis. The height of the image should be taken as positive for virtual images. However, it is to be taken as negative for real images. A negative sign in the value of the magnification indicates that the image is real. A positive sign in the value of the magnification indicates that the image is virtual.
Example 9.1
A convex mirror used for rear-view on an automobile has a radius of curvature of
Solution
Radius of curvature,
Object-distance,
Image-distance,
Height of the image,
Focal length,
Since
or,
The image is
Magnification,
The image is virtual, erect and smaller in size by a factor of 0.23 .
Example 9.2
An object,
Solution
Object-size,
Object-distance,
Focal length,
Image-distance,
Image-size,
From Eq. (10.1):
or,
The screen should be placed at
Also, magnification,
or,
Height of the image,
The image is inverted and enlarged.
Questions
1. Find the focal length of a convex mirror whose radius of curvature is
Show Answer
Answer
Radius of curvature,
Radius of curvature
Hence, the focal length of the given convex mirror is
2. A concave mirror produces three times magnified (enlarged) real image of an object placed at
Show Answer
Answer
Magnification produced by a spherical mirror is given by the relation,
Let the height of the object, ho
Then, height of the image,
Object distance,
Here, the negative sign indicates that an inverted image is formed at a distance of 30
9.3 REFRACTION OF LIGHT
Light seems to travel along straight-line paths in a transparent medium. What happens when light enters from one transparent medium to another? Does it still move along a straight-line path or change its direction? We shall recall some of our day-to-day experiences.
You might have observed that the bottom of a tank or a pond containing water appears to be raised. Similarly, when a thick glass slab is placed over some printed matter, the letters appear raised when viewed through the glass slab. Why does it happen? Have you seen a pencil partly immersed in water in a glass tumbler? It appears to be displaced at the interface of air and water. You might have observed that a lemon kept in water in a glass tumbler appears to be bigger than its actual size, when viewed from the sides. How can you account for such experiences?
Let us consider the case of the apparent displacement of a pencil, partly immersed in water. The light reaching you from the portion of the pencil inside water seems to come from a different direction, compared to the part above water. This makes the pencil appear to be displaced at the interface. For similar reasons, the letters appear to be raised, when seen through a glass slab placed over it.
Does a pencil appear to be displaced to the same extent, if instead of water, we use liquids like kerosene or turpentine? Will the letters appear to rise to the same height if we replace a glass slab with a transparent plastic slab? You will find that the extent of the effect is different for different pair of media. These observations indicate that light does not travel in the same direction in all media. It appears that when travelling obliquely from one medium to another, the direction of propagation of light in the second medium changes. This phenomenon is known as refraction of light. Let us understand this phenomenon further by doing a few activities.
Activity 9.7
- Place a coin at the bottom of a bucket filled with water.
- With your eye to a side above water, try to pick up the coin in one go. Did you succeed in picking up the coin?
- Repeat the Activity. Why did you not succeed in doing it in one go?
- Ask your friends to do this. Compare your experience with theirs.
Activity 9.8
- Place a large shallow bowl on a Table and put a coin in it.
- Move away slowly from the bowl. Stop when the coin just disappears from your sight.
- Ask a friend to pour water gently into the bowl without disturbing the coin.
- Keep looking for the coin from your position. Does the coin becomes visible again from your position? How could this happen?
The coin becomes visible again on pouring water into the bowl. The coin appears slightly raised above its actual position due to refraction of light.
Activity 9.9
- Draw a thick straight line in ink, over a sheet of white paper placed on a Table.
- Place a glass slab over the line in such a way that one of its edges makes an angle with the line.
- Look at the portion of the line under the slab from the sides. What do you observe? Does the line under the glass slab appear to be bent at the edges?
- Next, place the glass slab such that it is normal to the line. What do you observe now? Does the part of the line under the glass slab appear bent?
- Look at the line from the top of the glass slab. Does the part of the line, beneath the slab, appear to be raised? Why does this happen?
9.3.1 Refraction through a Rectangular Glass Slab
To understand the phenomenon of refraction of light through a glass slab, let us do an Activity.
Activity 9.10
- Fix a sheet of white paper on a drawing board using drawing pins.
- Place a rectangular glass slab over the sheet in the middle.
- Draw the outline of the slab with a pencil. Let us name the outline as
. - Take four identical pins.
- Fix two pins, say
and , vertically such that the line joining the pins is inclined to the edge AB. - Look for the images of the pins
and through the opposite edge. Fix two other pins, say and , such that these pins and the images of and lie on a straight line. - Remove the pins and the slab.
- Join the positions of tip of the pins
and and produce the line up to . Let meet at . Similarly, join the positions of tip of the pins and and produce it up to the edge . Let meet at . - Join
and . Also produce up to , as shown by a dotted line in Fig. 9.10.
In this Activity, you will note, the light ray has changed its direction at points
In Fig. 9.10, a ray EO is obliquely incident on surface
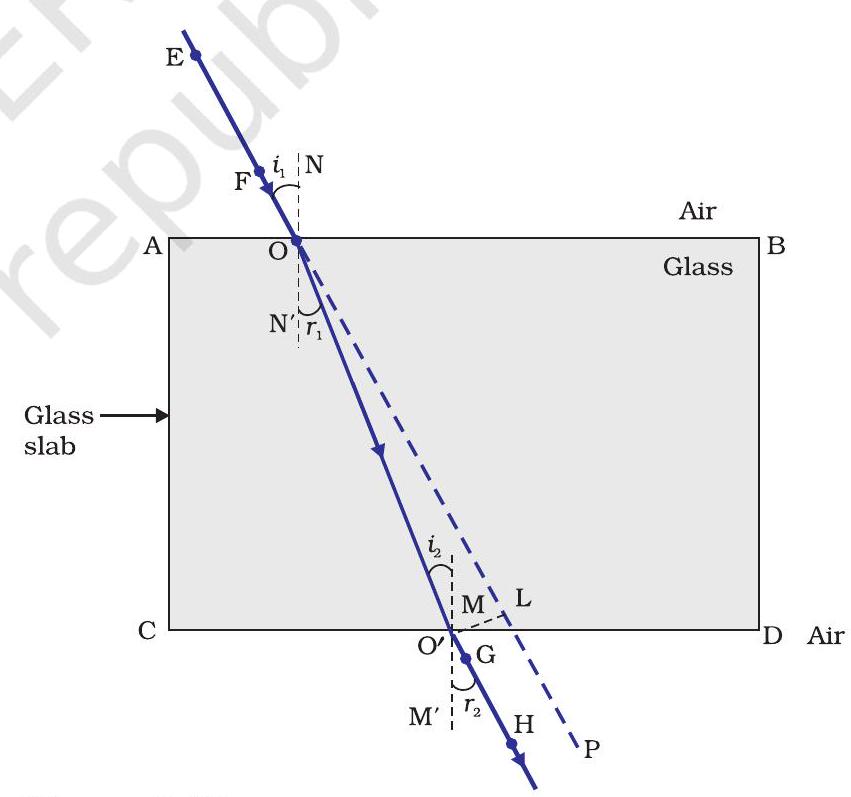
Figure 9.10 Refraction of light through a rectangular glass slab
Now you are familiar with the refraction of light. Refraction is due to change in the speed of light as it enters from one transparent medium to another. Experiments show that refraction of light occurs according to certain laws.
The following are the laws of refraction of light.
(i) The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the same plane.
(ii) The ratio of sine of angle of incidence to the sine of angle of refraction is a constant, for the light of a given colour and for the given pair of media. This law is also known as Snell’s law of refraction. (This is true for angle
This constant value is called the refractive index of the second medium with respect to the first. Let us study about refractive index in some detail.
9.3.2 The Refractive Index
You have already studied that a ray of light that travels obliquely from one transparent medium into another will change its direction in the second medium. The extent of the change in direction that takes place in a given pair of media may be expressed in terms of the refractive index, the “constant” appearing on the right-hand side of Eq.(9.4).
The refractive index can be linked to an important physical quantity, the relative speed of propagation of light in different media. It turns out that light propagates with different speeds in different media. Light travels fastest in vacuum with speed of
Consider a ray of light travelling from medium 1 into medium 2 , as shown in Fig.9.11. Let
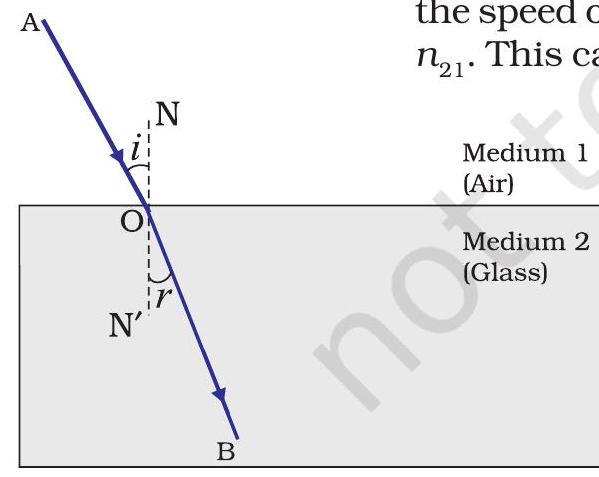
Figure 9.11
By the same argument, the refractive index of medium 1 with respect to medium 2 is represented as
If medium 1 is vacuum or air, then the refractive index of medium 2 is considered with respect to vacuum. This is called the absolute refractive index of the medium. It is simply represented as
The absolute refractive index of a medium is simply called its refractive index. The refractive index of several media is given in Table 9.3. From the Table you can know that the refractive index of water,
Table 9.3 Absolute refractive index of some material media
| Material medium | Refractive index | Material medium | Refractive index |
|---|---|---|---|
| Air | 1.0003 | Canada Balsam | 1.53 |
| Ice Water | 1.31 | Rock salt | 1.54 |
| Alcohol Kerosene | 1.33 | Carbon disulphide | 1.63 |
| Fused quartz | 1.44 | Dense flint glass | 1.65 |
| Turpentine oil Benzene | 1.46 | Ruby | 1.71 |
| Crown glass | 1.50 | Sapphire | 1.77 |
Note from Table 9.3 that an optically denser medium may not possess greater mass density. For example, kerosene having higher refractive index, is optically denser than water, although its mass density is less than water.
Do you know?
The ability of a medium to refract light is also expressed in terms of its optical density. Optical density has a definite connotation. It is not the same as mass density. We have been using the terms ‘rarer medium’ and ‘denser medium’ in this Chapter. It actually means ‘optically rarer medium’ and ‘optically denser medium’, respectively. When can we say that a medium is optically denser than the other? In comparing two media, the one with the larger refractive index is optically denser medium than the other. The other medium of lower refractive index is optically rarer. The speed of light is higher in a rarer medium than a denser medium. Thus, a ray of light travelling from a rarer medium to a denser medium slows down and bends towards the normal. When it travels from a denser medium to a rarer medium, it speeds up and bends away from the normal.
Questions
1. A ray of light travelling in air enters obliquely into water. Does the light ray bend towards the normal or away from the normal? Why?
Show Answer
Answer
The light ray bends towards the normal.
When a ray of light travels from an optically rarer medium to an optically denser medium, it gets bent towards the normal. Since water is optically denser than air, a ray of light travelling from air into the water will bend towards the normal.
2. Light enters from air to glass having refractive index 1.50. What is the speed of light in the glass? The speed of light in vacuum is
Show Answer
Answer
Refractive index of a medium nm is given by,
Speed of light in vacuum,
Refractive index of glass,
Speed of light in the glass,
3. Find out, from Table 9.3, the medium having highest optical density. Also find the medium with lowest optical density.
Show Answer
Answer
Material Refractive index Material medium Refractive
| medium | index | ||
|---|---|---|---|
| Air | 1.0003 | Canada Balsam | 1.53 |
| Ice | 1.31 | - | - |
| Water | 1.33 | Rock salt | 1.54 |
| Alcohol | 1.36 | - | - |
| Kerosene | 1.44 | Carbon disulphide | 1.63 |
| Fused | Dense | ||
| quartz | 1.46 | flint glass | 1.65 |
| Turpentine oil | 1.47 | Ruby | 1.71 |
| Benzene | 1.50 | Sapphire | 1.77 |
| Crown | 2.42 | ||
| glass | 1.52 | Diamond |
Highest optical density = Diamond
Lowest optical density
Optical density of a medium is directly related with the refractive index of that medium. A medium which has the highest refractive index will have the highest optical density and viceversa.
It can be observed from table 10.3 that diamond and air respectively have the highest and lowest refractive index. Therefore, diamond has the highest optical density and air has the lowest optical density.
4. You are given kerosene, turpentine and water. In which of these does the light travel fastest? Use the information given in Table 9.3.
Show Answer
Answer
Material Refractive indexMaterial medium Refractive
medium index
Air
| Ice | 1.31 | - | |
|---|---|---|---|
| Water | 1.33 | Rock salt | 1.54 |
| Alcohol | 1.36 | - | - |
| Kerosene | 1.44 | Carbon disulphide | 1.63 |
| Fused | |||
| quartz | 1.46 | Dense | |
| Turpentine oil | 1.47 | Ruby | 1.65 |
| Benzene | 1.50 | Sapphire | 1.71 |
| Crown | |||
| glass | 1.52 | Diamond | 2.42 |
Speed of light in a medium is given by the relation for refractive index (nm). The relation is given as
It can be inferred from the relation that light will travel the slowest in the material which has the highest refractive index and travel the fastest in the material which has the lowest refractive index.
It can be observed from table 10.3 that the refractive indices of kerosene, turpentine, and water are 1.44, 1.47, and 1.33 respectively. Therefore, light travels the fastest in water.
5. The refractive index of diamond is 2.42. What is the meaning of this statement?
Show Answer
Answer
Refractive index of a medium
Where,
The refractive index of diamond is 2.42 . This suggests that the speed of light in diamond will reduce by a factor 2.42 compared to its speed in air.
9.3.3 Refraction by Spherical Lenses
You might have seen watchmakers using a small magnifying glass to see tiny parts. Have you ever touched the surface of a magnifying glass with your hand? Is it plane surface or curved? Is it thicker in the middle or at the edges? The glasses used in spectacles and that by a watchmaker are examples of lenses. What is a lens? How does it bend light rays? We shall discuss these in this section.

(a)

(b)
Figure 9.12 (a) Converging action of a convex lens, (b) diverging action of a concave lens
A transparent material bound by two surfaces, of which one or surfaces are spherical, forms a lens. This means that a lens is bound by at least one spherical surface. In such lenses, the other surface would be plane. A lens may have two spherical surfaces, bulging outwards. Such a lens is called a double convex lens. It is simply called a convex lens. It is thicker at the middle as compared to the edges. Convex lens converges light rays as shown in Fig. 9.12 (a).
Hence convex lenses are also called converging lenses. Similarly, a double concave lens is bounded by two spherical surfaces, curved inwards. It is thicker at the edges than at the middle. Such lenses diverge light rays as shown in Fig. 9.12 (b). Such lenses are also called diverging lenses. A double concave lens is simply called a concave lens.
A lens, either a convex lens or a concave lens, has two spherical surfaces. Each of these surfaces forms a part of a sphere. The centres of these spheres are called centres of curvature of the lens. The centre of curvature of a lens is usually represented by the letter
A ray of light through the optical centre of a lens passes without suffering any deviation. The effective diameter of the circular outline of a spherical lens is called its aperture. We shall confine our discussion in this Chapter to such lenses whose aperture is much less than its radius of curvature and the two centres of curvatures are equidistant from the optical centre O. Such lenses are called thin lenses with small apertures. What happens when parallel rays of light are incident on a lens? Let us do an Activity to understand this.
Activity 9.11
CAUTION: Do not look at the Sun directly or through a lens while doing this Activity or otherwise. You may damage your eyes if you do so.
- Hold a convex lens in your hand. Direct it towards the Sun.
- Focus the light from the Sun on a sheet of paper. Obtain a sharp bright image of the Sun.
- Hold the paper and the lens in the same position for a while. Keep observing the paper. What happened? Why? Recall your experience in Activity 9.2.
The paper begins to burn producing smoke. It may even catch fire after a while. Why does this happen? The light from the Sun constitutes parallel rays of light. These rays were converged by the lens at the sharp bright spot formed on the paper. In fact, the bright spot you got on the paper is a real image of the Sun. The concentration of the sunlight at a point generated heat. This caused the paper to burn.
Now, we shall consider rays of light parallel to the principal axis of a lens. What happens when you pass such rays of light through a lens? This is illustrated for a convex lens in Fig. 9.12 (a) and for a concave lens in Fig.9.12 (b).
Observe Fig.9.12 (a) carefully. Several rays of light parallel to the principal axis are falling on a convex lens. These rays, after refraction from the lens, are converging to a point on the principal axis. This point on the principal axis is called the principal focus of the lens. Let us see now the action of a concave lens.
Observe Fig.9.12 (b) carefully. Several rays of light parallel to the principal axis are falling on a concave lens. These rays, after refraction from the lens, are appearing to diverge from a point on the principal axis. This point on the principal axis is called the principal focus of the concave lens.
If you pass parallel rays from the opposite surface of the lens, you get another principal focus on the opposite side. Letter
9.3.4 Image Formation by Lenses
Lenses form images by refracting light. How do lenses form images? What is their nature? Let us study this for a convex lens first.
Activity 9.12
- Take a convex lens. Find its approximate focal length in a way described in Activity 9.11.
- Draw five parallel straight lines, using chalk, on a long Table such that the distance between the successive lines is equal to the focal length of the lens.
- Place the lens on a lens stand. Place it on the central line such that the optical centre of the lens lies just over the line.
- The two lines on either side of the lens correspond to
and of the lens respectively. Mark them with appropriate letters such as and , respectively. - Place a burning candle, far beyond
to the left. Obtain a clear sharp image on a screen on the opposite side of the lens. - Note down the nature, position and relative size of the image.
- Repeat this Activity by placing object just behind
, between and at , between and . Note down and tabulate your observations.
The nature, position and relative size of the image formed by convex lens for various positions of the object is summarised in Table 9.4.
Table 9.4 Nature, position and relative size of the image formed by a convex lens for various positions of the object
| Position of the object | Position of the image | Relative size of the image | Nature of the image |
|---|---|---|---|
| At infinity | At focus |
Highly diminished, point-sized | Real and inverted |
| Beyond |
Between |
Diminished | Real and inverted |
| At |
At |
Same size | Real and inverted |
| Between |
Beyond |
Enlarged | Real and inverted |
| At focus |
At infinity | Infinitely large or highly enlarged | Real and inverted |
| Between focus |
On the same side of the lens as the object | Enlarged | Virtual and erect |
Let us now do an Activity to study the nature, position and relative size of the image formed by a concave lens.
Activity 9.13
- Take a concave lens. Place it on a lens stand.
- Place a burning candle on one side of the lens.
- Look through the lens from the other side and observe the image. Try to get the image on a screen, if possible. If not, observe the image directly through the lens.
- Note down the nature, relative size and approximate position of the image.
- Move the candle away from the lens. Note the change in the size of the image. What happens to the size of the image when the candle is placed too far away from the lens.
The summary of the above Activity is given in Table 9.5 below.
Table 9.5 Nature, position and relative size of the image formed by a concave lens for various positions of the object
| Position of the object | Position of the image | Relative size of the image | Nature of the image |
|---|---|---|---|
| At infinity | At focus |
Highly diminished, point-sized | Virtual and erect |
| Between infinity and optical centre |
Between focus |
Diminished | Virtual and erect |
What conclusion can you draw from this Activity? A concave lens will always give a virtual, erect and diminished image, irrespective of the position of the object.
9.3.5 Image Formation in Lenses Using Ray Diagrams
We can represent image formation by lenses using ray diagrams. Ray diagrams will also help us to study the nature, position and relative size of the image formed by lenses. For drawing ray diagrams in lenses, alike of spherical mirrors, we consider any two of the following rays -
(i) A ray of light from the object, parallel to the principal axis, after refraction from a convex lens, passes through the principal focus on the other side of the lens, as shown in Fig. 9.13 (a). In case of a concave lens, the ray appears to diverge from the principal focus located on the same side of the lens, as shown in Fig. 9.13 (b).

(ii) A ray of light passing through a principal focus, after refraction from a convex lens, will emerge parallel to the principal axis. This is shown in Fig. 9.14 (a). A ray of light appearing to meet at the principal focus of a concave lens, after refraction, will emerge parallel to the principal axis. This is shown in Fig.9.14 (b).

(iii) A ray of light passing through the optical centre of a lens will emerge without any deviation. This is illustrated in Fig.9.15(a) and Fig.9.15 (b).

The ray diagrams for the image formation in a convex lens for a few positions of the object are shown in Fig. 9.16. The ray diagrams representing the image formation in a concave lens for various positions of the object are shown in Fig. 9.17.

Figure 9.16 The position, size and the nature of the image formed by a convex lens for various positions of the object

Figure 9.17 Nature, position and relative size of the image formed by a concave lens
9.3.6 Sign Convention for Spherical Lenses
For lenses, we follow sign convention, similar to the one used for spherical mirrors. We apply the rules for signs of distances, except that all measurements are taken from the optical centre of the lens. According to the convention, the focal length of a convex lens is positive and that of a concave lens is negative. You must take care to apply appropriate signs for the values of
9.3.7 Lens Formula and Magnification
As we have a formula for spherical mirrors, we also have formula for spherical lenses. This formula gives the relationship between objectdistance
The lens formula given above is general and is valid in all situations for any spherical lens. Take proper care of the signs of different quantities, while putting numerical values for solving problems relating to lenses.
Magnification
The magnification produced by a lens, similar to that for spherical mirrors, is defined as the ratio of the height of the image and the height of the object. Magnification is represented by the letter
Magnification produced by a lens is also related to the object-distance
Magnification
Example 9.3
A concave lens has focal length of
Solution
A concave lens always forms a virtual, erect image on the same side of the object.
Image-distance
Focal length
Object-distance
Since
or,
or,
Thus, the object-distance is
Magnification
The positive sign shows that the image is erect and virtual. The image is one-third of the size of the object.
Example 9.4
A
Solution
Height of the object
Focal length
object-distance
Image-distance
Height of the image
Since
or,
or,
The positive sign of
Magnification
or,
Height of the image,
Magnification
or,
The negative signs of
9.3.8 Power of a Lens
You have already learnt that the ability of a lens to converge or diverge light rays depends on its focal length. For example, a convex lens of short focal length bends the light rays through large angles, by focussing them closer to the optical centre. Similarly, concave lens of very short focal length causes higher divergence than the one with longer focal length. The degree of convergence or divergence of light rays achieved by a lens is expressed in terms of its power. The power of a lens is defined as the reciprocal of its focal length. It is represented by the letter
The SI unit of power of a lens is ‘dioptre’. It is denoted by the letter D. If
Opticians prescribe corrective lenses indicating their powers. Let us say the lens prescribed has power equal to
More to know!
Many optical instruments consist of a number of lenses. They are combined to increase the magnification and sharpness of the image. The net power (P ) of the lenses placed in contact is given by the algebraic sum of the individual powers
… as The use of powers, instead of focal lengths, for lenses is quite convenient for opticians.During eye-testing, an optician puts several different combinations of corrective lenses of known power, in contact, inside the testing spectacles’ frame. The optician calculates the power of the lens required by simple algebraic addition. For example, a combination of two lenses of power + 2.0 D and + 0.25 D is equivalent to a single lens of power + 2.25 D. The simple additive property of the powers of lenses can be used to design lens systems to minimise certain defects in images produced by a single lens. Such a lens system, consisting of several lenses, in contact, is commonly used in the design of lenses of camera, microscopes and telescopes.
QUESTIONS
1. Define 1 dioptre of power of a lens.
Show Answer
#missing2. A convex lens forms a real and inverted image of a needle at a distance of 50 cm from it. Where is the needle placed in front of the convex lens if the image is equal to the size of the object? Also, find the power of the lens.
Show Answer
#missing3. Find the power of a concave lens of focal length 2 m.
Show Answer
#missingWhat you have learnt
- Light seems to travel in straight lines.
- Mirrors and lenses form images of objects. Images can be either real or virtual, depending on the position of the object.
- The reflecting surfaces, of all types, obey the laws of reflection. The refracting surfaces obey the laws of refraction.
- New Cartesian Sign Conventions are followed for spherical mirrors and lenses.
- Mirror formula,
- The focal length of a spherical mirror is equal to half its radius of curvature.
- The magnification produced by a spherical mirror is the ratio of the height of the image to the height of the object.
- A light ray travelling obliquely from a denser medium to a rarer medium bends away from the normal. A light ray bends towards the normal when it travels obliquely from a rarer to a denser medium.
- Light travels in vacuum with an enormous speed of
- The refractive index of a transparent medium is the ratio of the speed of light in vacuum to that in the medium.
- In case of a rectangular glass slab, the refraction takes place at both air-glass interface and glass-air interface. The emergent ray is parallel to the direction of incident ray.
- Lens formula,
- Power of a lens is the reciprocal of its focal length. The SI unit of power of a lens is dioptre.
EXERCISES
1. Which one of the following materials cannot be used to make a lens?
(a) Water
(b) Glass
(c) Plastic
(d) Clay
Show Answer
Answer
(d) A lens allows light to pass through it. Since clay does not show such property, it cannot be used to make a lens.
2. The image formed by a concave mirror is observed to be virtual, erect and larger than the object. Where should be the position of the object?
(a) Between the principal focus and the centre of curvature
(b) At the centre of curvature
(c) Beyond the centre of curvature
(d) Between the pole of the mirror and its principal focus.
Show Answer
Answer
(d) Between the pole of the mirror and its principal focus
3. Where should an object be placed in front of a convex lens to get a real image of the size of the object?
(a) At the principal focus of the lens
(b) At twice the focal length
(c) At infinity
(d) Between the optical centre of the lens and its principal focus.
Show Answer
Answer
(b) When an object is placed at the centre of curvature in front of a convex lens, its image is formed at the centre of curvature on the other side of the lens. The image formed is real, inverted, and of the same size as the object.
4. A spherical mirror and a thin spherical lens have each a focal length of
(a) both concave.
(b) both convex.
(c) the mirror is concave and the lens is convex.
(d) the mirror is convex, but the lens is concave.
Show Answer
Answer
(a) By convention, the focal length of a concave mirror and a concave lens are taken as negative. Hence, both the spherical mirror and the thin spherical lens are concave in nature.
5. No matter how far you stand from a mirror, your image appears erect. The mirror is likely to be
(a) only plane.
(b) only concave.
(c) only convex.
(d) either plane or convex.
Show Answer
Answer
(d) A convex mirror always gives a virtual and erect image of smaller size of the object placed in front of it. Similarly, a plane mirror will always give a virtual and erect image of same size as that of the object placed in front of it. Therefore, the given mirror could be either plane or convex.
6. Which of the following lenses would you prefer to use while reading small letters found in a dictionary?
(a) A convex lens of focal length
(b) A concave lens of focal length
(c) A convex lens of focal length
(d) A concave lens of focal length
Show Answer
Answer
(c) A convex lens gives a magnified image of an object when it is placed between the radius of curvature and focal length. Also, magnification is more for convex lenses having shorter focal length. Therefore, for reading small letters, a convex lens of focal length
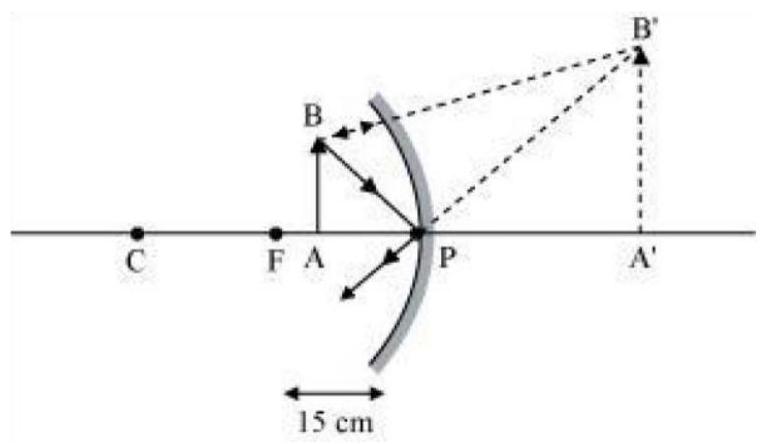
7. We wish to obtain an erect image of an object, using a concave mirror of focal length
Show Answer
Answer
Range of object distance
A concave mirror gives an erect image when an object is placed between its pole
Hence, to obtain an erect image of an object from a concave mirror of focal length
8. Name the type of mirror used in the following situations.
(a) Headlights of a car.
(b) Side/rear-view mirror of a vehicle.
(c) Solar furnace.Support your answer with reason.
Show Answer
Answer
(a) Concave (b) Convex (c) Concave
Explanation:
(a) Concave mirror is used in the headlights of a car. This is because concave mirrors can produce powerful parallel beam of light when the light source is placed at their principal focus.
(b) Convex mirror is used in side/rear view mirror of a vehicle. Convex mirrors give a virtual, erect, and diminished image of the objects placed in front of it. Because of this, they have a wide field of view. It enables the driver to see most of the traffic behind him/her.
(c) Concave mirrors are convergent mirrors. That is why they are used to construct solar furnaces. Concave mirrors converge the light incident on them at a single point known as principal focus. Hence, they can be used to produce a large amount of heat at that point.
9. One-half of a convex lens is covered with a black paper. Will this lens produce a complete image of the object? Verify your answer experimentally. Explain your observations.
Show Answer
Answer
The convex lens will form complete image of an object, even if its one half is covered with black paper. It can be understood by the following two cases.
10. An object
Show Answer
Answer
Object distance,
Object height, ho
Focal length,
According to the lens formula,
The positive value of
Magnification,
The negative sign shows that the image is real and formed behind the lens.
Magnification,
The negative value of image height indicates that the image formed is inverted.
The position, size, and nature of image are shown in the following ray diagram.
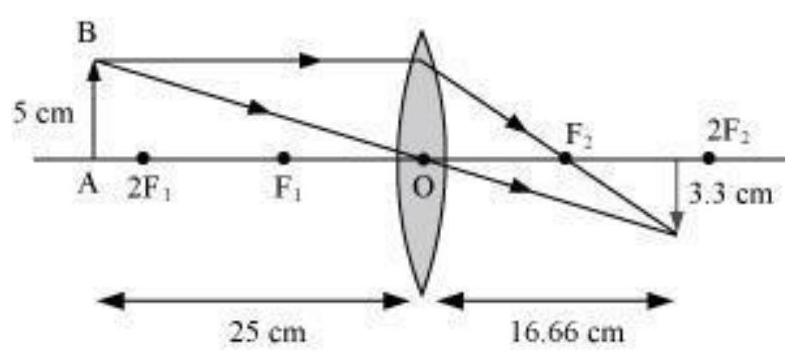
11. A concave lens of focal length
Show Answer
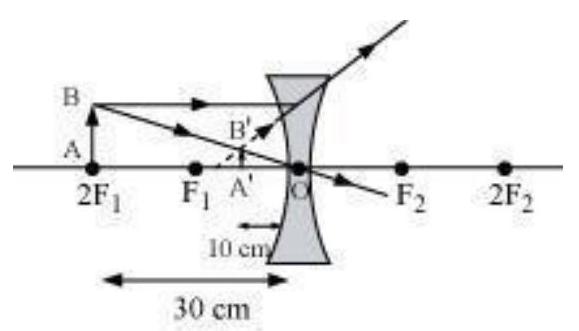
Answer
Focal length of concave lens (OF1),
Image distance,
According to the lens formula,
The negative value of
12. An object is placed at a distance of
Show Answer
Answer
Focal length of convex mirror,
Object distance,
According to the mirror formula,
The positive value of
Magnification,
The positive value of magnification indicates that the image formed is virtual and erect.
13. The magnification produced by a plane mirror is +1 . What does this mean?
Show Answer
Answer
Magnification produced by a mirror is given by the relation
Magnification,
The magnification produced by a plane mirror is +1 . It shows that the image formed by the plane mirror is of the same size as that of the object. The positive sign shows that the image formed is virtual and erect.
14. An object
Show Answer
Answer
Object distance,
Object height,
Radius of curvature,
Radius of curvature
According to the mirror formula,
The positive value of
Magnification,
The positive value of magnification indicates that the image formed is virtual.
Magnification,
The positive value of image height indicates that the image formed is erect.
Therefore, the image formed is virtual, erect, and smaller in size.
15. An object of size
Show Answer
Answer
Object distance,
Object height,
Focal length,
According to the mirror formula,
The screen should be placed at a distance of
Magnification,
The negative value of magnification indicates that the image formed is real.
Magnification,
The negative value of image height indicates that the image formed is inverted.
16. Find the focal length of a lens of power
Show Answer
Answer
A concave lens has a negative focal length. Hence, it is a concave lens.
17. A doctor has prescribed a corrective lens of power
Show Answer
Answer
A convex lens has a positive focal length. Hence, it is a convex lens or a converging lens.










