Chapter 06 Triangles Exercise-03
EXERCISE 6.3
1. State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

Show Answer
Solution
(i)
Therefore,
(ii)
[By SSS similarity criterion]
(iii)The given triangles are not similar as the corresponding sides are not proportional.
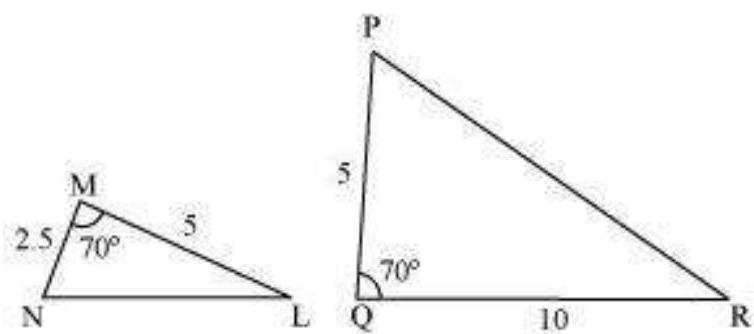
2. In Fig. 6.35,
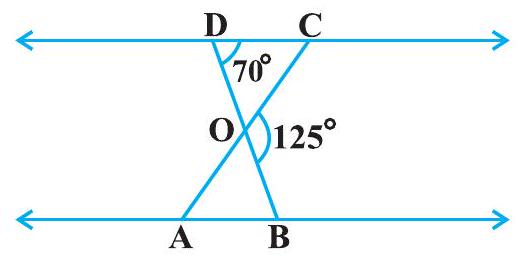
Fig. 6.35
Show Answer
Solution
DOB is a straight line.
In
(Sum of the measures of the angles of a triangle is
It is given that
3. Diagonals
Show Answer
#missing4. In Fig. 6.36,
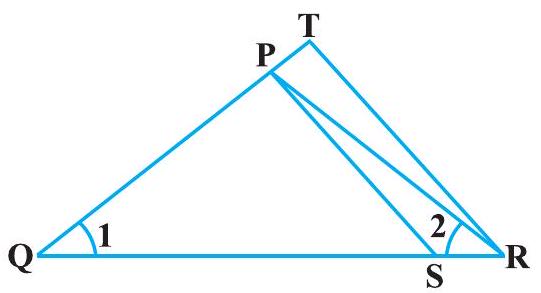
Fig. 6.36
Show Answer
Solution
In
Given,
Using
In
5.
Show Answer
Solution
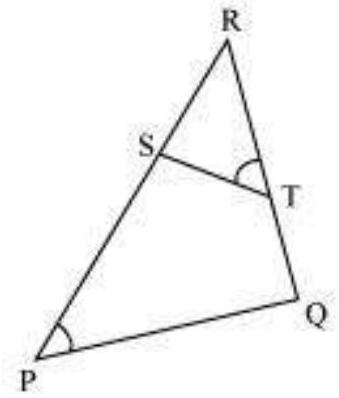
In
6. In Fig. 6.37, if
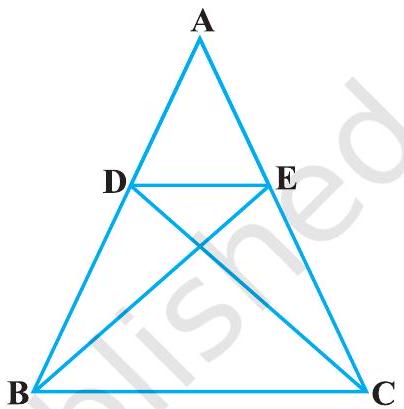
Fig. 6.37
Show Answer
Solution
It is given that
And,
In
[Dividing equation (2) by (1)]
7. In Fig. 6.38, altitudes
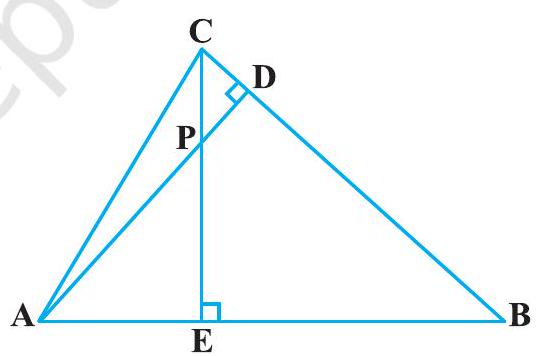
Fig. 6.38
(i)
(ii)
(iii)
(iv)
Show Answer
Solution
(i)
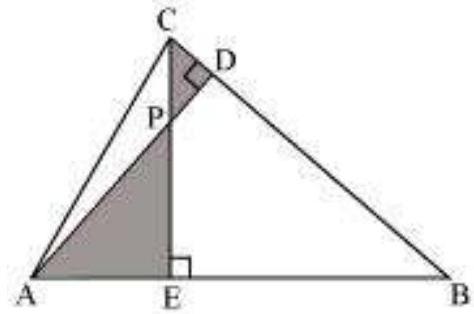
In
Hence, by using AA similarity criterion,
(ii)
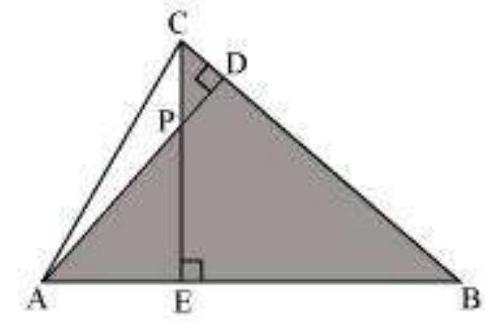
In
Hence, by using AA similarity criterion,
(iii)
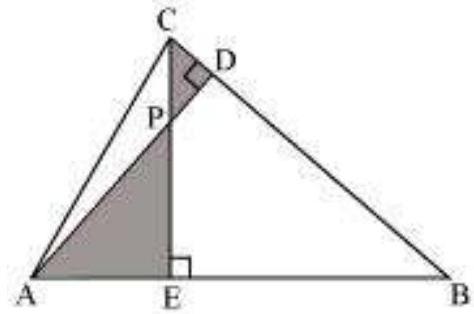
In
Hence, by using AA similarity criterion,
(iv)
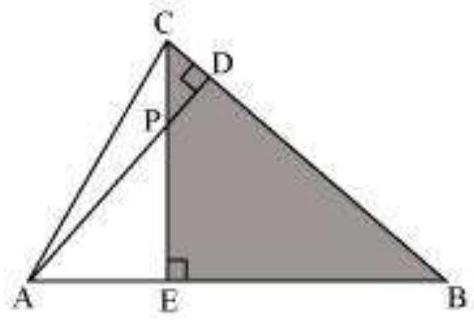
In
Hence, by using AA similarity criterion,
8.
Show Answer
Solution
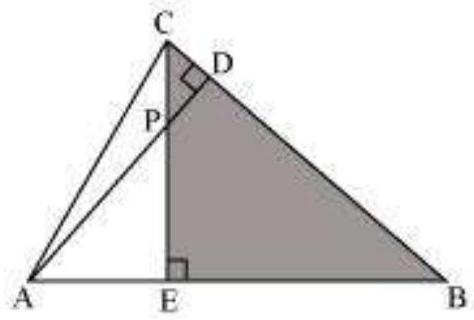
In
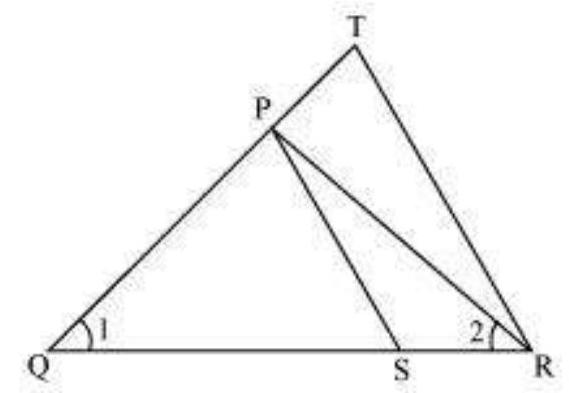
9. In Fig. 6.39,
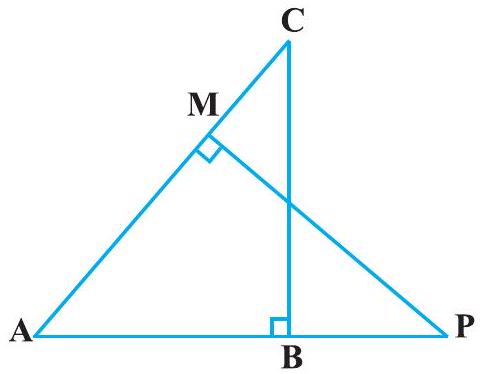
Fig. 6.39
(i)
(ii)
Show Answer
Solution
In
10.
(i)
(ii)
(iii)
Show Answer
Solution
Answer :

It is given that
And,
In
In
In
11. In Fig. 6.40,
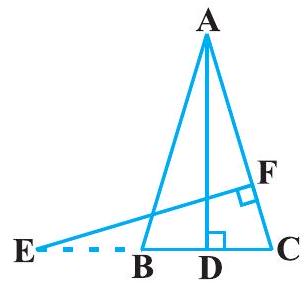
Fig. 6.40
Show Answer
Solution
It is given that
In
12. Sides
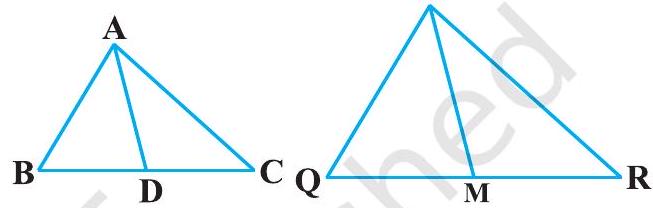
Fig. 6.41
Show Answer
Solution
Median divides the opposite side.
Given that,
In
In
13.
Show Answer
Solution
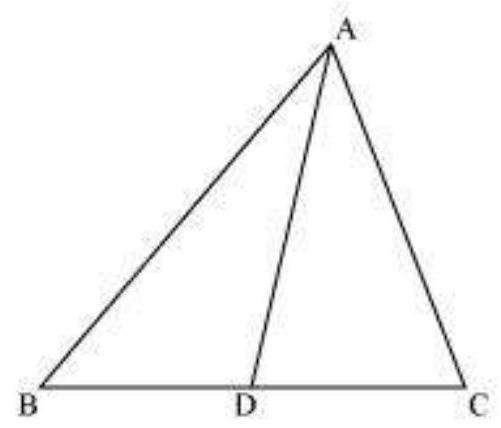
In
We know that corresponding sides of similar triangles are in proportion.
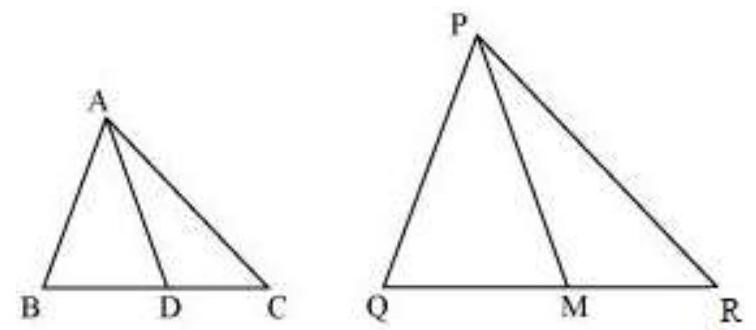
14. Sides
Show Answer
Solution
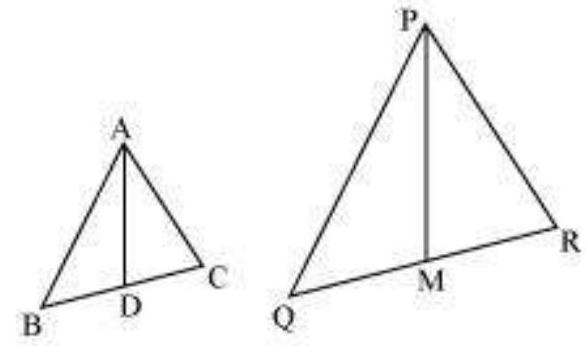
Given that,
Let us extend 
We know that medians divide opposite sides.
Therefore,
Also,
And,
In quadrilateral
Therefore, quadrilateral ABEC is a parallelogram.
Similarly, we can prove that quadrilateral
It was given that
We know that corresponding angles of similar triangles are equal.
Similarly, it can be proved that
Adding equation (1) and (2), we obtain
In
(Given)
15. A vertical pole of length
Show Answer
Solution
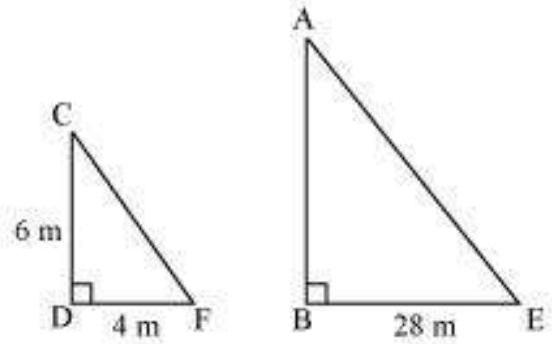
Let
Let the shadow of
At the same time, the light rays from the sun will fall on the tower and the pole at the same angle.
Therefore,
And,
Therefore, the height of the tower will be 42 metres.
16. If
Show Answer
Solution
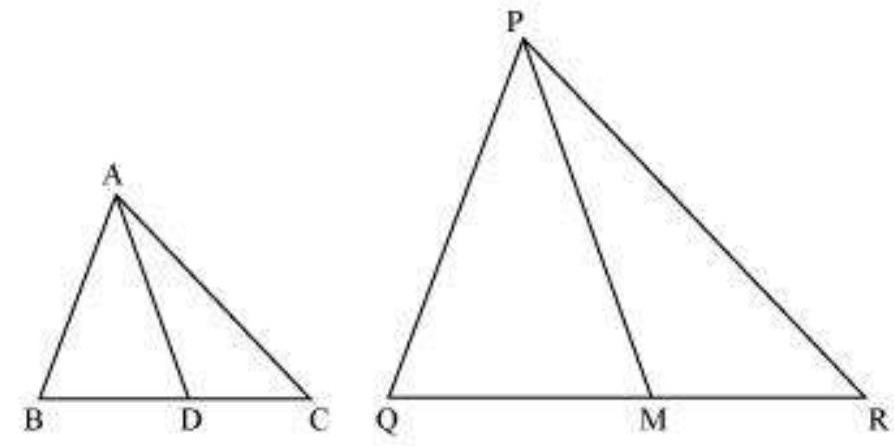
It is given that
We know that the corresponding sides of similar triangles are in proportion.
Also,
Since AD and PM are medians, they will divide their opposite sides.
From equations ( 1 ) and (3), we obtain
In










