Chapter 03 Pair of Linear Equations in Two Variables Exercise-01
EXERCISE 3.1
1. Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of Class $X$ took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Show Answer
Solution
(i) Let the number of girls be $x$ and the number of boys be $y$.
According to the question, the algebraic representation is
$x+y=10$
$x-y=4$
For $x+y=10$,
$x=10-y$
| $x$ | 5 | 4 | 6 |
|---|---|---|---|
| $y$ | 5 | 6 | 4 |
For $x-y=4$,
$x=4+y$
| $x$ | 5 | 4 | 3 |
|---|---|---|---|
| $y$ | 1 | 0 | -1 |
Hence, the graphic representation is as follows.
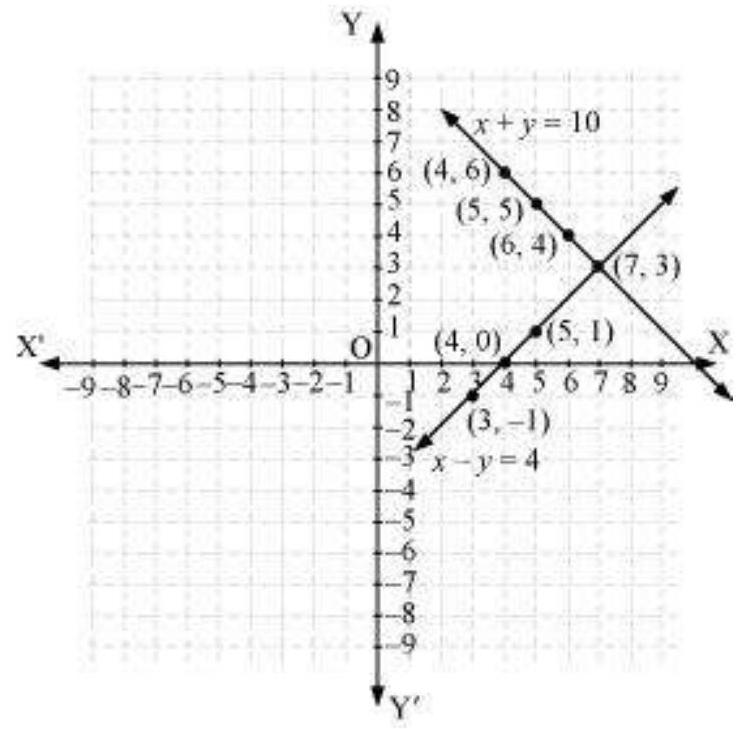
From the figure, it can be observed that these lines intersect each other at point $(7,3)$.
Therefore, the number of girls and boys in the class are 7 and 3 respectively.
(ii) Let the cost of 1 pencil be Rs $x$ and the cost of 1 pen be Rs $y$.
According to the question, the algebraic representation is
$5 x+7 y=50$
$7 x+5 y=46$
For $5 x+7 y=50$,
$x=\dfrac{50-7 y}{5}$
| $x$ | 3 | 10 | -4 |
|---|---|---|---|
| $y$ | 5 | 0 | 10 |
$7 x+5 y=46$
$x=\dfrac{46-5 y}{7}$
| $x$ | 8 | 3 | -2 |
|---|---|---|---|
| $y$ | -2 | 5 | 12 |
Hence, the graphic representation is as follows.
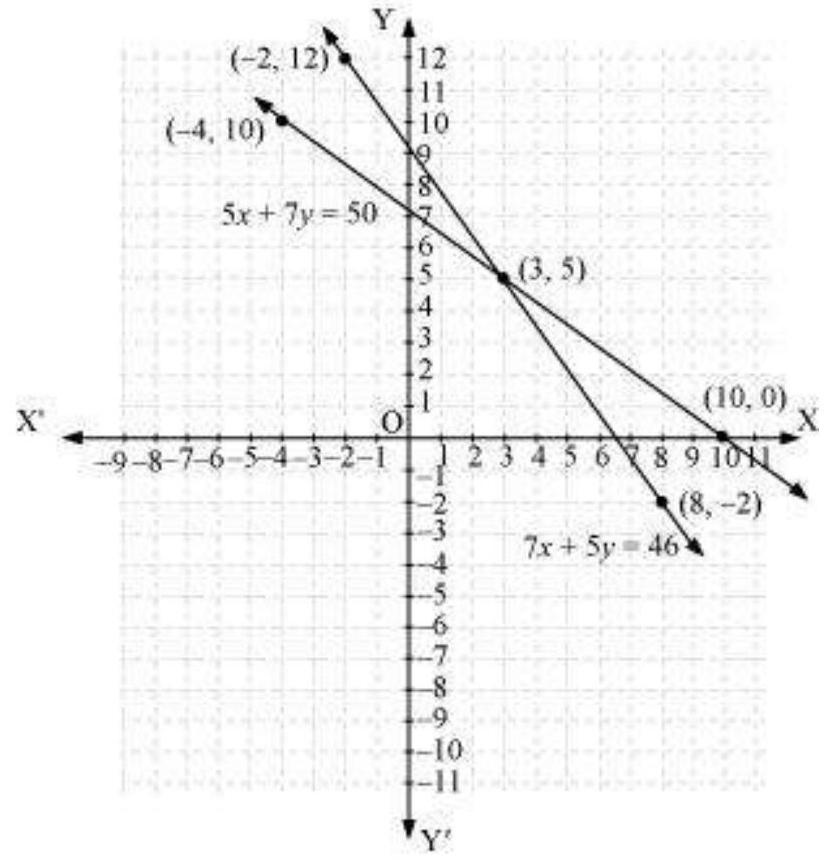
From the figure, it can be observed that these lines intersect each other at point $(3,5)$.
Therefore, the cost of a pencil and a pen are Rs 3 and Rs 5 respectively.
2. On comparing the ratios $\dfrac{a_1}{a_2}, \dfrac{b_1}{b_2}$ and $\dfrac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) $\begin{array}{r}5 x-4 y+8=0 \ 7 x+6 y-9=0\end{array}$
(ii) $9 x+3 y+12=0$ $18 x+6 y+24=0$
(iii) $6 x-3 y+10=0$ $2 x-y+9=0$
Show Answer
Solution
(i) $5 x-4 y+8=0$
$7 x+6 y-9=0$
Comparing these equations with $a_1 x+b_1 y+c_1=0$
and $a_2 x+b_2 y+c_2=0$, we obtain
$a_1=5, \quad b_1=-4, \quad c_1=8$
$a_2=7, \quad b_2=6, \quad c_2=-9$
$\dfrac{a_1}{a_2}=\dfrac{5}{7}$
$\dfrac{b_1}{b_2}=\dfrac{-4}{6}=\dfrac{-2}{3}$
Since $\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$,
Hence, the lines representing the given pair of equations have a unique solution and the pair of lines intersects at exactly one point.
(ii) $9 x+3 y+12=0$
$18 x+6 y+24=0$
Comparing these equations with $a_1 x+b_1 y+c_1=0$
and $a_2 x+b_2 y+c_2=0$, we obtain
$a_1=9, \quad b_1=3, \quad c_1=12$
$a_2=18, \quad b_2=6, \quad c_2=24$
$\dfrac{a_1}{a_2}=\dfrac{9}{18}=\dfrac{1}{2}$
$\dfrac{b_1}{b_2}=\dfrac{3}{6}=\dfrac{1}{2}$
$\dfrac{c_1}{c_2}=\dfrac{12}{24}=\dfrac{1}{2}$
Since $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}=\dfrac{c_1}{c_2}$,
Hence, the lines representing the given pair of equations are coincident and there are infinite possible solutions for the given pair of equations.
(iii) $6 x-3 y+10=0$
$2 x-y+9=0$
Comparing these equations with $a_1 x+b_1 y+c_1=0$ and $a_2 x+b_2 y+c_2=0$, we obtain
$a_1=6, \quad b_1=-3, \quad c_1=10$
$a_2=2, \quad b_2=-1, \quad c_2=9$
$\dfrac{a_1}{a_2}=\dfrac{6}{2}=\dfrac{3}{1}$
$\dfrac{b_1}{b_2}=\dfrac{-3}{-1}=\dfrac{3}{1}$
$\dfrac{c_1}{c_2}=\dfrac{10}{9}$
Since $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$
Hence, the lines representing the given pair of equations are parallel to each other and hence, these lines will never intersect each other at any point or there is no possible solution for the given pair of equations.
3. On comparing the ratios $\dfrac{a_1}{a_2}, \dfrac{b_1}{b_2}$ and $\dfrac{c_1}{c_2}$, find out whether the following pair of linear equations are consistent, or inconsistent.
(i) $3 x+2 y=5 ; \quad 2 x-3 y=7$
(ii) $2 x-3 y=8 ; 4 x-6 y=9$
(iii) $\dfrac{3}{2} x+\dfrac{5}{3} y=7 ; 9 x-10 y=14$
(iv) $5 x-3 y=11 ;-10 x+6 y=-22$
(v) $\dfrac{4}{3} x+2 y=8 ; 2 x+3 y=12$
Show Answer
Solution
(i) $3 x+2 y=5$
$2 x-3 y=7$
$\dfrac{a_1}{a_2}=\dfrac{3}{2}, \quad \dfrac{b_1}{b_2}=\dfrac{-2}{3}, \quad \dfrac{c_1}{c_2}=\dfrac{5}{7}$
$\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$
These linear equations are intersecting each other at one point and thus have only one possible solution. Hence, the pair of linear equations is consistent.
(ii) $2 x-3 y=8$ $4 x-6 y=9$
$\dfrac{a_1}{a_2}=\dfrac{2}{4}=\dfrac{1}{2}, \quad \dfrac{b_1}{b_2}=\dfrac{-3}{-6}=\dfrac{1}{2}, \quad \dfrac{c_1}{c_2}=\dfrac{8}{9}$
Since $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$,
Therefore, these linear equations are parallel to each other and thus have no possible solution. Hence, the pair of linear equations is inconsistent.
(iii) $\dfrac{3}{2} x+\dfrac{5}{3} y=7$
$9 x-10 y=14$
$\dfrac{a_1}{a_2}=\dfrac{\dfrac{3}{2}}{9}=\dfrac{1}{6}, \quad \dfrac{b_1}{b_2}=\dfrac{\dfrac{5}{3}}{-10}=\dfrac{-1}{6}, \quad \dfrac{c_1}{c_2}=\dfrac{7}{14}=\dfrac{1}{2}$
Since $\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$,
Therefore, these linear equations are intersecting each other at one point and thus have only one possible solution. Hence, the pair of linear equations is consistent.
(iv) $5 x-3 y=11$
$-10 x+6 y=-22$
$\dfrac{a_1}{a_2}=\dfrac{5}{-10}=\dfrac{-1}{2}, \quad \dfrac{b_1}{b_2}=\dfrac{-3}{6}=\dfrac{-1}{2}, \quad \dfrac{c_1}{c_2}=\dfrac{11}{-22}=\dfrac{-1}{2}$
Since $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}=\dfrac{c_1}{c_2}$
Therefore, these linear equations are coincident pair of lines and thus have infinite number of possible solutions. Hence, the pair of linear equations is consistent.
(v) $\dfrac{4}{3} x+2 y=8$
$2 x+3 y=12$
$\dfrac{a_1}{a_2}=\dfrac{\dfrac{4}{3}}{2}=\dfrac{2}{3}, \quad \dfrac{b_1}{b_2}=\dfrac{2}{3}, \quad \dfrac{c_1}{c_2}=\dfrac{8}{12}=\dfrac{2}{3}$
Since $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}=\dfrac{c_1}{c_2}$,
Therefore, these linear equations are coincident pair of lines and thus have infinite number of possible solutions. Hence, the pair of linear equations is consistent.
4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i) $x+y=5$, $\quad$ $2 x+2 y=10$
(ii) $x-y=8, \quad 3 x-3 y=16$
(iii) $2 x+y-6=0, \quad 4 x-2 y-4=0$
(iv) $2 x-2 y-2=0,4 x-4 y-5=0$
Show Answer
Solution
(i) $x+y=5$
$2 x+2 y=10$
$\dfrac{a_1}{a_2}=\dfrac{1}{2}, \quad \dfrac{b_1}{b_2}=\dfrac{1}{2}, \quad \dfrac{c_1}{c_2}=\dfrac{5}{10}=\dfrac{1}{2}$
Since $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}=\dfrac{c_1}{c_2}$
Therefore, these linear equations are coincident pair of lines and thus have infinite number of possible solutions. Hence, the pair of linear equations is consistent.
$x+y=5$
$x=5-y$
| $x$ | 4 | 3 | 2 |
|---|---|---|---|
| $y$ | 1 | 2 | 3 |
And, $2 x+2 y=10$
$x=\dfrac{10-2 y}{2}$
| $x$ | 4 | 3 | 2 |
|---|---|---|---|
| $y$ | 1 | 2 | 3 |
Hence, the graphic representation is as follows.
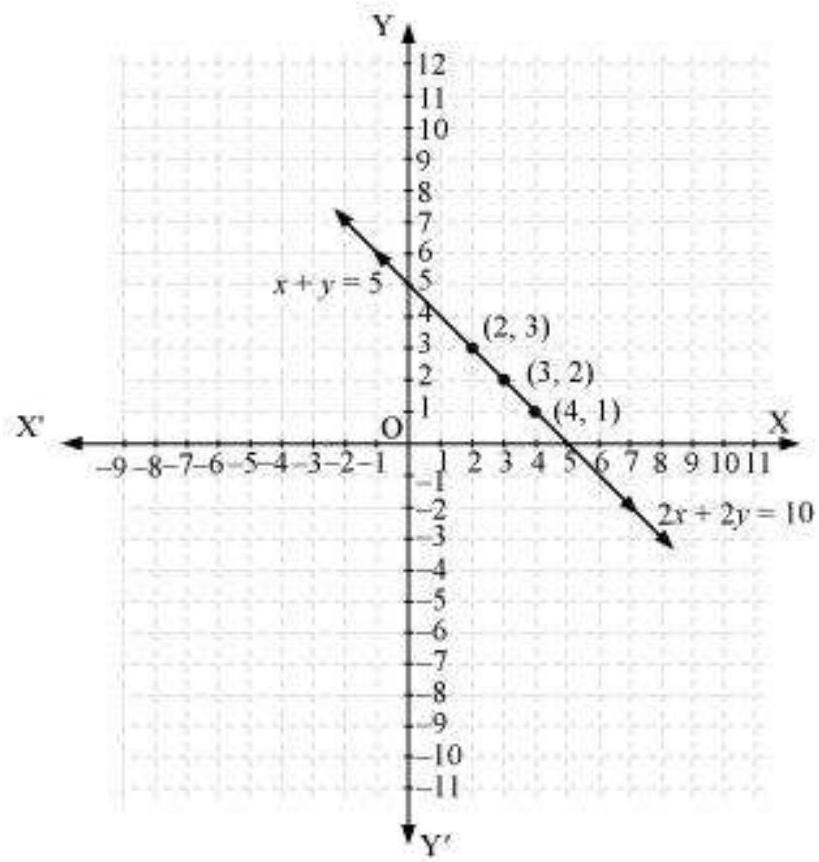
From the figure, it can be observed that these lines are overlapping each other. Therefore, infinite solutions are possible for the given pair of equations.
(ii) $x-y=8$
$3 x-3 y=16$
$\dfrac{a_1}{a_2}=\dfrac{1}{3}, \quad \dfrac{b_1}{b_2}=\dfrac{-1}{-3}=\dfrac{1}{3}, \quad \dfrac{c_1}{c_2}=\dfrac{8}{16}=\dfrac{1}{2}$
Since $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$,
Therefore, these linear equations are parallel to each other and thus have no possible solution. Hence, the pair of linear equations is inconsistent.
(iii) $2 x+y-6=0$
$4 x-2 y-4=0$
$\dfrac{a_1}{a_2}=\dfrac{2}{4}=\dfrac{1}{2}, \quad \dfrac{b_1}{b_2}=\dfrac{-1}{2}, \quad \dfrac{c_1}{c_2}=\dfrac{-6}{-4}=\dfrac{3}{2}$
Since $\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$,
Therefore, these linear equations are intersecting each other at one point and thus have only one possible solution. Hence, the pair of linear equations is consistent.
$2 x+y-6=0$
$y=6-2 x$
| $x$ | 0 | 1 | 2 |
|---|---|---|---|
| $y$ | 6 | 4 | 2 |
And $4 x-2 y-4=0$
$y=\dfrac{4 x-4}{2}$
| $x$ | 1 |
|---|
5. Half the perimeter of a rectangular garden, whose length is $4 m$ more than its width, is $36 m$. Find the dimensions of the garden.
Show Answer
Solution
Let the width of the garden be $x$ and length be $y$.
According to the question,
$y-x=4(1)$
$y+x=36(2)$
$y-x=4$
$y=x+4$
| $x$ | 0 | 8 | 12 |
|---|---|---|---|
| $y$ | 4 | 12 | 16 |
$y+x=36$
| $x$ | 0 | 36 | 16 |
|---|---|---|---|
| $y$ | 36 | 0 | 20 |
Hence, the graphic representation is as follows.
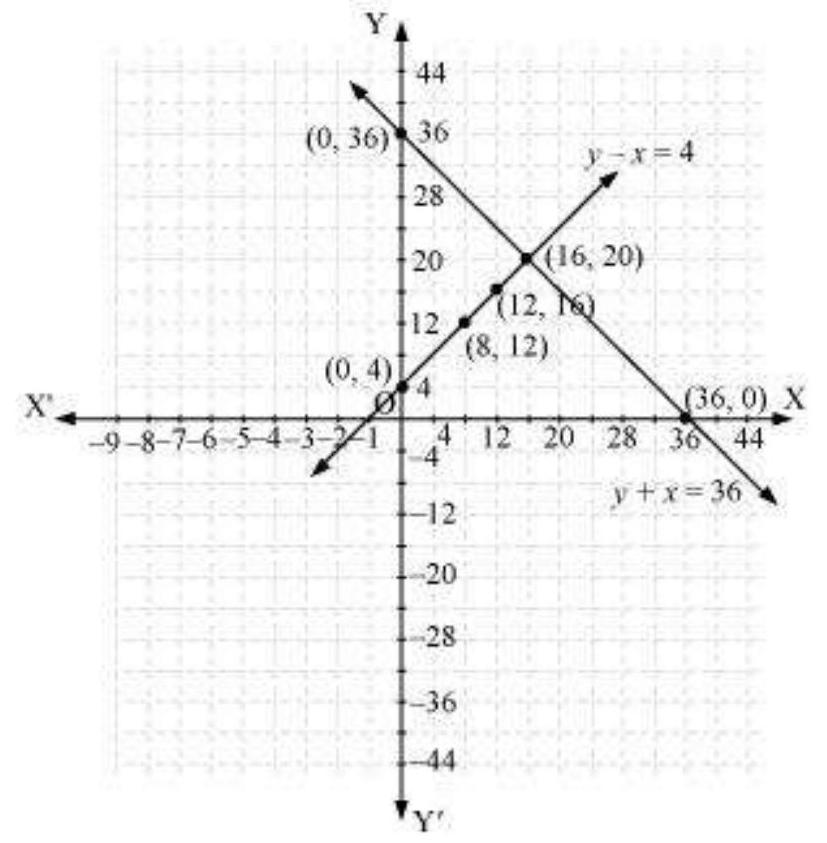
From the figure, it can be observed that these lines are intersecting each other at only point i.e., (16, 20). Therefore, the length and width of the given garden is $20 m$ and $16 m$ respectively.
6. Given the linear equation $2 x+3 y-8=0$, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Show Answer
Solution
(i)Intersecting lines:
For this condition,
$ \dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2} $
The second line such that it is intersecting the given line
is
$ 2 x+4 y-6=0 \quad \text{ as } \quad \dfrac{a_1}{a_2}=\dfrac{2}{2}=1, \quad \dfrac{b_1}{b_2}=\dfrac{3}{4} \text{ and } \dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2} \text{. } $
(ii) Parallel lines:
For this condition,
$\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$
Hence, the second line can be
$4 x+6 y-8=0$
as $\dfrac{a_1}{a_2}=\dfrac{2}{4}=\dfrac{1}{2}, \dfrac{b_1}{b_2}=\dfrac{3}{6}=\dfrac{1}{2}, \dfrac{c_1}{c_2}=\dfrac{-8}{-8}=1$
And clearly, $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$
(iii)Coincident lines:
For coincident lines,
$\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}=\dfrac{c_1}{c_2}$
Hence, the second line can be
$6 x+9 y-24=0$
as $\dfrac{a_1}{a_2}=\dfrac{2}{6}=\dfrac{1}{3}, \quad \dfrac{b_1}{b_2}=\dfrac{3}{9}=\dfrac{1}{3}, \dfrac{c_1}{c_2}=\dfrac{-8}{-24}=\dfrac{1}{3}$
And clearly, $\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}=\dfrac{c_1}{c_2}$
7. Draw the graphs of the equations $x-y+1=0$ and $3 x+2 y-12=0$. Determine the coordinates of the vertices of the triangle formed by these lines and the $x$-axis, and shade the triangular region.
Show Answer
Solution
$x-y+1=0$
$x=y-1$
| $x$ | 0 | 1 | 2 |
|---|---|---|---|
| $y$ | 1 | 2 | 3 |
$3 x+2 y-12=0$
$x=\dfrac{12-2 y}{3}$
| $x$ | 4 | 2 | 0 |
|---|---|---|---|
| $y$ | 0 | 3 | 6 |
Hence, the graphic representation is as follows.
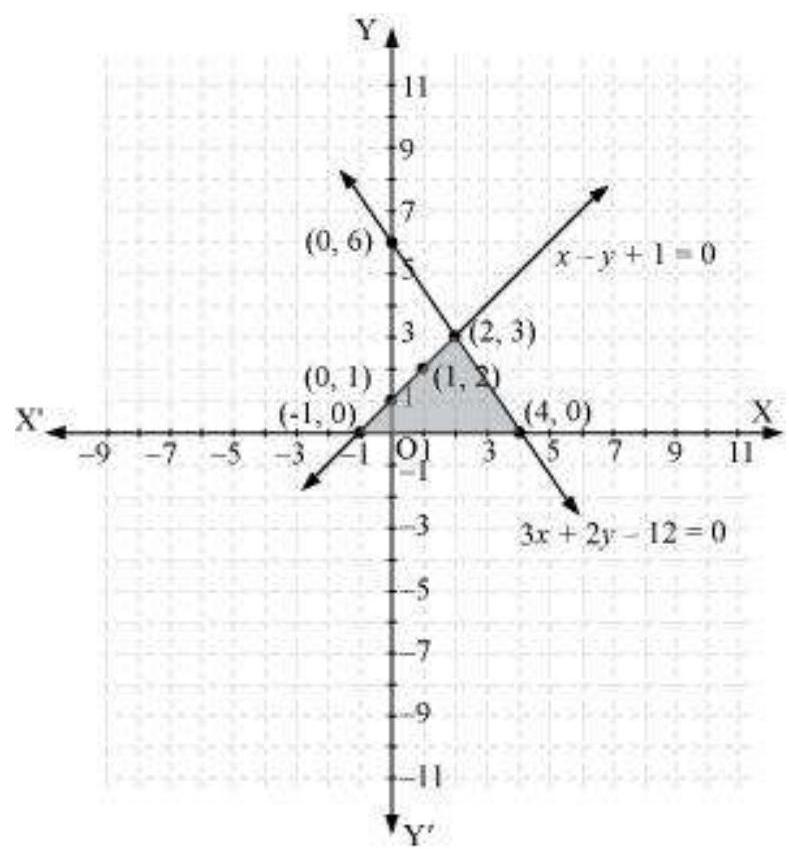
From the figure, it can be observed that these lines are intersecting each other at point $(2,3)$ and $x$-axis at $(-1,0)$ and $(4,0)$. Therefore, the vertices of the triangle are $(2,3),(-1,0)$, and $(4,0)$.










