CIRCLES

9.1 CIRCLE

A circle is the locus of a points which moves in a plane in such a way that its distance from a fixed point remains constant.

9.2 SECANT AND TANGENT :

$\Rightarrow$ Secant to a circle is a line which intersects the circle in two distinct points.

$\Rightarrow$ A tangent to a circle is a line that intersects the circle in exactly one point.

CIRCLES

9.3 THEOREM :

Statement : A tangent to a circle i perpendicular to the radius through the point of contact.

Given : $A$ circle $C(O,r)$ and a tangent $AB$ at a point $P$.

To prove : $OP\perp AB$

Construction : Take any points $Q$, other than $P$ on the tangent $AB$. Join $OQ$. Suppose $OQ$ meets the circle at $R$.

CIRCLES

Proof: $$ Among all line segments joining the point $O$ to a point on $AB$, the shorted one is perpendicular to $AB$. So, to prove that $OP\perp AB$, it is sufficient to prove that $OP$ is shorter than any other segment joining $O$ to any point of $AB$.

Clearly $OP=OR$ Now, $OQ$ $OR+RQ$

$\Rightarrow OQ>OR$ $\Rightarrow OQ>OP(\therefore OP=OR)$

Thus, $OP$ is shorter than any other segment joining $O$ to any point of $AB$.

Hence, $OP\perp AB$.

CIRCLES

9.4 THEORM :

Statement : Lengths of two tangents drawn from an external point to a circle are equal.

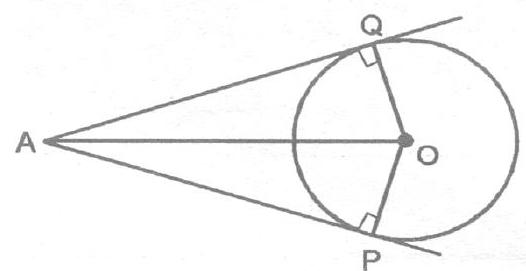
Given: $AP$ and $AQ$ are two tangents drawn from a point $A$ to a circle $C(O,r)$.

To prove $AP=AQ$

Construction : Join $OP,OQ$ and $OA$.

CIRCLES

Proof : $$ In $\mathrm{△}AOQ$ and $\mathrm{△}APO$

$\mathrm{\angle }OQA=\mathrm{\angle }OPA$ [Tangent at any point of a circle is perp. to radius through the point of contact]

$AO=AO$ [Common] $OQ=OP$ [Radius]

So, by R.H.S. criterion of congruency $\mathrm{△}AOQ\cong \mathrm{△}AOP$

$\therefore AQ=AP$ [By CPCT] Hence Proved.

CIRCLES

Result :

(i) If two tangents are drawn to a circle from an external point, then they subtend equal angles at the centre. $\mathrm{\angle }OAQ=\mathrm{\angle }OAP$ [By CPCT]

(ii) If two tangents are drawn to a circle from an external point, they are equally inclined to the segment, joining the centre to that point $\mathrm{\angle }OAQ=\mathrm{\angle }OAP$ [By CPCT]

CIRCLES

Ex. 1 If all the sides of a parallelogram touches a circle, show that the parallelogram is a rhombus.

CIRCLES

Sol. Given : Sides $AB,BC,CD$ and $DA$ of a $||gm$ ABCD touch a circle at $P,Q,R$ and $S$ respectively.

To prove $|{|}^{gm}ABCD$ is a rhombus.

Proof : $AP=AS$ …(i)
$BP=BQ$ …(ii)
$CR=CQ$ …(iii)
$DR=DS$ …(iv)

CIRCLES

[Tangents drawn from an external point to a circle are equal] Adding (1), (2), (3) and (4), we get

$\Rightarrow AP+BP+CR+DR=AS+BQ+CQ+DS$

$\Rightarrow (AP+BP)+(CR+DR)=AS+D{S}_{+}(BQ+CQ).$

$\Rightarrow AB+CD=AD+BC$

$\Rightarrow AB+AB=AD+AD$ $[\text{ In a }||\text{ gm }ABCD,\text{opposite side are equal] }$

$\Rightarrow 2AB=2AD\text{ or }AB=AD$

$\text{ But }AB=CD\text{AND}AD=BC$ $\text{[opposite side of a ||gm ]}$

$\therefore AB=BC=CD=DA\text{ Hence, }||\text{ gm }ABCD\text{ is a rhombus. }$

CIRCLES

Ex. 2 A circle touches the $BC$ of a $\mathrm{△}ABC$ at $P$ and touches $AB$ and $AC$ when produced at $Q$ and $R$ respectively as shown in figure, Show that $=\frac{1}{2}$ (Perimeter of $\mathrm{△}ABC$ ).

CIRCLES

Sol. Given : $A$ circle is touching side $BC$ of $\mathrm{△}ABC$ at $P$ and touching $AB$ and $AC$ when produced at $Q$ and $R$ respectively.

To prove : $AQ=\frac{1}{2}$ (perimeter of $.\mathrm{△}ABC)$

Proof :

$\begin{array}{rl}& AQ=AR\dots (i)\\ & BQ=BP\dots (ii)\\ & CP=CR\dots (iii)\end{array}$

CIRCLES

[Tangents drawn from and external point to a circle are equal]

Now, perimeter of $\mathrm{△}ABC$

$\begin{array}{rl}& =AB+BC+CA\\ & =AB+BP+PC+CA\\ & =(AB+BQ)+(CR+CA)\text{[From (ii) and (iii)]}\\ & =AQ+AR=AQ+AQ\text{[From (i)]}\\ AQ=\frac{1}{2}& \text{ (perimeter of }\mathrm{△}ABC).\end{array}$

CIRCLES

Ex. 3 Prove that the tangents at the extremities of any chord make equal angles with the chord.

CIRCLES

Sol. Let $AB$ be a chord of a circle with centre $O$, and let AP and BP be the tangents at $A$ and $B$ respectively. Suppose, the tangents meet at point $P$. Join OP. Suppose OP meets $AB$ at $C$.

We have to prove that $\mathrm{\angle }PAC=\mathrm{\angle }PBC$

In triangles PCA and PCB

$PA=PB$

CIRCLES

$[\therefore$ Tangent from an external point are equal]

$\mathrm{\angle }APC=\mathrm{\angle }BPC$ $[\therefore PA$ and $PB$ are equally inclined to OP]

And $PC=PC$ [Common]

So, by SAS criteria of congruence

$\mathrm{△}PAC\cong \mathrm{△}BPC\Rightarrow \mathrm{\angle }PAC=\mathrm{\angle }PBC$

[By CPCT]

CIRCLES

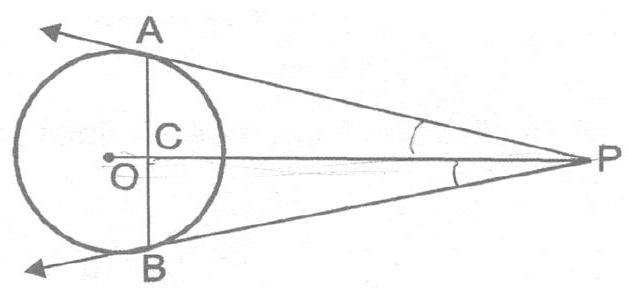
Ex. 4 Prove that the segment joining the points of contact of two parallel tangents passes through the centre.

CIRCLES

Sol. Let PAQ and RBS be two parallel tangents to a circle with centre O. Join OA and OB. Draw OC||PQ Now, $PA||CO$

$\begin{array}{ccc}\Rightarrow & \mathrm{\angle }PAO+\mathrm{\angle }COA={180}^{\circ }& [\text{ Sum of co-interior angle is }{180}^{\circ }]\\ \Rightarrow & {90}^{\circ }+\mathrm{\angle }COA={180}^{\circ }& [\therefore \mathrm{\angle }PAO=90]\\ \Rightarrow & \mathrm{\angle }COA={90}^{\circ }& \end{array}$

Similarly, $\mathrm{\angle }CON={90}^{\circ }$

$\therefore \mathrm{\angle }COA+\mathrm{\angle }COB={90}^{\circ }+{90}^{\circ }={180}^{\circ }$ Hence, $AOB$ is a straight line passing through $O$.

CIRCLES

DAILY PRACTICE PROBLEMS 9

OBJECTIVE DPP - 9.1

1. The length of the tangent drawn from a point $8cm$ away from the centre of a circle of radius $6cm$ is

(A) $\sqrt{7}cm$

(B) $\sqrt[2]{7}cm$

(C) $10cm$

(D) $5cm$

CIRCLES

CIRCLES

2. $A$ tangent $PQ$ at a point $P$ of a circle of radius $5cm$ meets a line through the centre $O$ at a point $Q$, so that $OQ=12cm$. Length of $PQ$ is :

(A) $12cm$

(B) $13cm$

(C) $8.5cm$

(D) $\sqrt{119}cm$

CIRCLES

CIRCLES

3. If tangents $PA$ and $PB$ from a point $P$ to a circle with centre $O$ are inclined to each other at an angle of ${80}^{\circ }$ then $\mathrm{\angle }POA$ is equal to

(A) ${50}^{\circ }$

(B) ${60}^{\circ }$

(C) ${70}^{\circ }$

(D) ${80}^{\circ }$

CIRCLES

CIRCLES

4. Two circle touch each other externally at $C$ and $AB$ is a common tangent to the circle. Then $\mathrm{\angle }ACB=$

(A) ${60}^{\circ }$

(B) ${45}^{\circ }$

(C) ${30}^{\circ }$

(D) ${90}^{\circ }$

CIRCLES

CIRCLES

5. $ABC$ is a right angled triangle, right angled at $B$ such that $BC=6$ am and $AB=8cm$. $A$ circle with centre $O$ is inscribed in $\mathrm{△}ABC$. The radius of the circle is

(A) $1cm$

(B) $2cm$

(C) $3cm$

(D) $4cm$

CIRCLES

CIRCLES

SUBJECTIVE DPP - 9.2

1. $ABCD$ is a quadrilateral such than $\mathrm{\angle }D={90}^{\circ }$. A circle $C(O,r)$ touches the sides $AB,BC,CD$ and $DA$ at $P,Q,R$ and $S$ respectively. If $BC=38cm,CD=25cm$ and $BP=27cm$, find $r$.

CIRCLES

Sol. 1. $14cm$

CIRCLES

2. Two concentric circles are of radius $5cm$ and $3cm$. Find the length of the chord of the larger circle which touches the smaller circle.

CIRCLES

Sol. 2. $8cm$

CIRCLES

3. In a circle of radius $5cm,AB$ and $AC$ are two chords, such that $AB=AC=6cm$. Find the length of chord BC.

CIRCLES

Sol. 3. $9.6cm$.

CIRCLES

4. The radius of the incircle of a triangle is $4cm$ and the segments into which one side is divided by the point of contact are $6cm$ and $8cm$. Determine the other two sides of the triangle.

CIRCLES

Sol. 4. $13cm$ and $15cm$

CIRCLES

5. In figure, $\ell$ and $m$ are two parallel tangents at $P$ and $R$. The tangent at $Q$ makes an intercept ST between $\ell$ and $m$. Prove that $\mathrm{\angle }SOT={90}^{\circ }$

CIRCLES

6. $PQR$ is a right angled triangle with $PQ=12cm$ and $QR=5cm$. A circle with centre $O$ and radius $x$ is inscribed in $\mathrm{△}PQR$. Find the value of $x$.

CIRCLES

Sol. 6. $2cm$

CIRCLES

7. From an external point $P$, two tangents $PA$ and $PB$ are drawn to the circle with centre $O$. Prove that $OP$ is the perpendicular dissector of $AB$.

CIRCLES

8. Two tangent $TP$ and $TQ$ are drawn to a circle with centre $O$ from an external point $T$. Prove that $\mathrm{\angle }PTQ=2\mathrm{\angle }OPQ$.

CIRCLES

9. A circle touches the sides of a quadrilateral $ABCD$ at $P,Q,R,S$ respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.

CIRCLES

10. In figure, a circle touches all the four sides of a quadrilateral $ABCD$ with $AB=6cm,BC=7cm$ and $CD=$ $4cm$. Find AD.

[CBSE - 2002]

CIRCLES

Sol. 10. $3cm$

CIRCLES

11. Prove that the lengths of the tangents drawn from an external point to a circle are equal.

Using the above, do the following :

In figure, $TP$ and $TQ$ are tangents from $T$ to the circle with centre $O$ and $R$ is any point on the circle. If $AB$ is a tangent to the circle at $R$, prove that

$TA+AR=TB+BR$

[CBSE - 208]

CIRCLES

12. In figure, if $\mathrm{\angle }ATO={40}^{\circ }$, find $\mathrm{\angle }AOB$

[CBSE - 2008]

CIRCLES

Sol. 12. ${100}^0$

CIRCLES

13. In figure $OP$ is equal to diameter of the circle. Prove that $ABP$ is an equilateral triangle.

[CBSE - 2008]