TRIANGLES

TRIANGLES

8.1 CONGRUENT AND SIMILAR FIGURES:

Two geometric figures having the same shape and size are known as congruent figures. Geometric figures having the same shape but different sizes are known as similar figures.

TRIANGLES

8.2 SIMILAR TRIANGLES:

Two triangles ABC and DEF are said to be similar if their

(i) Corresponding angles are equal. i.e. $\angle A=\angle D, \angle B=\angle E, \angle C=\angle F$ And,

(ii) Corresponding sides are proportional i.e. $\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}$

TRIANGLES

8.2 (a) Characteristic Properties of Similar Triangles :

(i) (AAA Similarity) If two triangles are equiangular, then they are similar.

(ii) (SSS Similarity) If the corresponding sides of two triangles are proportional, then they are similar.

(iii) (SAS Similarity) If in two triangle’s one pair of corresponding sides are proportional and the included angles are equal then the two triangles are similar.

TRIANGLES

8.2 (b) Results Based Upon Characteristic Properties of Similar Triangles :

(i) If two triangles are equiangular, then the ratio of the corresponding sides is the same as the ratio of the corresponding medians.

(ii) If two triangles are equiangular, then the ratio of the corresponding sides is same at the ratio of the corresponding angle bisector segments.

(iii) if two triangles are equiangular then the ratio of the corresponding sides is same at the ratio of the corresponding altitudes.

(vi) If one angle of a triangle is equal to one angle of another triangle and the bisectors of these equal angles divide the opposite side in the same ratio, then the triangles are similar.

(v) If two sides and a median bisecting one of these sides of a triangle are respectively proportional to the two sides and the corresponding median of another triangle, then the triangles are similar.

(vi) If two sides and a median bisecting the third side of a triangle are respectively proportional to the corresponding sides and the median another triangle, then two triangles are similar.

TRIANGLES

8.3 THALES THEOREM (BASIC PROPROTIONALITY THEOREM) :

Statement: If a line is drawn parallel to one side of a triangle to intersect the other sides in distinct points, then the other two sides are divided in the same ratio.

Given: $\quad$ A triangle $ABC$ in which a line parallel to side $BC$ intersects other two sides $AB$ and $AC$ at $D$ and E respectively.

To Prove :

$ \frac{AD}{DB}=\frac{AE}{EC} $

TRIANGLES

Construction : Join $BE$ and $CD$ and draw $DM \perp AC$ and $EN \perp AB$.

Proof : $\quad$ Area of $\triangle ADE(=\frac{1}{2}.$ base $\times$ height $)=\frac{1}{2} AD \times EN$.

Area of $\triangle ADE$ is denoted as are (ADE)

So, $\quad ar(ADE)=\frac{1}{2} DB \times EN \quad$ And $\quad ar(BDE)=\frac{1}{2} DB \times EN$,

Therefore, $\quad \frac{ar(ADE)}{ar(BDE)}=\frac{\frac{1}{2} AD \times EN}{\frac{1}{2} DB \times EN}=\frac{AD}{DB}$ …(i)

Similarly, $\quad ar(ADE=\frac{1}{2} AE \times DM.$ and $ar(DEC=\frac{1}{2} EC \times DM.$.

And

$ \frac{ar(ADE)}{ar(DEC)}=\frac{\frac{1}{2} AE \times DM}{\frac{1}{2} EC \times DM}=\frac{AE}{EC} $ …(ii)

Note that $\triangle BDE$ and $\triangle DEC$ are on the same base DE and between the two parallel lines $BC$ and $DE$.

So, $\quad ar(BDE)=ar(DEC)$ …(iii)

Therefore, from (i), (ii) and (iii), we have :

$ \frac{AD}{DB}=\frac{AE}{EC} \quad \text { Hence Proved. } $

TRIANGLES

Corollary : If in a $\triangle A B C$, a line $D E|| B C$, intersects $A B$ in $D$ and $A C$ in $E$, then

(i) $\frac{DB}{AD}=\frac{EC}{AE}$

(ii) $\frac{AB}{AD}=\frac{AC}{AE}$

(ii) $\frac{AD}{AB}=\frac{AE}{AC}$

(iv) $\frac{AB}{DB}=\frac{AC}{EC}$

(v) $\frac{DB}{AB}=\frac{EC}{AC}$

TRIANGLES

8.3 (a) Converse of Basic Proportionality Theorem :

If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.

TRIANGLES

8.3 (b) Some Important Results and Theorems :

(i) The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.

(ii) In a triangle $\mathbf{A B C}$, if $\mathbf{D}$ is a point on $\mathbf{B C}$ such that $\mathbf{D}$ divides $\mathbf{B C}$ in the ratio $\mathbf{A B}: \mathbf{A C}$, then $\mathbf{A D}$ is the bisector of $\angle A$.(iii) The external bisector of an angle of a triangle divides the opposite sides externally in the ratio of the sides containing the angle.

(iv) The line drawn from the mid-point of one side of a triangle parallel to another side bisects the third side. (v) The line joining the mid-points of two sides of a triangle is parallel to the third side.

(vi) The diagonals of a trapezium divide each other proportionally.

(vii) If the diagonals of a quadrilateral divide each other proportionally, then it is a trapezium.

(viii) Any line parallel to the parallel sides of a trapezium divides the non-parallel sides proportionally.

(ix) If three or more parallel lines are intersected by two transversal, then the intercepts made by them on the transversal are proportional.

TRIANGLES

Ex. 1 In a $\triangle A B C, D$ and $E$ are points on the sides $A B$ and $A C$ respectively such that $D E | B C$. If $A D=4 x-3$,

$AE=8 x-7, BD=3 x-1$ and $CE=5 x-3$, find the value of $x$. $\quad$ [CBSE - 2006]

TRIANGLES

Sol. In $\triangle ABC$, we have

$DE|| BC$

$ \begin{matrix} \therefore & \frac{AD}{DB}=\frac{AE}{EC} \quad \text { [By Basic Proportionality Theorem] } \\ \Rightarrow & \frac{4 x-3}{3 x-1}=\frac{8 x-7}{5 x-3} \\ \Rightarrow & 20 x^{2}-15 x-12 x+9=24 x^{2}-21 x-8 x+7 \\ \Rightarrow & 20 x^{2}-27 x+9=24 x^{2}-29 x+7 \\ \Rightarrow & 4 x^{2}-2 x-2=0 \\ \Rightarrow & 2 x^{2}-x-1=0 \\ \Rightarrow & (2 x+1)(x-1)=0 \\ \Rightarrow & x=1 \text { or } x=-\frac{1}{2} \end{matrix} $

TRIANGLES

So, the required value of $x$ is 1 .

$ [x=-\frac{1}{2} \text { is neglected as length can not be negative }] . $

TRIANGLES

Ex. 2 $D$ and $E$ are respectively the points on the sides $AB$ and $AC$ of a $\triangle ABC$ such that $AB=12 cm, AD=8 cm$, $AE=12 cm$ and $AC=18 cm$, show that $DE|| BC$.

TRIANGLES

Sol. We have,

$AB=12 cm, AC=18 m, AD=8 cm$ and $AE=12 cm$.

$\therefore \quad BD=AB-AD=(12-8) cm=4 cm$

$CE=AC-AE=(\begin{matrix} 18 & 12\end{matrix} ) cm=6 cm$

Now, $\quad \frac{AD}{BC}=\frac{8}{4}=\frac{2}{1}$

And, $ \frac{AE}{CE}=\frac{12}{6}=\frac{2}{1} \Rightarrow \frac{AD}{BD}=\frac{AE}{CE} $

TRIANGLES

Thus, $DE$ divides sides $AB$ and $AC$ of $\triangle ABC$ in the same ratio. Therefore, by the conserve of basic proportionality theorem we have $DE|| BC$.

TRIANGLES

Ex. 3 In a trapezium $A B C D A B|| D C$ and $D C=2 A B$. EF drawn parallel to $A B$ cuts $A D$ in $F$ and $B C$ in $E$ such that $\frac{BE}{EC}=\frac{3}{4}$. Diagonal $DB$ intersects $EF$ at $G$. Prove that $7 FE=10 AB$.

TRIANGLES

Sol.

TRIANGLES

From (i) and (ii), we get

$\frac{FG}{AB}=\frac{4}{7} \quad$ i.e. $FG=\frac{4}{7} A B$ …(iii)

In $\triangle BEG$ and $\triangle BCD$, we have

$\angle BEG=\angle BCD \quad$ [Corresponding angle $\therefore EG|| CD$ ]

$\angle GBE=\angle DBC \quad$ [Common]

$\therefore \quad \triangle BEG \sim \triangle BCD \quad$ [By AA rule of similarity]

$\therefore \quad \frac{BE}{BC}=\frac{EG}{CD}$

$\therefore \quad \frac{3}{7}=\frac{EG}{CD} \quad[\because \frac{BE}{EG}=\frac{3}{7}.$ i.e.. $.\frac{EC}{BE}=\frac{4}{3} \Rightarrow \frac{EC+BE}{BE}=\frac{4+3}{3}] \Rightarrow \frac{BC}{BE}=\frac{7}{3}$

$\therefore \quad EG=\frac{3}{7} CD=\frac{3}{7}(2 AB)[\because CD=2 AB$ (given) $]$

$\therefore \quad EG=\frac{6}{7} AB$ …(iv)

TRIANGLES

Adding (iii) and (iv), we get

$FG+EG=\frac{4}{7} AB+\frac{6}{7} AB=\frac{10}{7} AB$

$\Rightarrow \quad EF=\frac{10}{7} AB$ i.e., $7 EF=10 AB$.

Hence proved.

TRIANGLES

Ex. 4 In $\triangle A B C$, if $A D$ is the bisector of $\angle A$, prove that $\frac{\text { Area }(\triangle A B D)}{\text { Area }(\triangle A C D)}=\frac{A B}{A C}$

TRIANGLES

Sol. In $\triangle A B C, A D$ is the bisector of $\angle A$.

$\therefore \quad \frac{AB}{AC}=\frac{BD}{DC}$ ….(i) [By internal bisector theorem]

From A draw $AL \perp BC$

$\therefore \quad \frac{\text { Area }(\triangle ABD)}{\text { Area }(\triangle ACD)}=\frac{\frac{1}{2} BD \cdot AL}{\frac{1}{2} DC \cdot AL}=\frac{BD}{DC}=\frac{AB}{AC}$

[From (i)]

Hence Proved.

TRIANGLES

Ex. 5 $\angle BAC=90^{0}, AD$ is its bisector. IF $DE \perp AC$, prove that $DE \times(AB+AB)=AB \times AC$.

TRIANGLES

Sol. It is given that $A D$ is the bisector of $\angle A$ of $\triangle A B C$.

$\therefore \frac{AB}{AC}=\frac{BD}{DC}$

$\Rightarrow \frac{AB}{AC}+1=\frac{BD}{DC}+1 \quad \text { [Adding } 1 \text { on both sides] }$

$\Rightarrow \quad \frac{AB+AC}{AC}=\frac{BD+DC}{DC}$

$\Rightarrow \quad \frac{AB+AC}{AC}=\frac{BC}{DC}$ …(i)

In $\Delta^{\prime}$ s CDE and CBA, we have

$ \angle DCE=\angle BCA $ [Common]

$ \angle DEC=\angle BAC$ [Each equal to $90^{0}$ ]

TRIANGLES

So, by AA-criterion of similarity

$ \Delta CDE \sim \Delta CBA $

$\Rightarrow \quad \frac{CD}{CB}=\frac{DE}{BA} \quad \Rightarrow \quad \frac{AB}{DE}=\frac{BC}{DC}$ …(ii)

From (i) and (ii), we have

$\Rightarrow \quad \frac{AB+AC}{AC}=\frac{AB}{DE} \quad \Rightarrow \quad DE \times(AB+AC)=AB \times AC$

TRIANGLES

Ex. 6 In the given figure, $PA, QB$ and $RC$ are each perpendicular to $AC$. Prove that $\frac{1}{x}+\frac{1}{z}=\frac{1}{y}$

TRIANGLES

Sol. In $\triangle PAC$, we have $BQ|| AP$

$ \begin{aligned} & \Rightarrow \quad \frac{BQ}{AP}=\frac{CB}{CA} \\ & {[\therefore \Delta CBQ \sim \Delta CAP]} \\ & \Rightarrow \quad \frac{y}{x}=\frac{CB}{CA} …(i) \\ & \text { In } \triangle ACR \text {, we have } BQ|| CR \\ & \Rightarrow \quad \frac{BQ}{CR}=\frac{AB}{AC} \quad[\therefore \Delta ABQ \sim \Delta ACR] \\ & \Rightarrow \quad \frac{y}{z}=\frac{AB}{AC} …(ii) \\ \end{aligned} $

TRIANGLES

$ \begin{aligned} & \text { Adding (i) and (ii), we get } \\ & \frac{y}{x}+\frac{y}{z}=\frac{C B}{A C}+\frac{A B}{A C} \\ & \Rightarrow \quad \frac{y}{x}+\frac{y}{z}=\frac{A B+B C}{A C} & \Rightarrow \quad \frac{y}{x}+\frac{y}{z}=\frac{A C}{A C} \\ & \Rightarrow \quad \frac{y}{x}+\frac{y}{z}=1 & \Rightarrow \quad \frac{1}{x}+\frac{1}{z}=\frac{1}{y} \end{aligned} $

TRIANGLES

Ex. 7 In the given figure, $A B|| C D$. Find the value of $x$.

TRIANGLES

Sol. Since the diagonals of a trapezium divide each other proportionally.

$ \begin{matrix} \therefore & \frac{A O}{O C}=\frac{B O}{O D} \\ \Rightarrow & \frac{3 x-19}{x-3}=\frac{x-4}{4} \\ \Rightarrow & 12 x-76=x^{2}-4 x-3 x+12 \\ \Rightarrow & x^{2}-19 x+88=0 \\ \Rightarrow & x^{2}-11 x-8 x+88=0 \\ \Rightarrow & (x-8)(x-11)=0 \\ \Rightarrow & x=8 \text { or } x=11 . \end{matrix} $

TRIANGLES

8.4 AREAS OF SIMILAR TRIANGLS :

Statement: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

Given: $\quad$ Two triangles $ABC$ and $PQR$ such that $\triangle ABC \sim \triangle PQR \quad$ [Shown in the figure]

To Prove : $\quad \frac{ar(ABC)}{ar(PQR)}=(\frac{AB}{PQ})^{2}=(\frac{BC}{QR})^{2}=(\frac{CA}{RP})^{2}$

Construction: Draw altitudes $AM$ and $PN$ of the triangle $ABC$ an $PQR$.

TRIANGLES

Proof :

$ \begin{aligned} & ar(ABC)=\frac{1}{2} BC \times AM \\ & \text { And } ar(PQT)=\frac{1}{2} QR \times PN \\ & \text { So, } \quad \frac{ar(ABC)}{ar(PQR)}=\frac{\frac{1}{2} BC \times AM}{\frac{1}{2} QR \times PN}=\frac{BC \times AM}{QR \times PN} \end{aligned} $ …(i)

Now, in $\triangle ABM$ and $\triangle PQN$,

And $\angle B=\angle Q$ [As $\triangle ABC \sim \triangle PQR$ ]

$\angle M=\angle N$ $[90^{0}. each]$

So, $\quad \triangle ABM \sim \triangle PQN$ [AA similarity criterion]

Therefore, $\quad \frac{AM}{PN}=\frac{AB}{PQ}$ …(ii)

TRIANGLES

Also, $\quad \triangle ABC \sim \triangle PQR$ [given]

So, $\quad \frac{AB}{PQ}=\frac{BC}{QR}=\frac{CA}{RP}$ …(iii)

Therefore,

$\frac{ar(ABC)}{ar(PQR)}=\frac{BC}{QR} \times \frac{AB}{PQ}$ ${[\text { From (i) and (ii)}] } $

$=\frac{AB}{PQ} \times \frac{AB}{PQ}$ ${[\text { From (iii)}] } $

$=(\frac{AB}{PQ})^{2}$

$\text { Now using (iii), we get }$ $\frac{ar(\triangle ABC)}{ar(\triangle PQR)}=(\frac{AB}{PQ})^{2}=(\frac{BC}{QR})^{2}=(\frac{CA}{RP})^{2}$

TRIANGLES

8.4 (a) Properties of Areas of Similar Triangles :

(i) The areas of two similar triangles are in the ratio of the squares of corresponding altitudes.

(ii) The areas of two similar triangles are in the ratio of the squares of the corresponding medians.

(iii) The area of two similar triangles are in the ratio of the squares of the corresponding angle bisector segments.

TRIANGLES

Ex. 8 Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on this diagonals. $\quad$ [CBSE - 2001]

TRIANGLES

Sol. Given : A square $ABCD$. Equilateral triangles $\triangle BCE$ and $\triangle ACF$ have been described on side $BC$ and diagonals $AC$ respectively.

To prove : Area $(\triangle BCE)=\frac{1}{2}$. Area $(\triangle ACF)$

Proof : Since $\triangle BCE$ and $\triangle ACF$ are equilateral. Therefore, they are equiangular (each angle being equal to $60^{\circ}$ ) and hence $\triangle BCE \sim \triangle ACF$.

TRIANGLES

$ \begin{aligned} & \Rightarrow \quad \frac{\text { Area }(\triangle B C E)}{\text { Area }(\triangle ACF)}=\frac{BC^{2}}{A C^{2}} \\ & \Rightarrow \quad \frac{\text { Area }(\triangle BCE)}{\text { Area }(\triangle ACF)}=\frac{BC^{2}}{(\sqrt{2} B C)^{2}}=\frac{1}{2} \quad \begin{bmatrix} \because ABCD \text { is a square } \\ \because \text { Diagonal }=\sqrt{2}(\text { side }) \\ \Rightarrow A C=\sqrt{2} B C \end{bmatrix} \\ & \Rightarrow \quad \frac{\text { Area }(\triangle BCE)}{\text { Area }(\triangle ACF)}=\frac{1}{2} \quad \text { Hence Proved. } \end{aligned} $

TRIANGLES

8.5 PYTHAGOREOUS THEOREM :

Statement : In a right triangle, the square of the hypotenuse is equal to the sum of the square of the other two sides.

Given : $\quad A$ right triangle $A B C$, right angled at $B$.

To prove : $\quad A C^{2}=A B^{2}+B C^{2}$

Construction: $BD \perp AC$

Proof : $\Delta ADB$ & $\Delta ABC$

$∠DAB = ∠CAB $ $\quad$ [Common]

$∠BDA = ∠CBA $ $\quad$ [$90^\circ$ each]

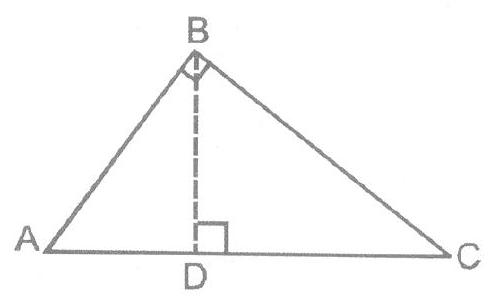
TRIANGLES

So, $∆ ADB$ ~ $∆ABC $ $\quad$ [By AA similarity]

$\frac{AD}{AB} = \frac{AB}{AC}$ $\quad$ [Sides are proportional]

or, $AD . AC = AB^2$ …..(i)

Similarly $∆ BDC ~ ∆ABC $

So, $\frac{CD}{BC} = \frac{BC}{AC}$

or $CD . AC = BC^2$ …..(ii)

Adding (i) and (ii),

$AD . AC + CD . AC = AB^2 + BC^2$

or, $AC (AD + CD) = AB^2 + BC^2$

or $AC.AC = AB^2 + BC^2$

or, $AC^2 = AB^2 + BC^2$ Hence Proved.

TRIANGLES

8.5 (a) Converse of Pythagoreans Theorem :

Statement : In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.

Given : $\quad$ A triangle $ABC$ such that $AC^{2}=AB^{2}+BC^{2}$

Construction : Construct a triangle DEF such that $DE=AB, EF=BC$ and $\angle E=90^{\circ}$

TRIANGLES

Proof :

In order to prove that $\angle B=90 .{ }^{0}$, it is sufficient to show $\triangle ABC \sim \triangle DEF$. For this we proceed as follows Since $\Delta$ DEF is a right - angled triangle with right angle at $E$. Therefore, by Pythagoras theorem, we have

$ \begin{matrix} DF^{2}=DE^{2}+EF^{2} & \\ \Rightarrow \quad DF^{2}=AB^{2}+BC^{2} & {[\therefore DE=AB \text { and } EF=BC \text { (By construction)] }} \\ \Rightarrow \quad DF^{2} 3=AC^{2} & {[\therefore AB^{2}+BC^{2}=AC^{2} \text { (Given) }]} \\ \Rightarrow \quad DF=AC \quad \ldots . .(i) & \\ \text { Thus, in } \triangle ABC \text { and } \triangle DEF \text {, we have } & \\ AB=DE, BC=EF & \text { [By construction] } \\ \text { And } \quad AC=DF & \text { [From equation (i)] } \\ \therefore \quad \Delta ABC \cong \Delta DEF & \text { [By SSS criteria of congruency] } \\ \Rightarrow \quad \angle B=\angle E=90^{0} & \\ \text { Hence, } \triangle ABC \text { is a right triangle, right angled at } B . \end{matrix} $

TRIANGLES

8.5 (b) Some Results Deduced From Pythagoreans Theorem :

(i) In the given figure $\triangle A B C$ is an obtuse triangle, obtuse angled at $B$. If $A D \perp C D$, then $AC^{2}=AB^{2}+BC^{2}+2 \mathbf{B C} \cdot \mathbf{B C}$

TRIANGLES

(ii) In the given figure, if $\angle B$ of $\triangle A B C$ is an acute angle and $\mathbf{A D} \perp \mathbf{B C}$, then $\mathbf{A C}^{2}=\mathbf{A B}^{2}+\mathbf{B C}^{2}-\mathbf{2 B C} \cdot \mathbf{B D}$

TRIANGLES

(iii) In any triangle, the sum of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of the median which bisects the third side.

(iv) Three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares o the medians of the triangle.

TRIANGLES

Ex. 9 In a $\triangle ABC, AB=BC=CA=2 a$ and $AD \perp BC$. Prove that

(i) $\quad AD=a \sqrt{3}$

(ii) area $(\triangle ABC)=\sqrt{3} a^{2}$

TRIANGLES

Sol. (i) Here, $AD \perp BC$.

Clearly, $\triangle ABC$ is an equilateral triangle.

Thus, in $\triangle ABD$ and $\triangle ACD$

$AD=AD \quad$

$\angle ADB=\angle ADC $

And $\quad AB=AC$

$\therefore \quad$ by RHS congruency condition

$\triangle ABD \cong \triangle ACD$

$\Rightarrow \quad BD=DC=a$

TRIANGLES

Now, $\triangle ABD$ is a right angled triangle

$\therefore \quad AD=\sqrt{AB^{2}-BD^{2}}$ [Using Pythagoreans Theorem]

$AD=\sqrt{4 a^{2}-a^{2}}=\sqrt{3} a$ or $a \sqrt{3}$

TRIANGLES

(ii)

$ \begin{aligned} \text { Area }(\triangle ABC)= & \frac{1}{2} \times BC \times AD \\ & =\frac{1}{2} \times 2 a \times a \sqrt{3} \\ & =a^{2} \sqrt{3} \end{aligned} $

TRIANGLES

Ex. 10 $BL$ and $Cm$ are medians of $\triangle ABC$ right angled at $A$. Prove that $4(BL^{2}+CM^{2})=5 BC^{2}$

[CBSE-2006]

TRIANGLES

Sol. In $\triangle B A L$

$BL^{2}=AL^{2}+AB^{2}$ …(i) [Using Pythagoreans theorem]

and In $\triangle CAM$

$CM^{2}=AM^{2}+AC^{2}$ …(ii) [Using Pythagoreans theorem]

TRIANGLES

Adding (1) and (2) and then multiplying by 4 , we get

$4(BL^{2}+CM^{2})=4(AL^{2}+AB^{2}+AM^{2}+AC^{2})$

$=4{AL^{2}+AM^{2}+(AB^{2}+AC^{2})} \quad[\therefore \Delta ABC$ is a right triangle $]$

$=4(AL^{2}+AM^{2}+BC^{2})$

$=4(ML^{2}+BC^{2})$ $[\therefore \Delta LAM $ is a right triangle]

$=\quad 4 ML^{2}+4 BC^{2}$

TRIANGLES

[A line joining mid-points of two sides is parallel to third side and is equal to half of it, $ML=BC / 2$ ]

$=\quad B C^{2}+4 BC^{2}=5 BC^{2}$

Hence proved.

TRIANGLES

Ex. 11 In the given figure, $BC \perp AB, AE \perp AB$ and $DE \perp AC$. Prove that $DE . BC=AD . AB$.

TRIANGLES

Sol. In $\triangle ABC$ and $\triangle EDA$,

We have

TRIANGLES

$ \begin{aligned} & \angle ABC=\triangle ADE \quad \\ & \angle ACB=\angle EAD \quad \\ \therefore \quad & By \quad AA \text { Similarity } \\ & \Delta ABC \sim \Delta EDA \\ \Rightarrow \quad & \frac{BC}{AB}=\frac{AD}{DE} \\ \Rightarrow \quad & DE \cdot BC=AD \cdot AB . \end{aligned} $

Hence Proved.

TRIANGLES

Ex. 12 $O$ is any point inside a rectangle $ABCD$ (shown in the figure). Prove that $OB^{2}+OD^{2}=OA^{2}+OC^{2}$

TRIANGLES

Sol. Through $O$, draw $PQ|| BC$ so that $P$ lies on $A$ and $Q$ lies on DC. [CBSE - 2006]

Now, $PQ|| BC$

Therefore,

$PQ \perp AB$ and $PQ \perp DC[\angle B=90^{\circ}.$ and $.\angle C=90^{\circ}]$

So, $\quad \angle BPQ=90^{\circ}$ and $\angle CQP=90^{\circ}$

Therefore, $BPQC$ and $APQD$ are both rectangles.

Now, from $\triangle OPB$,

$ OB^{2}=BP^{2}+OP^{2} $ …(i)

TRIANGLES

Similarly, from $\triangle ODQ$,

From $\Delta OQC$, we have

$ OD^{2}=OQ^{2}+DQ^{2} $ …(ii)

$ OC^{2}=OQ^{2}+CQ^{2} $ …(iii)

And form $\triangle OAP$, we have

$ OA^{2}=AP^{2}+OP^{2} $ …(iv)

TRIANGLES

Adding (i) and (ii)

$ \begin{aligned} & OB^{2}+OD^{2}=BP^{2}+OP^{2}+OQ^{2}+DQ^{2} \\ & =CQ^{2}+OP^{2}+OQ^{2}+AP^{2} \\ & \quad[As BP=CQ \text { and } DQ=AP] \\ & =CQ^{2}+OQ^{2}+OP^{2}+AP^{2} \\ & =OC^{2}+OA^{2} \quad[\text { From (iii) and (iv) }] \end{aligned} $

Hence Proved.

TRIANGLES

Ex. 13 $ABC$ is a right triangle, right-angled at $C$. Let $BC=a, CA \quad b, AB=c$ and let $p$ be the length of perpendicular

form $C$ on $AB$, prove that

(i) $\quad cp=ab$ (ii) $\quad \frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}$

TRIANGLES

Sol. Let $CD \perp AB$. Then $CD=p$

$\therefore \quad$ Area of $\triangle ABC=\frac{1}{2}$ (Base $\times$ height $)$

$=\quad \frac{1}{2}(AB \times CD)=\frac{1}{2} cp$

Also,

Area of $\triangle ABC=\frac{1}{2}(BC \times AC)=\frac{1}{2} ab$

$\therefore \quad \frac{1}{2} cp=\frac{1}{2} ab$

$\Rightarrow \quad CP=AB$.

TRIANGLES

(ii) Since $\triangle ABC$ is a right triangle, right angled at $C$.

$\therefore \quad AB^{2}=BC^{2}+AC^{2}$

$\Rightarrow \quad c^{2}=a . .+b^{2}$

$\Rightarrow \quad(\frac{ab}{p})^{2}=a^{2}+b^{2} \quad[\because cp=ab \Rightarrow c=\frac{ab}{p}]$

$\Rightarrow \quad \frac{a^{2} b^{2}}{p^{2}}=a^{2}+b^{2} \quad \Rightarrow \quad \frac{1}{p^{2}}=\frac{1}{b^{2}}+\frac{1}{a^{2}} \quad \Rightarrow \quad \frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}$

TRIANGLES

Ex. 14 In an equilateral triangle $A B C$, the side $B$ is trisected at $D$. Prove that $9 A^{2}=7 A B^{2}$.

TRIANGLES

Sol. $\quad ABC$ be can equilateral triangle and $D$ be point on $BC$ such that [CBSE - 2005]

$BC=\frac{1}{3} BC \quad$ (Given)

Draw $AE \perp BC$, Join $AD$.

$BE=EC$ (Altitude drown from any vertex of an equilateral triangle bisects the opposite side)

So, $\quad BE=EC=\frac{BC}{2}$

In $\quad \triangle ABC$

$ \begin{aligned} & A B^{2}=A E^{2}+E^{2} …(i)\\ & A D^{2}=A E^{2}+E^{2} …(ii) \end{aligned} $

TRIANGLES

From (i) and (ii)

$ \begin{aligned} & A B^{2}=A D^{2}-E^{2}+E^{2} \\ & A B^{2}=A D^{2}-\frac{B C^{2}}{36}+\frac{B C^{2}}{4}(\therefore B D+D E=\frac{B C}{2} \Rightarrow \frac{B C}{3}+D E=\frac{B C}{2} \Rightarrow D E=\frac{B C}{6}) \end{aligned} $

$AB^{2}+\frac{BC^{2}}{36}-\frac{BC^{2}}{4}=AD^{2} \quad(\therefore EB=\frac{BC}{2})$

$AB^{2}+\frac{AB^{2}}{36}-\frac{AB^{2}}{4}=AD^{2} \quad(\therefore AB=BC)$

$ \frac{36 AB^{2}+AB^{2}-9 AB^{2}}{36}=AD^{2} \Rightarrow \frac{28 AB}{36}=AD^{2} $

$7 AB^{2}=9 AD^{2}$

TRIANGLES

DAILY PRACTIVE PROBLEMS 8

OBJECTIVE DPP - 8.1

TRIANGLES

1. The perimeters of two similar triangles are $25 cm$ and $15 cm$ respectively. If one side of first triangle is 9 $cm$, then the corresponding side of the other triangle is

(A) $6.2 cm$ $\quad$

(B) $3.4 cm$ $\quad$

(C) $5.4 cm$ $\quad$

(D) $8.4 cm$

TRIANGLES

TRIANGLES

2. In the following figure, $AE \perp BC, D$ is the mid point of $BC$, hen $x$ is equal to

(A) $\frac{1}{a}[b^{2}-d^{2}-\frac{a^{2}}{4}]$ $\quad$

(B) $\frac{h+d}{3}$ $\quad$

(C) $\frac{c+d-h}{2}$ $\quad$

(D) $\frac{a^{2}+b^{2}+d^{2}-c^{2}}{4}$

TRIANGLES

TRIANGLES

3. Two triangles $ABC$ and $PQR$ are similar, if $BC: CA: AB=1: 2: 3$, then $\frac{QR}{PR}$ is

(A) $\frac{2}{3}$ $\quad$

(B) $\frac{1}{2}$ $\quad$

(C) $\frac{1}{\sqrt{2}}$ $\quad$

(D) $\frac{2}{3}$

TRIANGLES

TRIANGLES

4. In a triangle $A B C$, if angle $B=90^{0}$ and $D$ is the point in $B C$ such that $B D=2 D C$, then

(A) $AC^{2}=AD^{2}+3 CD^{2}(B)$ $\quad$

(B) $AC^{2}=AD^{2}+5 CD^{2} $ $\quad$

(C) $AC^{2}=AD^{2}+7 CD^{2}$ $\quad$

(D) $A C^{2}=A B^{2}+5 B D^{2}$

TRIANGLES

TRIANGLES

5. $P$ and $Q$ are the mid points of the sides $AB$ and $BC$ respectively of the triangle $ABC$, right-angled at $B$, then

(A) $AQ^{2}+CP^{2}=AC^{2}$ $\quad$

(B) $AQ^{2}+CP^{2}=\frac{4}{5} AC^{2}$ $\quad$

(C) $AQ^{2}+CP^{2}=\frac{5}{4} AC^{2}$ $\quad$

(D) $AQ^{2}+CP^{2}=\frac{3}{5} AC^{3}$

TRIANGLES

TRIANGLES

6. In a $\triangle A B C, A D$ is the bisector of $\angle A$, meeting side $B C$ at $D$.

If $A B=10 cm, A C=6 cm, B C=12 cm$, find $B D$.

(A) 3.3 $\quad$

(B) 18 $\quad$

(C) 7.5 $\quad$

(D) 1.33

TRIANGLES

TRIANGLES

7. In a triangle $A B C$, a straight line parallel to $B C$ intersects $A B$ and $A C$ at point $D$ and $E$ respectively. If the area of $ADE$ is one-fifth of the area of $ABC$ and $BC=10 cm$, then $DE$ equals

(A) $2 cm$ $\quad$

(B) $2 \sqrt{5} cm$ $\quad$

(C) $4 cm$ $\quad$

(D) $4 \sqrt{5} cm$

TRIANGLES

TRIANGLES

8. $\quad ABC$ is a right-angle triangle, right angled at $A$. A circle is inscribed in it. The lengths of the two sides containing the right angle are $6 cm$ and $8 cm$, then radius of the circle is

(A) $3 cm$ $\quad$

(B) $2 cm$ $\quad$

(C) $4 cm$ $\quad$

(D) $8 cm$

TRIANGLES

TRIANGLES

SUBJECTIVE DPP - 8.2

1. Given $\angle GHE=\angle DFE=90^{\circ}, DH=8, DF=12, DG=3 x-1$ and $DE=4 x+2$.

Find the lengths of segments DG and DE.

TRIANGLES

Sol. 1. $20$ $unit$ & $30$ $unit$ $\quad$

TRIANGLES

2. In the given figure, $DE$ is parallel to the base $BC$ of triangle $ABC$ and $AD: DB=5:3$. Find the ratio :-

(i) $\frac{AD}{AB}$ $\quad$

(ii) $\frac{\text { Area of } \triangle DEF}{\text { Area of } \triangle CFB}$

[CBSE - 2000]

TRIANGLES

Sol.2. (i) $\frac{5}{8}$ (ii) $\frac{25}{64}$ $\quad$

TRIANGLES

3. In Figure, $\triangle ABC$ is a right-angled triangle, where $\angle ACB=90^{\circ}$. The external bisector $BD$ of $\angle ABC$ meets $AC$ produced at $D$. If $AB=17 cm$ and $BC=8 cm$, find the $AC$ and $BD$.

TRIANGLES

Sol.3. $ 15 cm ., \frac{8 \sqrt{34}}{3} cm$. $\quad$

TRIANGLES

4. In figure, $\angle QPS=\angle RPT$ and $\angle PST=\angle PQR$. Prove that $\triangle PST \sim \triangle PQR$ and hence find the ratio $ST: PT$, if $PR: R=4: 5$.

TRIANGLES

Sol.4. $5: 4$ $\quad$

TRIANGLES

5. In the figure, $PQRS$ is a parallelogram with $PQ=16 cm$ and $QR=10 cm$. $L$ is a point on $PR$ such that $RL$ : $LP=2$ : 3. QL produced meets RS at $M$ and PS produced at $N$.

Find the lengths of PN and RM.

TRIANGLES

Sol.5. $PN=15 cm, RM=10.67 cm$. $\quad$

TRIANGLES

6. In $\triangle A B C, D$ and $E$ are points on $A B$ and $A C$ respectively such that $D E|| B C$. If $A D=2.4 cm, A E=3.2 cm$, $DE=2 cm$ and $BC=5 cm$, find $BD$ and $CE$.

TRIANGLES

Sol.6. $DB=3.6 cm, CE=4.8 cm$ $\quad$

TRIANGLES

7. In a triangle $PQR, L$ an $DM$ are two points on the base $QR$, such that $\triangle: PQ=\angle QRP$ and $\angle RPM=\angle RQP$. Prove that :

(i) $\quad \Delta PQL \sim \Delta RPM$

(ii) $\quad QL \times RM=PL \times PM$

(iii) $\quad PQ^{2}=QR \times QL$

TRIANGLES

8. In figure, $\angle BAC=90^{0}, AD \perp BC$. prove that $AB^{2}=BD^{2}-CD^{2}$.

TRIANGLES

9. In figure, $\angle ACB=90^{0}, CD \perp AB$ prove that $CD^{2}=BD \cdot AD$.

TRIANGLES

10. In a right triangle, prove that the square on the hypotenuse is equal to sum of the squares on the other two sides.

Using the above result, prove the following:

In figure $PQR$ is a right triangle, right angled at $Q$. If $QS=SR$, show that $PR^{2}=4 PS^{2}-3 PQ^{2}$.

TRIANGLES

11. In $\triangle ABC, \angle ABC=135^{0}$. Prove that $AC^{2}=AB^{2}+BC^{2}+4 ar(\triangle ABC)$.

TRIANGLES

12. In figure, $A B C$ and $D B C$ are two right triangles with the common hypotenuse $B C$ and with their sides $AC$ and $DB$ intersecting at $P$. Prove that $AP \times PC=DP \times PB$.

[CBSE- 2000]

TRIANGLES

13. Any point $O$, inside $\triangle ABC$, in joined to its vertices. From a point $D$ on $A O, DE$ is drawn so that $DE|| AB$ and $EF|| BC$ as shown in figure. Prove that $DF|| AC$.

[CBSE-2002]

TRIANGLES

14. In figure, $D$ and $E$ trisect $B C$. Prove that $8 A^{2}=3 A C^{2}+5 A D^{2}$

TRIANGLES

15. The perpendicular $A D$ on the base $B C$ of a $\triangle A B C$ meets $B C$ at $D$ so that $2 D B=3 C D$. Prove that $5 A B^{2}=$ $5 AC^{2}+BC^{2}$.

[CBSE - 2007]

TRIANGLES

16. Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares on their corresponding sides.

Using the above, do the following :The diagonals of a trapezium $A B C D$, with $A B | D C$, intersect each other point $O$. If $AB=2 CD$, find the ratio of the area of $\triangle AOB$ to the area of $\triangle COD$

[CBSE - 2008]

TRIANGLES

Sol.16. $4: 1$ $\quad$

TRIANGLES

17. $D, E$ and $F$ are the mid-points of the sides $A B, B C$ and $C A$ respectively of $\triangle A B C$. Find $\frac{ar(\triangle D E F)}{ar(\triangle A B C)}$. [ CBSE- 2008]

TRIANGLES

Sol.17. $1: 4$

TRIANGLES

18. $D$ and $E$ are points on the sides $CA$ and $CB$ respectively of $\triangle ABC$ right-angled at $C$. Prove that $AE^{2}+$ $BD^{2}=AB^{2}+DE^{2}$.

TRIANGLES

19. In figure, $DB \perp BC, DE \perp AB$ and $AC \perp BC$. Prove that $\frac{BE}{DE}=\frac{AC}{BC}$

[CBSE - 2008]

TRIANGLES