Introduction

All matters are composed of what is called ‘atom’. Atom is composed of fundamental particles and it has a nucleus in which its mass is concentrated.

The story of how atom was discovered is very long. But the brief story is that first of all Thomson provided something acceptable in scientific community about the atom. After him, Rutherford presented the modified and almost acceptable atomic model but it had also some discrepencies which was removed by Neils Bohr when he presented the most updated form of the atomic model in 1913.

This chapter provides us the structure of atom and its different features. The chapter also gives a glimpse of the nucleus and different phenomena occuring in it like radioactivity, fission, fusion etc.

You will also study the applications of these nuclear phenomena such as in atom bomb, hydrogen bomb, nuclear reactor and so on.

ATOMIC MODEL THOMSON ATOMIC MODEL

This model suggests an atom to be a tiny sphere of radius $\approx {10}^{-10}m$, containing the positive charge. The atom is electrically neutral. It contains an equal negative charge in the form of electrons, which are embedded randomly in this sphere, like seeds in a watermelon.

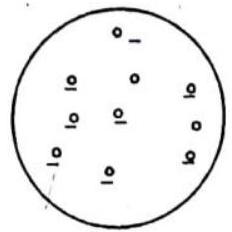
Fig 9.1 Thomson’s atomic model

This model failed to explain (i) large scattering angle of $\alpha$-particle (ii) origin of spectral lines observed in the spectrum of hydrogen atom.

RUTHERFORD’S ATOMIC MODEL

(a) Atom is sphere of diameter about ${10}^{-10}m$ and central part called nucleus contains positive charge and most of the masses of atom

(b) The diameter of the nucleus is of the order of ${10}^{-15}m$

(c) the space around the nucleus is almost empty. It is filled only with tiny sized electrons which revolve around the nucleus in different orbits.

(d) The electrostatic attraction between the nucleus and electron provides centripetal force required for circular motion

(e) Total positive charge in the nucleus is equal to total -ve charge at the atom.

Drawback of Rutherford Model

(1) The electron orbiting around the nucleus is under acceleration. So it must radiate energy. This may result in radius of orbits decreasing gradually.

(2) According to the Rutherford electron can revolve in all possible orbits hence the atom should emit radiation of all possible wave length. But in reality atoms are found to have line spectrum.

BOHR’S ATOMIC MODEL

In 1913 Bohr gave his atomic theory primarily to explain, the spectra of hydrogen & hydrogen-like atoms. His theory, contained a combination of views from Plank’s quantum theory, Einstein’s photon concept & Rutherford model of atom. The Bohr theory can explain, the atomic spectra of hydrogen atom & hydrogen-like ions such as $H{e}^{+},L{i}^{2+},B{e}^{3+}$……… (one electron ions). But his theory failed to explain, the spectra of more complex atom and ions. The basic postulates of Bohr’s model are

(i) The electron moves in circular orbits around the nucleus under the influence of coulombic force of attraction between the electron and the positively charged nucleus (as shown in figure below).

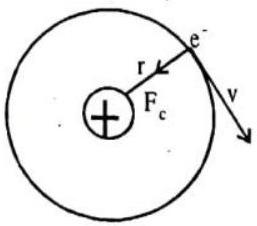
Fig.9.2 Bohr’s model of hydrogen atom

(ii) The electron rotates about the nucleus in certain stationary circular orbits, for which the angular momentum of electron about the nucleus is an integral multiple of $\frac{h}{2\pi }=\hslash$, where $h$ is plank’s constant i.e., $mvr=\frac{nh}{2\pi }=n\hslash \dots (n=1,2,3\dots \dots \dots$. where $n$ is principal quantum number)

(iii) When the electron is in one of its stationary orbits, it does not radiate energy, hence the atom is stable.These stationary orbits are called allowed orbits.

(iv) The atom radiates energy when the electron “jumps” from one allowed stationary state to another. The frequency of radiation follows the condition

$hn=E_i-E_f$ ……….. (2)

Where $E_i$ and $E_f$ are total energies of initial and final stationary states. This difference in energy $(E_i-E_f)$ between two allowed stationary states is radiated/absorbed in the form of a packet of electromagnetic energy ( $hn$ - one photon of frequency $n$ ) called a photon.

Now, we calculate the allowed energies of hydrogen atom, by using the model shown in fig (i), in which the electron travels in a circular orbital of radius $r$ with an orbital speed $v$.

For moving an electron in a circular orbit the required centripetal force is provided by the coulomb force of attraction which acts between nucleus $[Z{e}^{+}.$, here $Z=1$ (atomic number) for hydrogen atom $]$ & electron $(e^{-})$, i.e.,

$\frac{m{v}^2}{r}=\frac{k{e}^2}{r^2}$ ……….. (3)

where $k=\frac{1}{4\pi {\epsilon }_o}$ is electrostatic constant & ${\epsilon }_0$ is permittivity of free space.

Eliminating $v$ from (1) & (3) we obtain

$r=\frac{n^2{\hslash }^2}{mk{e}^2}=\frac{{\epsilon }_o{n}^2{h}^2}{\pi m{e}^2}(n=1,2,3\dots \dots .....)$ ……….. (4)

(radius of $n$th state)

Equation (4) gives the radii of various orbits (have discrete values).

The smallest radius (also called Bohr radius) corresponds to $n=1$ is

$r_0=\frac{{\hslash }^2}{mk{e}^2}\cong 0.529A^{\circ }$ ……….. (5)

$\Rightarrow r=0.529n^2\text{AA}$ for hydrogen atom and $r=0.529\times \frac{n^2}{Z}$ for hydrogen like ions.

From equations (4) & (1) we obtain, $v^2=\frac{n^2{\hslash }^2}{m^2{r}^2}=\frac{k^2{e}^4}{n^2{\hslash }^2}\Rightarrow v=\frac{k{e}^2}{n\hslash }$

or $v=\frac{e^2}{2{\epsilon }_{o}nh}=(\frac{c}{137})\times \frac{1}{n}$ (For hydrogen atom) ……….. (6)

(velocity in nth state)

$v=(\frac{c}{137})\frac{Z}{n}$ for hydrogen like ions

$\frac{c}{137}=2.19\times {10}^{6}m{s}^{-1}$

The total energy of electron is given by

$E=$ K.E. + P.E. $=$ Kinetic energy + Potential energy $=\frac{1}{2}m{v}^2+\frac{ke(-e)}{r}$

$E=\frac{-k{e}^2}{2r}=\frac{-m{e}^4}{8{\epsilon }_o{n}^2{h}^2}$ ……….. (7)

(Allowed energy state)

After substituting numerical values in Eq.(7), we obtain

$E=\frac{-13.6}{n^2}eV$ (For hydrogen atom) ……….. (8)

$E=\frac{-13.6Z^2}{n^2}eV/$ atom for hydrogen like ions.

KEEP IN MEMORY

1. Total energy $=-$ Kinetic energy $=\frac{\text{ Potential energy }}{2}$ 2. The reference level for potential energy has been taken as infinity 3. The energy gap between two successive levels decreases as the value of $n$ increases 4. The radius difference between the successive orbit (or shells) increases as the value of $n$ increases 5. The velocity of electrons around the nucleus goes on decreasing as $n$ increases 6. The time period of the electron in an orbit $T^2\propto r^3$ 7. Maximum number of spectral lines that can be emitted when an electron jumps from $n^{\text{th }}$ orbit is $\frac{n(n-1)}{2}$

$9.$ The first line of Lyman series is when electron jumps from $2\to 1$, It is also called $\alpha$-line

The second line of lyman series is when electron jumps from $3\to 1$, It is also called $\beta$-line

The limiting line of lyman series is when electron jumps from $\mathrm{\infty }\to 1$

The lowest energy state, or ground state, corresponds to $n=1$ is

$E_0=\frac{-m{e}^4}{8{\epsilon }_o{h}^2}=-13.6eV$

The next state corresponds to $n=2$ i.e., first excited state has an energy, $E=$ $-3.4eV$

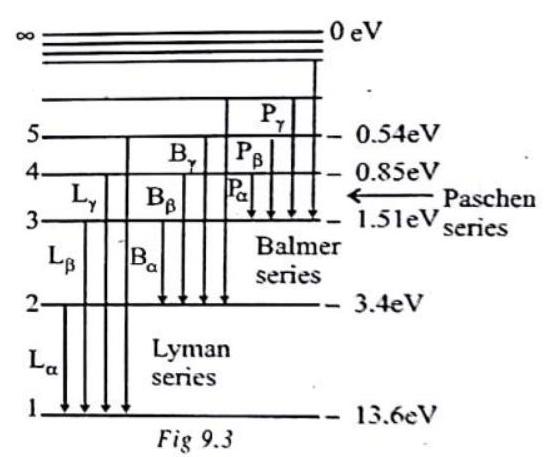
An energy level diagram of the hydrogen atom is shown in figure 2. The upper most level corresponding to $n\to \mathrm{\infty }$, represents the state for which the electron is completely removed from the atom.

Energy level diagram for hydrogen atom

Some transitions for Layman, Balmer & Paschen series are shown. The quantum numbers are at left & energies of levels are at right.

In this case …… $E=0$ for $r=\mathrm{\infty }$ (because $n=\mathrm{\infty }$ )

If the electron jumps from allowed state $n_i$ to allowed state $n_f$ then frequency of emitted photon is given by

$v=\frac{E_f-E_i}{h}=\frac{m{e}^4}{8{\epsilon }_o{h}^3}(\frac{1}{n_i^2}-\frac{1}{n_f^2})$ …… (9)

and the wavelength of emitted photon is $\frac{1}{\lambda }=\frac{v}{c}=\frac{m{e}^4}{8{\epsilon }_{o}c{h}^3}(\frac{1}{n_i^2}-\frac{1}{n_f^2})$

$\frac{1}{\lambda }=R(\frac{1}{n_i^2}-\frac{1}{n_f^2})$ for hydrogen atom …… (10)

and $\bar{v}=\frac{1}{\lambda }=R{Z}^2[\frac{1}{n_1^2}-\frac{1}{n_2^2}]$ (For H-like atoms)

Where $R=1.096776\times {10}^7{m}^{-1}$ is known as Rydberg constant. By using this expression (i.e., equation 10) we can calculate the wavelengths for various series (Layman, Balmer…) in hydrogen spectrum, i.e.

(i) Layman series $n_i=1\mathrm{\&}{n}_f=2,3,4$…………….

(iii) Paschen series $n_i=3\mathrm{\&}{n}_f=4,5,6$…………….

(v) $P$ fund series $n_i=5\mathrm{\&}{n}_f=6,7,8$…………….

(ii) Balmer series $n_i=2,\mathrm{\&}{n}_f=3,4,5$…………….

(iv) Brackett series $n_i=4\mathrm{\&}{n}_f=5,6,7$…………….

First three series of hydrogen atom are shown in figure. But in practice, the value of Rydberg constant varies between $\frac{R}{2}$ and $R$

This is because in above calculations we assumed that electron revolves around a massive fixed nucleus of mass $M$. But in reality, the electron & nucleus each revolve round their common center of mass i.e., the motion of nucleus cannot be ignored. The correction for nuclear motion amounts to replacing electronic mass $m$ by reduced mass $\mu$ which is defined as

$\mu =\frac{mM}{m+M}$

So total energy by taking this correction is

$E=\frac{-\mu e^4}{8{\epsilon }_o{h}^2{n}^2}$

If we are dealing with hydrogen like ions such as $-H{e}^{+},L{i}^{2+},B{e}^{3+}B{e}^{4+}$ (one electron ions) each can be considered as a system of two charges, the electron of mass $m$ and charge -e and nucleus of mass $M$ & charge $+Ze$, where $Z$ is atomic number. The radii of circular orbits for these one electron ions can be written as

$r=\frac{{\epsilon }_o{n}^2{h}^2}{\pi \mu Z{e}^2}=\frac{n^2{\hslash }^2}{\mu kZ{e}^2}(n=1,2,3\dots \dots \dots \dots ...)$ …… (13)

and the allowed energies are given by $E\cong \frac{-\mu Z^2{e}^4}{8{\epsilon }_o{h}^2{n}^2}(n=1,2,3\dots \dots ..$ …… (14)

WAVELENGTH LIMITS IN VARIOUS SPECTRAL SERIES OF HYDROGEN ATOM

(i) For Lyman series (in ultraviolet region)

${\lambda }_{\text{max }}=1216\text{AA},{\lambda }_{\text{min }}=912\text{AA}$

Here $n_i=1,n_f=2,3$ ……………

(ii) For Balmer Series (in visible region)

${\lambda }_{\text{max }}=6563\text{AA}\text{ and }{\lambda }_{\text{min }}=3646\text{AA}$

Here $n_i=2,n_f=3,4,5$ ……………

(iii) For Paschen series (in infrared region)

${\lambda }_{max}=18751\text{AA}\text{ and }{\lambda }_{min}=8107\text{AA}$

Here $n_i=3,n_f=4,5,6$ ……………

(iv) For Brackett series (in infrared region)

${\lambda }_{max}=40477\text{AA}\text{ and }{\lambda }_{min}=14572\text{AA}$

Here $n_i=4,n_f=5,6,7$ ……………

(v) For p-fund series (in infrared region)

${\lambda }_{\text{max }}=74515\text{AA}$ and ${\lambda }_{\text{min }}=22768\text{AA}$

Here $n_i=5,n_f=6,7,8$ ……………

KNOWLEDGE ENHANCER

If Bohr’s quantization postulate (angular momentum $=nh/2\pi$) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantization of orbits of planets around the sun?

Angular momentum $mvr=n\frac{h}{2\pi }$ associated with planetary motion are incomparably large relative to $h$. For example angular momentum of Earth in its orbital motion is of the order of ${10}^{70}\frac{h}{2\pi }$

For such large value of $n$, the difference in successive energies and angular momenta of the quantised levels of the Bohr model are so small that one can predict the energy level continuous.

LIMITATIONS OF BOHR’S MODEL

1. It could not explain the spectra of atoms containing more than one electron. 2. There was no theoretical basis for selecting $mvr$ to be an integral multiple of $h/2\pi$. 3. It involved the orbit concept which could not be checked experimentally. 4. It could not explain Zeeman & Stark effect and fine lines of spectra. 5. It was against De-broglie concept and uncertainty principle

KEEP IN MEMORY

1. Energy of electrons in different orbits in an atom varies inversely with the square of the number of orbits. So, energy of electrons increases (decreases in negative) as the orbit becomes higher. 2. If energy of a particular orbit is $E$ for $H$-atom then its value for a $H$-like atom with atomic number $Z$ is given by $E^{\prime }=E\times Z^2$. 3. If the radius of a particular orbit of $H$-atom is $R$ then its value for a $H$-like atom is given by $R^{\prime }=\frac{R}{Z}$. 4. If velocity of an electron in a particular orbit of $H$-atom be $v$ then its value for a $H$-like atom is given by $v^{\prime }=v\times Z$. 5. If kinetic energy and potential energy of an electron in a particular orbit of $H$-atom be $T$ and $V$ respectively them their corresponding values for a $H$-like atom are given by $T^{\prime }=T\times Z^2$ and $V^{\prime }=V\times Z^2$.

KNOWLEDGE ENHANCER

An electron drops from the fourth energy level in an atom to the third level and then to the first level. Two frequencies of light are emitted. How does their combined energy compare with the energy of the single frequency that would have been emitted if the electron had dropped from the fourth level directly to the first level?

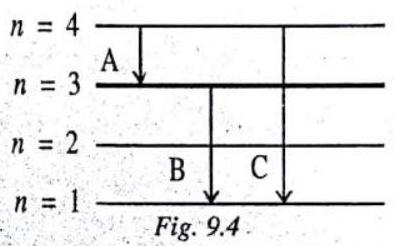
In this figure we have shown the drop of an electron from fourth energy level $(n=4)$ to third energy level $(n=3)$ and during this transition it emits photons of frequency A. In another transition from third energy level $(n=3)$ to first energy level $(n=1)$, it emits photons of frequency B. In case the electron drops from fourth level to first level, it emits photons of frequency $C$. From the above diagram we can easily see that the sum of frequencies (and energies) for transitions $A$ and $B$ equals the frequency (and energy) of transition $C$. Energy of transition $C=$ Energy of transition $A+$ Energy of transition $B$

ILLUSTRATION-9.1

Ionization potential of hydrogen atom is $13.6eV$. Hydrogen atom in the ground state are excited by monochromatic radiation of photon energy $12.1eV$. Which spectral lines will be emitted by hydrogen atoms according to Bohr’s theory?

Show Answer

SOLUTION:

Given that $(I.E.{)}_H=13.6eV$

$\therefore {\left(E_1\right)}_H=-(\text{ I.E. }{)}_H=-13.6\mathrm{eV}$.

After absorbing $12.1eV$ energy, the energy becomes

$-13.6eV+12.1eV=-1.5eV$.

This energy corresponds to $n=3$ level i.e., hydrogen atoms are excited to $n=3$ level.

Now following three transitions are possible

$n=3$ to $n=1,n=3$ to $n=2$, and $n=2$ to $n=1$.

ILLUSTRATION-9.2

The ionisation energy of Hydrogen atom is 13.6 eV. Following Bohr’s theory, what is the energy corresponding to a transition between the 3rd and the 4th orbit?

Show Answer

SOLUTION:

$\begin{array}{rl}& E_n=13.6/n^2\\ & E_3=-(13.9/9)=-1.51eV\\ & \text{ and }{E}_4=-(13.6/16)=-0.85eV\\ & \text{ Now }{E}_4-E_3=-0.85-(-1.51)=0.66eV\end{array}$

ILLUSTRATION-9.3

If the wavelength of the first line of the Lyman series for the hydrogen atom is $1210\text{AA}$, then what is the wavelength of the first line of the Balmer series of the hydrogen spectrum?

Show Answer

SOLUTION:

We know that, $\frac{1}{\lambda }=R[\frac{1}{n_1^2}-\frac{1}{n_2^2}]$

For first line of Lyman series, $n_1=1$ and $n_2=2$

$\therefore \frac{1}{{\lambda }_1}=R[\frac{1}{1}-\frac{1}{4}]=\frac{3R}{4}$ or $R=\frac{4}{3{\lambda }_1}$

for first line of Balmer series $n_1=2$ and $n_2=3$

$\therefore \frac{1}{{\lambda }_2}=R[\frac{1}{4}-\frac{1}{9}]=\frac{5R}{36}=\frac{5}{36}[\frac{4}{3{\lambda }_1}]$

or, $\frac{1}{{\lambda }_2}=\frac{5}{36}\times \frac{4}{3}\times \frac{1}{1210}$ or, ${\lambda }_2=\frac{36\times 3\times 1210}{5\times 4}=6434\text{AA}$

ILLUSTRATION-9.4

If the electron in hydrogen atom jumps from the third orbit to second orbit, what is the wavelength of the emitted radiation?

Show Answer

SOLUTION:

$\frac{1}{\lambda }=R[\frac{1}{n_1^2}-\frac{1}{n_2^2}]$ or $\frac{1}{\lambda }=R[\frac{1}{4}-\frac{1}{9}]=\frac{5R}{36}$

$\therefore \lambda =\frac{36}{5R}$

DISCHARGE TUBE EXPERIMENT

When a very strong potential difference is applied across the two electrodes in a discharge tube and the preacure of the sir is lowered gradually, then a stage is reached at which the current begins to flow through the air with cracking noise. The potential at which this happens is called sparking potential.

As pressure is lowered to $0.1m.m.Hg$ - cathode glow, Crooke’s dark space, negative glow, Faraday dark space and striations are observed.

At $0.01m.m$. Hg entire tube is dark (Crooke’s dark space) except the glass wall behind anode. Colour is yellowish-greza for socts glass and greyish-blue for lead glass.

The luminous streaks travelling from cathode to anode, below $0.01m.m$. Hg, are called cathode rays.

Fig. 9.5

PROPERTIES OF CATHODE RAYS

Emitted perpendicularly to cathode, travel in straight lines, carry energy, possess momentum, deflected by electric and magnetic fields, excite fluroescence, ionise gas, produce highly penetrating secondary radiation when suddenly stopped, effect photographic plate.

POSITIVE RAYS

Stream of +ve ions moving towards cathode in discharge tube.

PROPERTIES OF POSITIVE RAYS

(i) Rays are made up of positively charged particles.

(ii) Being heavy, their velocity is much less than that of cathode rays.

(iii) They ionise the gas through which they pass and ionising power of positive rays is more than that of cathode rays.

(iv) +ve rays are deflected by electric & magnetic field showing that they carry +ve charge with them.

PHOTO ELECTRIC EFFECT

In ${19}^{\text{th }}$ century, experiments showed that when light is incident on certain metallic surfaces, electrons are emitted from the surfaces. This phenomenon is known as the photo-electric effect & emitted electrons are called photo electrons. The first discovery of this phenomenon was made by Hertz (shown in fig.).

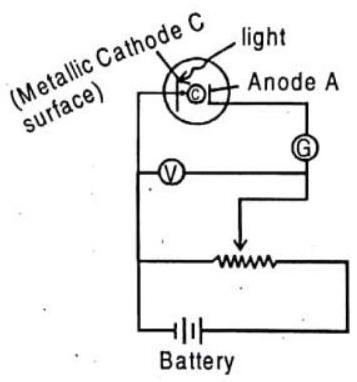
Fig. 9.6 When light strikes the cathode $C$ (metallic surface), photo electrons are ejected. Electrons are collected at Anode A, constituting a current in the circuit. (Photo electric effect)

Figure shows, when light strikes the cathode $C$, electrons are emitted & they are collected on anode $A$ due to potential difference provided by battery and constitutes the current in the circuit (observed by Galvanometer G.)

A plot of photoelectric current versus the potential difference $V$ between cathode & anode is shown in figure below.

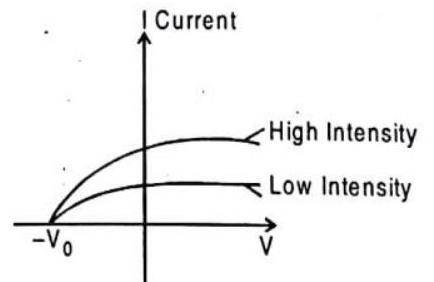
Fig. 9.7 Photoelectric current versus voltage for two light intensities. The current increases with intensity, but reaches a saturation. At voltage less than $-V_0$ the current is zero.

It is clear from figure that photo electric current increases as we increase the intensity of light & obtain saturation value at larger value of potential difference $V$ between cathode & anode. If $V$ is negative then, photoelectrons are repelle-1 by negative anode & only those electrons reaches anode, who have energy equal to or greater than $eV$. But if $V$ is equal to $V_0$, called stopping potential (i.e., cut off. potential), no electrons will reach the anode i.e.,

Maximum Kinetic energy of electron $=e{V}_0$

or $K_{max}=e{V}_0$ ……. (1)

where $e$ is charge of electron (i.e. $1.6\times {10}^{-19}$ coulomb).

But some features of photo electric effect can not be explained by classical physics & the wave theory of light.

(1) No photo electrons are emitted, if the frequency of incident light is less than some cut-off frequency (i.e., threshold frequency) $v_0$. It is inconsistent with the wave theory of light, which predicts that photo electric effect occurs at any frequency provided intensity of incident light is sufficiently high.

(2) The maximum kinetic energy of the photo electrons is independent of light intensiy, but increases with increasing the frequency of incident light.

(3) Electrons are emitted from surface almost instantaneously (less than ${10}^{-9}sec$ after the surface illumination), even at low intensity of incident light(classicaly we assume that the electrons would require some time to absorb the incident light before they acquire enough kinetic energy to escape from metal).

These above points were explained by Einstein in 1905 by treating the light as stream of particles. Taking Max Planck assumption, Einstein postulated that a beam of light consists of small packets of energy called photons or quanta. The energy $E$ of a photon is equal to a constant $h$ times its frequency $v$ i.e.,

$E=hv=\frac{hc}{\lambda }$ ……. (2)

Where $h$ is a Universal constant called Planck’s constant & numerical value of $h$ is

$\text{ i) }h=6.62607\times {10}^{-34}J.s$

When a photon arrives at surface, it is absorbed by an electron. This energy transfer is an All-or-Nothing process, in contrast to continuous transfer of energy in classical theory; the electrons get all photon’s energy or none at all. If this energy is greater than the work function $\varphi$ of the metal ( $\varphi$ i.e., work function is the minimum energy required to remove the electron from metal surface), the electron may escape from the surface. Greater intensity at a particular frequency means greater number of photons per second absorbed & consequently greater number of electrons emitted per second & so greater current.

To obtain maximum kinetic energy $K_{max}=\frac{1}{2}m{v}_{max}^2$ for an emitted electron, applied conservation of energy. According to it $K_{max}$ is

$\begin{array}{rl}& K_{max}=\frac{1}{2}m{v}_{max}^2=hv-\varphi \\ & K_{max}=h(v-v_0)\dots \dots (3)\\ or& e{V}_0=K_{max}=h(v-v_0)\dots \dots (4)\end{array}$

Where ${}_0=$ cut-off potential

$v_{max}=$ Maximum velocity obtained by photoelectrons

$v=$ Frequency of incident light i.e., photon

$v_0=$ Cut off frequency or threshold frequency.

$v_0$ is different for different metallic surfaces. For most metals the threshold frequency is in ultarviolet region of spectrum. (Corresponding to 1 between 200 & $300nm$ ), but for potassium & Cesium oxides, it is in the visible spectrum ($\lambda$ between 400 & $700nm)$.

VARIOUS GRAPHS RELATED TO PHOTO ELECTRIC EFFECT

Fig. 9.8

WORK FUNCTIONS OF SOME ELEMENTS :

Element	(Work function) (eV)
$Al(4.3)$	$Ni(5.1)$
$C$ (carbon) (5.0)	$Si(4.8)$
$Cu(4.7)$	$Ag(4.3)$
$Au$ (Gold) (5.1)	$Na(2.7)$

Where $1eV=1.602\times {10}^{-19}$ joule.

Within the frame work of photon theory of light (Quantum theory of light) we can explain above failures of classical physics.

(1) It is clear from eq. (3) that if energy of photon is less than the work function of metallic surface, the electrons will never be ejected from surface regardless of intensity of incident light.

(2) $K_{max}$ is independent of intensity of incident light, but it depends on the frequency of incident light [i.e., $K_{max}\propto v$ (frequency of light)].

(3) Electrons are emitted almost instantaneously consistent with particle view of light in which incident energy is concentrated in small packets (called photons) rather than over a large area (as in wave theory).

Knowledge ENHANCER

Every metal has a definite work function. Why do all photoelectrons not come out with the same energy if incident radiation is monochromatic? Why is there an energy distribution of photoelectrons?

By work function of a metal, we mean the minimum energy required for the electron in the highest level of conduction band to get out of the metal. Since all the electrons in the metal do not belong to that level but they occupy a continuous band of levels, therefore, for the given incident radiation, electrons knocked off from different levels come out with different energies.

X-RAYS

The X-rays were discovered by Prof. Roentgen, a German scientist in 1885. He was awarded Nobel Prize for this discovery in1901.

The modern apparatus for the production of X-rays was developed by Dr. Coolidge in 1913.

X-rays are produced when fast moving electrons are suddenly stopped on a metal of high atomic number.

Production of X-rays

$X$-rays are produced when fast moving cathode rays are stopped suddenly by a metal called target.

The modern device used in the production of X-ray is called the Coolidge tube, which consists of a highly evacuated glass tube as shown in the figure.

A filament $F$ emits electrons when it is heated by passing a low current through it. It also acts as a cathode. It is surrounded by a molybdenum cylinder $M$. The cylinder $M$ focusses the electrons on a fine beam. The target is tungesten which is embedded in copper anode $A$. The anode $A$ is inclined at ${45}^{\circ }$ to the horizontal. It is cooled by circulating water around it. To produce X-rays, high speed electrons are required. For this, the electrons emitted from the filament are accelerated by applying a high potential difference between the anode and the cathode.

The fast moving electrons produce X-rays when they strike the target.

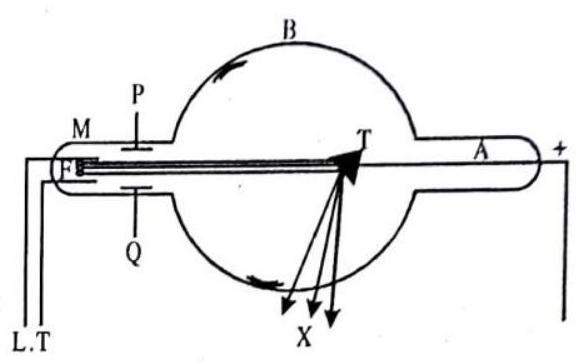
Fig. 9.9 Coolidge tube

Application of $x$-rays

$X$-rays have important and useful applications in surgery, medicine, engineering and studies of crystal structures.

1. Scientific Applications:

The diffraction of $X$-rays at crystals opened a new dimension to $X$-rays crystallography. Various diffraction patterns are used for determining internal structure of crystals. The spacing and dispositions of atoms of a crystal can be precisely determined using Bragg’s Law : $n\lambda =2d\sin \theta$.

2. Industrial Applications:

Since $X$-rays can penetrate through various materials, they are used in industry to detect defects in metallic structures is Big machines, railway tracks and bridges. X-rays are used to analyse the composition of alloys and pearls.

3. In Radio Therapy:

X-rays can cause damage to the tissues of body (cells are ionized and molecules are broken). So X-rays damages the malignant growths like cancer and tumors which are dangerous to life, when it used in proper and controlled intensities.

4. In Medicine and Surgery:

$X$-rays are absorbed more in heavy elements than in lighter ones. Since bones (containing calcium and phosphorus) absorb more X-rays than the surrounding tissues (containing light elements like $H,C,O$ ), their shadow is casted on the photographic plate. So the cracks or Fractures in bones can be easily located. Similarly intestine and digestive system abnormalities are also detected by $X$-rays.

ILLUSTRATION-9.5

The work function of cesium is $1.8eV$. Light of $5000\text{AA}$ is incident on it. Calculate (a) threshold frequency and threshold wavelength. (b) maximum K.E. of emitted electrons. (c) maximum velocity of emitted electrons (d) if the intensity of the incident light be doubled, then what will be the maximum K.E. of the emitted electrons? $(h=6.6\times {10}^{-34}.$ joule second, mass of electron $m=9.0\times {10}^{-31}kg$ and speed of light $c=3\times {10}^{8}m/s$ ).

Show Answer

SOLUTION:

(a) $W_0=h{v}_0$ or $v_0=h/W_0$

$W_0=1.8\times (1.6\times {10}^{-19})=2.9\times {10}^{-19}$ joule

$\therefore v_0=\frac{W_0}{h}=\frac{2.9\times {10}^{-19}\text{ joule }}{6.6\times {10}^{-34}\text{ joule second }}$

$=4.4\times {10}^{14}se{c}^{-1}$

Threshold wavelength

${\lambda }_0=\frac{c}{v_0}=\frac{3.0\times {10}^{8}m/s}{4.4\times {10}^{14}{s}^{-1}}=6.8\times {10}^{-7}$ metre $=6800\text{AA}$

(b) $E_k=h\nu -W_0=\frac{hc}{\lambda }-W_0$

$=\frac{(6.63\times {10}^{-34})(3\times {10}^8)}{5000\times {10}^{-10}}-(2.9\times {10}^{-19}\text{ joule })=(4.0-2.9)\times {10}^{-19}=1.1\times {10}^{-19}\text{ joule. }$

(c) $E_k=\frac{1}{2}m{v}_{max}^2$

$\begin{array}{rl}& \therefore v_{max}=\sqrt{(\frac{2E_k}{m})}=\sqrt{[\frac{2\times (1.1\times {10}^{-19})}{9.0\times {10}^{-31}}]}\\ & =5.0\times {10}^{5}m/sec.\end{array}$

(d) The K.E. of emitted electrons does not depend upon the intensity of light. Hence if the intensity of incident light be doubled, the energy will remain unchanged.

NUCLEAR FISSION

An atom’s nucleus can be split apart. When this is done, a tremendous amount of energy is released. The energy is both heat and light energy. Einstein said that a very small amount of matter contains a very large amount of energy. This energy, when let out slowly, can be harnessed to generate electricity. When it is let out all at once, it can make a tremendous explosion in an atomic bomb. The word fission means to split apart. Inside the reactor of an atomic power plant, uranium atoms are split apart in a controlled chain reaction.

${}_{92}{U}^{235}{+}_0{n}^1⟶{}_{92}{U}^{236}⟶{}_{56}B{a}^{141}{+}_{36}K{r}^{92}+3_0{n}^1+$ energy

$U^{235}$ nucleus captures a thermal neutron. This forms a compound nucleus $U^{236}$ in excited state.

The shape of nucleus is distorted and nucleus splits into two fragments emitting several neutrons.

Fig. 9.10

The energy released in fission of Uranium is about $200MeV$. The fission energy released per nucleon is about $0.84MeV$.

In a chain reaction, particles released by the splitting of the atom go off and strike other uranium atoms splitting those. Those particles given off split still other atoms in a chain reaction. In nuclear power plants, control rods are used to keep the splitting regulated so it doesn’t go too fast.

If the reaction is not controlled, you could have an atomic bomb. But in atomic bombs, almost pure pieces of the element Uranium235 or Plutonium, of a precise mass and shape, must be brought together and held together, with great force. These conditions are not present in a nuclear reactor.

The reaction also creates radioactive material. This material could hurt people if released, so it is kept in a solid form. The very strong concrete dome is designed to keep this material inside if an accident happens.

Energy released per gm of Uranium $=\frac{\text{ Avogadro number }}{\text{ mass number }}\times$ eniergy released per fission

$=\frac{6.023\times {10}^{23}}{235}\times 200=5.12\times {10}^{23}MeV$

Energy released by $1gm$ of $U^{235}=5.12\times {10}^{23}MeV=8.2\times {10}^{10}J=2.28\times {10}^{4}kWh=2\times {10}^{10}$ calorie

This energy is equivalent to

(i) energy obtained by burning $2560kg$ of coal

(ii) energy obtained by burning 20 tonne of explosive TNT

The energy is released in form of kinetic energy of fission fragments, $\gamma$-rays, heat, sound and light energy.

The fission process can take place at normal pressure and temperature.

NUCLEAR FUSION

Another form of nuclear energy is called fusion. Fusion means joining smaller nuclei to make a larger nucleus. The sun uses energy from nuclear fusion of hydrogen atoms into helium atoms. This gives off heat and light and other radiation.

Also given off in this fusion reaction is energy.

Scientists have been working on controlling nuclear fusion for a long time, trying to make a fusion reactor to produce electricity. But they have been having trouble learning how to control the reaction in a contained space.

Controlled nuclear fusion is believed by many scientists to be the ultimate solution to the world’s energy problems. The energy released in fusion reactions is many times greater than that released in fission reactions. To date, however, the technology has not been developed to make use of this source of energy. What’s better about nuclear fusion is that it creates less radioactive material than fission, and its supply of fuel can last longer than the sun’s.

$4_1{H}^1{⟶}_{2}H{e}^4+2_{+1}{e}^0+2v+Q$

Fusion is possible at high pressure $(\sim {10}^6.$ atom) and high temperature $(\sim {10}^{8\circ }C)$

The proton-proton cycle happens at lower temperature as compared to carbon-nitrogen cycle.

Nuclear fusion in possible at a place which has reactants in large quantity.

Hydrogen bomb works on principle of nuclear fusion.

The explosion of a hydrogen bomb needs an explosion of atom bomb to generate required temperature.

No harmful radiations are produced in fusion.

COMPARISON OF FISSION AND FUSION

Nuclear fission	Nuclear fusion
1. A heavy nucleus splits into two lighter nuclei.	1. Two lighter nuclei join to form a heavy nucleus.
2. Neutrons are required to start fission.	2. Protons are usually required to start fusion.
3. It takes place at normal pressure and temperature.	3. It takes place at very high pressure and temperature.
4. The energy released per nucleon is small $\sim 0.8MeV$.	4. The energy released per nucleon is large $\sim 6MeV$.
5. Fissionable material is expensive and not easily available.	5. Fusion material is cheap and abunduntly available.
6. Energy released in fission per cycle is large $\sim 200MeV$.	6. Energy released in fusion per cycle is small $\sim 24.7MeV$.

NUCLEAR REACTORS

A peaceful application of nuclear fission is the generation of electricity using heat from a controlled chain reaction in a nuclear reactor. A nuclear reactor is an arrangement in which the energy produced (in the form of heat) in a nuclear fission can be used in a controlled manner to produce steam, which can run the turbine and produce electricity.

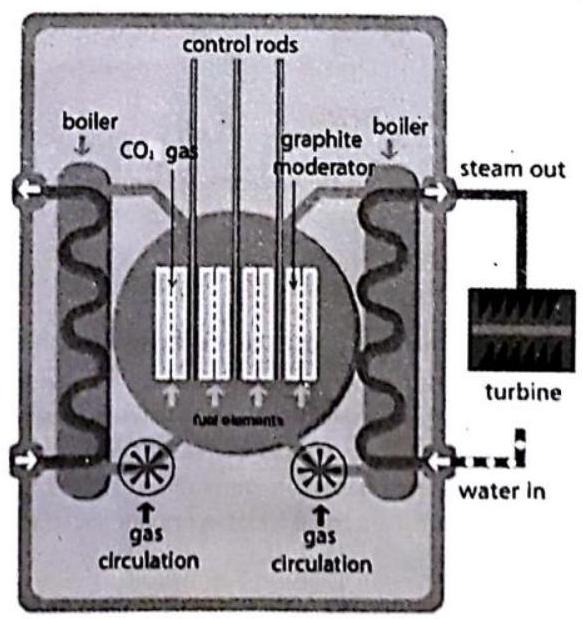
Fig. 9.11 : Nuclear Reactor

The main part of nuclear reactor

(a) Nuclear fuel:

It is the fissionable material used in nuclear reactors to produce energy by fission process. The nuclear fuel consists of uranium, usually in the form of its oxide, $U_3{O}_8$. Naturally occurring uranium contains about $0.7$ of uranium 235 isotope which is too low a concentration to sustain a chain reaction. For effective operation of reactor, uranium 235 must be enriched to a concentration of 3 or $4$.

(b) Moderator:

An important aspect of the fission process is the speed of the neutrons. Slow neutrons hit uranium-235 nuclei more efficiently than do the fast ones. Because fission reactors are highly exothermic, the neutrons produced usually move with high velocities. For greater collision efficiency, neutrons must be slowed down. For this purposes a substance is used that can reduce the kinetic energy of neutrons. Such a substance is called as a moderator. A good moderator should be a nontoxic and inexpensive substance. And it should resist conversion into radioactive substance by neutron bombardment. Graphite (C) or heavy water $(D_{2}O)$ are commonly used as moderators.

(c) Control rods:

In principle, the main difference between an atomic bomb and nuclear reactor is that the chain reaction that takes place in a nuclear reactor is kept under controlled conditions at all the times. The factor limiting the rate of the reaction is the number of neutrons present. This can be controlled by lowering cadmium or boron rods between the fuel elements.

(d) Coolant:

It is the substance which is circulated in pipes to absorb the heat given off by the nuclear reactor and transfer it outside the reactor core, where it is used to produce steam to drive an electric generator. Large quantity of water is used as coolant.

(e) Shield:

To prevent the losses of heat and to protect the people operating the reactor from the radiation and heat, the entire reactor core is enclosed in a heavy steel or concrete dome, called the shield.

A complete nuclear power plant essentially consists of the four parts: reactor core, steam generator, steam turbine, and steam condensing system.

ABOUT THE NUCLEUS

Rutherford proposed the existence of a nucleus in 1911 to explain the results of his $\alpha$ scattering experiment. Nucleus is the central core of an atom in which the entire positive charge and almost the entire mass of an atom is concentrated. The nucleus is made of elementary particles called neutrons and protons. All nuclei except hydrogen are made up of neutrons and protons. Hydrogen nucleus contains a single proton.

Neutron

Neutron is a neutral particle carrying no charge

(i) mass of neutron $m_n=1.6749\times {10}^{-27}kg=1.008665amu$

(ii) they are not deflected by external electric and magnetic fields

(iii) neutrons have high penetrating power and low ionizing power

(iv) neutrons are stable inside the nucleus. Outside the nucleus they are unstable with a half life of about 13 minutes

(v) neutron was discovered by James Chadwick in 1932 when he tried to explain results of collision of $\alpha$ particles with Berrylium

${}_{2}B{e}^4{+}_{2}H{e}^4{⟶}_6{C}^{13}{⟶}_6{C}^{12}{+}_0{n}^1+Q$

(vi) The spin angular momentum of a neutron is $\frac{1}{2}(h/2\pi )$

(vii) depending on speed they are classified as fast and slow (thermal) neutrons.

Proton

Proton is a charged particle carrying unit positive charge.

(i) mass of proton $m_p=1.6726\times {10}^{-27}kg=1.007825amu$

(ii) proton was discovered by Goldstein in 1919.

(iii) The number of protons present inside the nucleus of an atom is called atomic number ( $Z$ ) of an element.

(iv) As atom is electrically neutral so number of protons inside the nucleus is equal to number of electrons in an atom.

According to Heisenberg a proton and neutron can be regarded as two different charge states of same particle called nucleon. The total number of protons and neutrons present inside the nucleus is known as mass number $(A)$ of an element. Number of nucleons or Mass number $(A)=$ proton number $(Z)+$ neutron number $(N)$. In lighter nuclei the number of neutrons and protons are equal while in heavier nuclei number of neutrons is greater than number of protons.

A nuclide is a specific nucleus of an atom characterized as ${}_2{X}_N^A$ where $A$ is mass number, $Z$ is proton number and $N$ is neutron number

TYPES OF NUCLEI

Isotopes :

These are nuclei of same element having same $Z$ but different $A$

e.g. ${}_8{O}^{16}{,}_8{O}^{17}{,}_8{O}^{18}{;}_1{H}^1{,}_1{H}^2{,}_1{H}^3{;}_{92}{U}^{234}{,}_{92}{U}^{235}{,}_{92}{U}^{238}$

All isotopes of an element have same chemical properties. They occupy same place in periodic table. They cannot be separated by chemical analysis. They can be separated by mass spectrometers or mass spectrographs.

Isotones

These are nuclei of different elements having same $N$ but different $A$.

e.g. . ${}_6{C}_7^{13}$ and ${}_7{N}_7^{14};{}_1{H}_2^3$ and ${}_{2}H{e}_2^4;{}_{2}B{e}_5^9$ and ${}_5{B}_5^{10}$

Isotones are different elements with different chemical properties. They occupy different positions in periodic table. They can be separated by chemical analysis and mass spectrometers.

Isobars

These are nuclei of different elements having same $A$ but different $N$ and $Z$.

e.g ${}_6{C}^{14}$ and ${}_7{N}^{14}$; ${}_{18}A{r}^{40}$ and ${}_{20}C{a}^{40}$

Isobars are different elements with different chemical properties. They occupy different positions in periodic table. They can be separated by chemical analysis but cannot be separated by mass spectrometers.

Mirror nuclei

These are nuclei with same $A$ but in which neutron and proton number are interchanged.

${\text{ e.g. }}_{4}B{e}_3^7(Z=4,N=3){\text{ and }}_{3}L{i}_4^7(Z=3,N=4)$

Isomer nuclei

These are nuclei with same $A$ and same $Z$ but differ in their nuclear energy states. They have different life times and internal structure. These nuclei have different radioactive properties. e.g. $C{o}^{60}\mathrm{\&}C{o}^{60\ast }$

NUCLEAR FORCES

The strong forces of attraction which firmly hold the nucleons in the small nucleus and account for stability of nucleus are called as nuclear forces.

The nuclear force is a short range force

(i) They are appreciable when distance between nucleons is of the order of $2.2\times {10}^{-15}m$

(ii) They become negligible when distance between nucleons is greater than $4.2\times {10}^{-15}m$

(iii) When distance between two nucleons is less than $1\times {10}^{-15}m$ the nuclear forces become strongly repulsive

Nuclear forces are charge independent

(a) force between a pair of protons, a pair of neutrons and a pair of neutron and proton is equal.

$F(n-n)=F(p-p)=F(n-p)$

(b) The net force between pair of neutrons and a pair of neutron and proton is equal. This is slightly greater than force between pair of protons because force between protons is reduced due to electrostatic repulsion Net force $F(n-n)=$ Net force $F(n-p)>Net$ force $F(p-p)$

Nuclear forces are spin dependent

(a) Nuclear force depends on relative orientation of spins between two interacting nucleons. (b) The force of attraction between two nucleons with parallel spin is greater than force between nucleons with antiparallel spin.

(c) Deutron is formed in a bound state only if spins of neutron and proton are parallel.

Nuclear forces show saturation property

(a) The nucleon in nucleus interacts with its nearest neighbour only.

(b) It remains unaffected by the presence of other surrounding nucleons.

(c) The nuclear force between a pair of nucleons in light and heavy nucleus is equal.

Nuclear forces are non-central forces

(a) They do not act along line joining the centre of two nucleons.

(b) The non-central component depends on orientation of spins relative to line joining the centre of two nucleons.

Size of nucleus :

Rutherford in his $\alpha$ scattering experiment calculated the distance of closest approach at which $\alpha$ particle approaching nucleus is turned around by Coulomb repulsion.

When $\alpha$ particle is turned the kinetic energy must be converted to electric potential energy since collision is elastic

$\frac{1}{2}m{v}^2=\frac{K(2e)(Ze)}{d},\text{ distance of closest approach }d=\frac{4KZ{e}^2}{m{v}^2}$

$\begin{array}{rl}& \text{ for gold }Z=79,\frac{1}{2}m{v}^2=7MeV=7\times 1.6\times {10}^{-13}J\\ & \text{ so, }d=\frac{2\times 9\times {10}^9\times 79\times (1.6\times {10}^{-19}{)}^2}{7\times 1.6\times {10}^{-13}}=3.2\times {10}^{-14}m\end{array}$

Rutherford assumed the distance of closest approach as a measure of size of nucleus.

Radius of nucleus is related to mass number as $R=R_0{A}^{1/3}$ where $R_0$ is constant and $R_0=1.25\times {10}^{-15}m$

Density of nucleus :

Volume of nucleus $V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi R_0^{3}A$ So volume $V\propto A$.

mass of nucleus $=$ mass of protons + mass of neutrons $=mA$ where $m$ is mass of one nucleon

density of nucleus $\rho =\frac{\text{ mass of nucleus }}{\text{ volume of nucleus }}=\frac{mA}{\frac{4}{3}\pi R_0^{3}A}=\frac{3m}{4\pi R_0^3}$

The nuclear density is independent of mass number $A$.

The nuclear density is nearly constant and is equal to $\rho =\frac{3m}{4\pi R_0^3}=\frac{3\times 1.67\times {10}^{-27}}{4\times 3.14\times (1.25\times {10}^{-15}{)}^3}=2.04\times {10}^{17}kg/m^3$

The nuclear density is maximum at centre of nucleus and decreases as one moves away from the centre.

The distance from the centre of nucleus where density becomes $50$ of its density at centre is called nuclear radius.

The high density of nucleus indicates compactness of nucleus.

Atomic mass unit :

1 atomic mass unit $(amu)=\frac{1}{12}$ of mass of carbon ${(}_6{C}^{12})$ atom

$1amu=\frac{1}{12}(\frac{12}{6.023\times {10}^{23}})=1.66\times {10}^{-24}g=1.66\times {10}^{-27}kg$

Energy equivalent to 1 amu mass, $E=m{c}^2=1.66\times {10}^{-27}(3\times {10}^8{)}^2$ joule $=1.49\times {10}^{-10}$ joule $=931.5MeV$ $1amu=1.49\times {10}^{-10}J=931.5MeV$

MASS DEFECT

The mass of the nucleus is always less than the sum of masses of nucleons composing the nucleus. The difference between the

rest mass of nucleus and sum of rest masses of nucleons constituting the nucleus is known as mass defect. Mass defect $\mathrm{\Delta }m=[Z{m}_P+(A-Z)m_n]-M(Z^A)$

BINDING ENERGY

The energy required to break a nucleus into its constituent nucleons and place them at infinite distance is called binding energy

The energy equivalent to mass defect is called binding energy. This is the energy with which the nucleons are held together.

The binding energies $(\sim MeV)$ are very large as compared to molecular binding energies $(\sim eV)$

Binding energy $BE=(\mathrm{\Delta }m)c^2=c^2[Z{m}_p+(A-Z)m_n-M{(}_Z{X}^A)]$

rest mass of protons + rest mass of neutrons $=$ rest mass of nucleus $+BE$

NUCLEAR REACTION

The transformation of one stable nucleus into another nucleus by bombardment with suitable high energy particles like proton,neutron, $\alpha$ particle etc is known as nuclear reaction.

$\underset{\text{Target nucleus}}{{}_Z{X}^A}+\underset{\text{projectile}}{{}_{2}H{e}^4}$ $\to \underset{\text{compound nucleus}}{{}_{Z+2}{C}^{A+4}}$ $\to \underset{\text{product nucleus}}{{}_{Z+1}{Y}^{A+3}}+{}_1{H}^1+\underset{\text{energy change}}{Q}$

e.g. ${}_{13}A{l}^{27}{+}_{2}H{e}^4{⟶}_{15}{P}^{31}{⟶}_{14}S{i}^{30}{+}_{+1}{e}^0{+}_0{n}^1+Q$

The nuclear reactions obey following conservation laws

(a) conservation of linear momentum

(d) conservation of number of nucleons.

(b) conservation of total energy

(e) conservation of angular momentum.

ILLUSTRATION-9.6

What is the power output of ${}_{92}{U}^{235}$ reactor if takes 30 days to use up $2kg$ of fuel, and if each fission gives $185MeV$ of usable energy? Avogadro’s number $N=6.02\times {10}^{26}$ per kilomole.

Show Answer

SOLUTION:

Number of atoms in $2kg$ fuel

$=\frac{2}{235}$ kilomole $\times (6.02\times {10}^{26}$ per kilomole $)$

$=5.12\times {10}^{24}$

fission rate $=$ number of atoms fissioned in $1sec$.

$=\frac{5.12\times {10}^{24}}{30\times 24\times 60\times 60}=1.975\times {10}^{18}$ per second

Each fission gives $185MeV$ of energy.

Hence energy obtained in one second i.e. power output

$P=185\times (1.975\times {10}^{18})MeV$ per second

$=185\times (1.975\times {10}^{18})\times (1.6\times {10}^{-19})$ joule

$=58.46\times {10}^6$ joule per second (watt)

= 58.46 mega-Watt

ILLUSTRATION-9.7

Calculate the binding energy per nucleon for ${}_{17}{C}^{35}$. Given $M(C{l}^{35})$ = 34.9800 amu $m_n$ = 1.008665 amu and $m_p$ = 1.007825 amu.

Show Answer

SOLUTION:

$BE=Z{m}_p+(A-Z)m_n-M(C{l}^{35})=17\times 1.007825+18\times 1.008665-34.9800=0.308995amu$

$BE=0.308995\times 931.5=287.83MeV$

$\bar{B}=\frac{BE}{A}=\frac{287.75}{35}=8.22MeV/$ nucleon

ILLUSTRATION-9.8

A star initially has ${10}^{40}$ deutrons. It produces energy by processes.

$\begin{array}{c}{}_1{H}^2{+}_1{H}^2{⟶}_1{H}^3+p\\ {\text{ and }}_1{H}^2{+}_1{H}^3{⟶}_{2}H{e}^4+n\end{array}$

If average power radiated by star is ${10}^{16}W$ find time in which deutron is exhausted.

$M{(}_1{H}^2)=2.01471amu{M}_{2}H{e}^4)=4.00388amu$

$M_p=1.00783amu{m}_n=1.00866amu$

Show Answer

SOLUTION:

Adding the two equation $3_1{H}^2{⟶}_{2}H{e}^4+p+n$

mass defect = 3 $\times$ 2.01471 - 4.00388 - 1.00783 - 1.00866 = 0.02376 amu = 0.02376 $\times$ 931.5 MeV = 22.13 MeV

Power of star $={10}^{16}W={10}^{16}J/S$

Number of deutrons used per second

$=\frac{{10}^{16}}{1.6\times {10}^{-19}\times 22.13\times {10}^6}=2.82\times {10}^{27}$

Time in which deutrons will be used

$=\frac{\text{ number of deutrons }}{\text{ number of deutrons used per second }}=\frac{{10}^{40}}{2.82\times {10}^{27}}=3.5\times {10}^{12}sec.$

RADIOACTIVITY

The phenomenon of spontaneous emission of radiations from a substance is called radioactivity Radioactivity was discovered by Henry Becquerel in 1896 in Uranium salts. The substances like Uranium, Radium. Thorium, Polonium efc. which show radioactivity are called radioactive substances. Nuclei with $Z>83$ spontaneously disintegrate with emission of $\alpha$ and $\beta$ particles In radioactivity emission of alpha $(\alpha )$, Beta $(\beta )$ and gamma $(\gamma )$ radiation takes place. These are called radioactive radiations or Becquerel rays. The simultaneous emission of $\alpha$ and $\beta$ particles is not possible. Only one particle is emitted at a time. The emission of radiations causes a change in structure of nucleus. This causes transformation of an atom to new lighter atom or changes a radioactive element into element of lower atomic weight. All heavier radioactive elements emit radiations till they are converted to stable $P{t}^{206}$. It is a statistical process, so it is governed by the laws of probability. The disintegration of all atoms has equal probability. It is a spontaneous process which is independent of all external conditions. It is not affected by temperature, pressure. electric or magnetic field.

Types of radioactive processes

(a) Alpha decay

$z^{NH}$ (parent nucleus) ${⟶}_{2-2}{Y}^{N-1}$ (daughter nucleus) ${+}_{2}H{e}^4$ (alpha particle)

e.g. ${}_{92}{U}^{238}{⟶}_{90}T{h}^{24}{+}_{2}H{e}^4$

Alpha particle consists of 2 neitrons, 2 protons and carries positive charge in magnitude 2 electrons. It is doubly ionized helium nuclei. $\alpha$ emission takes place when size of nucleus becomes too large. The decay reduces the size of nucleus. $\alpha$ emission is explained on basis of quantum mechanical tunnel effect. The energy released in $\alpha$ decay $Q=(M_x-M_y-M_{\alpha })c^2$. The kinetic

energy of $\alpha$ particle $E_{\alpha }=(\frac{A-4}{A})Q$. Where $A$ is mass number and $Q$ is disintegration energy.

(b) Beta decay

(a) Electron emission ( ${\beta }^{-}$)

$\begin{array}{rl}& z^{X^A}{⟶}_{:+1}{Y}^N{+}_{-1}{e}^0({\beta }^{-}\text{particle })+\overline{v}\\ & {\text{ e.g. }}_6{C}^{+4}{⟶}_7{N}^{14}{+}_{-1}{e}^0+\overline{v}\text{ (antineutrino) }\end{array}$

${\beta }^{-}$ particles are fast moving electrons carrying negative charge. They are emitted when nucleus has too many neutrons relative to number of protons i.e. $N/Z$ ratio is larger than required. The emission of electron takes place when a neutron is converted to proton inside the nucleus. This helps in correction of $N/Z$ ratio.

$0^{n^1}{⟶}_1{p}^1{+}_{-1}{e}^0+\overline{v}$

The interaction responsible for $\beta$ decay is weak interaction.

(b) Positron emission

$\begin{array}{rl}& {}_z{X}^A{⟶}_{z-1}{X}^A{+}_{+1}{e}^0({\beta }^{+}\text{particle})+v\\ & {\text{ eg. }}_{29}C{u}^{6+}⟶28N{i}_{+1}^{6+}{e}^0+v\text{ (neutrino) }\end{array}$

${\beta }^{+}$particles are positrons with mass equal to an electron but carry a unit positive charge. They are emitted when nucleus has two many protons relative to number of neutrons i.e. $N/Z$ ratio is smaller than required. The emission of positron takes place when a proton is converted to neutron inside the nucleus. This increases $N/Z$ ratio.

${}_1{p}^1{=}_0{n}^1{+}_{+1}{e}^0+v$

(c) Gamma decay

$$ $$ ${}_Z{X}^{A^{\ast }}{⟶}_Z{X}^A+\gamma$

e.g. ${}_5{B}^{12}{⟶}_6{C}^{{12}^{\ast }}{+}_{-1}{e}^0+v$

$$ $$ ${}_6{C}^{{12}^{\ast }}{⟶}_6{C}^{12}+\gamma$

$\gamma$ rays are electromagnetic radiations which are chargeless, massless and emitted when nucleus has excess enengy. They are emitted when nucleus jumps from excited state to lower level or ground state. This reduces the enerny of nucleus. They are electromagnetic radiations of short wavelength $(-{10}^{-12}m)$ which travel with speed of light.

(d) Electron capture

${}_Z{X}^A{+}_{+1}{e}^0⟶{+}_{Z-1}{Y}^A+v$

${}_{4}B{e}^7{+}_{-1}{e}^0{⟶}_{3}L{i}^7+v$

This process takes place when nucleus has too many protons relative to number of neutrons. i.e. $N/Z$ ratio is larger than requirst. In the process parent nucleus captures one of its own orbital atomic electron and emits a neutrino.

Properties of $\alpha ,\beta$ and $\gamma$ rays

Property	$\alpha$ - rays	$\beta$ - rays	$\gamma$ - rays
1. Nature	These are doubly ionized helium atom ${}_{2}H{e}^4$ charge $q=+2e=3.2\times {10}^{-19}C$ mass $\begin{array}{rl}m& =2p+2n=4ama\\ & =4\times 1.6\times {10}^{-27}\mathrm{kg}\end{array}$	These are beam of fast moving electrons $({\beta }^{-})$and positions $({\beta }^{+})$ charge ${\beta }^{-}=-e=-1.6\times {10}^{-19}C$ ${\beta }^{+}=+e=1.6\times {10}^{-19}C$ $m({\beta }^{-})=m({\beta }^{+})=9.1\times {10}^{-31}kg$	These are electromagnetic radiations of high frequency and travel in form of photons. charge $q=0$ (chargeless) rest mass $=0$ effective mass $=\frac{hv}{c^2}=\frac{h}{\lambda c}$
2. Velocity	Speed ranges between $1.4\times {10}^7$ to $2.20\times {10}^{7}m/s$ $v_{\alpha }\sim 0.05c$	speed ranges from $1$ to $90$ of velocity of light $v_{\beta }\sim 0.9c$	speed equals velocity of light $v_{\gamma }=c$
3. Ionising power	These have maximum ionizing power $(1000)$	There ionizing power is less than $\alpha$ particles and more than $\gamma$ rays $(100)$	There ionizing power is least (1)
4. Penetration power	The penetration power is smallest. Can only penetrate through $0.01mm$ thick $Al$ sheet (1)	Penetration power is about 100 times that of $\alpha$ rays, can penetrate through 1 mm thick Al sheet $(100)$	Penetration power is very large. Can penetrale about $30cm$ thick Al sheet $(10000)$
5. Range	Range is very small (few cms in air)	Range is more than $\alpha$ rays. (few meters in air)	Range is very large (many hundreds of meter in air)
6. Nature of spectrum	Line spectrum	continuous spectrum	line spectrum
7. Interaction with matter	produces heat	produces heat	produces photoelectric effect Compton effect, pair production
8. Effect of electric and magnetic field	Suffers small deflection	suffers large deflection	pass undeflected
9. Effect of photo graphic plate and $ZnS$	Affects photographic plate and produces fluorescense	Affects photographic plate and produces fluorescence	Affects photographic plate and produces fluorescence.

SODDY AND FAJAN’S DISPLACEMENT LAWS

1. For $\alpha$ decay : When an element emits an $\alpha$ particle, the new element has mass number $A$ reduced by 4 and atomic number $Z$ reduced by 2 . The new element is displaced by two places on left in periodic table.

${}_z{X}^A⟶z-2Y^{A-4}{+}_2{H}^4$

2. For ${\beta }^{-}$decay : When an element emits a ${\beta }^{-}$particle the mass number $A$ remains unchanged and atomic number $Z$ is increased by 3. The new element is displaced by one place on right in periodic table

${}_z{X}^A⟶Z_{+1}{Y}^A{+}_{-1}{e}^0+\text{ antineutrino }(\overline{v})$

3. For ${\beta }^{+}$decay : When an element emits a ${\beta }^{+}$particle the mass number remains unchanged and atomic number $Z$ is decreased by one. The new element is displaced by one place on left in periodic table

${}_z{X}^A{⟶}_{z-1}{Y}^A{+}_{+1}{e}^0+\text{ neutrino }(v)$

4. For $\mathit{\gamma }$ decay : When an element emits a $\gamma$ particle the mass, charge or position of element in periodic table remains unchanged. Here the excited nucleus returns to ground state by emission of $\gamma$ ray photon.

RUTHERFORD - SODDY LAWS

The disintegration of a radioactive substance is random and spontaneous. Radioactive decay is purely a nuclear phenomenon and is independent of any physical and chemical conditions. The radioactive decay follows first order kinetics, i.e., the rate of decay is proportional to the number of undecayed atoms in a radioactive substance at any time $t$. If $dN$ be the number of atoms (nuclei) disintegrating in time $dt$, the rate of decay is given as $dN/dt$. From first order of kinetic rate law: $\frac{dN}{dt}=-\lambda N$ where $\lambda$ is called as decay or disintegration constant.

Let $N_0$ be the number of nuclei at time $t=0$ and $N_t$ be the number of nuclei after time $t$, then according to integrated first order rate law, we have:

$N_t=N_0{e}^{-\lambda t}\Rightarrow \lambda t=\ln \frac{N_0}{N_t}=2.303\log \frac{N_0}{N_t}$

The fraction of active atoms remaining at time $t$ is $\frac{N}{N_0}=e^{-\lambda t}$

The number of atoms that have decayed in time $t$ is

$N_0-N=N_0(1-e^{-\lambda t})$

The fraction of atoms that have decayed in time $t$ is

$\frac{N_0-N}{N_0}=1-e^{-\lambda t}$

Fig. 9.12

Decay Constant

Decay Constant $\lambda =\frac{-dN/dt}{N}=\frac{\text{ rate of decay }}{\text{ number of active atoms }}$

Decay Constant is rate of decay of radioactive atoms per active atom.

At $t=\frac{1}{\lambda };N=\frac{N_0}{e}$

The decay constant of radioactive element is equal to reciprocal of the time after which number of remaining active atoms reduce to $1/e$ times of original value.

$\begin{array}{cc}\text{ At }t=\frac{1}{\lambda }\text{ fraction of active nuclei left }& \frac{N}{N_0}=\frac{1}{e}=0.37\text{ or }37\mathrm{\%}\\ & \text{ fraction of decayed nuclei }\\ & 1-\frac{N}{N_0}=0.63=63\mathrm{\%}\end{array}$

$\lambda =\frac{dN/N}{dt}$. The decay constant is the probability of decay per active atom per unit time.

Unit of decay constant is second ${}^{-1}$ and dimension is $T^{-1}$

If their are more than one radioactive elements in a group then the resultant decay Constant is equal to sum of individual decay constants.

$\lambda ={\lambda }_1+{\lambda }_2+{\lambda }_3+\dots \dots \dots \dots \dots \dots \text{ or }\frac{1}{T}=\frac{1}{T_1}+\frac{1}{T_2}+\dots \dots .$

Half life (T) :

Period of a radioactive substance is defined as the time in which one-half of the radioactive substance is disintegrated. If $N_0$ be the number of nuclei at $t=0$, then in a half life $T$, the number of nuclei decayed will be $N_0/2$.

$N_t=N_0{e}^{-\lambda t}$ ……… (i)

$\frac{N_0}{2}=N_0{e}^{-\lambda T}$ ……… (ii)

From (i) and (ii)

$\frac{N_t}{N_0}=(\frac{1}{2}{)}^{t/T}=(\frac{1}{2}{)}^{n}k$

$n$ : number of half lives

Mean life $(\tau )$ :

The mean life of an atom in a radioactive substance is called average life of radioactive substance.

Mean life $\tau =\frac{\text{ the sum of lives of all active atoms }}{\text{ total number of active atoms }}\tau =\frac{{\int }_0^{N_0}tdN}{N_0}=\frac{N_0\lambda {\int }_0^{N_0}t{e}^{-\lambda }dt}{N_0}=\frac{1}{\lambda }$

Thus mean life is equal to reciprocal of decay constant $(\tau =1/\lambda )$

Half life $T=\frac{0.693}{\lambda }=0.693\tau$ and average life $\tau =\frac{T}{0.693}=1.44T$

$\tau >$ T i.e. average life is greater than half life.

Mean life is the time in which (a) number of active atoms reduces to $37$ of its initial value or (b) number of decayed atoms is $63$

$N=N_0{e}^{-\lambda t}$ so $\log \frac{N}{N_0}=-\lambda t$

Mean life is equal to magnitude of reciprocal of slope of $\log \frac{N}{N_0}v/st$ curve.

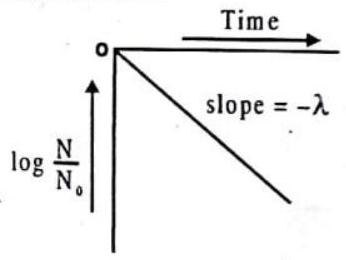
Fig. 9.13

ACTIVITY

The number of decays per unit time or decay rate is called activity.

Activity $A=\frac{dN}{dt}=N_0\lambda e^{-\lambda t}=A_0{e}^{-\lambda t}=N\lambda$

where $N_0\lambda =A_0$ is initial activity

$A=A_0{e}^{-\lambda t}$ is the activity law which shows activity decreases exponentially with time.

The activity of one gram of radioactive substance called specific activity.

Units of activity

Curie: The specific activity of $1gm$ of Radium 226 is called one curie.

1 curie $=3.7\times {10}^{10}$ disintegrations per second

Rutherford :

1 rutherford $={10}^6$ disintegrations per second

Becquerel :

I Becquerel $=1$ disintegration per second

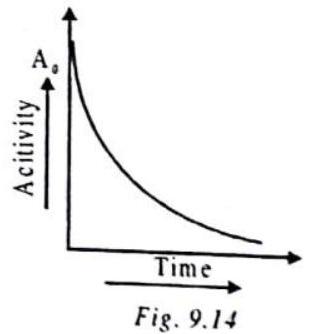
ILLUSTRATION-9.9

At any instant, the ratio of the amount of radioactive substances is $2:1$. If their half lives be respectively 12 and 16 hours. then after two days, what will be the ratio amount of the substances?

Show Answer

SOLUTION:

For first substance $n=\frac{48}{12}=4$

$\therefore N_1=N_{01}(\frac{1}{2}{)}^4=N_{01}/16$ …… (1)

For second substance, $n=\frac{48}{16}=3$

$N_2=N_{02}(\frac{1}{2}{)}^3=N_{02}/8$ …… (2)

Now, $\frac{N_1}{N_2}=\frac{N_{01}}{N_{02}}\times \frac{1}{2}=2\times \frac{1}{2}=1(\because N_{01}=2N_{02})$

$\therefore N_1:N_2=1:1$

ILLUSTRATION-9.10

Two radioactive substances $X$ and $Y$ initially contain equal number of nuclei. $X$ has a half life of 1 hour and $Y$ has half life of 2 hours. After two hours what is the ratio of the activity of $X$ to the activity of $Y$ ?

Show Answer

SOLUTION:

$\begin{array}{rl}& \frac{d{N}_x}{dt}={\lambda }_1{N}_x={\lambda }_1(N_0/4)(\because N=N_0/2^n)\text{ and }\frac{d{N}_Y}{dt}={\lambda }_2{N}_Y={\lambda }_2(N_0/2)\\ & \therefore (\frac{d{N}_X}{dt})/(\frac{d{N}_Y}{dt})=\frac{{\lambda }_1}{2{\lambda }_2}=\frac{T_2}{2T_1}=\frac{2}{2\times 1}=\frac{1}{1}(\because \lambda =\frac{0.693}{T})\end{array}$

ILLUSTRATION-9.11

The half life of radium is 1620 years and its atomic weight is 226 . What will be the number of atoms that will decay from its $1gm$ sample per second?

Show Answer

SOLUTION:

According to Avogadro’s hypothesis,

$N_0=\frac{6.02\times {10}^{23}}{226}=2.66\times {10}^{21}$

Half life $=T=\frac{0.6931}{\lambda }=1620$ years

$\therefore \lambda =\frac{0.6931}{1620\times 3.16\times {10}^7}=1.35\times {10}^{-11}{s}^{-1}$

Because half life is very much large as compared to its time interval, hence $N\approx N_0$

$\frac{dN}{dt}=\lambda N=\lambda N_0$ or $dN=\lambda N_{0}dt$

$\therefore dN=(1.35\times {10}^{-11})(2.66\times {10}^{21})(1)=3.61\times {10}^{10}$.

ILLUSTRATION-9.12

One gram of Radium emits $3.7\times {10}^{10}a$ particles per second. Calculate half life and mean life of Radium. Given Atomic mass of Radium $=226$

Show Answer

SOLUTION:

Rate of decay of Radium $=$ rate of emission of $\alpha$ particles

or $\frac{-dN}{dt}=\lambda N=3.7\times {10}^{10}$ per second

Number of active atoms $N=\frac{6.023\times {10}^{23}\times 1}{226}$

$\therefore \lambda N=\frac{0.693}{T}\times \frac{6.023\times {10}^{23}}{226}=3.7\times {10}^{10}$

or $T=1583$ years

Mean life $\tau =1.44T=1.44\times 1580=2279$ years

ILLUSTRATION-9.13

The activity of a radioactive substance drops to $1/32$ of its initial value in $7.5h$. Find the half life.

Show Answer

SOLUTION:

Using $\frac{A}{A_0}=(\frac{1}{2}{)}^{t/T}$ or $\frac{1}{32}=(\frac{1}{2}{)}^{7.5/T}$

or $(\frac{1}{2}{)}^5=(\frac{1}{2}{)}^{7.5/T}$ or $5=\frac{7.5}{T}$ i.e. $T=1.5$ hours

MISCELLANEOUS

SOLVED EXAMPLES

1. Find the ratio of the area of orbit of first excited state of electron to the area of orbit of ground level for hydrogen atom.

Show Answer

Solution. $A\propto r^2\propto n^4$

$\frac{A_2}{A_1}=[\frac{2}{1}{]}^4=\frac{16}{1}=16:1$

2. The activity of a radioactive substance drops to $1/32$ of its initial value in $7.5h$. Find the half life.

Show Answer

Solution. Using $\frac{A}{A_0}=(\frac{1}{2}{)}^{t/T}$ or $\frac{1}{32}=(\frac{1}{2}{)}^{7.5/T}$

$\text{ or }(\frac{1}{2}{)}^5=(\frac{1}{2}{)}^{7.5/T}\text{ or }5=\frac{7.5}{T}$

i.e. $T=1.5$ hours

3. The half life of a radioactive substance is 34.65 minute. If ${10}^{22}$ atoms are active at any time then find the activity of substance?

Show Answer

Solution. Activity $A=\frac{-dN}{dt}=\lambda N$

$\begin{array}{rl}A& =\frac{0.693}{T}\times N=\frac{0.693}{34.65\times 60}\times {10}^{22}\\ & =3.34\times {10}^{18}\text{ disintegration }/sec.\end{array}$

4. The mean life of a radioactive material for $\alpha$ and $\beta$ decay are 1620 years and 520 years. What is the half life of sample.

Show Answer

Solution. There are two channels of decay so $\frac{1}{\tau }=\frac{1}{{\tau }_{\alpha }}+\frac{1}{{\tau }_{\beta }}$

or $\tau =\frac{{\tau }_{\alpha }{\tau }_{\beta }}{{\tau }_{\alpha }+{\tau }_{\beta }}=\frac{1620\times 520}{1620+520}=394$ years

The half life $T=0.693\tau =0.693\times 394=273$ years

5. A nucleus breaks into two parts whose velocity is in ratio 2:1. Find the ratio of their radius.

Show Answer

Solution. as per conservation of momentum $m_1{v}_1+m_2{v}_2=0$

So $\frac{m_1}{m_2}=\frac{v_2}{v_1}$

ratio of radii $\frac{R_1}{R_2}=(\frac{A_1}{A_2}{)}^{1/3}=(\frac{m_1}{m_2}{)}^{1/3}=(\frac{1}{2}{)}^{1/3}$

so $R_1:R_2=1:2^{1/3}$

6. The binding energy of ${10}^{20}$ is $160.64MeV$. Find the atomic mass.

Show Answer

Solution. Given $m_P=1.007825$ amu and $m_n=1.008665amu$

$BE=\mathrm{\Delta }m{c}^2=c^2[Z{m}_P+(A-Z)m_n-M]$

$\begin{array}{rl}& M=\mathrm{Z}{m}_p+(A-Z)m_n-BE(\mathrm{amu})\\ & M=10\times 1.007825+10\times 1.008665-\frac{160.64}{931.25}=19.992\mathrm{amu}\end{array}$

7. The mass defect in a nuclear fusion reaction is $0.3$. What amount of energy is produced when $1kg$ of substance undergoes fusion.

Show Answer

Solution. Total mass converted to energy $=\frac{0.3}{1000}\times 1=3\times {10}^{-3}kg$

Energy liberated $=\mathrm{\Delta }m{c}^2=3\times {10}^{-3}\times (3\times {10}^8{)}^2$

$=27\times {10}^{13}\text{ joule }$

8. Determine the power output of $a_{92}{U}^{235}$ reactor if it takes 30 days to use $2kg$ of fuel. Energy released per fission is $200MeV$ and $N=6.023\times {10}^{26}$ per kilomole.

Show Answer

Solution. Number of atoms in $2kg$ fuel

$=\frac{2}{235}\times 6.023\times {10}^{26}=5.12\times {10}^{24}$

Number of fission per second

$=\frac{5.12\times {10}^{24}}{30\times 24\times 60\times 60}=1.978\times {10}^{18}$

Energy released per fission

$=200MeV=200\times 1.6\times {10}^{-13}=3.2\times {10}^{-11}J$

$\begin{array}{rl}\text{ Power output }& =3.2\times {10}^{-11}\times 1.978\times {10}^{18}=63.28\times {10}^{6}W\\ & =63.28MW\end{array}$

9. If $200MeV$ energy is released per fission of $U^{235}$ nuclei. Find the mass of $U^{235}$ consumed per day in a reactor of power $1MW$ assuming its efficiency as $80$.

Show Answer

Solution. Energy produced in one day $={10}^6\times 24\times 60\times 60$ joule

$\eta =0.8=\frac{\text{ output energy }}{\text{ input energy }}=\frac{{10}^6\times 24\times 60\times 60}{\text{ input energy }}$

So input energy $=\frac{{10}^6\times 24\times 60\times 60}{0.8}=10.8\times {10}^{10}J$

energy released in one fission

$=200\times {10}^6\times 1.6\times {10}^{-19}=3.2\times {10}^{-11}J$

no. of fissions per day $=\frac{10.8\times {10}^{10}}{3.2\times {10}^{-11}}=3.375\times {10}^{21}$

mass of $U^{235}$ required

$=$ no. of nuclei disintegrating per day $\times$ mass of $U^{235}$

$=3.375\times {10}^{21}\times 235\times 1.67\times {10}^{-27}=1.324mg$

10. Ultraviolet light of wavelength $2271\text{AA}$ from a $100W$ mercury source irradiates a photo-cell made of molybdenum metal. If the stopping potential is $-1.3V$, estimate the work function of the metal. How would the photo-cell respond to a high intensity $(-{10}^{5}Wm{m}^{-2})$ red light of wavelength $6328\text{AA}$ produced by a He-Ne laser?

Show Answer

Solution. Let us find energy of each photon of given ultraviolet light

$E=\frac{hc}{\lambda }=\frac{6.63\times {10}^{-34}\times 3^1\times {10}^8}{2271\times {10}^{-10}\times 1.6\times {10}^{-19}}=5.47eV$

Maximum kinetic energy of emitted electron can be judged by stopping potential of 1.3 volt.

$\frac{1}{2}m{v}_{max}^2=1.3eV$

Using Einstein’s equation $hv=W_0+\frac{1}{2}m{v}_{max}^2$

$5.47eV=W_0+1.3eV$

$W_0=4.17eV$

Red light of wavelength $6328\text{AA}$ will have energy of each photon

$E=\frac{hc}{\lambda }=\frac{6.63\times {10}^{-34}\times 3\times {10}^8}{6328\times {10}^{-10}\times 1.6\times {10}^{-19}}=1.96eV$

Thus energy of red light photons is less than work function $4.17eV$, hence irrespective of any intensity no emission will take place.

11. The total energy of an electron in the first excited state of the hydrogen atom is about $-3.4eV$.

(a) What is the kinetic energy of the electron in this state?

(b) What is the potential energy of the electron in this state?

(c) Which of the answer above would change if the choice of the zero of potential energy is changed?

Show Answer

Solution. Kinetic energy of an electron in an orbit, $=\frac{1}{4\pi {\epsilon }_0}\frac{e(Ze)}{2r}$

Potential energy of electron in the orbit $U=-\frac{1}{4\pi {\epsilon }_0}(\frac{Z{e}^2}{r})$

Total energy $E=K+U=-\frac{1}{4\pi {\epsilon }_0}(\frac{Z{e}^2}{2r})=-K=\frac{U}{2}$

It is given, total energy $E=(-3.4eV)$

(a) Kinetic energy of electron in this state $E=-K$

So, $K=E=-(-3.4eV)=3.4eV$

(b) Potential energy $E=U/2$

$U=2E=2(-3.4)=-6.8eV$

(c) If the zero of the potential energy is chosen differently, the kinetic energy remain the same. Althugh potential energy and hence total energy changes.

12. A radioactive isotope has a half-life of $T$ years. How long will it take the activity to reduce to (a) $3.125$,(b) $1$ of its original value?

Show Answer

Solution. Activity $R=R_0{e}^{-\lambda s}$

Also instantaneous activity, $R=-\lambda N$

$R=-\frac{0.693}{T}N$

Initital activity, $R_0=-\lambda N_0$

So, $R_0=-\frac{0.693}{T}{N}_0$

(a) $\begin{array}{rl}\frac{R}{R_0}& =\frac{N}{N_0}=\frac{3.125}{100}=\frac{1}{32}\text{ or }\frac{N}{N_0}={\left(\frac{1}{2}\right)}^n={\left(\frac{1}{2}\right)}^5\text{ or }n=5\\ \therefore t& =nT\text{ s years. }\end{array}$

(b) $\frac{R}{R_0}=\frac{N}{N_0}=\frac{1}{100}$

Required time, as can not be solved by direct calculation as in part (a).

$t=\frac{2.303}{\lambda }\log \frac{N_0}{N}=\frac{2.303T}{0.693}\log 100=\frac{2.303\times 2\times T}{0.693}\approx 6.65T$ years.

13. The half-life of ${}_{38}^{90}\mathrm{Sr}$ is 28 years. What is the distintegration rate of $15mg$ of this isotope?

Show Answer

Solution. Given $T_{1/2}=28$ years $=28\times 3.154\times {10}^{7}s$

Mass $m=15mg=0.015g$

Number of atoms in $0.015g$ sample of ${}_3{8}^{80}Sr$,

$N=\frac{m}{M}\times \text{ Avogadro’s number }=\frac{0.015\times 6.023\times {10}^{23}\text{ atoms }}{90}$

Activity of the sample,

$\begin{array}{rl}& R=\lambda /N=\frac{0.693}{T_{1/2}}N=\frac{0.693\times 0.015\times 6.023\times {10}^{23}}{28\times 3.154\times {10}^7\times 90}\\ & =7.877\times {10}^{10}\text{ disintegration }/sec=7.877\times {10}^{10}Bq\\ & =\frac{7.877\times {10}^{10}}{3.7\times {10}^{10}}Ci=2.13Ci\end{array}$

14. Calculate the compare the energy released by (a) fusion of $1.0kg$ of hydrogen deep within Sun and (b) the fission of $1.0kg$ of $235U$ in a fission reactor.

Show Answer

Solution. (a) In the fusion reactions taking place within core of sun, 4 hydrogen nuclei combines to form a helium nucleus with the release of $26MeV$ of energy.

$4_1^{1}H{\to }_2^{4}He+2e^{+}+26MeV$

Number of atoms in $1kg$ of ${}_1^{1}H$

$n=\frac{1000g\times 6\times {10}^{23}}{\text{ Atomic mass }}=\frac{1000g}{1g}\times 6\times {10}^{23}=6\times {10}^{26}=6\times {10}^{26}$ atoms

Energy released inthe fusion of $1kg$ of ${}_1^{1}H$

$E=\frac{6\times {10}^{26}\times 26}{4}MeV=39\times {10}^{26}MeV$

(b) Energy released per fission of U-235 is $200MeV$.

Number of atoms in $1kgU=235$

$n=\frac{1000g\times 6\times {10}^{23}}{235g}=25.53\times {10}^{23}$

Total energy released for fission of $1kg$ of uranium

$E=25.33\times {10}^{23}\times 200MeV=5.1\times {10}^{26}MeV$

So the energy released infusion of $1kg$ of Hydrogen is nearly 8 times the energy released in fission of $1kg$ of uranium-235.

1 EXERCISE

Fill in the Blanks :

DIRECTIONS: Complete the following statements with an appropriate word / term to be filled in the blank space(s).

1. The energy released during a nuclear reaction is called ………….. energy

Show Answer

Answer: nuclear

2. The nuclear fuel in the sun is …………..

Show Answer

Answer: hydrogen

3. U-238 has ………….. neutrons.

Show Answer

Answer: 146

4. In a nuclear reactor, nuclear energy is converted into …………..

Show Answer

Answer: electrical

5. If the binding energy per nucleon for ${}_{3}L{i}^7$ is 5.6 MeV, the total binding energy of a lithium nucleus is ………….. MeV.

Show Answer

Answer: 39.2

6. In plants and animals, the ratio of $C^{14}$ to $C^{12}$ is …………..

Show Answer

Answer: a constant, i.e., ${10}^{-12}$

7. The radioactive radiation which can be stopped easily is …………..

Show Answer

Answer: $\alpha$-rays

8. When an a-particle is ejected, the atomic number of the atom decreases by …………..

Show Answer

Answer: 2

9. The cathode rays emitted from a concave cathode meet at …………..

Show Answer

Answer: centre of curvature

10. Energy released in a nuclear reaction is given by …………..

Show Answer

Answer: E= $m{c}^2$

11. ………….. are used to absorb the neutrons in a nuclear reactor.

Show Answer

Answer: cadmium rods

12. The first experiment on radioactivily was done with the element …………..

Show Answer

Answer: radium

True / False

DIRECTIONS: Read the following statements and write your answer as true or false.

1. Atom bomb is based on the property of fission.

Show Answer

Answer: True

2. High energy neutrons are used in a nuclear reactor to initiate the fission reaction?

Show Answer

Answer: False

3. Cadmium rods are used as moderators in a nuclear reactor.

Show Answer

Answer: False

4. Higher the mass defect, higher will be the stability of the nucleus.

Show Answer

Answer: False

5. The e/m ratio of anode rays is constant irrespective of the gas filled inside the discharge tube.

Show Answer

Answer: False

6. Thorium series is also called 4n series.

Show Answer

Answer: True

7. Radioactive isotope of carbon is $C^{14}$

Show Answer

Answer: True

8. The radioactive isotope used in the treatment of cancer is a good source of $gamma$ rays radiations.

Show Answer

Answer: True

9. In all radioactive series, the end element formed is lead.

Show Answer

Answer: True

10. 4n + 2 series is called Uranium series.

Show Answer

Answer: True

Match the Following :

DIRECTIONS : Each question contains statements given in two columns which have to be matched. Statements $(A,B,C,D)$ in column I have to be matched with statements $(p,q,r,s)$ in column II.

1. Column II give fission probability relative to $U^{236}$ for nuclide given in column I match them correctly.

	Column I		Column II
(A)	$U^{236}$	(p)	0.001
(B)	$U^{239}$	(q)	1
(C)	$P{u}^{240}$	(r)	1.5
(D)	$A{m}^{244}$	(s)	0.0002

Show Answer

Answer: (A) $\text{rarr}q$; (B) $\text{rarr}p$; (C) $\text{rarr}r$; (D) $\text{rarr}s$

2. Match the following

	Column I		Column II
(A)	Coolidge tube	(p)	present in all natural radioactive series
(B)	$\alpha$ decay	(q)	istones
(C)	Radon	(r)	decrease in atomic number by two
(D)	${}_{14}{S}^{31}{,}_{15}{P}^{32}$	(s)	X-rays

Show Answer

Answer: (A) $\text{rarr}s$; (B) $\text{rarr}r$; (C) $\text{rarr}p$; (D) $\text{rarr}q$;

3. Match the following.

	Column I		Column II
(A)	Binding energy per nucleon	(p)	$E=m{c}^2$
(B)	Moderator	(q)	to slow down
(C)	Thermonuclear reaction	(r)	nuclear fusion
(D)	Mass energy equivalence	(s)	Stability of nucleus

Show Answer

Answer: (A) $\text{rarr}s$; (B) $\text{rarr}q$; (C) $\text{rarr}r$; (D) $\text{rarr}p$;

Very Short Answer Questions :

DIRECTIONS : Give answer in one word or one sentence.

1. In a discharge tube, at what pressure cathode rays are produced?

Show Answer

Answer: $0.01mm$ of Hg.

2. If the half-life period of a radioactive substance is 0.696 years, what is its decay constant?

Show Answer

Answer: $\lambda =\frac{0.693}{T}$

3. What happens when cathode rays are suddenly stopped?

Show Answer

Answer: X-rays are produced.

4. How can we say that cathode rays consist of negatively charged particles?

Show Answer

Answer: Direction of deflection in electric and magnetic fields.

5. Define binding energy.

Show Answer

Answer: Energy that results from the loss of mass when nucleus is formed.

6. How are $X$-rays produced?

Show Answer

Answer: When cathode rays are suddenly stopped by a metal target.

7. What forces are responsible for keeping the nucleons together in a nucleus?

Show Answer

Answer: Nuclear forces are responsible.

8. Which rays among $\alpha ,\beta$ and $\gamma$ are deflected most in a magnetic field? Which rays remain undeflected?

Show Answer

Answer: (i) $\beta$-rays $$ (ii) $\gamma$ - rays

9. What is a moderator? Give one example.

Show Answer

Answer: Used to slow down neutrons. Heavy water.

10. What is radioactive transformation or radioactive decay?

Show Answer

Answer: Disintegration of an unstable nucleus resulting in the formation of another nucleus.

11. Name the three radioactive series. Which series is referred to as $4n$ Series?

Show Answer

Answer: (i) Uranium series, actino-uranium series and thorium series.

$$ (ii) Thorium series.

12. What is a solar cell?

13. What are the advantages and disadvantages of a solar cell?

14. What energy transformation takes place in a solar cell?

15. What factors make a solar cell very expensive?

16. What is a solar panel?

17. Name the scientist who gave correct explanation of the source of sun’s energy.

Show Answer

Answer: Hans Bethe

18. What is the surface temperature of the sun?

Show Answer

Answer: $5500-{6000}^{\circ }C$

19. Name the fuel used in atomic reactors.

Show Answer

Answer: ${}_{92}{U}^{235}$

20. How much energy is released by one atomic mass unit of substance?

21. Name the process that forms the principle of a nuclear

$$ (i) atom bomb $$ (ii) hydrogen bomb

Show Answer

Answer: (i) Nuclear fission $$ (ii) Nuclear fusion

22. Which of the two processes is carried out at a higher temperature: nuclear fission or nuclear fusion?

Show Answer

Answer:

Nuclear fusion

23. What do you understand by nuclear wastes?

Show Answer

Answer: The discarded or unwanted materials of nuclear industry are all called nuclear wastes.

Short Answer Questions :

DIRECTIONS : Give answer in 2-3 sentences.

1. Define nuclear fission and fusion reactions.

2. What are advantages and disadvantages of nuclear reactors?

3. Mention any three harmful effects of nuclear radiation on our body.

Show Answer

Answer: (i) Damages of tissues to chromosomes enhancing mutation.

(ii) Initiation of unwanted cell division leading to cancerous growth.

(iii) Conversion of molecules of living cells into chemicallyreactive ions, which disrupt cell membranes resulting in serious illness.

4. A tremendous amount of energy is released during a nuclear fission reaction. Why?

Show Answer

Answer: In a nuclear reaction, the mass of the reactants is more than the mass of the products. Thus, the loss of mass in a nuclear reaction is converted into energy according to the massenergy equivalence equation, $E=m{c}^2$.

5. Give two applications of nuclear fission.

Show Answer

Answer: (i) The energy emitted during nuclear fission can trapped for peaceful uses like the generation of electricity.

(ii) It is used in warfare-for making atomic bombs which are produced by uncontrolled nuclear fission.

6. What would happen if all the hydrogen present in the sun is converted into helium?

Show Answer

Answer: In case all the hydrogen present in the sun is converted into helium, the temperature and pressure inside the sun will decrease. As a result of this, the sun will collapse due to its own gravity. When the size of sun decreases, its interior temperature will again rise and hydrogen nuclei will get liberated from the helium nuclei.

7. It is said that the energy produced from nuclear fusion would create fewer pollution problems than the energy produced by nuclear fission. Explain why?

Show Answer

Answer: The products obtained in nuclear fusion are not radioactive. Since they are not harmful, they can be disposed off easily. On the other hand, the products and by-products given out in nuclear fission are radioactive and hence are dangerous as they pollute water and air.

8. Cadmium rods play an important role in a nuclear reactor. What happens

(i) when they are completely inserted into nuclear fuel and

(ii) when they are slowly withdrawn from the nuclear fuel?

Show Answer

Answer: (i) All neutrons are absorbed, and the chain reaction stops. (ii) Correct number of neutrons are left behind to sustain the chain reaction and the reactor becomes critical.

9. “Obtaining of energy from nuclear fusion reactions is preferable to obtaining of energy from nuclear fission reactions”. Give two reasons to justify this statement.

Show Answer

Answer: (i) Nuclear fusion generates more energy than nuclear fission. (ii) The products formed in fusion reactions are nonradioactive and do not create radioactive pollutions.

10. What are radioactive isotopes? Mention two harmful effects of nuclear radiations.

Show Answer

Answer: Radioactive isotopes are those isotopes which release. spontaneously, $\alpha ,\beta ,\gamma$ radiations. The radiations cause, (i) Genetic disorder, (ii) Skin problems.

11. What is nuclear fusion reaction? Why are such reaction not possible in the school laboratory? State the amount of energy released by one gram of hydrogen in the sun.

Show Answer

Answer: Nuclear fusion reaction is the reaction in which lighter nuclei combine to form heavier nucleus, with the release of large amount of energy. These reactions are not possible in school laboratory, since the energy released is quite high and difficult to handle.

One gram of hydrogen releases $62,000,000,000eV$ or $62\times$ ${10}^{9}eV$ energy.

12. Name the process involved in the liberation of energy in (i) the sun and (ii) a nuclear reactor. Mention any two differences between the two processes.

Show Answer

Answer: (i) Fusion of Hydrogen, (ii) Fission.

Fission has been controlled and forms radioactive products and lighter elements. Fusion produces energy which is uncontrollable and heavier elements.

13. Indicate in symbols for any three isotopes of uranium. Which one among these is used for nuclear fission? What is meant by criticality of a nuclear reaction?

Show Answer

Answer: Isotopes of Uranium

${}_{92}^{235}\mathrm{U},{}_{92}^{238}\mathrm{U}$ and ${}_{92}^{239}\mathrm{U}$.

When sufficient ${}^{235}U$ is available to carry a chain. controllod reaction, the reactor is said to be in critical state.

14. What is the cause of release of unusually large energies in nuclear fission reactions? How is the energy per fission calculated?

Show Answer

Answer: The mass of nuclei obtained after the fission is less than the mass of the disintegrated nucleus. This difference in mass i.e., lost mass reappears in the form of large energy at a rate governed by the Einstein mass-energy relation.

To find energy per fission.

(i) Find the mass of reactants in kg or amu.

(ii) Find the mass of the nuclei obtained after fission in anu.

(iii) Find the difference in mass called mass defect $(\mathrm{\Delta }m)$.

Long Answer Questions :

DIRECTIONS : Give answer in four to five sentences.

1. Name the main components of the nuclear reactor and describe their function.

Show Answer

Answer: (i) A core [For nuclear fuel]

(ii) A moderator [For slowing down fast neutrons]

(iii) Control rods [To absorb (or remove) extra neutrons]

(iv) Coolant or heat exchanger [For transferring heat from the core]

(v) A Protective shield [To prevent harmful radiations from escaping to the surroundings]

Core : It contains nuclear fuel, which undergoes nuclear fission very rapidly to generate energy. Fuels commonly used in nuclear reactors are uranium-235 (U-235) and plutonium-239 (Pu-239).

Nuclear fuel : The nuclear fuel used in nuclear reactors is usually enriched ${}^{235}U(3$ or ${}^{239}Pu$. The fuel is sealed in aluminium cylinders, called fuel rods.

Moderator : The neutrons released are fast neutrons having energy of about $1MeV$. These neutrons are slowed down to energy of $0.025eV$ (thermal neutron) by using substances rich in protons. These substances are called moderators. The commonly used moderators are heavy water $(D_{2}O)$ and graphite.

Control rods : The rate of reaction is controlled by inserting or withdrawing rods made of elements whose nuclei absorb neutrons without undergoing fission. These rods are called control rods. Typical examples of control rods are those made of boron or cadmium.

Coolant : The purpose of the coolant is to carry the energy of the fission reaction from the core of the reactor and take it to a place of utilisation; i.e., a steam generator. The commonly used coolants are heavy water, molten sodium, molten potassium and pressurised $C{O}_2$

Protective shield : To stop the spreading of the harmful radiations from a nuclear reactor, the reactor is enclosed in thick concrete walls, often $10m$ in thickness.

2. Compare the energy during fission and fusion. What is the advantage of fusion over fission?

Show Answer

Answer: The energy given out during fusion is about seven times the energy given out during fission for the same mass. The advantage of the fusion reaction over the fission reaction is that the energy produced by fusion is clean and is not accompanied by the generation of any hazardous radioactive waste. Nuclear Fusion also has the following advantages over nuclear fission

(i) For the same masses of the reacting substances involved, fusion releases much more energy than fission.

(ii) The products of fusion reaction are not radioactive and are, therefore, easier to dispose off as compared to the products formed by fission reaction.

(iii) Nuclear fission requires urarium as a fuel which is limited and exhaustible substance, while nuclear fusion requires deuterium which can be obtained abundantly from sea water.

3. A radioactive sample is kept at the centre of a large evacuated sphere. How safe will it be?

Show Answer

Answer: For safety, the radiations $(\alpha ,\beta$ and $\gamma )$ emitted by the radioactive sample should not come out of the sphere. $\alpha$-particles have least penetrating power than all other radiations therefore, the walls of the sphere easily stops them. $\beta$-particles will not be stopped by the walls and there will be no absorption of $\beta$-particles inside the sphere as the air has been withdrawn from it. Some safety is obtained if the sphere is large because beta particles reaching out of the sphere will depend upon the radius of the sphere. $\gamma$-radiations are also not absorbed by the walls. Thus, for safety, the container should have lead walls and it should not be evacuated. The air will help in absorbing the radiations.

4. .Explain Bohr’s atomic model.

5. Explain in detail the nuclear hazards and the safety precautions to be taken.

6. Describe how cathode rays are produced in a discharge tube. Write down the properties and uses of cathode rays.

7. Describe in detail the process of $\beta$-decay and $\gamma$-decay.

8. Compare the properties of $\alpha ,\beta$ and $\gamma$ radiations.

2 EXERCISE

Multiple Choice Questions :

DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONLY ONE is correct.

1. In a nuclear power plant, uranium atoms

(a) combine and give off heat energy

(b) split and give off heat energy

(c) burn and give off heat energy

(d) split and give off electrons

Show Answer

Answer: (b)

2. Solar energy is produced by the following reaction

(a) Fission reaction

(b) Fusion reaction

(c) Chemical reaction

(d) None of the above

Show Answer

Answer: (b)

3. The volume occupied by an atom is greater then the volume of the nucleus by a factor of about

(a) ${10}^1$

(c) ${10}^{10}$

(b) ${10}^5$

(d) ${10}^{15}$

Show Answer

Answer: (c)

4. Which of the following is true for isotopes of specimen of $U^{235}$ and $U^{238}$ ?

(a) both contain same number of neutrons

(b) both contain same of number of proton, electron and neutron

(c) both contain same number of proton and electron but $U^{238}$ contains three more neutrons than $U^{235}$

(d) $U^{238}$ contain three less neutrons than $U^{235}$

Show Answer

Answer: (c)

5. Atomic nucleus contains

(a) electron & photon

(b) electron, proton & neutron

(c) electron & neutron

(d) proton & neutron

Show Answer

Answer: (d)

6. The atomic number & mass number of element is $Z\mathrm{\&}m$ then number of neutron will be

(a) $m\times z$

(c) $m/z$

(b) $m+z$

(d) $m-z$

Show Answer

Answer: (d)

7. Nuclei containing different number of protons but same number of neutrons are called

(a) Iso clinics

(c) isotones

(b) isobars

(d) isotopes

Show Answer

Answer: (c)

8. 1 amu is equivalent to

(a) $9.31MeV$

(b) $931KeV$

(c) $93.1MeV$

(d) $931MeV$

Show Answer

Answer: (d)

9. The dependence of density [d] of nuclear matter on the mass number $A$ is

(a) $d\propto A$

(b) $d\propto \sqrt{A}$

(c) $d=$ const.

(d) $d\propto 1/A$

Show Answer

Answer: (c)

10. The wrong statement is

(a) Nuclear forces are strongest

(b) Nuclear forces are very short range forces

(c) Nuclear force increase when the number of nucleons is increased

(d) Nuclear force is produced by the exchange of pions

Show Answer

Answer: (c)

11. Range of nuclear force is approximately

(a) $2\times {10}^{-10}m$

(b) $1.5\times {10}^{-20}m$

(c) $7.2\times {10}^{-4}m$

(d) $1.4\times {10}^{-15}m$

Show Answer

Answer: (d)

12. The mass number of a nucleus is equal to the number of

(a) Electron it contains

(b) Protons it contains

(c) Neutrons it contains

(d) Nucleons it contains

Show Answer

Answer: (d)

13. The neutron was discovered by

(a) Marie Curie

(b) Pierre Curie

(c) James Chadwick

(d) Rutherford

Show Answer

Answer: (c)

14. The order of magnitude of the density of nuclear matter is

(a) ${10}^{4}kg/m^3$

(c) ${10}^{27}kg/m^3$

(b) ${10}^{17}kg/m^3$

(d) ${10}^{34}kg/m^3$

Show Answer

Answer: (b)

15. Force between protons in nucleus will be

(a) only nuclear

(b) only coulomb

(c) nuclear & coulomb

(d) coulomb & gravitational

Show Answer

Answer: (c)

16. The mass equivalent of $931MeV$ energy is

(a) $1.66\times {10}^{-27}kg$

(b) $6.02\times {10}^{-24}kg$

(c) $1.66\times {10}^{-20}kg$

(d) $6.02\times {10}^{-27}kg$

Show Answer

Answer: (a)

17. Boron rods are used in nuclear reactor as

(a) moderator

(b) control rods

(c) coolant

(d) protective shield

Show Answer

Answer: (b)

18. Best moderator for neutron is

(a) berillium oxide

(b) pure water

(c) heavy water

(d) graphite

Show Answer

Answer: (c)

19. Nuclear fission was discovered by

(a) OttoHahn and strassman

(b) Fermi

(c) Bethe

(d) Rutherford

Show Answer

Answer: (a)

20. $200MeV$ of energy may be obtained per fission of $U^{235}$. A reactor is generating $1000kW$ of power. The rate of nuclear fission in the reactor is

(a) 1000

(c) $3.125\times {10}^{16}$

(b) $2\times {10}^8$

(d) 931

Show Answer

Answer: (c)

21. In the process of nuclear fusion

(a) Only heavy nucleus break into light nuclei

(b) Fusion of light nuclei at normal temperature

(c) Fusion of light nuclei at high pressure and low temperature

(d) Fusion of light nuclei at high pressure and high temperature

Show Answer

Answer: (d)

22. When ${}_{92}{U}^{235}$ undergoes fission $0.1$ of its original mass is changed into energy. How much energy is released if $1kg$ of ${}_{92}{U}^{235}$ undergoes fission

(a) $9\times {10}^{10}J$

(b) $9\times {10}^{11}J$

(c) $9\times {10}^{12}J$

(d) $9\times {10}^{13}J$

Show Answer

Answer: (a)

23. The cause of energy liberated in nuclear reaction is

(a) Change of potential energy into kinetic energy

(b) Kinetic energy of resultant nucleus

(c) Energy equivalent to mass lost

(d) None of these

Show Answer

Answer: (c)

24. Atom bomb consists of pieces of ${}_{92}{U}^{235}$ and a source of

(a) Proton

(b) Neutron

(c) Meson

(d) Electron

Show Answer

Answer: (b)

25. When four hydrogen nuclei fuse together to form helium nucleus, then in this process

(a) Energy is absorbed.

(b) Energy is liberated.

(c) Absorption and liberation of energy depends upon the temperature.

(d) Energy is neither liberated nor absorbed.

Show Answer

Answer: (b)

26. Two lighter nuclei are fused together to form a nucleus of medium atomic mass and energy is released in this process because

(a) Binding energy of lighter nuclei is more.

(b) Binding energy per nucleon of lighter nuclei is more.

(c) Binding energy per nucleon of medium nucleus is more.

(d) Energy is always released when two nuclei are fused.

Show Answer

Answer: (c)

27. Neutron ratio (available/used per fission in atomic reactor and atom bomb are

(a) $r>1$ in atomic reactor and $r<1$ in bomb.

(b) $r=1$ in atomic reactor and $r>1$ in bomb.

(c) $r>1$ in both atomic reactor and bomb.

(d) $r<1$ in both atomic reactor and bomb.

Show Answer

Answer: (b)

28. In atomic explosion, a temperature of about 10 million degrees is developed at the moment of explosion. The wavelength of light coming from the hot region of the atomic explosion lie in the region

(a) ultraviolet region

(b) visible region

(c) infrared region

(d) $x$-ray region

Show Answer

Answer: (d)

29. When light is incident on surface, photo electrons are emitted. For photoelectrons

(a) The value of kinetic energy is same

(b) Kinetic energy does not depend on the wave length of incident light

(c) The value of kinetic energy is equal to or less than a maximum energy

(d) None of the above

Show Answer

Answer: (c)

30. The phenomenon of photo electric emission depends on

(a) Only wave length of incident light

(b) Only work function of surface

(c) Only nature of surface

(d) All of the above

Show Answer

Answer: (d)

31. Photo electric effect is the phenomenon in which

(a) Photons come out of a metal when it is hit by a beam of electrons

(b) Photons come out of the nucleus of an atom under the action of an electric filed

(c) Electrons come out of metal with a constant velocity depending on frequency and intensity of incident light

(d) Electrons come out of a metal with different velocity not greater than a certain value which depends only on the frequency of the incident light wave and not on its intensity.

Show Answer

Answer: (c)

32. The electrons are emitted in the photo electric effect from a metal surface

(a) Only if the frequency of radiation is above a certain threshold value

(b) Only if the temperature of the surface is high

(c) At a rate that is independent of the nature of metal

(d) With a maximum velocity which is proportional to the frequency of incident radiation

Show Answer

Answer: (a)

33. Work function is

(a) Energy necessary to eject the electron from its orbit

(b) Energy necessary to eject the electron from metal

(c) Minimum necessary energy to eject the electron from metal

(d) Wavelength necessary for releasing an electron from a body

Show Answer

Answer: (c)

34. Einstein got noble prize for

(a) Photo electric effect

(b) Compton effect

(c) Theory of relativity

(d) None of the above

Show Answer

Answer: (a)

35. In a nuclear reactor, the moderator is

(a) uranium-234

(b) uranium-238

(c) cadmium

(d) heavy water

Show Answer

Answer: (d)

36. Which of the following is a good nuclear fuel?

(a) uranium-236

(b) neptunium-239

(c) thorium-236

(d) plutonium-239

Show Answer

Answer: (d)

37. A radioactive substance has a half life of four months. Three fourth of the substance will decay in

(a) Three months

(b) Four months

(c) Eight months

(d) Twelve months

Show Answer

Answer: (c) Substance left undecayed - $N_0-\frac{3}{4}{N}_0=\frac{1}{4}{N}_0$

$\begin{array}{rl}& \frac{N}{N_0}=\frac{l}{4}=(\frac{1}{2}{)}^n\\ & \therefore n=2\text{ i.e. in two half lives }\\ & \therefore t=nT=2\times 4=8\text{ months }\end{array}$

38. When hydrogen atom is in its first excited level, it’s radius is

(a) Four times, it ground state radius

(b) Twice times, it ground state radius

(c) Same times, it ground state radius

(d) Half times, it ground state radius.

Show Answer

Answer: (a) $r_n=r_0\cdot n^2$, where $r_0$ is radius of G-state & $r_n$ is radius of

$n^{\text{th }}$ state. (For first excited state $n=2$ ).

39. For a nuclear fusion process, suitable nucli are

(a) Any Nuclei

(b) Heavy Nuclei

(c) Light Nuclei

(d) Nuclei lying in the middle of periodic table

Show Answer

Answer: (c)

40. If $N_0$ is the original mass of the substance of half-life period $t_{1/2}=5$ years, then the amount of substance left after is years is

(a) $N_0/8$

(b) $N_0/16$

(c) $N_0/2$

(d) $N_0/4$

Show Answer

Answer: (a) Amount left $=N_0/2^n=N_0/8$ (Here $n=15/5=3$ )

41. If mass-energy equivalence is taken into account, when water is cooled to form ice, the mass of water should

(a) increase

(b) remain unchanged

(c) decrease

(d) first increase then decrease

Show Answer

Answer: (a) Because thermal energy decreases, therefore mass

42. Which of the following cannot be emitted by radioactive substances during their decay?

(a) Protons

(b) Neutrinoes

(c) Helium nuclei

(d) Electrons

Show Answer

Answer: (a)

More Than One Correct :

DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONE OR MORE may be correct.

1. $9.1\times {10}^{-34}kg$

(a) 0.51 MeV

(b) $9.1\times {10}^{-28}\text{gm}$

(c) 0.0005477 amu

(d) none of these

Show Answer

Answer: (b,c)

2. According to Bohr’s theory of hydrogen atom, for the electron in the $n^{th}$ allowed orbit, the

(a) linear momentum is proportional to $(1/n)$

(b) radius is proportional to $n$

(c) the kinetic energy is proportional to $(1/n^2)$

(d) the angular momentum is proportional to $n$

Show Answer

Answer: (a,c,d)

3. An electron orbiting in a circular orbit around the nucleus of an atom

(a) has a magnetic dipole moment

(b) exerts an electric force on the nucleus equal to that on it by the nucleus

(c) does produces a magnetic induction at the nucleus

(d) has a net energy inversely proportional to its distance from the nucleus

Show Answer

Answer: (a,b,c,d)

4. A particular hydrogen like atom has its ground state binding energy $122.4eV$. Then

(a) its atomic number is 3

(b) an electron witit $90eV$ energy can interact with it and excite it

(c) an $80eV$ electron emerges when an $80eV$ electron interacts with it

(d) an electron of $8.2eV$ and a photon of $91.8eV$ are emitted when a $100eV$ electron interacts with this atom

Show Answer

Answer: (a,c,d)

5. In which of the following situations the heavier of the two particles has smaller de Broglie wavelength? The two particles

(a) move with the same speed

(b) move with the same linear momentum

(c) move with the same kinetic energy

(d) have fallen through the same height

Show Answer

Answer: (a,c,d)

6. In the hydrogen atom in the ground state

(a) the kinetic energy of the electron is less than the potential energy which is positive

(b) the potential energy is less than the kinetic energy which is positive

(c) the potential energy is negative and the kinetic energy numerically less than the numerical value of potential energy

(d) the total energy is negative

Show Answer

Answer: (c,d)

7. Mark the correct options

(a) An atom with a vacancy has a smaller than the neutral atom

(b) $KX$-ray is emitted when a hole makes a jump from the $K$-shell to some other shell

(c) The wavelength of $KX$-ray is smaller than the wavelength of $LX$-ray of the same material

(d) The wavelength of $K_{\alpha }X$-ray is smaller than the wave length of $K_{\beta }X$-ray of the same material

Show Answer

Answer: (b,c)

8. Who was/were won the novel prize of physics in 1903?

(a) Pierre Curie

(b) Becquerel

(c) Rutherford

(d) Madame Curie

Show Answer

Answer: (a,b)

9. When the nucleus of an electrically neutral atom undergoes a radioactive decay process, it will remain neutral after the decay if the process is

(a) an $\alpha$-decay

(b) a $\beta$-decay

(c) a $\gamma$-decay

(d) a $K$-capture process

Show Answer

Answer: (c,d)

10. When a nucleus with atomic number $Z$ and mass number $A$ undergoes a radioactive decay process

(a) both $Z$ and $A$ will decrease if the process is $\alpha$-decay

(b) $Z$ will decrease but $A$ will not change if the process is ${\beta }^{+}$- decay

(c) $Z$ will increase but $A$ will not change, if the process is ${\beta }^{-}$- decay

(d) $Z$ and $A$ will remain unchanged if the process is $\gamma$ - decay

Show Answer

Answer: (a,b,c,d)

11. During a ${\beta }^{-}$- decay which of the following statements are correct?

(a) The daughter nucleus has one proton less than the parent nucleus

(b) The daughter nucleus has one proton more than the parent nucleus

(c) An electron which is already present within the nucleus is rejected

(d) A neutron in the nucleus decays emitting an electron

Show Answer

Answer: (b,d)

12. The decay constant of a radioactive substance is 173 $(\text{years}{)}^{-1}$. Therefore

(a) nearly $63$ of the radioactive substance will decay in 0.173 years

(b) half-life of the radioactive substance is (1/0.173) year

(c) one-fourth of the radioactive substance will be left after 8 years

(d) all the above statements are true

Show Answer

Answer: (a,c)

13. Which of the following reactions are not possible?

(a) $p\to n+$ positron + energy

(b) $n\to p+$ electron + energy

(c) ${}_{13}A{l}^{27}{+}_1{H}^2{\to }_{12}M{g}^{25}{+}_{2}H{e}^4$

(d) ${}_{92}{U}^{235}{+}_0{n}^1{\to }_{54}X{e}^{140}{+}_{38}S{r}^{95}+2_0{n}^1+\gamma$

Show Answer

Answer: (a,d)

14. The probability of disintegration per second of a nucleus in a given radioactive sample

(a) increases proportional to the life time lived by the nucleus

(b) decreases with the life time lived

(c) is independent of the life time lived

(d) depends on the total number of identical nuclei present in the sample

Show Answer

Answer: (c,d)

15. The heavier nuclei tend to have larger $N/Z$ ratio because

(a) a neutron is heavier than a proton

(b) a neutron is an unstable particle

(c) a neutron does not exert electric repulsion

(d) Coulomb force has longer range as compared to the nuclear force

Show Answer

Answer: (c,d)

16. ${}_{92}{U}^{235}$ is an alpha active nucleus. Then in a large quantity of the element

(a) the probability of a nucleus disintegrating during one second is lower in the first half-life and greater in the fifth half-life

(b) the probability of a nucleus disintegrating during one second remains constant for all the time

(c) quite an appreciable quantity of $U^{235}$ will remain, even after average life

(d) the energy of emitted $\alpha$-particle is less than the disintegration energy of the $U^{235}$ nucleus

Show Answer

Answer: (b,c,d)

17. During the radioactive decay

(a) atomic mass number cannot increase

(b) atomic number may increase

(c) atomic number may decrease

(d) atomic number may remain unchanged

Show Answer

Answer: (a,b,c,d)

18. An electron in a hydrogen atom makes a transition $n_1\to n_2$ where $n_1$ and $n_2$ are principle quantum numbers of the two state. Assume the Bohr model to be valid. The time period of the election in the initial state is eight times that in the final state. The possible values of $n_1$ and $n_2$ are

(a) $n_1=4,n_2=2$

(c) $n_1=8,n_2=1$

(b) $n_1=8,n_2=2$

(d) $n_1=6,n_2=3$

Show Answer

Answer: (a,d)

Fill in the Passage :

DIRECTIONS : Fill in the blanks in the following passage(s) from the words given inside the box.

I.

Atomic Bomb, powerful explosive nuclear weapon fueled by the splitting, or fission, of the nuclei of specific ……..1…….. of uranium or plutonium in a ……..2…….. The strength of the ……..3…….. created by an atomic bomb is on the order of the strength of the explosion that would be created by thousands of tons of TNT (Trinitrotoluene).

An atomic bomb must provide enough mass of plutonium or uranium to reach ……..4…….., the mass at which the nuclear reactions going on inside the material can make up for the neutrons leaving the material through its outside surface. Usually the plutonium or uranium in a bomb is separated into parts so that critical mass is not reached until the bomb is set to explode. At that point, a set of chemical explosives or some other mechanism drives all the different pieces of uranium or plutonium together to ……..5…….. a critical mass. After this occurs, there are enough neutrons bouncing around in the material to create a chain reaction of ……..6…….. . In the fission reactions, collisions between neutrons and uranium or plutonium atoms cause the atoms to split into pairs of nuclear fragments, releasing energy and more neutrons. Once the reactions begin, the neutrons ……..7…….. by each reaction hit other atoms and create more fission reactions until all the fissile material is exhausted or scattered.

Show Answer

Answer: 1. isotopes; 2. chain reaction; 3. explosion; 4. critical mass: 5. produce; 6 . fissions; 7. release

II.

Another form of nuclear energy is called fusion. Fusion means joining smaller nuclei to make a larger nucleus. The sun uses nuclear fusion of ……..1…….. atoms into ……..2…….. atoms. This gives off heat and light and other radiation. Also given off in this fusion reaction is energy.

Scientists have been working on controlling nuclear fusion for a long time, trying to make a fusion reactor to produce electricity. But they have been having trouble learning how to control the reaction in a contained space.

Controlled nuclear fusion is believed by many scientists to be the ultimate solution to the world’s energy problems. The energy released in ……..3…….. reactions is many times greater than that released in ……..4…….. reactions. To date, however, the technology has not been developed to make use of this source of energy. What’s better about nuclear fusion is that it creates less radioactive material than fission, and its supply of fuel can last longer than the sun

$4_1{H}^1{⟶}_{2}H{e}^4+2_{+1}{e}^0+2v+Q$

Fusion is possible at high pressure ( ${10}^6$ atom) and high temperature $(\sim {10}^8{}^{\circ }C)$.

The proton-proton cycle happens at lower temperature as compared to carbon-nitrogen cycle.

Nuclear fusion in possible at a place which has reactants in large quantity.

……..5…….. works on principle of nuclear fusion.

The explosion of a hydrogen bomb needs an explosion of ……..6…….. to generate required ……..7……..

No ……..8…….. radiations are produced in fusion.

Show Answer

Answer: 1. hydrogen; 2. helium; 3. fusion; 4. Fission; 5. Hydrogen bomb; 6. atom bomb; 7. temperature; 8. harmful

Passage Based Questions :

DIRECTIONS : Study the given paragraph(s) and answer the following questions.

PASSAGE-I

A physicist wishes to eject electrons by shining light on a metal surface. The light source emits light of wavelength of $450nm$. The table lists the only available metals and their work functions.

$\begin{array}{lc}\text{Metal}& {\mathbf{W}}_{\mathbf{0}}(\mathbf{eV})\\ \text{Barium}& 2.5\\ \text{Lithium}& 2.3\\ \text{Tantalum}& 4.2\\ \text{Tungsten}& 4.5\end{array}$

1. Which metal(s) can be used to produce electrons by the photoelectric effect from given source of light?

(a) Barium only

(b) Barium or lithium

(c) Lithium, tantalum or tungsten

(d) Tungsten or tantalum

Show Answer

Answer: (b) $DE=\frac{12400}{4.500\text{AA}}$

$\mathrm{\Delta }=2.75eV$

For photoelectric effect, $\mathrm{\Delta }E>W_0$ (work function).

2. Which option correctly identifies the metal that will produce the most energetic electrons and their energies?

(a) Lithium, $0.45eV$

(b) Tungston, $1.75eV$

(c) Lithium, $2.30eV$

(d) Tungston, $2.75eV$

Show Answer

Answer: (a) $\mathrm{\Delta }E=W_0+E;(E_k)=\mathrm{\Delta }E-W_0$

For maximum value of $(E_k),W_0$ should be minimum

$W_0$ for lithium $=2:3eV$

$\therefore (E_k)=2.75-2.3=0.45eV$

3. Suppose photoelectric experiment is done separately with these metals with light of wavelength $450nm$. The maximum magnitude of stopping potential amongst all the metals is-

(a) 2.75 volt

(b) 4.5 volt

(c) 0.45 volt

(d) 0.25 volt

Show Answer

Answer: (c) The.maximum magnitude of stopping potential will be for metal of least work function.

$\therefore$ required stopping potential is

$V_s=\frac{hv-{\varphi }_0}{e}=0.45$ volt.

PASSAGE-II

Gold nucleus ${(}_{79}{\text{Au}}^{198})$ can decay into mercury nucleus ${(}_{80}{\text{Hg}}^{198})$ by two decay schemes shown in figure. (i) it can emit a $\beta$ particle $({\beta }_1)$ and come to ground state by either emitting one $\gamma$ ray $({\gamma }_1)$ or emitting two $\gamma$ rays $({\gamma }_3\text{and}{\gamma }_4)$ (ii) it can emit one $\beta$ particle $({\beta }_2)$ and come to ground state by emitting ${\gamma }_2$ ray.

Atomic masses : ${}^{198}Au=197.9682amu$,

${}^{198}Hg=197.9662amu,1amu=930MeV/c^2$. The energy levels of the nucleus are shown in figure.

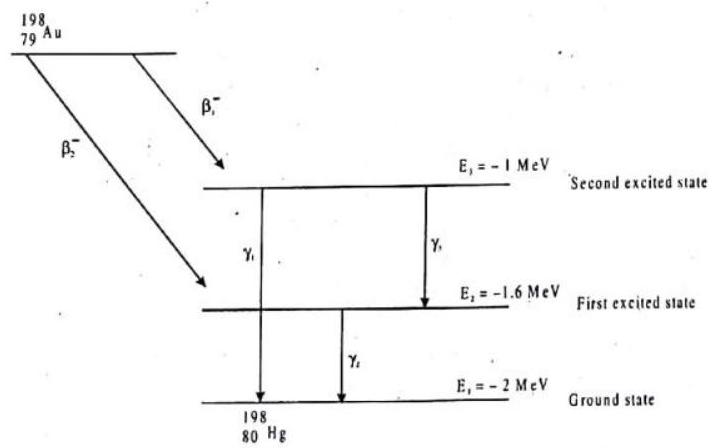
1. What is the maximum kinetic energy of emitted ${\beta }_2$ particles-

(a) $1.44MeV$

(b) $0.59MeV$

(c) $1.86MeV$

(d) $1.46MeV$

Show Answer

Answer: (d) Total energy released from $A{u}^{198}\to H{g}^{198}$ in ground state $=(\mathrm{\Delta }{m}_{\text{loss }})c^2=(197.9682-197.9662)(930)=1.86$ $MeV$

Energy released from ${}^{198}Hg$ in first excited state $arrowHg$ in ground state $=(-1.6)-(-2)MeV=0.4MeV$

$\Rightarrow$ Energy released from $A{g}^{198}\to H{g}^{198}$ second excited state $=1.86-0.4=1.46MeV=max$ K.E. of ${\beta }_2$ particle.

2. What is the maximum kinetic energy of emitted ${\beta }_1$ particle is -

(a) $1.28MeV$

(b) $0.77MeV$

(c) $1.86MeV$

(d) $0.86MeV$

Show Answer

Answer: (d) Similarly maximum kinetic energy of ${\beta }_1$ particle $=1.86-1=0.86MeV$

3. The wavelength of emitted $\gamma$ rays are in the other -

(a) ${\lambda }_{{\gamma }_2}>{\lambda }_{{\gamma }_3}>{\lambda }_{{\gamma }_1}$

(b) ${\lambda }_{{\gamma }_3}>{\lambda }_{{\gamma }_2}>{\lambda }_{{\gamma }_1}$

(c) ${\lambda }_{{\gamma }_1}>{\lambda }_{{\gamma }_2}>{\lambda }_{{\gamma }_3}$

(d) ${\lambda }_{{\gamma }_3}={\lambda }_{{\gamma }_2}={\lambda }_{{\gamma }_1}$

Show Answer

Answer: (a)

Assertion & Reason :

DIRECTIONS : Each of these questions contains an Assertion followed by Reason. Read them carefully and answer the question on the basis offollowing options. You have to select the one that best describes the two statements.

(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.

(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.

(c) If Assertion is correct but Reason is incorrect.

(d) If Assertion is incorrect but Reason is correct.

1. Assertion : Nuclear forces are independent of charges.

Reason : Nuclear force is not a central force.

Show Answer

Answer: (b)

2. Assertion : The strength of photoelectric current depends upon the intensity of incident radiation.

Reason : A photon of energy $E(=h\nu$ ) possesses a mass equal to $E/c^2$ and momentum equal to $E/c$.

Show Answer

Answer: (b)

3. Assertion : Binding energy (or mass defect) of hydrogen nucleus is zero.

Reason : Hydrogen nucleus contain only one nucleon.

Show Answer

Answer: (a)

4. Assertion : $U^{235}$ nucleus, by absorbing a slow neutron undergoes nuclear fission with the evolution of a significant quantity of heat

Reason : During nuclear fission a part of the original mass of $U^{235}$ is lost and gets converted into heat.

Show Answer

Answer: (a)

5. Assertion : The rest mass energy of a nucleus is smaller than the rest mass energy of its constituent nucleons in free state.

Reason : Nucleons are bound together in a nucleus.

Show Answer

Answer: (a)

6. Assertion : In a decay process of a nucleus, the mass of products is less than that of the parent.

Reason : The rest mass energy of the products must be less than that of the parent.

Show Answer

Answer: (a)

7. Assertion : In street light circuits, photo-cells are used to switch on and off the lights automatically at dusk and dawn.

Reason : A photocell can convert a change in intensity of illumination into a change in photocurrent that can be used to control lighting system.

Show Answer

Answer: (a)

Multiple Matching Questions :

DIRECTIONS : Following question has four statements $(A,B,C$ and $D$) given in Column I and four statements ( $p,q,r$ and $s$) in Column II. Any given statement in Column I can have correct matching with one or more statement(s) given in Column II. Match the entries in column I with entries in column II.

1. Match the processes in column I with their properties in Column II.

	Column I		Column II
(A)	Nuclear fission	(p)	involves weak nuclear forces
(B)	Nuclear fusion	(q)	involves conversion of matter into energy
(C)	$\beta$-decay	(r)	atoms of higher atomic number are used
(D)	Exothermic nuclear reaction	(s)	atoms of lower atomic reaction number are used

Show Answer

Answer: $(A)\to q,r;(B)\to q,s;(C)\to p;(D)\to q$

2. Match the following columns

	Column I		Column II
(A)	Nuclear fission	(p)	Converts some matter into energy
(B)	Nuclear fusion	(q)	Generally possible for nuclei with low atomic no.
(C)	$\beta$-decay	(r)	Generally possible for nuclei with higher atomic number
(D)	Exothermic nuclear	(s)	Essentially proceeds by weak nuclear forces

Show Answer

Answer: $(A)\to p,q;(B)\to p,r;(C)\to s,p;(D)\to p,q,r$

3. Match the entries of column I with the entries of column II.

	Column I		Column II
(A)	The sun	(p)	Nuclear fission
(B)	Nuclear reactor reaction	(q)	Nuclear fusion
(C)	Total binding energy in a process is increased	(r)	Energy is released
(D)	Total binding energy in a process is decreased	(s)	Energy is absorbed

Show Answer

Answer: $(A)\to q,r;(B)\to p,r;(C)\to r;(D)\to s$

HOTS Subjective Questions :

DIRECTIONS : Answer the following questions.

1. Name any one element that is used in making solar cells. On what property of the element in this use based?

Show Answer

Answer: Germanium or Silicon. The use is based on the semiconducting property.

2. Write any two harmful radiations emitted by nuclear wastes.

Show Answer

Answer: $\alpha ;\beta$ and $\gamma$ rays. (Any two)

3. Mention any two harmful effects of nuclear radiations on human body.

Show Answer

Answer: (i) Genetical disorders (ii) Skin cancer.

4. The mass number of elements $A,B$ and $C$ are 2,180 and 235 respectively. Which one of them is suitable to make (a) an atom bomb and (b) a hydrogen bomb? Name the process involved in each case.

Show Answer

Answer: (a) Atom bomb $\text{rarr}$ Element $C$ with Mass number $235\to$ nuclear fission.

(b) Hydrogen bomb $arrow$ Element A with Mass number $2\to$ nuclear fusion.

5. $48kJ$ of energy is produced in 60 seconds in a nuclear reactor. Find the number of fissions which would be taking place per second, if the energy released per fission is $3.2\times {10}^{-11}J$.

Show Answer

Answer: Energy $=48000J$, Time $=60$ seconds.

Energy per fission $=3.2\times {10}^{-11}J$

Number of fissions $=\frac{48000}{60\times 3.2\times {10}^{-11}}=250\times {10}^{11}$

6. If $786kJ$ of energy is produced per hour in a nuclear fission reactor, work out the number of fissions that would be taking place in it in 10 minutes, given that the energy released per fission is $3.2\times {10}^{-11}J$.

Show Answer

Answer: Energy released per hour $=786kJ$

Energy released in 10 minutes $=\frac{786\times 10}{60}=128kJ$

$=\frac{\text{ Total energy released }}{\text{ Energy released perfission }}=\frac{128\times 1000J}{3.2\times {10}^{-11}J}$

$=40\times {10}^{14}=4\times {10}^{15}$ fissions.

7. What is a nuclear reactor? What is a moderator? State the functions of moderator in a nuclear reactor. Name two substances used as moderators.

Show Answer

Answer: Nuclear reactor is a device where a nuclear fission reaction is carried out to generate electricity. Moderators are substances which slow down the neutrons and make them fit enough to induce fission in ${}^{235}U$ nuclei. Heavy water and Graphite act as moderators.

8. State the laws of radioactive emissions.

Show Answer

Answer: $N=N_o{e}^{-\lambda t}$,

Where $N_0$ and $N$ are the number of atoms of the substance at $t=0$ and ’ $t$ ’ respectively $\lambda$-disintegration constant.

9. Find the binding energy per nucleon for a lithium nucleus ${}_{3}L{i}^7$. Take mass of ${}_{3}L{i}^7=7u$, mass of proton $1.007825u$ and mass of neutron $=1.008665u$. Take $1u=931.5MeV$.

Show Answer

Answer: (i) Mass defect $=[3\times m_p+4\times m_n]-7u$

(ii) Binding energy $=$ mass defect $\times 931.5MeV$

(iii) Binding energy per nucleon $=\frac{\text{ Binding energy }}{7}$

10. What are prompt fission and delayed fission reactions?

Show Answer

Answer: (i) Fission takes place as soon as the heavy nucleus is bombarded with a neutron.

(ii) Neutron enters a heavy nucleus causing instability and eventually leading to the fission.

11. Mention the properties of cathode rays.

Show Answer

Answer: (i) Travel in straight line.

(ii) Exert mechanical force on the objects.

(iii) Deflect in presence of electric and magnetic fields.

(iv) Ionize the gas through which they pass.

(v) Affect photographic plates.

12. What is nuclear fusion? What are the conditions for a nuclear fusion reaction to take place?

Show Answer

Answer: (i) Two or more lighter nuclei combine to give a heavy nucleus.

(ii) High temperature.

13. Explain nuclear chain reactions.

Show Answer

Answer: (i) A series of nuclear fissions where by the neutrons produced in each fission cause additional fission, releasing enormous amount of energy.

14. Explain why the energy released during fusion cannot be used to produce electricity.

Show Answer

Answer: (i) fusion reactions are not chain reactions - Not possible to sustain the reaction

(ii) Requires a high temperature for nuclear reaction to take place.

(iii) Difficult to harness and convert the heat energy produced into mechanical energy.

15. Mention the properties of $X$-rays.

Show Answer

Answer: (i) Electromagnetic radiations.

(ii) Wavelength is of the order of $1A^{\circ }$

(iii) Affect photographic plates

(iv) Travel with velocity of light in straight line

(v) Produce fluorescence in certain materials.

(vi) Not affected by electric and magnetic fields.

16. What is a nuclear reactor? Name its different parts.

Show Answer

Answer: (i) A device, in which a self-sustaining controlled chain reaction is produced in a fissionable material

(ii) Nuclear fuel, moderator, coolant, shield, control rods.

17. Give any three uses of radio-isotopes.

Show Answer

Answer: (i) ${}_{11}N{a}^{24}$ - To detect a clot in the blood in the human body.

(ii) ${}_{27}C{o}^{60}-To$ kill cancer cells.

(iii) ${}_5{I}^{131}$ - To test the functioning of the thyroid gland.

18. Explain nuclear fission by giving an example.

Show Answer

Answer: (i) A process in which a heavy nucleus of a radioactive substance like uranium is split into lighter nuclei by the bombardment of a low energy neutrons.

(ii) ${}_{92}{U}^{235}{+}_0{}^1{⟶}_{36}K{r}^{92}{+}_{56}B{a}^{141}+3_0{}^{n^1+\text{ energy }}$

19. Using $E=m{c}^2$, find out the energy released, when $1u$ of mass disappears.

$$ Take $1u=1.66\times {10}^{-27}kg$.

Show Answer

Answer: $E=\mathrm{\Delta }m{c}^2$

20. What is a radioactive series? How is it formed? Explain.

Show Answer

Answer: (i) Sequential decay of a radioactive nucleus.

(ii) Results in the production of new nuclei at each stage.

(iii) Gives rise to a series of elements called radioactive decay series.