Chapter 03 Static Electricity
INTRODUCTION
Electricity is the cause of something present in matters called the ’electric charge’. Although charges are present in all matters but all of them do not produce electricity. Actually, electricity is produced by those matters which are ’electrically chas ged’ or by charges in motion. The electricity produced by charges at rest is known as static electricity and the electricity produced by charges in motion is called ‘current electricity’.
This chapter deals with the electricity produced by charges at rest. A static charge can produce an electric field but it can’t produce an electric current. Electric current can be produced only when the charges are in motion which is the subject matter of the next chapter. Electric charges can be stored and used as per requirement. The device which stores charges is known as ‘capacitor’ to be dealt with in this chapter.
Electric charge
We know that mass is responsible of gravitational force. Similarly, there is a property to every massive object which is responsible for another kind of force which can be attractive or repulsive unlike gravitational force which is only attractive. Also, this force is much more stronger than gravitational forces. This force is termed as electrical force. So, charge is responsible for electrical forces.
Electric eels can generate an electrical charge of up to 600 volts in order to stun prey and keep predators at bay. Up to 6,000 electroplates are arranged like a dry cell in the eel’s body. Its internal organs are all in a small area behind the head, with 7/8 of the eel being tail. The electrical shocks come from muscles mainly in the tail portion of the electric eel’s body. The body of an electric eel is similar to a battery. The tail end of the eel has a positive charge and the head region is negatively charged. When the eel touches its tail and head to other animals it sends electric shocks through their bodies. When the eel is at rest, there is no generation of electrical impulses.

Fig. 3.1 : Electric eels
HISTORICAL PREVIEW
It was discovered centuries ago that certain types of materials would mysteriously attract one another after being rubbed together. For example: after rubbing a piece of silk against a piece of glass, the silk and glass would tend to stick together. Indeed, there was an attractive force that could be demonstrated even when the two materials were separated:
Glass and silk aren’t the only materials known to behave like this. Anyone who has ever brushed up against a latex balloon only to find that it tries to stick to them has experienced this same phenomenon. Paraffin wax and wool cloth are another pair of materials early experimenters recognized as manifesting attractive forces after being rubbed together.
 This phenomenon became even more interesting when it was discovered that identical materials, after having been rubbed with
their respective cloths, always repelled each other:
This phenomenon became even more interesting when it was discovered that identical materials, after having been rubbed with
their respective cloths, always repelled each other:
Glass rod
(a)
It was also noted that when a piece of glass rubbed with silk was exposed to a piece of wax rubbed with wool, the two materials would attract one another:
Furthermore, it was found that any material demonstrating properties of attraction or repulsion after being rubbed could be classed into one of two distinct categories: attracted to glass and repelled by wax, or repelled by glass and attracted to wax. It was either one or the other: there were no materials found that would be attracted to or repelled by both glass and wax, or that reacted to one without reacting to the other.
More attention was directed toward the pieces of cloth used to do the rubbing. It was discovered that after rubbing two pieces of glass with two pieces of silk cloth, not only did the glass pieces repel each other, but so did the cloths. The same phenomenon held for the pieces of wool used to rub the wax:
Now, this was really strange to witness. After all, none of these objects were visibly altered by

by the rubbing, yet they definitely behaved differently than before they were rubbed. Whatever change took place to make these materials attract or repel one another was invisible.
Some experimenters speculated that invisible “fluids” were being transferred from one object to another during the process of rubbing, and that these “fluids” were able to effect a physical force over a distance. Charles Dufay was one the early experimenters who demonstrated that there were definitely two different types of changes brought by rubbing certain pairs of objects together. The fact that there was more than one type of change manifested in these materials was evident by the fact that there were two types of forces produced: attraction and repulsion. The hypothetical fluid transfer became known as a charge.
One pioneering researcher, Benjamin Franklin, came to the conclusion that there was only one fluid exchanged between rubbed objects, and that the two different “charges” were nothing more than either an excess or a deficiency of that one fluid. After experimenting with wax and wool, Franklin suggested that the coarse wool removed some of this invisible fluid from the smooth wax, causing an excess of fluid on the wool and a deficiency of fluid on the wax. The resulting disparity in fluid content between the wool and wax would then cause an attractive force, as the fluid tried to regain its former balance between the two materials. Postulating the existence of a single “fluid” that was either gained or lost through rubbing accounted best for the observed behavior: that all these materials fell neatly into one of two categories when rubbed, and most importantly, that the two active materials rubbed against each other always fell into opposing categories as evidenced by their invariable attraction to one another. In other words, there was never a time where two materials rubbed against each other both became either positive or negative.
Following Franklin’s speculation of the wool rubbing something off of the wax, the type of charge that was associated with rubbed wax became known as “negative” (because it was supposed to have a deficiency of fluid) while the type of charge associated with the rubbing wool became known as “positive” (because it was supposed to have an excess of fluid). Little did he know that his innocent conjecture would cause much confusion for students of electricity in the future.
Precise measurements of electrical charge were carried out by the French physicist Charles Coulomb in the 1780’s using a device called a torsional balance measuring the force generated between two electrically charged objects. The results of Coulomb’s work led to the development of a unit of electrical charge named in his honor, the coulomb. If two “point” objects (hypothetical objects having no appreciable surface area) were equally charged to a measure of I coulomb, and placed I meter (approximately I yard) apart, they would generate a force of about 9 billion newtons (approximately 2 billion pounds), cither attracting or repelling depending on the types of charges involved.
It was discovered much later that this “fluid” was actually composed of extremely small bits of matter called electrons, so named in honour of the ancient Greek word for amber: another material exhibiting charged properties when rubbed with cloth Experimentation has since revealed that all objects are composed of extremely small “building-blocks” known as atoms, and that these atoms are in turn composed of smaller components known as particles. The three fundamental particles comprising atoms are called protons, neutrons, and electrons.
The result of an imbalance of this “fluid” (electrons) between objects is called static electricity. It is called “static” because the displaced electrons tend to remain stationary after being moved from one material to another.
Activity : Take any two materials from the following list and then rubbed with each other. We can always find that the former one is positively charged and the later one is negatively charged.
Fur
When a charged body is close enough to a neutral body, they attract each other. One of the applications of this effect is to use tiny paint droplets to paint the automobiles uniformly.
CHECK POINT :
When one material is rubbed against another, electrons jump readily from one to the other, but protons do not. Why is this? (Think in atomic terms.)
Show Answer
SOLUTION
Protons are bound with the nucleus of an atom but electrons revolve round it. Therefore, electrons can easily be dislodged from an atom but it is difficult to take out a proton from the atom. This is why, when one material is nubbed against another, electrons jump readily from one to the other, but protons do not.
PROPERTIES OF CHARGES :
1. Charge is conserved
That is, net charge can neither be created nor destroyed. Note the term net charge. Although charges can be created or destroyedin some processes but the net charge always remains conserved.
2. Charge is quantized
Charge on any particle can never be less than the charge of an electron (i.e.,
In other words, the total charge on any particle is an integral multiple of the charge of electron
It means that a charge of
3. Unlike charges repel each other and like charges attract each other. 4. A charge at rest produces an electric field in the space around it. A uniformly moving charge produces both electric and magnetic field and a non-uniformly moving charge radiates energy.
ILLUSTRATION-3.1
Calculate the net charge on a substance consisting of (a)
Show Answer
SOLUTION:
(a) The charge of one electron is
(b) Similarly the net charge on a substance consisting of a combination of
(
ILLUSTRATION-3.2
When a piece of polythene is rubbed with wool, a charge of
Show Answer
SOLUTION:
No. of electrons transferred,
Mass transferred
CONDUCTORS AND INSULATORS
Suppose you charge a rubber rod and then touch it to a neutral object. Some charge, repelled by the negative charge on the rod, will be transferred to the originally-neutral object. What happens to that charge then depends on the material of which the originally-neutral object consists. In the case of some materials, the charge will stay on the spot where the originally neutral object is touched by the charged rod. Such materials are referred to as insulators, materials through which charge cannot move, or, through which the movement of charge is very limited. Examples of good insulators are quartz, glass, and air. In the case of other materials, the charge, almost instantly spreads out all over the material, in response to the force of repulsion (recalling that force causes acceleration which leads to the movement) that each elementary particle of the charge exerts on every other elementary particle of charge. Materials in which the charge is free to move about are referred to as conductors. Examples of good conductors are metals and saltwater.
When you put some charge on a conductor, it immediately spreads out all over the conductor. The larger the conductor, the more it spreads out. In the case of a very large object, the charge can spread out so much that any chunk of the object has a negligible amount of charge and hence, behaves as if were neutral. Near the surface of the earth, the earth itself is large enough to play such a role. If we bury a good conductor such as a long copper rod or pipe, in the earth, and connect to it another good conductor such as a copper wire, which we might connect to another metal object, such as a cover plate for an electrical socket, above but near the surface of the earth, we can take advantage of the earth’s nature as a huge object made largely of conducting material. If we touch a charged rubber rod to the metal cover plate just mentioned, and then withdraw the rod, the charge that is transferred to the metal plate spreads out over the earth to the extent that the cover plate is neutral. We use the expression “the charge that was transferred to the cover plate has flowed into the earth.” A conductor that is connected to the earth in the manner that the cover plate just discussed is connected is called “ground.” The act of touching a charged object to ground is referred to as grounding the object. If the object itself is a conductor, grounding it (in the absence of other charged objects) causes it to become neutral.
CHARGING BY INDUCTION
When a charged particle is taken near to neutral metallic object then the electrons move to one side and there is excess of electrons on that side making it negatively charged and deficiency on the other side making that side positively charged. Hence charges appear on two sides of the body (although total charge of the body is still zero). This phenomenon is called induction and the charge produced by it is called induced charge.

A body can be charged by means of (a) friction, (b) conduction, (c) induction, (d) thermoionic ionisation, (e) photoelectric effect and (f) field emission.
COULOMB’S LAW
The force exerted by one point charge on another acts along the line joining the two charges. It varies inversely as the square of the distance separating the charges and is proportional to the product of the charges. The force depends on the medium. The force is repulsive if the charges have the same sign and attractive if the charges have opposite signs.
The magnitude of the electric force exerted by a charge

Where
If
Where
It is common practice to express
If some dielectric (insulator) is present in the space between the charges, the net force acting on each charge is altered. The force decreases
Here,
For vacuum or air
CHECK POINT:
How does the magnitude of electric force compare with the charge between a pair of charged particles when they are brought to half their original distance of separation? To one-quarter their original distance? To four times their original distance? (What law guides your answers?)
Show Answer
SOLUTION:
According to inverse-square law, the electric force between two charges is inversely proportional to the square of the distance of their separation. Therefore, when the charges are brought to half their original distance of separation, the electric force between them increases by four times.
If the separation distance is made one-quarter their original distance, the force increases by sixteen times.
Similarly, the force between the charges decreases by sixteen times when the separation distance between them is made four times their original distance. (The inverse square law guides our answer).
ILLUSTRATION-3.3
Three identical point charges are placed at the corners of an equilateral triangle. If the electrostatic force between the any towcharges is
Show Answer
SOLUTION:
Three identical points charges, say, positive and having magnitude %, ure placed at the corners of’ an equilateral triangle, as shown. The change at the top conner experiences two electrostatic repulsive forces
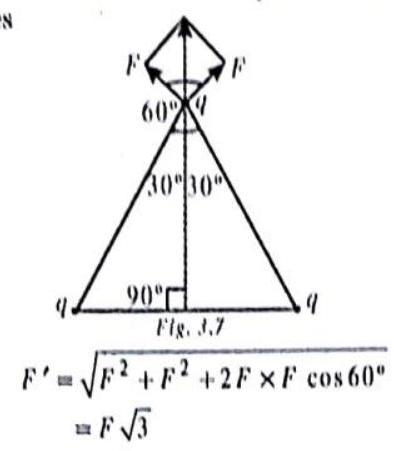
and acts in direction perpendicular to the base of triangle, as shown.
ILLUSTRATION-3.4
Tow points charges
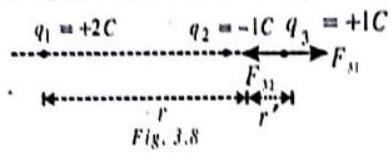
Show Answer
SOLUTION:
The third charge
which is the distance of
ILLUSTRATION-3.5
Electric force between two point charges
Show Answer
SOLUTION:
(a) As electric force between two body interaction, i.e., force between two particles, is independent of presence or absence of other particles, the force between
(b) An electric force is proportional to the magnitude of charges, total force on
i.e., The resultant force on
ELECTRIC FIELD
If we place a charge in any region of space, it is observed that any other charge placed in that region experiences a force. The space around an electric charge is filled with a field called electric field.
The intensity of electric field is a vector quantity which at a point, is defined as the force experienced by a unit positive charge placed at that point. Its direction is in the direction of the electric field if the charge is positive and opposite to it if the charge is negative. Mathematically,
The unit of electric field is newton per coulomb (N/C).
ILLUSTRATION-3.6
A particle of mass
Show Answer
SOLUTION:
The particle experiences an electric force of magnitude
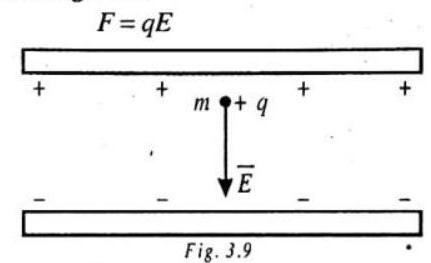
in the downward direction. This force does a positive work
on the particle and the particle gains a kinetic energy equal to this work done, when it is released in the electric field and moves downwards through the distance
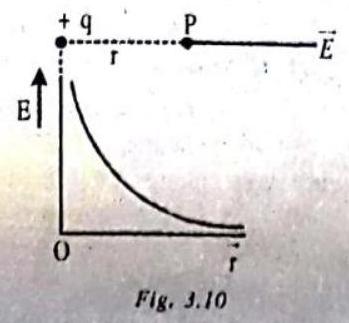
Electric field due to Single Point Charge
The electric field
and direction along the line joining the point charge
Electric field due to Many Point Charges
The electric field due to many point charges
at a point
from the charges
where
For example, the electric field at the origin
and the minus
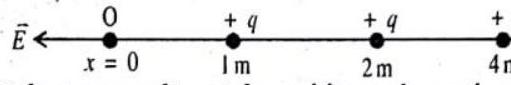
If the infinite number of point charges are alternately positive and negative, then the electric field has the magnitude
and the minus

Charged Conductor Carrying no Currents
Any charge given to a conductor spreads over the whole external-most surfaces
The electric field
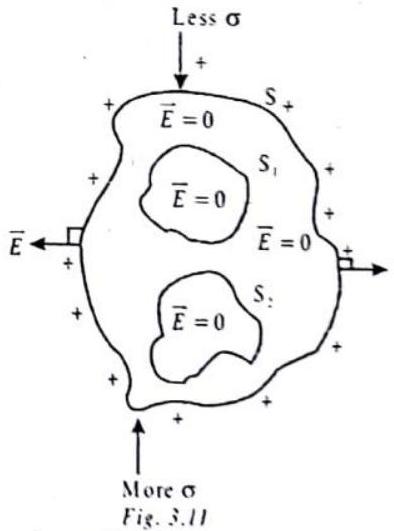
which shows that the field is independent of the position and depends on the surface charge density
ELECTRIC LINES OF FORCE OR ELECTRIC FIELD LINES
(i) The concept of electric field was introduced by Michael Faraday.
The magnitude of electric field strength at any point is measured by the number of electric lines of force passing per unit small area around that point normally and the direction of field at any point is given by the tangent to the line of force at the point.
(ii) An electric line of force is that imaginary smooth curve drawn in an electric field along which a free isolated unit positive (initially at rest) charge moves.
Properties:
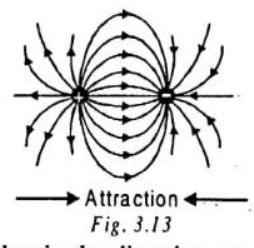
(1) The lines of force diverge out radially from a +ve charge and converge at a - ve charge. More correctly the lines of force are always directed from higher to lower potential.

Fig. 3.12 (2) The tangent drawn at any point on line of force gives the direction of force acting on a positive charge placed at that point.
(3) Two lines of force never intersect. If they are assumed to intersect, there will be two directions of electric field at the point of intersection, which is impossible.
(4) These lines have a tendency to contract in tension like a stretched elastic string. This actually explains attraction between opposite charges.
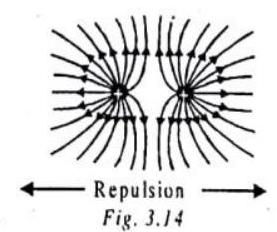
(5) These lines have a tendency to separate from each other in the direction perpendicular to their length. This explains repulsion between like charges.
(6) The no. of lines originating or terminating on a charge is proportional to the magnitude of charge. In rationalised MKS system
(7) Total lines of force may be fractional as lines of force are imaginary.
(8) Lines of force ends or strarts normally on the surface of a conductor.
(9) If there is no electric field there will be no lines of force.
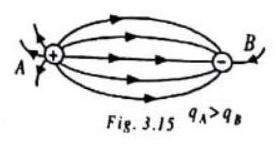 (10) Lines of force per unit area normal to the area at a point represents magnitude of intensity, crouded lines represent strong field
while distant lines represent weak field.
(10) Lines of force per unit area normal to the area at a point represents magnitude of intensity, crouded lines represent strong field
while distant lines represent weak field.
(11) Electric lines of force differ from magnetic lines of force.
(a) Electric lines of force never form closed loop while magnetic lines are always closed or extended to infinity.
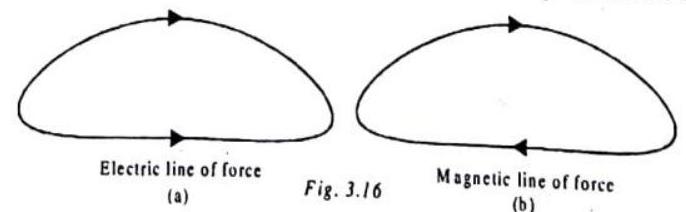 (b) Electric lines of force always emerge or terminate normally on the surface of charged conductor, while magnetic lines emerge or terminate on the surface of a magnetic material at any angle.
(b) Electric lines of force always emerge or terminate normally on the surface of charged conductor, while magnetic lines emerge or terminate on the surface of a magnetic material at any angle.
(c) Electric lines of force do not exist inside a conductor but magnetic lines of force may exist inside magnetic material. Lines of force do not exist inside a conductor (as field inside a conductor is zero) as shown. (Electrostatic shielding)

CHECK POINT:
Which among the curves shown in Figure cannot possibly represent electrostatic field lines?


Show Answer
SOLUTION
(a) It is wrong, because electric field lines must be normal to the surface of conductor outside it.
(b) It is wrong because field lines cannot start or originate from negative charge, and also cannot end or submerge into positive charge.
(c) It is correct
(d) It is wrong because electric field lines never intersect each other.
(e) It is wrong because electric field lines cannot form closed loops.
ELECTRIC FLUX
A surface
where
where the summation is performed over all the elementary parts of
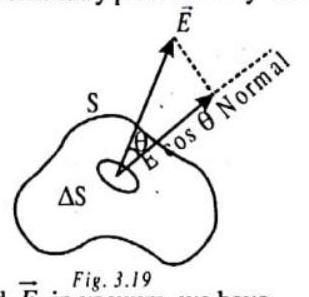
For a closed surface
where
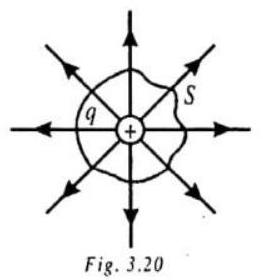
If a charge
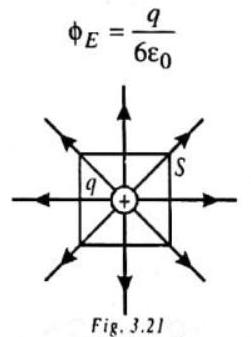
If the charge
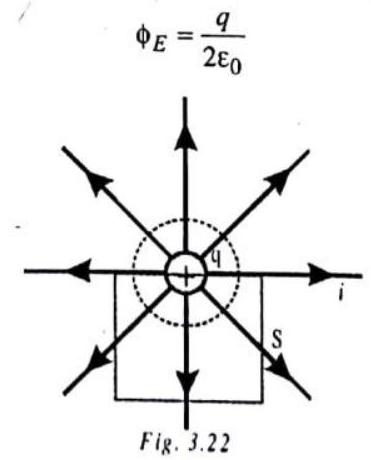
If the charge
and then, the electric flux through each of the three faces meeting at that corner is zero and the electric flux through each of the other three faces is
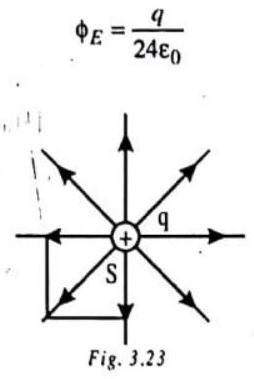
ILLUSTRATION-3.7
A surface encloses an electric quadrupole. What is the total electric flux through the surface?
Show Answer
SOLUTION:
An electric quadrupole consists of the two electric dipoles, each one having the two point charges
ILLUSTRATION-3.8
A cylinder of radius
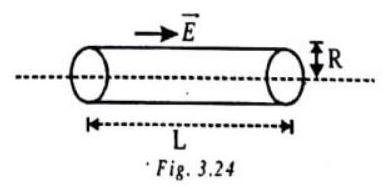
Show Answer
SOLUTION:
The cylinder is simply placed in the uniform electric field
ELECTRIC POTENTIAL
Electric potential at a point in electric field is defined to be equal to the minimum work done by an external agent in moving a unit positive charge from infinity or a reference point to that point against the electrical force of the field.
Electric potential at a point in electric field is numerically equal but opposite in sign to the work performed by electrical force to bring unit positive charge from infinity to that point.
If
Unit of potential is joule/coulomb or volt. (S.I. unit)
Potential due to Many Point Charges
The electrostatic potential due to many point charges
where
For example, the electrostatic potential at the origin

If the infinite number of point charges are alternately positive and negative, then

ELECTRIC POTENTIAL DIFFERENCE
Potential deference between two points is equal to the minimum work done in moving a unit positive test charge from one point to the other.
UNDERSTANDING POTENTIAL DIFFERENCE
When the ends of a heat conductor are at different temperatures, heat energy flows from the higher temperature to the lower temperature. The flow ceases when both ends reach the same temperature. Similarly, when the ends of an electrical conductor are at different electric potentials - when there is a potential difference - charges in the conductor flow from the higher potential to the lower potential. The flow of charge persists until both ends reach the same potential. Without a potential difference, no flow of charge will occur.
To attain a sustained flow of charge in a conductor, some arrangement must be provided to maintain a difference in potential while charge flows from one end to the other. The situation is analogous to the flow of water from a higher reservoir to a lower one fig. Water will flow in a pipe that connects the reservoirs only as long as a difference in water level exists. The flow of water in the pipe, like the flow of charge in a wire, will cease when the pressures at each end are equal. (We imply this phenomenon when we say that water seeks its own level.) A continuous flow is possible if the difference in water levels - hence the difference in water pressures - is maintained with the use of a suitable pump (in Figure).

(a) Water flows from the reservoir of higher pressure to the reservoir of lower pressure. The flow will cease when the difference in pressure ceases.
(b) Water continue to flow because a difference in pressure is maintained with the pump. Fig. 3.25
A sustained electric current requires a suitable pumping device to maintain a difference in electric potential - to maintain a voltage. Chemical batteries or generators are “electrical pumps” that can maintain a steady flow of charge. These devices do work to pull negative charges apart from positive ones. In chemical batteries, this work is done by the chemical disintegration of zinc or lead in acid, and the energy stored in the chemical bonds is converted to
electric potential energy.
Fig.3.26 Each coulomb of charge that is made to flow in a circuit that connects the ends of this 1.5V. Flashlight cell is energized with 1.5J.
Generators separate charge by electromagnetic induction, a process we will describe in the next chapter. The work that is done (by whatever means) in separating the opposite charges is available at the terminals of the battery or generator. This energy per charge provides the difference in potential (voltage) that provides the “electrical pressure”. to move electrons through a circuit joined to those terminals.
A common automobile battery will provide an electrical pressure of 12 volts to a circuit connected across its terminals. Then 12 joules of energy are supplied to each coulomb of charge that is made to flow in the circuit.
EQUIPOTENTIAL SURFACES
A surface of constant, or uniform, potential
lines form an orthogonal system, i.e., they are mutually perpendicular. The equipotential surfaces do not intersect each other and they are closer in the region of stronger electric field and widely separated in the region of weaker electric field.
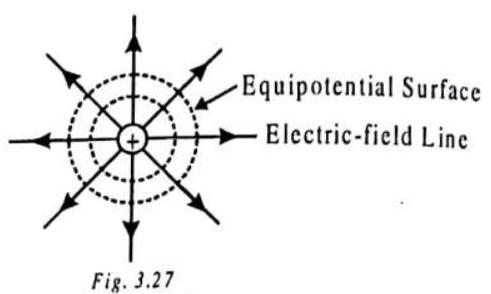
A volume of constant, or uniform, potential
CHECK POINT:
Two charges
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?
Show Answer
SOLUTION
(a) Since it is an electric dipole, so a plane normal to
(b) Normal to the plane in the direction
ILLUSTRATION-3.9
Ten positively charged particles have the charges
Show Answer
SOLUTION:

The electric potential at the origin
ILLUSTRATION-3.10
A uniform electric field of
Show Answer
SOLUTION:
The increase in the electric potential
ILLUSTRATION-3.11
A radioactive source, in the form of a metallic sphere of the radius
Show Answer
SOLUTION:
Say, the electric potential of the source is raised to the
and the number of
The fotal charge of these
and hence, the total charge which appears on the radioactive source is
Due to this charge, the source, being spherical and of radius
ELECTROSTATIC POTENTIAL ENERGY
The electrostatic potential energy of a point charge
i.e., it is the work done in displacing the point charge
where
The electrostatic potential energy of a system of two point charge
which is defined as the amount of work done in assembling the two point charges from the infinite separation between them. The electrostatic potential energy of a system of three point charges
which is equal to the amount of work done in assembling the system of three point charges from the intinite separations between them.
CHECK POINT:
A balloon may easily be charged to several thousand volts. Does that mean it has several thousand joules of energy? Explain.
Show Answer
SOLUTION:
No, it doesn’t mean that the balloon has several thousand joules of energy always. It can have several thousand joules of energy only if the balloon acquires high charge.
ILLUSTRATION-3. 12
Three point charges
Show Answer
SOLUTION:
The three charges are at the corners of an equilateral triangle, as shown.
The total electrostatic potential energy of the system is
When one of the charges, say,
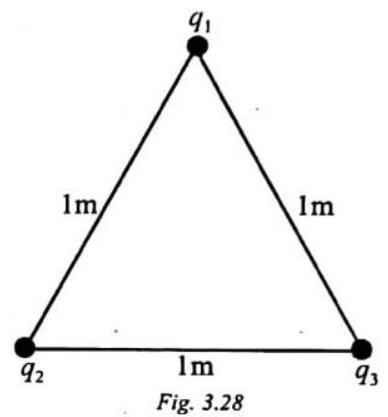

the total electrostatic potential energy of the system will be
Then, the total energy supplied to the system becomes
As the power supplied to the system is
ILLUSTRATION-3.13
Two identical point charges,
when it is displaced by a distance
Show Answer
SOLUTION:
Before the displacement of the point charge
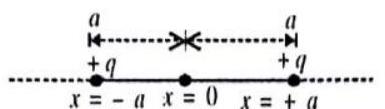
When
Now, the change, i.e., increase, in the electrostatic potential energy of
ELECTRIC DIPOLE
An electric dipole is a system of two unlike point charges
where
The torque
Then

The work done in rotating the dipole from equilibrium through an angle
If
Workdone in rotating an electric dipole in uniform electric field from
Time period of a dipole in uniform electric field is
where I = Moment of Inertia of the dipole about the axis of rotation.
Potential energy of an electric dipole in an electric field is.
where
We can also write
Electric field due to an electric dipole
(a) Axial line (end-on position)
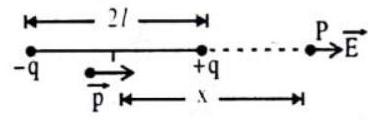
(b) Equatorial line (Broad - side on potential)

(c) At any point (for first dipole)
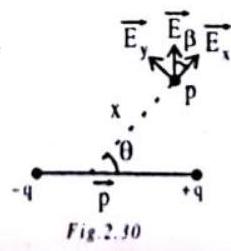
(d) Electric field intensity due to a point charge varies inversely as cube of the distance and in case of quadrupole it varies inversely as the fourth power of distance from the quadrupole.
ILLUSTRATION-3.14
Calculate the electric intensity due to a dipole of length
Show Answer
SOLUTION:
The electric intensity on the axial line of the dipole is given by
Here
CAPACITORS AND CAPACITANCE
A capacitor or condenser consists of two conductors separated by an insulator or dielectric. The conductors carry equal and opposite charges
The capacitance of a conductor is gently increased when an earth connected conductor is placed near it.
Capacitance
When charge is given to an isolated body its potential increases
i.e.,
if,
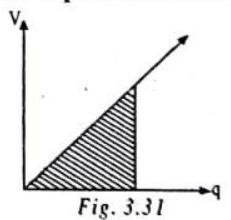
(1) The ability to store charge is called capacitance of the capacitor. Capacitance of a body is numerically equal to the change required to raise the potential by unit.
(2) Units : SI unit of
C.G.S. unit
Dimensions :
In case of spherical conductor
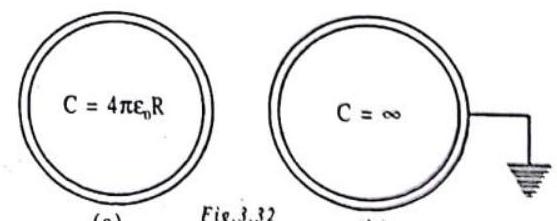
(b)
If we assume the earth to be a conducting sphere of radius
(3) The capacity of the body is independent of the charge given to the body or its potential raised and depends on its shape and size only.
Capacitance depends on :
(a) Area of the conductor: If the surface area of a conductor is increased keeping charge q const. Its potential decreases and hence the capacity increases
(b) The presence of other conductor in the vicinity of the charged conductor. The presence of other conductor near a charged conductor decreases the potential of the charged conductor, there by the capacity increases.
(c) The medium around the charged conductor: If the capacity of the conductor is
140 Static Electricity I Physics I
ENERGY STORED IN A CAPACITOR
When a conductor is charged its potential changes from 0 to
The energy is stored in the electric field between the plates of the capacitor
The energy stared per unit valume in the electric field between the plates is called energy dersidy
WORK DONE BY BATTERY
Work done by battery is given by
Whenever there is a charging of capacitor, work done by battery, in part is stored as electrostaric enargy in termeen carwicior plates and remaining is dissipated as heat due to charge flow through connecting wires.
In general, heat produced is given by
TYPES OF CAPACITORS
Capacitors are mainly of three types:
(1) Parallel plate capacitor
(2) Spherical capacitor
(3) Cylindrical capacitor
(1) Parallel plate capacitor (PPC)
A PPC consists of two equal parallel metal plates facing each other and sparand by 2 dielectric
Let us consider a parallel-plate capacitor, having a charge
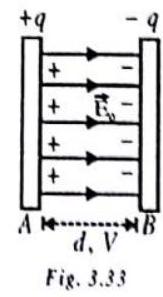
and electric potential difference across them is
Then, the capacitance of capacitor becomes
In case of PCC
(i) Capacity is directly proportional to effective over-laping area of the plate
(ii) Capacity is inversely proportional to the distance between the plate fie.
(iii) Capacity is independent of charge given, potential raised or nature of metal and thichness of plates
(2) Spherical capacitor
(i) Outer Spherical Conductor Grounded
Let us consider a spherical capacitor, having the two spherical conductors
The electric potential of the inner spherical conductor
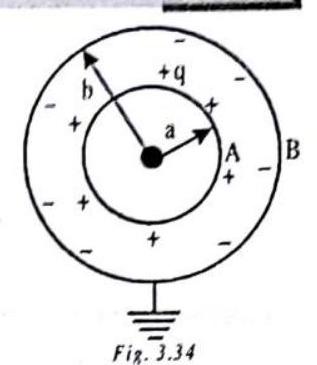
The electric potential of the outer spherical conductor
Then, the capacitance of the spherical capacitor, having the two spherical conductors
When the outer conductor
The capacitance of our earth which is assumed to be spherical conductor of mean radius of
(ii)Inner Spherical Conductor Grounded
Let us, now, consider a spherical capacitor, having the two spherical conductors
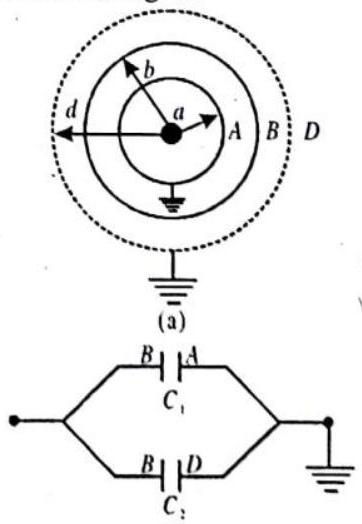
(b)
Fig. 3.35
When the conductor
which is more than the capacitance of the system, with the outer spherical conductor
ILLUSTRATION-3.15
The radius of circular plates of a parallel-plate capacitor is
Show Answer
SOLUTION:
The capacitance of parallel-plate capacitor, with the air as dielectric, is
where
we have,
(3) Cylindrical capacitor
A cylindrical capacitor consists of the two coaxial cylindrical conductors
The electric field between the cylindrical conductors at the distance
which gives the potential for the two cylindrical conductors
The electric potential difference between the two cylindrical conductors becomes
and then, the capacitance of the cylindrical capacitor becomes
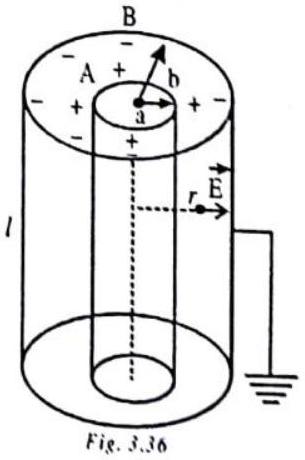
where the charge on the capacitor is
To increase the capacity of a cylindrical capacitor
(i)
(ii) b/a should be less i.e.
(iii) Length of the cylinder (L) should be more.
ILLUSTRATION-3.16
Two cylindrical capacitors, each of the capacitance of
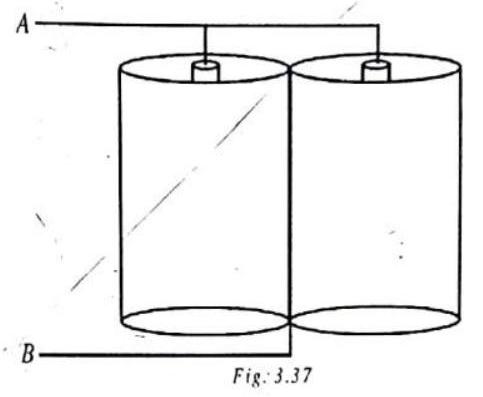
Show Answer
SOLUTION:
The given system is a parallel combination of two cylindrical capacitors, each of capacitance of
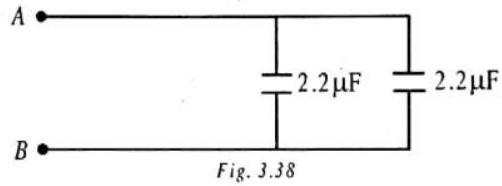
Therefore, the equivalent capacitance of system as a whole is
CHECK POINT:
What meaning would you give to the capacitance of a single conductor?
Show Answer
SOLUTION:
It means thata single conductor is a capacitor whose other plate can be considered to be at infinity.
COMBINATION OF CAPACITORS
Series Combination
Let us consider a number of capacitors, connected in series, as shown.
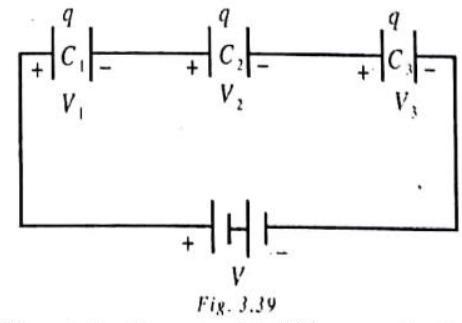
They have the same charge
Therefore, the equivalent capacitance
Evidently, therefore, the equivalent capacitance
Parallel Combination
We, now, consider a number of capacitors, connected in parallel, as shown. They have the same electric potential difference
The total charge of the combination is
from which we have the equivalent capacitance of the combination, i.e.,
Evidently, therefore, the equivalent capacitance
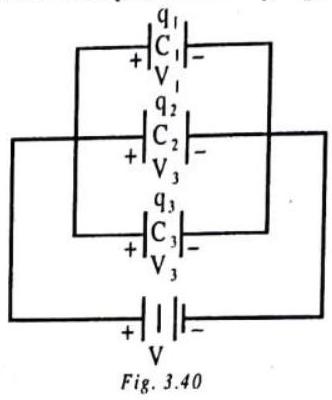
ILLUSTRATION-3.17
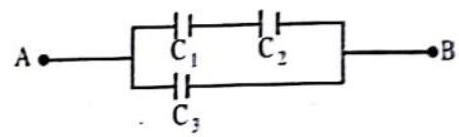
A circuit is shown in figure.
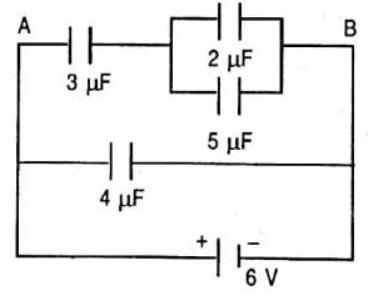
Find the charge on the condenser having a capacity of
Show Answer
SOLUTION:
Potential difference between
The capacitance between
Total charge
Total potential difference across
Hence the common potential difference across the condensers in parallel is
So, the charge on
ILLUSTRATION-3.18
In the given circuit, consisting of the four capacitors and a battery, the potential difference across the
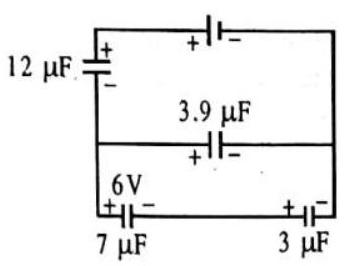
Fig. 3.42
Show Answer
SOLUTION:
The capacitors of
The potential difference across the parallel combination of
which is in series with the capacitor of
and then, the battery emf becomes
LOSS OF ENERGY ON JOINING TWO CHARGED CONDUCTORS OR CAPACITORS
When the two charged conductors, having the capacitances
The same thing, as outlined above, happens, when the two charged capacitors are connected, with the plates of the like polarities together, by the conducting wires. Before connecting together, the total energy of the charged conductors, or capacitors, is

After connecting together, the total energy of charged conductors, or capacitors, will be
Then, the loss of energy becomes
which is mainly as the heat and also as the light and sound due to the sparking taking place. This loss is zero, when
i.e., the charges of the two conductors, or capacitors, before joining together are in the ratio of their capacitances. After connecting together, the charges on the two conductors, or capacitors, will also be in the ratio of their capacitancces, i.e.,
ILLUSTRATION-3.19
A
Show Answer
SOLUTION:
The electrostatic potential energy of the first capacitor of
MISCELLANEOUS
SOLVED EXAMPLES
1. .Two protons in a molecule is separated by
Show Answer
Solution.
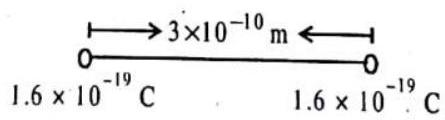
According to Coulomb’s law, the electrostatic force
Here,
So,
2. Two negative charges of unit magnitude each and a positive charge
Show Answer
Solution . Let the charge
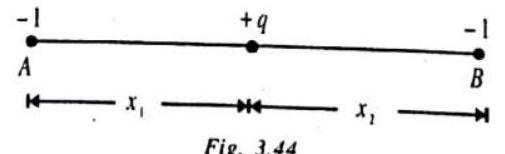
For equilibrium of
For equilibrium of unit negative charge at
Force on
Stability : If
However, if
3. A
Show Answer
Solution .
As
4. Electric force between two point charges
Show Answer
Solution .
(a) As electric force between two body interaction, i.e., force between two particles, is independent of presence or absence of other particles, the force between
(b) An electric force is proportional to the magnitude of charges, total force on
i.e., The resultant force on
5. Calculate the electric field strength required to just support a water drop of mass
Show Answer
Solution . Here,
Step 1 : Let
Force acting on the water drop due to electric field
Weight of drop acting downward,
Step 2 : Drop will be supported if
i.e.,
or
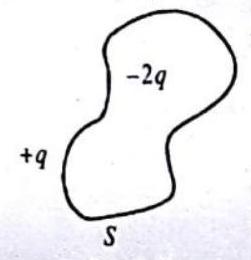
6. The following figure shows a surface
Show Answer
Solution . According to Gauss law, the net flux is
Fig. 3.45
(because
7. In which Figure, the electric flux is maximum?
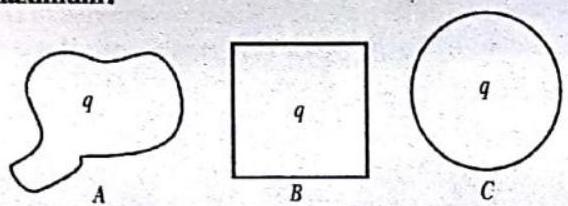
Fig. 3.46
Show Answer
Solution . According to Gauss Law, the electric flux linked with a closed surface depends only on net charge enclosed by that surface. It does not depend on the shape and size of that closed surface. Hence electric flux linked in above three figures are same i.e.,8. A charge
Show Answer
Solution . According to Gauss theorem the total electric flux
Since cube has six faces. Hence electric flux linked with each face
9. A charge
Show Answer
Solution . According to Gauss’s law
So flux from any one of surface of cube
10.
Show Answer
Solution . As Volume remains constant, therefore,
1 EXERCISE
Fill in the Blanks:
DIRECTIONS : Complete the following statements with an appropriate word / term to be filled in the blank space(s).
1. Electric is of two types viz. positive and negative charge.
Show Answer
Answer: (charge)2. Proton is said to be charged and electron is said to be charged
Show Answer
Answer: (positively, Negatively)3. Like charges
Show Answer
Answer: (repuls, attract)4. A proton repels a and unlike charges
Show Answer
Answer: (proton/electron)5. The force of attraction or repulsion between two is given by
Show Answer
Answer: (charges, Coulomb’s law)6. Charge can neither be nor
Show Answer
Answer: (created, destroyed)7. The charge from one body can be to another body but the total charge of a system remains
Show Answer
Answer: (transferred, constant)8. The static electricity deals with electric charges at and their
Show Answer
Answer: (rest, effects)9. Charge flows from a body at to a body at
Show Answer
Answer: (higher potential, lower potential)10. To bring a unit positive charge from to a point in an electric field, some work has to done which is called
Show Answer
Answer: infinity, electric potential11. An electric dipole is a system of two point charges
Show Answer
Answer: urilike12. The capacitance of conductor depends on the and of conductor and the surrounding medium.
Show Answer
Answer: shape, size13. A system of two insulated from each other, is called a capacitor.
Show Answer
Answer: Conductors14. The equivalent capacitance
Show Answer
Answer:15. The equivalent capacitance
Show Answer
Answer:True /False:
DIRECTIONS : Read the following statements and write your answer as true or false.
1. The electric charge is of two types viz, positive and negative charge.
Show Answer
Answer: True2. Like charges attracts to each other and unlike charges repels to each other.
Show Answer
Answer: False3. A proton repels an electron.
Show Answer
Answer: False4. A nutron repels a proton.
Show Answer
Answer: False5. Charge can neither be created nor destroyed.
Show Answer
Answer: True6. Proton is said to be charged positively and electron is said to be charged negatively.
Show Answer
Answer: True7. The branch of electricity which deals with the properties -of electrified bodies due to a moving charge is called electrostatics.
Show Answer
Answer: False8. In nature charge
Show Answer
Answer: True9. Charge can be in fraction of e, i.e. 1.7e, 0.8e, or -1.3e.
Show Answer
Answer: False10. The electronic charge ’
Show Answer
Answer: False11. The device used to detect the presences of charge and to Identify the nature of charge on a body, is called an electroscop.
Show Answer
Answer: True12. An electric dipole is a pair of equal and same charges.
Show Answer
Answer: False13. The mutual electrostatic force between two point charges
Show Answer
Answer: False14. Electric field due to a point charge
Show Answer
Answer: False15. Potential at a point is the force due to electric dipole.
Show Answer
Answer: False16. For capacitors in the series combination, the total capacitance
Show Answer
Answer: FalseMatch The Following:
DIRECTIONS: Each question contains statements given in tavo columns which have to be matched. Statements (A, B, C, D) in column I have to be matched with statements
1.
Show Answer
Answer:2.
Show Answer
Answer: (A)3. Two point charges
Show Answer
Answer:Very Short Answer Questions:
DIRECTIONS : Give answer in one word or one sentence.
1. Write the physical quantity which has its unit coulomb/ volt? Is it a vector or a scalar quantity?
Show Answer
Answer: The quantity is capacitance2. Write down the relation between electric field and potential at a point.
Show Answer
Answer:3. Is electrostatic potential necessarily zero at a point where electric field strength is zero?
Illustrate your answer.
Show Answer
Answer: No, it is not necessary.
Ex: The electric field inside a hollow spherical conductor is zero but potential is not zero.
4. What is the workdone in moving a charge of
Show Answer
Answer: Workdone to move the charge5. Draw an equipotential surface in a uniform electric field.
Show Answer
Answer: 
It is a plane surface perpendicular to the electric field.
6. What is the ratio of electric field intensities at any two points between the plates of a parallel plate capacitor?
Show Answer
Answer: Required ratio is7. The work done in moving a charge of
Show Answer
Answer:8. In a parallel plate capacitor, the capacitance increases from
Show Answer
Answer:
9. The equivalent capacitance of the combination between

Show Answer
Answer:
10. Two large conducting spheres carrying charges
Show Answer
Answer: No, because charge distributions on the spheres will not be uniform.11. If Coulomb’s law involved
Show Answer
Answer: No.12. A small test charge is released at rest at a point in an electrostatic field configuration. Will it travel along the field line passing through that point?
Show Answer
Answer: Not necessarily. (True only if the field line is a straight line.) The field line gives the direction of acceleration, not that of velocity, in general.13. We know that electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?
Show Answer
Answer: No, potential is continuous.14. What meaning would you give to the capacitance of a single conductor?
Show Answer
Answer: A single conductor is a capacitor with one of the ‘plates’ at infinity.15. What meaning would you give to the capacitance of a single conductor?
Show Answer
Answer: A water molecule has permanent dipole moment. However, detailed explanation of the value of dielectric constant requires microscopic theory and is beyond the scope of the book.16. Name the physical quantity whose SI unit is (a) newton/ coulomb, (b) joule/coulomb.
Show Answer
Answer: Newton/coulomb is the SI unit of electric field strength.
(b) Joule/coulomb is the SI unit of electric potentials.
17. What orientation of an electric dipole in a uniform electric field corresponds to its stable equilibrium?
Show Answer
Answer: If the dipole is placed along the direction of the field, its equilibrium is stable18. Calculate the no. of electrons in
Show Answer
Answer:
19. Draw lines of force to represent a uniform electric field.
Show Answer
Answer: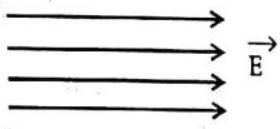
20. Which particles are responsible for the flow of current in conductors?
Show Answer
Answer: Electrons.21. What is the SI unit of electric potential?
Show Answer
Answer: In SI, electric potential is measured in volt22. Write the mathematical expression for electric potential.
Show Answer
Answer: Mathematically, electric potential is written as
Short Answer Questions:
DIRECTIONS : Give answer in 2-3 sentences.
1. Two point electric charges of unknown magnitude and sign are placed at a distance ’
Show Answer
Answer: (a) The two charges are of opposite sign so that force will be attractive in nature.
(b) The two charges have different magnitudes - the charge of smaller magnitude will be nearer to the point where the total field intensity is zero.
2. Electric charge is distributed uniformly on the surface of a spherical rubber balloon. Show how the value of. electric intensity vary (i) on the surface (ii) inside and (iii) outside?
Show Answer
Answer: (i) On the surface,
(ii) Inside the surface,
(iii) Out side the surface,
3. A surface encloses an electric quadrupole. What is the total electric flux through the surface?
Show Answer
Answer: An electric quadrupole consists of the two electric dipoles, each one having the two point charges4. What is the force between two small charged spheres having charges of
Show Answer
Answer: Given,
By Formula,
5. When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Show Answer
Answer: Charge is neither created nor destroyed. It is merely transferred from one body to another. Electrons are transferred from glass to silk, so glass has positive charge and silk has negative charge.6. (a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
(b) Explain why two field lines never cross each other at any point?
Show Answer
Answer: (a) They start from a positive charge and end at a negative charge. They are continuous, because force is continuous. They do not have sudden breaks, otherwise a moving test charge will have to take jumps.
(b) Two lines of force do not intersect each other. If they intersect at a point, there will be two directions of field at that point. Since it is impossible, hence they don’t intersect.
7. Three capacitors each of capacitance
Show Answer
Answer: (A)
(B)
8. Calculate the value of
Show Answer
Answer: 
The
9. What is an equipotential surface? Show that the electric field is always directed perpendicular to an equipotential surface.
Show Answer
Answer: An equipotential surface is that at every point of which electric potential is same. Consider two points A and B on the equipotential surface.
By definition, potential difference between two points
10. Equipotential surfaces are perpendicular to field lines. Why?
Show Answer
Answer: On an equipotential surface, no work is done in moving a charge from one point to another. Therefore, the component of electric field intensity along the equipotential surface is zero. So equipotential surfaces are perpendicular to field lines.11. Distinguish between electric potential and potential energy.
Show Answer
Answer: Electric potential at a point is the amount of workdone in moving a unit positive charge from infinity to that point.
Potential energy is the amount of workdone in carrying the total charge from infinity to that point against the electrostatic forces.
12. Is it possible for a metal sphere of
Show Answer
Answer: We have
So, it is not possible for a metallic sphere to hold a charge of
13. What is the relation between dielectric constant and electric susceptibility?
Show Answer
Answer: The relation between dielectric constant and electrical susceptibility of a material is
The electrical susceptibility describes the electrical behaviour of a dielectric. It has different values for different dielectrics. For vacuum
14. An electric dipole is free to move in a uniform electric field. Explain its motion when it is placed (i) parallel to the field and (ii) perpendicular to the field.
Show Answer
Answer: The torque acting on a dipole placed in a uniform electric field at an angle
(i) When the dipole is parallel to the field,
(ii) When the dipole is perpendicular to the field is perpendicular to
15. Two capacitors of capacitances
Show Answer
Answer: 
Energy stored
Long Answer Questions:
DIRECTIONS : Give answer in four to five sentences.
1. (a) Explain the meaning of the statement ’electric charge of a body ‘is quantised’.
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large scale charge?
Show Answer
Answer: (a) Quantization of electric charge. It is now a well known fact that all charges occurring in nature are positive or negative integral multiples of a basic unit of electric charge which we take as the magnitude of the charge on an electron. We use symbol
(b) At the macroscopic level one deals with charges that are enormous compared to the magnitude of charge
2. A capacitor is charged to potential
Derive an expression for the common potential of the combination of capacitor.
Show Answer
Answer: Let
Before sharing, total charge
When the capacitors are joined by a wire, charge will flow from higher to lower potential till both the potentials are equal. This equal potential is called common potential
If
3. Derive the expression for the capacitance of a parallel plate capacitor filled with dielectric.
Show Answer
Answer: 
Let
potential is same,
Capacitance
4. How is Coulomb’s law similar to Newton’s law of gravitation? How is it different?
Show Answer
Answer: Coulomb’s law states that, for two charged objects that are much smaller than the distance between them, the force between them varies directly as the product of their charges and inversely as the square of the separation distance and it acts along a straight line from one charge to the other. It can be expressed as where,
where,
From equations (1) and (2), it seems that Coulomb’s law and Newton’s law of gravitation are similar in the way that both follow the inverse square law and take the same form. But the two laws are different in the way that Coulombian force can be attractive or repulsive according as the nature of charges but gravitational force between two masses is always attractive in nature.
5. How does the magnitude of electric force compare with the charge between a pair of charged particles when they are brought to half their original distance of separation? To One-quarter their original distance? To four times their original distance? (What law guides your answers?)
Show Answer
Answer: According to inverse-square law, the electric force between two charges is inversely proportional to the square of the distance of their separation. Therefore, when the charges are brought to half their original distance of separation, the electric force between them increases by four times.
If the separation distance is made one-quarter their original distance, the force increases by sixteen times.
Similarly, the force between the charges decreases by sixteen times when the separation distance between them is made four times their original distance.
(The inverse square law guides our answer).
2 EXERCISE
Multiple Choice Questions:
DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
1. An electric dipole, consisting of two opposite charges of
(a)
(b)
(c)
(d)
Show Answer
Answer: (c) Charges
(d)
2. If the potential of a capacitor having capacity
(a)
(b)
(c)
(d)
Show Answer
Answer: (c) Capacitance of capacitor
The increase in energy
3. Intensity of an electric field (E) depends on distance
(a)
(b)
(c)
(d)
Show Answer
Answer: (c) Intensity of electric field due to a Dipole
4. A charge
(a)
(b)
(c)
(d)
Show Answer
Answer: (a) At equilibrium, net force is zero
or
5. The formation of a dipole is due to two equal and unlike point charges placed at a
(a) short distance
(b) long distance
(c) above each other
(d) none of these
Show Answer
Answer: (a) Dipole is formed when two equal and unlike charges are placed at a short distance.6. A parallel plate condenser with oil between the plates (dielectric constant of oil
(a)
(b)
(c)
(d)
Show Answer
Answer: (d) When oil is placed between space of plates
When oil is removed
On compari both equations, we get
7. When air is replaced by a dielectric medium of force constant
(a) decreases
(b) increases
(c) remains unchanged
(d) becomes
Show Answer
Answer: (a) In air,
In medium,
8. A capacitor is charged to store an energy
(a)
(b)
(c)
(d)
Show Answer
Answer: (a) In 1st case when capacitor
In Ind case after disconnect of battery similar capacitor is artached in parallel with Ist capacitor then
Now,
9. A charge
(a)
(b)
(c)
(d)
Show Answer
Answer: (d) According to Gauss’s theorem,
electric flux through a closed surface
where
10. In a parallel plate capacitor, the distance between the plates is
(a)
(b)
(c)
(d)
Show Answer
Answer: (b) Energy stored per unit volume
11. Energy stored in a capacitor is
(a)
(b)
(c)
(d)
Show Answer
Answer: (a) Energy stored in capacitor
12. Three capacitors each of capacity
(a) connecting two in parallel and one in series
(b) connecting all of them in series
(c) connecting them in parallel
(d) connecting two in series and one in parallel
Show Answer
Answer: (d) For series,
For parallel,
13. When a body is charged by induction, then the body
(a) becomes neutral
(b) does not lose any charge
(c) loses whole of the charge on it
(d) loses part of the charge on it
Show Answer
Answer: (b) Charging by induction involves transfer of charges from one part to the other of the body. No loss of charge is involved.14. If a body is positively charged, then it has
(a) excess of electrons
(b) excess of protons
(c) deficiency of electrons
(d) deficiency of neutrons
Show Answer
Answer: (c) Positive charge is due to deficiency of electrons.15. On charging by conduction, mass of a body may
(a) increase
(b) decreases
(c) increase or decrease
(d) none
Show Answer
Answer: (c) On charging by conduction, body may gain mass, if it acquires negative charge. It may lose mass, if it acquires positive charge.16. Coulomb’s law is true for
(a) atomic distances
(b) nuclear distances
(c) charged as well as uncharged particles
(d) all the distances
Show Answer
Answer: (d) Coulomb’s law is true for all distances small and large. Hence it is called a long range force.17. Two charges are placed a certain distance apart. A metallic sheet is placed between them. What will happen to the force between the charges?
(a) increase
(b) decrease
(c) remains unchanged
(d) either ’
Show Answer
Answer: (b)18. Which of the following is best insulator?
(a) Carbon
(c) Graphite
(b) Paper
(d) Ebonite
Show Answer
Answer: (d) Ebonite is the best insulator.19. Two spheres
(a) remains unaffected
(c) mass of
(b) mass of
(d) nothing can be said
Show Answer
Answer: (c) A loses electrons and B gains electrons. Therefore, mass of20. What happens when some charge is placed on a soap bubble?
(a) its radius decreases
(b) its radius increases
(c) the bubble collapses
(d) none of the above
Show Answer
Answer: (b) The radius of soap bubble increases because of outward force acting on the bubble due to charging.21. Quantisation of charge implies
(a) charge cannot be destroyed
(b) charge exists on particles
(c) there is a minimum permissible charge on a particle
(d) charge, which is a fraction of a coulomb is not possible.
Show Answer
Answer: (d)
Coulomb
22. Two charges are placed a certain distance apart in air. If a glass slab is introduced between them, the force between them will
(a) increase
(b) decrease
(c) remains the same
(d) be zero
Show Answer
Answer: (b)
As
23. A charge
(a) decreases
(b) increases
(c) remains unchanged
(d) increases if
Show Answer
Answer: (c) The force of24. A positively charged rod is brought near an uncharged conductor. If the rod is then suddenly withdrawn, the charge left on the conductor will be
(a) positive
(b) negative
(c) zero
(d) not sure
Show Answer
Answer: (c) Positively charged rod induces negative charge on the side of the sphere closer to the rod and an equal positive charge on the side away from the rod. When the rod is withdrawn, the negative changes move to neutralise the equal positive change. The charge left is zera25. The ratio of electric force between two electrons to two protons separated by the same distance in air is
(a)
(b)
(c)
(d) none
Show Answer
Answer: (a)26. The dielectric constant of a metal is
(a)
(b) 0
(c) 1
(d) none
Show Answer
Answer: (a) Metal is a good conductor. So, its27. A metallic particle having no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
(a) towards the plate
(b) away from the plate
(c) parallel to the plate
(d) zero
Show Answer
Answer: (d)28. If a body is charged by rubbing it, its weight
(a) remains precisely constant
(b) increases slightly
(c) decreases slightly
(d) may increase slightly or may decrease slightly
Show Answer
Answer: (d) The weight can be increased slightly, if it acquire negative charge & weight can be decreased slightly, if it acquires positive charge.29. An electric field can deflect
(a) neutrons
(b) X-rays
(c)
(d)
Show Answer
Answer: (d) An electric field can deflect only a charged particle.30. A hollow sphere of charge does not have electric field at
(a) outer point
(b) interior point
(c) beyond
(d) beyond
Show Answer
Answer: (b)31. If one penetrates a uniformly charged solid sphere, the electric field
(a) increases
(b) decreases
(c) is zero at all points
(d) remains same as at the surface
Show Answer
Answer: (b) E decreases as we move from the surface of the sphere to its centre.32. If one penetrates a uniformly charged spherical cloud, electric field strength
(a) decreases directly as the distance from the centre
(b) increases directly as the distance from the centre
(c) remains constant
(d) none of the above
Show Answer
Answer: (a) A spherical cloud behaves as a solid sphere. Therefore, E decreases directly with the decreasing distance from the centre.33. Electric lines of force about a negative point charge are
(a) circular anticloc
(b) circular clockwise
Show Answer
Answer: (c) For a single negative point charge, electric lines of force are radial and inwards.34. Electric lines of force
(a) exist everywhere
(b) exist only in the immediate vicinity of electric charges
(c) exist only when both positive and negative charges are near one another
(d) are imaginary
Show Answer
Answer: (d) Electric lines of force are imaginary.35. Debye is the unit of
(a) electric flux
(b) electric dipole moment
(c) electric potential
(d) electric field intensity
Show Answer
Answer: (b) Debye is the unit of electric dipole moment.36. An electric dipole will experience a net force when it is placed in
(a) a uniform electric field
(b) a non-uniform electric field
(c) both the above cases
(d) none of these
Show Answer
Answer: (b) Net force (as well as torque) are experienced by the dipole in a non uniform electric field.37. An electric dipole is kept in a uniform electric field. it experiences
(a) a force and a torque
(b) a force, but no torque
(c) A torque but no force
(d) neither a force nor a torque
Show Answer
Answer: (c) In a uniform electric field, net force38. A charge
(a)
(b)
(c)
(d)
Show Answer
Answer: (d). Aceording to Gauss theorem-the total electric flux
Since cube has six faces. Hence electric flux linked with each face
39. A charge
(a)
(b)
(c)
(d)
Show Answer
Answer: (c) We require eight cubes to surround completely this corner charge. So, the flux through one cube is40. Positive electric flux indicates that electric lines of force are directed
(a) outwards
(b) inwards
(c) outwards or inwards
(d) none of these
Show Answer
Answer: (a) Positive electric flux is due to + charge. So lines of force are directed outwards.41. Electric flux at a point in an electric field is
(a) positive
(b) negative
(c) zero
(d) none of these
Show Answer
Answer: (c) As area of a point is zero,42. Electric flux over a surface in an electric field may be
(a) positive
(b) negative
(c) zero
(d) positive, negative, zero
Show Answer
Answer: (d) Though electric flux is scalar, yet its value may be positive, negative or zero.43. The electric potential at a point on the equatorial line of an electric dipole is
(a) directly proportional to distance
(b) inversely proportional to distance
(c) inversely proportional to square of the distance
(d) none of the above
Show Answer
Answer: (d) At a point on equatorial line of electric dipole, V=0.More Than One Correct:
DIRECTIONS: This section contains multiple choice questions. Each question has 4 choices
1. Four electric charges are arranged as shown in the figure at the four corners of a square of side a. The potential energy of the system is:
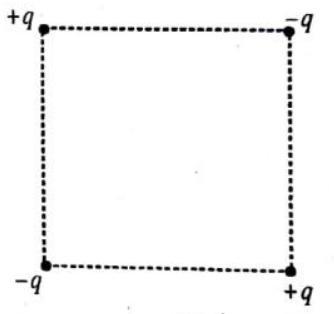
(a) zero
(b) negative
(c) positive
(d) greater than
(e) less than
Show Answer
Answer: (b,c)2. Three charged particles are in equilibrium under their electrostatic forces only:
(a) the particles must be collinear
(b) all the charges cannot have the same magnitude
(c) all the charges cannot have the same sign
(d) the equilibrium is unstable
Show Answer
Answer: (a,b,c,d)3. Inside a uniformly charged spherical conductor, the electric:
(a) potential is zero everywhere
(b) potential is non-zero and same everywhere
(c) field is zero everywhere
(d) field has the same magnitude everywhere but it is not zero
Show Answer
Answer: (b,c)4. Four charges, all of the same magnitude are placed at the four corners of a square. At centre of the square, the potential is
(a)
(b)
(c)
(d)
Show Answer
Answer: (a,b,c,d)5. Consider two identical charges placed at a distance
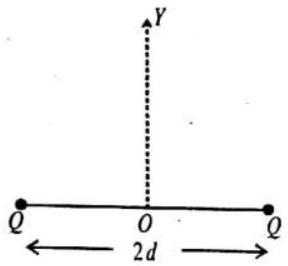
(a) neutral
(b) stable for displacement along the
(c) stable for displacement along the
(d) unstable for displacement along the
Show Answer
Answer: (b,c,d)6. Across the surface of a charged conductor, the electric:
(a) field is continuous
(b) potential is continuous
(c) field is discontinuous
(d) potential is discontinuous
Show Answer
Answer: (b,c)7. A point charge is brought in an electric field. The electric field at a nearby point:
(a) will increase if the charge is positive
(b) will decrease if the charge is negative
(c) may increase if the charge is positive
(d) may decrease if the charge is negative
Show Answer
Answer: (c,d)8. Which of the following quantities do not depend on the choice of zero potential or zero potential energy?
(a) Potential at a point
(b) Potential difference between the points
(c) Potential energy of a two charge system
(d) Change in potential energy of a two charge system
Show Answer
Answer: (b,d)9. An electric dipole is placed at the centre of a sphere. Mark the correct option:
(a) the flux of the electric field through the sphere is zero
(b) the electric field is zero at every point of the sphere
(c) the electric field is not zero anywhere on the sphere
(d) the electric field is zero on a circle on the sphere
Show Answer
Answer: (a,c)10. In a uniform electric field, equipotential surfaces must:
(a) be plane surfaces
(b) be normal to the direction of the field
(c) be placed such that surfaces having equal differences in potential are separated by equal distances
(d) have decreasing potentials in the direction of the field
Show Answer
Answer: (a,b,c,d)11.
(a)
(b)
(c) in the region between
(d) a line of force from
Show Answer
Answer: (a,c,d)12. Which of the following is/are proportional to the inverse square of the distance
(a) The potential at a distance
(b) The electric field at a distance
(c) The force per unit length between two thin, straight, infinitely long current carrying conductors, parallel to each other, separated by a distance
(d) The gravitational attraction between two small bodies kept at a distance
Show Answer
Answer: (a,c)13. A positive charge
(a) the electric field at any point outside the shell is zero
(b) the electrostatic potential at any point outside the shell is
(c) the outer surface of the spherical shell is an equipotential shell
(d) the electric field at any point inside the shell, other than
Show Answer
Answer: (b,c)14. A parallel plate capacitor is charged to a definite potential and the charging battery is disconnected. Now if the plates of capacitor are moved apart, then:
(a) the stored energy of the capacitor increases
(b) charge on the capacitor increases
(c) voltage of the capacitor increases
(d) the capacitance increases
Show Answer
Answer: (a,c)15. A capacitor of capacity
(a) its time constant is
(b) during time
(c) during its time constant charge left on the capacitor is 0.63 times to its maximum charge
(d) during its time constant, charge left on the capacitor is 0.37 times to its maximum change
Show Answer
Answer: (a,b,d)16. Two parallel plate capacitors are constructed one by a pair of iron plates and the second by a pair of copper plates of same area and same spacings. Then:
(a) the copper plate capacitor has a greater capacitance than the iron one
(b) both capacitors have equal, non-zero capacitances in the uncharged state
(c) both capacitors will have equal capacitances only if they are charged equally
(d) the capacitances of the two capacitors are equal even if they are unequally charged
Show Answer
Answer: (b,d)17. Mark the correct statements?
(a) A given conducting sphere can be charged to any extent.
(b) A given conducting sphere cannot be changed to a potential greater than a certain valuc.
(c) A given conducting sphere cannot be charyed to a potential less than a certain minimum value.
(d) None of the above
Show Answer
Answer: (b,c)Fill In the Passage
DIRECTIONS : Fill in the blanks in the following passage(s) from the words given inside the box.
I.
Electric charge is developed due to actual transfer of ……1……. When two substances are rubbed against each other, energy is provided from outside to overcome ……2……. between them. This energy is used to remove electrons from one substance and …….3……. them to the other. The transfer takes place from the material in which electrons are held less tightly to the material in which electrons are held more tightly. The material which loses electrons acquires …….4……. and which gains electrons acquires an equal ……5……..
Show Answer
Answer:
-
electrons
-
friction
-
transferring
-
positive charge
-
Negative charge
II.
Any charge exists in discrete lumps or packets of a certain minimum charge …………… where
Show Answer
Answer:
-
-
quantization
-
multiple
-
electron
-
+ne
-
integral number
III.
The force of interaction between any two point charges is …..1……… proportional to the product of the charges and …….2……. proportional to the square of the distance between them.
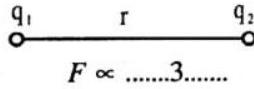
where,
where,
between two charges
Dividing we get,
Show Answer
Answer:
-
directly
-
inversely
-
-
-
Permittivity
Passage Based Questions:
DIRECTIONS : Study the given paragraph(s) and answer the following questions.
Passage - I
Three large plates A, B and C are placed parallel to each other and charges are given as shown.
1. The charge that appears on the left surface of plate
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)2. The charge on inner surface of plate
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)3. The charge on left surface of
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)Passage -II
Related to the following diagram of two charges,
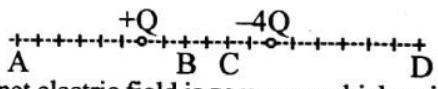
1. The net electric field is zero near which point?
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)2. At which point does the net electric field vector point to the left?
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)3. At which point would a small positive charge
(a)
(b)
(c). C
(d)
Show Answer
Answer: (c)Passage-III
Two fixed charges
1. All the points in the
(a) straight line
(b) circle
(c) parabola
(d) ellipse
Show Answer
Answer: (b)2. The expression for the potential
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)Assertion & Reason:
DIRECTIONS : Each of these questions contains an Assertion followed by Reason. Read them carefully and answer the question on the basis of following options. You have to select the one that best describes the two statements.
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
1. Assertion : Consider two identical charges placed distance

The equilibrium of a positive test charge placed at the point
Reason: Force on test charge is zero.
Show Answer
Answer: (c) If +ve charge is displaced along2. Assertion : A deuteron and an
Reason: Forces will be same in electric field.
Show Answer
Answer: (d)
Further,
and
3. Assertion : Four point charges
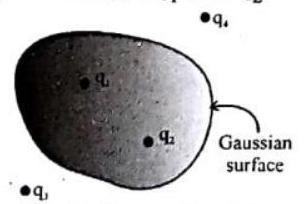
Reason: Electric field at all points on Gaussian surface depends only on charges
Show Answer
Answer: (d) Electric field at any point depends on presence of all charges.4. Assertion : The positive charge particle is placed in front of a spherical uncharged conductor. The number of lines of forces terminating on the sphere will be more than those emerging from it.
Reason: The surface charge density at a point on the sphere nearest to the point charge will be negative and maximum in magnitude compared to other points on the sphere.
Show Answer
Answer: (a) No. of lines entering the surface5. Assertion: Charges are given to plates of two plane parallel plate capacitors
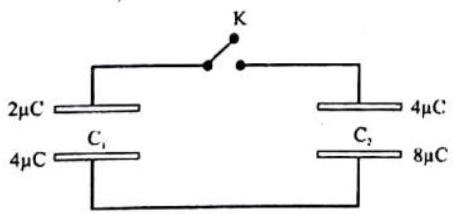
Reason: In a parallel plate capacitor both plates always carry equal and opposite charge.
Show Answer
Answer: (d) Charge distribution on each surface makes both capacitor of same potential difference hence charge will not flow.6. Assertion : Each of the plates of a parallel-plate capacitor is given equal positive charge
Reason: A negative charge (
Show Answer
Answer: (d) The charge on each of two facing surfaces will be zero.7. Assertion : Electric potential and electric potential energy are different quantities.
Reason: For a system of positive test charge and point charge electric potential energy
Show Answer
Answer: (d) Potential and potential energy are different quantities and cannot be equated.8. Assertion : Two equipotential surfaces cannot cut each other.
Reason: Two equipotential surfaces are parallel to each other.
Show Answer
Answer: (d) Two equipotential surfaces are not necessarily parallel to each otherMultiple Matching Questions:
DIRECTIONS : Each question has four statements
1. For the situation shown in the figure below, match the entries of column I with the entries of column II.
Show Answer
Answer: (A)2. In the circuit shown in figure, plates of capacitor

Show Answer
Answer: (A)3. In the circuit shown in the following figure,

Show Answer
Answer: (A)4. In the given figure, the separation between the plates of
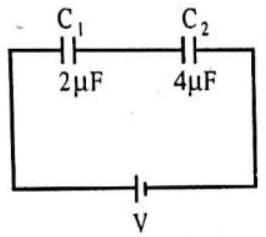
Show Answer
Answer: (A)5. Match the entries of colun I with the entries of column II. Column I Column II
| Column I | Column II |
|---|---|
| (A) When a dielectric slab is gradually inserted between the plates of an isolated parallel plate capacitor | (p) is gradually inserted between the plates of an isolated parallel plate capacitor |
| (B) When a dielectric slab is gradully inserted between the plates of a parallel plate capacitor and its potential is kept constant | (q) is gradully inserted between the plates of a parallel plate capacitor and its potential is kept constant |
| (C) When the plates of a parallel plate capacitor are pulled apart, keeping its potential constant | (r) parallel plate capacitor are pulled apart, keeping its potential constant |
| (D) When the plates of a parallel plate capacitor are pulled apart, keeping its charge constant. | (s) work done by extrnal agent is negative |
Show Answer
Answer: (A)Subjective Questions:
DIRECTIONS : Answer the following questions.
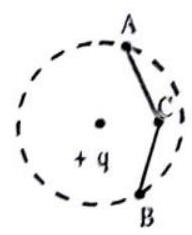
1. If a point charge
Show Answer
Answer: Work done will be same in both the paths as electrostatic force is conservative in nature, so work done doesn’t depend on the path followed.2. Find the electric field between two metal plates
Show Answer
Answer:3. Calculate the electric potential at the surface of a gold nucleus. Given, the radius of the nucleus
Show Answer
Answer: Charge on gold nucleus
4. Calculate the potential at a point
Show Answer
Answer:5. At a point due to a point charge, the values of electric field intensity and potential are
Show Answer
Answer:
6. A parallel plate capacitor with air has a capacitance of
Show Answer
Answer:
7. Each plate of a parallel plate capacitor has an area of
Show Answer
Answer:
8. A given charge situated at a distance from an electric dipole in the end on position, experiences a force
Show Answer
Answer: For an electric dipole,
9. In a parallel plate capacitor the potential difference of
Show Answer
Answer: 
Electric field between the plates of a capacitor is uniform that is constant at every point
10. Two protons
Show Answer
Answer: 
The field between the two parallel plates is uniform. So, the protons will experience same force.
11.
Show Answer
Answer: Charge will be same, as
Here,
12. How much energy will be stored by a capacitor of
Show Answer
Answer: Energy13. How does the force between two point charges change if the dielectric constant of the medium in which they are kept increases?
Show Answer
Answer: Force in a medium14. Is electrostatic potential a scalar quantity or a vector quantity?










