Chapter 02 Human Eye And Colourful World
Introduction
Light enables us to see things. But light alone can’t show us things visible. It does so with the help of ’eyes’. When eyes get defective, some visual aids are required. These aids can be in the form of spectacles. To see things bigger than their actual size, optical instruments are used. With the help of these instruments we can see distant objects like stars, sun, moon and other celestial objects very clearly. We can also see very small things very clearly with their aid. Light makes our world colourful. When light passes through a prism, a very beautiful band of seven colours is obtained on a nearby screen. When sun light falls on water droplets just after raining, a beautiful rainbow is observed. This chapter is an attempt to provide a description of the eye, its defects and remedies, optical instruments and phenomena which makes our world colourful.
THE HUMAN EYE
The human eye is the organ which gives us the sense of sight, allowing us to learn more about the surrounding world than we do with any of the other four senses. We use our eyes in almost every activity we perform, whether reading, working, watching television, writing a letter, driving a car, and in countless other ways. Most people probably would agree that sight is the sense they value more than all the rest.

The eye allows us to see and interpret the shapes, colors, and dimensions of objects in the world by processing the light they reflect or emit. The eye is able to see in bright light or in dim light, but it cannot see objects when light is absent.
PROCESS OF VISION
Light waves from an object (such as a tree) enter the eye first through the cornea, which is the clear dome at the front of the eye. The light then progresses through the pupil, the circular opening in the center of the colored iris. Next, the light passes through the crystalline lens, which is located immediately behind the iris and the pupil.
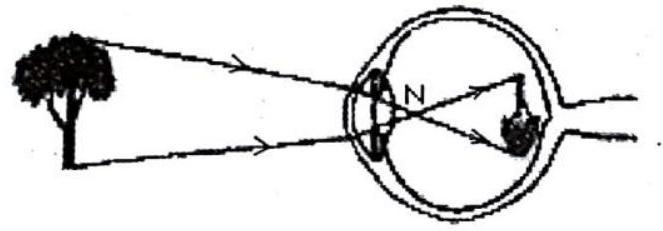
Fig. 2.2
Initially, the light waves are bent or converged first by the cornea, and then further by the crystalline lens, to a nodal point (N) locatedimmediately behind the back surface of the lens. At that point, the image becomes reversed (turned backwards) and inverted (turned upside-down).
The light continues through the vitreous humor, the clear gel that makes up about
Within the layers of the retina, light impulses are changed into electrical signals and then sent through the optic nerve, along the visual pathway, to the cortex at the posterior or back of the brain. Here, the electrical signals are interpreted or “seen” by the brain as a visual image. When the light entering the eyes is bright enough, the pupils will constrict (get smaller), due to the pupillary light response.
Actually, then, we do not “see” with our eyes but, rather, with our brains. Our eyes merely are the beginnings of the visual process. You might have experienced that you are not able to see objects clearly for some time when you enter from bright light to a room with dim light. After sometime, however, you may be able to see things in the dim-lit room. The pupil of an eye acts like a variable aperture whose size can be varied with the help of the iris.
When the light is very bright, the iris contracts the pupil to allow less light to enter the eye. However, in dim light the iris expands the pupil to allow more light to enter the eye. Thus, the pupil opens completely through the relaxation of the iris.
POWER OF ACCOMMODATION
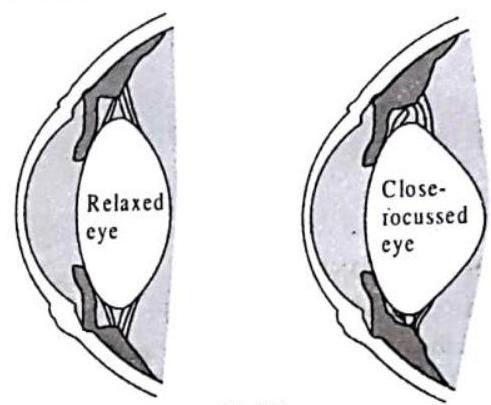
The ability of the lens to change its shape to focus near and distant objects is called accommodation is done.
| Object | Ciliary musicles | Suspensory ligamesnts | Musicle tension on lens | lens shape |
| near | contract | slackened | low | fat |
| distant | relax | stretched | high | thin |
When the eye is relaxed and the interior lens is the least rounded, the lens has its maximum focal length for distant viewing. As the muscle tension around the ring of muscle is increased and the supporting fibres are thereby loosened, the interior lens rounds out to its minimum focal length. The minimum distance, at which objects can be seen most distinctly without strain, is called the least distance of distinct vision. It is also called the near point(N.P.) of the eye. For a young adult with normal vision, the near point is about
 If an eye has the ability to assume a focal length of
If an eye has the ability to assume a focal length of Many animals can see clearly both in water and on land. Some have extraordinary accommodation ranges, and others have developed other strategies. Cormorants and dippers can vary the refractive power of their lenses by
DEFECTS OF VISION AND THEIR CORRECTION
NEARSIGHTEDNESS: If the eyeball is too long or the lens too spherical, the image of distant objects is brought to a focus in front of the retina and is out of focus again before the light strikes the retina. Nearby objects can be seen more easily. Eyeglasses with concave lenses correct this problem by diverging the light rays before they enter the eye. Nearsightedness is called myopia. Myopia most commonly develops in childhood or early teens (between 8 and 14). The risk of developing myopia is increased if there is a family history of it. There may also be a link between myopia and prolonged close-up work, súch as reading or sitting close temporary short-sightedness, called pseudomyopia, can be caused by a number of diseases or certain drugs. For example, myopia may be the first sign of type-2 (non insulin-dependent) diabetes. Symptoms of pseudomyopia usually clear up if the underlying cause is treated to the television, although there is little scientific evidence for this.
This defect can be corrected by using a concave lens of suitable focal length. A concave lens diverges the rays coming from the object so that they get focused at the retina.

Let a person can see an object at a maximum distance
Let a nearsighted person can see upto a maximum distance

FARSIGHTEDNESS: If the eyeball is too short or the lens too flat or inflexible, the light rays entering the eye - particularly those from nearby objects - will not be brought to a focus by the time they strike the retina. Eyeglasses with convex lenses can correct the problem. Farsightedness is called hypermetropia or hyperopia. Squinting, eye rubbing, lack of interest in school, and difficulty in reading are often seen in children with hyperopia.

Let the farsighted eye can see a minimum distance
By lens formula.
PRESBYOPIA (“AFTER 40” VISION)
After age 40, and most noticeably after age 45, the human eye is affected by presbyopia, which results in greater difficulty in maintaining a clear focus at a near distance with an eye which sees clearly at a far away distance. This is due to a lessening of flexibility of the crystalline lens, as well as to a weakening of the ciliary muscles which control lens focusing, both attributable to the ageing process.
Person suffering from presbyopia require bifocal lenses. A common type of bi-focal lenses consists of both concave and convex lenses. The upper portion consists of a concave lens. It facilitates distant vision. The lower part is a convex lens. It facilitates near vision. These days, it is possible to correct the refractive defects with contact lenses or through surgical interventions.
ASTIGMATISM
Astigmatism is the most common refractive problem responsible for blurry vision. Most of the eyeball’s focusing power occurs along the front surface of the eye, involving the tear film and cornea (the clear ‘window’ along the front of the eyeball). The ideal cornea has a perfectly rourtd surface. Anything 12 other than perfectly round contributes to abnormal corneal curvature-this is astigmatism. Here’s a good way to demonstrate the effects of astigmatism. Look at your reflection in the curved surface of a round soup spoon and compare it with your reflection in an oval teaspoon. The cornea is the transparent layer over the colored part of the eye. It bends (refracts) light rays and helps focus the light onto the retina in the back of the eye so people can see. When the cornea is oblong shaped, it causes light rays to focus on two different points on the retina, instead of just one. As a result, people with significant astigmatism may have distorted or blurry vision. Astigmatism may cause eye strain and also may be combined with nearsightedness or farsightedness. Astigmatism can start in childhood or in adulthood. Cylindrical lens is use to correct astigmatism

If the figure shown was constructed with all the radial lines of equal sharpness and contrast a person without astigmatism would see all these radial lines as perfectly sharp and with the same contrast. The diagram shown has been fudged to illustrate how it might appear to a person with astigmatism.
CATARACTS
A cataract is a clouding of the lens in the eye. With people age, cataracts grow progressively darker and more dense, preventing light from easily passing through the lens. This results in vision loss.
Patients with cataracts have difficulty seeing in poorly lit environments. Many people also experience increased sensitivity to light and glare, double vision (or “ghost images”), and fading colors (blue may appear green; white may appear dull beige, etc.). Most cataracts are highly treatable. Cataract surgery is one of the most common surgeries performed in the world with
Complicated cataracts cannot be extracted like normal cataracts because of potential complications such as other eye conditions, lack of vision in the other eye, or health concerns such as diabetes.
CHECK POINT
Does short-sightedness (myopia) or long-sightedness (hypermetropia) imply necessarily that the eye has partially lost its ability of accommodation? If not, what might cause these defects of vision?
Show Answer
SOLUTION
A person with normal ability of accommodation may be myopic or hyperopic due to deflective eye structure. When the eye ball from front to back gets too elongated the “myopic” defect occure, similarly when the eye ball from front to back gets too shortened the “hypermetropia” defect occur.
When the eye ball has normal length but the eyelens loses partially its ability of accommodation, the defect is called “presbyopia” and is corrected in the same manner as myopia or hypermetropia.
ILLUSTRATION-2.1
A man who wears the corrective lenses of power +3D, has to hold a newspaper at
Show Answer
SOLUTION:
The corrective lenses have the focal length
and the lens formula gives
which means that the corrective lenses used by man form the clear images at
ILLUSTRATION-2.2
What should be the focal length of corrective lenses required by a person for reading a book, if his near point is at
Show Answer
SOLUTION:
The book is kept at the least distance of distance vision
REFRACTION OF LIGHT THROUGH A PRISM
Prism is a transparent medium bounded by any number of surfaces in such a way that the surface on which light is incident and the surface from which light emerges are plane and non-parallel.
Consider a triangular glass prism. It has two triangular bases and three rectangular lateral surfaces. These surfaces are inclined to each other. The angle between its two lateral faces is called the angle of the prism. In figure you can see the incident ray, the refracted ray inside the prism and the emergent ray. You may note that a ray of light is entering from air to glass at the first surface. The light ray on refraction has bent towards the normal. At the second surface, the light ray has entered from glass to air. Hence it has bent away from the normal.
The peculiar shape of the prism makes the emergent ray bend at an angle to the direction of the incident ray. This angle is called the angle of deviation. It’s not only the shape that matters but importantly difference of refractive index of prism material from surrounding makes ray to deviate, if glass prism is placed in a fluid with same refractive index as that of glass ray will pass without deviation.

Activity :
Fix a sheet of white paper on a drawing board using drawing pins.
Place a glass prism on it in such a way that it rests on its triangular base. Trace the outline of the prism using a pencil.
Draw a straight line
Fix two pins, say at points
Look for the images of the pins, fixed at
Fix two more pins, at points
Remove the pins and the glass prism.
The line
Draw perpendiculars to the refracting surfaces
Mark the angle of incidence
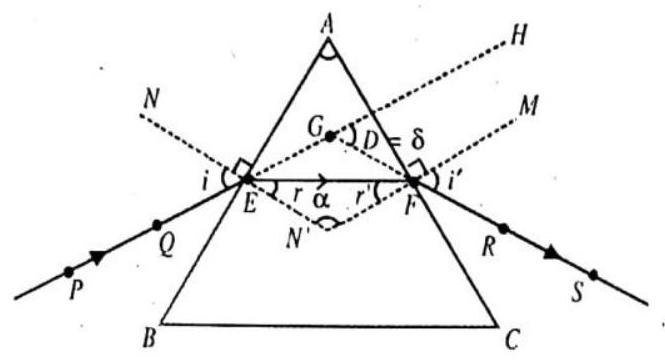
Fig. 2.9: Refraction of light through a triungular glass prism
ANGLE OF DEVIATION (
The angle between the emergent ray and incident ray is called angle of deviation (
In quadrilateral, (see above activity) the sum of its four angles should be
In
From(1)&(2),
In
ANGLE OF MINIMUM DEVIATION
For each angle of incidence
Condition when
i.e., when angle of incidence equals to the angle of emergence.
78 Human Eye and Colourful World | Physics |
Now,
FOR A SMALL ANGLED PRISM
If
Putting these values in above-derived formula, we get
It is generally written as below
Enowedge
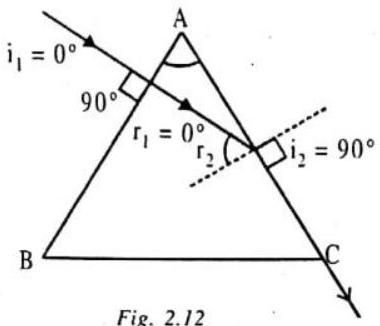
1.Condition of no emergence of a ray from a prism
The light will not emerge out of a prism for all values of angle of incidence if at face
at face
(1)
Now from Snell’s law, at face
i.e.,
So from eq. (1) and (2),
However, in a prism,
So from eq. (3) and (4),
or
i.e., A ray of light will not emerge out of a prism (whatever be the angle of incidence)
if
2.Maximum deviation from a prism
Deviation will be maximum when angle of incidence
so eq. reduces to :
However, when
i.e.,
and as in a prism
So at surface AC,
or
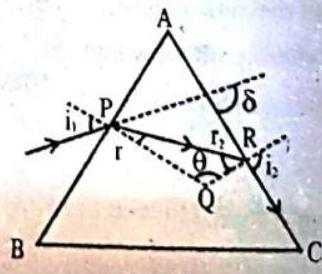
Fig. 2.II
ILLUSTRATION-2.3
A ray of light falls normally on a refracting face of a prism of the refractive index
Show Answer
SOLUTION:
The angle of incidence of the ray of light at the refracting face
At the second refracting face
ILLUSTRATION-2.4
An equilateral prism is having the refractive index
Show Answer
SOLUTION:
For minimum deviation
(i)
(ii) For the maximum deviation
Then, by the Snell’s Law, we have
ILLUSTRATION-2.5
Find the angle of deviation suffered by a ray of light is passing through a thin prism, as shown. The refractive index of prism material is
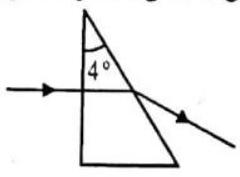
Show Answer
SOLUTION
The angle of deviation suffered by the ray of light in passing through the thin prism of angle
DISPERSION OF WHITE LIGHT BY A GLASS PRISM
The refraction law underlies the phenomenon of the dispersion of light, that is the decomposition of the white light into the component colours when passing through a prism or through a transparent object delimited by non parallel surfaces. A beam of light containing all the visible spectrum of the light is white, because the sum of all the colors generates the white color. Normally the light we use is white. It’s the light containing all the colors mixed together. We can realize this fact when the beam of light passes through a glass prism: the light is decomposed in all the component colours, Violet, Indigo, Blue, Green, Yellow, Orange and Red, called as VIBGYOR. The band of the coloured components of a light beam is called its spectrum.
The phenomenon can be explained by thinking that light of different colours (different wavelengths) has different velocities while travelling in a medium:
Hence, the change in velocity of light observed when the light passes from the air to the glass, depends on the wavelength.
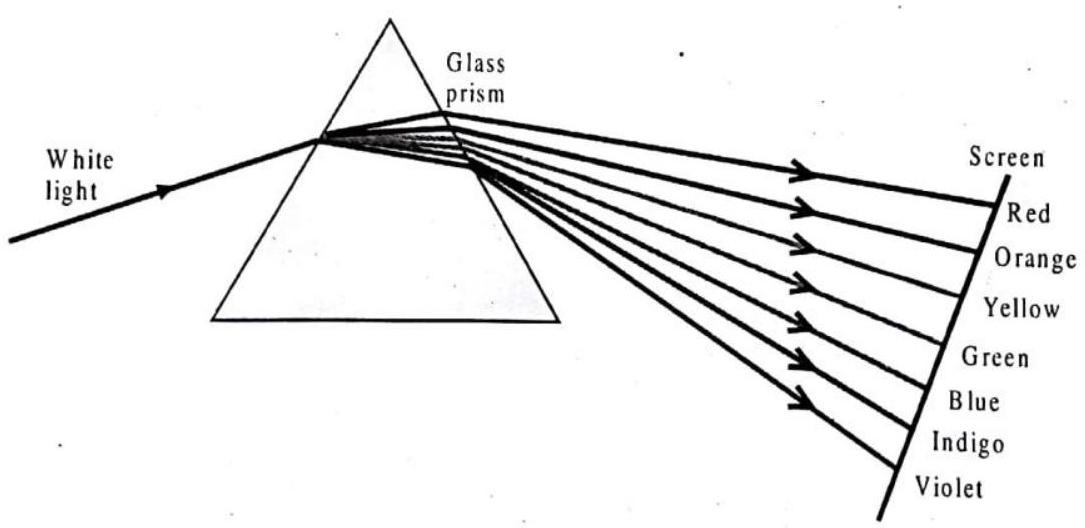
Fig. 2.14
By passing the interface air-glass, lower is the wavelength lower becomes the velocity of the light, so, for example, red light rays are faster than violet light rays. This change in velocity coupled with the direction of the light beam to the air-glass interface explains the decomposition of a white light ray in the component colours while it is passing through a prism.
This phenomenon is known as “dispersion of light through a prism” and it is also responsible for rainbows during storms: as a matter of fact, each raindrop can be regarded as a little prism; when a light ray strikes a raindrop it is refracted and decomposed, spreading out all the visible colours ranging from red to violet.
ANGLE OF DISPERSION
The angle between the rays of the extreme colours in the refracted (dispersed) light is called the angle of dispersion
DISPERSIVE POWER
Dispersive power of the medium of the material of prism is given by
For small angled prism
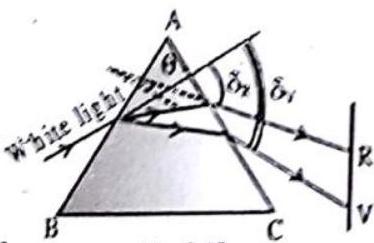
Fig. 2.15
CAUSE OF DISPERSION
The cause of dispersion is the dependence of the refractive index
The different colours of light corresponds of different refractive index of the prism. Hence, different colours have different velocities in the prism and hence get separated from one another.
Combination of Two Prisms
If two prisms of prism angles
and
(a) For deviation without dispersion (Achromatic Prism)
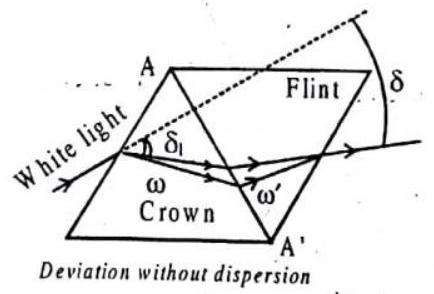
Fig. 2.16 (a)
But as
Usually
(b) For dispersion without deviation (Direct vision prism)
In this situation,
i.e.,
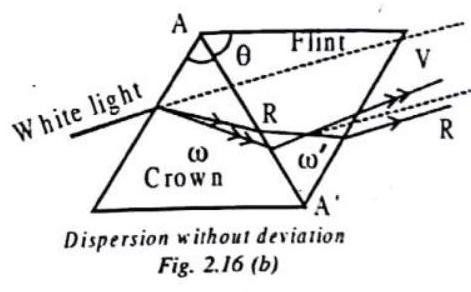
If
ILLUSTRATION-2.6
White light passes through a thin prism of angle
Show Answer
SOLUTION:
The angular dispersion produced by the prism is
ILLUSTRATION-2.7
In the previous Illustration, calculate the dispersive power of prism material.
Show Answer
SOLUTION:
ILLUSTRATION-2.8
The crown glass has the refractive indices 1.51 and 1.49 for the blue and red lights, respectively, and the flint glass has the refractive indices 1.77 and 1.73 for the blue and red lights, respectively. A beam of white light is incident on a combination of two thin isosceles prisms, one of crown glass of angle
Show Answer
SOLUTION:
The net deviation of light produced by the combination of two prisms is zero and therefore,
where the minus sign indicates that the second prism of flint glass of angle
Then the net angular dispersion of light produced by the combination is
TOTAL INTERNAL REFLECTION (TIR):
THE PHENOMENON : In case of refraction of light, from snell’s law we have
If light is passing from denser to rarer medium through a plane boundary then
i.e.,
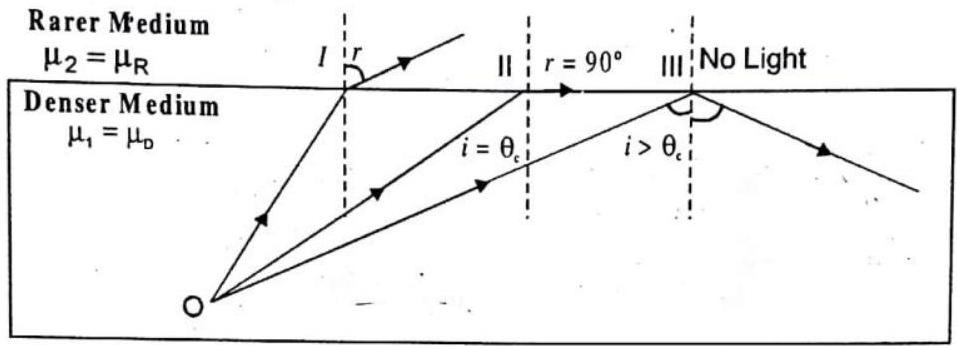
Fig. 2.17
So, as angle of incidence
And hence eqn. (2) in terms of critical angle can be written as
So, if
For total internal reflection to take place light should pass from a denser medium to a rarer medium. It light passes from air to water (or glass) or from water to glass, total internal reflection can-never take place.
When light is passing from denser to rarer medium, total internal reflection will take place only if angle of incidence is greater than
a certain value called critical angle given by :
In case of total internal reflection, as all (i.e. 100%) incident light is reflected back into the same medium there is no loss of intensity while in case of reflection from mirror or refraction from lenses, there is some loss of intensity as all light can never be reflected or refracted. This is why image formed by TIR are much brighter than formed by mirror or lenses.
CRITICAL ANGLE
In case of propagation of light from denser of rarer medium through a plane boundary, critical angle is the angle of incidence for which angle of refraction is
For a given pair of medium critical angle depends on wavelength of light used i.e., greater the wavelength of light lesser will be
This is why in case of
Glass air
As
Water air
As
Glass Water
As

Fig. 2.18 : All rays reflect internally, but the top three rays reflect only a small percentage internally; most energy leaves the prism. The fourth and fifth rays are reflected
i.e.,
i.e.,
i.e.,
So
FISH LOOKING UP THROUGH WATER
It is interesting to see that to a fish at a depth

From the geometry of figure, we have
where
In another situation, if a source of light is placed at the position of eye of fish, those rays of light from the source which are incident on the water surface outside the circle at an angle
APPLICATIONS OF TIR
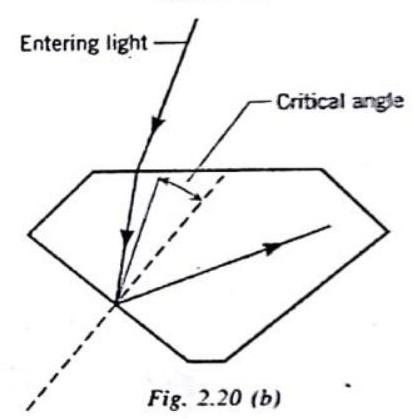
1.Sparkling of diamond
A diamond sparkles because, when it is held in a certain way, the intensity of the light coming from it is greatly enhanced. Fig. helps to explain that this enhancement is related to total internal reflection. Part of the drawing shows a ray of light striking a bottom face of the diamond at an angle of incidence exceeding the critical angle, the ray is totally reflected back into the diamond, eventually exiting the top surface to give the diamond its sparkle. The critical angle is
Now consider what happens to the same ray of light within the diamond when the diamond is placed in water. Because water has a larger index of refraction than air, the critical angle increases to

Fig.
2. Optical fibre
Take a thin solid wire (called strand) made up of glass or quartz, etc. Coat it from outside with some material whose
Hence, in effect, light can travel axially within an optical fibre, although the axis of fibre may be flexible having bent or wavy profile.
A bundle of optical fibres is called a light pipe and is able to send image of an extended object from one end to another by picking up images of small-small parts of the object and sending them likewise to the other end.
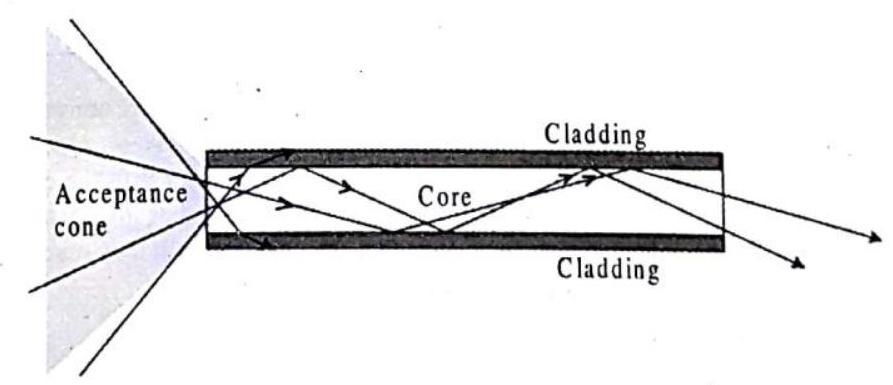
Fig. 2.21(a) : Optical fibre showing total internal reflection of light.

Fig.
Use of Optical fiber
(a) For medical examination inside the stomach, intestines etc., called endoscopy.

(b) The recent trend is to send even electrical signals through optical fibres, by converting them into electromagnetic radiations/light waves.
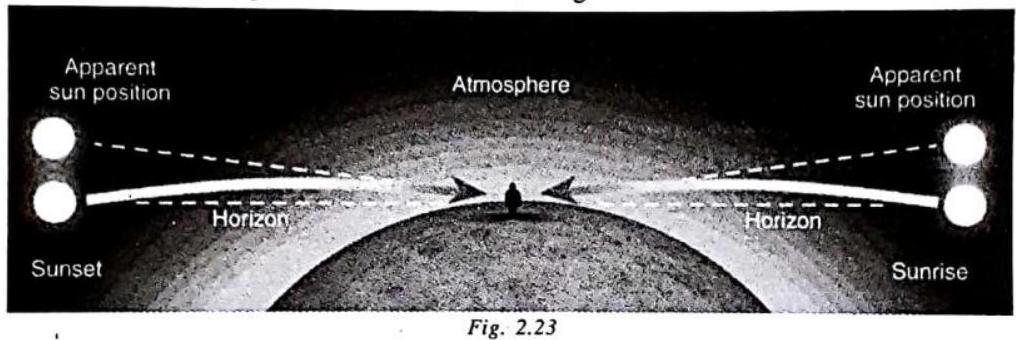
3.Duration of Sun’s Visibility
In presence of atmosphere (in which
4. Mirage
It is an optical illusion, in which inverted image of a distant object can be seen, as it reflected from a pond or a lake in hot regions due to continuous atmospheric refraction and total internal reflection.
In deserts, because of intense heat, the layers of air, near the surface of the earth, get heated so soon that the density adjusment does not take place, hence the densities and refractive indices of the layers immediately above the sand are lower than those of the layers higher up. The rays of light from a distant object, after passing through layers, which are gradually less refracting, bend more and more away from normal, till they fall on a layer at an angle, greater than the critical angle and it gets totally reflected. These reflected rays then travel up and undergo a series of refractions, but in a direction opposite to those in first case, they now pass through layers which are gradually more and more refracting, till they reach the eye of the observer, who sees an image of the object, as though reflected from the surface of a lake of water.
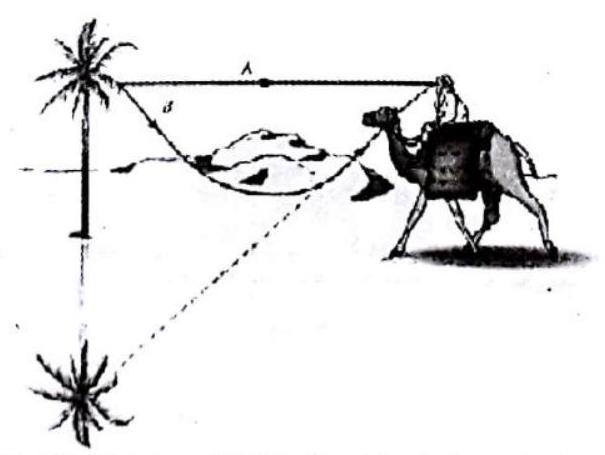
Fig 2.24(a) Hot air near desert has a lower index of refraction than the cooler air above.

Fig. 2.24 (b) : There’s no water on the road; but it appears so due to total internal reflection.
5.Looming
It is an optical illusion in which inverted image of a distant object can be seen, as if reflected from a pond or lake or sometimes, as if suspended in the atmosphere in cold regions due to continuous atmospheric refraction and total internal reflection. In cold region, air above water is cold (denser) whereas above it, it is hot (rarer). So, when light ray from the object travels from cold to warm air (denser to rarer) it undergoes continuous atmospheric refraction, and causes total internal reflections in downward directions due to which we see objects hanging up in sky.
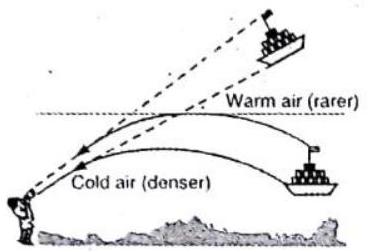
Fig. 2.25 : Looming observed in very cold region is caused by the total internal reflection of light coming from the ship (or any other object)
CHECK POINT
Rays of light in water that shine up to the water-air boundary at angles of more than
Show Answer
SOLUTION
Total internal reflection only takes place when light goes from denser to rarer medium as from water to air. It cannot take place other way around, like the case in which light rays in air meets air-water boundary. Light rays coming from air and incident on water surface will always be refracted. There is not any angle at which light rays in air meeting air-water boundary will be reflected totally. Some light will be refracted at all angles except when the ray of light grazes the air-water interface.
ILLUSTRATION-2.9
A light ray falls on a square glass slab at an angle of incidence
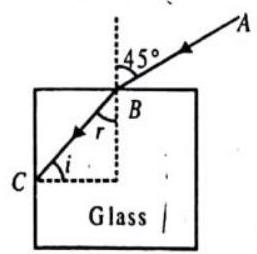
Fig. 2.26
Show Answer
SOLUTION :
If the light ray is to undergo the total internal reflection at the point
and then, by the Snell’s law,
Equating
which is the minimum refractive index of glass for the total internal reflection to occur at the point
ILLUSTRATION-2.10
A point source
Show Answer
SOLUTION:
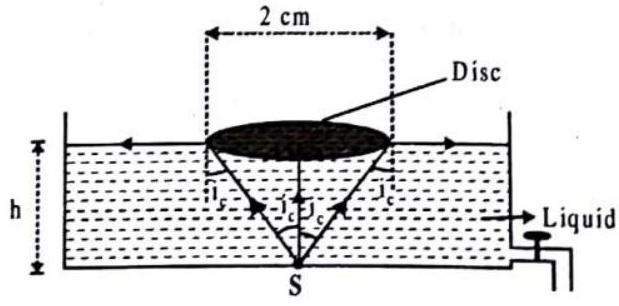
Fig. 2.27
When the height of liquid above the point source
If
which gives the maximum value of
RAINBOW
You must have observed most spectacular light shown on earth i.e., rainbow. Indeed
the traditional rainbow is sunlight spread out into its spectrum of colours and diverted
to the eye of the observer by water droplets. The “bow” part of the word describes the
fact that the rainbow is a group of nearly circular arcs of color all having a common
center.
Rainbows are generated through refraction and reflection of light in small rain drops.
The sun is always behind you when you face a rainbow, and that the center of the
circular arc of the rainbow is in the direction opposite to that of the sun. The rain, of
course, is in the direction of the rainbow i.e., rain drops must be ahead of you and the
angle between your line-of-sight and the sunlight will be

Fig. 2.28
After rain, there are still some tiny water droplets remained in the air. If there is sunshine, a white sunbeam will be reflected and refracted by these tiny droplets. Different colors of light have different refractivity. They will be reflected in slightly in different directions inside a water droplet. Since, water is more dense than air, light is refracted as it enters the drop-red is bent less, blue more. Some of the light will reflect off the back of the drop if the angle is larger than the critical angle
The light is then refracted again as it leaves the drop (act like a small prism), the colours of white light have been dispersed.
- violet light will leave the drop at an angle of
- red light will leave the drop at an angle of

Fig. 2.29
However, you can not see the blue light and red light refracted from the same drop.
So, many drops are involved in producing the rainbow
you can only see one wavelength of light refracted from one drop.
So, to see a rainbow, you need to see light refracted from many drops.
Hence, red will be on the top and blue will be on the bottom of the rainbow.
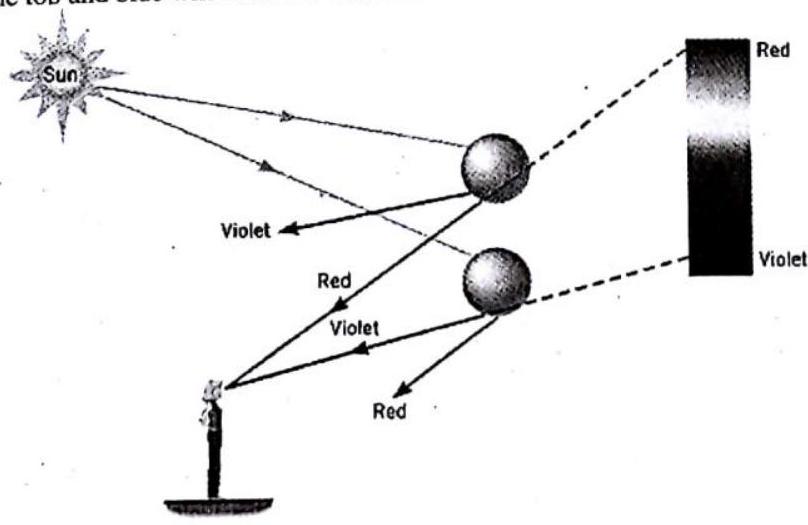
Fig. 2.30 : Forming a Rainbow.
Both the primary and secondary rainbows are phenomena that are formed by the reflection and refraction of sunlight in tiny water droplets. When a sunbeam is being refracted twice and reflected once by the droplet, a primary rainbow will form. If the beam is being refracted twice and reflected twice, a secondary rainbow will form. As the secondary rainbow is formed by one more reflection than the primary rainbow, it is much fainter and rare to see. On the other hand, since the paths of sunbearns in a primary rainbow and a secondary rainbow are different, the colours of the secondary sainhow are arranged in just the reverse order of the primary one.

CHECK POINT:
A rainbow viewed from an airplane may form a complete circle. Where will the shadow of the air-plane appear? Explain
Show Answer
SOLUTION
A rainbow viewed from an airplane may form a complete circle because the earth doesnot come in the way of the airplane and rainbow and as a rainbow is a three dimensional cone of dispersed light it will appear as a complete circle. The shadow of the airplane will appear with in the circle of the rainbow.
ATMOSPHERIC REFRACTION
Twinkling of stars
The scientific name for the twinkling of stars is stellar scintillation (or astronomical scintillation). Stars twinkle when we see them from the Earth’s surface because we are viewing them through thick layers of turbulent (mov’:
Stars (except for the Sun) appear as tiny dols in the sky; as their light travels through the many layers of the Earth’s atmosphere, the light of the star is bent (refracted) many times and in random directions (light is bent when it hits a change in density-like a pocket of cold air or hot air). This random refraction results in the star winking out (it looks as though the star moves a bit, and our eye interprets this as twinkling).
Stars closer to the horizon appear to twinkle more than stars that are overhead this is because the light of stars near the horizon has to travel through more air than the light of stars overhead and so is subject to more refraction.
Also, planets do not usually twinkle, because they are so close to us; they appear big enough that the twinkling is not noticeable (except when the air is extremely turbulent).
Stars would not appear to twinkle if we viewed them from outer space (or from a planet/moon that didn’t have an atmosphere.
Since the atmosphere bends starlight towards the normal, the apparent position of the star is slightly different from its actual position. The star appears slightly higher (above) than its actual position when viewed near the horizon. Further, this apparent position of the star is not stationary, but keeps on changing slightly, since the physical conditions of the earth’s atmosphere are not stationary.

Fig. 2.32
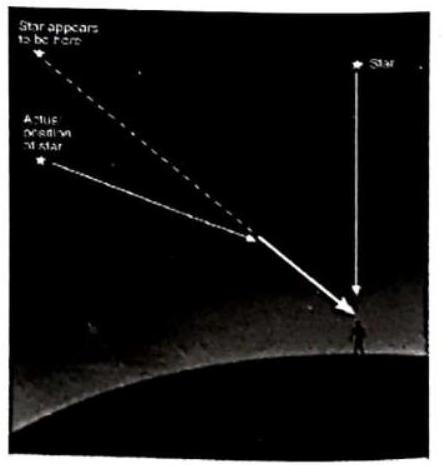
Fig. 2.33
SCATTERING OF LIGHT
The interplay of light with objects around us gives rise to several spectacular phenomena in nature. The blue colour of the sky, colour of water in deep sea, the reddening of the sun at sunrise and the sunset are some of the wonderful phenomena we are familiar with all this is because of scattering of light.
When sunlight enters the earth atmosphere, air and water vapour molecules will absorb part of the light and reradiate it to all directions. This is called scattering. Generally two types of scattering are consider mie and rayleigh.
Mie Scattering
large particles in the atmosphere are able to scatter all wavelengths of white light equally
when all wavelengths of white light are scattered equally, then Mie scattering is occurring
this is why clouds appear white.
Rayleigh scattering
The selective scattering of the shorter wavelengths of visible light (violet and blue) by atmospheric gases. Note that Rayleigh scattering involves much smaller scattering particles than Mie scattering
Orange/red sunsets in a clean atmosphere
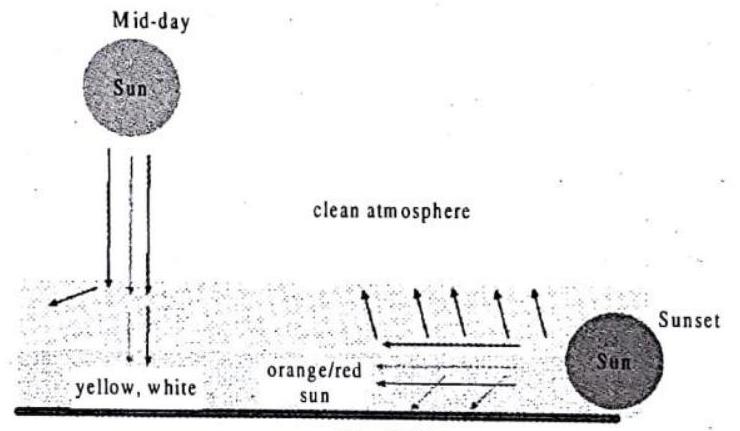
Fig. 2.34

Fig. 2.35
At mid-day, only a bit of the short wavelengths of visible light are scattered since the radiation is passing through a small distance in the atmosphere.
At sunset, however, the radiation must pass through a much thicker layer of the atmosphere.
When the sun is at an angle of
Hence, much more blue light, and some green light are scattered.
Therefore, the sun appears to look orange/red.
Orange/red sunsets in a dirty atmosphere
When pollution is present, the atmosphere contains more particles such as aerosols having larger diameters than the atmospheric gases. Hence, more of the intermediate wavelengths of visible light such as yellow and green are scattered in addition to the blue light what largely remains is red light, hence the sun appears red.
OPTICAL INSTRUMENTS
The size of the image on the retina determines how large an object appears to be. However, the size of the image on the retina is
difficult to measure. Alternatively, the angle
Visual angle with instrument
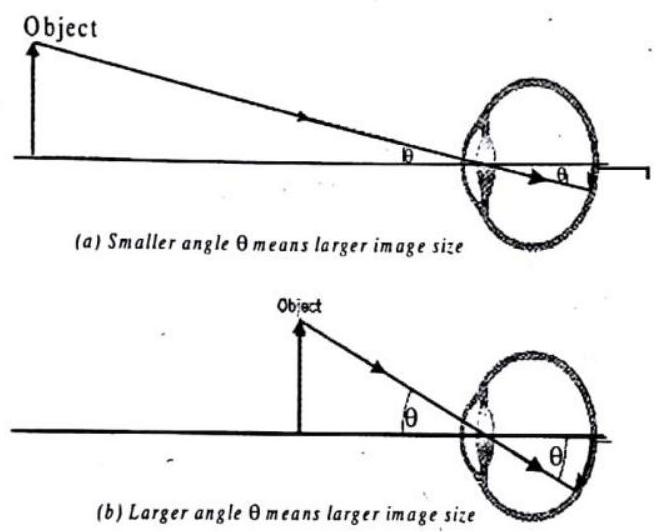
Fig. 2.36 : In both (a) and (b) the objects have the same size, but in (b) the image on the retina is larger because the object is closer to the eye. The angle
SIMPLE MICROSCOPE (MAGNIFYING GLASS OR READING LENS)
It is also known as magnifying glass or simply magnifier and consists of a convergent lens with object between its focus and optical centre and eye close to it. The image formed by it is erect, virtual enlarged and on same side of lens between object and infinity.
Magnification by a simple microscope
The magnifying power (MP) or angular magnification of a simple microscope (or an optical instrument) is defined as the ratio of visual angle with instrument to the maximum visual angle for clear vision when eye is unadded (i.e., when the object is at least distance of distinct vision)
i.e.,
Case 1: Eye focussed at near point i.e., the image is formed at a distance

In this case,
Now, according to our sign convention
Case 2: Eye focussed at infinity (Normal adjustment)
In this case, we find out angular magnification. If the object is viewed directly by the eye, keeping the object at the near point, then
Now, let us find the angle subtended by its image, if the image is fcrmed at
In this case,
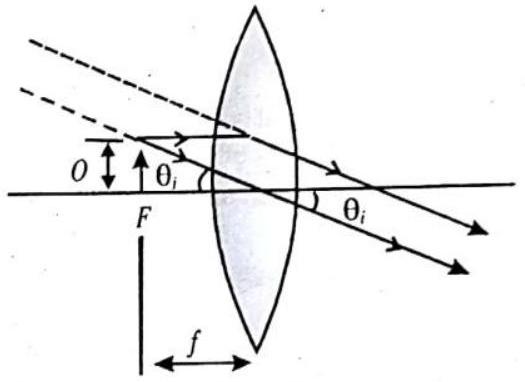
Fig. 2.38
This is one less than the magnification when the image is formed at the near point, but, naturally, viewing is more comfortable and the difference in magnification usually small.
For example, if we want a magnification of six,
For all practical purposes, it is not possible to have magnification
USES
The watch makers use of convex lens to have a magnified view of the small parts of the watch. The magnified glass is also used to see slides. It is also used in laboratories to note vernier readings.
CHECK POINT:
The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification?
Show Answer
SOLUTION
In magnifying glass the object is placed closer than
COMPOUND MICROSCOPE
Construction: It consists of two convergent lenses of short focal lengths and apertures arranged co-axially. Lens (of focal length
Magnification of a compound microscope
Now
or
Put (2) in (1) to get
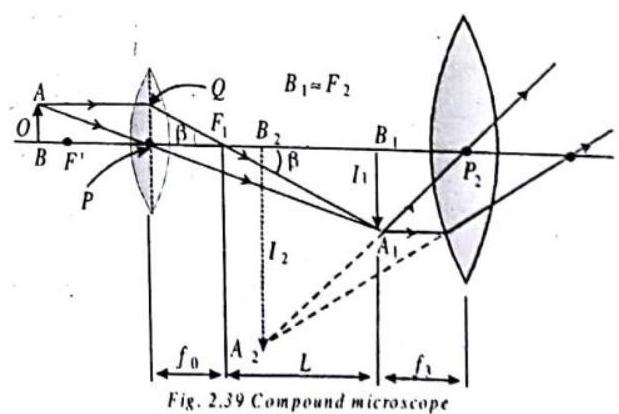
Now, let the eye is focussed at
where, for all practical purposes
If the eye is focussed at near point,
Therefore the total magnification will become,
CHECK POINT:
When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why ? How much should be that short distance between the eye and eyepiece?
Show Answer
SOLUTION
If we place our eye too close to the eyepiece, we shall not collect much of the light and also reduce our field of view. When we position our eye slightly away and area at the pupil of our eye is greater,
Now our eye collects all the light refracted by the objective, and a clear image is observed by the eye.
TELESCOPE
Telescope is used to provide angular magnification of distant objects. It is of many types, general categories are :
(i) Refracting type (lenses are used)
(ii) Reflecting type (mirrors are used)
(iii) Astronomical, to view celestial objects
(iv) Terrestial, to view objects on earth.
Thus, prism binoculars are also terrestial telescopes.
A refracting type astronomical telescope, used to see the distant objects at larg distances, consists of objective, i.e., a converging lens, or lens combination of larger focal length
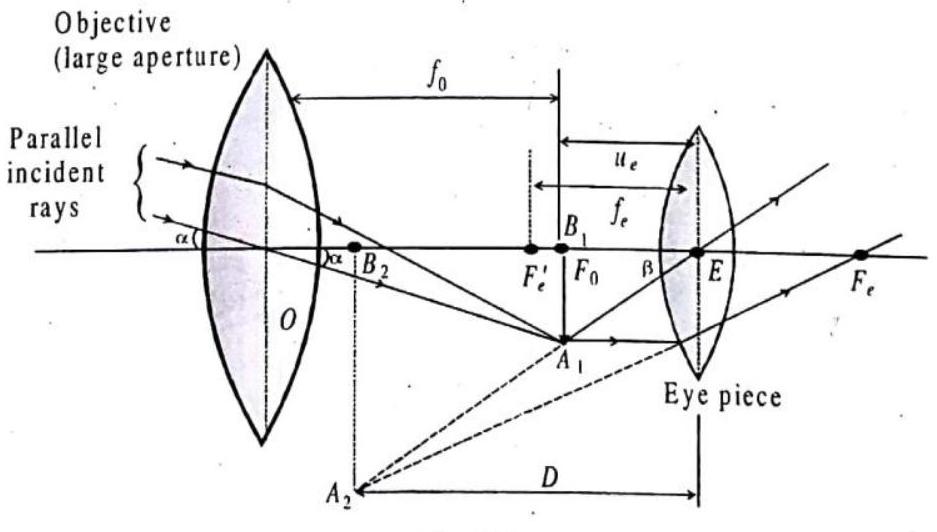
Fig. 2.40
Magnifying power (M)
Magnifying power
Using sign convention and taking
This is the general formula for magnifying power of a telescope.
For the eyepiece,
Using lens formula, we get
Put (2) in (1), we get
In this case, the length of the telescope is
In this case, as already explained, we have
Put (4) in (1) to get
In this case, the length of the telescope
This is the reason why the focal length of objective is taken large and of eyepiece small in case of a telescope. This also increases the resolving power of the telescope.
Further, linear or lateral magnification does not convey much meaning in case of a telescope because the size of final images too is negligible compared to actual size of the objects which are generally planets or stars.
Difference between Compound Microscope and Astronomical Telescope
| Compound Microscope | Astronomical Telescope |
|---|---|
| 1. It is used to increase visual angle of near tiny object. | 1. It is used to increase visual angle of distant large objects. |
| 2. In it field and eye lens both are convergent, of short focal length and aperture. | 2. In it objective lens is of large focal length and aperture while eye lens of short focal length and aperture and both are convergent. |
| 3. Final image is inverted. Virtual and enlarged and at a distance D to∞ from the eye. | 3. Final image is inverted, virtual and enlarged at a distance D to∞ from the eye. |
| 4. MP does not change appreciably if field and eye lens are interchanged [MP~ (LD/fof)] | 4. MP becomes (1/m²) times of its initial value if objective and eye- lenses are interchanged as MP - [fo/f] |
| 5. MP is increased by decreasing the focal length of both the lenses. | 5. MP is increased by increasing the focal length of objective lens (and by decreasing the focal length of eye-piece. |
| 6. RP is increased by decreasing the wavelength of light used. | 6. RP is increased by increasing the aperture of objective. |
ILLUSTRATION-2.11
If the tube length of an astronomical telescope is
Show Answer
SOLUTION:
For the normal adjustment, i.e., for the normal vision (relaxed eye), The magnifying power is of magnitude
and the tube length is
Solving the above equations, we have
ILLUSTRATION-2.12
A compound microscope has the magnifying power of magnitude 30 . The focal length of it’s eyepiece is
Show Answer
SOLUTION:
The magnifying power of compound microscope is
Therefore, the magnification produced by the objective is
where the minus sign indicates that the image formed by the objective is inverted.
ILLUSTRATION-2.13
An astronomical telescope, consisting of an objective of focal length
Show Answer
SOLUTION:
The magnifying power of telescope has the magnitude
Then, the angular size of the final image of moon will be
and it’s linear size will be
ILLUSTRATION-2.14
The objective and eyepiece of a compound microscope, separated by
Show Answer
SOLUTION:
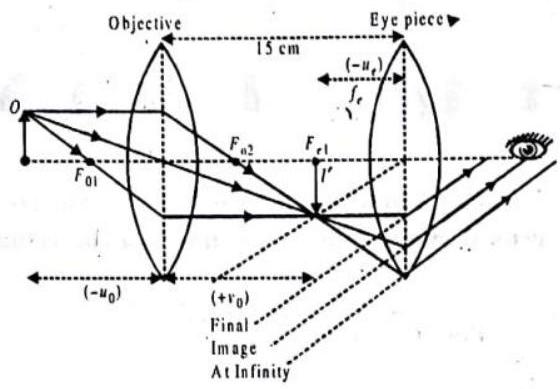
Fig. 2.41
Applying the lens formula for the eyepiece, we have
which means that the image
Then, applying the lens formula for the objective, we have
i.e., the object distance from the objective is
LENS CAMERA
In it a converging lens whose aperture and distance from the film can be adjusted is used. Usually object is real and between
In photography of an object, the image is first focused on the film by adjusting the distance between lens and film (called focusing). After focusing, aperture is set to a specific value (for desired effect) and then film is exposed to light for a given time through a shutter.
However, light transmitting area of a lens is proportional to the square of its aperture
(1) If aperture is kept fixed,
(2) If intensity is kept fixed,
Increasing the time of exposure by reducing the aperture increases the depth of field.
The following table will explain this relationship in detail.
MISCELLANEOUS
SOLVED EXAMPLES
1. A person needs a lens of power -5.5 dioptres for correcting his distant vision. For correcting his near vision he necds a lens of power +1.5 dioptre. What is the focal length of the lens required for correcting (i) distant vision, and (ii) near vision?
Show Answer
Solution. (i) Focal length of distance viewing
(ii) Focal length in near vision
2. Make a diagram to show how hypermetropia is corrected. The near point of a hypermetropic eye is
Show Answer
Solution.

To correct the defect, the image of an object at
So, a convex lens of focal length
Power,
3. Why is a normal eye not able to see clearly the objects placed closer than
Show Answer
Solution. The maximum accommodation of a normal eye is reached when the object is at a distance of4. The angle of crown glass
Show Answer
Solution. For a direct vision spectroscope
or
5. The refracting angle of the prism is
Show Answer
Solution. For minimum deviation
From snell’s law
6. A farsighted person cannot focus clearly an objects that are less than
Show Answer
Solution. The near point is
Hence,
7. A certain eye has a near point of
Show Answer
Solution. (a) We want to move the far point to infinity, so
(b) We have,
So that
(c) For the near point at
8. Complete the path of the monochromatic ray of light in each of the right angled isosceles triangle. Critical angle for the glass is 
Show Answer
Solution.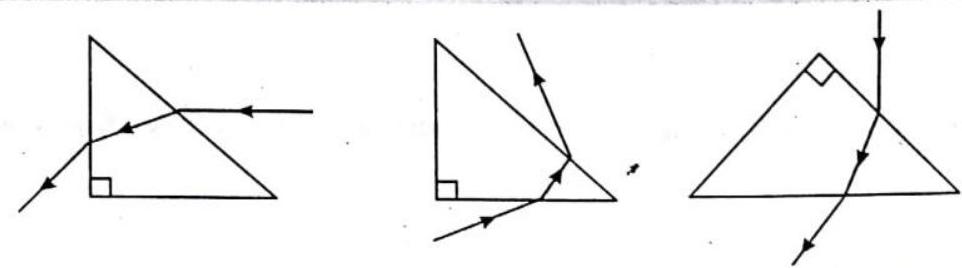
9. A figure divided into squares, each of size
(i) What is the magnification (image size/object size) produced by the lens? How much is the area of each square in the virtual image?
(ii) What is the angular magnification (magnifying power) of the lens?
(iii) Is the magnification in (i) equal to the magnifying power in (ii) ? Explain.
Show Answer
Solution. (i)
Magnification
Since, magnification is 10 therefore the area of each square in the virtual image is
(ii) Angular magnification
(iii) No. Magnification of an image by a lens and aigular magnification (or magnifying power) of an optical instrument are two separate things. The latter is the ratio of the angular size of the object (which is equal to the angular size of the image even if the image is magnified) to the angular size of the object if placed at the near point
10. A lady uses +1.5D glasses to have normal vision from
Show Answer
Solution. (a)
(b) focal length of glasses
1 EXERCISE
Fill in the Blanks.
DIRECTIONS: Complete the following statements with an appropriate word / term to be filled in the blank space(s).
1. The coloured diaphragm between the cornea and the lens is …………
Show Answer
Answer: IRIS2. The middle point of the iris has a hole, which is called……………….
Show Answer
Answer: pupil3 The screen on which the image is formed by the lens system of the human eye is called………..
Show Answer
Answer: retina4. …………….. responds to the intensity of light.
Show Answer
Answer: Rods5. ……………respond to colour by generating electrical nerve pulses.
Show Answer
Answer: Cones6. For young adult with normal vision, least distance of distict vision
Show Answer
Answer: 25cm.7. The closest distance at which the eye can focus clearly is called the ……………………
Show Answer
Answer: near8. For a normal eye, the range of vision is from ……………………
Show Answer
Answer: 25cm to infinity9. The eye which suffers from myopia as well as from hypermetropia is said to suffer from ……………………
Show Answer
Answer: presbyopia.10. The eye which cannot simultaneously see with the same distinctness all objects or lines making different inclinations is said to suffer from. ……………………
Show Answer
Answer: astigmatsm11. The defect of the eye due to which a person is unable to distinguish between certain colours, known as ……………………
Show Answer
Answer: colour blindness12. Newton demonstrated that white light is made up of …………………… constituent colours.
Show Answer
Answer: seven13. The phenomenon of splitting of white light into its constituent colours is called. ……………………
Show Answer
Answer: dispersion14. The band of colours produced on the screen is called……………………
Show Answer
Answer: spectrum.15. The ability of the eye to focus both near and distant objects, by adjusting its focal length, is called the ……………………
Show Answer
Answer: accommodation of the eye.16. The smallest distance, at which the eye can see objects clearly without strain, is called the …………………… of the eye.
Show Answer
Answer: near point17. The common refractive defects of vision include …………………… , ……………………and……………………
Show Answer
Answer: myopia, hypermetropia, prebyopia.18. The splitting of white light into its component colours is called ……………………
Show Answer
Answer: dispersion.19. …………….. causes the blue colour of sky and the reddening of the Sun at sunrise and sunset.
Show Answer
Answer: Scattering of light20. Sunlight comprises …………………… colours.
Show Answer
Answer: 721. The wavelength of violet colour is ……………………
Show Answer
Answer:22. The wavelength of red colour is………………………
Show Answer
Answer:23. In the minimum deviation position, the path of ray of light entering a prism is such that the angle of…………………… is………………… to the angle of emergence; also the refracted ray in the prism is…………………. to the base of the prism
Show Answer
Answer: incidence, equal, parallelTRUE / FALSE
DIRECTIONS: Read the following statements and write your answer as true or false.
1. Lens which is used for correcting the presbyopia defect of the eye is concave.
Show Answer
Answer: False2. The colour that deviates maximum while passing through a glass prism is violet.
Show Answer
Answer: True3. Water droplets act as tiny prism in the formation of rainbow.
Show Answer
Answer: True4. The transparent spherical membrane covering the front of the eye is known as comea.
Show Answer
Answer: True5. The eye which can see near object clearly is said to suffer from hypermetropia.
Show Answer
Answer: False6. The eye which cannot see distant objects clearly is said to suffer from myopia.
Show Answer
Answer: True7. Colour blindness is a genetic disorder which occurs by inheritance. '
Show Answer
Answer: True8. In Myopia the image of distant objects is focussed before the retina.
Show Answer
Answer: True9. Hypermetropia is corrected by using a convex lens of suitable power.
Show Answer
Answer: True10. The refractive index of diamond is 2.4 . Its critical angle is
Show Answer
Answer: True11. For total internal reflection to take place, the angle of incidence in the given (denser) medium must be less than the critical angle for that medium.
Show Answer
Answer: False12. In the minimum deviation position of a prism, the refracted ray is always parallel to its base.
Show Answer
Answer: False13. A person suffering from myopia cannot see distant objects clearly.
Show Answer
Answer: True14. The focal length of a given lens depends on the surrounding medium.
Show Answer
Answer: True15. Prismatic periscopes use the principle of total internal reflection.
Show Answer
Answer: True16. A dentist uses a convex mirror to view the inner parts of a patient’s mouth.
Show Answer
Answer: False17. The solar spectrum in general is an absorption spectrum.
Show Answer
Answer: TrueMATCH THE FOLLOWING
DIRECTIONS (Qs. 1-3) : Each question contains statements given in two columns which have to be matched. Statements
1. Match the following :
| Column I | Column II |
|---|---|
| (A) Inverted crown-flint | (p) Deviation |
| glass prism | |
| (B) Achromatism | (q) Deviation without dispersion |
| (C) Hollow prism | (r) Absence of chromatic aberration |
| (D) Glass slab | (s) Dispersion without deviation |
Show Answer
Answer: (A)2. Column II gives lens that can be use to correct the defect of vision given in column I, match them correctly. Column I
| Column I | Column II |
|---|---|
| (A) Myopia | (p) convex lens |
| (B) Hyperopia | (q) concave lens |
| (C) Astigmatism | (r) cylindrical lens |
| (D) Presbyopia | (s) bi-focal lens |
Show Answer
Answer: (A)3. Match the following:
| Column I | Column II |
|---|---|
| (A) Plane mirror | (p) Primary colours |
| (B) Convex lens | (q) |
| (C) Spectroscope | (r) Incoherent scattering |
| (D) Atmospheric scattering of light | (s) Magnification always one |
| (E) RB RBG | (t) Terrestrial telescope |
| (F) Optic fibre | (i) Burglar alarm |
| (G) Sol Solid angle in a sphere | (v) Virtual and magnified image |
| (H) Photo electric effect | (w) Blue colour of effect the sky |
| (I) Raman effect | (x) Observing and studying spectrum |
| (J) Erecting lens | (y) Total internal reflection |
Show Answer
Answer: (A)Very Short Answer Questions:
DIRECTIONS : Give answer in one word or one sentence.
1. When a monochromatic light passes through a prism, will it show dispersion?
Show Answer
Answer: No, it will not show any dispersion but will show only deviation.2. Will a star appear to twinkle if seen from free space (say moon)?
Show Answer
Answer: A pure spectrum is the one in which the colours are separated from one another using a narrow source of light.3. What do you mean by a pure spectrum?
Show Answer
Answer: Myopia.4. What is the common name for short sightedness?
Show Answer
Answer: Spherical aberration.5. Name the defect which is corrected by using an astigmatic lens.
Show Answer
Answer: A rainbow is a natural spectrum appearing in the sky.6. Name a natural spectrum.
Show Answer
Answer: The ability of the eye to see objects at all distances is called accomodation7. Name the ability of the eye to see objects at all distances.
Show Answer
Answer: No, because there is no atmosphere in free space for refraction to take place.8. Will a star appear to twinkle if seen from free space (say moon)?
Show Answer
Answer: Our arm describes a cone, and our finger sweeps out a circle. Likewise with rainbows.9. Suppose you point to a wall with your arm extended. Then you sweep your arm around, making an angle of about
Show Answer
Answer: No, as there won’t be dispersion and total internal reflection.10. If light travelled at the same speed in raindrops as it does in air, would we have rainbows?
Show Answer
Answer: The earth comes in the way of the rainbow and prevents it to form a complete circle.11. What prevents rainbows from being seen as complete circles?
Show Answer
Answer: The rainbow - colored fringe formed at the edges of a spot of white light coming from a beam of lantern or slide projector is due to diffraction of light rays coming from different part of the beam.12. What is responsible for the rainbow-coloured fringe commonly seen at the edges of a spot of white light from the beam of lantern or slide projector?
Show Answer
Answer: Back of the observer must be towards the sun.13. What is the essential condition for observing a rainbow?
Show Answer
Answer: No, this is because dispersion of light cannot occur on passing through air contained in a hollow prism.14. Does a beam of light give spectrum on passing through a hollow prism containing air, explain?
Show Answer
Answer: This is because in the formation of a secondary rainbow, light enters from the bottom of the drop, instead of entering from the top as in case of primary rainbow and suffers two total internal reflections instead of one.15. Why does a secondary rainbow have inverted colours ?
Show Answer
Answer: The statement is true, because a short-sighted person has difficulty in observing far off objects.16. A short-sighted person may read a book without spectacles. Comment.
Show Answer
Answer: No, the statement is false. A hypermetropic person can observe far off objects without any problem.17. A hypermetropic person has problem in driving without spectacles, comment on this.
Show Answer
Answer: This problem is due to astigmatism of the eye. This defect is removed using a cylindrical lens with appropriate axis and suitable radius of curvature.18. A person looking at a mesh of crossed wires is able to see the vertical wires more distinctly than the horizontal wires. Why ? How can it be corrected?
Show Answer
Answer:19. A short-sighted person cannot see clearly beyond
Show Answer
Answer:20. A myopic person can see things clearly only when they lie between
Show Answer
Answer: True21. A person can see the objects lying between
Show Answer
Answer: Eye is the most developed sensory organ of a human being.22. Which is the most developed sensory organ of a human being?
Show Answer
Answer: Cornea causes the first refraction.23. Which part of the eye causes the first refraction?
Show Answer
Answer: Iris gives the characteristic colour of the eye.24. Which part of the eye gives the characteristic colour of the eye?
Show Answer
Answer: Ciliary muscles can only compress or squeeze the crystalline lens to decrease its focal length; they cannot pull the lens to have larger focal length. Thus the power of accommodation is caused by the action of ciliary muscles.25. What is the function of the ciliary muscles ?
Show Answer
Answer: Fovea is on the principal axis of the crystalline lens on the retina. Blind spot is a point on the retina where the optic nerve-fibres join together to form the optic nerve. 27. The size of the image increases as the object is brought nearer.26. Where are fovea and blind spot located in the eye ?
Show Answer
Answer: The distance of the watch from the eye must be such that its virtual image is formed at27. How does the size of the image on the retina change as an object is brought nearer and nearer to the eye?
Show Answer
Answer: Persistence of vision is the impression of an image on the retina for an instant after its withdrawal. Successive images produce an impression of continuity. This principle is used28. What is the distance at which a watch repairer holds the watch when he is wearing a magnifying glass, if his distance of most distinct vision is
Show Answer
Answer: The distance of the watch from the eye must be such that its virtual image is formed at29. What is meant by persistence of vision?
Show Answer
Answer: Persistence of vision is the impression of an image on the retina for an instant after its withdrawal. Successive images produce an impression of continuity. This principle is used in cinema.Short Answer Questions.
DIRECTIONS : Give answer in 2-3 sentences.
1. Can a beam of white light when passed through a hollow prism give spectrum ? Explain.
2. What is Cataract?
Show Answer
Answer: The crystalline lens of eye in older persons sometimes becomes milky and cloudy. This condition is called cataract. This causes partial or complete loss of vision.3. What is colour blindness?
Show Answer
Answer: Colour blindness is a defect of the eye due to which a person is unable to distinguish between certain colours, sometime even the primary colours.4. How do we see colours?
Show Answer
Answer: The retina of human eye has a large number of light sensitive cells. These cells are of two types i.e., rod cells and cone cells. The rod shaped cells show response towards the intensity of light rays, while the cone shaped cells respond to colour. It is these cone cells, which make it possible for a man to see different colours and distinguish between them.5. A person having a myopic eye uses a concave lens of focal length
Show Answer
Answer: Focal length,
Now, Power,
Thus, the power of this concave lens is -2 dioptres
6. What are fibre cables?
Show Answer
Answer: Fibre optic cables : Fibre optic cables consisting of thousand glass fibres transmit thousands of telephonic conversations at the same time over long distances.7. Why do different coloured rays deviate differently in the prism?
Show Answer
Answer: Different coloured rays deviate differently in the prism because the angle of refraction of different colours is different while passing through the glass prism.8. Why does a diamond sparkle?
Show Answer
Answer: The refractive index of diamond is very high. The faces of diamond are cut in such a way that the light entering into the diamond suffers total internal reflection repeatedly.9. Who do stars twinkle on a clear night?
Show Answer
Answer: The continuously changing atmosphere causes refraction which is able to cause variation in the light coming from a point-sized star, thus the stars appear to be twinkling.10. A person having the nearest distance of distinct yision of
Show Answer
Answer:
Now
11. A man who wears glasses of power 3 dioptre must hold a newspaper at least
Show Answer
Answer: As here
formula
or
i.e.
i.e., the lens shifts the object from
12. Why does it take some time to see objects in a dim room when you enter the room from bright sunlight outside?
Show Answer
Answer: In the bright sunlight, iris causes the pupil to become smaller so that only a small portion of light enters the eye and rods of the retina are also adjusted in the same way. But when a person enters into a dimly-lit room, each iris takes some time to increase the diameter of the pupil, so that more amount of light can enter the eyes to see the object clearly and rod cells of the retina also take some time to adjust themselves to get the picture of the object in the dim light.13. Does a single raindrop illuminated by sunlight disperse a spectrum of colours? Does a viewer see a spectrum from a single far away drop?
Show Answer
Answer: A single raindrop illuminated by sunlight disperse the light to produce seven colors of the spectrum.
A viewer cannot see a full spectrum from a single raindrop because the colours of the spectrum formed by a single raindrop are separated by a large distance. A viewer sees the colours of a continuous spectrum dispersed by different raindrops. Millions of drops produce the entire spectrum of visible light.
14. Two observers standing apart from one another do not see the “same” rainbow. Explain.
Show Answer
Answer: All the rain drops that disperse the light to form rainbow lie within a cone of semi vertical angle15. How is a rainbow similar to the halo sometimes sen around the moon on a frosty night? How are seen around the moon on a frosty night? How are rainbows and halos different?
Show Answer
Answer: Halos and seen around the moon are due to refraction of light by the crystals of ice in the atmosphere. Both rainbows and halos are seen in the form of arches.
The difference between rainbows and halos is that halos are formed due to refraction of light whereas rainbows are formed due to total internal reflection of light and refraction of light.
16. A 45 year old person is suffering from a defect in his vision due to which he uses spectacles of bi-focal lenses. (a) Which defect pe is suffering from?
(b) What is a bi-focal lens?
Show Answer
Answer: (a) The person is suffering from presbyopia.
(b) A bi-focal lens consists of both concave and convex lenses. The upper portion consists of a concave lens and the lower portion consists of a convex lens.
17. What is dark adaptation of the eye?
Show Answer
Answer: In a dark room or at very low level of illumination the supply of light sensitive chemicals in the rods of the retina increases to make the rods respond to that very low intensity of illumination; this takes half an hour to happen and this process is called dark adaptation.18. A person having short sight (near sight) unable to see clearly beyond
Show Answer
Answer: For distant vision, defect is short sight Focal length
For near vision,
Long Answer Questions:
DIRECTIONS : Give answer in four to five sentences.
1. Why does it take some time to see objects in a dim room when you enter the room from bright sunlight outside?
Show Answer
Answer: In the bright sunlight, iris causes the pupil to become smaller so that only a small portion of light enters the eye and rods of the retina are also adjusted in the same way. But when a person enters into a dimly-lit room, each iris takes some tome to increase the diameter of the pupil, so that more amount of light can enter the eyes to see the object clearly and rod cells of the retina also take some time to adjust themselves to get the picture of the object in the dim light.2. Explain the construction and working of a compound microscope with a ray diagram. Derive the expression for magnification when image is formed at infinity.
Show Answer
Answer: Objective, eye piece
Ray diagram, find the values of
3. Explain the formation of mirages.
Show Answer
Answer: Total internal reflection.4. A prism causes dispersion of white light while a rectangular glass block does not. Explain.
Show Answer
Answer: In a prism the refraction of light takes place at the two slant surfaces. The dispersion of white light occurs at the first surface of prism where its constituent colours are deviated through different angles. At the second surface, these split colours suffer only refraction and they get further separated. But in a rectangular glass block, the refraction of light takes place at the two parallel surfaces. At the first surface, although the white light splits into its constituent colours on refraction, but these split colours on suffering refraction at the second surface emerge out in form of a parallel beam, which give an impression of white light.5. How will you investigate the existence of the radiation beyond the red and violet extremes of the spectrum?
Show Answer
Answer: If a blackened bulb thermometer is moved from violet end towards the red end, first a steady rise in temperature is observed, but as the thermometer goes beyond the red end, there is rapid rise in temperature. This shows the existence of some kind of radiation producing the heating effect beyond the red end of the spectrum. If the radiations from the red end to the violet end are made to fall on the silver chloride solution, it almost remains unaffected beyond the violet end of the spectrum.6. When yellow paint and blue paint are mixed we get green colour. When yellow light and blue light are mixed, white light is obtained. Give reasons.
Show Answer
Answer: Yellow light is ‘made up’ of two of the primary colours, namely red and green. Hence, when this light is mixed with the light of the third primary colour, namely blue light, we get white light.
Yellow light + Blue light
The effect of mixing of two paints of different colours is not the same as that of mixing of two pure spectral lights. This is because each paint appears to have a colour that depends on the lights that it can reflect. Yellow paint is known to reflect red, green and yellow lights. Similarly blue paint reflects blue and green lights. Hence, when these two paints are mixed, the mixture can reflect only green light and thus appears green in colour.
7. Explain why in day light an object appears red when seen through a red glass and black when seen through a blue glass?
Show Answer
Answer: We will have these observations if the given object is able to reflect red light but is not able to reflect blue light. This would be possible if the object is either of red or of yellow (8. How would you show the presence of UV and IR rays in the spectrum?
Show Answer
Answer: If a blackened bulb thermometer is moved from violet end towards the red end, first a steady rise in temperature is observed, but as the thermometer goes beyond the red end, there is rapid rise in temperature. This shows existence of some kind of radiation producing the heating effect beyond the red end of the spectrum. If the radiations from the red end to the violet end are made to fall on the silver chloride solution, it almost remains unaffected beyond the violet end of the spectrum.2-EXERCISE
Multiple Choice Questions:
DIRECTIONS: This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
1. Angle of deviation (
(a)
(b)
(c)
(b)
Show Answer
Answer: (a)2. The human eye forms the image of an object at its
(a) cornea
(b) iris
(c) pupil
(b) retina
Show Answer
Answer: (d)3. The least distance of distinct vision for a young adult with normal vision is about
(a)
(b)
(c)
(b)
Show Answer
Answer: (c)4. The change in focal length of an eye lens is caused by the action of the
(a) pupil
(b) retina
(c) ciliary muscles
(b) iris
Show Answer
Answer: (c)5. Prism angle of a prism is
(a) 0.5
(b) 0.15
(c) 0.019
(b) 0.032
Show Answer
Answer: (c) Dispersive power of prism
but
Therefore
6. Prism angle and refractive index for a prism for a
(a)
(b)
(c)
(b)
Show Answer
Answer: (b)
7. Diameter of the moon is
(a)
(b)
(c)
(b)
Show Answer
Answer: (c)
Angle subtended by the moon at the objective
Thus angular diameter of the image
8. A telescope consisting of an objective of focal length
(a)
(b)
(c)
(b)
Show Answer
Answer: (b)
9. A near sighted person cannot see distinctly beyond
(a) +50
(b) -50
(c) +2
(b) -2
Show Answer
Answer: (d)10. The following one is not a primary colour
(a) Yellow
(b) Red
(c) Green
(b) Blue
Show Answer
Answer: (a)11. Fraunhofer lines in the sun’s spectrum are present because
(a) Vapours of certain elements present in the atmosphere absorb certain colours
(b) The temperature of the sun is very high
(c) The sun does emit certain light
(d) Certain elements present in the sun interfere
Show Answer
Answer: (d)12. When a mirror is rotated an angle the reflected ray moves through double that angle, the instrument based on the above principle is
(a) Periscope
(b) Odometer
(c) Refractometer
(d) Sextant
Show Answer
Answer: (d)13. Rainbow is caused due to
(a) Reflection of sun light air
(b) Dispersion of sun light from water drops
(c) Refraction of sun light from water drops
(d) Diffraction of sun rays from water drops
Show Answer
Answer: (b)14. In the visible spectrum the colour having the shortest wavelength is
(a) Green
(b) Red
(c) Violet
(d) Blue
Show Answer
Answer: (c)15. The splitting of white light into several colours on passing through a glass prism is due to
(a) refraction
(c) interference
(b) reflection
(d) diffraction
Show Answer
Answer: (a) Disperssion arises because of basic phenomenon refraction.16. At the moment dew formation starts on a cool night, the air
(a) Must loose all water vapour
(b) Must remain unsaturated
(c) Must get mixed up with some other vapour
(d) Must become saturated
Show Answer
Answer: (d)17. At sun rise or at sun set the sun appears to be reddish while at mid-day it looks white. This is because
(a) Scattering due to dust particles and air molecules causes this phenomenon
(b) The sun is cooler at sun rise or at sunset
(c) Refraction causes this phenomenon
(d) Diffraction sends red rays to the earth at these times.
Show Answer
Answer: (a)18. Sometimes blurred and less sharply defined images are formed. This defect is called
(a) Chromatic aberration
(b) Spherical aberration
(c) Blurred lens
(d) None of the above
Show Answer
Answer: (b)19. A person cannot see objects clearly which are nearer than
(a) Astigmatism
(b) Myopia
(c) Hypermetropia
(d) Presbyopia
Show Answer
Answer: (c)20. On entering a glass prism, sun rays are
(a) Deviated but not dispersed
(b) Deviated and dispersed
(c) Dispersed but not deviated
(d) Neither deviated nor dispersed
Show Answer
Answer: (b)21. A piece of cloth looks red in sun light. It is held in the blue portion of a solar spectrum, it will appear
(a) red
(b) black
(c) blue
(d) white
Show Answer
Answer: (b)22. The angle of minimum deviation of a ray of light of glass prism is greatest for the light of colour
(a) violet
(b) orange
(c) yellow
(d) red
Show Answer
Answer: (a)23. To get line spectrum, the substances are excited in their
(a) solid state
(b) molecular state
(c) gaseous state
(d) atomic state
Show Answer
Answer: (d)24. A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)

25. The frequency of light whose wavelength is
(a)
(b) 5000 cycles per second
(c)
(d)
Show Answer
Answer: (c)26. The pupil of the eye changes in size to adjust for
(a) objects at different distances
(b) objects of different sizes
(c) different colors
(d) different amounts of light
Show Answer
Answer: (d)27. To use a magnifying glass, the object should be placed
(a) as close to the lens as possible
(b) just within the lens’ focal point
(c) just beyond the focal point
(d) some distance beyond the focal point
Show Answer
Answer: (b)28. A camera employs a ………… lens to form .. images
(a) diverging …….. real
(b) diverging …….. virtual
(c) converging … real
(d) converging … virtual
Show Answer
Answer: (c)29. In the eye, the position of the image on the retina is adjusted by changing the
(a) position of the lens
(c) diameter of the pupil
(b) focal length of the lens
(d) length of the eyeball
Show Answer
Answer: (b)30. What power lens is needed to correct for nearsightedness where the uncorrected far point is
(a) +2.5 diopters
(b) -2.5 diopters
(c) +0.4 diopters
(d) -0.4 diopters
Show Answer
Answer: (d)31. What power lens is needed to correct for farsightedness where the uncorrected near point is
(a) + 3.6 diopters
(b) -3.6 diopters
(c) +0.28 diopters
(d) -0.28 diopters
Show Answer
Answer: (a)32. In a room, artificial rain is produced at one end and a strong source of white light is switched on at the other end. To observe the rainbow an observer must
(a) Look anywhere in the room
(b) Look towards the source
(c) Look towards the raindrops
(d) Look in a direction equally inclined to the source of raindrops
Show Answer
Answer: (c)33. For which of the following pairs the critical angle is smallest
(a) Water to air
(b) Glass to water
(c) Glass to air
(d) Glass to glass
Show Answer
Answer: (c)34. For which colour the critical angle is maximum in water-air system
(a) Red
(b) Violet
(c) Yellow
(d) It is same for all colours
Show Answer
Answer: (a)35. A direct vision spectrometer uses the phenomenon of
(a) Diffraction
(b) Interference without deviation
(c) Dispersion without deviation
(d) Deviation without dispersion
Show Answer
Answer: (c)36. Astigmatism can be corrected by
(a) Bifocal lenses
(b) Cylindrical lenses
(c) Concave lenses
(d) Planoconvex lenses
Show Answer
Answer: (b)37. For seeing a cricket match, we prefer binoculars to the terrestrial telescope, because
(a) Binoculars give three-dimensional view
(b) Terrestrial telescope gives inverted image
(c) To avoid chromatic aberration
(d) To have larger magnification
Show Answer
Answer: (a)38. The electromagnetic radiation of frequency
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)39. The convex lens is not used
(a) in camera
(b) as glasses to correct for short sight
(c) as glasses to correct for light sight
(d) all of the above
Show Answer
Answer: (b)40. When blue light is used in a thin convex lens then the focal length is found to be
(a) equal to
(b) less than
(c) greater than
(d) nothing can be predicted
Show Answer
Answer: (c)41. One of the refracting surfaces of a prism is silvered, and the angle of prism is A. It is found that a ray of light incident at an angle of incidence
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)42. A diver at a depth of
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)43. The refractive index of water is
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)44. Relation between critical angles of water and glass is
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)45. Critical angle for light going from medium (i) to (ii) is
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)46. If light travels a distance
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)47. Dispersion is the term used to describe
(a) the propagation of light in straight lines
(b) The splitting of a beam of light into component colours
(c) The bending of a beam of light when it strikes a mirror
(d) The change that takes place in white light after passage through red glass.
Show Answer
Answer: (b)48. In a glass prism
(a) Blue light is dispersed more than red light
(b) Red light is dispersed more than blue light
(c) Both red light and blue light are equally dispersed
(d) None of these
Show Answer
Answer: (a)49. Deviation
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)50. If for a given prism the angle of incidence is changed from
(a) Increases
(b) Decreases
(c) First decreases and then increases
(d) First increases and then decreases
Show Answer
Answer: (c)51. Consider telecommunication through optical fibres:
Which of the following statement is not true
(a) Optical fibres can be of graded refractive index
(b) Optical fibres have extremely low transmission loss
(c) Optical fibres are subject to electromagnetic interference from outside
(d) Optical fibres may have homogeneous core with a suitable cladding
Show Answer
Answer: (c)52. The refracting angle of a prism is
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)53. A ray is incident at an angle of incidence
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)54. An optician while testing the eyes finds the vision of a patient to be 6/12. By this he means that
(a) The person can read the letters of 6 inches from a distance of
(b) The person can read the letters of 12 inches from
(c) The person can read the letters of
(d) The focal length of eye lens had become half that of the normal eye
Show Answer
Answer: (c)55. A person cannot see objects clearly beyond
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)56. A long sighted person has a minimum distance of distinct vision of
(a) Concave lens of focal length
(b) Convex lens of focal length
(c) Convex lens of focal length
(d) Concave lens of focal length
Show Answer
Answer: (c)57. A long-sighted person cannot see objects clearly at a distance less than
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)58. In which of the following cases, is total internal reflection not possible
(a) A ray incident from water to glass
(b) A ray incident from glass to water
(c) A ray incident from glass to air
(d) A ray incident from water to air
Show Answer
Answer: (a)59. Critical angle of light passing from glass to air is maximum for
(a) violet
(b) blue
(c) yellow
(d) red
Show Answer
Answer: (d)60. A mirage occurs because
(a) The refractive index of atmosphere increases with height
(b) The refractive index of atmosphere decreases with height
(c) The hot ground acts like a mirror
(d) Refractive index remains constant with height
Show Answer
Answer: (a)61. A well cut diamond appears bright because
(a) Of reflection of light
(b) Of dispersion of light
(c) The total internal reflection
(d) Of refraction of light
Show Answer
Answer: (c)62. Twinkling of stafs is on account of
(a) Large distance of stars and storms in air
(b) Small size of stars
(c) Large size of stars
(d) Large distance of stars and fluctuations in the density of air.
Show Answer
Answer: (d)63. You are under the water in a clear lake looking at the surface and see the image of a fish due to total internal reflection. What is the minimum angle that the light leaving the fish makes with the normal to the surface of the lake?
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)64. A ray of light passing through a prism having
(a)
(b)
(c)
(d)
Show Answer
Answer: (d) i=2r65. White light is incident at an angle to the surface of a triangular piece of glass. Which color of light deviates most from its original path after leaving the glass?
(a) red
(b) orange
(c) green
(d) blue
Show Answer
Answer: (d)More than One Correct:
DIRECTIONS: This section contains multiple choice questions. Each question has 4 choices
1. The human eye can focus objects at different distances by adjusting the focal length of the eye lens. Choose those options which are not accountable for this happening.
(a) presbyopia
(b) accommodation
(c) near-sightedness
(d) far-sightedness
Show Answer
Answer: (a,c,d)2. The change in focal length of an eye lens is not caused by the action of the
(a) pupil
(b) retina
(c) ciliary muscles
(d) iris
Show Answer
Answer: (a,b,d)3. The following is/are a primary colour
(a) Yellow
(b) Red
(c) Green
(d) Blue
Show Answer
Answer: (b,c,d)4. When a mirror is rotated an angle the reflected ray moves through double that angle, the instruments which are not based on the above principle, are
(a) Periscope
(b) Odometer
(c) Refractometer
(d) Sextant
Show Answer
Answer: (a,b,c)5. A combination is made of two lenses of focal length
(a)
(b)
(c)
(d)
Show Answer
Answer: (a,b,c)6. In case of hypermetropia
(a) The image of near objects is formed in front of retina
(b) The image of near objects is formed behind the retina
(c) A concave lens should be used for correction
(d) A convex lens cannot be used for correction
Show Answer
Answer: (b)7. Astigmatism is / are
(a) Bifocal lenses
(b) Cylindrical lenses
(c) Concave lenses
(d) Planoconvex lenses
Show Answer
Answer: (a,c,d)8. The defect that may occur in a lens are
(a) spherical aberration and chromatic aberration
(b) coma and astigmation
(c) distortion
(d) none of the above
Show Answer
Answer: (a,b,c)9. Out of the following, which statements are correct
(a) Sunlight filtering through a tree often makes circular patches on the ground because sun is round
(b) A beam of white light passing through a hollow prism gives no spectrum
(c) The number of images observable between two parallel plane mirrors is infinite
(d) A virtual object placed between the pole and the principal focus of a convex mirror produces an image which is virtual, diminished and upright.
Show Answer
Answer: (b,c)10. Due to refraction of light in atmosphere
(a) Stars appear to twinkle
(b) The sun appears to be oval in morning and evening
(c) The period of visibility of the sun is increased
(d) The phenomena of mirage and looming take place
Show Answer
Answer: (all)11. White light is incident on an equilateral prism. In the position of minimum deviation
(a) Angle of incidence is equal to angle of emergence
(b) The ray inside the prism is parallel to its base
(c) The angle of refraction inside the prism is equal to the angle of prism
(d) The dispersion of all colours is same
Show Answer
Answer: (a,b)12. Out of the following, select the correct statements
(a) Refractive index varies inversely as the fourth power of the wavelength of light.
(b) When the moon is near the horizon, it appears bigger. This is due to optical illusion.
(c) The colour of light which travels with the maximum speed in glass is red.
(d) If sun is shining brightly in one part of the sky after rain, two rainbows are usually observed.
Show Answer
Answer: (b,c,d)13. In which of the following cases, is total internal reflection possible
(a) A ray incident from water to glass
(b) A ray incident from glass to water
(c) A ray incident from glass to air
(d) A ray incident from water to air
Show Answer
Answer: (b,c,d)14. The optical phenomenon which Newton’s theory of light failed to explain is
(a) interference
(b) polarization
(c) diffraction
(d) none of the above three
Show Answer
Answer: (a,b,c)15. A convex mirror is not used
(a) by a dentist
(b) for shaving
(c) as a rear view mirror in vehicles
(d) as a light reflector for obtaining a parallel beam of light.
Show Answer
Answer: (a,b,d)16. Spectrometer is used to measure
(a) angle of prism
(b) refractive index of material of a prism
(c) the dispersion
(d) none of the above
Fill in the Passage:
DIRECTIONS : Complete the following passage(s) with an appropriate word/term to be filled in the blank spaces.
1.

The figure shown demonstrates ……..1…… It is the in ability to see …..2……… objects. This defect occurs due to slight elongation of the eye ball. A a result the distance between eye lens and retina is greater (focal length of lens decreases) and the image is formed …….3…….. the retina. This defect can be corrected using a …….4…… lens of suitable focal length.
Show Answer
Answer:
(1) myopia
(2) distant
(3) infront of
(4) concave
2.
When light passes from one medium to other, it bends.
Suppose a ray of light is made incident at a certain angle of incidence ’
Show Answer
Answer:
(1) critical
(2)total internal refrection
(3)denser
(4)rarer
(5)mirage
Passage Based Questions:
DIRECTIONS : Study the given paragraph(s) and answer the following questions.
Passage-I
Image formation by thin lenses follows the reaction
We know that for real objects, a concave lens forms a virtual image whereas a convex lens forms an image that could be real or virtual. Consider a lens and a small object placed at right-angles to its optic axis at a position (1) such that the image formed is six times magnified. The object is now shifted away from the lens to another position (2) at a distance
1. Distance of positions (1) and (2) of the object from the optic centre are, respectively
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)2. Distance of position (3)
(3) from optic centre is
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)3. Focal length of lens is
(b)
(a)
(d)
(c)
Show Answer
Answer: (a)
Passage-II
The ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained the curvature of lens increases (that means radius of curvature decreases) and focal length decreases. For a clear vision the image must be on retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye-lens. It is about
A person can theoretically have clear vision of objects situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown-up person minimum distance of object should be around
A person suffering for eye defects uses spectacles (Eye glass). The function of lens of spectacles is to form the image of the objects within the range in which person can see clearly. The image of the spectacle-lens becomes object for eye-lens and whose image is formed on retina.
The number of spectacle-lens used for the remedy of eye defect is decided by the power of the lens required and the number of spectacle-lens is equal to the numerical value of the power of lens with sign. For example power of lens required is
For all the calculations required you can use the lens formula and lens maker’s formula. Assume that the eye lens is equiconvex lens. Neglect the distance between eye lens and the spectacle lens.
1. Minimum focal length of eye lens of a normal person is
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)2. Maximum focal length of eye lens of normal person is
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)3. A nearsighted man can clearly see object only upto a distance of
(a) +1
(b) -1
(c) +3
(d) -3
Show Answer
Answer: (b)
Here
For
For near sighted man lens should make the image of the object within
For lens
Passage-III
All objects referred to the subsequent problems lie on the principal axis.
1. If light is incident on surface
(a) real for a real object
(b) virtual for a real object
(c) real for a virtual object
(d) virtual for a virtual objec
Show Answer
Answer: (b)2. In above question if the object is real, then the final imag formed after two refractions
(a) may be real
(c) must be virtual
(b) may be virtual
(d) Both (a) and (b)
Show Answer
Answer: (d)3. If light is incident on surface 2 from right then which of th following is true for image formed after a single refraction
(a) Rcal object will result in a rcal image
(b) Virtual object will result in a virtual image
(c) real object will result in a virtual in a virtual image
(d) Virtual object will result in a real image
Show Answer
Answer: (d)
i.e. for real object image is always virtual.
Consider object on left side of spherical surface seperating two media. If real object is in rarer media i.e.
Then,
Hence image shall be virtual for a real object lying on concave side with rare media.
If real object is in denser media i.e.,
or
and image is virtual if
From statements 1, 2 and 3 we can easily conclude the answers.
Assertion & Reason
DIRECTIONS : Each of these questions contains an Assertion followed by reason. Read them carefully and answer the question on the basis of following options. You have to select the one that best describes the two statements.
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
1.Assertion : There exists two angles of incidence for the same magnitude of deviation (except minimum deviation) by a prism kept in air.
Reason : In a prism kept in air, a ray is incident on first surface and emerges out of second surface. Now if another ray is incident on second surface (of prism) along the previous emergent ray, then this ray emerges out of first surface along the previous incident ray. This particle is called principle of reversibility of light.
Show Answer
Answer: (a) Reason is correct explanation of Assertion.2.Assertion : Keeping a point object fixed, if a plane mirror is moved, the image will also move.
Reason : In case of plane mirror, distance of object and its image is equal from any point on the mirror.
Show Answer
Answer: (d) If the mirror is shifted parallel to itself such that the velocity of the mirror is parallel to its surface, the image shall not shift. Hence statement 1 is false.3.Assertion : The formula connecting
Reason : Laws of reflection are strictly valid for plane surfaces, but not for large spherical surfaces.
Show Answer
Answer: (c) Assertion : The mirror (spherical) formula
Reason : Laws of mirror are valid for plane as well as large spherical surfaces.
Therefore, statement 2 is wrong.
4.Assertion : A lens having large aperture will produce image of a point source not as a point but as a diffused bright spot. This error of optical system is called spherical aberration.
Reason : Pâraxial rays are focused at a different point compared to marginal rays.
Show Answer
Answer: (a) The formula5.Assertion : A ray is incident from outside on a glass sphere surrounded by air as shown. This ray may suffer total internal reflection at second interface.

Reason : For a ray going from a denser to a rarer medium, the ray may suffer total internal reflection.
Show Answer
Answer: (d) From symmetry the ray shall not suffer TIR at second interface, because the angle of incidence at first interface equals to angle of emergence at second interface. Hence Assertion is false.Multiple Matching Questions
DIRECTIONS : Following question has four statements
1.
| Column I | Column II |
|---|---|
| (A) Spectrometer | (p) refraction |
| (B) Mirrage | (q) deviation without dispersion |
| (C) Hollow prism | (r) to measure angle of prism |
| (D) Glass slab | (s) to measure the dispersion Column II |
Show Answer
Answer: (A)2.
| Column I | Column II |
|---|---|
| (A) Myopia | (p) convex lens |
| (B) Hyperopia | (q) concave lens |
| (C) Vivtual image | (r) plane mirror |
| (D) Magnification always one | (s) convex mirror |
Show Answer
Answer: (A)3.
| Column I | Column II |
|---|---|
| (A) Plane mirror | (p) Primary colours |
| (B) Convex lens | (q) |
| (C) Spectroscope | (r) Incoherent scattering |
| (D) Atmospheric scattering of light | (s) Magnification always one |
| (E) RBG | (t). Refraction |
| (F) Optic fibre | (u) Burglar alarm |
| (G) Solid angle in a sphere | (v) Virtual and magnified image |
| (H) Photo electric effect | (w) Blue colour of effect the sky |
| (I) Raman effect | (x) Observing and studying spectrum |
| (J) Mirrage | (y) Total internal reflection |
Show Answer
Answer: (A)HOTS Subjective Questions:
DIRECTIONS : Answer the following questions.
1. A person with a myopic eye cannot see objects beyond
Show Answer
Answer: In normal eye, the far point is infinity. The lens used should be such that an object at infinity forms virtual image at
Now,
We know
or
Power,
A concave (or divergent) lens of focal length
2. The far point of a myopic person is
Show Answer
Answer: The far point of this myopic person is
Using lens formula,
or
or
The negative (-) sign indicates that the lens is concave.
Now, Power
The concave lens of power
3. A person cannot see objects nearer than
Show Answer
Answer: The defect of the vision is hypermetropia. The formula used
is
Given,
Power of the lens
4. A person can see clearly only up to 3 metres. Prescribe a lens for spectacles so that he can see clearly up to 12 metres. Defect is myopia.
Show Answer
Answer: Here,
A concave lens of focal length
5. The far point of a myopic person is
Show Answer
Answer: A myopic person needs a concave lens for the correction of his eyesight.
His
So,
6. A person with a defective eye-division is unable to see the objects nearer than
Show Answer
Answer: This person is hypermetropic
So, his
Focal length of corrective lens :
- sign shows that he needs a convex lens of focal length
7. A ray of light is travelling in water medium falls on the water-air interface at an angle of
Show Answer
Answer: From the relationship between critical angle
In the case of water,
so,
But, the angle of resistance is
8. Complete the ray diagram (figure) to show the nature of light produced on the screen.

Show Answer
Answer: The light on the screen is white with faint colour at the edges.
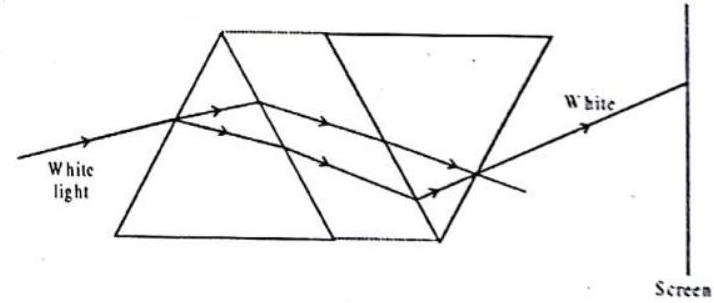
This is because the dispersion caused by the first prism is compensated by the second prism. The emergent beam is parallel to the incident beam. The two prisms together behave like a glass block with parallel sides.
9. Study the figure given below and answer the questions that follow.
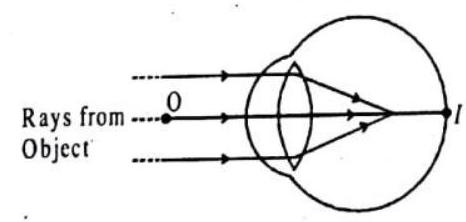
(a) Which defect of vision has been shown in the figure?
(b) What do the points
(c) Which lens is used to correct this defect?
(d) Redraw the figure with the corrective lens.
Show Answer
Answer: (a) Myopia or near-sightedness has been shown in the figure.
(b) The points
(c) A concave lens of proper focal length is used to correct this defect.
(d)
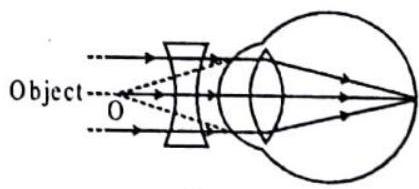
Correctness for myopia
10. In the diagram given below, a defective eye has been corrected. Study the diagram and answer the questions that follow.
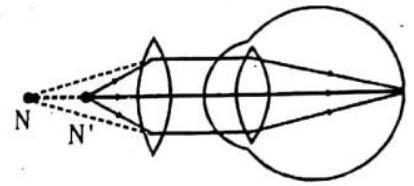
(a) Name the defect which has been corrected.
(b) Name the point
(c) Why a convex lens, instead of a concave lens, has been used?
(d) Redraw the figure of the defective eye without the corrective lens.
Show Answer
Answer: (a) Hypermetropia or long-sightedness has been corrected.
(b) The point represent the near point of the hypermetropic eye.
(c) In a hypermetropic eye, the rays of light coming from a near object don’t converge in appropriate way so as to focus at retina but they get focussed beyond the retina. When a convex lens is used before the eye, extra focussing power is provided and the rays are focussed at the retina.
If a concave lens, on the other hand, will be used then it will diverge the rays and they will get focussed at a point more beyond the retina.
(d)
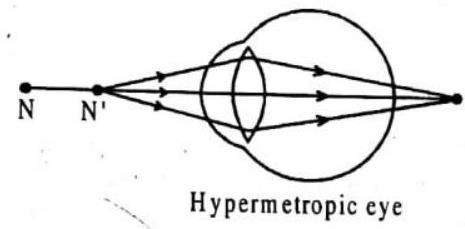
11. The diagram given below shows the mechanism how stars twinkle due to atmospheric refraction. But there is something wrong with the drawing. Study the diagram carefully and predict the wrongness with it. Also redraw the correct diagram.
Show Answer
Answer: Twinkling of stars takes place as a result of atmospheric refraction. The starlight, on entering the earth’s atmosphere, undergoes refraction at its different layers. The refractive index of the atmosphere gradually increases downwards. But in the diagram it has been shown to decrease. This is what is wrong with the diagram.
The correct diagram is given below.
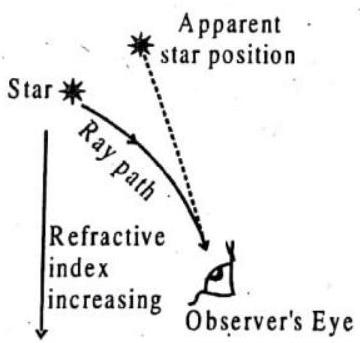
12. A watch-repairer has his near point at
Show Answer
Answer:
13. One eye is sufficient to form the image of an object. What is the advantage of having two eyes?
Show Answer
Answer: The area seen clearly with one eye is comparatively less than that seen with two eyes. Further two eyes give beter judgement of distances of distant objects than one eye only. Also, left eye sees more portion of the right side of the object and the right eye sees more of the left side. Thus, two eyes do not form exactly similar images and the fusion of these two dissimilar images in the brain gives the three dimensional or the stereoscopic vision.14. Although each eye perceives separated image, we do not see to thing in double with both eyes open. Why?
Show Answer
Answer: The axes of the two eyes are directed towards the same object. Therefore there appears to be only one object. The two separate images formed by the two eyes get fused in the brain. The optic nerves lead to the same point in the brain producing only one sensation. Hence, we see only one object with two eyes.15.
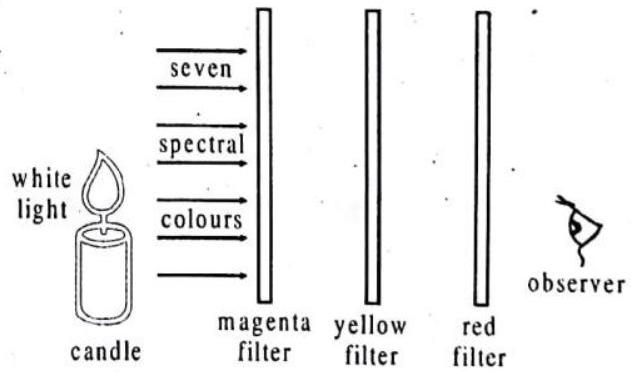
In the above diagram, extend the lines to show which of the seven spectral colours would pass through the magenta filter, the yellow filter and finally the red filter. Label the colour of each line.
Show Answer
Answer: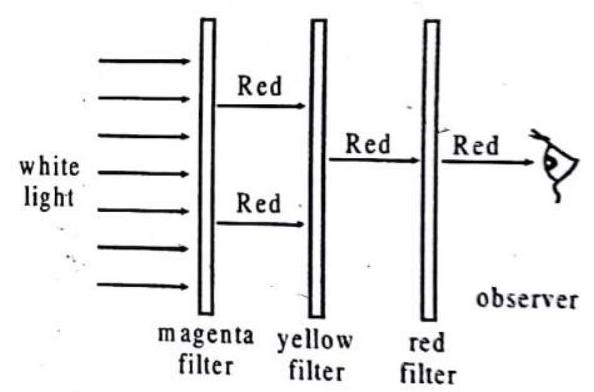
16. How is presbyopia different from hypermetropia ?
Show Answer
Answer: Presbyopia is a defect only for near vision due to insufficient power of accommodation arising out of the inability of the ciliary muscles to squeeze the crystalline lens beyond 3 particular power i.e., to the full extent as in a normal defectless eye, so the near point is beyond
In a hypermetropic eye the crystalline lens has berome kss powerful (in the relaxed condition) and so it has to exercise power of accommodation to see infinitely distant objects also straining the ciliary muscles. Hypermetropia is the defect for near vision.










