11.1 Surface Area of a Right Circular Cone

We have already studied the surface areas of cube, cuboid and cylinder. We will now study the surface area of cone. So far, we have been generating solids by stacking up congruent figures. Incidentally, such figures are called prisms. Now let us look at another kind of solid which is not a prism (These kinds of solids are called pyramids.). Let us see how we can generate them.

Activity : Cut out a right-angled triangle $\mathrm{ABC}$ right angled at $\mathrm{B}$. Paste a long thick string along one of the perpendicular sides say AB of the triangle [see Fig. 11.1(a)]. Hold the string with your hands on either sides of the triangle and rotate the triangle about the string a number of times. What happens? Do you recognize the shape that the triangle is forming as it rotates around the string [see Fig. 11.1(b)]? Does it remind you of the time you had eaten an ice-cream heaped into a container of that shape [see Fig. 11.1(c) and (d)]?

Fig. 11.1

This is called a right circular cone. In Fig. 11.1(c) of the right circular cone, the point $\mathrm{A}$ is called the vertex, $\mathrm{AB}$ is called the height, $\mathrm{BC}$ is called the radius and $AC$ is called the slant height of the cone. Here $B$ will be the centre of circular base of the cone. The height, radius and slant height of the cone are usually denoted by $h,r$ and $l$ respectively. Once again, let us see what kind of cone we can not call a right circular cone. Here, you are (see Fig. 11.2)! What you see in these figures are not right circular cones; because in (a), the line joining its vertex to the centre of its base is not at right angle to the base, and in (b) the base is not circular.

Fig. 11.2

As in the case of cylinder, since we will be studying only about right circular cones, remember that by ‘cone’ in this chapter, we shall mean a ‘right circular cone.’

Activity : (i) Cut out a neatly made paper cone that does not have any overlapped paper, straight along its side, and opening it out, to see the shape of paper that forms the surface of the cone. (The line along which you cut the cone is the slant height of the cone which is represented by $l$ ). It looks like a part of a round cake.

(ii) If you now bring the sides marked A and B at the tips together, you can see that the curved portion of Fig. 11.3 (c) will form the circular base of the cone.

Fig. 11.3

(iii) If the paper like the one in Fig. 11.3 (c) is now cut into hundreds of little pieces, along the lines drawn from the point $\mathrm{O}$, each cut portion is almost a small triangle, whose height is the slant height $l$ of the cone.

(iv) Now the area of each triangle $=\frac{1}{2}\times$ base of each triangle $\times l$.

So, area of the entire piece of paper

$$\begin{array}{rl}& =\text{ sum of the areas of all the triangles }\\ & =\frac{1}{2}{b}_{1}l+\frac{1}{2}{b}_{2}l+\frac{1}{2}{b}_{3}l+\cdots =\frac{1}{2}l(b_1+b_2+b_3+\cdots )\\ & =\frac{1}{2}\times l\times \text{ length of entire curved boundary of Fig. 11.3(c) }\end{array}$$

$$(as $b_1+b_2+b_3+\dots$ makes up the curved portion of the figure)

But the curved portion of the figure makes up the perimeter of the base of the cone and the circumference of the base of the cone $=2\pi r$, where $r$ is the base radius of the cone.

So, Curved Surface Area of a Cone $=\frac{1}{2}\times l\times 2\pi r=\pi rl$

where $r$ is its base radius and $l$ its slant height.

Note that $l^2=r^2+h^2$ (as can be seen from Fig. 11.4), by applying Pythagoras Theorem. Here $h$ is the height of the cone.

Therefore, $l=\sqrt{r^2+h^2}$

Fig. 11.4

Now if the base of the cone is to be closed, then a circular piece of paper of radius $r$ is also required whose area is $\pi r^2$.

So, Total Surface Area of a Cone $=\pi rl+\pi r^2=\pi r(l+r)$

Example 1 : Find the curved surface area of a right circular cone whose slant height is $10\mathrm{cm}$ and base radius is $7\mathrm{cm}$.

Solution : Curved surface area $=\pi rl$

$$\begin{array}{rl}& =\frac{22}{7}\times 7\times 10{\mathrm{cm}}^2\\ & =220{\mathrm{cm}}^2\end{array}$$

Example 2 : The height of a cone is $16\mathrm{cm}$ and its base radius is $12\mathrm{cm}$. Find the curved surface area and the total surface area of the cone (Use $\pi =3.14$ ).

Solution : Here, $h=16\mathrm{cm}$ and $r=12\mathrm{cm}$.

So, from $l^2=h^2+r^2$, we have

$$l=\sqrt{{16}^2+{12}^2}\mathrm{cm}=20\mathrm{cm}$$

So, curved surface area $=\pi rl$

$$\begin{array}{rl}& =3.14\times 12\times 20{\mathrm{cm}}^2\\ & =753.6{\mathrm{cm}}^2\end{array}$$

Further, total surface area $=\pi rl+\pi r^2$

$$\begin{array}{rl}& =(753.6+3.14\times 12\times 12){\mathrm{cm}}^2\\ & =(753.6+452.16){\mathrm{cm}}^2\\ & =1205.76{\mathrm{cm}}^2\end{array}$$

Example 3 : A corn cob (see Fig. 11.5), shaped somewhat like a cone, has the radius of its broadest end as $2.1\mathrm{cm}$ and length (height) as $20\mathrm{cm}$. If each $1{\mathrm{cm}}^2$ of the surface of the cob carries an average of four grains, find how many grains you would find on the entire cob.

Fig. 11.5

Solution : Since the grains of corn are found only on the curved surface of the corn cob, we would need to know the curved surface area of the corn cob to find the total number of grains on it. In this question, we are given the height of the cone, so we need to find its slant height.

Here, $l=\sqrt{r^2+h^2}=\sqrt{(2.1{)}^2+{20}^2}\mathrm{cm}$

$$=\sqrt{404.41}\mathrm{cm}=20.11\mathrm{cm}$$

Therefore, the curved surface area of the corn cob $=\pi rl$

$$=\frac{22}{7}\times 2.1\times 20.11{\mathrm{cm}}^2=132.726{\mathrm{cm}}^2=132.73{\mathrm{cm}}^2\text{ (approx.) }$$

Number of grains of corn on $1{\mathrm{cm}}^2$ of the surface of the corn cob $=4$

Therefore, number of grains on the entire curved surface of the cob

$$=132.73\times 4=530.92=531\text{ (approx.) }$$

So, there would be approximately 531 grains of corn on the cob.

EXERCISE 11.1

$$\text{ Assume }\pi =\frac{22}{7}\text{, unless stated otherwise. }$$

1. Diameter of the base of a cone is $10.5\mathrm{cm}$ and its slant height is $10\mathrm{cm}$. Find its curved surface area.

2. Find the total surface area of a cone, if its slant height is $21\mathrm{m}$ and diameter of its base is $24\mathrm{m}$.

3. Curved surface area of a cone is $308{\mathrm{cm}}^2$ and its slant height is $14\mathrm{cm}$. Find (i) radius of the base and (ii) total surface area of the cone.

4. A conical tent is $10\mathrm{m}$ high and the radius of its base is $24\mathrm{m}$. Find

(i) slant height of the tent.

(ii) cost of the canvas required to make the tent, if the cost of $1{\mathrm{m}}^2$ canvas is ₹ 70 .

Show Answer

Solution

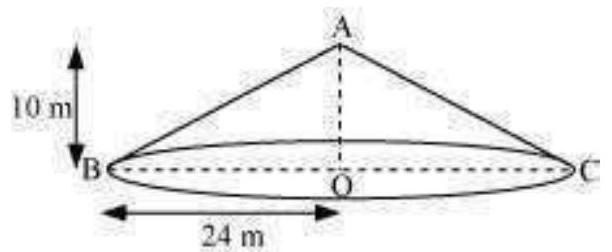
(i) Let $ABC$ be a conical tent.

Height ( $h$ ) of conical tent $=10m$

Radius ( $r$ ) of conical tent $=24m$

Let the slant height of the tent be I.

In $\mathrm{△}ABO,A{B}^2=A{O}^2+$

$B{O}^2$

$\begin{array}{rl}& I^2=h^2+r^2\\ & =(10m{)}^2+(24m{)}^2\\ & =676m^2\\ & \therefore I=26m\end{array}$

Therefore, the slant height of the tent is $26m$.

(ii) CSA of tent $=\pi rl$

$\begin{array}{rl}& =(\frac{22}{7}\times 24\times 26)m^2\\ & =\frac{13728}{7}{m}^2\end{array}$

Cost of $1m^2$ canvas $=$ Rs 70

Cost of 7 canvas $=$

$\frac{13728}{7}{m}^{2}Rs(\frac{13728}{7}\times 70)$

$=$ Rs 137280

Therefore, the cost of the canvas required to make such a tent is Rs 137280 .

5. What length of tarpaulin $3\mathrm{m}$ wide will be required to make conical tent of height $8\mathrm{m}$ and base radius $6\mathrm{m}$ ? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately $20\mathrm{cm}$ (Use $\pi =3.14$ ).

6. The slant height and base diameter of a conical tomb are $25\mathrm{m}$ and $14\mathrm{m}$ respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per $100{\mathrm{m}}^2$.

7. A joker’s cap is in the form of a right circular cone of base radius $7\mathrm{cm}$ and height $24\mathrm{cm}$. Find the area of the sheet required to make 10 such caps.

8. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of $40\mathrm{cm}$ and height $1\mathrm{m}$. If the outer side of each of the cones is to be painted and the cost of painting is ₹ 12 per ${\mathrm{m}}^2$, what will be the cost of painting all these cones? (Use $\pi =3.14$ and take $\sqrt{1.04}=1.02)$

11.2 Surface Area of a Sphere

What is a sphere? Is it the same as a circle? Can you draw a circle on a paper? Yes, you can, because a circle is a plane closed figure whose every point lies at a constant distance (called radius) from a fixed point, which is called the centre of the circle. Now if you paste a string along a diameter of a circular disc and rotate it as you had rotated the triangle in the previous section, you see a new solid (see Fig 11.6). What does it resemble? A ball? Yes. It is called a sphere.

Fig. 11.6

Can you guess what happens to the centre of the circle, when it forms a sphere on rotation? Of course, it becomes the centre of the sphere. So, a sphere is a three dimensional figure (solid figure), which is made up of all points in the space, which lie at a constant distance called the radius, from a fixed point called the centre of the sphere.

Note : A sphere is like the surface of a ball. The word solid sphere is used for the solid whose surface is a sphere.

Activity : Have you ever played with a top or have you at least watched someone play with one? You must be aware of how a string is wound around it. Now, let us take a rubber ball and drive a nail into it. Taking support of the nail, let us wind a string around the ball. When you have reached the ‘fullest’ part of the ball, use pins to keep the string in place, and continue to wind the string around the remaining part of the ball, till you have completely covered the ball [see Fig. 11.7(a)]. Mark the starting and finishing points on the string, and slowly unwind the string from the surface of the ball.

Now, ask your teacher to help you in measuring the diameter of the ball, from which you easily get its radius. Then on a sheet of paper, draw four circles with radius equal to the radius of the ball. Start filling the circles one by one, with the string you had wound around the ball [see Fig. 11.7(b)].

Fig. 11.7

What have you achieved in all this?

The string, which had completely covered the surface area of the sphere, has been used to completely fill the regions of four circles, all of the same radius as of the sphere.

So, what does that mean? This suggests that the surface area of a sphere of radius $r$ $=4$ times the area of a circle of radius $r=4\times \left(\pi r^2\right)$

So,$$Surface Area of a Sphere $=4\pi r^2$

where $r$ is the radius of the sphere.

How many faces do you see in the surface of a sphere? There is only one, which is curved.

Now, let us take a solid sphere, and slice it exactly ’through the middle’ with a plane that passes through its centre. What happens to the sphere?

Yes, it gets divided into two equal parts (see Fig. 11.8)! What will each half be called? It is called a hemisphere. (Because ‘hemi’ also means ‘half’)

Fig. 11.8

And what about the surface of a hemisphere? How many faces does it have?

Two! There is a curved face and a flat face (base).

The curved surface area of a hemisphere is half the surface area of the sphere, which is $\frac{1}{2}$ of $4\pi r^2$.

Therefore, Curved Surface Area of a Hemisphere $=\mathbf{2}\mathit{\pi }{r}^2$

where $r$ is the radius of the sphere of which the hemisphere is a part.

Now taking the two faces of a hemisphere, its surface area $2\pi r^2+\pi r^2$

So, Total Surface Area of a Hemisphere $=3\pi r^2$

Example 4 : Find the surface area of a sphere of radius $7\mathrm{cm}$.

Solution : The surface area of a sphere of radius $7\mathrm{cm}$ would be

$$4\pi r^2=4\times \frac{22}{7}\times 7\times 7{\mathrm{cm}}^2=616{\mathrm{cm}}^2$$

Example 5 : Find (i) the curved surface area and (ii) the total surface area of a hemisphere of radius $21\mathrm{cm}$.

Solution : The curved surface area of a hemisphere of radius $21\mathrm{cm}$ would be

$$=2\pi r^2=2\times \frac{22}{7}\times 21\times 21{\mathrm{cm}}^2=2772{\mathrm{cm}}^2$$

(ii) the total surface area of the hemisphere would be

$$3\pi r^2=3\times \frac{22}{7}\times 21\times 21{\mathrm{cm}}^2=4158{\mathrm{cm}}^2$$

Example 6 : The hollow sphere, in which the circus motorcyclist performs his stunts, has a diameter of $7\mathrm{m}$. Find the area available to the motorcyclist for riding.

Solution : Diameter of the sphere $=7\mathrm{m}$. Therefore, radius is $3.5\mathrm{m}$. So, the riding space available for the motorcyclist is the surface area of the ‘sphere’ which is given by

$$\begin{array}{rl}4\pi r^2& =4\times \frac{22}{7}\times 3.5\times 3.5{\mathrm{m}}^2\\ & =154{\mathrm{m}}^2\end{array}$$

Example 7 : A hemispherical dome of a building needs to be painted (see Fig. 11.9). If the circumference of the base of the dome is $17.6\mathrm{m}$, find the cost of painting it, given the cost of painting is ₹ 5 per $100{\mathrm{cm}}^2$.

Fig. 11.9

Solution : Since only the rounded surface of the dome is to be painted, we would need to find the curved surface area of the hemisphere to know the extent of painting that needs to be done. Now, circumference of the dome $=17.6\mathrm{m}$. Therefore, $17.6=2\pi r$.

So, the radius of the dome $=17.6\times \frac{7}{2\times 22}\mathrm{m}=2.8\mathrm{m}$

The curved surface area of the dome $=2\pi r^2$

$$\begin{array}{rl}& =2\times \frac{22}{7}\times 2.8\times 2.8{\mathrm{m}}^2\\ & =49.28{\mathrm{m}}^2\end{array}$$

Now, cost of painting $100{\mathrm{cm}}^2$ is ₹ 5.

So, cost of painting $1{\mathrm{m}}^2$=₹ 500

Therefore, cost of painting the whole dome =₹ 500 $\times 49.28$ = ₹ 24640

EXERCISE 11.2

$\text{ Assume }\pi =\frac{22}{7}\text{, unless stated otherwise. }$

1. Find the surface area of a sphere of radius:

(i) $10.5\mathrm{cm}$

(ii) $5.6\mathrm{cm}$

(iii) $14\mathrm{cm}$

2. Find the surface area of a sphere of diameter:

(i) $14\mathrm{cm}$

(ii) $21\mathrm{cm}$

(iii) $3.5\mathrm{m}$

3. Find the total surface area of a hemisphere of radius $10\mathrm{cm}$. (Use $\pi =3.14$ )

Show Answer

Solution

Radius ( $r$ ) of hemisphere $=10cm$

Total surface area of hemisphere $=$ CSA of hemisphere + Area of circular end of hemisphere

$\begin{array}{rl}& =2\pi r^2+\pi r^2\\ & =3\pi r^2\\ & =[3\times 3.14\times (10{)}^2]c{m}^2\\ & =942c{m}^2\end{array}$

Therefore, the total surface area of such a hemisphere is $942c{m}^2$.

4. The radius of a spherical balloon increases from $7\mathrm{cm}$ to $14\mathrm{cm}$ as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.

5. A hemispherical bowl made of brass has inner diameter $10.5\mathrm{cm}$. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per $100{\mathrm{cm}}^2$.

6. Find the radius of a sphere whose surface area is $154{\mathrm{cm}}^2$.

7. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.

8. A hemispherical bowl is made of steel, $0.25\mathrm{cm}$ thick. The inner radius of the bowl is $5\mathrm{cm}$. Find the outer curved surface area of the bowl.

9. A right circular cylinder just encloses a sphere of radius $r$ (see Fig. 11.10). Find

(i) surface area of the sphere,

(ii) curved surface area of the cylinder,

(iii) ratio of the areas obtained in (i) and (ii).

Fig. 11.10

Show Answer

Solution

(i) Surface area of sphere $=4\pi r^2$

(ii) Height of cylinder $=r+r=2r$

Radius of cylinder $=r$

CSA of cylinder $=2nrh$

$=2\pi r(2r)$

$=4\mathrm{\Gamma }{r}^2$

(iii)

Required ratio $=\frac{\text{ Surface area of sphere }}{\text{ CSA of cylinder }}$

$=\frac{4\pi r^2}{4\pi r^2}$

$=\frac{1}{1}$

Therefore, the ratio between these two surface areas is $1:1$.

11.3 Volume of a Right Circular Cone

In earlier classes we have studied the volumes of cube, cuboid and cylinder

In Fig 11.11, can you see that there is a right circular cylinder and a right circular cone of the same base radius and the same height?

Fig. 11.11

Activity : Try to make a hollow cylinder and a hollow cone like this with the same base radius and the same height (see Fig. 11.11). Then, we can try out an experiment that will help us, to see practically what the volume of a right circular cone would be!

Fig. 11.12

So, let us start like this.

Fill the cone up to the brim with sand once, and empty it into the cylinder. We find that it fills up only a part of the cylinder [see Fig. 11.12(a)].

When we fill up the cone again to the brim, and empty it into the cylinder, we see that the cylinder is still not full [see Fig. 11.12(b)].

When the cone is filled up for the third time, and emptied into the cylinder, it can be seen that the cylinder is also full to the brim [see Fig. 11.12(c)].

With this, we can safely come to the conclusion that three times the volume of a cone, makes up the volume of a cylinder, which has the same base radius and the same height as the cone, which means that the volume of the cone is one-third the volume of the cylinder.

So, $\text{ Volume of a Cone }=\frac{1}{3}\pi r^{2}h$

where $r$ is the base radius and $h$ is the height of the cone.

Example 8 : The height and the slant height of a cone are $21\mathrm{cm}$ and $28\mathrm{cm}$ respectively. Find the volume of the cone.

Solution : From $l^2=r^2+h^2$, we have

$$r=\sqrt{l^2-h^2}=\sqrt{{28}^2-{21}^2}\mathrm{cm}=7\sqrt{7}\mathrm{cm}$$

So, volume of the cone $=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\times \frac{22}{7}\times 7\sqrt{7}\times 7\sqrt{7}\times 21{\mathrm{cm}}^3$

$=7546{\mathrm{cm}}^3$

Example 9 : Monica has a piece of canvas whose area is $551{\mathrm{m}}^2$. She uses it to have a conical tent made, with a base radius of $7\mathrm{m}$. Assuming that all the stitching margins and the wastage incurred while cutting, amounts to approximately $1{\mathrm{m}}^2$, find the volume of the tent that can be made with it.

Solution : Since the area of the canvas $=551{\mathrm{m}}^2$ and area of the canvas lost in wastage is $1{\mathrm{m}}^2$, therefore the area of canvas available for making the tent is $(551-1){\mathrm{m}}^2=550{\mathrm{m}}^2$.

Now, the surface area of the tent $=550{\mathrm{m}}^2$ and the required base radius of the conical tent $=7\mathrm{m}$

Note that a tent has only a curved surface (the floor of a tent is not covered by canvas!!).

Therefore, curved surface area of tent $=550{\mathrm{m}}^2$.

That is,$\pi rl=550$

or, $\frac{22}{7}\times 7\times l=550$

or, $l=3\frac{550}{22}\mathrm{m}=25\mathrm{m}$

Now,$l^2=r^2+h^2$

$$\begin{array}{rl}\text{Therefore,}h=\sqrt{l^2-r^2}& =\sqrt{{25}^2-7^2}\mathrm{m}=\sqrt{625-49}\mathrm{m}=\sqrt{576}\mathrm{m}\\ & =24\mathrm{m}\end{array}$$

So, the volume of the conical tent $=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\times \frac{22}{7}\times 7\times 7\times 24{\mathrm{m}}^3=1232{\mathrm{m}}^3$.

EXERCISE 11.3

Assume $\pi =\frac{22}{7}$, unless stated otherwise.

1. Find the volume of the right circular cone with

(i) radius $6\mathrm{cm}$, height $7\mathrm{cm}$

(ii) radius $3.5\mathrm{cm}$, height $12\mathrm{cm}$

2. Find the capacity in litres of a conical vessel with

(i) radius $7\mathrm{cm}$, slant height $25\mathrm{cm}$

(ii) height $12\mathrm{cm}$, slant height $13\mathrm{cm}$

3. The height of a cone is $15\mathrm{cm}$. If its volume is $1570{\mathrm{cm}}^3$, find the radius of the base. (Use $\pi =3.14$ )

4. If the volume of a right circular cone of height $9\mathrm{cm}$ is $48\pi {\mathrm{cm}}^3$, find the diameter of its base.

5. A conical pit of top diameter $3.5\mathrm{m}$ is $12\mathrm{m}$ deep. What is its capacity in kilolitres?

6. The volume of a right circular cone is $9856{\mathrm{cm}}^3$. If the diameter of the base is $28\mathrm{cm}$, find

(i) height of the cone

(ii) slant height of the cone

(iii) curved surface area of the cone

7. A right triangle $\mathrm{ABC}$ with sides $5\mathrm{cm},12\mathrm{cm}$ and $13\mathrm{cm}$ is revolved about the side $12\mathrm{cm}$. Find the volume of the solid so obtained.

Show Answer

Solution

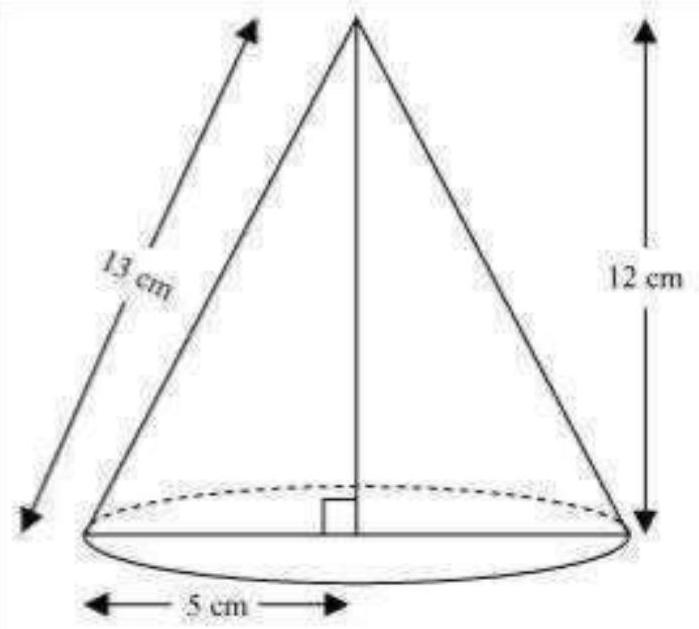
When right-angled $\mathrm{△}ABC$ is revolved about its side $12cm$, a cone with height $(h)$ as 12 $cm$, radius ( $r$ ) as $5cm$, and slant height (I) $13cm$ will be formed.

$=\frac{1}{3}\pi r^{2}h$

Volume of cone

$=[\frac{1}{3}\times \pi \times (5{)}^2\times 12]c{m}^3$

$=100\pi c{m}^3$

Therefore, the volume of the cone so formed is $100nc{m}^3$.

8. If the triangle $\mathrm{ABC}$ in the Question 7 above is revolved about the side $5\mathrm{cm}$, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.

Show Answer

Solution

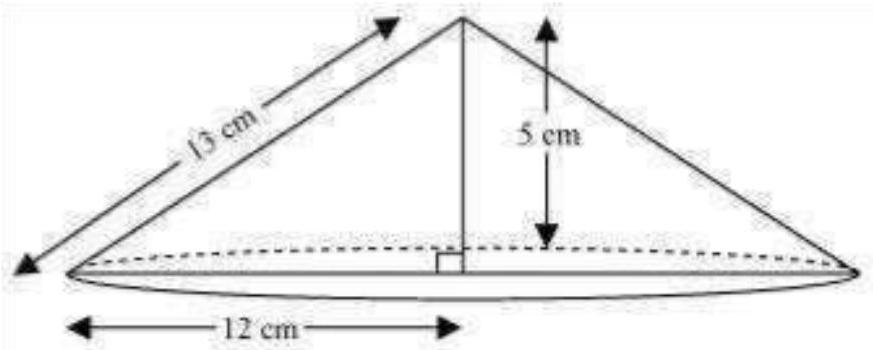
When right-angled $\mathrm{△}ABC$ is revolved about its side $5cm$, a cone will be formed having radius ( $r$ ) as $12cm$, height ( $h$ ) as $5cm$, and slant height $(I)$ as $13cm$.

$\begin{array}{rl}& =\frac{1}{3}\pi r^{2}h\\ & \text{ Volume of cone }\\ & =[\frac{1}{3}\times \pi \times (12{)}^2\times 5]c{m}^3\\ & =240\pi c{m}^3\\ & =\frac{100\pi }{240\pi }\\ & \text{ Reauired ratio }\\ & =\frac{5}{12}=5:12\end{array}$

9. A heap of wheat is in the form of a cone whose diameter is $10.5\mathrm{m}$ and height is $3\mathrm{m}$. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.

11.4 Volume of a Sphere

Now, let us see how to go about measuring the volume of a sphere. First, take two or three spheres of different radii, and a container big enough to be able to put each of the spheres into it, one at a time. Also, take a large trough in which you can place the container. Then, fill the container up to the brim with water [see Fig. 11.13(a)].

Now, carefully place one of the spheres in the container. Some of the water from the container will over flow into the trough in which it is kept [see Fig. 11.13(b)]. Carefully pour out the water from the trough into a measuring cylinder (i.e., a graduated cylindrical jar) and measure the water over flowed [see Fig. 11.13(c)]. Suppose the radius of the immersed sphere is $r$ (you can find the radius by measuring the diameter of the sphere). Then evaluate $\frac{4}{3}\pi r^3$. Do you find this value almost equal to the measure of the volume over flowed?

Fig. 11.13

Once again repeat the procedure done just now, with a different size of sphere. Find the radius $R$ of this sphere and then calculate the value of $\frac{4}{3}\pi R^3$. Once again this value is nearly equal to the measure of the volume of the water displaced (over flowed) by the sphere. What does this tell us? We know that the volume of the sphere is the same as the measure of the volume of the water displaced by it. By doing this experiment repeatedly with spheres of varying radii, we are getting the same result, namely, the volume of a sphere is equal to $\frac{4}{3}\pi$ times the cube of its radius. This gives us the idea that

$$ Volume of a Sphere $=\frac{4}{3}\pi r^3$

where $r$ is the radius of the sphere.

Later, in higher classes it can be proved also. But at this stage, we will just take it as true.

Since a hemisphere is half of a sphere, can you guess what the volume of a hemisphere will be? Yes, it is $\frac{1}{2}$ of $\frac{4}{3}\pi r^3=\frac{2}{3}\pi r^3$.

So, $$ Volume of a Hemisphere $=\frac{\mathbf{2}}{\mathbf{3}}\pi r^3$

where $r$ is the radius of the hemisphere.

Let us take some examples to illustrate the use of these formulae.

Example 10 : Find the volume of a sphere of radius $11.2\mathrm{cm}$.

Solution : Required volume $=\frac{4}{3}\pi r^3$

$$=\frac{4}{3}\times \frac{22}{7}\times 11.2\times 11.2\times 11.2{\mathrm{cm}}^3=5887.32{\mathrm{cm}}^3$$

Example 11 : A shot-putt is a metallic sphere of radius $4.9\mathrm{cm}$. If the density of the metal is $7.8\mathrm{g}\mathrm{per}{\mathrm{cm}}^3$, find the mass of the shot-putt.

Solution : Since the shot-putt is a solid sphere made of metal and its mass is equal to the product of its volume and density, we need to find the volume of the sphere.

Now, volume of the sphere $=\frac{4}{3}\pi r^3$

$$\begin{array}{rl}& =\frac{4}{3}\times \frac{22}{7}\times 4.9\times 4.9\times 4.9{\mathrm{cm}}^3\\ & =493{\mathrm{cm}}^3\text{ (nearly) }\end{array}$$

Further, mass of $1{\mathrm{cm}}^3$ of metal is $7.8\mathrm{g}$.

Therefore, mass of the shot-putt $=7.8\times 493\mathrm{g}$

$$=3845.44\mathrm{g}=3.85\mathrm{kg}\text{ (nearly) }$$

Example 12 : A hemispherical bowl has a radius of $3.5\mathrm{cm}$. What would be the volume of water it would contain?

Solution : The volume of water the bowl can contain

$$\begin{array}{rl}& =\frac{2}{3}\pi r^3\\ & =\frac{2}{3}\times \frac{22}{7}\times 3.5\times 3.5\times 3.5{\mathrm{cm}}^3=89.8{\mathrm{cm}}^3\end{array}$$

EXERCISE 11.4

Assume $\pi =\frac{22}{7}$ , unless stated otherwise.

1. Find the volume of a sphere whose radius is

(i) $7\mathrm{cm}$

(ii) $0.63\mathrm{m}$

2. Find the amount of water displaced by a solid spherical ball of diameter

(i) $28\mathrm{cm}$

(ii) $0.21\mathrm{m}$

3. The diameter of a metallic ball is $4.2\mathrm{cm}$. What is the mass of the ball, if the density of the metal is $8.9{\mathrm{g}}_{\text{per }}{\mathrm{cm}}^3$ ?

4. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?

5. How many litres of milk can a hemispherical bowl of diameter $10.5\mathrm{cm}$ hold?

6. A hemispherical tank is made up of an iron sheet $1\mathrm{cm}$ thick. If the inner radius is $1\mathrm{m}$, then find the volume of the iron used to make the tank.

7. Find the volume of a sphere whose surface area is $154{\mathrm{cm}}^2$.

8. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of ₹ 4989.60. If the cost of white-washing is ₹ 20 per square metre, find the

(i) inside surface area of the dome,

(ii) volume of the air inside the dome.