Chapter 09 Circles Exercise-03
EXERCISE 9.3
1. In Fig. 9.23, $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are three points on a circle with centre $\mathrm{O}$ such that $\angle \mathrm{BOC}=30^{\circ}$ and $\angle \mathrm{AOB}=60^{\circ}$. If $\mathrm{D}$ is a point on the circle other than the $\operatorname{arc} \mathrm{ABC}$, find $\angle \mathrm{ADC}$.
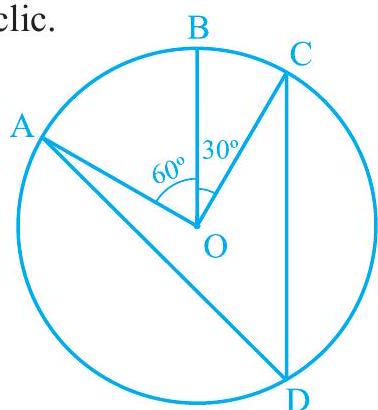
Fig. 9.23
Show Answer
Solution
It can be observed that
$\angle A O C=\angle A O B+\angle B O C$
$=60^{\circ}+30^{\circ}$
$=90^{\circ}$
We know that angle subtended by an arc at the centre is double the angle subtended by it any point on the remaining part of the circle.
$ \angle ADC=\frac{1}{2} \angle AOC=\frac{1}{2} \times 90^{\circ}=45^{\circ} $
2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Show Answer
Solution
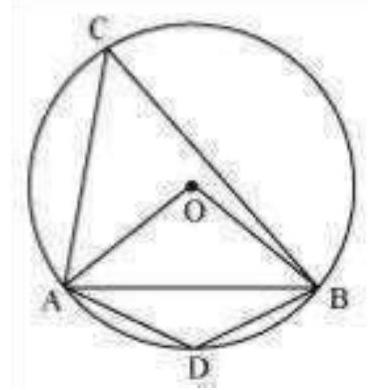
In $\triangle OAB$,
$A B=O A=O B=$ radius
$\angle \triangle OAB$ is an equilateral triangle.
Therefore, each interior angle of this triangle will be of $60^{\circ}$. $\angle \angle AOB=60^{\circ}$
$\angle ACB=\frac{1}{2} \angle AOB=\frac{1}{2}(60^{\circ})=30^{\circ}$
In cyclic quadrilateral $A C B D$,
$\angle ACB+\angle ADB=180^{\circ}$ (Opposite angle in cyclic quadrilateral)
$\angle \angle ADB=180^{\circ}-30^{\circ}=150^{\circ}$
Therefore, angle subtended by this chord at a point on the major arc and the minor arc are $30^{\circ}$ and $150^{\circ}$ respectively.
3. In Fig. 9.24, $\angle \mathrm{PQR}=100^{\circ}$, where $\mathrm{P}, \mathrm{Q}$ and $\mathrm{R}$ are points on a circle with centre $\mathrm{O}$. Find $\angle \mathrm{OPR}$.
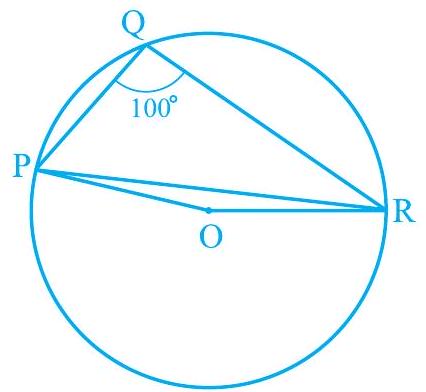
Fig. 9.24
Show Answer
Solution
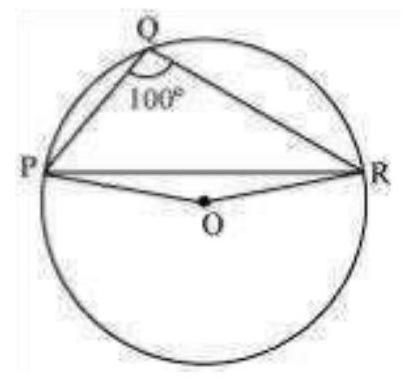
Consider PR as a chord of the circle.
Take any point $S$ on the major arc of the circle.
PQRS is a cyclic quadrilateral.
$\angle PQR+PSR=180^{\circ}$ (Opposite angles of a cyclic quadrilateral)
$\angle P S SR=180^{\circ}-100^{\circ}=80^{\circ}$
We know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle. $\angle \angle POR=2 \angle PSR=$ $2(80^{\circ})=160^{\circ}$
In $\triangle POR$,
$OP=OR$ (Radii of the same circle)
$\angle$ OPPR $=$ ORP (Angles opposite to equal sides of a triangle)
$\mathrm{OPR}+\mathrm{ORP}+\mathrm{POR}=180^{\circ}$ (Angle sum property of a triangle)
$\angle \mathrm{OPR}+160^{\circ}=180^{\circ} 2$
$\angle \mathrm{OPR}=180^{\circ}-160^{\circ}=20^{\circ} 2$
$\angle \mathrm{OPR}=10^{\circ}$
4. In Fig. 9.25, $\angle \mathrm{ABC}=69^{\circ}, \angle \mathrm{ACB}=31^{\circ}$, find $\angle \mathrm{BDC}$.
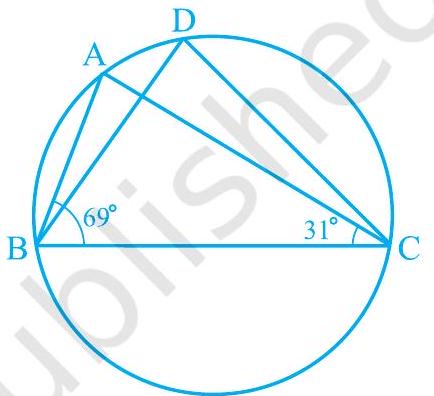
Fig. 9.25
Show Answer
Solution5. In Fig. 9.26, A, B, C and D are four points on a circle. $\mathrm{AC}$ and $\mathrm{BD}$ intersect at a point $\mathrm{E}$ such that $\angle \mathrm{BEC}=130^{\circ}$ and $\angle \mathrm{ECD}=20^{\circ}$. Find $\angle \mathrm{BAC}$.
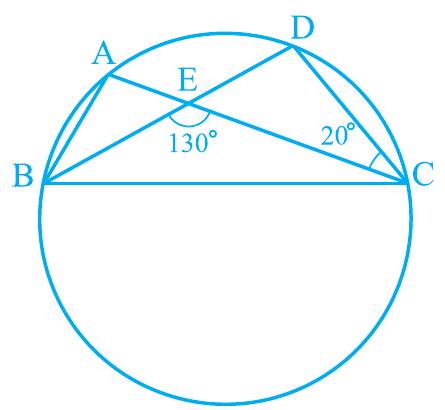
Fig. 9.26
Show Answer
Solution
$\angle CDE+DCE=\angle CEB$ (Exterior angle)
$\angle C D E+20^{\circ}=130^{\circ}$
$\angle CDE=110^{\circ}$
For chord CD,
$<\quad<$
$\angle CAD=70^{\circ}$
$ \begin{aligned} & \angle \quad \angle \quad B C D+B A=180^{\circ} \text{ (Opposite angles of a } By \\ & +100^{\circ}=180^{\circ} \quad BCD \\ & \angle BCD=80^{\circ} \\ & \text{ In } \triangle ABC \text{, } \\ & AB=BC \text{ (Given) } \\ & \angle \angle BCA=\angle CAB \text{ (Angles opposite to equal sides of a triangle) } \\ & \angle \angle BCA=30^{\circ} \end{aligned} $
$ \angle \quad \angle \quad BCD+BAD=180^{\circ} \text{ (Opposite angles of a cyclic quadrilateral) } \angle $
However, $\angle BAC=\angle CDE$ (Angles in the same segment of a circle)
$\angle \angle BAC=110^{\circ}$
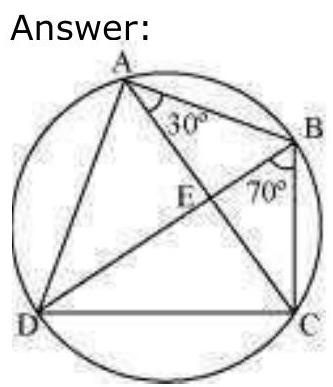
6. $\mathrm{ABCD}$ is a cyclic quadrilateral whose diagonals intersect at a point $\mathrm{E}$. If $\angle \mathrm{DBC}=70^{\circ}$, $\angle \mathrm{BAC}$ is $30^{\circ}$, find $\angle \mathrm{BCD}$. Further, if $\mathrm{AB}=\mathrm{BC}$, find $\angle \mathrm{ECD}$.
Show Answer
Solution
$BAD=BAC+CAD=30^{\circ}+70^{\circ}=100^{\circ}$
CD + BAD $=180^{\circ}$ (Opposite angles of a cyclic quadrilateral) $\angle$
We have, $B^{\prime} C D=80^{\circ}$
$ \begin{aligned} & \angle B^{\prime} C A+A C D=80^{\circ} \\ & \circ+A C D=80^{\circ} 30 \quad A C D \\ & \angle=\angle 50^{\circ} \\ & \angle \angle \\ & E C D=50^{\circ} \end{aligned} $
7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Show Answer
Solution
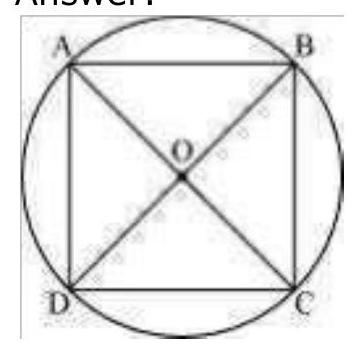
Let $A B C D$ be a cyclic quadrilateral having diagonals $B D$ and $A C$, intersecting each other at point $O$.
$ \angle BAD=\frac{1}{2} \angle BOD=\frac{180^{\circ}}{2}=90^{\circ} $
$ \begin{aligned} & \angle BCD+\angle BAD=180^{\circ} \text{ (Cyclic quadrilateral) (Consider } BD \text{ as a chord) } \\ & \angle BCD=180^{\circ}-90^{\circ}=90^{\circ} \\ & \angle ADC=\frac{1}{2} \angle AOC=\frac{1}{2}(180^{\circ})=90^{\circ} \\ & \angle ADC+\angle ABC=180^{\circ}(\text{ Cyclic quadrilateral })^{\circ} \\ & +\angle ABC=180^{\circ} 90 \end{aligned} $
$\angle A B C=90^{\circ}$
(Considering $AC$ as a chord)
Each interior angle of a cyclic quadrilateral is of $90^{\circ}$. Hence, it is a rectangle.
8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Show Answer
Solution
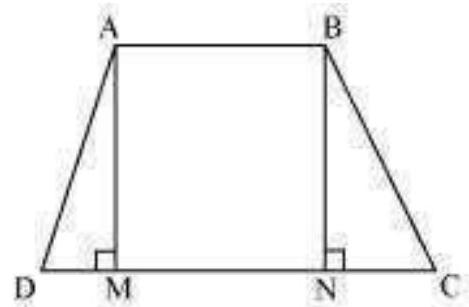
Consider a trapezium $A B C D$ with $A B|| C D$ and $B C=A D$.
Draw $AM \angle CD$ and $BN \angle CD$.
In $\triangle A M D$ and $\triangle B N C$,
$A D=B C$ (Given)
$\angle AMD=\angle BNC(.$ By construction, each is $.90^{\circ})$
$AM=BM$ (Perpendicular distance between two parallel lines is same)
$\angle \triangle AMD \triangle BNC$ (RHS congruence rule)
$\angle A D C=B C \mathscr{C}(C P C T) \ldots$
${ }^{\angle} B A D$ and $A D C$ are on the same side of transversal AD.
$\angle BAD+\stackrel{\angle ADC}{ }=180^{\circ}$.
$\angle \quad \angle$
$B A D+B C D=180^{\circ}[$ Using equation (1)]
This equation shows that the opposite angles are supplementary.
Therefore, $A B C D$ is a cyclic quadrilateral.
9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at $\mathrm{A}, \mathrm{D}$ and $\mathrm{P}$, $Q$ respectively (see Fig. 9.27). Prove that $\angle \mathrm{ACP}=\angle \mathrm{QCD}$.
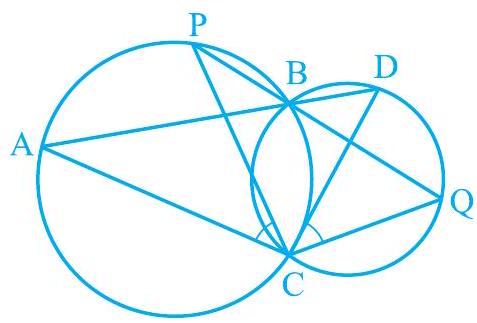
Fig. 9.27
Show Answer
Solution
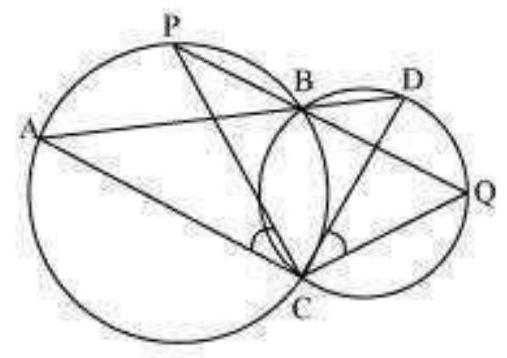
Join chords AP and DQ. $\quad \angle \angle$
For chord AP,
$\angle PBA=\angle ACP$ (Angles in the same segment) …
For chord DQ,
$\angle DBQ=\Phi CD$ (Angles in the same segment) … (2) ABD and
PBQ are line segments intersecting at $B$.
$\angle PBA=$ DBQ (Vertically opposite angles) … (
From equations ( 1 ), ( 2 ), and ( 3 ), we obtain $\angle A C P$
$=\angle QCD$
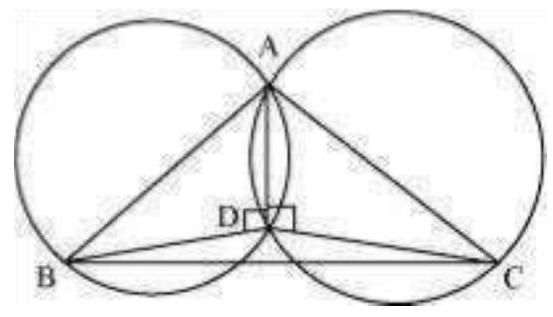
10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Show Answer
Solution
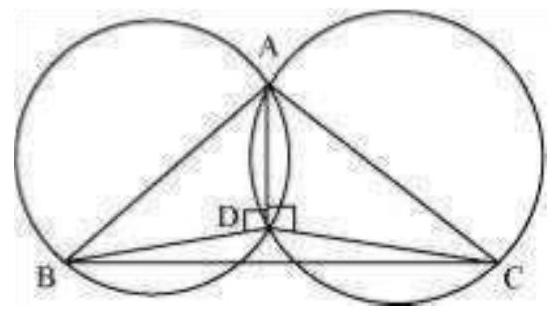
Consider a $\triangle ABC$.
Two circles are drawn while taking $A B$ and $A C$ as the diameter.
Let they intersect each other at $D$ and let $D$ not lie on $B C$.
Join AD.
$\angle ADB=90^{\circ}$ (Angle subtended by semi-circle)
$\angle ADC=90^{\circ}$ (Angle subtended by semi-circle)
$\angle$
$ BDC=\angle ADB+\angle ADC=90^{\circ}+90^{\circ}=180^{\circ} $
Therefore, BDC is a straight line and hence, our assumption was wrong.
Thus, Point $D$ lies on third side $B C$ of $\triangle A B C$.
11. $\mathrm{ABC}$ and $\mathrm{ADC}$ are two right triangles with common hypotenuse $\mathrm{AC}$. Prove that $\angle \mathrm{CAD}=\angle \mathrm{CBD}$.
Show Answer
Solution
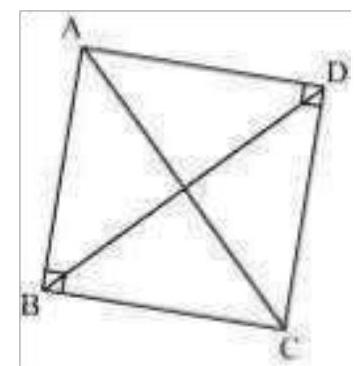
In $\triangle ABC$,
$«<$
$\angle 90^{\circ}+\angle BCA+\angle CAB=180^{\circ}$
$\angle \angle BCA+\angle CAB=90^{\circ} \ldots$ (1) $ABC+BCA+CAB=180^{\circ}$ (Angle sum property of a triangle)
In $\triangle ADC$,
$\angle C D A+A C D+D A C=180^{\circ}$ (Angle sum property of a triangle)
$\angle 90^{\circ}+A^{\prime} C D+D^{\prime} C=180^{\circ}$
${ }^{\angle} A C D+D A C=90^{\circ}$
Adding equations (1) and (2), we obtain
$ BCA+CAB+ACD+DAC=180^{\circ} $
$\angle(BCA+\stackrel{\angle}{\angle} \angle ACD)+(CAB+DAC)=180^{\circ}$
$$ \begin{equation*} BCD+DAB=180^{\circ} \tag{3} \end{equation*} $$
However, it is given that
$\angle B+D=90^{\circ}+90^{\circ}=180^{\circ} \ldots$
From equations (3) and (4), it can be observed that the sum of the measures of opposite angles of quadrilateral $A B C D$ is $180^{\circ}$. Therefore, it is a cyclic quadrilateral.
Consider chord CD.
$\angle CAD=\angle CBD$ (Angles in the same segment)
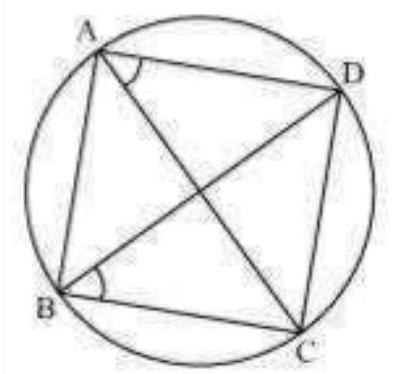
12. Prove that a cyclic parallelogram is a rectangle.
Show Answer
Solution
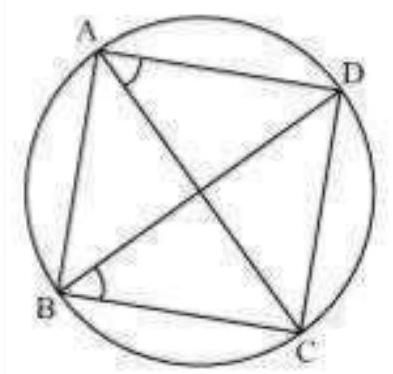
Let $A B C D$ be a cyclic parallelogram. $\angle<$ A $+C=180^{\circ}$ (Opposite angles of a cyclic quadrilateral) … (1)
$\angle A=\angle C$ and $\angle B=\angle D$ We know that opposite angles of a parallelogram are equal. $\angle$
From equation (1), $\angle A+\angle C=180^{\circ}$
$\angle \angle A+\angle A=180^{\circ}$
$\angle 2 \angle A=180^{\circ}$
$\angle \angle A=90^{\circ}$
Parallelogram $ABCD$ has one of its interior angles as $90^{\circ}$. Therefore, it is a rectangle.










