EXERCISE 8.2
1. is a quadrilateral in which and are mid-points of the sides and (see Fig 8.20). AC is a diagonal. Show that :
(i) and
(ii)
(iii) is a parallelogram.
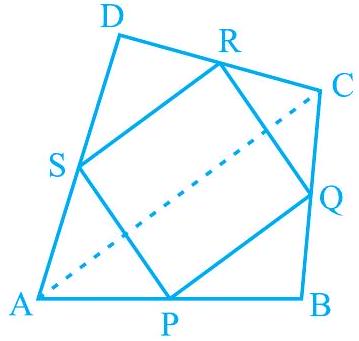
Fig. 8.20
Show Answer
Solution
(i) In and are the mid-points of sides and respectively. In a triangle, the line segment joining the mid-points of any two sides of the triangle is parallel to the third side and is half of it.
and .
(ii) In and are mid-points of sides and respectively. Therefore, by using mid-point theorem,
and
Using equations (1) and (2), we obtain
and (3)
(iii) From equation (3), we obtained
Clearly, one pair of opposite sides of quadrilateral PQRS is parallel and equal.
2. is a rhombus and and are the mid-points of the sides and respectively. Show that the quadrilateral is a rectangle.
Show Answer
Solution

b e
and
In ,
In and are the mid-points of sides and respectively.
AC (Using mid-point theorem) … (1)
and are the mid-points of and respectively. and (Using mid-point theorem)
From equations (1) and (2), we obtain
and
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.
Let the diagonals of rhombus intersect each other at point .
In quadrilateral OMQN,
I| OM ( QR || BD)
Therefore, OMQN is a parallelogram.
However, (Diagonals of a rhombus are perpendicular to each other)
Clearly, PQRS is a parallelogram having one of its interior angles as .
Hence, is a rectangle.
3. is a rectangle and and are mid-points of the sides and respectively. Show that the quadrilateral is a rhombus.
Show Answer
Solution

Let us join and .
In ,
and are the mid-points of and respectively.
and Mid-point theorem
Similarly in
,
and (Mid-point theorem) … (2)
Clearly, and
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.
and (Opposite sides of parallelogram)
In and are the mid-points of side and respectively.
and (Mid-point theorem) …
However, the diagonals of a rectangle are equal. /
By using equation (1), (2), (3), (4), and (5), we obtain PQ
Therefore, is a rhombus.
4. is a trapezium in which is a diagonal and is the mid-point of . A line is drawn through parallel to intersecting at (see Fig. 8.21). Show that is the mid-point of .
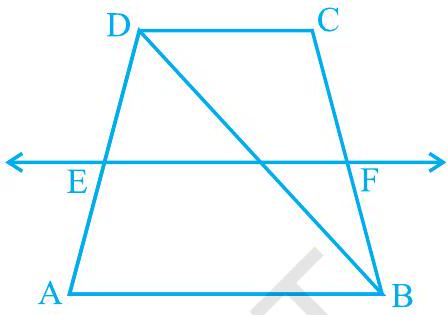
Fig. 8.21
Show Answer
Solution
Let intersect at .

By converse of mid-point theorem, we know that a line drawn through the mid-point of any side of a triangle and parallel to another side, bisects the third side.
In ,
and is the mid-point of .
Therefore, will be the mid-point of .
As and ,
(Two lines parallel to the same line are parallel to each other)
In and is the mid-point of line . Therefore, by using converse of mid-point theorem, is the mid-point of .
5. In a parallelogram and are the mid-points of sides and respectively (see Fig. 8.22). Show that the line segments AF and trisect the diagonal .

Fig. 8.22
Show Answer
Solution
is a parallelogram.
And hence, AE I| FC
Again, (Opposite sides of parallelogram ABCD)
and are mid-points of side and
In quadrilateral , one pair of opposite sides (AE and ) is parallel and equal to each other. Therefore, AECF is a parallelogram. EC (Opposite sides of a parallelogram)
In is the mid-point of side and (as ). Therefore, by using the converse of mid-point theorem, it can be said that is the mid-point of
DQ.
Similarly, in is the mid-point of side and (as ).
Therefore, by using the converse of mid-point theorem, it can be said that is the mid-point of .
From equations (1) and (2), DP
Hence, the line segments and trisect the diagonal .
6. is a triangle right angled at . A line through the mid-point of hypotenuse and parallel to intersects at . Show that
(i) D is the mid-point of AC
(ii)
(iii)
Show Answer
Solution

(i) In ,
It is given that is the mid-point of and .
Therefore, is the mid-point of . (Converse of mid-point theorem)
(ii) As DM || and is a transversal line for them, therefore,
(Co-interior angles)
(iii) Join MC.
In and ,
( is the mid-point of side ) (Each 90)
(Common)
(By SAS
Therefore, (By CPCT)

congruence rule)
However, (M is the mid-point of
Therefore, it fan be said that


















