EXERCISE 8.1
1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Show Answer
Solution
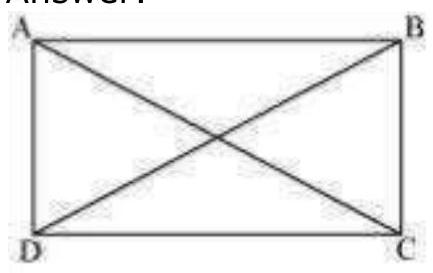
Let be a parallelogram. To show that is a rectangle, we have to prove that one of its interior angles is .
In and ,
(Opposite sides of a parallelogram are equal)
Common)
(Given)
(By SSS Congruence rule)
It is known that the sum of the measures of angles on the same side of transversal is .
Since is a parallelogram and one of its interior angles is is a rectangle.
2. Show that the diagonals of a square are equal and bisect each other at right angles.
Show Answer
Solution
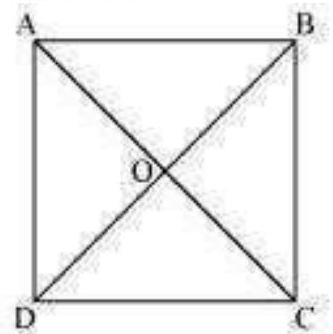
Let be a square. Let the diagonals and intersect each other at a point . To prove that the diagonals of a square are equal and bisect each other at right angles, we have to prove , and .
In and ,
(Sides of a square are equal to each other)
All interior angles are of )
(Common side)
(By SAS congruency)
Hence, the diagonals of a square are equal in length.
In and ,
(Vertically opposite angles)
(Alternate interior angles)
(Sides of a square are always equal)
(By AAS congruence rule)
and (By CPCT)
Hence, the diagonals of a square bisect each other.
In and ,
As we had proved that diagonals bisect each other, therefore,
(Sides of a square are equal)
(Common)
(By SSS congruency)
However, (Linear pair)
Hence, the diagonals of a square bisect each other at right angles.
3. Diagonal of a parallelogram bisects (see Fig. 8.11). Show that
(i) it bisects also,
(ii) is a rhombus.
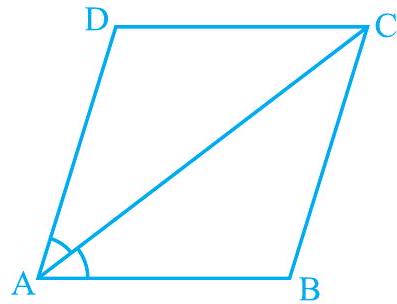
Fig. 8.11
Show Answer
Solution
(i) is a parallelogram.
(Alternate interior angles) ..
And, (Alternate interior angles) … (2) However, it is given that bisects .
From equations (1), (2), and (3), we obtain
.
DCA
Hence, bisects .
(ii)From equation (4), we obtain
(Side opposite to equal angles are equal)
However, and (Opposite sides of a parallelogram)
Hence,
is a rhombus.
4. is a rectangle in which diagonal bisects as well as . Show that:
(i) is a square
(ii) diagonal bisects as well as .
Show Answer
Solution
(i) It is given that is a rectangle.
(Sides opposite to equal angles are also equal)
However, and (Opposite sides of a rectangle are equal)
is a rectangle and all of its sides are equal.
Hence, is a square.
(ii) Let us join BD.
In ,
(Sides of a square are equal to each other)
(Angles opposite to equal sides are equal)
However, (Alternate interior angles for )
bisects .
Also, (Alternate interior angles for )
BD bisects b.
5. In parallelogram , two points and are taken on diagonal such that (see Fig. 8.12). Show that:
(i)
(ii)
(iii)
(iv)
(v) APCQ is a parallelogram
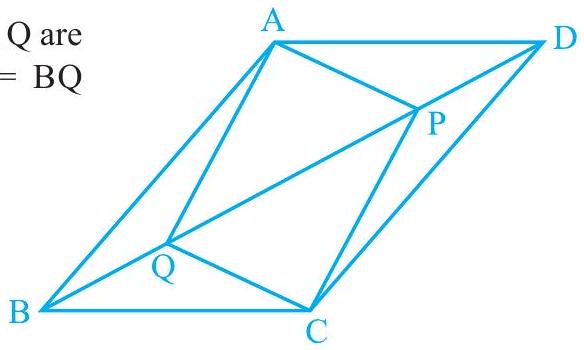
Fig. 8.12
Show Answer
Solution
(i) In and ,
(Alternate interior angles for )
(Opposite sides of parallelogram ABCD)
(Given)
(Using SAS congruence rule) ii)
As we had observed that
(iii) In and ,
(Alternate interior angles for )
(Opposite sides of parallelogram ABCD)
(Given)
(Using SAS congruence rule) iv)
As we had observed that , (
(v) From the result obtained in (ii) and (iv),
and
Since opposite sides in quadrilateral APCQ are equal to each other, APCQ is a parallelogram.
6. is a parallelogram and and are perpendiculars from vertices and on diagonal (see Fig. 8.13). Show that
(i)
(ii)
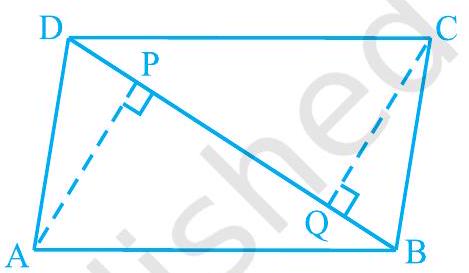
Fig. 8.13
Show Answer
Solution
(i) In and ,
Each
(Opposite sides of parallelogram
CDQ (Alternate interior angles for )
(By AAS congruency)
(ii) By using the above result
, we obtain
7. is a trapezium in which and (see Fig. 8.14). Show that
(i)
(ii)
(iii)
(iv) diagonal diagonal
[Hint: Extend and draw a line through parallel to intersecting produced at .]
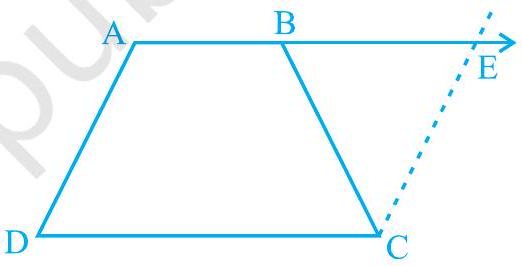
Fig. 8.14
Show Answer
Solution
Let us extend . Then, draw a line through , which is parallel to , intersecting at point . It is clear that AECD is a parallelogram.
(i) (Opposite sides of parallelogram AECD)
However, (Given)
Therefore,
(Angle opposite to equal sides are also equal)
Consider parallel lines AD and CE. AE is the transversal line for them.
(Angles on the same side of transversal)
(Using the relation )
However, (Linear pair angles) (2)
From equations (1) and (2), we obtain
(ii)
(Angles on the same side of the transversal)
Also, (Angles on the same side of the transversal)
However, [Using the result obtained in (i) D
(iii) In and ,
Common side)
(Given)
(Proved before)
(SAS congruence rule)
(iv) We had observed that,
















