EXERCISE 7.3
1. and are two isosceles triangles on the same base and vertices and are on the same side of (see Fig. 7.39). If is extended to intersect at , show that
(i)
(ii)
(iii) AP bisects as well as .
(iv) is the perpendicular bisector of .
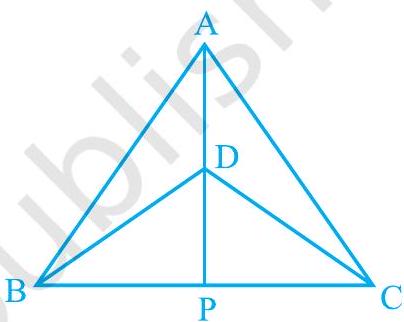
Fig. 7.39
Show Answer
Solution
(i) In and ,
(ii) In and ,
(iii) Since
So, bisects
i.e. AP bisects …..(iii)
In and ,
DP DP …common side
…from (ii)
…(since is isosceles)
….SSS test of congruence
….c.a.c.t.
bisects
So, AP bisects
From (iii) and (iv),
AP bisects as well as .
(iv) We know that
(angles in linear pair)
Also, … from (ii)
and
Hence, is perpendicular bisector of .
2. is an altitude of an isosceles triangle in which . Show that
(i) bisects
(ii) bisects .
Show Answer
Solution
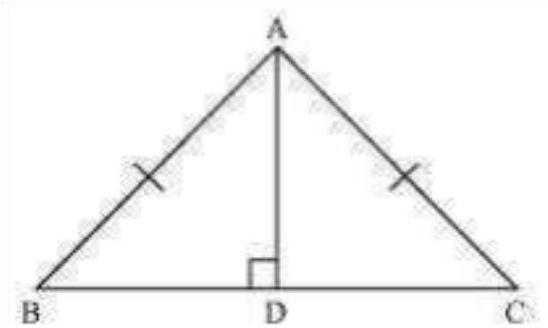
(i) In and ,
(Each as AD is an altitude)
(Given)
(Common)
(By RHS Congruence rule)
Hence, bisects .
(ii) Also, by CPCT,
Hence,
bisects A. :
3. Two sides and and median of one triangle are respectively equal to sides and and median of (see Fig. 7.40). Show that:
(i)
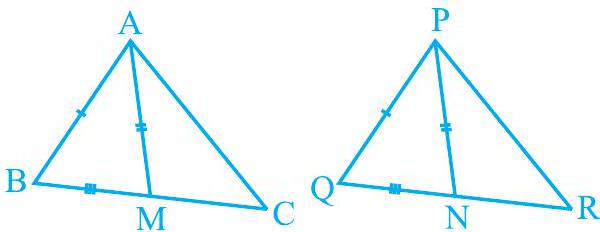
(ii)
Fig. 7.40
Show Answer
Solution
(i) In is the median to .
However,
(1)
In and , In is the median to .
(ii) In and ,
(Given)
[From equation (2)]
(Given)
(By SAS congruence rule)
4. and are two equal altitudes of a triangle . Using RHS congruence rule, prove that the triangle is isosceles.
Show Answer
Solution
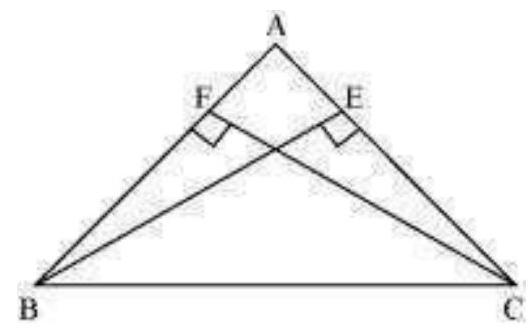
In and ,
Each
(Common)
(Given)
(By RHS congruency)
(Sides opposite to equal angles of a triangle are equal)
Hence, is isosceles.
5. is an isosceles triangle with . Draw to show that .
Show Answer
Solution
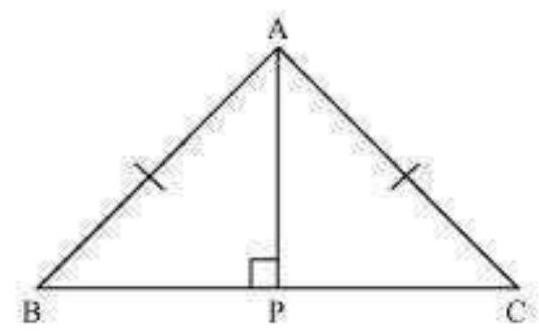
In and ,
Each
Given
Common
(Using RHS congruence rule)
(By using CPCT)















