Chapter 07 Triangles Exercise-02
EXERCISE 7.2
1. In an isosceles triangle $\mathrm{ABC}$, with $\mathrm{AB}=\mathrm{AC}$, the bisectors of $\angle \mathrm{B}$ and $\angle \mathrm{C}$ intersect each other at $\mathrm{O}$. Join $\mathrm{A}$ to $\mathrm{O}$. Show that :
(i) $\mathrm{OB}=\mathrm{OC}$
(ii) $\mathrm{AO}$ bisects $\angle \mathrm{A}$
Show Answer
Solution
(i) It is given that in triangle $A B C, A B=A C$
$\Rightarrow \angle A C B=\angle A B C$ (Angles opposite to equal sides of a triangle are equal)
$ \begin{aligned} & \Rightarrow \frac{1}{2} \angle A C B=\frac{1}{2} \angle A B C \ & \Rightarrow \angle O C B=\angle O B C \end{aligned} $
$\Rightarrow \mathrm{OB}=\mathrm{OC}$ (Sides opposite to equal angles of a triangle are also equal)
(ii) In $\triangle O A B$ and $\triangle O A C$,
$\mathrm{AO}=\mathrm{AO}$ (Common)
$A B=A C($ Given $)$
$O B=O C$ (Proved above)
Therefore, $\triangle O A B \cong \triangle O A C$ (By SSS congruence rule)
$\Rightarrow \angle B A O=\angle C A O$ (CPCT)
$\Rightarrow \mathrm{AO}$ bisects $\angle \mathrm{A}$.
2. In $\triangle \mathrm{ABC}, \mathrm{AD}$ is the perpendicular bisector of $\mathrm{BC}$ (see Fig. 7.30). Show that $\triangle A B C$ is an isosceles triangle in which $\mathrm{AB}=\mathrm{AC}$.
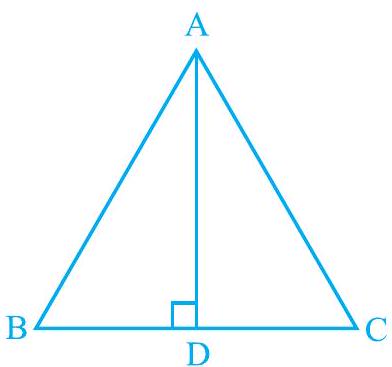
Fig. 7.30
Show Answer
Solution
In $\triangle A D C$ and $\triangle A D B$,
$A D=A D$ (Common)
$\therefore A D C=\therefore A D B($ Each 90) $C D=B D(A D$ is the perpendicular bisector of $B C)$
$\therefore \quad \triangle ADC \therefore \triangle ADB$ (By SAS congruence rule)
$\therefore \quad AB=AC(By CPCT)$
Therefore, $A B C$ is an isosceles triangle in which $A B=A C$.
3. $\mathrm{ABC}$ is an isosceles triangle in which altitudes $\mathrm{BE}$ and $\mathrm{CF}$ are drawn to equal sides $\mathrm{AC}$ and $\mathrm{AB}$ respectively (see Fig. 7.31). Show that these altitudes are equal.
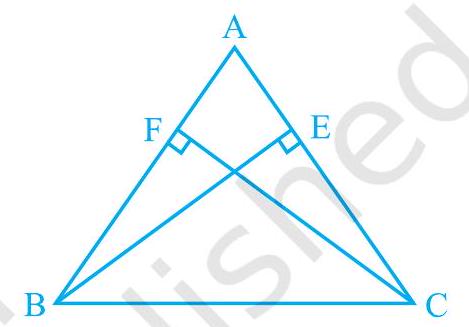
Fig. 7.32
Show Answer
Solution
In $\triangle A E B$ and $\triangle A F C$,
$\therefore A E B$ and $A F C(.$ Each $.90^{\circ}) \quad A=$
$\therefore A$ (Common angle) $A B=A C$ (Given)
$\therefore \triangle AEB \therefore \triangle AFC$ (By AAS congruence rule) $\therefore BE=$ $CF$ (By CPCT)
4. $\mathrm{ABC}$ is a triangle in which altitudes $\mathrm{BE}$ and $\mathrm{CF}$ to sides $A C$ and $A B$ are equal (see Fig. 7.32). Show that
(i) $\triangle \mathrm{ABE} \cong \triangle \mathrm{ACF}$
(ii) $\mathrm{AB}=\mathrm{AC}$, i.e., $\mathrm{ABC}$ is an isosceles triangle.
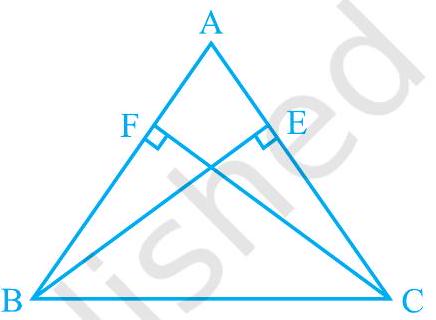
Fig. 7.32
Show Answer
Solution
(i) In $\triangle A B E$ and $\triangle A C F$,
$\therefore ABE$ and $ACF(.$ Each $90^{\circ}$ )
$\therefore A=A^{\prime}$ (Common angle)
$B E=C F$ (Given)
$\therefore \triangle ABE \therefore \triangle ACF$ (By AAS congruence rule)
(ii) It has already been proved that
$\triangle ABE \bullet \triangle ACF$
$\therefore A B=A C(B y C P C T)$
5. $\mathrm{ABC}$ and $\mathrm{DBC}$ are two isosceles triangles on the same base BC (see Fig. 7.33). Show that $\angle \mathrm{ABD}=\angle \mathrm{ACD}$.
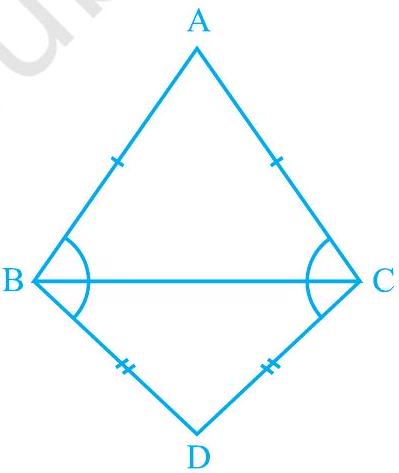
Fig. 7.33
Show Answer
Solution
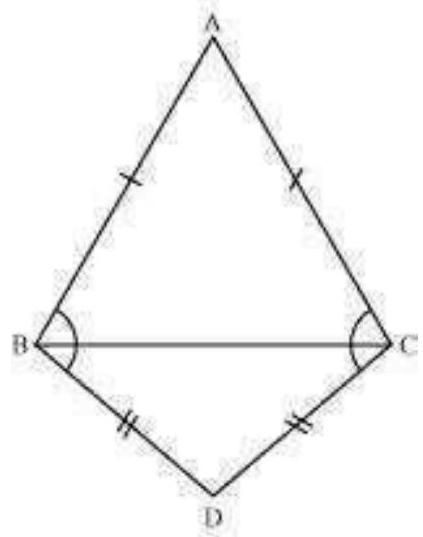
Let us join $A D$.
In $\triangle A B D$ and $\triangle A C D$,
$A B=A C$ (Given)
$B D=C D$ (Given)
$A D=A D$ (Common side)
$\therefore \triangle ABD \cong \quad \triangle ACD$ (By SSS congruence rule)
$\therefore \quad \therefore ABD=A ACD(By CPCT)$
6. $\triangle \mathrm{ABC}$ is an isosceles triangle in which $\mathrm{AB}=\mathrm{AC}$. Side $\mathrm{BA}$ is produced to $\mathrm{D}$ such that $\mathrm{AD}=\mathrm{AB}$ (see Fig. 7.34). Show that $\angle B C D$ is a right angle.
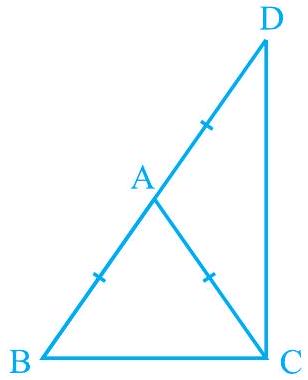
Fig. 7.34
Show Answer
Solution
In $\triangle ABC$,
$A B=A C$ (Given)
$\therefore \therefore ACB=\therefore ABC$ (Angles opposite to equal sides of a triangle are also equal)
In $\triangle ACD$,
$A C=A D$
$\therefore \therefore$ ADC $=: A C D$ (Angles opposite to equal sides of a triangle are also equal)
In $\triangle B C D$,
$\therefore A B C+B C D+A D C=180^{\circ}$ (Angle sum property of a triangle)
$\therefore A \dot{C B}+ACB+ACD+\therefore ACD=180^{\circ}$
$\therefore \quad \therefore 2(ACB+ACD)=180^{\circ}$
$\therefore \quad \therefore \quad 2(BCD)=180^{\circ}$
$\therefore B C D=90^{\circ}$
7. $\mathrm{ABC}$ is a right angled triangle in which $\angle \mathrm{A}=90^{\circ}$ and $\mathrm{AB}=\mathrm{AC}$. Find $\angle \mathrm{B}$ and $\angle \mathrm{C}$.
Show Answer
Solution
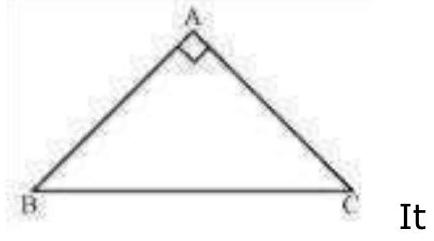
It is given that
$A B=A C$
$\therefore \dot{C}=B$ (Angles opposite to equal sides are also equal)
In $\triangle ABC$
$\therefore A+\dot{B}+C=180^{\circ}$ (Angle sum property of a triangle)
$\therefore 90^{\circ}+\stackrel{\therefore}{B}+C \stackrel{\therefore}{=} 180^{\circ}$
$\therefore 90^{\circ}+\stackrel{\therefore}{B}+B \stackrel{\therefore}{=} 180^{\circ}$
$\therefore \quad \therefore \quad 90^{\circ}$
$\therefore$ :
$B=450$
$B=C=45^{\circ}$
8. Show that the angles of an equilateral triangle are $60^{\circ}$ each.
Show Answer
Solution
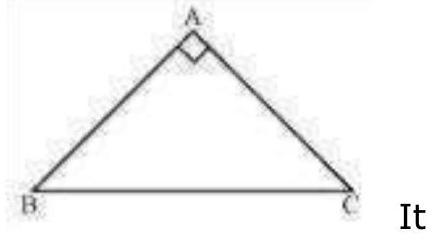
Let us consider that $A B C$ is an equilateral triangle.
Therefore, $A B=B C=A C$
$A B=A C$
$\therefore C=B$ (Angles opposite to equal sides of a triangle are equal)
Also,
$AC=BC$
$\therefore B=A$ (Angles opposite to equal sides of a triangle are equal)
Therefore, we obtain $\therefore$ A
$=B \cdot C \therefore$
In $\triangle ABC$,
$\therefore A+B+C=180^{\circ}$
$\therefore A^{\circ}+A+A+180^{\circ}$
$\therefore 3 \dot{A}=180^{\circ}$
$\therefore \dot{A}=60^{\circ}$
$\therefore \dot{A}=B \stackrel{\Delta}{=} C=\ddot{6} 0^{\circ}$ Hence, in an equilateral triangle, all interior angles are of measure $60^{\circ}$.
