Chapter 07 Triangles Exercise-01
EXERCISE 7.1
1. In quadrilateral $\mathrm{ACBD}$, $\mathrm{AC}=\mathrm{AD}$ and $\mathrm{AB}$ bisects $\angle \mathrm{A}$ (see Fig. 7.16). Show that $\triangle \mathrm{ABC} \cong \triangle \mathrm{ABD}$. What can you say about $\mathrm{BC}$ and $\mathrm{BD}$ ?
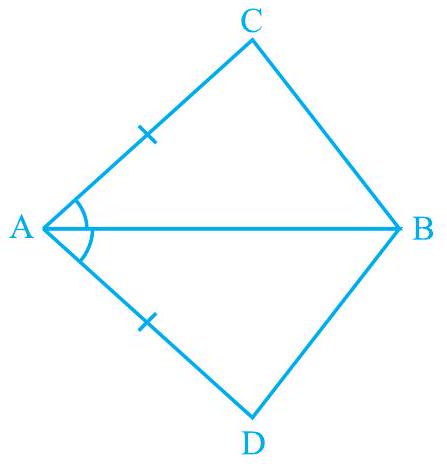
Fig. 7.16
Show Answer
Solution
$\triangle A B C \quad \triangle A B D$. What can you say about $B C$ and $B D$ ?
In $\triangle A B C$ and $\triangle A B D$,
$A C=A D$ (Given)
$\angle CAB=\angle DAB(AB$ bisects $\angle A)$
$A B=A B$ (Common)
$\therefore \quad \triangle ABC \cong \triangle ABD$ (By SAS congruence rule)
$\therefore \quad BC=BD(By CPCT)$
Therefore, BC and BD are of equal lengths.
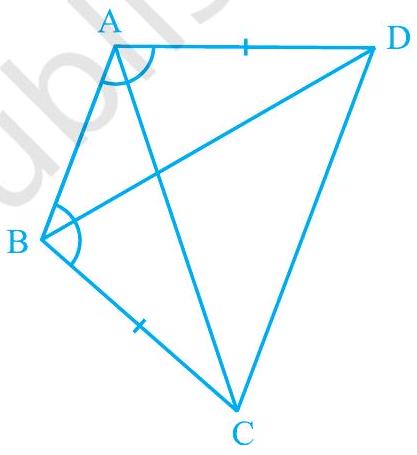
2. $A B C D$ is a quadrilateral in which $A D=B C$ and $\angle \mathrm{DAB}=\angle \mathrm{CBA}$ (see Fig. 7.17). Prove that
(i) $\triangle \mathrm{ABD} \cong \triangle \mathrm{BAC}$
(ii) $\mathrm{BD}=\mathrm{AC}$
(iii) $\angle \mathrm{ABD}=\angle \mathrm{BAC}$.
Show Answer
Solution
In $\triangle A B D$ and $\triangle B A C$,
$A D=B C($ Given)
$\angle \angle$
$DAB=CBA($ Given)
$AB=BA$ (Common)
$\therefore \triangle ABD \cong \triangle BAC$ (By SAS congruence rule)
$\therefore BD=AC$ (By CPCT) And, $\angle ABD$
$=\widehat{B A C}(B y C P C T)$
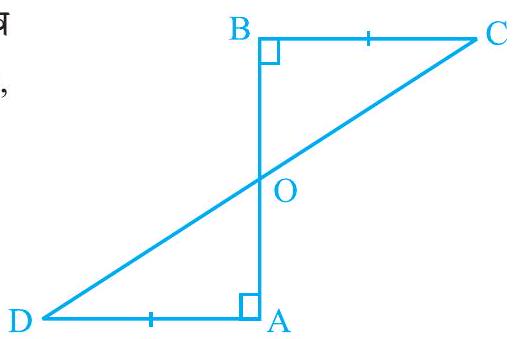
3. $\mathrm{AD}$ and $\mathrm{BC}$ are equal perpendiculars to a line segment $A B$ (see Fig. 7.18). Show that CD bisects $\mathrm{AB}$.
Show Answer
Solution
In $\triangle B O C$ and $\triangle A O D$,
$ \begin{aligned} & \angle \quad \angle BOC=AOD \text{ (Vertically opposite angles) } \\ & \angle \quad CBO=DAO(\text{ Each } 90^{\circ}) \\ & BC=AD \text{ (Given) } \\ & \therefore \quad \triangle BOC \cong \triangle AOD \text{ (AAS congruence rule) } \\ & \therefore \quad BO=AO(By C P C T) \\ & \Rightarrow \quad CD \text{ bisects } AB . \end{aligned} $
4. $\quad l$ and $m$ are two parallel lines intersected by another pair of parallel lines $p$ and $q$ (see Fig. 7.19). Show that $\triangle \mathrm{ABC} \cong \triangle \mathrm{CDA}$.
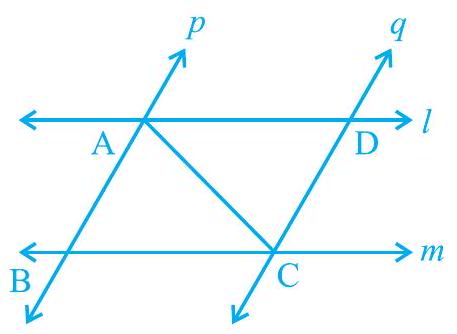
Fig. 7.19
Show Answer
Solution
In $\triangle ABC$ and $\triangle CDA$,
$ \begin{aligned} & \angle BAC=\angle DCA \text{ (Alternate interior angles, as } p | q) \\ & AC=CA \text{ (Common) } \\ & \angle \quad \angle BCA=DAC \text{ (Alternate interior angles, as } \mid | m \text{ ) } \\ & \therefore \quad \therefore \quad \triangle ABC \triangle CDA(By \text{ ASA congruence rule) } \\ & \text{ Question 5: } \end{aligned} $
5. Line $l$ is the bisector of an angle $\angle \mathrm{A}$ and $\mathrm{B}$ is any point on $l$. $\mathrm{BP}$ and $\mathrm{BQ}$ are perpendiculars from $\mathrm{B}$ to the arms of $\angle A$ (see Fig. 7.20). Show that:
(i) $\triangle \mathrm{APB} \cong \triangle \mathrm{AQB}$
(ii) $\mathrm{BP}=\mathrm{BQ}$ or $\mathrm{B}$ is equidistant from the arms of $\angle \mathrm{A}$.
Fig. 7.20
Show Answer
Solution
In $\triangle A P B$ and $\triangle A Q B$,
$ \begin{aligned} & \therefore \quad \therefore \quad APB=AQB(\text{ Each 90) } \\ & \therefore \quad \therefore \quad PAB=QAB(I \text{ is the angle bisector of } \therefore A) \end{aligned} $
$A B=A B$ (Common)
$\therefore \triangle APB \therefore \triangle AQB$ (By AAS congruence rule) $\therefore BP=$
BQ (By CPCT)
rms of $\therefore A$. Or, it can be said that $B$ is equidistant from the a
6. In Fig. 7.21, $\mathrm{AC}=\mathrm{AE}, \mathrm{AB}=\mathrm{AD}$ and $\angle \mathrm{BAD}=\angle \mathrm{EAC}$. Show that $\mathrm{BC}=\mathrm{DE}$.
Fig. 7.21
Show Answer
Solution
It is given that $\therefore B A D=\therefore E A C$
$\therefore BAD+\therefore DAC=\therefore EAC+\therefore DAC$
$\therefore B A C=\therefore DAE$
In $\triangle B A C$ and $\triangle D A E, A B=A D$
(Given) $\therefore BAC=$
$\therefore$ DAE (Proved above)
$A C=A E($ Given)
$\therefore \quad \triangle BAC \therefore \triangle DAE$ (By SAS congruence rule)
$\therefore \quad BC=DE(By CPCT)$
7. $\mathrm{AB}$ is a line segment and $\mathrm{P}$ is its mid-point. $\mathrm{D}$ and $\mathrm{E}$ are points on the same side of $\mathrm{AB}$ such that $\angle \mathrm{BAD}=\angle \mathrm{ABE}$ and $\angle \mathrm{EPA}=\angle \mathrm{DPB}$ (see Fig. 7.22). Show that
(i) $\triangle \mathrm{DAP} \cong \triangle \mathrm{EBP}$
(ii) $\mathrm{AD}=\mathrm{BE}$
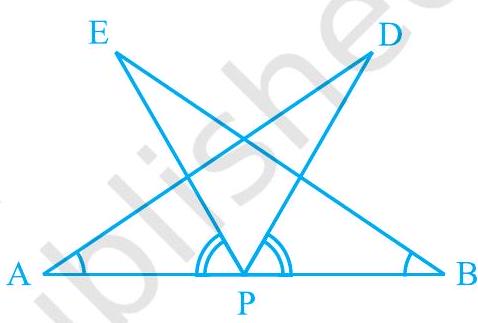
Fig. 7.22
Show Answer
Solution
It is given that EPA $=$ DPB
$\therefore \quad \therefore E P A+D ’ P E=D P B+D P E$
$\therefore \therefore$ DPA $=$ ÉPB
In $\sqrt{\Delta} \sqrt{\Delta}$ EBP,
$\therefore$ DAP $=$ 岸 (Given)
$A P=B P(P$ is mid-point of $A B)$
$\therefore \quad \therefore \quad$ DPA $=$ EPB (From above)
$\therefore \quad \therefore \quad \triangle$ DAP $\triangle$ EBP (ASA congruence rule)
$\therefore \quad AD=BE(By CPCT)$
8. In right triangle $A B C$, right angled at $C, M$ is the mid-point of hypotenuse AB. C is joined to $\mathrm{M}$ and produced to a point $\mathrm{D}$ such that $\mathrm{DM}=\mathrm{CM}$. Point $\mathrm{D}$ is joined to point $\mathrm{B}$ (see Fig. 7.23). Show that:
(i) $\triangle \mathrm{AMC} \cong \triangle \mathrm{BMD}$
(ii) $\angle \mathrm{DBC}$ is a right angle.
(iii) $\Delta \mathrm{DBC} \cong \triangle \mathrm{ACB}$
(iv) $\mathrm{CM}=\frac{1}{2} \mathrm{AB}$
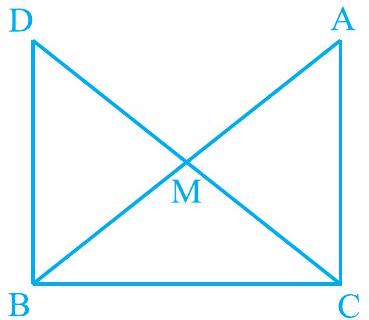
Fig. 7.23
Show Answer
Solution
(i) In $\triangle A M C$ and $\triangle B M D$,
$A M=B M$ ( $M$ is the mid-point of $A B$ )
$\therefore$ AMC $=\therefore$ BMD (Vertically opposite angles)
$CM=DM$ (Given)
$\therefore \quad \triangle AMC \therefore \triangle BMD$ (By SAS congruence rule)
$\therefore \quad AC=BD(By C P C T)$ And,
$\therefore$ ACM $=: BDM(By$ CPCT) ii)
$\therefore \quad ACM=` BDM($
However, AेंCM and ¿BDM are alternate interior angles.
Since alternate angles are equal,
It can be said that $D B | A C$
$ \begin{aligned} & \therefore \quad DBC+\therefore ACB=180^{\circ} \text{ (Co-interior angles) } \\ & \therefore \quad \therefore \quad DBC+90^{\circ}=180^{\circ} \\ & \therefore \quad \therefore \quad DBC=90^{\circ} \end{aligned} $
(iii) In $\triangle DBC$ and $\triangle ACB$,
$DB=AC$ (Already proved)
$\therefore DBC=\therefore ACB(.$ Each 90 $.{ }^{\circ})$
$BC=CB$ (Common)
$\therefore \triangle DBC \quad \triangle ACB$ (SAS congruence rule) iv)
$\triangle DBC \triangle ACB($
$\therefore \quad AB=DC(By CPCT)$
$\therefore \quad AB=2 CM$
$\therefore CM=\frac{1}{2} AB$
