Chapter 06 Lines And Angles Exercise-01
EXERCISE 6.1
1. In Fig. 6.13, lines $\mathrm{AB}$ and $\mathrm{CD}$ intersect at $\mathrm{O}$. If $\angle \mathrm{AOC}+\angle \mathrm{BOE}=70^{\circ}$ and $\angle \mathrm{BOD}=40^{\circ}$, find $\angle \mathrm{BOE}$ and reflex $\angle \mathrm{COE}$.
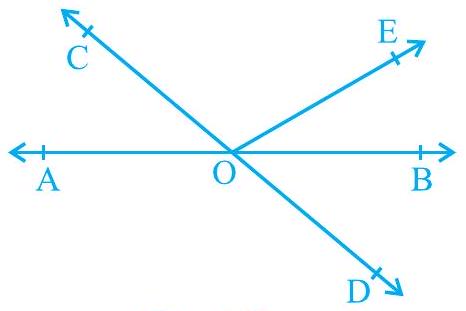
Fig. 6.13
Show Answer
Solution
$A B$ is a straight line, rays $O C$ and $O E$ stand on it.
$\therefore \angle AOC+\angle COE+\angle BOE=180^{\circ}$
$\Rightarrow(\angle AOC+\angle BOE)+\angle COE=180^{\circ}$
$\Rightarrow 70^{\circ}+\angle COE=180^{\circ}$
$\Rightarrow \angle COE=180^{\circ}-70^{\circ}=110^{\circ}$
Reflex $\angle COE=360^{\circ}-110^{\circ}=250^{\circ}$
$CD$ is a straight line, rays $OE$ and $OB$ stand on it.
$\therefore \angle COE+\angle BOE+\angle BOD=180^{\circ}$
$\Rightarrow 110^{\circ}+\angle BOE+40^{\circ}=180^{\circ}$
$\Rightarrow \angle BOE=180^{\circ}-150^{\circ}=30^{\circ}$
2. In Fig. 6.14, lines $X Y$ and $M N$ intersect at $O$. If $\angle \mathrm{POY}=90^{\circ}$ and $a: b=2: 3$, find $c$.
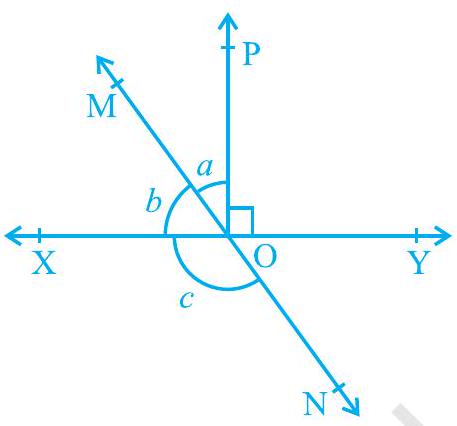
Fig. 6.14
Show Answer
Solution
Let the common ratio between $a$ and $b$ be $x . \quad \therefore$
$X Y$ is a straight line, rays OM and OP stand on it.
$\therefore X O M+MOP+\angle POY=180^{\circ} b+a+POY=180^{\circ}$
$3 x+2 x+90^{\circ}=180^{\circ} 5 x=90^{\circ} x=18^{\circ} a=$
$2 x=2 \times 18=36^{\circ} b=$
$3 x=3 \times 18=54^{\circ}$
MN is a straight line. Ray OX stands on it.
$\therefore b+c=180^{\circ}$ (Linear Pair)
$54^{\circ}+c=180^{\circ} c=180^{\circ}-$
$54^{\circ}=126^{\circ} \quad \therefore c=126^{\circ}$
3. In Fig. 6.15, $\angle \mathrm{PQR}=\angle \mathrm{PRQ}$, then prove that $\angle \mathrm{PQS}=\angle \mathrm{PRT}$.
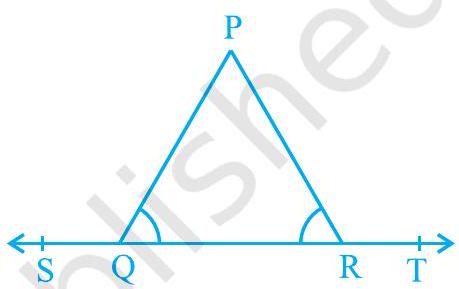
Fig. 6.15
Show Answer
Solution
In the given figure, ST is a straight line and ray QP stands on it.
$\therefore 4 Q S+P Q R=180^{\circ}$ (Linear Pair)
$\angle PQR=180^{\circ}-\angle PQS(1)$
PRT $+\angle PRQ=180^{\circ}$ (Linear Pair)
${ }^{\angle} PRQ=180^{\circ}-PRT$ (2)
It is given that $4 PQR=\angle PRQ$.
Equating equations (1) and (2), we obtain
$ \begin{aligned} & 180^{\circ}-\stackrel{\angle}{ }{ }^{PQS}=180^{\circ}-PRT \angle PQS \\ & =\angle PRT \end{aligned} $
4. In Fig. 6.16, if $x+y=w+z$, then prove that $\mathrm{AOB}$ is a line.
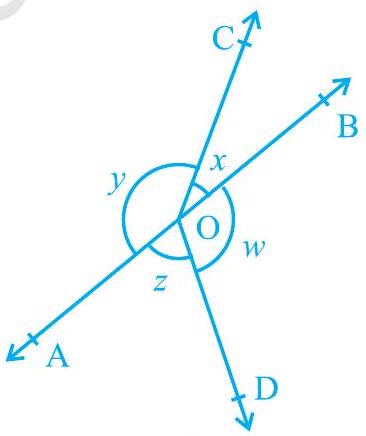
Fig. 6.16
Show Answer
Solution
It can be observed that, $x+y+z+w$ then prove that $A O B$ is a line.
$=360^{\circ}$ (Complete angle) It is given
that, $x+y=z+w \quad \therefore x+y+x+y$
$=360^{\circ}$
$2(x+y)=360^{\circ} x$
$+y=180^{\circ}$
Since $x$ and $y$ form a linear pair, $A O B$ is a line.
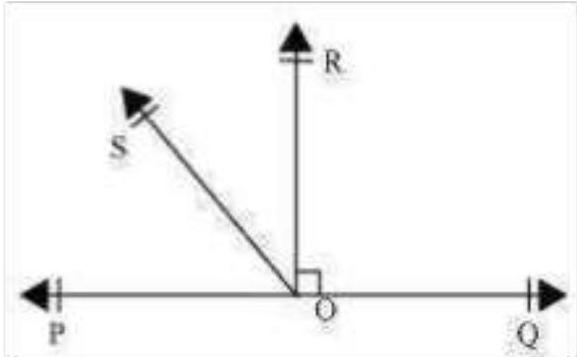
5. In Fig. 6.17, $\mathrm{POQ}$ is a line. Ray $\mathrm{OR}$ is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
$\angle \mathrm{ROS}=\frac{1}{2}(\angle \mathrm{QOS}-\angle \mathrm{POS})$.
Show Answer
Solution
It is given that $OR PQ \quad \perp$
$\therefore \quad \therefore POR=90^{\circ}$
$\therefore \quad \therefore POS+\therefore SOR=90^{\circ}$
$\therefore ROS=90^{\circ}-\therefore POS$.
$\therefore QOR=90^{\circ}$ (As OR $.\therefore PQ)$
$\therefore QOS-\therefore ROS=90^{\circ}$
$\therefore ROS=\therefore QOS-90^{\circ}$
On adding equations (1) and (2), we obtain
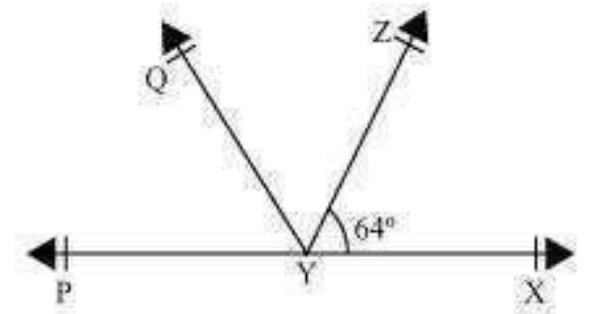
6. It is given that $\angle \mathrm{XYZ}=64^{\circ}$ and $\mathrm{XY}$ is produced to point $\mathrm{P}$. Draw a figure from the given information. If ray $\mathrm{YQ}$ bisects $\angle \mathrm{ZYP}$, find $\angle \mathrm{XYQ}$ and reflex $\angle \mathrm{QYP}$.

Fig. 6.17
Show Answer
Solution
It is given that line YQ bisects $\therefore P Y Z$.
Hence, $\therefore QYP=\therefore ZYQ$
It can be observed that $PX$ is a line. Rays $YQ$ and $YZ$ stand on it.
$\therefore X Y Z+Z Y Q+\therefore Q Y P=180^{\circ}$
$\therefore 64^{\circ}+2 QYP=180^{\circ}$
$\therefore 2$ Q̈PP $=180^{\circ}-64^{\circ}=116^{\circ}$
$\therefore \dot{Q} QP=58^{\circ}$
Also, $\stackrel{\grave{Z}}{ZYQ}=\therefore QYP=58^{\circ}$
Reflex QYP $=360^{\circ}-58^{\circ}=302^{\circ}$
$X Y Q=X Y Z+a Z Y Q$
$=64^{\circ}+58^{\circ}=122^{\circ}$










