Chapter 03 Coordinate Geometry Exercise-02
EXERCISE 3.2
1. Write the answer of each of the following questions:
(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.
Show Answer
Solution
(i) The name of horizontal lines and vertical lines drawn to determine the position of any point in the Cartesian plane is $x$-axis and $y$-axis respectively.
(ii) The name of each part of the plane formed by these two lines, $x$-axis and $y$-axis, is quadrant (one-fourth part).
(iii) The name of the point where these two lines intersect is the origin.
2. See Fig.3.14, and write the following:
(i) The coordinates of $\mathrm{B}$.
(ii) The coordinates of $\mathrm{C}$.
(iii) The point identified by the coordinates $(-3,-5)$.
(iv) The point identified by the coordinates $(2,-4)$.
(v) The abscissa of the point $\mathrm{D}$.
(vi) The ordinate of the point $\mathrm{H}$.
(vii) The coordinates of the point $\mathrm{L}$.
(viii) The coordinates of the point $\mathrm{M}$.
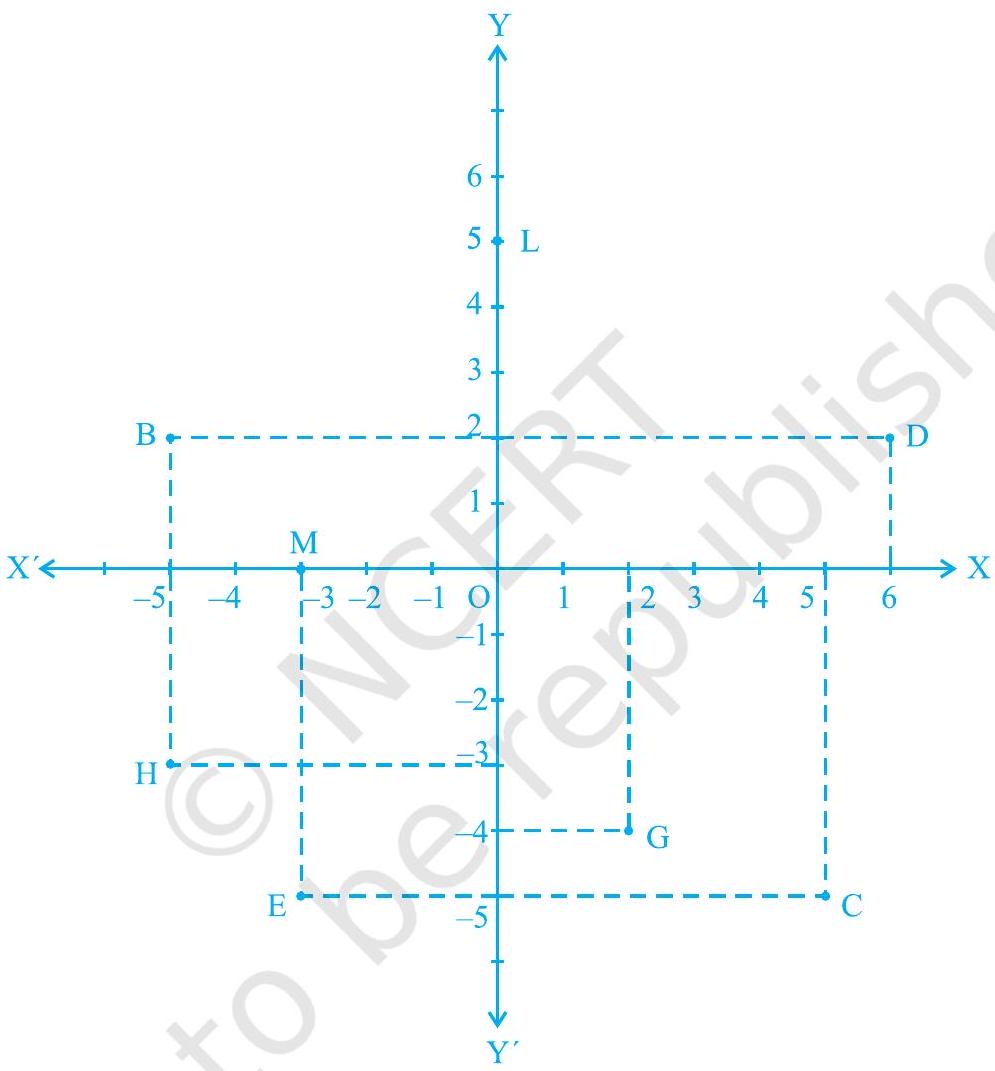
Fig. 3.14
Show Answer
Solution
(i) The $x$-coordinate and the $y$-coordinate of point $B$ are -5 and 2 respectively. Therefore, the coordinates of point $B$ are $(-5,2)$.
(ii) The $x$-coordinate and the $y$-coordinate of point $C$ are 5 and -5 respectively. Therefore, the coordinates of point $C$ are $(5,-5)$.
(iii) The point whose $x$-coordinate and $y$-coordinate are -3 and -5 respectively is point $E$.
(iv) The point whose $x$-coordinate and $y$-coordinate are 2 and -4 respectively is point $G$.
(v) The $x$-coordinate of point $D$ is 6 . Therefore, the abscissa of point $D$ is 6 . (vi) The $y$-coordinate of point $H$ is -3 . Therefore, the ordinate of point $H$ is -3 . (vii) The $x$-coordinate and the $y$-coordinate of point $L$ are 0 and 5 respectively. Therefore, the coordinates of point $L$ are $(0,5)$.
(viii) The $x$-coordinate and the $y$-coordinate of point $M$ are -3 and 0 respectively. Therefore, the coordinates of point $M$ is $(-3,0)$.










