Solution

(i) ${}^{2-\sqrt{5}}=2-2.2360679\dots$

$=-0.2360679\dots$

As the decimal expansion of this expression is non-terminating non-recurring, therefore, it is an irrational number.

(ii)

$(3+\sqrt{23})-\sqrt{23}=3=\frac{3}{1}\text{ number. form, therefore, it is a }$

As it can be represented in $\frac{p}{q}$

(iii) $\frac{2\sqrt{7}}{7\sqrt{7}}=\frac{2}{7}$ : $\frac{2\sqrt{7}}{7\sqrt{7}}=\frac{2}{7}$, which is a rational number.

(iv) $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}=0.7071067811\dots$

As the decimal expansion of this expression is non-terminating non-recurring, therefore, it is an irrational number. ( $v)$

$2п=2(3.1415\dots )$

$=6.2830\dots$

As the decimal expansion of this expression is non-terminating non-recurring, therefore, it is an irrational number.

Solution

$\begin{array}{rl}& (3+\sqrt{3})(2+\sqrt{2})=3(2+\sqrt{2})+\sqrt{3}(2+\sqrt{2})\\ & =6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}\\ & (3+\sqrt{3})(3-\sqrt{3})=(3{)}^2-(\sqrt{3}{)}^2\\ & \text{ (ii) }\\ & =9-3=6\\ & \text{ (iii) }(\sqrt{5}+\sqrt{2}{)}^2=(\sqrt{5}{)}^2+(\sqrt{2}{)}^2+2(\sqrt{5})(\sqrt{2})\\ & =5+2+2\sqrt{10}=7+2\sqrt{10}\\ & \text{ (iv) }(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})=(\sqrt{5}{)}^2-(\sqrt{2}{)}^2\\ & =5-2=3\end{array}$

Solution

There is no contradiction. When we measure a length with scale or any other instrument, we only obtain an approximate rational value. We never obtain an exact value. For this reason, we may not realise that either $c$ or $d$ is irrational. Therefore,

the $\frac{c}{d}$ fraction is irrational. Hence, $\pi$ is irrational.

Solution

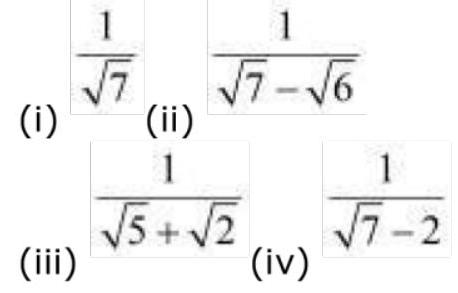
Mark a line segment $OB=9.3$ on number line. Further, take $BC$ of 1 unit. Find the midpoint D of OC and draw a semi-circle on OC while taking D as its centre. Draw a

(i)

$\frac{1}{\sqrt{7}}=\frac{1\times \sqrt{7}}{1\times \sqrt{7}}=\frac{\sqrt{7}}{7}$

perpendicular to line $OC$ passing through point $B$. Let it intersect the semi-circle at $E$.

Taking B as centre and BE as radius, draw an arc in tersecting number line at $F$. BF is $\sqrt{9.3}$.

Solution

(i)

$\begin{array}{rlr}{64}^{\frac{1}{2}}& =(2^6{)}^{\frac{1}{2}}& =2^2=4\\ & =2^{6\times \frac{1}{2}}& [(a^m{)}^n=a^{mm!}{]}_{(16{)}^{\frac{3}{4}}=(2^4{)}^{\frac{3}{4}}}^{(iii)}\\ & =2^3=8& \end{array}$

$=2^{5\times \frac{2}{3}}[(a^m{)}^{n\prime }=a^{mmn}]$

(ii)

$\begin{array}{rl}{32}^{\frac{1}{5}}& =(2^5{)}^{\frac{1}{5}}\\ & =(2{)}^{5\times \frac{1}{5}}\\ & =2^1=2\end{array}$

$\begin{array}{rl}& =2^{4\times \frac{3}{4}}\\ & [(a^m{)}^n=a^{mm}]\\ & [(a^m{)}^n=a^{mm}{]}_{(125{)}^{\frac{-1}{3}}}^{(iv)}=\frac{1}{(125{)}^{\frac{1}{3}}}\\ & =2^3=8\end{array}$

$(125{)}^{\frac{1}{3}}=(5^3{)}^{\frac{1}{3}}$

$\begin{array}{ccc}=5^{3\times \frac{1}{3}}& [(a^m{)}^n=a^{mm}]& =\frac{1}{5^{3\times \frac{1}{3}}}\\ =5^1=5& =\frac{1}{5}\end{array}$

$[a^{-m}=\frac{1}{a^m}]$