Himanshu- 12-2-24, Foundation Class09 Physicsbook1-Smartedu(2018) (40 Pages)
There are quite a few errors in this book. Read with your own risk. Errors are Printing errors, Calculation Errors, Conceptual Errors etc

There are quite a few errors in this book. Read with your own risk. Errors are Printing errors, Calculation Errors, Conceptual Errors etc
PART A
Chapter 0 Basic Mathematics for Physics
Chapter 1 Measurement
chapter 2 Motion in a Straight Line 30
chapter 3 Motion in a Plane
chapter 4 Force and Laws of Motion 107.156
chapter 5 Work, Energy and Power
CHAPTER 0
Basic Mathematics For Physics
If you want to excel in science field, it is very important to have good mathematical aptitude. This chapter is presenting Basic Mathematics that is very useful for developing problem solving strategies whenever required. It includes application in physics section that will develop your scientific temper. Go through it twice or thrice before start learning physics. Take your teacher help wherever you feel any doubt or require more illustrations. “Mathematics is the language of physics”.
TRIGONOMETRIC IDENTITIES
DIFFERENTIAL CALCULUS
The derivative
Where
A useful expression to remember when
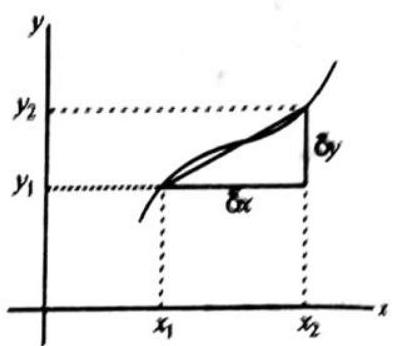
If
Examples, we evaluate the derivatives of several well-behaved functions.
Illustration :
SOLUTION: Applying equation 2 to each term independently, and remembring that
We have
SPECIAL PROPERTIES OF THE DERIVATIVE
(a) Derivative of the Product of Two Functions. If a function
(b) Derivative of the Sum of Two Functions. If a function
(c) Chain Rule of Differential Calculus. If
Then
(d) The Second Derivative. The second derivative of
TABLE 1 : DERIVATIVES FOR SEVERAL FUNCTIONS
MAXIMA AND MINIMA
To find the maxima and minima for a function or extreme values of the function
STEP-I : Find
STEP-II : Put
STEP-III : Find
STEP-IV : Find the values of
STEP-V : If
If
STEP-VI : If
i.e. a point which is neither MINIMA nor MAXIMA.
INTEGRAL CALCULUS
Integration is the inverse of differentiation.
TABLE 2 : SOME INDEFINITE INTEGRALS
VECTOR
Physical Quantities (Anything which can be measured)
| Scalar | Vector |
|---|---|
| 1. Physical quantities which need only magnitude to express them. | Physical quantities which need both magnitude and direction to express them & they should obey vector rules. |
| 2. They may have direction but not needed for their expression. | |
| Example : Mass, energy, work, distance, speed, pressure, current, Time, |
Examples: Velocity, Displacement, Accelaration, Force, Momentum, Current density, |
VECTOR REPRESENTATION
Vectors are represented either graphically or by symbols as following :
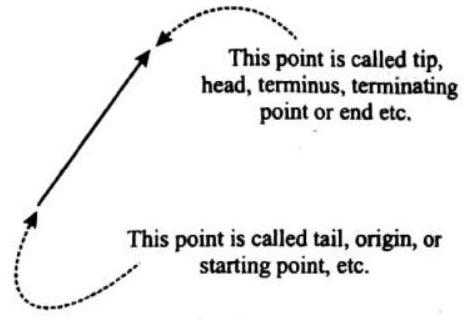
Graphical Representation of Vectors
Vectors are represented by directed line segments. Their terminology is as shown in the figure.
The length of the line segment represents the magnitude of the vector and its arrow-head depicts its direction. The \to head can be put on the extreme end of the line or at any other point of the line.
represent a vector whose direction is perpendicular to the plane of this paper, coming out of the paper i.e. towards you. Similarly,
Symbolic representation of vector
- Vectors are represented in either of the following two ways.
Either as
- Magnitude (also called modulus or mod values) of vectors are represented by normal alphabets, e.g.
Magnitude of
- Unit vectors (detail study in types of vector) (i.e. whose magnitude is one unit) are represented as
TYPES OF VECTOR
1. Equal vectors : Two vectors
2. Parallel vector: Two vectors
(i) Both have same direction.
(ii) One vector is scalar (positive non-zero) multiple of another vector.
Use : If a vector is shifted parallel to itself their will be no change in it.
3. Anti-parallel vectors : Two vectors
(i) Both have opposite direction.
(ii) One vector is scalar (non-zero negative) multiple of another vector. Use : In subtraction of vector.
4. Collinear vectors: When the vectors under consideration can share the same support or have a common support then the considered vectors are colinear.
5. Zero vector
Properties of zero vector:
(i) The sum of a finite vector
(ii) The multiplication of a zero vector by a finite number
(iii) The multiplication of a finite vector
Examples : The position vector of the origin in a system of coordinates is a zero vector. If an object is stationary, then its displacement in a finite time is a zero vector.
6. Unit vector : A vector divided by its magnitude is a unit vector. Unit vector for
Since,
7. Position vector
It is gencrally represented by
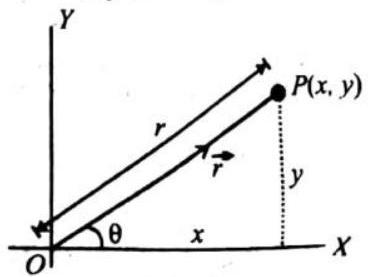
8. Displacement vector
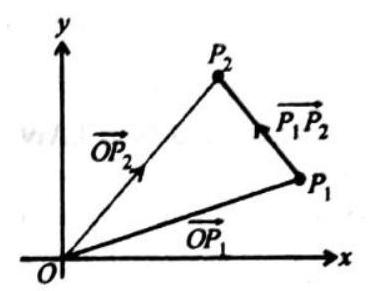
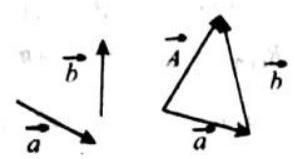
LAWS OF VECTOR ADDITION
Triangle law of vector addition of two vector
It states that if two vectors acting on a particle at the same time are represented in magnitude and direction by the two sides of a triangle taken in one order, their resultant vector is represented in magnitude and direction by the third side of the triangle taken in opposite order.
Let the two vector
Magnitude of
Direction of
Note: (l) Vector does not obey ordinary algebra.
(ii) In above formulation remember
In above diagram you can see
Value of
Thus
Like the vector sum of the forces of
Note: 1. To a vector only a vector of same type can be added that represents the same physical quantity and the resultant is a vector of the same type
- Vector addition is commutative, i.e.,
- Vector addition is associative, i.e.,
- If the vectors
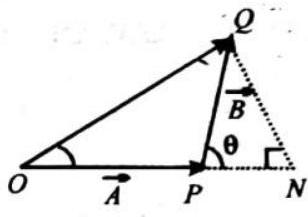
PARALLELOGRAM LAW OF VECTOR ADDITION
It states that if two vectors are represented in magnitude and direction by the two adjacent sides of a parallelogram then their resultant is represented in magnitude and direction by the diagonal of the parallelogram.
Let the two vectors
If
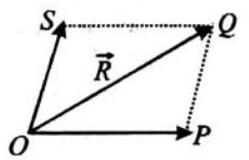
If
POLYGON LAW OF VECTOR ADDITION
If a number of non zero vectors are represented by the
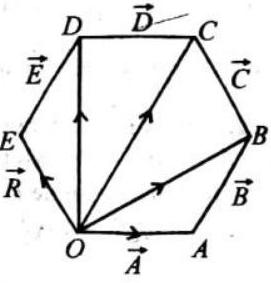
Note :
- Resultant of two unequal vectors cannot be zero.
- Resultant of three co-planar vectors may or may not be zero.
- Resultant of three non coplanar vectors cannot be zero, Minimum number of non coplanar vectors whose sum can be zero is four.
- Polygon law should be used only for diagram purpose for calculation of resultant vector (For addition of more than 2 vector) we use components of vector.
- Minimum no. of coplanar vector for zero resultant is 2 (for equal magnitude) & 3 (for unequal magnitude)
SUBTRACTION OF VECTOR
Subtraction of a vector
Note: 1. Addition of a viector to its own negative vector or null vector
- Subtraction is not comnutative, i.e.,
(a)
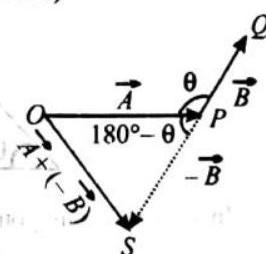
(b)
- Change in a vector physical quantity means subtraction of initial vector from the final vector
COMPONENTS OF VECTOR
If
We say that
The process of splitting a single vector into two or more vectors, which together produce the same effect as is produced by single vector alone, is called resolution of vectors.
The vectors into which the given single vector is splitted are called component vectors. (Resolution of a vector is just opposite to composition of vectors).
Consider a vector 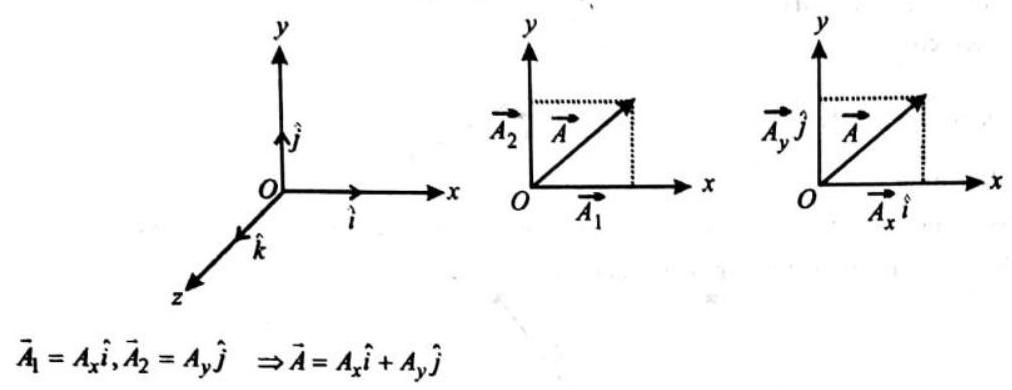
The quantities
Its clear from above equation that a component of a vector can be positive, negative or zero depending on the value of
(a) Its magnitude
(b) Its components
Note: If
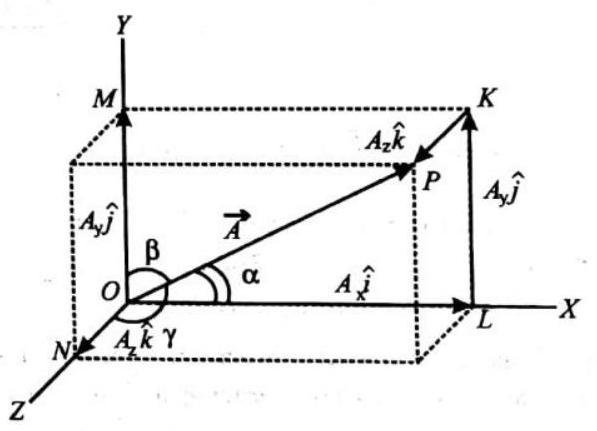
In three dimensions, a vector
See following diagram carefully
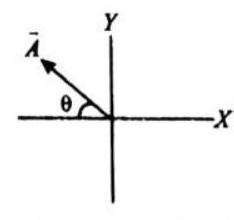
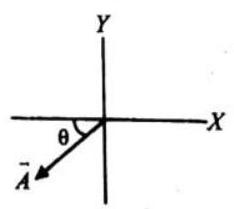
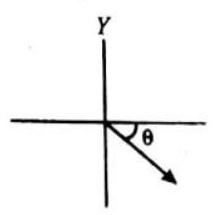
MULTIPLICATION OF VECTORS
Scalar Product
The scalar product or dot product of any two vectors
Properties
(a) It is always a scalar.
(b) It is commutative, i.e.,
(c) It is distributive, i.e.,
(d) As by definition
(e)
The angle between the vector
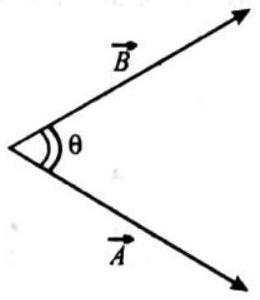
Geometrically, 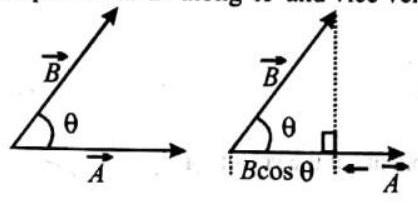
Component of
Component of
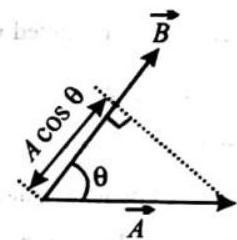
(f) Scalar product of two vectors will be maximum when
(g) If the scalar product of two nonzero vectors vanishes then the vectors are orthogonal.
(h) The scalar product of a vector by itself is termed as self dot product and is given by
(i) In case of unit vector
(j) In case of orthogonal unit vectors,
(k)
Illustration 2 :
Prove that vectors
SOLUTION : Here,
Two vectors are perpendicular to each other if,
Now
Since
CHAPTER 1
MEASUREMENT
INTRODUCTION
The process of comparing an unknown physical quantity with respect to a known quantity is known as measurement. For example, when we say that the length of our bedroom is 10 feet it implies that the bedroom is 10 times the known quantity ‘feet’. So, measurement of any physical quantity consists of two parts - (i) a numerical value and (ii) the known quantity. In above example, the numerical value is 10 and the known quantity is the ‘feet’. The known quantity is called the unit of that physical quantity. The Seet’, therefore, is the unit of length.
Physical quantities are of two types-fundamental and derived. A derived quantity can be expressed in Chers of fundamental quantities. A derived quantity expressed in terms of fundamental quantities is said to have ‘dimensions’.
Ceasurement of a quantity has in general, inaccuracy or ’errors’. In this chapter we will learn measurement, unit, dimensions and errors in measurement.
PHYSICAL QUANTITIES
Quantities which can be measured are called physical quantities. Velocity, acceleration, force, area, volume, pressure, etc. are some examples of physical quantities.
Kinds of Physical Quantities
There are two kinds of physical quantities
(i) Fundamental Physical Quantities : Fundamental physical quantities are those which do not depend on other quantities and also independent of each other. They are seven in number viz; length, mass, time, thermodynamic temperature, electric current, luminuous intensity and amount of substance.
(ii) Derived Physical Quantities : Derived physical quantities are those which are derived from fundamental physical quantities. For example, velocity is derived from the fundamental quantities length and time, hence it is a derived physical quantity.
UNIT
To measure a physical quantity it is compared with a standard quantity. This standard quantity is called the unit of that quamtity. For example, to measure the length of a desk, it is compared with the standard quantity known as ‘metre’. Thus, ‘metre’ is said to be the unit of length.
The starting point in any study of measurement is an understanding of the need for universal standardisation of the units. In early times, man used body parts as a standard of measure. With progress, these rough inaccurate measurements were discarded for accurate systems of measurement. Also, as world trade increased, there developed a need for universal standards of units of measure with opportunity for all countries to adopt such established standards.
Do you Know !!
The unit named to commemorate a scientist is not written with capital initial letter. For example, the unit of force is written as newton (and not as Newton), the unit of current is written as ampere (and not as Ampere). etc.
The symbols for units named after scientists are usually the first initial letter of their names in capital. For example,
Types of Units
There are two types of units :
(i) Fundamental units and
(ii) Derived units
Fundamental units
Fundamental units are those units which cannot be derived from any other unit, and they cannot be resolved into any basic or fundamental unit, for example, length, mass, time, temperature, luminous intensity and current.
Derived units
Any unit which can be obtained by the combination of one or more fundamental units are called derived unit for example, area speed, density, volume, momentum, acceleration, force, etc.
System of Units
Depending upon the units of fundamental physical quantities, there are four main systems of units, namely
- CGS (Centimeter, Gramme or Gram, Second)
- FPS (Foot, Pound, Second)
- MKS (Meter, Kilogram, Second)
- SI (Systeme International d’ Unites)
The first three of these systems recognize only three fundamental dimensions i.e. length
An international organization, the Conference Generale des Poids et Measures, or CGPM is internationally renogmeed as the authority on the definition of units. In English, this body is known as “General Conference on Wrights and Akrasun”. The Systeme International de Unites, or SI system of units, was set up in 1960 by the CGPM
Do you Know !!
The units do not have plural forms. For example, it is wong in write a forre of 10 mown (os
No full stop is put hetween the symbols for units. l’or example, it is wrong to write new:rm metre as N.m. One should write it us Nm.
Characteristics of a Standard Unit
A standard unit must have following features to be accepted world wide.
(i) It should have a convenient size.
(ii) It should be very well defined.
(iii) It should be independent of time and place.
(iv) It should be easily available so that all laboratories can duplicate and use it as per requirement.
(v) It should be independent of physical conditions like temperature, pressure, humidity etc.
(vii) It should be easily reproducible.
Advantages of SI
(i) Coherent System : All the derived units are obtainable directly from the basic units.
(ii) Rational System : Only one unit for one physical quantity.
(iii) Metric System : This makes calculations easier.
(iv) This system is universally accepted.
Disadvantages of SI
As it is a coherent system, all the derived units are not practical e.g. 1 coulomb (unit of electric charge), 1 farad (unit of electric capacitance), 1 bel (unit of loudness of sound) are too large units to be practical.
Fundamental Units of SI
The following table shows the seven fundamental units of S.I.
| S. No. | Physical quantity | Unit of measurement | Symbol for unit |
|---|---|---|---|
| 1. | Length | Metre | |
| 2. | Mass | Kilogram | |
| 3. | Time | Second | |
| 4. | Electric current | Ampere | |
| 5. | Temperature | Kelvin | |
| 6. | Luminous intensity | Candela | cd |
Supplementary Units of SI
The following table shows the two supplementary units of SI
| S.No. | Physical quantity | Unit of measurement | Symbol for unit |
|---|---|---|---|
| 1. | Plane Angle | Redian | rad |
| 2. | Solid Angle | Steradian | sr |
Definitions of SI units
- Metre: The metre is the length of the path travelled by light in vacuum during a time interval of
- Kilogram: The kilogram is equal to the mass of the international prototype of the kilogram (a platinum-iridium alloy cylinder) kept at International Bureau of Weights and Measures, at Sevres, near Paris, France
- Second: The second is the duration of
- Ampere: The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 metre apart in vacuum, would produce between these conductors a force equal to
- Kelvin: The kelvin, is the
- Candela: The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency
- Mole: The mole is the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon - 12 .
| FACTOR | PREFIX | SYMBOL |
|---|---|---|
| yotta - | ||
| zeeta - | ||
| exa - | ||
| peta - | ||
| tera - | ||
| giga - | ||
| mega - | ||
| kilo - | ||
| hecto - |
| FACTOR | PREFIX | SYMBOL |
|---|---|---|
| deca - | ||
| deci - | ||
| centi - | ||
| mili - | ||
| micro- | ||
| nano- | ||
| pico- | ||
| femto- | ||
| atto- | ||
| zepto- | ||
| yocto– |
Some units of smaller lengths
(i) 1 centimetre
(ii) 1 millimetre
(iii) 1 micron
(iv) 1 nanometre
(v) 1 angstrom
(vi)
(vii) 1 fermi (f) or femto-metre
Some units of bigger lengths
- 1 kilometre (km): This is unit for expressing terrestrial distances.
- Astronomical Unit (AU): It is the mean distance of the centre of sun from the centre of earth.
- Light Year (ly): It is distance travelled by light in vacuum in one year.
1 light year
- Parallactic Second (parsec) : It is the distance at which an arc of length
SI DERIVED UNITS WITH SPECIAL NAMES
| Physical quantity | SI Unit | |||
|---|---|---|---|---|
| Name | Symbol | Expression in terms of other units | Expression in terms of SI base units | |
| Frequency | hertz | |||
| Force | newton | |||
| Pressure, stress | pascal | |||
| Energy, work, quantity of heat |
joule | |||
| Power, radiant flux | watt | |||
| Quantity of electricity, electric charge |
coulomb | As | ||
| Electric potential, potential difference, electromotive force |
volt | or |
||
| Capacitance | farad | |||
| Electric resistance | ohm | V/A | ||
| Conductance | siemens | |||
| Magnetic flux | weber | |||
| Magnetic field, magnetic flux density, magnetic induction |
tesla | T | ||
| Inductance | henry | |||
| Luminous flux, luminous power |
lumen | |||
| Illuminance |
Important Conversions and Units
(A) (i) 1 Light year
(ii) 1 Astronomical unit
(iii)
(iv)
(v)
(vi)
(vii) 1 mile
(viii)
(ix)
(x)
(B) (i) 1 atomic mass unit
(ii)
(iii) 1 tonne
(iv)
(v)
(vi)
(vii)
(viii)
(ix) 1 h.p. =746 watt
(x)
(C) (i)
(ii)
(iii) 1 weber =
(iv) 1 degree =
(v) 1 shake =
Rules for Writing Units and Their Symbols
(i) Units named after scientists are not written with initial letter in capital, e.g. it is incorrect to write 10 Newton, the correct way is 10 newton.
(ii) But the symbols of the units named after scientists must be written in capital letter for example,
(iii) If the symbols of unit is not from a name then small letters must be used.
(iv) For derived units index notation must be used e.g.
(v) Units and symbol should not be written in plural form e.g. write 25 centimeter in place of 25 centimeters.
DIMENSIONS OF A PHYSICAL QUANTITY
We have seen that derived physical quantities can be obtained from fundamental units or base quantities. When we write a physical quantity in terms of base quantities it can be expressed as product of powers of the base quantity. For example :
The exponent of the base quantity in the expression of a physical quantity is called dimensions of the quantity. Thus force has dimensions as 1 in mass, 1 in length and -2 in time. While finding dimensions, magnitudes of quantities are not considered. The above expression can also be written as
An expression for a physical quantity in terms of fundamental quantities is known as dimensional formula.
So the dimensional formula for force is
The dimensional formulae of various derived quantities can be obtained from their relations with other quantities, in the following table dimensional formulae of various physical quantities are derived.
Do you know !!
A physical quantity may be dimensionless but still may have units. For example, plane angle is dimensionless but has radian as its unit.
A physical quantity that does not have any unit must be dimensionless.
Illustration 1 :
Derive the dimensional formulae for the following quantities :
(i) Pressure (ii) Torque (iii) Angular momentum
solution: (i) Pressure
(ii) Torque
(iii) Angular Momentum
- The division of energy and time is X. Among momentum, power, torque and electric field, which has the same dimensional formula of
Check Your Answer
Power is defined as the ratio of work (or energy) to time. Therefore,
Dimensiona of Some Physical Quantities
| S.No. | Physical Quantity | Relation with other quantities |
Dimensional formula |
Unit |
|---|---|---|---|---|
| 1. | Length, displacement, distance | |||
| 2. | Area | length |
||
| 3. | Volume | |||
| 4. | Mass | |||
| 5. | Mass Density | |||
| 6. | Linear Mass Density | |||
| 7. | Relative Density | Unitless, dimensionless | ||
| 8. | Specific gravity | Unitless, dimensionless | ||
| 9. | Speed | |||
| 10. | Velocing | |||
| 11. | Acceleration | |||
| 12. | Fonce | |||
| 13. | Coefficient of friction | Unitless, dimensionless | ||
| 14. | Work | |||
| 15. | Kinetic Energy | |||
| 16. | All forms of Energy | - | ||
| 17. | ||||
| 18 . | Linear Momentum | |||
| 19. | Linear Impulse | |||
| 20. | Power | |||
| 21. | Pressure | |||
| 22. | Stress | |||
| 23. | Young’s Modulus | |||
| 24. | Shear Modulus | |||
| 25 . | Bulk Modulus | |||
| 26. | Strain | Unitless, dimensionless | ||
| 27. | Universal constant of gravitation | |||
| 28. | Poisson Ratio | Unitless, dimensionless | ||
| 29. | Surface Tension | |||
| 30. | Frequency | |||
| 31. | Angular velocity | |||
| 32. | Radius of gyration | length | ||
| 33. | Moment of Inertia | |||
| 34. | Angular Momentum | |||
| 35. | Rotational kinetic energy | |||
| 36. | Wavelength | |||
| 37. | Coefficient of visosity | |||
| 38. | Reynolds number | Unitless dimensionless | ||
| 39. | Temperature | |||
| 40. | Heat Energy |
|||
| 41. | Specific Heat . | |||
| 42. | Heat Capacity | |||
| 43. | Latent Heat of fusion or vaporisa- tion |
|||
| 44. | Gas constant | |||
| 45. | Boltzmann constant | |||
| 46. | Stefan’s constant | |||
| 47. | Power of a lens | |||
| 48. | Planck constant | |||
| 49. | Electric current | A | ||
| 50. | Electric charge | As |
||
| 51 . | Electric potential | |||
| 52 . | Absolute permittivity | |||
| 53. | Electric field | |||
| 54. | Electric dipole moment | |||
| 55. | Electrostatic potential Energy | |||
| 56. | Electric resistance | |||
| 57. | Resistivity | |||
| 58. | Capacitance | |||
| 59. | Magnetic field strength/ Induction | |||
| 60. | Magnetic flux | |||
| 61. | Coefficient of self-induction |
Uses of Dimensional Analysis
The following are the uses of dimensional analysis.
(i) To convert a unit from one system to other
Dimensions are quite useful for finding the conversion factor for the unit of a physical quantity from one system to another. We know that
where
So,
Illustration 2 :
Convert 1 pascal
SOLUTION : Pascal is unit of pressure whose dimensional formula is
Given
Using the formula
Illustrotion 3 :
What will be the value of 100 newton in a new system which has
SOLUTION : Dimensional formula for force is
Using
(ii) To check the correctness of a physical equation
According to the principle of homogeneity of dimensions, only those physical quantities can be added or subtracted which have the same dimensions. In other words an equation which is containing several terms separated from each other by the equality, plus or minus must be of the same dimensions. An equation will be dimensionally correct only and only if all the terms have the same dimensions. For example in the equation
Thus the equation
Illustration 4 :
Verify dimensional accuracy of the formula
SOLUTION : LHS
RHS
As dimensions of both sides of equation are the same, so, the formula is dimensionally correct.
(iii) To establish relation among different physical quantities
If the dependence of a physical quantity on other physical quantities is of product type then using dimensions the formula for the given physical quantity can be deduced. This method is also based on the principle of homogeneity of dimensions. For example a mass attached with a spring oscillates in the vertical direction, we assume that the time period of oscillation
where
Thus: by dimensional analysis we have deduced that time period of a spring-mass system is independent of gravity, directly proportional to square root of mass and is inversely proportional to square root of spring constant.
Illustration 5 :
Viscous force
SOLUTION :
Taking dimensions on both the sides
The value of
Limitations of Dimensional Analysis
(a) For deriving a formula, we should know the quantities on which a particular quantity depends.
(b) The method works only if dependence of physical quantities is of product type only.
(c) The method does not give any information about the dimensionless constant.
(d) We cannot derive the formulae which contain exponential, logarithmic and trigonometrical functions.
(e) The method works only if there are as many equations available to us as there are unknowns. For example if in mechanics a physical quantity depends upon more than three other physical quantities then the method fails.
(f) - An equation can be dimensionally correct but otherwise incorrect. As
Do you know !!
In composite relations, each term has the same dimensi ons. It is because, only like quantities can be added and subtracted from one another.
Types of Physical Quantities on Basis of Dimensions
According to dimensions there are four types of physical quantities.
(a) Dimensional constants : Those quantities which have fixed value but possesses dimensions. For example (i) Gravitational constants (ii) Planck’s constant (iii) Velocity of light etc.
(b) Dimensionless constant : Those quantities which have fixed value but does not have dimensions. For example (i)
(c) Dimensional variables : Those quantities which have dimensions but do not have fixed value. For example velocity, volume, force, etc.
(d) Dimensionless variables : Those quantities which do not have dimensions and fixed value. For example (i) strain (ii) relative density (iii) angle etc.
ERRORS IN MEASUREMENT
Measurement is an important and essential part of our life. Generally measured value of a quantity is different from the true value of the physical quantity. The difference between the true value and measured value is called error. Before we discuss about errors let us understand two important terms :
(a) Accuracy : It is the measure of how close the measured value is to the true value of the physical quantity.
(b) Precision : It tells us about the limit or resolution upto which the quantity is measured.
Suppose certain body has true value of its mass as
Types of Errors
(i) Systematic errors : Those errors which tend to be in one direction, either positive or negative, generally their cause is known. These errors can be minimised by improving experimental techniques selecting better equipments and removing personal bias. Some of the sources of systematic errors are:
(a) Instrumental errors: This type of error arises due to imperfect design or calibration of the measuring instrument, for example zero mark of varnier scale may not coincide with zero mark of main scale in a vernier callipers.
(b) Imperfection in experimental procedure : For example, measuring temperature of a human body by placing thermometer under armpit would give lower temperature than the actual body temperature, ignoring force of buoyancy during the measurement of weight a body etc.
(c) Personal error : This type of error arise due to lack of proper setting of the apparatus, individual bias, or due to carelessness while taking observation. For example if you hold your head too much towards while reading ammeter or voltmeter there will be some error due to parallax.
(d) Errors due to external factors like variation in temperature, humidity pressure wind etc. may introduce errors. For example wind may introduce error while taking the time period of a simple pendulum.
(ii) Random Errors : These arise due to unpredictable and random variations in experimental conditions like temperature, voltage supply, personal (unbiased) error by observer etc. These errors are also called ‘chance’ errors as these occurs irregular and are random with respect to sign (negative or positive) and size.
Random errors can be minimised by taking the observation several times and taking the arithmetic mean of all the observation. The error associated with the resolution of an instrument is called least count error. The smallest division on the scale of a measuring instrument is called its least countr. By using instrument of high precision and improving experimental technique we can minimise least count errors.
(iii) Gross Errors : These arise entirely due to carelessness of the observer like reading an instrument without proper setting, recording observation incorrectly etc. This type of errors can be minimised if the observer is mentally alert and sincere.
Other Types of Errors
(a) Absolute error : The magnitude of the difference between the true value and the individual measured value is called absolute error of the measurement.
Suppose individual values obtained in various observations are
Then the true mean value is given by
Then the absolute errors are :
Absolute errors can be negative or positive or zero also.
(b) Mean absolute error : It is the arithmetic mean of magnitudes of absolute errors in all measurements.
Final measurement in the terms of mean absolute error is expressed as
Remember the mean absolute error has the same unit as that of the measured quantity.
(c) Relative or fractional error : It is equal to the ratio of mean absolute error to the mean (true) value of measured quantity.
Relative Error does not a unit.
If it is expressed in terms of percentage then it is called percentage error
(
(
Final measurement in terms of the percentage error will be expressed as (
COMBINATION OF ERRORS
Suppose a physical quantity depends upon a number of other quantities which are to be measured experimentally. When we measure those quantities, there will be errors which we also affect the final measurement. In order to estimate the error in the final measurement we should know how individual errors combine in addition, subtraction, multiplication and division.
(a) Error in the sum of quantities: Let
There is a physical quantity
Then,
or
So
So, when two physical quantities are added the mean absolute error in the final measurement is equal to the sum of individual mean absolute errors.
(b) Error in difference of quantities : Suppose a physical quantity
Then
So, when two physical quantities are subtracted then the mean absolute error in the final measurement is given by the sum of individual mean absolute errors.
(c) Error in product of quantities :
Let
Then
So, when two quantities are multiplied the fractional error (or percentage error) in the result is equal to the sum of individual fractional (or percentage) errors.
(d) Error in division of quantifios : Suppose a physical quantity is given as :
$$ P=\frac{A}{B} $
Then
hence neglected
Or
So, in division of quantities fractional error (or percentage error) in the final result is equal to the sum of individual fractional error (or percentage error).
(e) Errer in quantity ralsed to some power:
If
Then
In General,
If
then
So, the fractional error (or percentage error) in a physical quantity raised to the power is equal to power times the fractional error (or percentage error). Therefore the physical quantities which are raised to some powers should be measured with maximum accuracy (least error).
Illustration 6 :
Two resiatances
Solution : In series combination of resistances, the resultant is given by
So,
Resistance in terms of mean absolute error
Percentage Error
Sa. resistance in terms of
Illustration 7 :
If
solution: As
So, the final length
Now, percenage error
So, final length in terms of percentage error
Illustration 8 :
Leagth and breadth of a rectangle are given as
solution: As in multiplication percentage errors are added so,
percentage error in area
where
Hence, area in terms of percentage error
Now,
Illustration 9 :
Find mean abselute error and percentiage error in
solution:
Using
Note : Percentage error in
Illustrotion 10
A physical quantity
The percentage errors of measurement in
solution : Given
So,
Hence,
SIGNIFICANT FIGURES
Significants digits or figures give information about the accuracy of a measurement. It tells us about the number of digits in which we have confidence. Suppose a particular measurement is reported to be
Rule-1. All the non-zero digits are significant-For example 2134 has four significant digits and 27184 has five significant digits.
Rule-2. All the zeros between two non-zero digits are significant, no matter where the decimal point is, if at all. For example 25089 has five significant digits, 12.0021 has six significant digits.
Rule-3. In a number which is less than one all zeros to the right of decimal point and to the left of a non-zero digit are not significant.
Rule-4. All the zeros on the right of last non-zero digits are significant in a number with a decimal point. For example in 3,500 there are four significant digits and in
Rule-5. All the zeros on the right on a non-zero digit are not significant in a number without decimal point. For example 15800 has only three significant digits, 18930000 has only four significant digits.
Rule-6. All the zeros on the right on a non-zero digit are taken to be significant when these come from a measurement. For example some distance is measured to be
Rule-7. A change of system of units does not change the number of significant digits in a measurement. Also when a number is written in scientific notation
Illustration 11 :
Write down the number of significant figures in the following :
(i)
solution: (i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii) 91.000 has five significant figures.
Rules for Arithmetic Operations with significant Figures
(a) Addition and subtraction : The final result should retain as many decimal places as there are in the number with the least decimal places. For example if we add
(b) Multiplication and division : In multiplication and division the final result should retain least number of significant digits from among all the numbers. Suppose density of a material is
But according to the rule of significant digits it may be
As the number 6.921 has 4 significant digits, 2.11 has 3 significant digits so the final answer must contain only ’ 3 ’ significant digits.
Obtain the value of
Check Your Answer
Illustration 12 :
Each side of a cube is measured to be
solution : Here, the side of cube is measured upto ’ 4 ’ significant digits, so the calculated area and volume should be rounded off to 4 singnificant digits.
Surface area
Surface area
Volume
Volume
ROUNDING OFF A NUMBER
(a) Uncertainity : It is taken a half of the least count of the measuring instrument. Suppose length and breadth of a rectangular piece of paper are measured with the help of a meter scale with least count of
If, we find the area of rectangular sheet of paper then uncertainity in the final result will equal to the square root of the sum of square of percentage uncertainities:
Area
(b) Rounding off the uncertain digit :
Rule-1. Preceding digit is increased by one if the insignificant (uncertain) digit which is to be rounded off is more than 5.
For example a number
Rule-2. Preceding digit remains the same if the insignificant digit which is to be rounded off is less than 5. Suppose the number is 9.873 then after rounding off to 3 significant digits it will become 9.87 .
Rule-3. If the digit to be rounded off is 5 and preceding digit is even then the preceding digit is left unchanged. For example the number to be rounded off is
Rule-4. If the digit to be rounded off is 5 and preceding digit is odd then the preceding digit is increased by one.
For example if the number is
Illustration 13
Round off the numbers 8121, 978.5, 12.68, 5.735, 8.925, 11.2 2
Solution :
| SL. No | Number to be rounded off | Rounded off number | Rule |
|---|---|---|---|
| 1. | 8100 | 2 | |
| 2. | 978 | 3 | |
| 3. | 12.7 | 1 | |
| 4. | 5.74 | 4 | |
| 5. | 8.92 | 3 | |
| 6. | 11.2 | 2 |
EXERCISE 1
DIRECTIONS : Complete the following statements with an appropriate word / term to be filled in the blank space(s).
- There are fundamental and supplementary units in S.I. system.
- The measurement of a physical quantity is the prouduct of the numerical value and the
- In C.G.S. system, force is measured in
- Metre per second is a of that quantity. unit.
- Candela is a unit.
- There are two supplementary units in S.I. system. They are and
- Ampere is an S.I. unit for the quantity called
- The dimensions of force are
- The dimensional analysis can be used to check the of a given relationship.
- If errors in the measurement of the length and the breadth of a rectangle are
- The number of significant figures in 12345 is
- The number 1040 has significant figures.
- A physical relation which is correct is not necessarily physically correct.
- Angstrom is a unit for
- S.I. unit of luminous intensity is …..
- The dimensions of ……………….. in force is -2 .
- Instrumental error belong to ………………… errors.
- Number of significant figures in 4.00 is
- 1 Angstrom is equal to ..
- The word RADAR stands for ranging.
- ……………….. waves are used in SONAR.
- Mass of electron is or order of
- S.I unit of angle is to obtain accurate value of the quantity.

DIRECTIONS : Read the following statements and write your answer as true or false.
- Light year is a unit of time.
- The magnitude of a quantity change with change in the unit of system.
- A quantity has same dimensions in different system of units.
- After rounding off the number 0.05857 to two significant figures we get 0.059 .
- The S.I. unit of the amount of substance is mole.
- The S.I. unit of acceleration is
- The unit of surface tension is newton per metre
- The dimensions of force are
- The units of work and torque are same.
- The error in the measurement in the radius of a sphere is
- Dimensional analysis is not applicable in case of trigonometrical and logarithmic function.
- A constant has the dimension of length.
- The dimensional equation for acceleration is [Acceleration]
- The equation
- The unit of magnetic energy is same as that of the unit of mechanical energy.
- A unitless quantity must be dimensionless.
- If numerical value of a quantity is
- If
- If
- Light year is a unit of time.
- Parsec is largest practical unit of length.
- Two different quantities may have same dimensions.
- Speed and velocity have same dimensions.
- Zero error is a constant error
- Random error can be removed completely.

**DIRECTIONS : **Each question contains statements given in two columns which have to be matched. Statements
| Column I | Column II |
|---|---|
| (Quantity) | (Unit) |
| (A) Area | (p) |
| (B) Speed | (q) |
| (C) Force | (r) |
| (D) Work | (s) |
| Column I | Column II |
|---|---|
| (Quantity) | (Dimension) |
| (A) Momentum | (p) |
| (B) Coefficient of viscosity | (q) |
| (C) Force | (r) |
| (D) Energy | (s) |
| Column I | Column II |
|---|---|
| (Quantity) | (C.G.S unit) |
| (A) Acceleration due to gravity | (p) |
| (B) Specific heat capacity | (q) |
| (C) Impulse | (r) |
| (D) Power | (s) ergs |
- Match the quantities (Column I) with their respective dimensions (Column II).
| Column I | Column II |
|---|---|
| (A) Velocity | (p) |
| (B) Force | (q) |
| (C) Acceleration | (r) |
| (D) Displacement | (s) |
- Match the quantities (Column I) “with their S.I units (Column II)
| Column I | Column II |
|---|---|
| (A) Mass | (p) kelvin |
| (B) Length | (q) kilogram |
| (C) Electric current | (r) metre |
| (D) Temperature | (s) ampere |

DIRECTIONS : Give answer in one word or one sentence.
- What is meant by unit?
- What should we know in order to measure a physical quantity?
- Is light year a unit of time?
- Define light year.
- What is the unit for measuring wavelength of light ?
- How many times a kg is larger than a
- What are the dimensions of angular displacement?
- What are the dimensions of angular momentum ?
- What are the dimensional formulae for the following: (i) pressure, (ii) power, (iii) density and (iv) angle
- Find dimensional formula of latent heat.
- Name two physical quantities which have same dimensions as that of work.
- Can a quantity have units but still be dimensionless ?
- Are all constants dimensionless ?
- What is the unit of pressure in SI?
- Define significant figures.
DIRETIONS : Give answer in 2-3 sentences.
- What importance do we attach to zeroes immediately after the decimal point?
- Subtract with due regard to significant figures:
- Solve the following with due regard to significant figures:
- What are the dimensions of gravitational constant ?
- Give the dimensional formula of thermal conductivity.
- Write four pairs of physical quantities, which have the same dimensional formula.
- What is the advantage of expressing physical quantities in terms of dimensional equations?
- In the equation
- Derive the SI unit of joule (
- What is the advantage in choosing the wavelength of a light radiation as a standard of length ?

DIRECTIONS : Give answer in four to five sentences.
- What do you mean by the unit of a physical quantity? Explain the types and systems of units.
- What is S.I. system of units ? Write its fundamental and derived units.
- Define the fundamental units of S.I. system.
- What do you mean by dimension of a physical quantity? Write the uses of dimensional analysis.
- How the dimensional method is used to convert a unit from one system to another? Explain with the help of an illustration.
- What is significant figure? Mention the rules to write the number of significant figures.
EXERCISE

DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b). (c) and (d) out of which ONLY ONE is correct.
- Which of the following systems of units is not based on units of mass, length and time alone?
(a) SI
(b) MKS
(b) CGS
(d) FPS
- Unit of latent heat is
(a)
(c)
(b)
(d)
- Which of the following is not a unit of time?
(a) Solar year
(b) Tropical year
(c) Leap year
(d) Light year
- Dyne-sec is the unit of
(a) momentum
(b) force
(c) work
(d) angular momentum
- One shake is equal to
(a)
(b)
(c)
(d)
- One torr is equal to
(a)
(b) Atmosphere
(c)
(d)
- What are the units of magnetic permeability?
(a)
(c)
(b)
(d)
- The ampere-second is a unit of
(a) current
(b) charge
(c) energy
(d) power
- The SI unit of coefficient of mutual inductance of a coil is
(a) henry
(b) volt
(c) farad
(d) weber
- SI unit of magnetic flux is
(a) gauss
(b) weber
(c) oersted
(d) ampere/metre
- Unit of specific resistance is
(a)
(b) ohm
(c) ohm - m
(d)
- Light year is
(a) Light emitted by the sun in one year.
(b) Time taken by light to travel from sun to earth.
(c) The distance travelled by light in free space in one year.
(d) Time taken by earth to go once around the sun.
- SI unit of pressure is
(a) atmosphere
(b) bar
(c) pascal
(d)
- Electron volt is a unit of
(a) potential difference
(b) change
(c) energy
(d) capacity
- Dimension of impulse are
(a)
(c)
(b)
(d)
- Units of coefficient of viscosity are
(a)
(b)
(c)
(d) None of these
- What are the dimensions of Action?
(a)
(b)
(c)
(d)
- Which is dimensionless?
(a) Force/acceleration
(b) Velocity/acceleration
(c) Volume/area
(d) Energy/work
- Potential is measured in
(a) joules/coulomb
(c) newton-second
(b) watt/coulomb
(d) none of these
- One second is defined to be equal to
(a) 1650763.73 periods of the Krypton clock
(b)
(c) 1650763.73 periods of the Cesium clock
(d) 9192631770 periods of the Cesium clock
- If
(a)
(c)
(b)
(d)
- The dimensions of electromotive force in terms of current A are
(a)
(c)
(b)
(d)
- The expression
(a) pressure
(b) power
(c) stress
(d) Young’s modulus
- The dimensions of universal gas constant are
(a)
(c)
(b)
(d)
- Dimensions of specific heat are
(a)
(b)
(c)
(d)
- Which physical quantities have same dimension?
(a) Moment of couple and work
(b) Force and power
(c) Latent heat and specific heat
(d) Work and power
- Distance travelled by a particle at any instant ’
(a)
(c)
(b)
(d)
- In the eqn.
(a) dyne
(b) dyne
(c)
(d) dyne
- Error in the measurement of radius of a sphere is
(a)
(b)
(c)
(d)
- A quantity is represented by
(a)
(b)
(c)
(d) None of these
- Subtract
(a)
(c)
(b)
(d)
- Multiply 107.88 by 0.610 and express the result with correct number of significant figures
(a) 65.8068
(b) 65.807
(c) 65.81
(d) 65.8
- When 97.52 is divided by 2.54 , the correct result is
(a) 38.3937
(b) 38.394
(c) 38.39
(d) 38.4
- The radius of a thin wire is
(a) 0.08
(b) 0.080
(c) 0.0804
(d) 0.80384
- S.I. unit of surface tension is
(a) degree/
(b)
(c)
(d)
- Weber
(a) Tesla
(c) Watt
(b) Henry
(d) None
(a) Force
(b) Moment of force
(c) Momentum
(d) Power
- Which of the following is not the name of a physical quantity?
(a) Displacement
(b) Momentum
(c) Metre
(d) Torque
- Watt-hour meter measures
(a) current
(b) voltage
(c) power
(d) electric energy
- If
(a)
(b)
(c)
(d)
- If time
(a)
(c)
(b)
(d)
- The number of significant figures in
(a) 1
(b) 2
(c) 3
(d) 4
- In a simple pendulum experiment for the determination
of acceleration due to gravity, time period is measured with an accuracy of
(a)
(b)
(c)
(d)
(a)
(b)
(c)
(d)
More than One correct
DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONE OR MORE may be correct.
- Which of the following pairs have same dimensions?
(a) Light year and wavelength
(b) Torque and work
(c) Angular momentum and work
(d) Energy and Young’s modulus
- Choose the correct statements :
(a) A dimensionally incorrect equation may be incorrect
(b) A dimensionally correct equation may be incorrect
(c) A dimensionally incorrect equation may be correct
(d) A dimensionally correct equation may be correct
- Which of the following are not a unit of time?
(a) Light year
(b) Second
(c) Parsec
(d) Micron
- When a wave traverses a medium the displacement of a particle located at
where
Which of the following are dimensionless quantities?
(a)
(b)
(c)
(d)
- Which of the following are the units of mass?
(a) amu
(b) Quintal
(c)
(d) Metric ton
- Which of the following are true regarding significant figures?
(a) The zeros appearing in the middle of a number are significant, while those at the end of a number without a decimal point are ambiguous.
(b) All non-zero digits are significan
(c) Greater the number of significant figures in a measurement smaller is the percentage error
(d) The power of 10 are counted while counting the number of significant figures.
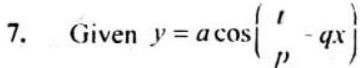
where
(a) The unit of
(b) The :nit of
(c) The unit of
(d) The unit of
- Identify the pairs having ickntical dimensions
(a) Strain and ingle
(b) Planck constant and angulan momintum
(c) Linear momentun and moment of force
(d) Pressure and modulus of clasticils
Multiple Matching Questions
DIRECTIONS : Following question has lon’ velt mem. A. B.
- Match the quantities having same dimensions: Column I
| Column I | Column II |
|---|---|
| (A) Stress | (p) Force |
| (B) Pressure | (q) Strain |
| (C) Tension | (r) Angle |
| (D) Refractive index | (s) Young’s modulus |
| (t) Energy per unit volum |
- If
| Column I | Column II |
|---|---|
| (A) |
(p) |
| (B) |
(q) |
| (C) |
(r) |
| (D) |
(s) |
| (t) |
Fill in the Passage
DIRECTIONS : Complete the following passage(s) with an appropriate word/term to be filled in the blank spaces.
minimised, instrumental errors, environmental errors, Systematic errors. random errors, personal errors.
I. No measurement can be perfect, some errors are always associated with the measurement. The errors cause of which are known ____ (1) ____ . This type of errors can again of three types. The errors caused due to faulty instrument are called ____ (2) ____ the crrors caused due to carelessness of the observer are called ____ (3) ____ and the errors caused due to environmental factors are called ____ (4) ____ The other category of errons fier which cause of errors is not known are called ____ (5) ____ This type of errors cannot be eluminated completely but can be ____ (6) ____ by taking more and more observations .
kg. S.I system. seven, independent, second, ampere,Fundamental, derived
II. Physical quantities are mainly of two types ____ (1) ____ quantities are the quantities which are basic in nature and cannot be derived from other quantities. There are a total of ____ (2) ____ such quantities. On the other hand ____ (3) ____ quantities are the physical quantities which can be derived from other quantities. The chose of basic quantities is not, i.e. any quantity can be taken a basic but all such quantities must be ____ (4) ____ of each other. There are different systems of units used for measurement of physical quantities but the system which is internationally accepted is called ____ (5) ____ In this system, unit of time is ____ (6) ____ unit of electric current is ____ (7) ____ and unit of mass is ____ (8) ____
Passage Based Questions
DIRECTIONS: Stuly the given paragraph(s) and answer the following yuctions.
Passage - I
Dimensions are the powers to which fundamental quantities must be raised to represent a given physical quantity. Again the choice of fundamental quantities is not unique. A set of physical quantities which are independent of each other may be taken as fundamental quantities. Based on the above information and knowledge of dimensions, answer the following.
- Which of the following set of quantities cannot be taken as fundamental?
(a) force, length, time
(b) momentum, length, time
(c) acceleration, length, time
(d) mass, velocity, acceleration.
- If momentum
(a)
(c)
(b)
(d)
- In the previous case, the dimensional formula for force will be
(a)
(c)
(b)
(d)
Passage II
the mas of a cube measured with a balance of least cont
- The pereentage error in the measurement of mass of the cule is
(a)
(b) 4”:"
(c)
(d)
- Nevolute ctror in the measurement of volume is
(i)
(b)
(c)
(d)
- Wholute error in the measurement af density is
(i)
(i)
(b)
(d)
Assertion & Reason
DIRECTIONS : Each of these questions contains an Assertion followed in Reason. Redl them carefully and answer the question an the basis of following options. You have to select the one that best describes the two statements.
(a) II both Assertion and Reason are correct and Reason is the correct explanation of Assertion
(b) If hoth Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
- Assertion : Light year and wavelength both measure distance.
Reason : Both have dimensions of time.
- Assertion : Force cannot be added to pressure.
Reason : Their dimensions are different.
- Assertion : Density is a derived physical quantity.
Reason : Density cannot be derived from the fundamental physical quantitics.
- Assertion : The graph between
Reason: The straight line graph means that
- Assertion : Number of significant figures in 0.005 is one and that in 0.500 is three.
Reason : This is because zeros are not significant.
- Assertion : Radian is the unit of distance.
Reason : One radian is the angle subtended at the centre of a circle by an arc equal in length to the radius of the circle.
Hots subjective Questions
DIRECTIONS: Answer the following questions.
- Each side of a cube is measured to be
- 5.74 g of a substance occupiev
- The mass of a box measured by a grocer’s balance is
- Find the dimensions of
- The formula
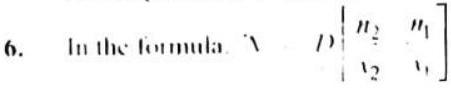
D diffusion coefficients
- A gas bubble from an explosion under water, oscillates with a period T proportionaly to P d F where p isthe state pressure, d isthe density of water and b is the total energy of explosion. Find the values of a, b and c
- If velocity. force and time are taken to be furdiamental quantities, find dimensional formula tor (a) Masses and (b) Energy.
- Let us consider an equation
- A calorie is a unit of heat or energy and it equals about 4.2 J where 1J is
- What is the dimensions of physical quantity 1 m the equation Force
- If force, acceleration and time are taken as fundamental quantities, then find the dimensions of length.
- Check the dimensional consistency of the equation :
where
- Check the correctness of the relation by dimensional analysis :
where the letters have their usual meanings.
EXERCISE - I
FILL IN THE BLANKS
- seven, two
- unit
- dyne
- derived
- fundamenta
- radian, steradian
- electric current
- velocity
- correctness
- 3.5 %
Hint : Area
- five
- three
- dimensionally
- length
Hint : Angstrom
- Candela
- time
- systematic
- three
- radio
- ultrasonic
- radian
- subtracted
TRUE/FALSE
- False
- True
- True
- True
- True
- False
- True
- True
- True
- False
Hint: Volume
- True
- False
Hint: A constant has no dimension
- True
- True
- True
Hint : All kind of energy has same unit.
- True 17. False 18. True
- False 20. False 21. True
- True 23. True 24. True
- False
MATCH THE COLUMNS
VERY SHORT ANSWER QUESTIONS
-
The unit of a physical quantity is a standard of the same kind chosen in order to measure that quantity.
-
Its unit and the number of times the unit is contained in the physical quantity.
-
No, it is a unit of distance.
-
One light year is defined as the distance travelled by light in one year.
-
Angstrom
-
-
Since angular displacement
-
-
(i)
-
[Latent heat]
-
Torque and energy
-
Yes. For example, unit of angle is radian, but it is a dimensionless quantity.
-
No. For example,
-
-
The digits, whose values are accurately known in a particular measurement, are called its significant figures.
SHORT ANSWER QUESTIONS
-
All zeros to the right of a decimal point and to the left of a non-zero digit are never significant. 0.00967 contains three significant figures. The single zero conventionally placed to the left of the decimal point in such an expression is also never significant. All zeroes to the right of a decimal point are significant, if they are not followed by a non-zero digit. 30.00 contains four significant figures. All zeros to the right of the last non-zero digit after the decomal point are significant. 0.07800 contains four significant figures.
-
Now,
Since each of
3.52 has least number of significant figures i.e., three. Therefore, rounding off the result to three significant figures,
we have
- We know,
- The coefficient of thermal conductivity is given by
Where,
Note: Here, the coefficient of thermal conductivity has been denoted by
6. 1. Work and energy
-
Pressure and stress
-
Velocity gradient and frequency
-
Angular momentum and Planck’s constant.
7. The dimensional formula of a physical quantity indicates the fundamental units on which the physical quantity depends. It further tells the powers of the fundamental units, on which the given physical quantity depends.
- Since, angle is dimensionless, both
Therefore,
and
- Joule is unit of work. We know that
work
- The advantages in choosing the wavelength of a light radiation as a standard of length are as follows :
- The wavelength of light is not affected by time and environment.
- This standard of length does not undergo any change with place.
EXERCISE - 2
MULTIPLE CHOICE QUESTIONS
-
(a)
-
(a)
-
(b) Tropical year is the year in which there is total solar eclipse. Light year represents distance.
-
(a) As force
- (a)
- (d)
- (a) From Biot Savart’s law
- (b) charge
- (a)
- (b) According to Faraday’ Law
so dimensionally
and the S.I unit of magnetic flux is volt
- (c)
- (c) 1 light year speed of light in vacuum no. of seconds in one year
- (C) 1 pascal “1 N:
- (c) Electron volt is a unitof energy &
-
(a) Impulse - force
-
(d) coefficient of viscosity (
Force required per unit area to maintain unit velocity gradient
- (C) Action means, force & the dimension of force is
- (d) Both energy and work have same unit energy/work is a pure number
- (a) Potential is work done per unit charge
- (d)
- (d) 1 to
- (d) I:lectromotse lisec pulential dillewence
- (h)
- (a)
Where
-
(d)
-
(a) Moment of couple = force
-
(b) InS
-
(b)
- (C)

- (a) Subtraction is correct upto one place of decimal, correspending to the least number of decinal places.
- (d) Number of significant figures in multiplication is three, corresponding to the minimum number
- (d)
- (b) Radius,r 0.16 mm
Area of cross section
- (b) Surface tension
- (a) Weber
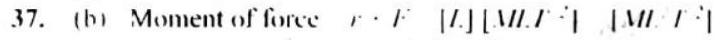
- (c) The meter is a unit and not a physical quantity?
- (d) W hr is a unit of energy
- (d)
- (C)
- (b) According to rules of significant figures.
- (c)
- (c) |at| - [F] amd
MORE THAN ONE CORRECT
- (a. b)
- (a. b. d)
- (a. c. d)
- (a. c. d)
凡. $$ \frac{y}{a}$ are dumensionless
- (a, b, c, d)
- (a, b, c)
- (a, b, d)
[P] [t] & |q|,
- (a, b, d)
MULTIPLE MATCHING QUESTIONS
- (A)
- (A)
FILL IN THE PASSAGE
I. (1) Systematic errors (2) instrumental errors (3) personal errors (4) environmental errors (5) random crrors (6) minimised.
II. (1) Fundamental (2) seven (3) derived (4) independent (5) S.I system (6) second (7) ampere (8) kg.
PASSAGE BASED QUESTIONS
- (c) Acceleration can be derived from length and time, i.e.
- (b) We have, momentum
or
- (b) We have
or
- (c) Here, mass of cube,
or
- (a)
- (d)
ASSERTION & REASON
- (c)
- (a) Quantities having different dimensions cannot be added or subtracted.
- (c)
- (d) Graph between
- (c)
(d) Radian is unit of distance
HOTS SUBJECTIVE QUESTIONS
- The number of sigmticant figures in the measured length is 4. The calculated area and the volume should therefore be rounded off to 4 , significant figures.
Surface area of the cube
volume of the cube
- There are 3 significant figures in the measured mass whereas there are only 2 significant figures in the measured volume. Hence the density should be expressed to only 2 significant figures.
Density
- (a) Total mass
(b) Difference
- Dimensionally
Also dimensionally V - b [ By principle of homogenity]
- Dimension on left
Dimension on right
- By Homogencity theory of I Dimension
Dimension of
- Given that,
Equating both sides dimensionally,
Equating the exponents of similar quantities,
Solving these equations, we get
- Let the quantity be
Assuming that the function is the product of power functions of
where
The above equation dimensionally becomes.
i.e.,
Now, (a)
So, Eq. (2) becomes
which on solving yields
Substituting it in Eqn. (1), we get
(b)
So Eqn. (2) becomes,
which in the light of principle of homogeneity yields
Which on solving yields,
So Eqn. (1) becomes,
- The dimensions of LHS are
The dimensions of RHS are
The dimensions of LHS and RHS are the same and hence the equation is dimensionally correct.
Dimensional formula of energy is
Comparing with
Now,
11.
12.
Hence,
- We have,
Dimensional formula of
Dimensional formula of
Dimensional formula of
- Here
Dimensional formula of wavelength
Therefore, dimensional formula of L.H.S.
Dimensional formula of Plank’s constant
Dimensional formula of mass
Dimensional formula of velocity
Therefore, dimensional formula of R.H.S.
As dimensional formula of L.H.S. is the same as that of R.H.S, the given relation is correct.
CHAPTER 2

The car is moving in a straight line
Motion in a Straight Line
INTRODUCTION
Motion is everywhere. It is fundamental to our human existence. We need motion for growing, for learning, for thinking and for enjoying life. We use motion for walking through a forest, for listening to its noises and for talking about all this.
Like all animals, we rely on motion to get food and to survive dangers. Like all living beings, we need motion to reproduce, to breathe and to digest; like all objects, motion keeps us warm.
Motion in an object can take place in different ways and style. When an object moves in one direction it is called motion in a straight line or motion in one dimension. When an object moves along two directions at the same time, it is called motion in a plane or motion in two dimensions and when an object moves on a circular path, the motion is called circular motion. This chapter deals with the different aspects of the motion in one dimension.
REST AND MOTION
Rest : An object is said to be at rest if it does not change its position with respect to its surroundings with the passage of time Motion : A body is said th he in motion if its position changes continuously with respect to the surroundings (or with respect to an observer) with the passage of time.
We know that earth is rotating about its axis and revolving around the sun. The stationary objects like your class-room, a tree and the lamp posts etc. do not change their position with respect to each other i.e. they are at rest. Although carth is in motion. To an observer situated outside the earth say in a space ship, your classroom, trees etc. would appear to be in motion. Therefore, all motions are relative. There is nothing like absolute motion. If you move with book in your hand, book is not moving with respect to you
Rest and Motion are Relative Terms
Rest and motion are relative terms. A particle at rest with respect to an observer can be in motıon with respect to another observer. To the passengers in a moving bus or train, trees, buildings and people on the roadsides observe that the bus or the train and its passengers are moving in the forward direction. At the same time, each passenger in a moving bus or train finds that fellow passengers are not moving, as the distance between them is not changing.
If you will observe the man moving on moving flat car from ground your observation will be different from what man himself will observe. Similarly, if you will observe pendulum in moving car from ground your observation will be different from what person inside car will observe.
Frame of Reference
To locate the position of object we need a frame of reference. A convenient way to set up a frame of reference is to choose three mutually perpendicular axes and name them
DISTANCE AND DISPLACEMENT
Motion is related to change of position. The length traveled in changing position may be expressed in terms of distance, the actual path length between two points. Distance is a scalar quantity, which has only a magnitude with no direction.
The direct straight line pointing from the initial point to the final point is callectadisplacement (change in position). Displacement only measures the change in position, not the details involved in the change in position Displacement is a vector quantity. which has both magnitude and direction. In the figure shown, an object goes from point
If one states ’the car has travelled
The displacement can be zero even if the distance is not %ero. For example when a body is thrown vertically upwards from a point on the ground, after sometime it returns back to the same point, then the displacement of the body is zero but the distance travelled by the body is not zero, it is
Similarly, if a body is moving in a circular or closed path and reaches its original position after one rotation, then the displacement in one rotation is zero, but the distance travelled is equal to the circumference of the circular path
Do you know !!
The actual distance travelled by an object in a given time interval can he equal to or greater than the magnitude of displacement. It can never be less than the magnitude of displacement.
The displacement of an object in a given time interval can be positive, zero or negative. However. distance covered by the object in a given time interval is always positive.
AVERAGE SPEED
Average speed is defined as the distance traveled divided by the time interval to travel that distance. Average speed
It is a scalar quantity.

The Cheetah averages
Instantaneous Speed
Instantaneous speed is the speed at a particular time instant (
Uniform and Non-uniform Speed
A body is said to be moving with uniform speed if it covers equal distances in equal time intervals and with non-uniform or variable speed if covers unequal distances in the same time intervals.
Do you know !!
The velocity of an object may be positive, zero or negative, but the speed of an object can never be negative.
AVERAGE VELOCITY
Average velocity is defined as the ratio of change in position or displacement to the time taken.
Here
Also,
It is a vector quantity, its unit is
- Under what condition is the average velocity equal to instantaneous velocity?
Check Your Answer
- When the displacement-time curve is a straight line, i.e., when the body is moving with uniform velocity.
Illustration 1 :
A particle moved from point
SOLUTION : Let us take,
(i) As particle comes back to the same point, displacement
(ii) Total distance covered = length of path
(iii) Average velocity
(As displacement is zero)
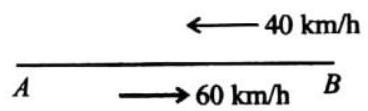
For average speed, total time
So, average speed

(i) If a particle covers two consecutive equal distances with speeds
(ii) If a particle covers three consecutive equal distances with speeds
(iii) If a particle has speed
Illustration 2 :
A particle moves in a circular path of radius
SOLUTION :
**For
Displacement
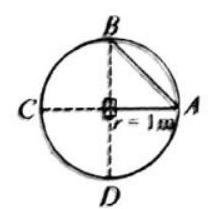
Average velocity
Average speed
(ii) For
Displacement
Average velocity
Average speed 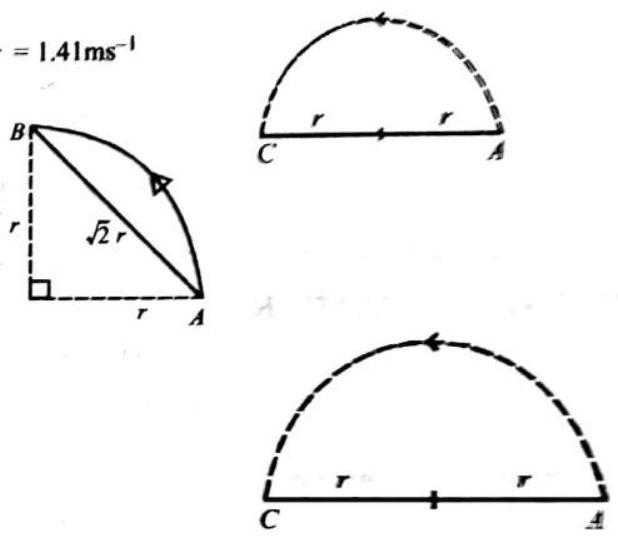
(iii) For
Displacement
Average velocity
Average speed
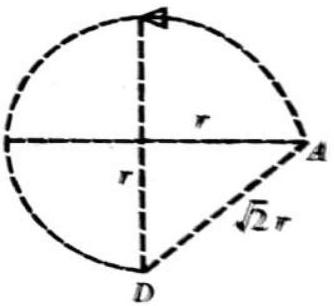
(iv) For
Displacement
Average velocity
Average speed

Instantaneous Velocity
Velocity of a body at a particular instant or moment of time is called instantaneous velocity.
Then the instantaneous velocity will be given as
Instantaneous velocity is a vector quantity, as it has direction as well as magnitude, its unit is
Illustration 3
Displacement
Solution : We know that,
So,
(i) at
(ii) at
ss,
(iii) For average velocity we use,
where
AVERAGE ACCELERATION
Average acceleration is defined as the change in velocity divided by the time interval to make the change
Instantaneous Acceleration
Instantaneous acceleration of the particle is the acceleration at particular instant, mathematically, it will be
Instantaneous acceleration is also referred to as ‘acceleration’,
Types of Acceleration :
(i) Positive acceleration : If the velocity of an object increases in the same direction, the object has a positive acceleration
(ii) Negative acceleration (Retardation) : If the velocity of a body decreases in the same direction, the body has a negative acceleration or it is said to be retarding e.g : A train slows down.
IDEA BOX
Misconception
A common misconception about velocity and acceleration has to do with their directions. Since vekecity has benth masyintoute and direction, a change in either magnilude (specl) and/or direction will result in a change in velecily, therefure an acceleratum. We can accelerate objects either by speeding them up on down (change magninde) and/on by changing lineer directune of travel.
For motion in one-dimension, when the velocity and acceleration of an whject are in the arene directum they hase the same directional signs), the velocity incieases and the object speeds up (acceleratim). When the velusity and seceration are in opposite direction, the velocity decreases and the object slows down deceleration.

When velocity of a particle increases with time, it is said to he accelerated motion i.e both aceceleration and selkeity will be positive and speed (magnitude of velocity) would increase.
When both acceleration and velocity are negative, that would mean that the direction of inotion is in the opprsite direction but in this case also speed of particle would increase with time.
If acceleration and velocity are of opposite signs, in that case speed of the particle would decrease. Iheceration is equivalent to negative of acceleration.
Factors Characterising the Motion of a Particle
Time (
Position

Speed is constant. Direction is changing Hence velocity is not constant
The values that
Velocity
- Can the velocity of an object ever be in the direction other that the direction of the acceleration of the object?
Check Your Answer
Yes, instantaneous acceleration is independent of instantaneous velocity. So the direction of velocity has no relation to the direction of its acceleration.
UNIFORM AND NON-UNIFORM MOTION
Uniform Rectilinear Motion
It is a motion in which a material point moves in a straight line and covers equal distances in equal intervals of time.
The path length of a body in a uniform rectilinear motion is equal to the magnitude of the displacement. Consequently, the path length in the motion is equal to the magnitude of the velocity multiplied by the time :
Do you know !!
No force is required to keep an object in uniform motion. When an object has uniform motion along a straight line in a given direction, the magnitude of displacement is equal to actual distance covered.
Non-uniform motion
It is a motion in which the velocity varies with time.
The change in the velocity of a material point in nonuniform motion is characterized by acceleration.
Uniformly variable motion is a motion with a constant acceleration.
Uniformly variable motion can be curvilinear like circular motion.
If a uniformly variable motion is rectilinear, i.e., the velocity
Non-uniform acceleration
If during motion of a body its velocity increases by unequal amounts in equal intervals of time.
IDEA BOX
General method of approaching numerical problems.
- Draw a ‘sketch’ diagram wherever possible.
- Copy down the numerical information given in the question.
- Write down the relevant formula.
- Substitute the given values into the formula.
- Calculate the answer, remembering to show all steps in the working out and giving the correct units for our fioal answer.
Illustration 4 :
An object moving to the right has a decrease in velocity from
SOLUTION : Given
Find
According to the definition of average acceleration,
The negative sign means the acceleration is opposite to velocity (deceleration). The result means that the object decreases its velocity by
Illustration 5
A car covers the
SOLUTION : Suppose the total distance covered is 25 . Then time taken to cover first’s distance with speed
Time taken to cover second
Illustration 6 :
The table below shows the distance in
| Time | Distance (in cm) covered in each second by |
||
|---|---|---|---|
| Object |
Object |
Object |
|
| 1st second | 20 | 20 | 20 |
| 2nd second | 20 | 36 | 60 |
| 3rd second | 20 | 24 | 100 |
| 4th second | 20 | 40 | 140 |
| 5th second | 20 | 48 | 180 |
(I) Which object is moving with constant speed ? Give a reason for your answer.
(ii) Which object is moving with a constant acceleration? Give a reason.
(iii) Which object is moving with irregular acceleration?
SOLUTION : The object
(i) The object
(ii) The object
| 1 | 4 | 9 | 16 | 25 | |
|---|---|---|---|---|---|
| 20 | 80 | 180 | 320 | 500 |
(iii) The object
EQUATIONS OF MOTION (KINEMATIC EQUATIONS)
Kinematic equations can be used to describe the motion with constant acceleration.
The symbols used in the kinematic are :
First equation :
By definition, Acceleration
Second equation :
Distance travelled - tverage velocity
But from eq. (1),
Third equation :
Distance travelled - Average velocity
But from eq. (1),v::
Among the three cyuations listed can be used to solve the majority of kinematic problems.
Which equation should you select for a particular problem? The equation you select must have the unknown quantity in it and everything clse musi be gıven, because we can only solve for one unknown in one equation.
Distance Covered by Body in
Tips to solve problem on kinematic equations :
- Make a drawing to represent the situation being studied.
- Decide which directions are to be called positive
- In an organized way, write down the values (with appropriate plus and minus signs) that are given for any of the five kinematic variables
- Before attempting to solve a problem, verify that the given information contains values for at least three of the five kinematics variables.
- When the motion of an object is divided into segments, remember that the final velocity of one segment is the initial velocity for the next segment.
Illustration 7 :
An automobile accelerates uniformby from reat to
SOLUTION
Given :
Since
Since
Illustration 8 :
A car is moving at a speed
solution : Here,
and
Since
Illustration 9 :
A bus moving with a veloeity of
solution :
as
Illustration 10 :
A bullet moving with
solution :
Illustration 11 :
A body covers a distance of 20m in the 7th second and 24m inthe 9th second. How much distance shall it cover in 15th sec.
SOLUTION :
also
From (1) equation
Substituting this value in (2),
Use this value in (3).
Now,
Illustration 12
A body with an initial velocity of
SOLUTION :
(i) Acceleration
(ii) Initial velocity
Acceleration,
and distance
From equation of motion
GRAPHICAL INTERPRETATION OF MOTION IN A STRAIGHT LINE
In physics we often use graphs ds important tools for picturing certain concepts. Below concepts of displacement, velocity and acceleration.
Displacement-Time Graphs
Belon is a graph showing the displationent of the cyclist from
This graphs shows us how. in III seconds lime, the cyclist has moved from
Do you know !!
The
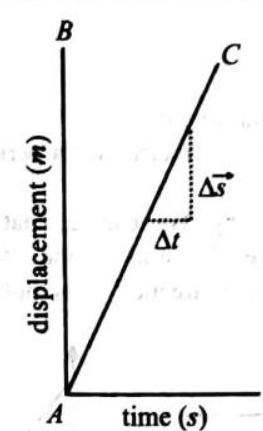
The slope is the same all the way from
(a) Shows the graph for an object stationary over a period of time. The gradient is zero, so the object has zero velocity.
(b) Shows the graph for an object moving at a constant velocity. You can see that the displacement is increasing as time goes on. The gradient, however, stays constant (remember is the slope of straight line) so the velocity is constant. Here the gradient is positive, so the object is moving in the direction we have defined as positive.
(c) Shows the graph for an object moving at a constant acceleration. You can see that both the displacement and the velocity (gradient of the graph) increase with time. The gradient is increasing with time, thus the velocity is increasing with time and the object is accelerating.
Velocity-Time Graphs
Look at the velocity-time graph below:
This is the velocity-time graph of a cyclist traveling from
Do you know !!
The
The slope of a velocity-time graph gives the acceleration.
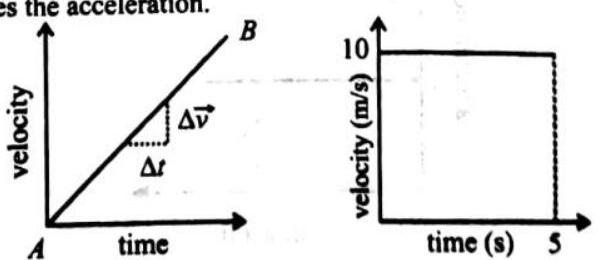
We can also calculate displacement traveled from velocity-time graph.
This graph shows an object moving at a constant velocity of
(a) Shows the graph for an object moving at a constant velocity over a period of time. The gradient is zero, so the object is not accelerating.
(b) Shows the graph for an object which is decelerating. You can see that the velocity is decreasing with time. The gradient, however, stays constant (remember: its the slope of a straight line), so the acceleration is constant. Here the gradient is negative, so the object is accelerating in the opposite direction to its motion, hence it is decelerating.
(a)
(b)
Acceleration-Time Graphs
In this chapter on rectilinear motion we will only deal with objects moving at a constant acceleration, thus all acceleration-time graphs will look like these two:
(a)
(b)
Deseription of the graphs
(a) Shows the graph for an object which is either stationary or traveling at a constant velocity. Either way, the acceleration is zero over time.
(b) Shows the graph for an object moving at a constant acceleration. In this case the acceleration is positive - remember that it can also be negative.
We can obtain the velocity of a particle at some given time from an acceleration time graph-it is just given by the area between the graph and the time-axis. In the graph below, showing an object at a constant positive acceleration, the increase in velocity of the object after 2 seconds corresponds to the portion.
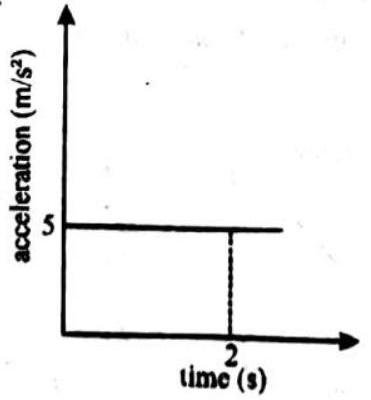
Its useful to remember the set of graphs below when working on problems. Figure shows how displacement, velocity and time relate to each other. Given a displacement-time graph like the one on the left, we can plot the corresponding velocity-time graph by remembering that the slope of a displacement-time graph gives the velocity. Similarly, we can plot an acceleration-time graph from the gradient of the velocity-time graph.
Fig. A relationship between displacement, velocity and acceleration
- A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is
Check Your Answer
Here, length of each step
time required to take one step
It follows that when the drunkard takes 5 steps forward, he will cover a distance of
GRAPHICAL DERIVATION OF EQUATION OF MOTION
(i) First Equation
It can be derived from
From line
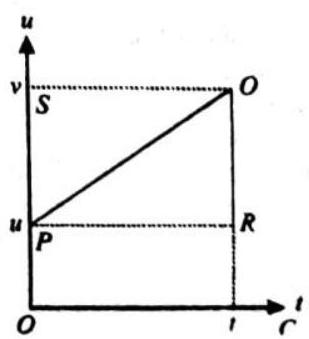
(ii) Second Equation
It can also be derived from
From relation,
Distance covered
Putting values,
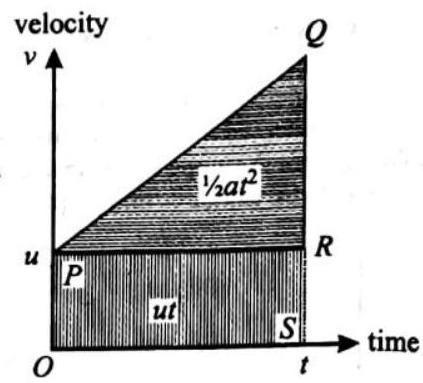
(iii) Third equation
or
From above graph
On putting the values,
Illustration 13 :
Given the displacement-time graph below, draw the corresponding velocity-time and acceleration-time graphs, and then describe the motion of the object.
SOLUTION
Step 1 : Decide what information is supplied
The question explicitly gives a displacement-time graph.
Step 2 : Decide what is asked?
3 things are required:
- Draw a velocity-time graph
- Draw an acceleration-time graph
- Describe the behavior of the object
Step 3 : Velocity-time graph - 0-2 seconds
For the first 2 seconds we can see that the displacement remains constant - so the object is not moving, thus it has zero velocity during this time. We can reach this conclusion by another path too: remember that the gradient of a displacement velocity. For the first 2 seconds we can see that the displacement-time remer that the gradient of a displacement-time graph is the the velocity during this time is zero and the object is stationary.
Step 4 : Velocity-time graph - 2-4 seconds
For the next 2 seconds, displacement is increasing with time so the object is moving. Looking at the gradient of the displacement graph we can see that it is not constant. In fact, the slope is getting steeper (the gradient is increasing) as time goes on. Thus, remembering that the gradient of a displacement-time graph is the velocity, the velocity must be increasing with time during this phase.
Step 5 : Velocity-time graph - 4-6 seconds.
For the final 2 seconds we see that displacement is still increasing with time, but this time the gradient is constant, so we know that the object is now travelling at a constant velocity, thus the velocity-time graph will be a horizontal line during this stage.
So our velocity-time graph looks like this one below. Because we haven’t been given any values on the vertical axis of the displacement-time graph, we cannot figure out what the exact gradients are and hence what the values of the velocity are. In this type of question it is just important to show whether velocities are positive or negative, increasing, decreasing or constant.
Once we have the velocity-time graph its much easier to get the acceleration-time graph as we know that the gradient of a velocitytime graph is the just the acceleration.
Step 6 : Acceleration-time graph - 0-2 seconds
For the first 2 seconds the velocity-time graph is horizontal at zero, thus it has a gradient of zero and there is no acceleration during this time. (This makes sense because we know from the displacement time graph that the object is stationary during this time, so it can’t be accelerating).
Step 7 : Acceleration-time graph - 2-4 seconds
For the next 2 seconds the velocity-time graph has a positive gradient. This gradient is not changing (i.e. its constant) throughout these 2 seconds so there must be a constant positive acceleration.
Step 8 : Acceleration-time graph - 4-6 seconds
For the final 2 seconds the object is traveling with a constant velocity. During this time the gradient of the velocity-time graph is once again zero, and thus the object is not accelerating.
The acceleration-time graph looks like this:
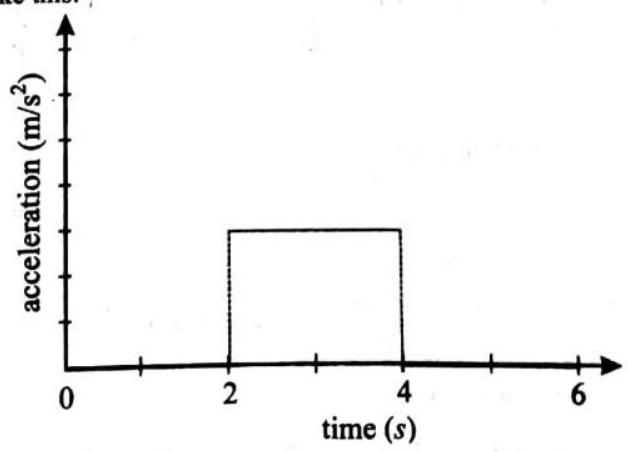
Step 9 : A description of the object’s motion
A brief description of the motion of the object could read something like this:
At
Illustration 14 :
The graph represents the velocity of a particle as a function of time.
(a) What is the acceleration at
(b) What is the acceleration at
(c) What is the average acceleration between 0 and
(d) What is the average acceleration for the
(e) What is the displacement for the
solution :
(a) Acceleration is the slope of the line
(b) The slope of the line is zero and
(c)
(d)
(e) The net area equals the displacement.
The area of a rectangle is length
Illustration 15
A train starts from rest and accelerates uniformly at
solution : The velocity-time graph is shown in figure.
Acceleration
or
Final velocity
(I) The maximum velocity reached
(ii) The retardation in the last 5 minutes
(iii) Total distance travelled
(iv) Average velocity
MOTION UNDER GRAVITY
It is a common experience that when a body is dropped form a certain height it experiences acceleration due to gravity and its motion is in a straight path. Sthilarly, when a body is thrown vertically up, it goes to a certain height and then starts falling again, experiencing acceleration due to gravity throughout the motion. The value of acceleration due to gravity
Case-I : Body thrown downward :
In this case, initial motion of the body is downward so according to the sign convention, downward direction will be taken as positive and upward direction as negative. So, the kinematic equations will be :
In a special case when the body is dropped/let fall/allowed to fall we will take the initial velocity
Case-II : Body thrown upward : If a body is thrown vertically up with an initial velocity
Maximum height reached by the body
Time of Ascent : The time taken by body thrownup to reach maximum height ’
Hence time of ascent
Time of Descent : The time taken by a freely falling body to reach the ground is called the time of descent.
and
But, we know that
Time of flight : Time of flight is the time for which a body remains in the air and is given by sum of time of ascent and time of descent.
Therefore,
Velocity on reaching ground : When a body is dropped from a height
but
Case-III : Body projected vertically up from the top of a tower:
If a body is projected vertically up from the top of a tower of height ’
displacement after time
velocity after time
Its velocity on reaching the ground is
Its maximum height above the ground is
Illustration 16 :
A body is allowed to fall from a height of
solution :
Given
Since, the body is falling downward we will use the following equations.
For velocity,
For distance travelled in the last second of motion
Illustration 17 :
A body is thrownward from a tower of height
solution : Given
For time taken to hit the ground, we use
So,
Velocity just before hitting the ground
Now, velocity after two seconds
(Using
Then
Illustration 18 :
A person sitting on the top of a tower drops ball at regular intervals of one second. Find the position of 1st, 3rd and 5th ball when the sixth ball is being dropped. (Use
solution : You can see from the adjoining figure that when the
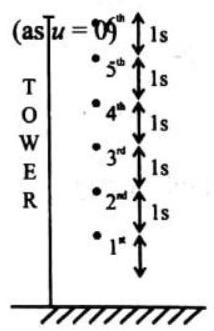
The third ball has fallen for three seconds
The fifth ball has fallen for one second only
Illustration 19
A body is projected vertically upwards. If
solution : As the initial direction of motion is upward it will be taken as positive and downward direction as negative. So using
This equation is a quadratic equation which has two roots
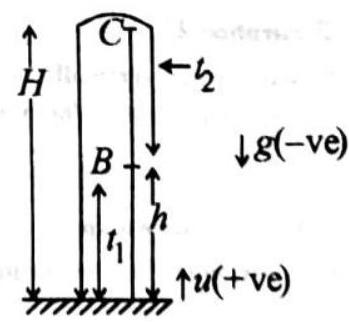
So, the velocity of projection,
Now the product of rook
Fer maxion heride
So the neal time of firis
Illustration 20
 is:
is:
 spositive. Sa
spositive. Sa
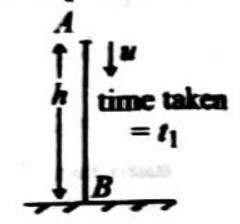
 downond so
downond so
Let
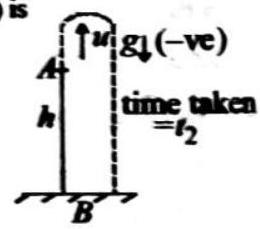
Non, aniphing (i) by
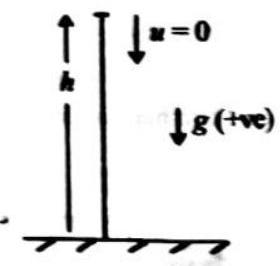
Substing tis
Illustration 21
Fer the then :
For the stone thrown downward :
downward direction +ve as it is the initial direction of motion upward direction -ve, so
Adding (i) and (ii)
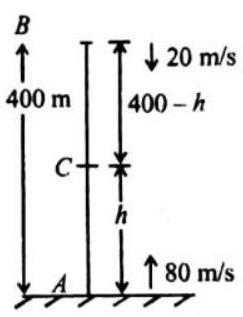
Substituting in (i)
Illustration 22
A ball is thrown vertically upwards with a velocity of
Solution We solve this problem by two methods, so that your concepts become crystal at the same time you will be able to use sign conventions properly so that a problem can be solved in the shortest time possible.
Method-1 : Upward motion
time to reach
downward motion
Now, the motion from
or
So, the total time
Method-2 : Now let us take the point of projection to be the
(
EXERCISE 1
Fill in the blanks
DIRECTIONS : Complete the following statements with an appropriate word / term to be filled in the blank space(s).
- Distance traveled divided by elapsed time gives ____
- If a car starts at rest and accelerates uniformly, the distance it travels is proportional to the ____ of the time it travels.
- All objects in free fall at a given place have the same All ____
- If a car is going.northward and the driver jams on its brakes, the direction of its acceleration is ____
- When an object is going in a circular path at constant speed, the direction of its acceleration is ____
- The length of second’s hand in a watch is
- A truck travelling due north at
- A particle is moving eastward with a velocity of
- If a particle moves in a circle describing equal angles in equal interval of times, its velocity vector ____
- A particle moves with a velocity
- The ratio of angular speeds of minute hand and hour hand of watch is ____
- A ball thrown vertically upwards return to its starting point in
- A body falling freely from the rest has a velocity
- A body, dropped from a tower with zero velocity, reaches the ground in
- The magnitude of average velocity ____ equal to the average speed.
True and false
DIRECTIONS : Read the following statements and write your answer as true or false.
- Area under velocity-time graph shows displacement.
- Magnitude of displacement can be equal to or lesser than distance.
- If particle speed is constant, acceleration of the particle must be zero
- A particle moving with a uniform velocity must be along a straight line.
- A particle is known to be at rest at time
- The equation
- A ball is thrown vertically upwards in vacuum. Then the time of ascent is equal to the time of descent.
- In a journey, numerical value of displacement
- An object covers distances in direct proportional to the square of the time elapsed. Its acceleration is increasing.
- A particle in one dimensional motion with positive value of acceleration must be speeding up.
- In circular motion the centripetal and centrifugal forces acting in opposite directions balance each other and the net force on the revolving particle is zero.
- Magnitude of acceleration is constant in the rotating motion along a circular path.
- Forces responsible for uniform circular motion are called centrifugal force.
- Centrifugal force is the reaction of the centripetal force.
- If a body is moving on a curved path with constant speed, then its acceleration is perpendicular to the direction of motion.
MATCH THE COLUMN
DIRECTIONS : Each question contains statements given in two columns which have to be matched. Statements
1.
| Column I | Column II |
|---|---|
| (A) Uniform speed | (p) Unequal distance in equal time |
| (B) Constant speed | (q) Zero acceleration |
| (C) Uniform acceleration | (r) Unequal velocity in equal time change |
| (D) Non-uniform acceleration | (s) Equal distance in equal time |
| (E) Non-uniform speed | (t) Equal velocity change in equal time |
2.
| Column I | Column II |
|---|---|
| (A) Average velocity | (p) |
| (B) Acceleration | (q) D/T |
| (C) Final velocity | (r) |
| (D) Distance | (s) |
| (E) Speed | (t) u+at |
3.
| Column I | Column II |
|---|---|
| (A) Slope of displacement-time graph | (p) acceleration |
| (B) Slope of velocity-time graph | (q) velocity |
| (C) Area under velocity-time graph intercepted with time-axis. | (r) change in velocity |
| (D) Area under acceleration-time graph intercepted with time-axis. | (s) Displacement |
Very short answer question
DIRECTIONS : Give answer in one word or one sentence.
- What does the speedometer record - the average speed or instantaneous speed?
- Can a body moving with a uniform velocity be in equilibrium?
- Two particles
- Under what condition the average velocity of a body is equal to its instantaneous velocity?
- When the magnitude of average velocity is same as that of average speed?
- Identify the type of motions? (a) a carom coin is striking against the side of a board and not rebounding smoothly but hoping up as it rebounds, (b) a car going along a zigzag path on a road.
- Can a particle has varying speed but a constant velocity?
- What is the acceleration of a particle moving with uniform velocity?
- Under what condition will the distance and displacement of a moving object have the same magnitude?
- What does the slope of position and time graph represent for uniform motion?
- If the velocity of a particle is non-zero, can its acceleration ever be zero? Explain.
- If the velocity of a particle is zero, can its acceleration ever by non-zero? Explain.
- If a car is traveling eastward, can its acceleration be westward? Explain.
- What does slope of
- A ball is thrown straight up. What is its velocity and acceleration at the top?
Short answer question
DIRECTIONS : Give anss ’er in 2-3 sentences.
- A car,
- A body moving along
- A stone released with zero velocity from the top of the tower reaches the ground in 4 second. What is the approximate height of the tower?
- A particle moves along
- In the previous example, what is the acceleration of the particle?
- The displacement of a body is given to be proportional to the cube of time elapsed. What will be the acceleration of the body?
- What is the distance travelled by a body falling freely from rest in the first, second and third seconds.
- A stone is thrown upwards with a velocity
- A body is projected vertically upwards with a velocity of
- The velocity of a body moving with a uniform acceleration of
- A motor car moving with a uniform velocity of
- A wooden block of mass
- Draw the position time graph for particle moving with positive and negative velocities.
- A car travels half the distance with constant velocity
- For a particle in one dimensional motion, the instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?
Long Answer Questions
DIRECTIONS : Give answer in four to five sentences.
- Establish the three equations of uniformly accelerated motion graphically.
- Draw velocily-lime graph of a uniformly accelerated mintion
- Draw position-time graph of an uniformly accelerated motion.
- Derive the distance travelled by body performing a motion with constant acceleration at the
- Define (a) instantaneous velocity (b) instantaneous acceleration (c) average velocity and (d) average acceleration.
- What do you mean by the distance and displacement covered by a particle? Explain with examples.
EXAMPLE 2
Multiple choice Questions
DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONLY ONE is correct
- If the displacement of a particle varies with time as
(a) velocity of the particle is inversely proportional to
(b) velocity of the particle is proportional to
(c) velocity of the particle is proportional to
(d) the particle moves with a constant acceleration
- The initial velocity of a particle is
Which of the following relation is valid
(a)
(b)
(c) ,
(d)
- The poution, “l’ a particle varies with time
(i)
(h)
(c)
(d) terr
- If a car at rest accelerates uniformly to a speed of
(a)
(b)
(c)
(d)
- The relation between time
where
(a)
(b)
(c)
(d)
- The coordinates of a moving particle at time
(a)
(c)
(b)
(d)
- The displacement of a particle is given by
The initial velocity and acceleration are respectively
(a)
(b)
(c)
(d)
- The displacement
What is the acceleration of the particle?
(a)
(c)
(b)
(d)
- The displacement-time graphs of two particles
(a)
(b)
(c)
(d)
- A car accelerates from rest at a constant rate
(a)
(b)
(c)
(d)
- A person travels along a straight road for the first half time with a velocity
(a)
(b)
(c)
(d)
- A passenger travels along the straight road for half the distance with velocity
(a)
(b)
(c)
(d)
- A point moves with uniform acceleration and
(a)
(b)
(c)
(d)
- A bus starts moving with acceleration
(a)
(b)
(c)
(d)
- When the speed of a car is
(a)
(b)
(c)
(d)
- The velocity of a particle at an instant is
(a)
(b)
(c)
(d)
- A rubber ball is dropped from a height of 5 metre on a plane where the acceleration due to gravity is not known. On bouncing, it rises to a height of
(a)
(b)
(c)
(d)
- A stơne thrown vertically upwards with a speed of
(a)
(c)
(b)
(d)
- A particle covers half of the circle of radius
(a)
(b)
(c)
(d)
- A bod
(a) from rest and moves with uniform velocity
(b) from rest and moves with uniform acceleration
(c) with an initial velocity and moves with uniform acceleration
(d) with an initial velocity and moves with uniform velocity
- A ball released from a height falls
(a)
(b)
(c)
(d)
- A food packet is released from a helicopter rising steadily at the speed of
(a)
(b)
(c)
(d) nonc of the above
- The speed of the car is
(a)
(b)
(c)
(d)
- A stone thrown upward with a speed
(a)
(c)
(b)
(d)
- A rifle bullet loses
(a) 5
(b) 10
(c) 11
(d) 20
- A stone is dropped into a well in which the level of water is
(a)
(b)
(c)
(d)
- A body dropped from a height ’
(a)
(b)
(c)
(d)
- The acceleration of a particle is increasing linearly with time
(a)
(b)
(c)
(d)
- A ball is dropped downwards, after
(a)
(b)
(c)
(d)
- Two trains are each
(a)
(b)
(c)
(d)
- If a ball is thrown vertically upwards with a velocity of
(a)
(b)
(c)
(d)
- A car moving with a vpecd of
(a)
(b)
(c)
(d)
- A stone is thrown vertically upwards. When the particle is at a height half of its maximum height, its speed is
(a)
(b)
(c)
(d)
- The acceleration due to gravity on planet
(a)
(b)
(c)
(d)
- A ball is released from the top of a tower of height
(a)
(b)
(c)
(d)
- An automobilc travelling with a speed of
(a)
(b)
(c)
(d)
- The motion of a particle is described by the equation
(a)
(b)
(c) 6 m
(d)
- For the velucity tumc graph ,hown in the figure below the distance coveral hy the turly in the last two seconds of its motion is what fraction of the total distance travelled by it in all the seven seconds?
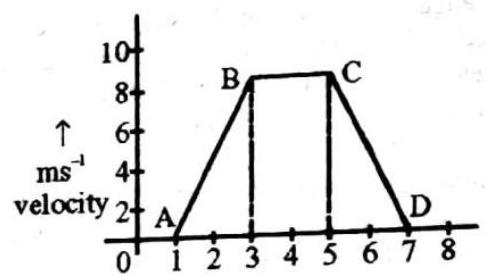
(a)
(b)
(c)
(d)
- A stone is just released from the window of a train moving along a horizontal straight track. The stone will hit the ground following a
(a) straight line path
(b) circular path
(c) parabolic path
(d) hyperbolic path
- A particle is moving eastwards with a velocity of
(a)
(b)
(c)
(d) zero
- A parachutist after bailing out falls
(a)
(b)
(c)
(d)
More than one correct
DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONE OR MORE may be correct.
- A vector quantity is a physical quantity which needs
(a) magnitude
(b) direction
(c) distance
(d) time
- Which of the following are examples of uniform velocity?
(a) Motion of moon around earth
(b) Motion of planet around sun
(c) Motion of car on crowded road
(d) Motion of a moving fan
- Average velocity can be calculated by
(a)
(b)
(c)
(d)
- Which of the following are vector quantities ?
(a) Speed
(b) Distance
(c) Velocity
(d) Acceleration
- If a body starts from rest, its
(a)
(b)
(c) velocity increases
(d) velocity decreases
- If a body moves with uniform velocity, its
(a)
(b)
(c)
(d)
- Velocity time graph of a body moving with variable acceleration is
- Which of the following is correct about the given below graph?
(a) Velocity is zero
(b) Velocity is constant
(c) Acceleration is zero
(d) Acceleration is constant
- Which of the following statements are true for displacements?
(a) It can be zero
(b) It cannot be zero
(c) Its magnitude is greater than distance travelled
(d) Its magnitude is lesser than distance travelled
- The speed of an object is
(a) distance per unit tims
(b) a scalar quantity
(c) displacement per unit times
(d) a vector quantity
Multiple matching questions
DIRECTIONS : Following question has four statements (A,
| Column I | Column II |
|---|---|
| (A) |
(p) |
| (B) |
(q) |
| (C) |
(r) Final Velocity |
| (D) |
(s) |
| (t) Initial Velocity | |
| (u) |
| Column I | Column II |
|---|---|
| (A) Acceleration | (p) |
| (B) Speed | (q) centripetal force |
| (C) Circular motion | (r) |
| (D) Displacement | (s) |
| (t) scalar quantity | |
| (u) vector quantity |
- A body is in motion for some time, then at a centain insent of time.
| Column I | Column II |
|---|---|
| (A) Distance | (p) may be positive |
| (B) Displacement | (q) may be negative |
| (C) Speed | (r) may be zero |
| (D) Velocity | (s) may be increasing |
| (t) may be decreasing |
- Match the following for the
| Column I | Column II |
|---|---|
| (A) At point A | (p) Speed is increasing |
| (B) At point B | (q) Acceleration is positive |
| (C) At point C | (r) Acceleration is negative |
| (D) At point |
(s) Acceleration is zero |
| (t) Speed is zero |
Fill in the Passage
DIRECTIONS : Complete the following passage(s) with an appropriate word/term to be filled in the blank spaces.
I. Straight, distance, equal, directly, distance
When a body moves with uniform speed, it travels equal ____ (1) ____ in ____ (2) ____ intervals of time. This means the ____ (3) ____ travelled is ____ (4) ____ proportional to time. Therefore the graph obtained is a ____ (5) ____ line passing through the origin.
II. speed, direction, centrifugal, radial, centripetal
When a body moves in a circular path, its ____ (1) ____ changes at every moment. ____ (2) ____ of the body may remain constant or change. When the force exerted is such that it keeps the body in a circular path, it is called ____ (3) ____ or ____ (4) ____ force whereas if the force exerted throws the body out of circular motion, it is called ____ (5) ____ force.
III. displacement, vector, scaler, less than, zero, distance, velocity, speed,
When a body moves from one point to another, the total length of path covered by the body is called and the shortest distance between the initial and the final position is called ____ (1) ____. Distance is a ____ (2) ____ quantity while displacement is a ____ (3) ____ quantity. The magnitude of distance can never be ____ (4) ____ that of displacement. Displacement of the body in a round trip is always ____ (5) ____ The time rate of change of distance is called ____ (6) ____ while that of displacement is called ____ (7) ____
IV. zero, straight line, parabola, increasing, decreasing, acceleration.
Equations of motion are valid only if the ___ (1) ____ of the body is constant. For such a motion, velocity-time graph is ____ (2) ____ and it passes through origin if initial velocity of the body is ____ (3) ____. Displacement time graph for such a motion is ____(4) ____. If the acceleration of the body is positive w.r.t its velocity, slope of displacement time graph is ____ (5) ____ and if its acceleration is negative w.r.t velocity, slope of displacement-time graph is ____ (6) ____
Passage based questions
DIRECTIONS : Study the given paragraph(s) and answer the following questions.
PASSAGE - 1
Consider the motion of a batsman in a cricket game. The length of the pitch is
- The total distance travelled by batsman is
(a)
(b)
(c)
(d)
- How far is the batsman from his starting point ?
(a)
(b)
(c)
(d)
- What is the net displacement of the batsman ?
(a)
(b)
(c)
(d)
PASSAGE - II
The velocity of any moving body, in ordinary circumstances, does not always remain constant. For example, a bus gains velocity while leaving a station and loses velocity while approaching a station. Similarly, when a store is dropped from a certain height, its velocity goes on increasing as it comes to the ground. But if a stone is thrown upwards its velocity goes on decreasing, till it becomes zero and then its velocity starts increasing as it approaches the ground.
- The rate of change of velocity with time is known as
(a) Acceleration
(b) Speed
(c) Intial velocity
(d) Final velocity
- What can be concluded about acceleration if velocity increases continously?
(a) Acceleration is positive
(b) Acceleration is constant
(c) Acceleration is negative
(d) Acceleration is zero
- Which of the following case represents a negative acceleration?
(a) Car starting from rest
(b) A stone falling from height
(c) Train coming to halt
(d) Bus moving with uniform velocity
PASSAGE-III
A ball is projected upwards from ground. It is observed from a
- What is the velocity of projection of the ball?
(a)
(b)
(c)
(d)
- The maximum height attained by the ball above the ground
(a)
(c)
(b)
(d)
- Total time of flight of the ball is
(a)
(b)
(c)
(d)
PASSAGE-IV
A thief is running on a motorcycle at a constant speed of 25
- After how much time will the police catch the thief?
(a) 1 minute
(b) 1.5 minute
(c) 2 miniutes
(d) 50 seconds
- How much distance will the jeep cover to reach the thief ?
(a)
(b)
(c)
(d)
- What should be the minimum acceleration of the thief to escape from police.
(a)
(b)
(c)
(d)
Assertion and Reason
DIRECTIONS : Each of these questions contains an Assertion followed by Reason. Read them carefully and answer the question on the basis of following options. You have to select the one that best describes the two statements.
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
1. Assertion : The distance-time graph of uniform motion is a straight line.
Reason : Independent variable is taken along
2. Assertion : The velocity of a body is a vector quantity.
Reason : A vector quantity has only magnitude and no direction.
3. Assertion : Motion of moon around earth is a non-uniform motion.
Reason : The size of moon is smaller than that of earth.
4. Assertion: If a body moves with uniform velocity, its acceleration is zero.
Reason : Rate of change of velocity is zero in case of body moving with uniform velocity.
5. Assertion : Instantaneous speed is the speed of a body over a long period of time.
Reason : The graph representing non-uniform speed will be a curve with increasing or decreasing slope.
6. Assertion: Displacement of a body may be zero when distance travelled by it is not zero.
Reason: The displacement is the longest distance between initial and final positive ions.
7. Assertion: The displacement time graph of a body moving with uniform acceleration is a straight line.
Reason: The displacement is proportional to square of time for uniformly accelerated motion.
Hots Subjectve Questions
DIRECTIONS : Answer the following questions.
- Sailing fun, especially on a windy day. consider the top views of the two boats betow, one sailing with the wind and the other across the wind. Which can sail faster than wind speeds?
- What will be the acceleration of a rock thrown straight upward at the moment it reaches the tippity-top of its trajectory?
- Two balls of different masses are thrown vertically upwards with the same speed. They pass through the point of projection in their downward motion with the same speed (Neglect air resistance). Is it possible?
- A particle is moving eastwards with a velocity of
- Two bodies,
- A body starts from rest and moves with a uniform acceleration. Find the ratio of the distance covered in the
- A body is moved along a straight line by a machine delivering constant power. How is the distance moved by the body proportional to time
- A stone is dropped into a well in which the level of water is
- A rocket is fired upward from the earth’s surface such that it creates an acceleration of
- When a particle is thrown vertically upward with some initial velocity, draw velocity-time and acceleration-time graph.
- Acceleration-time graph of a particle moving in a straight line is given as shown in fig. Plot its velocity-time graph. What is the maximum velocity of the particle. Initially particle was at rest.

EXERCISE - I
Fill in the Blanks
- Average speed
- Square
- Accelaration
- South
- Centripetal
- changes in direction
- 3
- 80
- may or may not be
True/Flase
| 1. True | 2. True | 3. Flase |
| 4. True | 5. False | 6. True |
| 7. True | 8. True | 9. False |
| 10. False | 11. False | 12. True |
| 13. False | 14. True | 15. True |
Match The Columns
- (A)
- (A)
- (A)
Very Short Answer Questions
- Instantaneous speed.
- Yes, since the net force acting on it is zero.
- No effect.
- When the body is moving with constant velocity, the average velocity of a body is equal to its instantaneous velocity.
- When the body is moving with a constant velocity, the magnitude of average velocity is same as that of average speed.
- (a) three dimensional motion (b) two dimensional motion
- No since both speed and velocity remain constant in uniform motion.
- Zero.
- If the object is moving along a straight line.
- Velocity.
- Acceleration
15 Velocity at the top
Short Answer Questions
- Relative velocity of
- Ditferentiating the given equation,
Difterentiating again, frodor
Therefive, anceleration
Therefive,
Therefore, after differentiating, we get the velocity, v=ds/dt = -5 + 12t
For initial velocity,
-
-
-
Distance travelled in first second of motion
Distance travelled in first two seconds of motion
Distance travelled in first three seconds of motion
Distance travelled in 2nd second
Distance travelled in 3rd second
The required ratio will be
- We know,
From this relation, we get,
Therefore,
We know,
Therefore,
- Let the block and the bullet meet at a height
for block,
For bullet,
We get.
Therefore,
Therefore,
- The
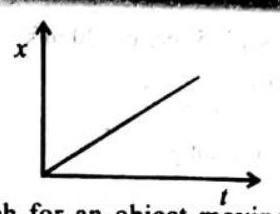
The
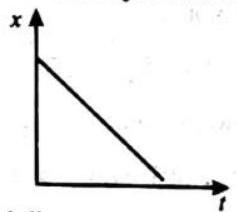
- Let
Therefore, average velocity,
- In an accelerated motion, the velocity of an object always keeps on changing. Therefore, one has to measure the instantaneous velocity. However, when accelerated motion takes place along a straight line, the velocity of the body changes only due to change in magnitude of velocity. Therefore, the instantaneous speed is always equalto the magnitude of instantaneous velocity of the particle in one dimensional motion.
EXERCISE - 2
Multiple Choice Questions
- (b)
- (b)
Note : Do not use
- (c) Given that
and acceleration
For acceleration to be zero
- (b)
Now
- (a) Since
so
and
- (d)
- (c)
(
Now
- (c)
- (d)
- (d) Let the car accelerates for a time
Let the car decelerates for a time
or
- (a) Let for the first half time
For second half time,
Now,
- (d)
- (b) Let
and
Now
So,
and
- (b) Let after a time
- (d)
Maximum retardation,
When the initial velocity is
From the formula
- (c) Downward motion
Also for upward motion
Fractional loss
- (a) From third equation of motion
In first case initial velocity
final velocity
and max. height obtained is
In second case
and max. height is
It implies that
- (b) When a particle cover half of circle of radius
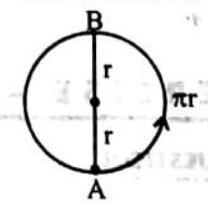
- (c) The distance covered in
where
From equations (1) & (2) we get
and moves with uniform accoleration
- (d) Since,
where
In this case
so, distance travelled in
- (c) The food packet has an initial velocity of
- (b) In first case retardations,
In second case retardation is,
but
- (b) The stone rises up till its vertical velocity is zero and again reached the top of the tower with a speed
the base is
- (c) Let
suppose the velocity becomes zero after passing through
or
- (b) Time taken by the stone to reach the water level
Time taken by sound to come to the mouth of the well,
- (c) From third equation of motion,
where
For first case
For second case
&
so
or
- (c)
At
Now,
Integrating we get,
- (a)
For first body
For second body
So difference between them after
If
- (b) Relative speed of each train with respect to each other be,
Here distance covered by each train
- (b) From first equation of motion
here
so,
- (a) From third equation of motion :
So,
for second case
So
- (b) From third equation of motion
Given,
Therefore
or
- (c) Since the initial velocity of jump is same on both planets
So,
or
- (a)
now for
given by,
- (d) Speed
Let deceleration be a
or
(2)divided by (1) gives,
- (d) Equation of motion is
we know that
integrating it we get,
- (b) Distance in last two second
Total distance
- (c) The horizontal velocity of the stone will be the same as that of the train. In this way, the horizontal motion will be uniform motion. The vertical motion will be controlled by the force of gravity, i.e., vertical motion is accelerated motion. Thus the resultant motion will be along a parabolic trajectory.
- (c) Average acceleration
Average acceleration
which means
- (d) Initial velocity of parachute after bailing out,
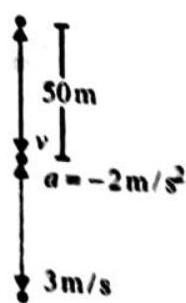
The velocity at ground,
Initially he has fallen
More Than One Correct
| 1. (a,b) | 2. (a,b) | 3. (a,b) | 4. (c,d) |
| 5. (a,c) | 6. (a,d) | 7. (a,d) | 8. (b,c) |
| 9. (a,d) | 10. (a,b) |
Multiple Matching Questions
- (A)
- (A)
- (A)
- (A)
Fill In The Passage
I. (1) distance
(2) equal
(3) distance
(4) directly
(5) straight
II. (1) direction
(2) Speed
(3) centripetal
(4) radial
(5) centrifugal
III. (1) distance
(2) displacement
(3) scalar
(4) vector
(5) less than
(6) zero
(7) speed
(8) velocity
IV. (1) acceleration
(2) straight line
(3) zero
(4) parabola
(5) increasing,
(6) decreasing
Passage based questions
- (d) The total distance travelled is
- (a)
- (a) Net displacement
- (a)
- (a)
- (c)
- (b) Let
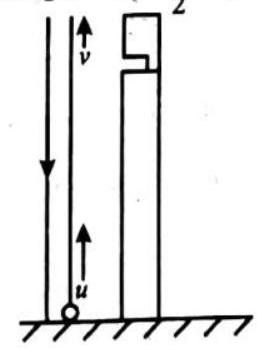
Now using
We get
or
- (a)
- (c)
- (d) Initial velocity of police jeep w.r.t thief’s motorcycle,
Acceleration of police jeep w.r.t thief’s motorcycle,
Using,
or
or
but time cannot be -ve,
- (a) Distance covered by jeep in
- (b) Let
We have
Thief will escape from police if,
or
or
Assertion and Reason
- (b)
- (c)
- (d)
- (a)
- (d)
- (c) Displacement is shortest possible distance between initial and final position.
- (d)
- (a)
- (d) Motion of body is uniform only if direction of motion is same or opposite to the initial velocity.
- (b)
- (a)
If
- (d) Velocity of the bus will change as direction of motion is changing.
Hots Subjective Questions
- The boat that sails directly with the wind can sail no faster than wind speed. Why? Even sailing as fast as the wind, there would be no wind impact against the sail. It would sag. But when sailing crosswind, there would still be wind impact against the sail, and speeds greater than wind speed can be achieved.
- Although its speed and velocity at the top will both instantaneously be zero, its acceleration will be
- Yes.
When the two balls are thrown vertically upwards with the same speed
Here,
Thus, we find that final velocity is independent of mass.
- Average acceleration
To find the resultant of
Since,
Therefore,
- Let
For first body,
For second body,
Further distance covered in
or
- Time taken by the stone to reach the water level
Time taken by sound to come to the mouth of the well,
- Velocity when the engine is switched off
- Between 0 to 5 sec.
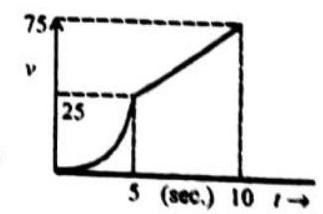
Velocity at
Between 5 to 10 second
so,
CHAPTER 3
Motion in a Plane
INTRODUCTION
In last chapter we studied the motion in a straight line. This chapter is all about a different mode of motion in which the object does/does not move in a straight line but it can be assumed to be moving along two perpendicularly placed straight lines at the same time. Such type of motion is named as the motion in a plane or motion in two dimensions. The motion of a swimmer in a river is an expmple of this type of motion. Oher common examples of such a motion are the circular motion and the projectile motion.
Actually, motion in a plane is a combination of two motion in a straight line. Therefore, to study the motion in a plane we don’t need extra knowledge or equations but we just apply the knowledge or - motions which we studied in the last chapter on motion in a straight line. This chapter will be rstudied under the parts - (i) projectile motion, (ii) circular motion and (iii) relation motion.
MOTION IN A PLANE AS A COMBINATION OF TWO MOTIONS IN A STRAIGHT LINE
When position of a moving particle can be completely described by two dimensions it is said to be a two dimensional motion. If a particle is at
For motion along
(i)
(ii)
(iii)
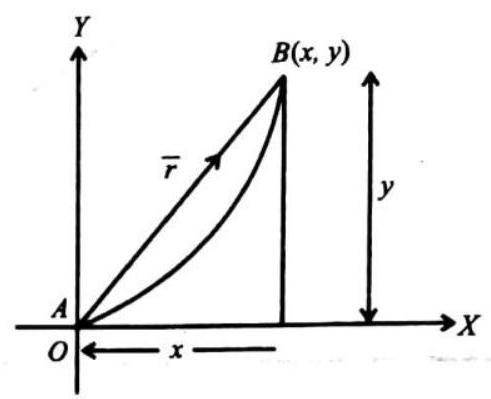
Here,
For motion along
(i)
(ii)
(iii)
Here,
In vector form :
Examples of motion in two dimension are (i) projectile motion (ii) circular motion and (iii) relative motion. Now we will discuss projectile motion in detail.
Projectile motion
Projectile is the name given to a body thrown with some initial velocity in any arbitrary direction an the influence of a constant acceleration. The motion of a projectile is called projectile motion.
Example : A football kicked by the player, a stone thrown from the top of building motion. The path followed by the projectile is called a trajectory.
Terms Related to Projectile Motion
1. Trajectory : The path followed by a projectile is called its trajectory. Generally, the trajectory of a projectile is parabolic
2. Maximum Helght
3. Horizontal Range (R) : The horizontal distance between the point of projection and the point of landing of a projectile is called its horizontal range.
4. Time of Flight
Study of Motion of a Projectile
Let us consider a projectile projected from a point
The different kinematic parameters along horizontal and vertical directions are given below.
Horizontal direction
Initial velocity,
Acceleration,
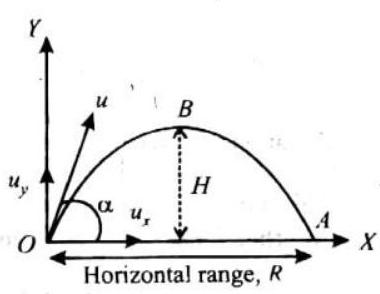
Vertical direction
Initial velocity,
Acceleration,
Do you know !!
A projectile returns to ground at the same angle and with the same velocity with which it is projected.
The time of flight (T):
This is the time taken for the particle to travel along its path from
At any time
When the particle is at
Therefore,
i.e., the time of flights is
The maximum height
At any time
When the particle is at
So
Then,
i.e., the greatest height is given by
The horizontal range (R) : This is the distance from the initial position to the limal position on a horrzntal planc through the point of projection, i.e.
At any time
So, for
Do you know !!
When a projectile is at the highest point of its trajactory.
(i) It possess velocity only along horizontal.
(ii) the velocity and acceleration of the projectile are perpendicular to each other:
Equation of trajectory : L.et us say particle is at
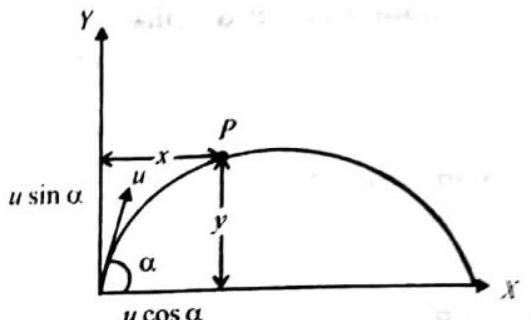
Equation is of type
This represents a parabola
Another form of the equation of trajectory: Multiply by
Various Common Results
1. Velocity at any time
In projectile motion
Magnitude :
Direction :
2. Velocity at any position P(x, y):
IDEA BOX
When a projectile is thrown at
(i) its range is maximum and is equal to
(ii) the maximum height attained by the proiectile is equal to one fourth of its maximum range i.e. equal to
3. Maximum Range : For given speed, range varies with angle of projection. It is maximum at
In many practical applications (javelin throw, shot put etc.), the initial and final elevations may not be equal, and other consideration are important. For example, in the shot put. the hall ends its flight when it hits the ground, but it is projected from an initial height of about
4. Two angles of projection for same range :
If speed is constant then for angle of projection
Thus for given
like
For these two angles of projection range is same but maximum height and time of flight will be different.
- As a projectile moves in its parabolic path, is there any point along its path where the velocity and acceleration vectors are (a) perpendicular to each other? (b) parallel to each other?
- In the absence of air resistance, why does the horizontal component of a projectile’s motion not change, while the vertical component does?
Check Your Answer
- (a) At the top of its flight,
(b) If the object is thrown straight up or down, then
- In the absence of air resistance, the force acting on the projectile is only the force of gravity acting vertically downward. No component of the force due to gravity acts in the horizontal direction therefore the horizontal component of the projectile motion remains unchanged.
Whereas the vertical component of motion undergoes changes. The vertical component of motion decreases while rising against gravity and increases during downward motion.
Illustration 1 :
A ball is thrown at an angle of
Solution : Given
Using
Time of flight,
Horizontal Range,
Illustration 2 :
A body is projected at an angle of
Solution : At
Illustration 3 :
A particle projected with some velocity at an angle
Solution : As
For vertical heights, we can use
So,
Illustration 4 :
A body, when projected at angles of
Solution: Remember,
Illustration 5 :
A staircase contains 3 steps cach
Solution : In order to hit the lower most plane and ’
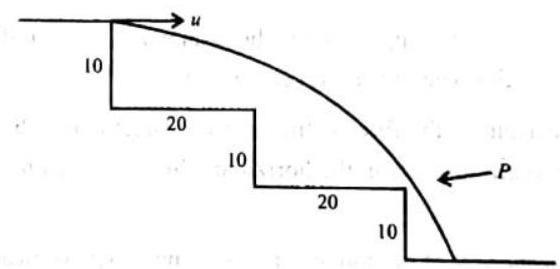
Note : If
HORIZONTAL PROJECTILE
Suppose a projectile is projected horizontally with initial speed ’
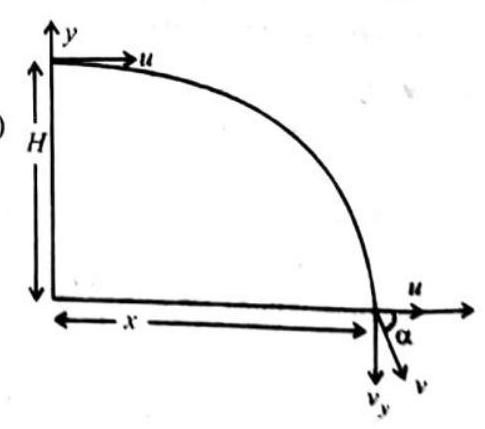
Here
Suppose it reaches the ground in time
and
Angle with hori/untal
- A bullet is fired horizontally towards a target directly in front of the gun. The target starts falling freely the moment bullet is fired, will the bullet hit the target.

Check Your Answer
Suppose the bullet takes ’
Illustration 6 :
An aeroplane flying horizontally at an altitude of
Solution :
Using,
For time
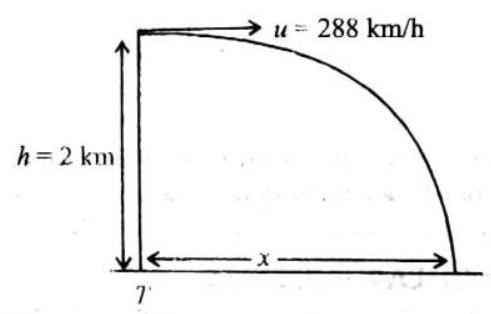
CIRCULAR MOTION
Motion of a particle (small body) along a circle (circular path), is called a circular motion. If the body covers equal distances along the circumference of the circle, in equal intervals of time, the motion is said to be a uniform circular motion,
Explanation :
Consider a boy running along a regular hexagonal track (path) as shown in l’ig. As the hoy runs along the sidc of the hexagon at a uniform speed, he has to take a turn at each corner changing direction but keeping the speed same. In onc round he has to take six turns at regular intervals. If the same boy runs along the side of a regular octagonal track with same uniform speed, he will have to take eight turns in one round at regular intervals but the interval, will become smaller.
By increasing the number of sides of the regular polygon, we find the number of turns per round becomes more and the interval between two turns become still shorter. A circle is a limiting case of a polygon with an infinite number of sides On the circular track, the turning becomes a continuous process without any gap in between the boy running along the sides of such a track will be performing a circular motion. Hence, circular motion is the motion of a body along the sides of a polygon of infinite number of sides with uniform speed, the direction changing continuously.
Examples of uniform circular motion are
(i) Motion of moon around the earth.
(ii) Motion of satellite around its planet.
Angular Position and Angular Displacement
Angular position : Angle made by radius to the particle with a reference radius is known as angular position. In figure
Angular displacement : Angular displacement is defined as the angle traced out by the radius vector at the axis of the circle in a given time.
Here
Its units are degree, radian revolution, etc
Angular Velocity
It is defined as the rate of change of angular displacement. If
Unit of
Some Terms Related to Circular Motion
Time period : It is defined as the time taken by the particle to complete one revolution on its circular path. It is denoted by
Frequency : It is defined as number of revolutions completed by particle in its circular path in unit time It is denoted by
Relation between time period and frequency :
Relation between
Acceleration and Force in Uniform Circular Motion
Any change of velocity-speeding up, slowing down, or turning a corner is an acceleration. We distinguish these different kinds of accelerated motion by assigning a direction to the acceleration. In other words, acceleration is a vector.
If you are traveling in a straight line and speed up, your change in velocity its
Now suppose you do not change speed but are making a turn. This is a change in only the direction of velocity, since velocity is a vector, this is surely a change in velocity-an acceleration. Figure shows how to find the direction of this acceleration. The dotted line shows what the path of the car would be if its motion were not accelerated that is, if it traveled at constant speed in a straight line.
The arrow is a vector representing the change in the velocity of the car, that is, the vector that must be added to the old velocity to get the new velocity. The acceleration is in the same direction as the change in velocity. When the car turns to the right, its acceleration is to the right, perpendicular to its velocity, this acceleration is called centripetal acceleration and its value is
Do you know !!
- If circular motion of the object is uniform, the object will possess only centripetal acceleration.
- If circular motion of the object is non-uniform, the object will possess both centripetal and transverse accelerations.
IDEA BOX
Nothing will follow a circular path unless it is forced to.
If
This force is known as the centripetal force.
Illustration 7 :
The planet Neptune travels in a nearly circular orbit of radius,
Solution :
Illustration 8 :
A grinding wheel (radius
(a) What is the speed of a point on the outer edge of the wheel?
(b) What is the centripetal acceleration of the point?
Solution :
The period of motion is
Su,
Illustration 9 :
Rishabh, a
Solution : Here,
(i) Centripetal acceleration,
(ii) (entripetal force,
Relative Motion
The motion of an object
observers
Relative Velocity
The velocity of point
Let two objects
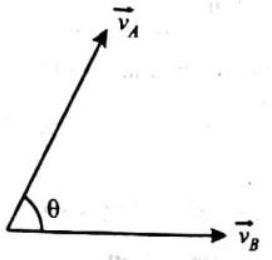
To find the magnitude and direction of the velocity
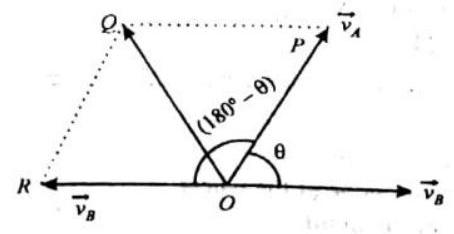
Now, we complete the parallelogram
The resultant of
- When will the relative velocity of two moving objects be zero ?
Check Your Answer
When the two objects are moving with equal velocities (i.e. same speed and in the same direction.)
Do you know !!
The relative velocity of an object A w.r.t. another object B is equal to resultant of the velocity of A and negative of the velocity of B. mathematically
Illustration 10 :
A man standing on a road has to hold his umbrella at
Solution : Given that the velocity of rain drops with respect to road is making an angle
hence
The situation is shown in velocity triangle in figure.
It shows clearly that,
and
Illustration 11
A plane is to fly due north. The speed of the plane relative to the air is
Solution : Since the wind is blowing toward the east, the plane must head west of north as shown in figure. The velocity of the plane relative to the ground
(a) 1. The velocity of the plane relative to the ground is given by equation:
- The sine of the angle
(b) Since
Illustration 12 :
A man swims at an angle
Solution :
Illustration 13
On a two-lane road, car
Solution :
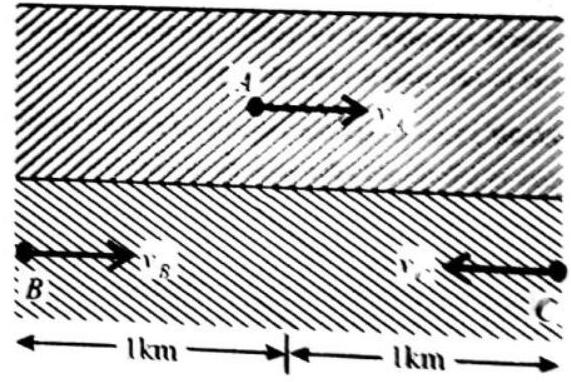
Relative velocity of
Relative velocity of
Time taken by
Now, for
On simplification,
Illustrotion 14 :
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial spend the cam. rymal
Solution :
This is time taken by the ball to reach the maximum height. The time of descent is also
The uniform velocity of the lift does not change the relative motion of ball and lift. So, the hall woukd take the sanke notal time i.c. it would come back after 10 second.
EXERCISE 1
Fill in the blanks
DIRECTIONS : Complete the following statements with an appropriate word / term to be filled in the blank space(s).
- The maximum height attained by a projectile is maximum when the angle of projection is ____
- The range of a projectile is maximum when the angle of projection is ____
- The maximum horizontal range for a projectile thrown with velocity
- Horizontal range is same for a projectile at the angle of projection
- The maximum height of a projectile thrown with velocity
- The angle between the velocity and acceleration of a projectile at the highest point is ____
- Time taken by an object to complete one round of the circular path on which it is moving is called its
- The S.I. unit of angular speed is ____
- Centripetal acceleration always acts towards the ____ of the circular path.
- Centrifugal force acts ____ the circular path.
- The horizontal range of a projectile is maximum when the angle of projection is ____
- A projectile thrown with a velocity of
- Two buses
- The maximum height attained by a projectile at a fixed angle of projection varies directly with the ____ of velocity of projection.
- A projectile projected at some angle with the horizontal has an acceleration ____ along horizontal.
True/False
DIRECTIONS : Read the following statements and write your answer as true or false.
- In uniform circular motion, the speed is constant but the velocity changes.
- The acceleration in non-uniform circular motion directs towards the centre of the path.
- The relative velocity of a car
- The relative velocity of a
- A bus
- The velocity of a projectile at the highest point is along the vertical.
- The velocity of a projectile at the highest point is along the horizontal.
- The horizontal distance covered by a projectile during its time of flight is known as its trajectory.
- Projectile is a body which moves under the action of a variable acceleration.
- The relative velocity of car moving with a velocity
- Projectiles projected at angles of projection
Match the Columns
DIRECTIONS : Each question contains statements given in two columns which have to be matched. Statements
- A body of mass
| Column I | Column II |
|---|---|
| (A) |
(p) |
| (B) |
(q) |
| (C) |
(r) |
| (D) |
(s) |
- A particles completes one and a half-round of a circular track of radius
| Column I | Column II |
|---|---|
| (A) Distance covered | (p) 4 S.I units |
| (B) Displacement covered | (q) 7 S.I units |
| (C) Time taken | (r) 28 S.I units |
| (D) Average velocity | (s) 132 S.I units |
- A particle is projected from ground with a speed
| Column I | Column II |
|---|---|
| (A) Time of flight | (p) |
| (B) Horizontal range | (q) |
| (C) Maximum height | (r) |
| (D) Speed of the particle at the highest point of its trajectory | (s) |
Very Short Answer Questions
DIRECTIONS : Give answer in one word or one sentence.
- Does a uniform acceleration in two-dimensional motion necessarily imply motion along a straight-line path?
- What will be the effect on horizontal range of a projectile when its initial velocity is doubled, keeping the angle of projection identical?
- What will be the effect on maximum height of a projectile if its angle of projection is changed from
- Is the maximum height attained by projectile is largest when its horizontal range is maximum?
- If the velocity at the maximum height of a projectile is half its initial velocity of projection
- Write down the expression for the equation of trajectory of a projectile.
- What is the nature of the trajectory of a particle having a uniformly accelerated motion in a plane?
- If the two bodies are projected at an angle
- If the two bodies are projected at the same initial velocity at angles
- In a projectile motion the range
- A body of mass
- If the greatest height to which a man can throw a body is ’
- Define angular speed. What is its SI unit?
- A particle moves along a circle of radius
- Two cars are going around two concentric circular paths at the same angular speed. Does the inner or the outer car have the larger linear speed?
- Among the angular velocities of hour hand and that of earth, which will be greater?
- The range of a particle when launched at angle of
- Give two examples of circular motion with constant speed.
- What is the direction of velocity vector of a particle in circular motion?
- What furnishes centripetal acceleration for earth to go round the sun?
- What provides the centripetal force to satellite revolving round the earth?
Short Answer Questions
DIRECTIONS : Give answer in 2-3 sentences.
- Justify the statement that a uniform circular motion is an accelerated motion.
- For uniform circular motion, does the direction of the centripetal force depend upon the sense of rotation?
- A stone tied to the end of a string is whirled in a circle. If the string breaks, the stone flies away tangentially. Why?
- Passengers are thrown outwards, when the bus takes a circular turn. Why?
- The outer rail of a curved railway track is generally raised over the the inner. Why?
- A bucket containing water is rotated in vertical circle Explain, why the water does not fall?
- A body is dropped freely from the window of a train. Will the time of the free fall be equal, if the train is stationary, the train moves with a constant velocity, the train moves with an acceleration?
- A person sitting in a moving train throws a ball vertically upwards. How does the ball appear to move to an observer (i) inside the train (ii) outside the train?
- A ship is sailing westward at
- While firing, one has to aim a little above the target and not exactly on the target. Why ?
- The magnitude of the velocity of projection being fixed, how does the range of projectile depend upon its angle of projection? Is there any optimum value for the angle of projection so that range may be maximum ?
Long Answer Questions
DIRECTIONS : Give answer in four to five sentences.
- Find the time of flight, maximum height, horizontal range of projectile projected with speed
- What do you mean by a projectile? A projectile is fired with velocity
- A projectile is fired making an angle
(a) Find mathematically the nature of its path
(b) Derive relations for its horizontal range and maximum horizontal range.
- Show that there are two angles of projection for a projectile to have the same horizontal range. What will be the maximum heights attained in the two cases? Compare the two heights for
- Show that the velocity with which a projectile hits the ground is same with which it was initially projected and the angle made by the trajectory with the horizontal is same as the angle of projection.
- Define angular displacement, angular speed, angular acceleration, time period and frequency as regards circular motion. How are linear velocity and linear acceleration related to angular speed and angular acceleration respectively?
- What are centripetal acceleration and centripetal force ? Derive expressions for them.
EXAMPLE 2
Multiple choice Questions
DIRECTIONS: This section contains multiple choice questions Each. question has 4 choices (a), (b), (c) and (d) out of which ONLY ONE is correct
- A projectile is projected with a kinetic energy
(a)
(c)
(b)
(d)
- The range of a particle when launched at an angle of
(a)
(c)
(b)
(d)
- A gun fires two bullets at
(a)
(c)
(b)
(d)
- Two balls are projected at an angle
(a)
(b)
(c)
(d)
- A body is projected at an angle of
(a)
(b)
(c)
(d)
- If range is double the maximum height of a projectile, then
(a)
(b)
(c)
(d)
- A body is projected such that its
(a)
(b)
(c)
(d)
- A projectile can have the same range
(a)
(c)
(b)
(d)
- A particle having a mass
(a) 0.5
(b) 49
(c) 98
(d) 490
- The velocity of projection of a body is increased by
(a)
(b)
(c)
(d)
- A body is thrown with a velocity of
(a)
(b)
(c)
(d)
- If the horizontal range of a projectile is equal to the maximum height reached, then the corresponding angle of projection is
(a)
(b)
(c)
(d)
- The co-ordinates of a moving particle at any time ’
(a)
(b)
(c)
(d)
- Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
(a) The acceleration vector points to the centre of the circle
(b) The acceleration vector is tangent to the circle
(c) The velocity vector is tangent to the circle
(d) The velocity and acceleration vectors are perpendicular to each other.
- A body moves
(a)
(c)
(b)
(d)
- In uniform circular motion, the velocity vector and acceleration vector are
(a) perpendicular to each other
(b) same direction
(c) opposite direction
(d) not related to each other
- The circular motion of a particle with constant speed is
(a) periodic but not simple harmonic
(b) simple harmonic but not periodic
(c) periodic and simple harmonic
(d) neither periodic nor simple harmonic
- Two projectiles are fired from the same point with the same speed at angles of projection
(a) Their maximum height will be same
(b) Their range will be same
(c) Their landing velocity will be same
(d) Their time of flight will be same
- From a
(a) It is not possible to calculate which one of the two stones will reach the ground first
(b) Both the stones (
(c) A stone reaches the ground earlier than
(d) B stone reaches the ground earlier than
- An aeroplane flying at a constant speed releases a bomb.
As the bomb moves away from the aeroplane, it will
(a) always be vertically below the aeroplane only if the aeroplane was flying horizontally
(b) always be vertically below the aeroplane only if the aeroplane was flying at an angle of
(c) always be vertically below the aeroplane
(d) gradually fall behind the aeroplane if the aeroplane was flying horizontally.
- The time of flight of a projectile on an upward inclined plane depends upon
(a) angle of inclination of the plane
(b) angle of projection
(c) the value of acceleration due to gravity
(d) all of these
- At the highest point on the trajectory of a projectile, its
(a) potential energy is minimum
(b) kinetic energy is maximum
(c) total energy is maximum
(d) kinetic energy is minimum.
- Two bullets are fired horizontally, simultaneously and with different velocities from the same place. Which bullet will hit the ground earlier?
(a) It would depend upon the weights of the bullets.
(b) The slower one.
(c) The faster one.
(d) Both will reach simultaneously.
- In the case of a projectile fired at an angle equally inclined to the horizontal and vertical with velocity
(a)
(b)
(c)
(d)
- A bomb is released by a horizontal flying acroplane. The trajectory of bomb is
(a) a parabola
(b) a straight line
(c) a circle
(d) a hyperbola
- The greatest height to which a man can throw a ball is
(a)
(b)
(c)
(d)
- The
(a)
(b)
(c)
(d) zero.
- A cricket ball is hit with a velocity
(a)
(b)
(c)
(d)
- A plane flying horizontally at a height of
(a)
(b)
(c)
(d)
- A projectile is thrown horizontally with a speed of
(a)
(b)
(c)
(d)
- A ball is projected at such an angle that the horizontal range is three times the maximum height. The angle of projection of the ball is
(a)
(b)
(c)
(d)
- If a particle is projected at
(a)
(c)
(b)
(d) none of these
- The equation of trajectory of projectile is given by
The maximum range of the projectile is
(a)
(b)
(c)
(d)
- A projectile can have the same range for two angks of projection. If
(a)
(b)
(c)
(d) none of these
- A bullet is fired with a speed of
(a)
(b)
(c)
(d) directly towards the target
- A wheel rotates with constant acceleration of
(a) 32
(b) 24
(c) 16
(d) 8
- A projectile of mass
(a)
(b)
(c)
(d)
- A projectile is thrown in the upward direction making an angle of
(a)
(b)
(c)
(d)
- A bomb is dropped from an aeroplane moving horizontally at constant speed. If air resistance is taken into consideration, then the bomb
(a) falls on earth exactly below the aeroplane
(b) falls on the earth exactly behind the aeroplane
(c) falls on the earths ahead of the aeroplane
(d) flies with the aeroplane
- A cyclist moving at a speed of
(a) is doubled
(b) is halved
(c) becomes four times
(d) becomes
- A projectile can have the same range ’
(a)
(b)
(c)
(d)
- A person swims in a river aiming to reach exactly on the opposite point on the bank of a river. His speed of swimming is
(a)
(b)
(c)
(d)
- The relative velocity
(1) greater than velocity of body
(2) greater than velocity of body
(3) less than the velocity of body
(4) less than the velocity of body
(a) (1) and (2) only
(b) (3) and (4) only
(c) (1), (2) and (3) only
(d) (1), (2), (3) and (4).
More Than One Correct
DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a). (b), (c) and (d) own of which ONE OR MORE may be correct.
- The following quantities may remain constant during uniform circular motion :
(a) magnitude of acceleration
(b) acceleration
(c) speed
(d) velocity
- A cart moves with a constant speed along a horizontal circular path. From the cart, a particle is thrown up vertically with respect to the cart. Then the particle will :
(a) land outside the circular path
(b) land somewhere on circular path
(c) follow a parabolic path
(d) follow an elliptical path
- A man on a moving cart, facing in the direction of motion, throws a ball straight upwards with respect to himself. Then the ball will
(a) fall behind him if the cart moves with some acceleration
(b) return to him if the cart moves with a constant velocity
(c) never return to him
(d) always return to him
- Which of the following represent the projectiles ?
(a) A stone thrown horizontally from the top of the tower
(b) A bullet fired from the gun
(c) A rocket fired into space
(d) A ball thrown upwards
- A particle is acted upon by a force of constant magnitudk which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that:
(a) it moves in a circular path
(b) velocity is constant
(c) acceleration is constant
(d) kinetic energy is constant
- A bullet fired with a certain muzzle speed at an angle of
(a)
(b)
(c)
(d)
- A ball is projected upwards at a certain angle with the horizontal. Which of the following statements are correct, at the highest point?
(a) The acceleration of the projectile is vertically downwards.
(b) The velocity of the projectile is along the horizontal direction
(c) The velocity of the projectile is zero
(d) The acceleration of the projectile is zero
- A body is moving in a circle of radius
(a)
(b)
(c)
(d)
- Two vectors of the same physical quantity are unequal if :
(a) they have the same magnitude but different directions
(b) they have different magnitudes and different directions
(c) they have different magnitudes but the same direction
(d) they have the same magnitude and the same direction
- Two particles are projected from the same point with the same speed, at different angles
(a)
(b)
(c)
(d)
- Let
(a)
(b)
(c)
(d)
- The maximum height attained by the projectile depends upon the following factors
(a) mass of the projectile
(b) acceleration of the projectile
(c) angle of projectile
(d) magnitude of initial velocity
- A particle is moving along a circular path. The angular velocity, linear velocity, and centripetal acceleration of the particle at any instant respectively are
(a)
(b)
(c)
(d) None
- Two balls
(a)
(b)
(c)
(d)
- For a projectile motion, which of the following depend on angle of projection?
(a) Time of flight
(b) Horizontal range
(c) Horizontal component of velocity
(d) Acceleration
Multiple Matching Questions
DIRECTIONS : Following question has four statements (A,
- Match the following for a uniform circular motion.
| Column I | Column II |
|---|---|
| (A) Speed | (p) Constant |
| (B) Direction of velocity | (q) Variable |
| (C) Magnitude of acceleration | (r) Towards the centre acceleration of the circular path |
| (D) Direction of acceleration | (s) Along the tangent to the circular path |
| (t) Circular Path | |
| (u) |
- A particle is projected from ground at a certain angle. Match the following for the motion of the particle.
| Column I | Column II |
|---|---|
| (A) Speed of the particle | (p) Constant |
| (B) Acceleration of the particle | (q) Variable |
| (C) Horizontal component of velocity | (r) First increases then decreases |
| (D) Vertical displacement | (s)First decreases then increases |
| (t) Always donwards |
Fill in the Blanks
DIRECTIONS : Complete the following passage(s) with an appropriate word/term to he filled in the blank spaces.
(I) non-uniform, centre, centripetal acceleration, magnitude, direction, perpendicular, uniform.
When a body exccutes circular motion, its speed is (1) ____ but its velocity is ____ (2) ____ The acceleration of the particle is always directed towards ____ (3) ____ of the circular path, hence is always ____ (4) ____ to its velocity. The acceleration responsible for change in direction of velocity during circular motion is called ____ (5) ____, it is constant in ____ (6) ____ but varies in ____ (7) ____.
(II) verticily &uwnwards. constant, horizontal, minimum, horizonui range, parabola, equal to.
When a particle is projected from ground making some angle with the horizontal. its acceleration is ____ (1) ____ and is directed ____ (2) ____. At the highest point of its trajectory, the velocity of the particle is along ____ (3) ____ and its magnitude is ____ (4) ____ at that point. The straight line distance between the point of projection and the point of landing is called ____ (5) ____. The speed with which the particle strikes the ground is ____ (6) ____ the speed of proiection. The path of projectile is always a ____ (7) ____.
Passage Based Questions
DIRECTIONS : Study the given paragraph(s) and answer the following yuestions
PASSAGE - I
A boy moves along a straight line with a uniform speed of
- The displacement covered by the boy from the beginning to the instant when it takes sixth turn is :
(a)
(b)
(c)
(d)
- The average relocity of the boy between the instant of begining of its motion to the instant when it takes fifth turn is :
(a)
(b)
(c)
(d) zero
- The average acceleration of the body from the beginning to the instant just after it takes second turn is :
(a)
(b)
(c)
(d) zero
PASSAGE - II
A particle is projected from ground with an initial speed
Then (take
- The time of flight of the particle is :
(a)
(b)
(c)
(d)
- The horizontal range of the particle is :
(a)
(b)
(c)
(d)
- Velocity of the particle at the highest point of its trajectory is:
(a)
(b)
(c)
(d) zero
PASSAGE - III
A particle is projected horizontally with a speed of
- How much time will the particle take to reach the ground?
(a)
(b)
(c)
(d)
- At what distance from the bottom of the tower will the particle hit the ground?
(a)
(c)
(b)
(d)
- The speed with which the particle hit the ground is :
(a)
(b)
(c)
(d)
PASSAGE - IV
A particle is moving along a circular track of radius
- How much time will it take to complete one complete round?
(a)
(c)
(b)
(d)
- What is the average velocity of the particle in one complete round?
(a)
(c)
(b)
(d) Zero
- The acceleration of the particle is
(a)
(b)
(c)
(d) 0
Assertion and Reason
DIRECTIONS : Each of these questions contains an Assertion followed by reason. Read them carefully and answer the question on the basis of following options. You have to select the one that best describes the two statements.
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect
(d) If Assertion is incorrect but Reason is correct
1. Assertion : When a body is dropped or thrown horizontally from the same height, it would reach the ground at the same time.
Reason : Horizontal velocity has no effect on the vertical motion.
2. Assertion : Horizontal range of a projectile is same for angles of projection
Reason : Horizontal range does not depend on angle of projection.
3. Assertion : If the rain is falling vertically, to a man walking on a horizontal road, the apparent speed of rain to the man will always be greater than its actual speed.
Reason : As velocity of the rain and the man are mutually perpendicular.
4. Assertion : In a uniform circular motion, acceleration of the body is constant.
Reason : In uniform circular motion, the body has only centripetal acceleration.
5. Assertion : Horizontal component of velocity of projectile is constant.
Reason : Acceleration of the projectile is along the vertical.
6. Assertion : In projectile motion, acceleration is always perpendicular to the velocity.
Reason - Path of projectile is a parabola.
Hots Subjective Questions
DIRECTIONS : Answer the following questions.
- A ball is thrown horizontally from the top of a tower with a speed of
- A ball is projected from ground with a velocity of
- A particle is projected “ith a velocity " " that its horizontal range is twice the greatest height attained. Find the horizontal range of it
- The angular velocity of a particle moving in a circle of radius
- A body is moving in a circle of radius
- A stone tied to the end of string
- A wheel is
- An aircraft executes a horizontal loop of radius
- A cyclist is riding with a speed of
- What is the centripetal acceleration of the carth is it moves in its orbit around the sun?
- The height
- How does the vertical distance a projectile falls helow an otherwise straight-line path compare with the vertical distance it would fall from rest in the same time?
- In the absence of air resistance, why does the horizontal component of a projectile’s motion not change, while the vertical component does?
- At what point in its trajectory does a batted baseball have its minimum speed? If air resistance can be neglected, how does this speed compare with the horizontal component of its velocity at other points?
- Two golfers each hit a ball at the same speed. one at
- When you jump upward, your hang time is the time you feet are off the ground. Does hang time depend on the vertical component of your velocity when you jump, on the horizontal component of your velocity, or on both? Defend your answer.
- A projectile can have the same range for two angles of projection. If
SOLUTIONS
EXERCISE - 1
FILL IN THE BLANKS
- angular speed
- away
- centre
- 1.25
Hint :
Hint :
Velocity of
- Square
Hint :
Here.
- zero.
TRUE/FALSE
- True
- True
- False
- True
- True
Hint : Relative velocity of passengers in each bus
- False
- True
- False
- False
Hint :
Projectile moves under the action of a constant acceleration
- False
Hint :
Required relatwe selocity (50 30
- True
Hint :
The horizontal range of the projectiles is same at two angles of projection
Match The Column
- (A)
Hint :
- (A)
Distance
Displacement
Time taken
Average velocity
Time of flight,
Horizontal range,
Maximum height,
At the highest point of trajectory,
Very Short Answer Questions
1. No
2. It will be four times the initial horizontal range.
3. It will be three times the initial vertical height.
4. Maximum height will be attained at
5.
6. The equation of trajectory of a projectile having initial speed
7. Parabolic.
8.
9. Horizontal range,
(i) when
(ii) when
10. Here,
11. Horizontal range,
(i) when
and
(ii) when
12. We know, maximum height,
Similarly, maximum horizontal range,
13. The angular displacement per unit time is known as angular speed. Mathematically, angular speed = angular displacement / time taken
14.
15. The linear speed is given by
16. For hour hand of watch, time period,
Angular velocity,
17. Here,
or,
Horizontal range,
18. 1. The motion of the hour or the minute hand of a watch. 2. The motion of the blades of the fan, when the electric fan has attained constant speed.
19. At every point along tangent to the circular path.
20. The gravitational pull of the sun on the earth.
21. Garavitational force of attraction on the satellite due to the earth.
Short Answer Questions
-
In uniform circular motion, the speed of the body remains the same but the direction of motion of the body changes continuously. Since velocity is a vector quantity, the continuous change in the direction of motion of.the body implies continuous change in the velocity of the body. As the rate of change of velocity is acceleration. a uniform circular motion is an accelerated motion.
-
The direction of the centripetal force does not depend, whether the body is moving in clockwise or anticlockwise direction. It is always directed along the radius and towards the centre of the circle.
-
The instantaneous velocity of the stone going around the circular path is tangential to the circle. When the string breaks, the centripetal force ceases to act. Due to inertia. the stone continuous its motion along the tangent to the circular path. That is why, it flies away tangentially.
-
When the bus takes a turn, the centripetal acceleration of the bus acts towards the centre of the circular turn and along its radius. Due to inertia, the passengers are thrown outwards. The force experienced by the passengers is called the centrifugal force.
. When the outer rail of a curved railway track is raised, the weight of the train gives a component of its weight along the radius of the curved track. This component of the weight provides the train the necessary centripetal force so as to enable it to move along the curved path.
- Fig shows a bucket containing water and whirled in a vertical circle.
Let
-
The motion of the train only alfects the magnitude of the horizontal component of velocity and the acceleration of the body along the horizontal, if any. It does not atficy the nature of the motion along the vertical. Therefior, in all the three cases, the time of thee fall of the body will be cqual.
-
(i) To the observer inside the train, the ball will appear to move straight vertically upwards and then downwards
(ii) The observer outside the train, the ball will appear to move along the parabolic path.
- The bolt will drop just at the foot of the mast. It is because, when the bolt drops, it will possess the following two motions :
(i) Motion towards west with uniform velocity of
(ii) Vertically downwards motion with initial velocity zero and acceleration equal to
4 0: a
Now
In 2s, the bolt will thavel a distance of
- During the time interval, the bullet moves up to the target, it falls through some vertical distance under the effect of gravity. As a result, it will not hit the target at the point, it wals aimed at It will hit a little below. Therefore, so as to hit the target exactly at that point, one has to aim a little above that point on the target.
- The horizontal range of a projectile is given by
As the magnitude of the velocity is fixed and
i.e., range of the projectile is directly proportional to sin of the twice of the angle of projection.
For
EXERCISE - 2
Multiple Choice Questions
1. (b) K.E. is minimum at the highest point. So, the horizontal distance is half of the range
2. (b)
or
3. (b) The bullets are fired at the same initial speed
4. (d)
5. (a)
As vertical velocity
Angle with horizontal
It is a state, when a particle reach to a highest point of its path.
6. (d)
7.
(a)
or
8. (a)
where
9. (b) There is no change in horizontal velocity, hence no change in momentum in horizontal direction. The vertical velocity at
so change in momentum in vertical direction is
10. (c) We know that,
11. (d) Time of flight
12. (c)
13. (b)
14. (b) Acceleration vector is always radial (i.e . towards the centre) for uniform circular motion.
15. (a)
Now, taking initial position at origin. Final position in vector form is given by
16. (a) In uniform circular motion speed is constant. So, ne tangential acceleration.
It has only radial acceleration
and its velocity is always in tangential direction. So these two are perpendicular to each other.
17. (a) In circular motion of a particle with constant speed, particle repeats its motion after a regular interval of time but does not oscillate about a fixed point. So, motion of particle is periodic but not simple harmonic.
18. (b) Given,
In lst case, we know that range
In IInd case when (1) in then
(we get same value of innues).
19. (b)
20. (c) Since horizontal component of the velocity of the bomb will be the same as the velocity of the aeroplane. therefore horizontal displacements remain the same at any instant of time.
21. (d)
22. (d) Velocity and hence kinetic energy is minimum at the highest point.
23. (d) The initial velocity in the vertically downward direction is zero and same height has to be covered.
24. (a)
25. (a) A parabola
26. (d)
27. (c)
28. (c)
29. (b) Horizontal distance covered should be same for the lime ol collision
30. (c) Even after 5 second, the horizontal velocity
Now,
31. (d) Given
32. (a) We have,
33. (b) Comparing the given equation with the equation of trajectory of a projectile,
we get,
and
Now,
34. (a)
Range
or,
35. (c) The bullet performs a horizontal journey of
The bullet performs vertical journey for this time.
For vertical journey,
or,
or,
The gun should be aimed
36. (c) For circular angular motion, the formula for angular displacement
where
or
or
or 100 radian are covered in
37. (b)
As the figure drawn above shows that at pouns in and
Hence, change in momentum is given by
38. (c)
Velocity of projectile
angle of projection
Let, the time taken by the projectile from
For vertical motion,
39. (b) If there is no resistance, bomb will drop at a place exactly below the flying aeroplane. But when we take into account air resistance, bomb will face deceleration in its velocity. So, it will fall on the earth exactly behind the aeroplane.
40. (d) When a cyclist moves on a circular path, it experiences a centrifugal force which is equal to
41. (c) The time of flight of a projectile is given as,
A projectile can have same range if angle of projection are complementary i.e.,
and
where range
42. (c) Here
so
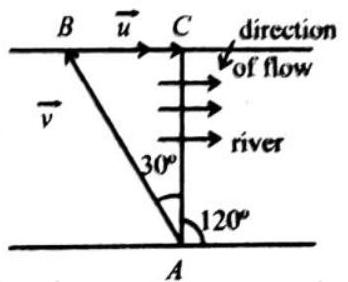
43. (d) All options are correct :
(i) When two bodies
(ii) When two bodies
More Than One Correct
In uniform circular motion, magnitude of acceleration and velocity is constant but not their directions.
The particle has initially horizontal as well as vertical velocity hence its motion is projectile.
- (a,d)
Motion of the particle will be uniform circular.
- (b, d)
For a projectile motion,
or
Centripetal acceleration,
For same horizontal range
For circular motion
- (b, c, d)
In uniform circular motion, velocity, angular velocity and centripetal acceleration are mutually perpendicular.
- (a, d)
For horizontal projection,
As
Multiple Matching Questions
- (A)
- (A)
Fill In The Passage
(I)
(1) uniform
(2) non-uniform
(3) centre
(4) perpendicular
(5) centripetal acceleration
(6) magnitude
(7) direction.
(II)
(1) constant
(2) vertically downwards
(3) horizontal
(4) minimum
(5) horizontal range
(6) equal to
(7) parabola
Passage Based Questions
- (b) Let the boy starts from point
Displacernent
- (a) At the instant of fith turn, boy will be at point
- (a) Change in velocity,
- (b) Time of flight
- (b) Horizontal range,
- (b) At the highest point of trajectory.
- (c) Time of flight,
- (c) Horizontal range,
- (c) Speed with which the particle hits the ground
-
(a)
-
(d) Displacement of the particle in one complete round is zero, hence average velocity of the particle in one complete round is zero.
-
(b) Acceleration
Assertion And Reasons
- (a) Time of flight depends only on vertical motion and not on the horizontal motion.
- (c) Horizontal range depends on angle of projection and is equal for two angles of projection
- (a) Both assertion and reason are true and reason is correct explanation of assertion.
- (c) Centripetal acceleration is not constant as it varies in direction.
- (a) Acceleration due to gravity acts vertically downwards hence horizontal velocity does not change.
- (d) In projectile motion, acceleration is perpendicular to velocity only at the heighest point of its trajectory.
Hots Subjective Questions
- Ans :
Hint :
- Ans :
Hint :
- Ans :
Hint :
- Ans.
Hint : (a)
- Ans.
Hint :
- Here,
Now,
The acceleration of uniform circular motion is given by
The acceleration is directed along the radius of the circular path and towards the centre of the circle.
- Here,
We know,
- Here,
Now, the centripetal acceleration is given by
Now,
or
- Here,
Centripetal acceleration,
Suppose that the cyclist applies brakes at the puint
Thus,
Therefore, total acceleration is given by
If
or,
at
so
-
The vertical distance a projectile falls below an otherwise straight line path is the same vertical distance it would fall from rest in the same time because the distance covered in vertical direction in both the cases is given by
-
In the absence of air resistance, the force acting on the projectile is only the force of gravity acting vertically downward. No component of the force due to gravity acts in the horizontal direction therefore the horizontal component of the projectile motion remains unchanged.
Whereas the vertical component of motion undergoes changes. The vertical component of motion decreases while rising against gravity and increases during downward motion.
-
A batted baseball has the minimum speed at the top of its trajectory. The vertical component of velocity is zero at the top. The baseball has only the horizontal component of velocity which remains the same at any point on the trajectory.
-
Both of the two golf balls will hit the ground at the same distance from the point of projection because the same range is obtained from two different launching angles when the angles add up to
The ball thrown at an angle of
- When anybody jumps upwards the hang time in air depends on the vertical component of velocity not on the horizontal component of velocity.
This is because the vertical component and horizontal component of velocity are perpendicular to each other and hence are independent of each other.
The vertical component of velocity matters only for the motion in vertical direction and there is no contribution of the horizontal component of velocity.
Range
or,
CHAPTER 4
FORCE AND LAWS OF MOTION
INTRODUCTION
In last couple of chapters we dealt with different kinds of motion. We didn’t bother about their cause. This chapter is concerned about the cause of motion (i.e. force) and its effect (i.e. acceleration) and their Melationship. We will read different kinds of force.
When force is applied on a body, some acceleration is produced in it. These two quantities-force and acceleration are closely related. The existence of one causes the existence of other.
The great physicist sir Isaac Newton formulated three laws which govern the motion and its cause. This chapter deals with all the three laws of motion given by Newton and their applications in day to day life.
The chapter also gives us detailed knowledge of linear momentum, its conservation, impulse and their practical applications.
Force
In our daily life we find that a body at rest can be moved and one that is moving can be stopped. The doors and windows of a house are pushed to open and pulled to shut them. In games like cricket, hockey and football, players on the ground sometimes stop a moving ball or manage to deflect it to some other direction. The boatsman pulls a boat with a rope in order to bring it to the shore or pushes it to get it into the water. This push or pull is called the force in every day language.
Force is a vector quantity (it has both magnitude and direction). There must be a net force (unbalanced force) acting on an object for the object to change its velocity (either magnitude and/or direction), or to accelerate.
If we want the car to stop, we have to do something to it. That is what our brakes are for : to exert a force that decreases the car’s velocity.
In a basketball, a player launches a shot by pushing on the ball.
Thus it can be said that the force is a physical influence which can change the state of motion or state of rest of a body. A force can change the direction of motion of a body
Therefore, a force can change the speed and direction of motion of a body. A force is that physical quantity which tries to change or changes the state of rest or of uniform motion of a body.
To obtain a complete information about the force acting on an object one should know
(i) the point of application of force
(ii) the magnitude of force
(iii) the direction in which the force acts.
- If an object experiences no acceleration, is no force acting on it?
Check Your Answer
If an object has no acceleration, you cannot conclude that no forces act on it. In this case, you can only say that the net forceon the object is zero.
Some Common Forces
(i) Contact forces
When a body
Practical examples
(a) The pulling of a trolley by a coolie.
(b) The pulling of a cart by a horse.
(c) The pushing of a door to close it.
(d) The stretching of a spring by suspending a load.
(e) The squeezing of a gum tube to extract the gum.
(ii) Elastic recoil
The special property of solids, in contrast to liquids and gases, is that they resist any change in their shape. When we push on a solid, it pushes back. The plank exerts an upward force against the hand because the hand is changing the shape of the board. The floor pushes up when our weight pushes down on it, because our weight changes its shape
(iii) Tension
This is a special type of elastic recoil, resulting from stretching something. In a tug-of-war, the rope is under great tension, so it pulls back on the teams at the opposite ends. The spring scale is actually a tension-measuring device. The harder you pull on both ends of the spring, the more it stretches, and the harder it pulls back.
(iv) Compression
This is the opposite of tension. Pushing on a window pole shortens the pole-a little-and the pole pushes back. Actually, the bending board exerts its recoil because its upper surface is compressed and its lower surface is tensed.
(v) Buoyancy
Anything submerged in a liquid or a gas experiences an upward force. A rock under water feels lighter than the same rock in the air. If buoyancy is greater than weight, as for a cork under water or a helium-filled balloon in the air, the object rises. If we are under water, we can rise to the top until we emerge into the air. Then, buoyancy and gravity are equal, and we float.
(vi) Viscous drag
Anything moving through a liquid or gas feels a retarding, friction-like force. That is why a boat needs an engine, why we cannot swim fast enough to get into the Olympics, why automobiles are streamlined, and why a parachute is advisable if we plan to fall out of an airplane.
(vii) Normal force
If contact force between the bodies is perpendicular to the surface in contact, the force is known as normal force. Let us consider a block on a table. The table pushes the block upwards and block pushes the table down wards. Then forces are perpendicular to the surfaces of block and table. Thus the table applies a normal force on block in the upward direction and block applies a normal force on table in downward direction.
(viii) Friction
Two bodies placed in contact can also exert forces parallel to the surfaces in contact, such a force is called force of friction or simply friction. Suppose a body is placed on the table. Following three forces acts on it.
(1) Force by earth in downward direction
(2) Normal force due to table in upward direction.
(3) Applied force towards right.
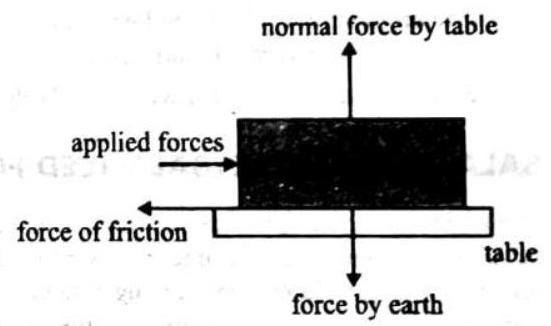
Body is not moving, so all the forces must be balanced, normal force due to table and force by earth balanced each other. To balance the applied force there must be an equal and opposite force. This force is known as force of friction. If we increase the applied force the body is still at rest. It means force of friction is also increased till it is balanced by the applied force. The force of friction is self adjusting force. On increasing the applied force, the force of friction will increase up to a limit. It is known as limiting friction. After it on increasing the applied force, the body will start to move.
(ix) Spring Force
A spring is made of a coiled metallic wire. A spring has a definite length when it has been neither pushed nor pulled. The length is called natural length. At natural length the spring does not exert any force on the objects attached to its ends. If the spring is pulled at the ends its length becomes larger than natural length. It is known as stretched or extended spring. Extended spring pulls objects attached to its ends.

If the spring is pushed at the ends its length becomes less than natural length. It is known as compressed spring. A compressed spring pushes the block attached to its ends.
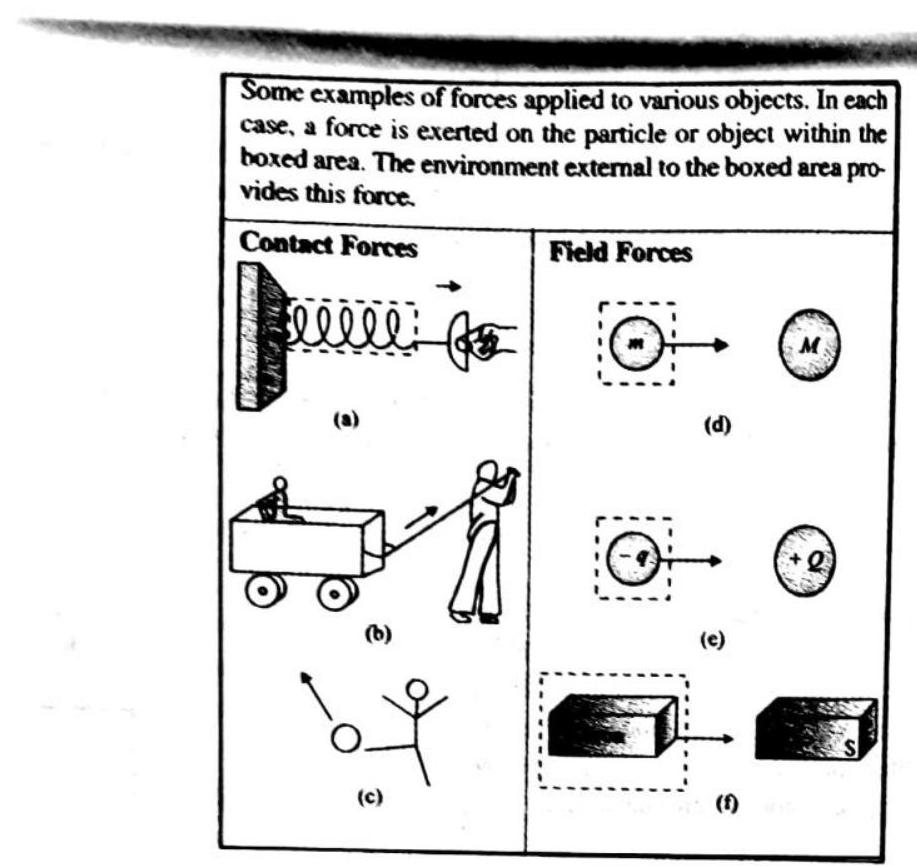
Weight
The earth attracts all the bodies towards its centre. The force exerted by the earth on the body is known as the weight of the body. It acts in vertically downward direction. These forces are not contact forces. If mass of the body is
Balanced and Unbalanced Forces
One effect of a force is to alter the dimension or shape of a body on which the force acts; like by loading a spring, there occurs an increase in its length. By hammering a small piece of silver sheet, thin foil is made. The steam pushing out from a pressure cooker occupies a large volume. On pressing a piece of rubber, its shape changes. In a cycle pump, when the piston is lowered, the air is compressed to occupy less volume. Another is to alter the state of motion of the body. A player applies force with a hockey stick to change the speed and direction of motion of a ball. When more force is applied on the pedal by a cyclist, speed of the cycle increases. In many situations we may find that a body remains at rest or moves uniformly even if it is acted on by a force ! For example try to push a heavy stone or a heavy iron safe, probably we may not be able to move it. Does it mean that something is wrong with the definition of force? What happens actually is that there exists another force which is acting on the body in a direction opposite to your push and exactly compensating it. In effect there is no net force acting on the body. This force which we have not taken into account is the force of friction.
When several forces act on a body simultaneously, their effects can compensate one another with the result there is no change in the state of rest or motion. When this is the case, the body is said to be in equilibrium. Equivalently, one can say that the net force acting on the body is zero for balanced forces. Balanced forces do not change the speed. This means that the body as a whole either remains at rest or moves in a straight line with constant rate.
Fig. : Balanced forces
An object in equilibrium may or may not be at rest. A parachutist, descending at constant speed, is in equilibrium. His weight is just balanced by the viscous drag on the parachute-which is why he put it on in the first place.
Balancing the vertical forces is not enough to produce equilibrium. An airplane traveling at constant speed, as in figure, is in equilibrium under the influence of four forces, two vertical and two horizontal.
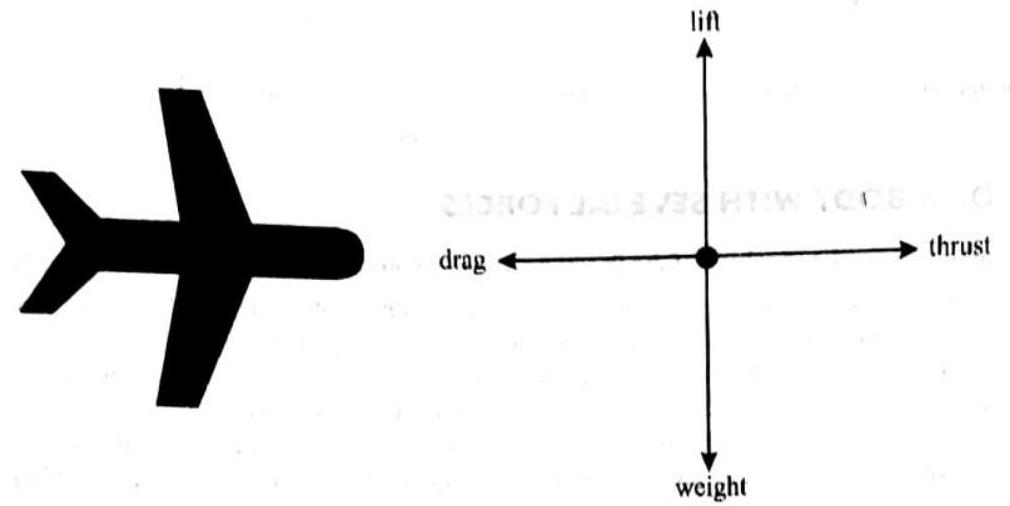
Vertical : gravity (down) is just balanced by the lift produced by the flow of air across the wing. I/orizontal : viscous drag is just balanced by the thrust of the engines. Both the vertical and the horizontal velocities are constant.
When the resultant force or net force acting on a body is not zero we say that it is acted on by an unbalanced force. A net or unbalanced force when acts on a body it changes its state of rest or uniform motion.
To imagine unbalanced force, imagine see saw. If the people on either side push down with the same force, they cancel each other. The see-saw is balanced and does not move [(fig. (a)]. In fig (b), there is an unbalanced force of
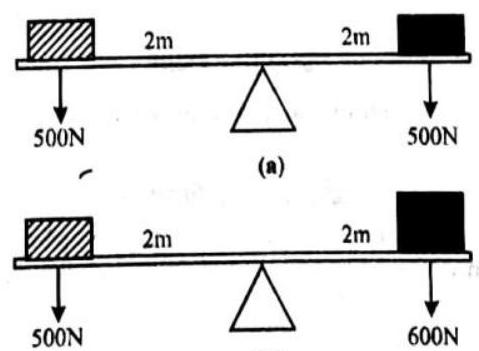
(b)
Component of a Force
The crate of figure is being dragged along the floor by means of a rope, which is not horizontal. The rope makes an angle
The tension in the rope, acting on the crate, does two things to it. First, it drags the crate across the floor. Second, it tends to lift the crate off the floor. The smaller the angle
How can you find out how much force is being used to drag the crate? Force is a vector, and it obeys the same mathematical rules as velocity vectors and displacement vectors. The dragging force is the component of the tension in the rope acting parallel to the floor, that is, the horizontal component.
Similarly, the component of the force tending to lift the crate is the vertical component and is given by
Equilibrium of a body with several forces
For the purpose of making a complete analysis of the forces acting on an object, a vector diagram is a useful device.
Figure is a vector diagram showing the forces on a brick being dragged along a tabletop. Four forces act: gravity (weight), friction, elastic recoil of the tabletop, and tension in the cord. Each force is represented by a vector, drawn at the correct angle and with its length proportional to the force. For the purpose of analysis, all vectors are represented by components along a pair of axes perpendicular to each other. In this case, we elect to use horizontal and vertical axes, since three of the forces are already on these axes. To do the analysis, we have to resolve the tension vector into its components on the vertical and horizontal axes. Then we can write two equations: one says that there is no net vertical force, and the other says that there is no net horizontal force.
At the moment an object that has been tossed upward into the air reaches its highest point, is it in equilibrium? Defend your answer.
Check Your Answer
When an object reaches at the highest point of its path, when it is tossed upwards in air, its velocity is zero. The force due to gravity acts in the downward direction which balances upward force with which it is thrown. So it is in equilibrium..
Units of Force
(i) The S.I. unit of force is newton.
One newton is the force which when acts on a body of mass
(ii) In C.G.S. system, the unit of force is dyne.
One dyne is the force which when acts on a body of mass 1 gramme, produces an acceleration of
(iii) Units of force in terms of force due to gravity
In MKS system, the unit of force is the kilogramme force (kgf).
One kilogramme force is the force due to gravity on 1 kilogramme mass.
Thus,
Since the average value of
Illustration 1
The 2.5 kilogram brick of figure in above section is being pulled by a cord that makes an angle of
Solution : (a) On the horizontal axis, the friction must be equal to the horizontal component of the tension, so
(b) On the vertical axis, the downward force (weight) must equal the sum of upward forces, so
Illustration 2
A block of weight
Solution : There are three forces on the body:
(i)
(ii)
(iii)
As the block is at rest, the resultant force on it must be zero. The total downward force is
NEWTON’S LAWS OF MOTION

Newton, Sir Isaac (1642-1727), mathematician and physicist, one of the foremost scientific intellects of all time. Born at Woolsthorpe, near Grantham in Lincolnshire, where he attended school, he entered Cambridge University in 1661; he was elected a Fellow of Trinity College in 1667, and Lucasian Professor of Mathematics in 1669 . He remained at the university, lecturing in most years, until 1696. Of these Cambridge years, in which Newton was at the height of his creative power, he singled out 1665-1666 (spent largely in Lincolnshire because of plague in Cambridge) as “the prime of my age for invention”. During two to three years of intense mental effort he prepared Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy commonly known as the Principia, although this was not published until 1687 .
Newton’s First Law of Motion
It gives qualitative definition of force. It states : An object continues in a state of rest or in a state of motion at a constant speed along a straight line, unless compelled to change that state by a net force. In other words, if a body is in a state of rest, it will remain in the state of rest and if it is in the state of motion, it will remain moving in the same direction with the same velocity unless an external force is applied on it.
Do you know !!
A common misconception about Newton’s first law is that a force is required to keep an object in motion. This is not so. Experiments done on air tracks (where there is a negligible friction) show that no force is required to keep an object moving with constant velocity. We get this misconception because friction is always present in our everyday lives
Do you know !!
To maintain constant velocity of a moving car; you have to push the accelerator. Does this contrudict Newton’s first law? No! It is seen clearly in the diagram on the right that the forward force on the car is equal in magnitude and opposite to the backward friction force (air friction plus ground friction) and so they cancel each other. resulting in a zero net force. Therefore, there is still no net force and the car moves away with constant velocity.
Inertia and mass
A greater net force is required to change the velocity of some objects than of others. For instance, a net force that is just enough to cause a bicycle to pick up speed will cause an imperceptible change in the motion of a freight train. In comparison to the bicycle, the train has a much greater tendency to remain at rest. Accordingly, we say that the train has more inertia than the bicycle. Quantitatively, the inertia of an object is measured by its mass. Inertia is the natural tendency of an object to remain at rest or in motion at a constant speed along a straight line. The mass of an object is a quantitative measure of inertia. The greater for the mass, the greater is the inertia of body. The definition of inertia and mass indicates why Newton’s first law is sometimes called the law of inertia.
Although the law of inertia was first clearly enunciated by Galileo, the English natural philosopher Issac Newton (1642-1727) incorporaled the law into the solid logical basis on which he founded the science of mechanics in his great 1687 work, commonly called Principia.
Do you know !!
According to Aristotle, an external force is required to keep a body in motion. His observation was based on common day experience. He was led to this wrong conclusion due to the reason that friction was not known in those days!
Examples :
(i) Coin drops into the glass when sudden force is applied on the cardboard.
(ii) Slow continue force breaks the upper string while if a sudden jerk is applied lower string breakout.

(iii) During the downward motion hammer’s sudden stop tighten the hammerhead.
(iv) Too little force, too little time to overcome “inertia” of tableware.


Galileo Galilei, bom in Pisa, Italy in 1564 was a key figure in the Scientific Revolution in Europe about four centuries ago. Galileo invented the concept of acceleration. From experiments on motion of bodies on inclined planes or falling freely, he contradicted the Aristotelian notion that a force was required to keep a body in motion, and that heavier hodies fall down faster under gravity. The law of inertia he thus arrived at was the starting point of the subsequent epochal work of Isaac Newton.
With Galileo came a turning point in the very method of scientific inquiry, Science was no longer merely observations of nature and logicul inferences from them. Science incant devising and doing experiments to verify or refute theories. Science meant measurement of quantities and a search for mathematical relations between them. Not undeservedly, many regard Galileo as the father of modern science.
The Law of Inertia
Galileo studied the motion of objects on an inclined plane. Objects moving down an inclined plane accelerate, while those going up the plane suffer retardation. Motion on a horizontal plane is an intermediate situation. Galileo concluded that at ubject moving on a horizontal plane must neither have acceleration nor retardation, i.e. it should move with constant velocity.
Another experiment of Galileo leading to the same conclusion involves a double inclined plane. A ball released from rest on one of the planes rolls down and climbs up the other. If the two planes are not very rough. the final height of the ball is nearly the same (a little less but never greater) as the initial height. In the ideal situation, when friction is completely eliminated, the final height of the ball should equal its initial height?
If now the slope of the second plane is decreased and the experiment repeated, the ball will still reach the same height, but in doing so it will travel a longer distance. In the limiting case, when the slope of the second plane is zero (i.e. it is a borizontal plane) the ball travels an infinite distance. In other words, its motion will never cease. This is, of course, an idealised situation. In practice, the ball does come to a stop after in motion continues to move with uniform velocity. This property of every object in nature is called inertia. Inertia means ‘resistance to change]. A body does not change its state of rest or of uniform motion, unless an external force compels it to change that state.
Types of Inertia
(I) Inertia of rest
The tendency of the body to continue in state of rest even when some external unbalanced force is applied on it is called inertia of rest.
Example 1 :
When a carpet is suddenly jerked the dust fly off, because due to the sudden moment the carpet moves but the dust on account of inertia of rest is left behind.
Example 2 :
The passenger standing in a bus tends to fall backwards when the bus suddenly starts, this is because his feet are in direct contact with the floor of the bus and the friction at the contact is high this friction does not allow the feet to slip on the floor, the feet therefore move forward with the floor the upper part of the body is still at rest for a while thus the passenger gets a jerk.
Example 3 :
On shaking a tree, the fruits fall down. The reason is that when the stem or branches are shaken, they come in motion while the fruits remain in the state of rest due to the inertia of rest. Thus the fruits get detached from the branches and fall down due to the pull of gravity.
(ii) Inertia of motion
The tendency of the body to continue in its state of motion even when some unbalanced force is applied on it is called the inertia of motion.
Example 1 :
It is dangerous to jump out of a moving vehicle (bus/train), because the jumping man, who is moving with the high speed of the vehicle would tend to move with the high speed of the vehicle. On reaching the ground his feet come to rest but upper part of the body continues to move with the speed of vehicle and the person falls forward on the ground. It is dangerous to jump out of a moving train and it is better to come out when it halts. However if in case of some emergency if some person wants to jump safely from a moving vehicle he should run for quite a while in the direction of motion of the vehicle after the jump so that his entire body remains in motion for sometime.
Example 2 :
When a running car stops suddenly, the passenger is jerked forward. The reason is that in a running a car, the whole body of passenger is in the state of motion. As the car stops suddenly, the lower part of his body being in contact with the car, comes to rest but his upper part remains in the state of motion due to the inertia of motion. Thus he gets jerked forward.
Example 3 :
In an event of long jump, an athlete runs fast before making the jump. Due to inertia of motion he is able to jump to a longer distance.
Example 4 :
A person riding a bicycle along a level road does not come to rest immediately after he stops pedaling. The bicycle continues to move forward due to the inertia of motion. But eventually it comes to rest as a result of the retarding action of friction etc.
Example 5 :
When we shake a wet piece of cloth, cloth as well as water in it comes to motion but when cloth comes to rest, the water is still moving due to the inertia of motion and falls forward on the front body of the person.
Example 6 :
When a person jumps out of a moving train, he falls down. This is so because inside the train, his complete body was in a state of motion with the train. On jumping out of the moving train as soon as his feet touch the ground, the lower part of his body being in contact with the car, comes to rest but his upper part remains in the state of motion due to the inertia of motion. Thus he gets jerked forward.
Is it possible to have motion in the absence of a force? Is it possible to have force in the absence of motion?
Check Your Answer
Motion requires no force. Newton’s first law says an object in motion continues to move by itself in the absence of external forces. It is possible for forces to act on an abject with no resulting motion if the forces are balanced.
MOMENTUM
Most of us know from our experience of playing cricket that a cricket ball moving with a high speed could be fatal. Is it due to the velocity of the ball only? Had it been so, a dust particle moving with the same velocity would have been equally fatal. On the other hand, it could not be only due to the mass of the ball as we can safely hold a stationary (or a slowly moving) cricket ball in our hand without any fear. From this and many such examples we conclude that a quantity consisting the product of mass and velocity (mv) is of much significance. This quantity is so important in physics that it is given its own name and symbol. We call this quantity as momentum and represent it by symbol p.
Momentum is a measure of the quantity of motion in a body.
Example: Consider, a truck and a rickshaw moving with same velocities, heading towards each other and eventually ending up in a head on collision. Needless to say, that the rickshaw might get deformed to such an extent, that it would be difficult for us to make it, were it was a rickshaw before ! However, the truck might get some minor damages. Why is it so ? The first thing that comes to mind, is because the truck has more mass. Exactly! But in this context, it is more wise to say that, it all happens because the truck has more quantity of motion (i.e., momentum).
The momentum of a moving body is defined as the product of its mass and velocity. If we represent the mass and velocity of a body by
The direction of momentum of a body is same as that of its velocity. If only the magnitude is considered, then
The SI unit of momentum is kilogram meter per second
Illustration 3
A ball of mass
Solution : Given mass of the ball
Newton’s Second Law of motion
It states that the rate of change of momentum of a body is directly proportional to the applied unbalanced force.
Rate of change in momentum
Do you know !!
When a body is travelling at constant speed, the net force on it is zero.
If a body is moving with initial velocity
Initial momentum of the body
Final momentum of body
Change in momentum in time
So, rate of change of momentum
But according to Newton’s second law
Here
So
If
Hence,
So, the magnitude of the resultant force acting on a body is equal to the product of mass of the body and the acceleration produced. Direction of the force is same as that of the acceleration.
Newton’s First and Second Laws : The logical connection between them
Newton’s first law asserts that a body tends to move with constant velocity. Newton’s second law provides a quantitative measure of the force that will produce a given acceleration of the mass.
At first glance, it may seem that the Newton’s first law is not an independent law of nature at all, but merely the special case of Newton’s second law,
Do you Know !!
Illustration 4
A force acts for
Solution : When force ceases to act the body shall move with the constant velocity since it moves a distance
i.e.
Acceleration
From the relation
Force
Illustration 5
Calculate the force required to impart to a car a velocity of
Solution : Here, Mass,
Let us calculate the value of acceleration by using the first equation of motion.
Now, Initial velocity,
Final velocity,
And, Time taken,
Now, putting these values in the equation :
We get,
or acceleration,
Now, putting
We get,
Thus, the force required in this case is of 4500 newtons.
Illustration 6
A motorcar is moving with a velocity of
Solution : The initial velocity of the motorcar
and the final velocity of the motorcar
The total mass of the motorcar along with its passengers
We have the magnitude of the force
On substituting the values, we get
The negative sign tells us that the force exerted by the brakes is opposite to the direction of motion of the motorcar.
Illustration 7
A force of
(i) the acceleration of the body’
(ii) velocity at the end of
(iii) displacement at the end of
Solution : Given :
From
(i) Thus, acceleration
(ii)
Using
(iii)
From
Illustration 8
A ball of mass
(i) the initial momentum of ball
(iii) the rate of change of momentum
Solution : Given :
(i) Initial momentum of ball
(ii) Final momentum of the ball
(iii) Rate of change of momentum
(iv) Acceleration
(v) Force
Newton’s Third Law Of Motion
Newton’s first two laws of motion describe what happens to a single object that has forces acting on it while Newton’s third law deals with the relationship between the forces objects exert on each other.
If we push on a wall it pushes back. This doesn’t hurt if you push gently, but if you punch a wall hard it hurts very much. Newton hypothesized that any time two objects interact in such a way that a force is exerted on one of them, there is always a force that is equal in magnitude exerted in the opposite direction on the other object. This hypothesis is called Newton’s third law.
Newton’s third law of motion states that ‘if a body
Motor cars are able to move along a road because the reaction of the road pushes the car along in response to the action of the wheels pushing on the road.
(i) A swimmer pushes (or applies force) the water with his hands and feet to move in the forward direction in water. It is the reaction to this force that pushes the swimmer forward.
(ii) The propellers of an aeroplane pushes the air backwards and the forward reaction of the air makes the aeroplane move forward.
(iii) When a bullet is fired from a gun, the force sending the bullet forward is equal to the force sending the gun backward. But due to the high mass of the gun, it moves only a little distance backward and gives a kick to the shoulder of the gunman. The gun is said to have recoiled.
(iv) Consider, a horse cart being driven by a horse. The horse pulls forward, the cart with a force
The forward thrust,
Thus, the net force on the system, acting forwards is given by
Now, if
and hence the system would start moving with an acceleration
where
But if
(v) Action and reaction are equal in magnitude but both act on the body in opposite direction.
For an orbiting satellite action of earth on the satellite is the force exerted on the satellite by the gravitational pull of the earth.
Reaction of the satellite on the earth. It is the gravitational pull of the satellite on the earth.
(vi) Hammer pushes on stake then stake pushes on hammer and the hammer acts, the stake re-acts.
Do you know !!
The paired forces (called action and reaction) always act on different bodies. There is no way one of them can balance the other one!
(vii) When car moves tyre pushes the road and road pushes on the tyre as a reaction force.
Misconcept
Consider a book on the table. The table pushes the book upward i.e. normal force. Student feels weight and normal force are action and reaction but they aren’t action and reaction. Reason : The book does not fly up because there is another force on the book pulling it downward this is the force exerted by the earth i.e. the weight of the book as book does not accelerate so, we conclude that the forces acting on the book are balanced but they are not action and reaction pair because the action and reaction acts on different bodies.
There is another misconception concerning the third law. The third law states that the two forces Weight example, an egg and a stone collide with each other, the egg breaks and the stone is intact.
Since the egg breaks, we often conclude that the force by the stone on the egg is greater than the force by the egg on the same. This is not so. The forces are always equal. The egg breaks because it is simply easier to break. It takes a smaller force to break the egg then to break the stone.
Newton’s Third Law from Newton’s Law
Let us consider two bodies 1 and 2. Let
Extermal force
Experiment : The ring of a spring balance
Fig. : Demonstration of action and reaction
Guidelines to solve problem based on NLM
(i) Draw a free-body diagram for each object involved in the analysis.
(ii) Select a rectangular coordinate system. The solutions will be much easier if you seloct the
(iii) Resolve all forces not pointing in the
(iv) Add, algebraically, all the
(v) Set
Since you have choosen the
- Mayank strongman and some small pull on opposite ends of rope in a tag of war. Who exerts the greater force on the rope.

Check your answer
Both of them would exert the same force on the rope. Mayank can pull no harder on the rope than Sonu. Rope tension is the same all along the rope, including the ends. Just as a wheel on ice can exert no more force on the ice than the ice exerts on the wheel and just as one cannot punch an empty paper bag with any more force than the bag can exert on the puncher. Mayank can exert no more force on his end of the rope than Sonu exerts on his end.
Do you know !!
Atwood’s machine gives us a direct way of demonstrating Newton’s laws of motion in the laboratory.
Illustration 9
A water skier is towed by a motorboat at a constant velocity of magnitude
Solution : Two major forces act on the water skier, one of these forces is that exerted on her hands by the towrope. The other is the resistance of the water (and to a lesser extent the air). When the skier is moving in a straight line at a constant
When the skier is moving at
But so is the resistive force. Again, the net force on the skier must be zero because her velocity is constant.
Illustration 10
What thrust is needed to fire a 350-kilogram rocket straight up with an acceleration of 8.0 meters per second squared?
Solution : The net force needed to produce this acceleration is
However, there is a downward force acting on it as well, equal to
The net force is the thrust minus the weight, or
thrust
so the rocket engine must product a thrust of
Illustration 11
A pile driver of mass
Solution :
Illustrotion 12
A force of
Solution : For mass
then
For mass
then
When
then
Free Body Diagram
To study the motion of an individual body of a system, a diagram is drawn which represents different types of interactions with surrounding in terms of forces. This diagram is said to be the Free Body Diagram (FBD) of that body. To draw the free body diagram, the object is first made isolated from its surroundings and then all forces acting on it are represented by \tos
Illustration 13
Two blocks of mass
- Block
- Block
- Pulley 1
- Pulley 2
Solution :
Illustration 14
Three blocks
- Block A
- Block B
- Block C
- Pulley
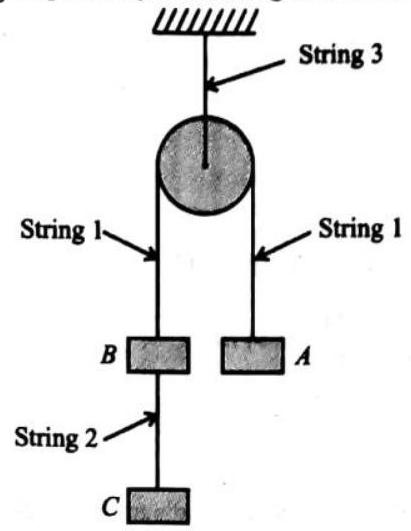
Solution :
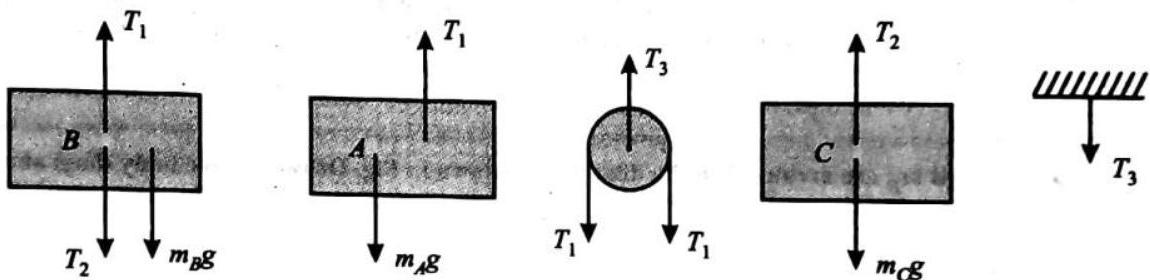
Illustration 15
Find acceleration and contact force between the two bodies
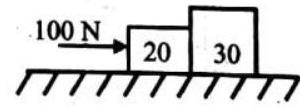
Solution:
Illustration 16
Find acceleration of each mass and tension in the string (
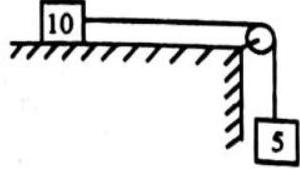
Solution :
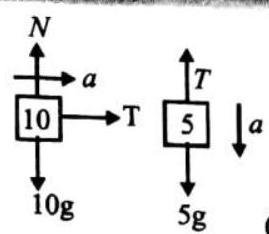
(Both masses will have the same acceleration as string is inelastic)
From (i) and (ii)
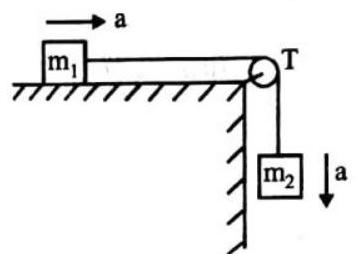
NOTE : For this system,
Illustration 17
Draw free-body diagram of each body in the system
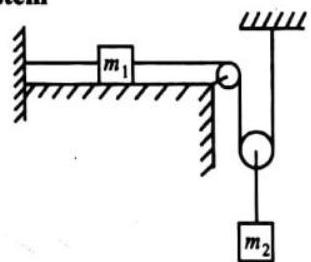
Solution :
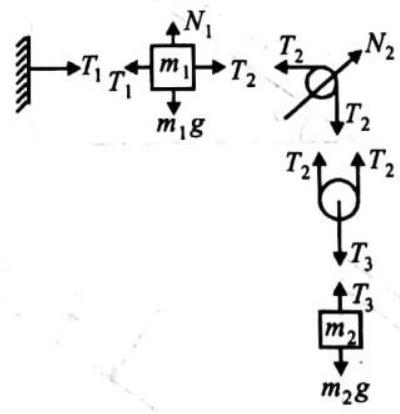
Illustration 18
Find acceleration of masses and tension in the strings, pulley is massless and frictionless and strings are massless and inelastic.
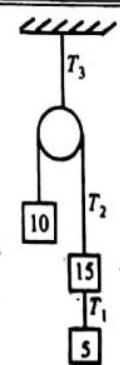
Solution :
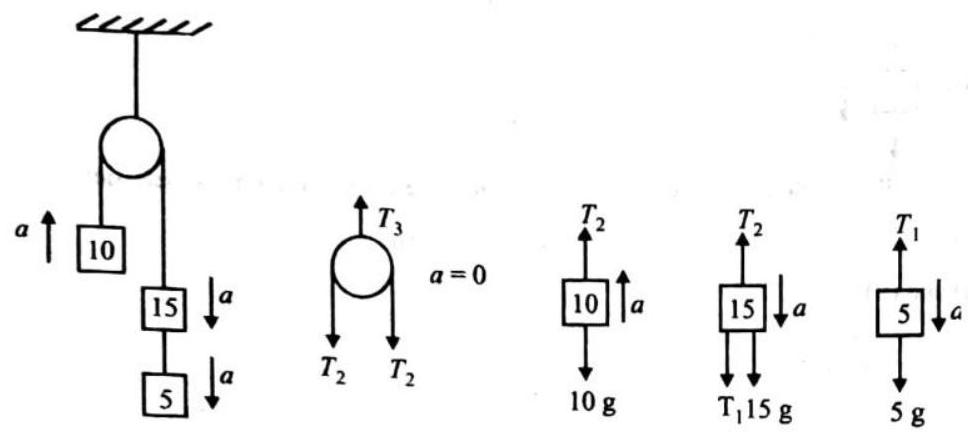
Adding (ii), (iii) and (v)
Illustration 19
Draw F.B.D. of the system shown
Solution :
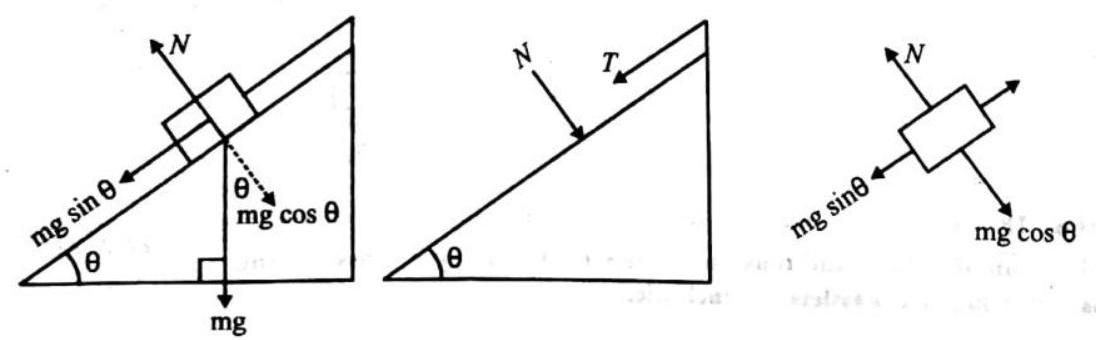
Impulse
From Newton’s second law,
Impulse-momentum is very useful in explaining some everyday phenomena like a cricket player while taking a catch always moves his hands backward, because the total change in momentum
Do you know !!
The change in momentum of a body depends on the magnitude and direction of the applied force and the period of time over which it is applied; i.e. it depends on its impulse.
Thus the hands of the player are not hurt while taking a catch. Similarly the idea of the impulse of a force is important when considering a hammer driving a nail into a block of wood, a boy kicking a football and a girl striking a hockey ball.
Example :
(i) A girl standing at rest with her right foot on a skateboard thrusts backwards on the ground with her left foot as Figure. The push of the ground on her left foot will increase the forward momentum of the girl and skateboard. From

(ii) A body throwing a javelin is shown in figure. For a javelin of a given mass, the distance it will travel depends upon the force exerted by the boy’s arm and the time for which it is exerted.

(iii) During the collision of a truck with the wall, wall exerts great impulse on truck
Illustration 20
A 650-kilogram rocket is to be speeded up from 440 meters per second to 520 meters per second in outer space. If the thruet of the engine is 1200 newtons, for how long must the engine be fired ?
Solution : The change in the momentum of the rocket is
IIlustration 21
A 0.10 kilogram ball is dropped onto a table top. The speeds of the ball right before hitting the table top and right after hitthy the table top are
Solution : Given :
The velocity of the ball before the collision is downward and the velocity of the ball after the collision is upward. Since these two velocities are opposite, we have to assign signs (+ or - ) to them to find the change in velocity,
From impulse-momentum theorem, we have
So,
The positive sign indicates that the force on the ball by the tabletop is upward, which makes sense.
Illustration 22
A boy of mass
Solution : Assume there is zero unbalanced horizontal force in the horizontal direction and that left to right is the positive (+) direction.
Momentum before interaction
Momentum after interaction
Equating momenta
Conservation of Momentum
The greatest value of the concept of momentum is in the calculation of what happens when two or more objects interact. It turns out that we can often find out the results of a collision, for example, without knowing anything at all about the for interact. It turns out long they persist.
The explanation is this : Think of two objects,
Now, impulse is equal to change in momentum. It follows that, in the collision, the change in the momentum of
Think of using this rule whenever dealing with an interaction between two objects. For example, a little girl is standing on a wagon, and jumps off to the rear of it. To do so, she has to kick the wagon so that it moves forward. Before she jumped, the total momentum of the system was zero, so it must continue to forward.
In other words, the principle of conservation of momentum states that “if there is a direction in which there is zero unbalanced force acting on a system then the total momentum of that system in that direction is constant even if the bodies act on each other’.
Note that other forces, e.g. the pull of the Earth, do act on the bodies, but the result can still be used if there is a direction in which the external forces are balanced.
The law of conservation of Linear momentum by third law of motion :
Suppose two objects
The change in momentum of object
The force on
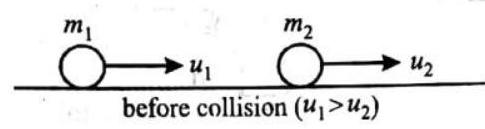
IDEA BOX

The change in momentum of object

The force on
By Newton’s third law
Example :
(1) A bomb shell initially at rest is shown in figure. Now the bomb shell suddenly explodes in two fragments having masses in the ratio
Let the masses of the two fragments be
or
Thus the smaller fragment of mass
(2) Recoil of the Gun : Initially, before a bullet is fired from the gun, both, the bullet and the gun are at rest. So, before a bullet is fired, the initial momentum of the system (gun + bullet) is zero.
Now, when a bullet is fired it leaves the barrel with some velocity, that is it has some momentum. According to the law of conservation of momentum, the final momentum should be equal to the initial momentum which is in this case is zero. The final momentum could be zero only if the gun has a momentum equal and opposite to that of the bullet. The gun is said to be recoiled. Although their momenta are equal but as the mass of the gun is much higher than that of the bullet the recoil velocity of the gun is much smaller compared to the velocity of the bullet.
(3) Jet Engines and Rockets : The working of jet engines and rockets can also be described on the basis of the law of conservation of momentum. A rocket standing at the launching pad has produced.
Theses gases pass out through the tail nozzle of the rocket in downward direction in the form of jet with tremendous velocity. Therefore the rocket moves up with such a velocity so as to make the momentum of the system (rocket + emitted gases) zero again.
Think it Overt
Tie the mouth of a balloon tightly to a small piece of discarded ballpoint refill or a plastic tube having a narrow bore and inflate it. Close the opening of the tube with your finger to prevent the air to escape (fig. (a)). Now let the air escape from the opening of the tube (fig. (b)). In which direction does the balloon move? Why does it move in a direction opposite to the direction in which the air escapes?
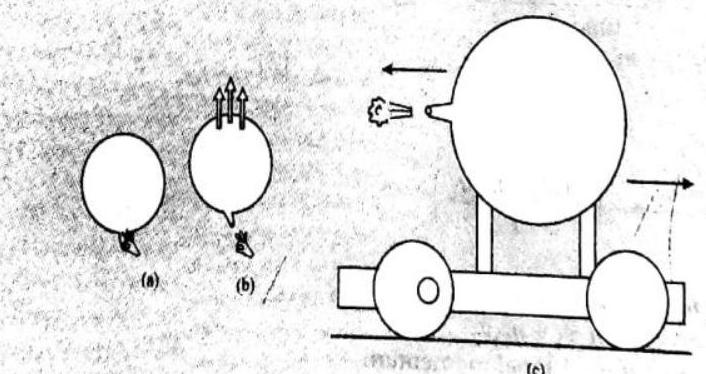
In doing this activity you may also fix the inflated balloon on the top of (fig. c). You will notice that the toy car moves in the direction opposite to the direction a trolley before you let the air escape principle involved in the working of jet engines and rookets. In jet engines, a large volume which the air escapes. This is the basic of fuel is allowed to escape through a jet and as a result, it moves the forward.
Illustration 23
A bullet of mass
Solution : Choose a suitable direction (the horizontal direction) in which the effect of the external forces is zero. Choose a sign
convention for the direction of the velocities : here left to right is positive ( + ). Let
Momentum after gun is fired
Momentum before firing
In hand-held guns the recoil can be absorbed by the person holding the gun. In very large guns which fire massive shells at high velocity the recoil could rip the gun from its mounting unless special provision is made to absorb the force.
Illustration 24
A 1.2-kilogram basketball traveling at 7.5 meters per second hits the back of a 12-kilogram wagon and bounces off at 3.8 meters per second, sending the wagon off in the original direction of travel of the ball. How fast is the wagon going?
Solution :
The momentum of the ball before it hit has to equal the sum of the momenta of the two objects after the collision. Let’s call the original direction of travel of the ball positive. Then the equation becomes
Illustration 25
Two particles of mass
Solution : Since the particles are released from rest, so initial momentum of the system of particles is zero. Further, since the interaction between the particles is mutual, so the forces acting on them are purely internal, and hence the momentum of the system remains constant (and is zero) with time.
The negative sign indicates that the direction of velocity of larger mass is opposite to that of the smaller mass.
More About Friction
We studied back that friction is a resistance to the relative motion between two objects in contact (in case of solid objects) or the body and its surroundings (in case object is moving in a fluid). Actually, when two objects are kept in contact, a reaction force

force
It is not appreciated that the existence of friction between surfaces does not depend on their roughness or smoothness in the everyday sense of these words. In fact there can be very large frictional force between two highly polished flat metal surfaces. Consequently, it is important, in mechanics, to interpret smooth as frictionless rather than free from projections.
The results of experimental investigation into the behaviour of frictional forces confirm that:
(a) frictional forces opposes the movement of an object across the surface of another with which it is in rough contact.
(b) the direction of the frictional force is opposite to the potential direction of motion.
(c) the magnitude of the frictional force is only just sufficient to prevent movement and increases as the tendency to move increases, up to a limiting value. When the limiting value is reached, the frictional force cannot increase any further and motion is about to begin (limiting equilibrium). When the frictional force
The constant
In general
Do you know
The atomic and molecular forces of attraction between the two surfaces at the point of contact give rise to friction between the surfaces.
Static Frictional Force
When there is no relative motion between the contact surfaces, frictional force is called static frictional force. It is a self-adjusting force, it adjusts its value according to requirement (of no relative motion).
In the taken example static frictional force is equal to applied force. Hence one can say that the portion of graph
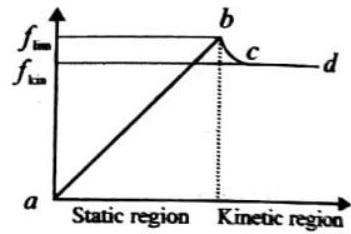
Limiting Frictional Force
This frictional force acts when body is about to move. This is the maximum frictional force that can exist at the contact surface. We calculate its value using laws of friction.
Kinetic Frictional Force
Once relative motion starts between the surfaces in contact, the frictional force is called as kinetic frictional force. The magnitudeof kinetic frictional force is also proportional to normal force.
From the previous observation we can say that
Angle of friction
At a point of rough contact, where slipping is about to occur, the two forces acting on each object are the normal reaction
IDEA BOX
The friction between two surfaces increases (rather than to decrease), when the surfaces are made highly smooth.
The resultant of these two forces is
The angle
At a point of rough contact when slipping is about to occur we can, therefore, use either.
components
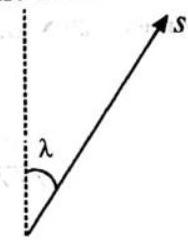
The use of
- When the surfaces of two objects in rough contact tend to move relative to each other, equal and opposite frictional forces act on the objects, opposing the potential movement.
- Up to a limiting value, the magnitude of a frictional force,
- When the limit is reached
- At all times
- The resultant of
Angle of Repose
Suppose a body is kept above a rough inclined surface, whose angle of inclination is slowly increased such that at angle ’
So,
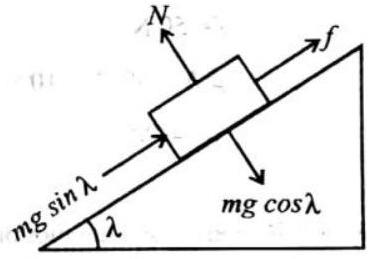
In case
so
If body is projected upward on the inclined plane, then
Illustration 26
Find acceleration and friction force for the body as shown in figure (
Solution : Applied force,
Limiting force of friction
As the applied force is less than the limiting force of friction the body will not accelerate and hence, force of friction will be equal to the applied force
So,
Illustration 27
In Ilustration-26 if the applied force is
Solution :
so,
Illustration 28
When a force of
Solution : As on the application of
When the body is set into motion then kinetic friction will come into play, that is why the same force will produce accelerativil
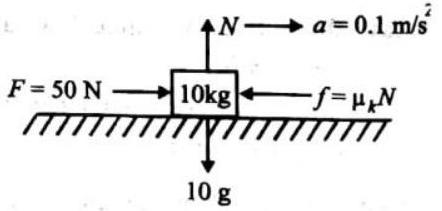
Illustration 29
Find acceleration of masses and tension in the string for the system shown
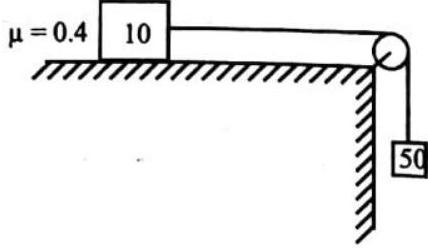
Solution :
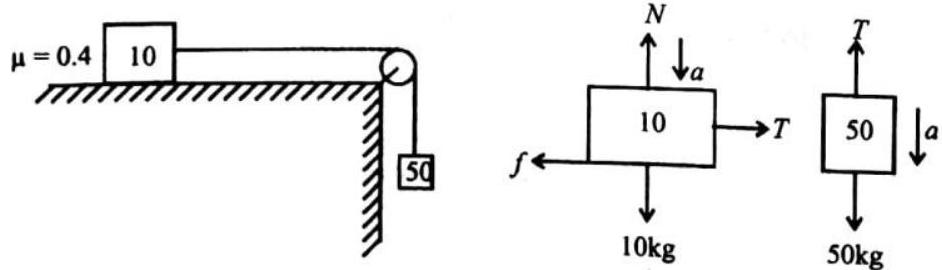
So,
and
Illustration 30
Find acceleration of masses and tension in the string for the system shown in fig
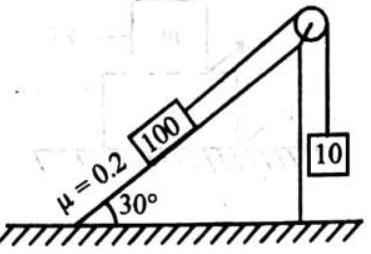
Solution : Drawing F.B.D of two masses
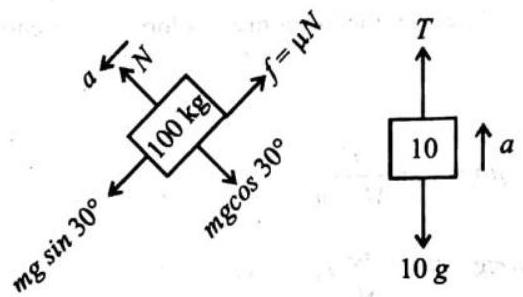
Illustrotion 31
Find maximum force applied on the lower mass so that the two masses move together, for the system of masses shown.
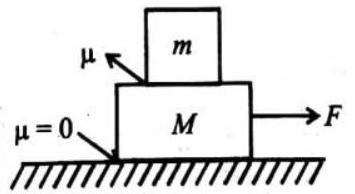
Solution : In order to find the direction of friction on the mass
(As friction on the upper body is in forward direction so on the lower body it will be in backward direction i.e. action -reaction pair)
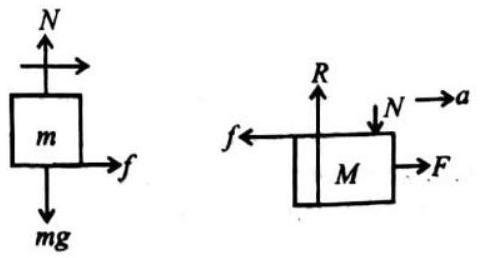
Illustration 32
In illustration-31 if force is applied on the upper mass then what will be your answer.
Solution :
As the two masses are moving together so
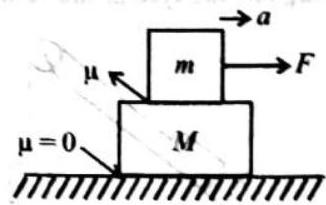
(As the upper mass is likely to slide over the lower mass in forward direction, friction will be in backward direction)
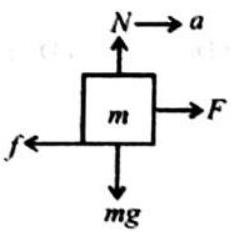
Illustration 33
Explain why it is easier to pull than push a box on a rough surface
Solution : Pushing a box
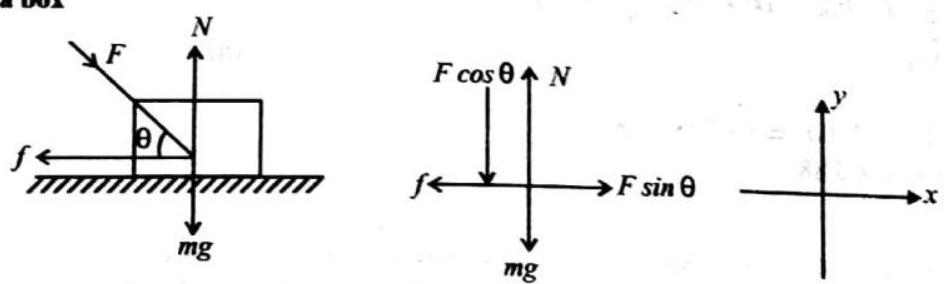
Along
Pulling a box
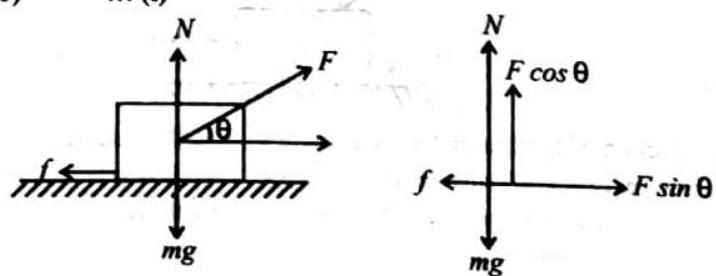
Along
So,
Illustration 34
A mass of
Solution :
Using
But
So,
Friction force,
Illustration 35
A chain of mass ’
Solution :
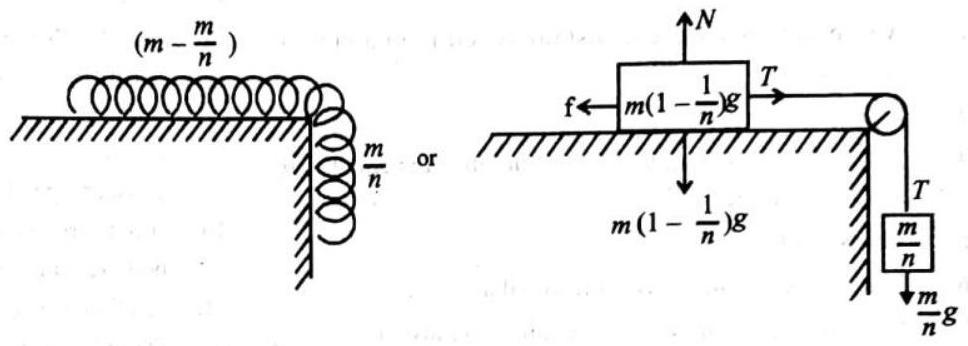
From F.B.D
Illustration 36
Find acceleration and contact force between two masses in the given fig
Solution :
Drawing F.B.D (Two mass will slide down together as
and
Adding (i) and (ii)
(from (i))
EXERCISE 1
Fill in the blanks
DIRECTIONS : Complete the following statements with an appropriate word / term to be filled in the blank space(s).
- Application of a force changes the ____ object.
- An object moving at constant speed is in a state of ____
- Impulse is the product of force and ____
- The change in the momentum of an object is equal to the ____ applied to it.
- The SI unit of force is the ____
- It takes about 4.45 newtons to ____
- If a force of 200 newtons is required to move a wagon up a frictionless hill at constant speed, the force needed to lef the wagon roll downhill at constant speed is ____
- In any interaction between two or more isolated objects, the total ____ does not change.
- An object will move in a circular path at constant speed if a force is applied to it in a direction that is kept ____ to its velocity.
- The change in the velocity of an object is proportional to the ____ applied to it.
- The ratio of net force applied to an object to the acceleration it produces is the ____ of the object.
- If there are several forces on an object, its acceleration depends on its mass and the ____ force.
- Magnitude of kinetic friction ____ with increase in inclination of the inclined plane.
- Conical shape of rockets reduce ____
- ____ is equal to change in momentum.
True/False
DIRECTIONS : Read the following statements and write your answer as true or false.
- When we push our foot against the ground backwards (action), the ground exerts an equal and opposite force (reaction) on our foot which causes us to more forward.
- It is easier to start motion in a lighter body than a heavier body.
- A rocket can propel itself in a vacuum.
- Action and reaction force acts on the same object.
- Particle of different masses falls with different acceleration on earth.
- Particle is at rest, if force is zero.
- Particle moves in the direction of force.
- If particle is initially at rest then it moves in direction of net force.
- No net force acts on a rain drop falling vertically with a constant speed.
- If net force acting on the body is zero, momentum of the body remains constant.
- Friction is electromagnetic in nature.
- Static friction is self-adjusting.
- Magnitude of kinetic friction is constant.
- Forces of action and reaction cancel each other
- A body can be in equilibrium under the action of three coplaner forces.
Match the Columns
DIRECTIONS : Each question contains statements given in two columns which have to be matched. Statements
| Column I | Column II |
|---|---|
| (A) To every action there is | (p) Momentum |
| (B) During collision, there is conservation of | (q) Force |
| (C) Rate of change of velocity is | (r) Reaction |
| (D) Rate of change of momentum is | (s) Acceleration |
| (E) Force that opposes motion | (t) Force of Friction |
- A block of mass
| Column I | Column II |
|---|---|
| (A) Lift moving upwards with some acceleration | (p) Equal to |
| (B) Lift moving downwards with some acceleration | (q) Greater than |
| (C) Lift moving upwards with constant velocity | (r) Less than |
| (D) Lift falling freely under gravity | (s) Zero |
- Consider the arrangement shown in the figure. There is no friction between block
| Column I | Column II |
|---|---|
| (A) |
(p) |
| (B) |
(q) |
| (C) |
(r) |
| (D) |
(s) |
Very short answer questions
DIRECTIONS : Give answer in one word or one sentence.
- A person sitting in the compartment of a train moving with a uniform speed throws a ball in the upward direction. What path of the ball will appear to him? What to a person standing outside?
- The length of an ideal spring increases by
- The two ends of a spring-balance are pulled each by a force of
- A retarding force is applied to stop a motorcar. If the speed of the motorcar is doubled, how much more distance will it cover before stopping under the same retarding force?
- A ball of
- A body of mass
- A body is suspended from the ceiling of a transparent cabin falling freely towards the earth. Describe the motion of the body as observed by an observer (a) sitting in the cabin, (b) standing on the earth.
- A force of
- What is the angle of friction between two surfaces in contact, if coefficient of friction is
- Under what circumstances is Newton’s first law same as Newton’s second law.
- Write the equation of Newton’s second law when the body is moving opposite to the direction in which force is applied.
- What is friction?
- Why do we call friction a self adjusting force?
- Why is friction a non-conservative force ?
- It is easier to roll a barrel than to pull it along the road. Why?
Short Answer Questions
DIRECTIONS : Give answer in 2-3 sentences.
- Vehicles stop on applying brakes. Does this phenomenon violate the principle of conservation of momentum?
- Four blocks of the same mass

Determine the tensions
- Two bodies of masses
- A bird is sitting on the floor of a closed glass cage in the hands of girls. Will the girl experience any change in the weight of the cage when the bird (i) starts flying in the cage with a constant velocity? (ii) flies upwards with acceleration ? (iii) flies downwards with acceleration ?
- The driver of a truck travelling with a velocity
- Derive a formula for the acceleration of a body moving down rough inclined plane.
- Derive a relation between angle of friction and angle of repose.
- What is inertia ? Why do we call the Newton’s first law as the law of inertia? Explain.
- Show that the Newton’s first law of motion gives the qualitative definition of force and the second law gives the measure (or quantitative definition) of force.
- State Newton’s second law of motion. With the help of this law, establish a relationship between the force and acceleration produced in a body.
- State Newton’s second law of motion. Show that it gives the measure of force.
- Prove that Newton’s second law of motion is the only real law of motion.
- What is force? What are its absolute and gravitational units ? How are these related to each other?
- Define the terms momentum and impulse. Obtain the relation between impulse and momentum.
- State the principle of conservation of linear momentum. Explain, how you will prove this law. Explain one example, where we make use of this law.
Long Answer Question
DIRECTIONS : Give answer in four to five sentences.
- State Newton’s second law of motion. Hence, derive the equation of motion
- State Newton’s laws of motion and the principle of conservation of momentum. Prove the principle of conservation of momentum from (i) Newton’s second (ii) third law of motion.
- What is friction ? Why is it called a self adjusting force? Give the old and modern view of the cause of friction.
- Explain fully the terms ‘friction’ and ’limiting friction’.
State the laws of limiting friction. Justify the statement that friction is a necessity and an evil. Give some familiar methods for reducing friction.
EXERCISE 2
Multiple Choice Questions
DIRECTIONS: This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
- A force
(a) 2
(c) 6
(b) 4
(d) 8
- A field gun of mass
(a)
(b)
(b)
(d)
- A feather of 20 grams is dropped from a height. It is found to fail down arts a constant velocity. The net force acting on it is
(a)
(b)
(c)
(d) zero
- A body of mass
(a) 2 sec.
(b) 3 sec.
(c)
(d)
- If a constant force acts on a body initially kept at rest the distance moved by the body in time
(a)
(b)
(c)
(d)
- By applying a force of one Newton, one can hold a body of mass
(a) 102 gram
(b)
(c)
(d) None of these
- The speed of a falling body increases continuously, this is because
(a) no force acts on it
(b) it is very light
(c) the air exert the frictional force
(d) the earth attract it
- A gun of mass
(a)
(b)
(c)
(d)
- If an object is in a state of equilibrium
(a) it is at rest
(b) it is in motion at constant velocity
(c) it is in free fall
(d) may be more than one of the above
- A fish is swimming upward at an angle of
(a) upward
(b) downward
(c) horizontal
(d) at an angle upward
- If a boat is moving along a constant speed, it may be assumed that
(a) a net force is pushing it forward
(b) the sum of only vertical forces is zero
(c) the buoyant force is greater than gravity
(d) the sum of all forces is zero
- An astronaut with all her equipment has a mass of 95 kilograms. How much will she weigh on the moon, where the acceleration due to gravity is 1.67 meters per second squared?
(a)
(b)
(c)
(d)
- How much is the viscous drag acting on a rocket-driven sled that is going at constant speed against a frictional force of 22000 newtons when the thrust of the engine is 31000 newtons-
(a)
(b)
(c)
(d)
- To slow down a car, a braking force of 1200 newtons is applied for 10 seconds. How much force would be needed to produce the same change in velocity in 6 seconds -
(a)
(b)
(c)
(d)
- A frictionless wagon is pushed from rest, with a force of 60 newtons for 14 seconds. If it then strikes a wall and comes to rest in 0.15 second, how much average force does the wall exert on it ?
(a)
(b)
(c)
(d)
- What force is needed to a accelerate a 60 -kilogram wagon from rest to 5.0 meters per second in 2.0 seconds
(a)
(b)
(c)
(d)
- A frictionless wagon going at 2.5 meters per second is pushed with a force of
(a)
(b)
(c)
(d)
- A 2.0 kilogram weather balloon is released and begins to nse against 6.5 newtons of viscous drag. If its buoyancy is 32 newtons, what is its acceleration
(a)
(c)
(b)
(d)
- What braking force is needed to bring a 2200 kilogram car going 18 meters per second to rest in 6.0 seconds?
(a)
(b)
(c)
(d)
- The 35 kilogram girl is standing on a 20 kilogram wagon and jumps off, giving the wagon a kick that sends it off at 3.8 meters per second. How fast is the girl moving
(a)
(b)
(c)
(d)
- A
(a)
(c)
(b)
(d)
- In outer space, a
(a) 17 newton
(c) 3000 newton
(b) 750 newton
(d) 3200 newton
- Two stars of masses
(a)
(b)
(c)
(d)
- A moving object can come to rest only if it
(a) has a frictional force acting on it
(b) has no net force acting on it
(c) is completely isolated
(d) applies an impulse to something else
- If a jet engine provides a thrust of 45000 newtons, how long must it fire to produce 1 million newton-seconds of impulse?
(a)
(b)
(c)
(d)
- A rocket-driven sled speeds up from 40 meters per second to 55 meters per second in 5.0 seconds, using an engine that produces 3500 newtons of thrust. How much thrust would be needed to get the same increase in speed in 2.0 seconds
(a) 8550
(b) 8750
(c) 8700
(d) 8500
- What force is needed to speed up a frictionless
(a)
(b)
(c)
(d)
- What force must the brakes and tires apply to a
(a)
(b)
(c)
(d)
- A
(a)
(b)
(c)
(d)
- A
(a)
(b)
(c)
(d)
- The recoil velocity of a
(a)
(b)
(c)
(d)
- A
(a)
(b)
(c)
(d)
- When a body is stationary
(a) There is no force acting on it
(b) The force acting on it not in contact with it
(c) The combination of forces acting on it balances each other
(d) The body is in vacuum
- A rider on horse falls back when horse starts running, all of a sudden because
(a) rider is taken back
(b) rider is suddenly afraid of falling
(c) inertia of rest keeps the upper part of body at rest while lower part of the body moves forward with the horse
(d) none of the above
- A man getting down a running bus, falls forward because
(a) due to inertia of rest, road is left behind and man reaches forward
(b) due to inertia of motion upper part of body continues to be in motion in forward direction while feet come to rest as soon as they touch the road
(c) he leans forward as a matter of habit
(d) of the combined effect of all the three factors stated in (a), (b) and (c)
- The heart is pumping blood at
(a)
(c)
(b)
(d) zero
- A force of 50 dynes is acted on a body of mass
(a)
(b)
(c)
(d)
- A force
(a)
(b)
(c)
(d)
- Swimming is possible on account of
(a) First law of motion
(b) Second law of motion
(c) Third law of motion
(d) Newton’s law of gravitation
- The distance
(a) Newton’s first law
(b) Newton’s second law
(c) Newton’s third law
(d) none of these
- Gravels are dropped on a conveyor belt at the rate of
(a) 1
(b) 2
(c) 4
(d) 0.5
- A cricket ball of mass
(a)
(b)
(c)
(d)
- The average force necessary to stop a hammer having momentum
(a)
(b)
(c)
(d)
- A force of 100 dynes acts on mass of
(a)
(b)
(c)
(d)
- The Newton’s laws of motion are valid in
(a) inertial frames
(b) non-inertial frames
(c) rotating frames
(d) accelerated frames
- Newton’s third law is equivalent to the
(a) law of conservation of linear momentum
(b) law of conservation of angular momentum
(c) law of conservation of energy
(d) law of conservation of energy and mass
- When we jump out a boat standing in water it moves
(a) forward
(b) backward
(c) side ways
(d) none of the above
- A man is at rest in the middle of a pond on perfectly smooth ice. He can get himself to the shore by making use of Newton’s
(a) first law
(b) second law
(c) third law
(d) all the laws
- A parrot is sitting on the floor of a closed glass cage which is in a boy’s hand. If the parrot starts flying with a constant speed, the boy will feel the weight of the cage as
(a) unchanged
(b) reduced
(c) increased
(d) nothing can be said
- A cannon after firing recoils due to
(a) conservation of energy
(b) backward thrust of gases produced
(c) Newton’s third law of motion
(d) Newton’s first law of motion
- Newton’s third law of motion leads to the law of conservation of
(a) angular momentum
(b) energy
(c) mass
(d) momentum
More than one correct
DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONE OR MORE may be correct.
- Acceleration of a body can be calculated using
(a)
(b)
(c)
(d)
- Which physical quantity has its unit as ‘Newton’?
(a) Friction
(b) Acceleration
(c) Force
(d) Momentum
- The acceleration produced by a force of
(a)
(c)
(b)
(d)
- What force would be required to produce an acceleration of
(a)
(c)
(b)
(d)
- Which of the following is/are a vector quantity ?
(a) Speed
(b) Acceleration
(c) Momentum
(d) Velocity
- A body is in translatory equilibrium if
(a) it is in uniform motion
(b) resultant force on it is zero
(c) it is at rest
(d) it is in accelerated motion
- If a particle under the action of a force
(a)
(c)
(b)
(d)
- If the tension in the cable supporting a lift is equal to the weight of the lift, the lift may be
(a) going up with uniform speed
(b) going up with increasing speed
(c) going down with uniform speed
(d) going down with increasing speed
- In which of the following cases, the net force is zero?
(a) A car moving with constant speed of
(b) A drop of train falling down with terminal velocity
(c) A cork of mass
- A metal sphere is hung by a string fixed on a wall. The force acting on the sphere are shown in the figure. Which of the following statements are correct?
(a)
(b)
(c)
(d)
- A block of mass
(a) Force of friction on the block is
(b) Contact iorce between the block and the belt is
(c) Force of friction on the block is
(d) Contact force between the block and the belt is
- A monkey of mass
(a) the tension in the slope is
(b) the force of friction exerted by the rope on the monkey is
(c)
(d)
- A man pulls a block heavier than himself with a light rope.
The coefficient of friction is the same between the man and the ground and between the block and the ground. Then
(a) if both move, the acceleration of the man is greater than the acceleration of the block.
(b) the block will not move unless the man also moves
(c) the man can move even when the block is stationary.
(d) none of these assertions is correct.
- A man tries to remain in equilibrium by pushing with his hands and feet against two parallel walls. For equilibrium:
(a) the coefficient of friction must be the same between both walls and the man
(b) he must exert equal forces on the two walls
(c) the forces of friction at the two walls must be equal
(d) friction must be present on both walls
- The pulley arrangements of following figures (a) and (b) are identical. The mass of the rope is negligible. In figure (a), the mass
(a)
(b)
(a) The acceleration of mass
(b) The acceleration of mass
(c) The tension in the string in figure (a) is
(d) The tension is the string in figure (b) is
- System shown in figure consists of two blocks of masses
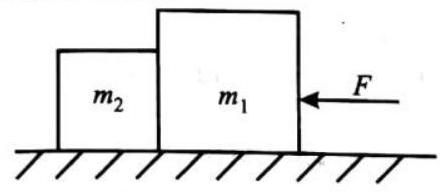
(a) The reaction force of
(b) The acceleration of the system is
(c) The acceleration of mass
(d) None of the above
- Refer to the figure, the pulleys and the string are light.
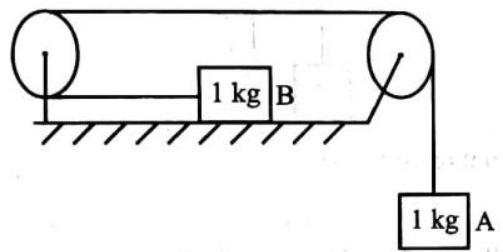
(a) The acceleration of the system is
(b)
(c) The acceleration of the system is
(d)
Multiple matching questions
DIRECTIONS : Following question has four statements
| Column I | Column II |
|---|---|
| (A) Newton’s first law | (p) Dust coming out of carpet beaten with stick |
| (B) Newton’s second law | (q) Recoil of gun |
| (C) Newton’s third law | (r) Law of inertia |
| (D) Law of conservation of momentum | (s) Catching a cricket ball |
| (t) Use of seat belts in car | |
| (u) Flying of rockets and aeroplanes |
- For the system shown in the figure, the incline is frictionless and the string is massless and inextensible pulley is light and frictionless. As the system is released from rest.
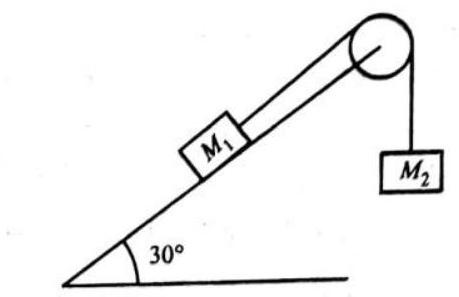
| Column I | Column II |
|---|---|
| (A) |
(p) |
| (B) |
(q) |
| (C) |
(r) |
| (D) |
(p) Tension in string equals the weight of either block |
- If
Fill in the blanks
DIRECTIONS : Complete the following passage(s) with an appropriate word/term to be filled in the blank spaces.
I. force, simultaneously, opposite, equal, Opposite, different, equal
To every action there is an ____ (1) ____ and ____ (2) ____ reaction. Action and reaction act on two ____ (3) ____ bodies, but they act ____ (4) ____. Whenever one body exerts a ____ (5) ____ on another body, the second body exerts an ____ (6) ____and ____ (7) ____ force on the first body.
II.
Motion, force, second, direction, Newton, momentum, directly directly
According to Newton’s ____ (1) ____ law of ____ (2) ____, the rate of change of ____ (3) ____ of a body is ____ (4) ____ proportional to the ____ (5) ____. It takes place in the ____ (6) ____ in which the force acts. The S.I. unit of force is ____ (7) ____ or
III. electromagnetic, Contact, tend to move, chemical bonding, kinetic, constant, static, depends, relative motion, does not depend
Friction is an opposing force which act between two surfaces in ____ (1) ____ whenever the surfaces move or ____ (2) ____ w.r.t. each other. The force of friction is ____ (3) ____ in nature and its cause is ____ (4) ____ between the surfaces contact. When there is no relative motion between the surface, friction is called ____ (5) ____ and when there is relative motion between the surfaces, friction is called ____ (6) ____ and its magnitude is ____ (7) ____ The magnitude of friction ____ (8) ____ on nature of surfaces in contact and ____ (9) ____ on area of contact. Friction always opposes ____ (10) ____ between the surfaces.
Passage Based Questions
DIRECTIONS : Study the given paragraph(s) and answer the following questions.
PASSAGE-I
A block of mass
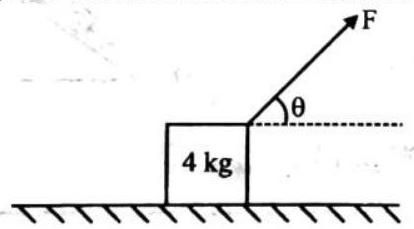
- For what value of
(a)
(b)
(c)
(d)
- What is the minimum value of force
(a)
(b)
(c)
(d)
- If the value of
(a)
(b)
(c)
(d)
PASSAGE-II
Two blocks
- Acceleration of blocks is
(a)
(b)
(c)
(d)
- If at
(a)
(b)
(c)
(d)
- What will be the velocity of the blocks, just after the string becomes taut?
(a)
(b)
(c)
(d)
PASSAGE-III
Consider the situation shown in the adjoining figure, strings are massless and inextensible, pulleys are massless and frictionless, the inclined surface is rough having coefficient of friction
- The minimum value of ratio
(a) 1
(b)
(c) 2
(d)
- If the ratio
(a)
(b)
(c) 3
(d) zero
- The maximum value of ratio
(a) 2
(b) 3
(c)
(d)
Assertion & Reasan
DIRECTIONS : Each of these questions contains an Assertion followed by reason. Read them carefully and answer the question on the basis of following options. You have to select the one that best describes the two statements.
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
- Assertion: When a bullet is fired from a gun, there is a forward force on the bullet and recoil of gun.
Reason: Every action has an equal and opposite reaction.
- Assertion: When astronauts throw something in space, that object would continue moving in the same direction and with the same speed.
Reason: The acceleration of an object produced by a net applied force is directly related to the magnitude of the force, and inversely related to the mass of the object.
- When we sit on a chair, our body exerts a force downward and
Assertion: That chair needs to exert an equal force upward or the chair will collapse.
Reason: The third law says that for every action there is an equal and opposite reaction.
- Assertion: The wings of a bird push air upwards and the air must be pushing the bird downwards.
Reason: For every action there is an equal and opposite reaction.
- Assertion: When a firefly hits a bus, each of them exerts the same force
Reason: Firefly has more mass as compared to the windshield.
- Assertion: Force exerted by the ground on the man moves him forward.
Reason: It is a reactional force.
- Assertion: A quick collision between two bodies is more violent than a slow collision, even when the initial and the final velocities are identical.
Reason: Because the rate of change of momentum which determines the force is greater in the first case.
- Assertion: Change in momentum is impulse.
Reason: Impulse is the area between
- Assertion: A body is momentarily at rest when it reverses the direction.
Reason: A body cannot have acceleration if its velocity is zero at a given instant of time.
- Assertion: For stable equilibrium force has to be zero and potential energy should be minimum.
Reason: For equilibrium, it is not necessary that the force is not zero.
- Assertion: While walking on ice, one should take small steps to avoid slipping.
Reason: This is because smaller steps ensure smaller friction.
- Assertion: Force required to accelerate a mass in two perpendicular directions is never same.
Reason: The presence of
Hots Subjective Questions
DIRECTIONS : Answer the following questions.
- On which of these hills does the ball roll down with increasing speed and decreasing acceleration along the path? (Use this example if you wish to explain to someone the difference between speed and acceleration.)
- If you drop an object, its acceleration toward the ground is
- Two
- Suppose two carts, one twice as massive as the other, fly apart when the compressed spring that joins them is released. How fast does the heavier cart roll compared with the lighter cart?
- If you exert a horizontal force of
- Two people of equal mass attempt a tug-of-war with a 12-m rope while standing on frictionless ice. When they pull on the rope, each person slides toward the other. How do their accelerations compare, and how far does each person slide before they meet?
- When your hand turns the handle of a faucet, water comes out. Do your push on the handle and the water coming out comprise an action-reaction pair? Defend your answer.
- A stone is shown at rest on the ground.
(a) The vector shows the weight of the stone. Complete the vector diagram showing another vector that results in zero net force on the stone.
(b) What is the conventional name of the vector you have drawn?
- Here a stone at rest suspended by a stringe.
(a) Draw force vectors for all the forces that act on the stone.
(b) Should your vectors have a zero resultant? Why, or why not?

- Suppose that the string in the preceding exercise breaks and that the stone slows in its upward motion. Draw a force diagram of the stone when it reaches the top of its path.
- What is the net force on the stone in the preceding exercise when it is at the top of its path? What is its instantaneous velocity? Its acceleration?
- Here is the stone sliding down a friction-free incline (a) Idenitify the forces that act on it, and draw appropriate force vectors. (b) By the parallelogram rule, construct the resultant force on the stone.
(carefully showing that it has a direction parallel to the incline- the same direction as the stone’s acceleration).
- Here is the stone at rest, interacting with both the surface of the incline and the block. (a) Identify all the forces that act on the stone and draw appropriate force vectors. (b) Show that the net force on the stone is zero. (b) Show that the net force on the stone is zero. (Hint 1 : There are two normal forces on the stone. Hint
- A force produces an acceleration of
- A
- A force of
- A gun weighing
SOLUTIONS
EXERCISE - I
Fill in the blanks
- velocity
- equilibrium
- time
- impulse
- newton
- pound
- 200 newtons
- momentum
- perpendicular
- impulse
- mass
- net unbalanced
- decrease
- atmospheric friction
- impulse
True/False
| 1. True | 2. True | 3. True | 4. False |
| 5. False | 6. False | 7. False | 8. True |
| 9. True | 10. True | 11. True | 12. True |
| 13. True | 14. False | 15. True |
Match the columns
- (A)
- (A)
- (A)
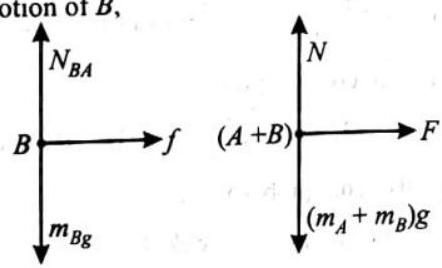
d
but
For system
Both
Now, if
if
if
if
hence
Very Short Answer Questions
1. It will appear to fall in vertically downward direction to the person in the compartment and parabolic to a person standing outside.
2. It would increase in length by
3.
4. Since distance
5. Change in linear momentum
6. Physical balance will show no change whereas, spring balance will show higher reading.
7. (a) The body will appear stationary in air, (b) The body will appear falling freely under the acceleration in air.
8.
9.
10. When the force applied on a body is zero, Newton’s first law becomes a special case of Newton’s second law.
11.
12. The opposing force that is set up between the surfaces of contact, when one body slides or rolls or tends to do so on the surface of another body is called friction.
13. When applied force is zero, friction is zero. As the applied force is increased, friction also increases and becomes equal to the applied force. It happens so, till the body does not start moving. For this reason, friction is called self adjusting force.
14. It is because, work done against friction along a closed path is non-zero.
15. The rolling friction is lesser as compared to the sliding friction.
Short Answer Questions
1. Vehicle stops on applying brakes, which is in accordance with the law of conservation of momentum. When brakes are applied, opposition force acts on the vehicle. In pursuit, car will be at rest. Loss of momentum of the vehicle is exactly equal to the impulse of the applied force.
2.

Let a be the common acceleration of the whole system.
Force equation,
3. No. Net force on the body of mass
4. In closed glass cage, air inside is bound with the cage. Therefore, (i) no change in weight of the cage, when bird flies with constant velocity, (ii) cage will be heavier, when bird flies with upward acceleration, (iii) cage will be lighter, when bird flies with downward acceleration.
5. While applying brakes, let
For taking a turn radius
6.
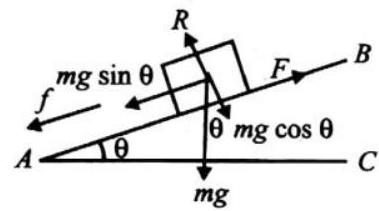
i.e.
7.
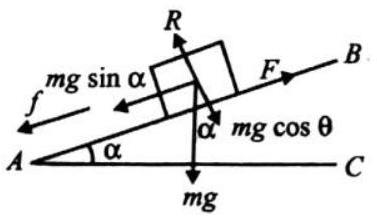
If
By definition, coefficient of friction,
Multiple Choice Questions
| 1. (a) | 2. (b) | 3. (b) | 4. (a) | 5. (b) |
| 6. (a) | 7. (d) | 8. (a) | 9. (d) | 10. (b) |
| 11. (d) | 12. (a) | 13. (b) | 14. (a) | 15. (b) |
| 16. (c) | 17. (a) | 18. (b) | 19. (a) | 20. (d) |
| 21. (b) | 22. (b) | 23. (c) | 24. (d) | 25. (a) |
| 26. (b) | 27. (a) | 28. (c) | 29. (d) | 30. (a) |
| 31. (b) | 32. (a) | 33. (c) | 34. (c) | 35. (b) |
| 36. (a) | 37. (c) | 38. (b) | 39. (c) | 40. (b) |
| 41. (a) | 42. (d) | 43. (d) | 44. (c) | 46. (a) |
| 47. (b) | 48. (c) | 49. (a) | 50. (c) | 51. (d) |
More than one correct
- (a, b)
- (a, c)
- (c, d)
- (a, d)
- (b, c, d)
- (a, b, c)
For translatory equilibrium
- (a, d) For equilibrium,
- (a, c) If
- (a, c, d)
- (c, d)
- (b, c, d)
For motion of block
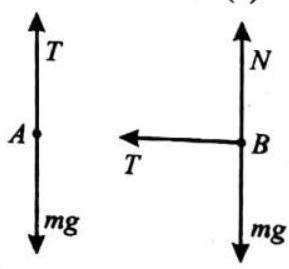
For motion of block
On solving
Multiple Matching Questions
- (A)
- (A)
- (A)
Fill In The Passage
I. (1) equal
(2) opposite
(3) different
(4) simultaneously
(5) force
(6) equal
(7) opposite
II. (1) second
(2) motion
(3) momentum
(4) directly
(5) force
(6) direction
(7) Newton
III. (1) Contact
(2) tend to move
(3) electromagnetic
(4) chemical bonding
(5) static
(6) kinetic
(7) constant
(8) depends
(9) does not depend
(10) relative motion,
Passage Based Questions
1. (b) FBD of the block is shown below, Here,
or
Block will move if,
or
or
Now
Now, maximum value of
2. (b) Here
3. (a) If
or
4. (b)
Here,
On solving
5. (a) Speed of
The string will become taut again when distance covered by both the blocks is equal, i.e.
or
6. (b) Let
Let
impulse of
or
7. (d) For
or 
As
or
or
8. (b)
9. (c) As the block
or
Assertion and Reasons
- (a)
- (b)
- (a)
- (d)
- (c)
- (b)
- (a)
- (b)
- (c)
- (c)
- (a)
- (c)
Hots Subjective Questions
- When the ball rolls down the hill as shown in the figure, a component of weight of the ball acts downwards along the inclined plane. It is in the opposite direction of the force of friction. The net force along the inclined plane remains constant throughout the motion and hence the acceleration is also constant. Since a constant acceleration is acting on the ball, therefore the ball rolls down with increasing speed.
When the ball rolls down the hill-as shown in the figure, its acceleration starts decreasing after a certain height because the slope of the hill is not constant. When the ball rolls down from the top of the hill its acceleration increases but as soon as it reaches the point from where the slope is lesser, the acceleration starts decreasing.
- If an object is dropped from rest i.e. its initial speed is zero, it falls under gravity with an acceleration
- When two weights are attached to a spring scale then the forcas acting on the strings of the scale are as shown in fig.

The spring balance will show
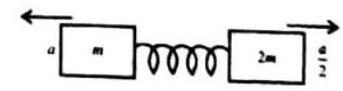
The two carts have masses say
Let the accelerations of the two carts be
This means that cart twice as massive has half the acceleration as compared with the other.
If the crate slides on the floor with a constant velocity then it means that there is no net force acting on the crate. It means that the force with which we are pushing the crate is exactly equal in magnitude to the force of friction that is opposing the motion of the crate so that there is not net acceleration of the crate but only constant speed. This implies that the force of friction is equal to
Yes, the force of friction is equal and opposite to the
Since the two people pulling each other in a tug-of-war are of equal mass, and the ground is frictionless, this means that they both exert equal and opposite force on each other. Assuming that the rope does not extend or slag in length then the action-reaction pair of forces which are formed by the pull of both persons would accelerate both of them towards each other with equal magnitude no friction is present to retard their motion. This means that both persons slide towards each other with same speed and same distance
(acceleration
Hence they would meet each other after sliding equal distances from their initial positions.
This means they would meet at the centre of the rope length i.e, they meet after sliding
- When our hand turns the handle of a faucet, the faucet in turn applies a pressure on our fingers. These two forces i.e, the push of our hand on the handle of the tap and the push of the tap on our hand make the action-reaction pair.
When force is applied by our hand turns the faucet which moves the screw inside the tap and releases the water which flows out of the nozzle of the tap. The force of screw of the tap on the water and force of water on it make another action-reaction pair. But this means that our push on the handle and the water coming out of the tap do not make an action-reaction pair since our hand and water is not touching each other.
- (a)
The figure shows a stone resting on the ground. The net force on the stone is zero as its acceleration is zero. One of the force that acts on stone is the weight force of the stone, due to earth’s gravitational pull, acting in the downward direction. This force acts on the ground and pushes it down. As a reaction to this force the ground also exerts an equal and opposite force on the stone in the upward direction. As a result the two forces cancel and no net force acts on the stone. The force vectors can be represented as shown in figure 1
(b) The downward weight force is balanced by an upward force. This upward force is conventionally called reaction force of the ground that prevents the ground from sinking and keeps the stone at rest. It acts normal to the surface of the ground
- The various force vectors that act on the stone are shown in the figure.
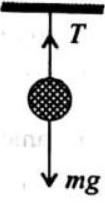
Net force
(a) There is a downward force of weight of the stone given as
(b) Since the stone is at rest and shows no acceleration this means that there is no net force on the stone. This happens because the tension and weight force are equal and opposite. They both cancel each other and net force on stone is zero. That is,
Therefore resultant of two vectors is zero.
(c) The stone suspended by the string shows no motion which means its acceleration is zero and net force is also zero.
This happens because downward weight force is balanced by upward tension in the string. Since these two forces are action and reaction forces hence they cancel each other and give the resultant force as zero.
- The string attached to the stone puils it upward. This means that an external force is applied from the fixed point to pull the stone up. The stone accelerates in upward direction because the upward force (of pull) is greater than the downward force of weight
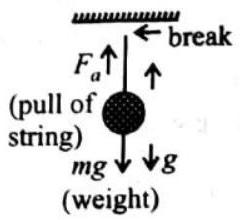
When the string breaks from the fixed point then this upward force (of pull) on the stone stops acting on it and the stone is under the influence of its weight force only when this happens then there is no upward force on the stone. At the top of its path the stone is momentarily at rest because its upward velocity becomes zero due to deceleration. The only force acting on it at that point is the force of gravity which is represented by weight of the stone as shown in the figure.
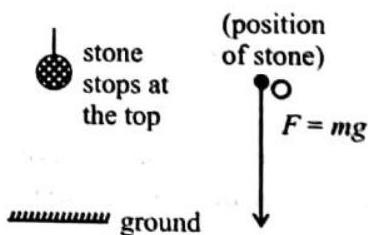
- At the top of the path the stone is at rest. This happens because the upward acceleration of the stone is balanced by the downward acceleration due to gravity. The net force on the stone at the top is the force due to gravity
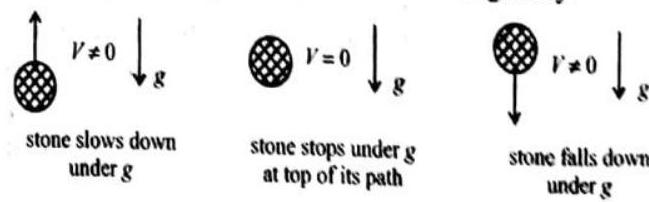
At that moment, its instantaneous velocity Vinst is zero (rest point). The acceleration of the stone is not zero but it is equal to ’
(a) The various forces that act on the stone sliding down are
(i) Weight of the stone given as
(ii) reaction force of the incline acting in a normal direction to the incline.
When a stone slides on an frictionless incline then the force of gravity acts on it at all points a vertically downward direction. This is due to the fact that acceleration due to gravity always acts forwards the centre of the earth and hence its direction is always given by a downward vertical \to. Secondly, the motion of the stone on the incline pushes the ground which produces a reaction force by the ground which is always perpendicular to the surface and acts on the moving object in a direction away from it this force of reaction is represented by vector
Since it is a frictionless incline so we do not consider frictional force.
(b) The two forces acting on the stone form a parallelogram as shown in fig 2. and their resultant is given by the diagonal of the parallelogram. As seen in the figure the diagonal vector
(a) Here fig. 1 the stone sliding on a frictionless surface is stopped by a block so that the stone is at rest. The various forces that act on the stone are
(1) weight of the stone acting in a vertically downward direction and represented by ’
(2) the normal reaction of the surface to its weight force acting perpendicularly upward from the surface on the stone and represented by vector
These two forces form two adjacent sides of a parallelogram and their resultant is the diagonal of the parallelogram given by vector
(3) This reaction force of the block on the stone is the third force acting on the stone
(b) As the action-reaction forces cancel i.e,
14.
Hints:
15.
Hints:
16.
Hints: Horizontal component of force
17.
Hints:
From conservation of momentum,
Resultant momentum before and after firing is zero as no external froce is acting on it.
CHAPTER 5
WORK, ENERGY AND POWER
Introduction
In common sense, all physical activities such as reading, writing, carrying a bag, pushing a wall etc. are considered to be work. Let, for example, you employ a worker to push and move a high wall of a building. He tries his best whole day but he doesn’t become able to move the wall a little bit. But he asks for his labouring charge. Would you pay him the charge or not? Definitely, your answer would be ‘yes’because he has performed his task or work. But in language of physics he hasn’t done any work.
The meaning of work in physics is a big different from its meaning in common language. Actually, in physics work has a meaning only when a displacement is caused on a body by the applied force on it. If there is no displacement in a body by an applied force, no work is said to be done on the body by the force.
Suppose Pari gets tired after four hours of study but Dolly doesn’t tire even after eight hours of study. Who does more work-Pari or Dolly? We can’t answer it. But we can surely say that Dolly has more capacity of doing work than Pari. The capacity of doing work is defined as the ‘Energy’. Also, the rate of doing work is termed as the ‘Power’.
This chapter is all about Work, Energy and Power.
Work
In physics work is defined if force applied on object displaces the object in direction of force. Here all three terms force, displacement and direction of force are important. If force is zero, work is zero; if force is non-zero but displacement is zero (like pushing the wall) work is zero and if force is non-zero, displacement is non-zero but no part of force is in the direction of displacement, work in zero. Hence, we define the work as the product of the force and displacement in the direction of applied force or product of displacement and force in the direction of displacement.
Note that the force in above formula is the component of force is the direction of displacement in the diretion fo force
Unit of Work
The
Abbreviated as
When a force of
Other units of work
In c.g.s. system of measurement force is measured in dyne, displacement in
From
if
Thus, if a force of 1 dyne, displaces the point of application, by
Relation between 1 joule and erg is as follows.
Higher units of work are
Do you know !!
If nothing is actually moving, no work is done-no matter how great the force involved!
Work Done By A Force Applied At An Angle
Let Rishabh pulls a toy car through a string, then as shown in figure the force applied by him is along the string (direction
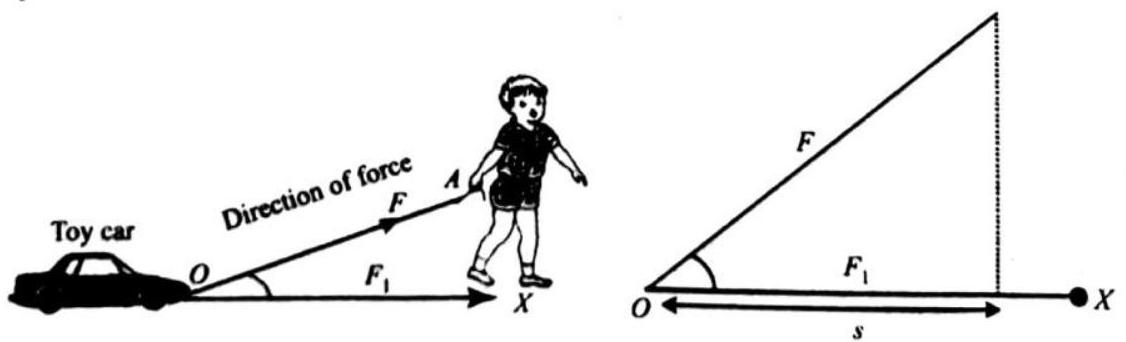
Values of
Thus, if the displacement (of the point of application) has a component along the direction of applied force, then/work done is positive. On the other hand, if the displacement has a component opposite to the direction of applied force, then work done will be negative.
If the applied force and particle’s displacement be mutually perpendicular, then work done by the force on the particle is zero. (
It is important to understand that work done by the force does not depend on the time taken in the displacement of point of action. For example, one porter takes 5 minutes to put a box on the roof of a bus while other put the same box on the roof in 10 minutes, work done by both the porter is same.
Do you know !!
Work is a scalar quantity but you can have positive and negative work. Positive work is where the force pulls in the same direction as the movement. Negative work is where the force is in the opposite direction.
Example:
(i) If the wall doesn’t move, the person does no work.

(ii) A body attached to a string revolves in a horizontal circle (figure). The tension
(iii) A coolie with a luggage on his head, moving on a horizontal platform, does no work, since the direction of force is vertically up and displacement horizontal (even though he might feel physically tired).
(iv) If a boy tries to push a heavy boulder, by applying a force, but unable to displace it, then work done by the boy is zero.
(v) When a horse pulls a cart, the applied force and the displacement are in the same direction. So, work done by the horse is positive.
(vi) When brakes are applied to a moving vehicle, the work done by the braking force is negative. This is because the braking force and the displacement act in opposite directions.
(vii) When a spring is compressed then the force applied by the spring and the displacement will be in opposite to cach other, so work done by the spring will be negative.
Work Done-Against Gravity
Consider a body of mass
The work done by the weight is
If an agent, such as crane, is responsible for lifting the body, then
Work Done By A Moving Vehicle
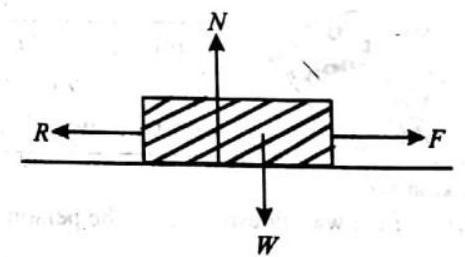
The diagram shows the forces that commonly act on a moving vehicle.
The work done by
If the vehicle is not accelerating, the forces acting on it are in equilibrium.
KNOWLEDG NHANCER
(ii) Internal work:
Suppose that a man sets himself in motion backward by pushing against a wall. The forces acting on the man are his weight ’
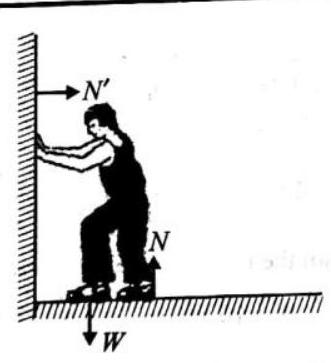
The new feature in this situation is that the man is a composite system with several parts that can move in relation to each other and thus can do work on each other, even in the absence of any interaction with externally applied forces. Such work is called internal work. Although internal forces play no role in acceleration of the composite system, their points of application can move so that work is done; thus the man’s kinetic energy can change even though the external forces do no work
Figure shows four situations in which a force acts on a box while the box slides rightward a distance
(A)
(B)
(C)
(D)
Check Your Answer
We know that the positivity or negativity of work depends upon the angle between the force and the displacement caused by the force. The work done becomes less positive as
D, C, B, A
Illustration 1
How much work is done by a force of
Solution : The work done is calculated by the formula
Illustration 2
A body of mass
Solution : The force of gravity on the body, is the force exerted by earth on it and is
Now from
Illustration 3
A child pulls a toy car through a distance of 10 meters on a horizontal floor. The string held in child’s hand makes an angle of
Solution : In this case, as the applied force and the displacement are not in same direction, we will calculate the work done by the formula.
Here, Force
Magnitude of the displacement
So substituting these values in the above formula, we get
From the table of natural cosines
Illustration 4
A man lifts 20 boxes each of mass
Solution :
The work done against gravity in lifting one box
Illustration 5
From the graph (figure given below) of force versus displacement of a particle, find the total work done by the force.
Solution :
The total work done
Illustrotion 6
A force of
Solution : Force,
Angle between force and displacement,
Work done,
then,
Energy
Some people have a lot of energy when they get up in the morning. Carbohydrates are high-energy foods. Oil is the main source of the energy that keeps incustry and cars going. The centre in a football formation has to put a lot of energy into his attack.
The word energy has a different meaning in each of those four sentences. As used in physics, the word has a very precise meaning, although it is a little difficult to define because energy takes many different forms. We can approach a definition by noting the relationship between energy and work. Energy is defined as the capacity to do work.
In other words, anything which has the capacity to do work is said to possess energy. The implies that work can be done only at the expense (cost) of energy i.e., to do work, we need to spend energy, whatsoever be its form.
Unit of Energy: Its unit is same as that of work i.e., joule (J).

IDEA BOX
Let us understand energy-work equivalence with some examples
(i) When a fast moving cricket ball hits a stationary stump, the stump is thrown away. Here the work is done on the stump by the ball and the ball has the capacity to do this work because of its motion (kinetic energy).
(ii) A body can acquire the ability to do work when it is deformed temporily. For example, a compressed watch spring is able to drive the wheels of a watch.
(iii) If a boy (mass
Do you know !!
Energy is a promise of work to be done in future. It is the stored ability to do work.
Mechanical Energy
The energy in a body may be by virtue of its motion (kinetic energy) or by virtue of its position (potential energy). Energy in a body due to these conditions is called mechanical energy. For example, energy of water in a water tank on the roof, energy of moving bullet, energy of small spring in ball-pen, energy of moving air etc. are the forms of mechanical energy.
Kinetic Energy
Energy possessed by a body by virtue of its state of motion is called kinetic energy. Kinetic energy is always positive and is a scalar. The fact, that moving bodies carry energy with them is proved by some of the several happenings in day to day life.
Examples :
(i) A stone thrown with some velocity, breaks the window pane.
(ii) A moving vehicle, when accidently happens to collide with another vehicle at rest or motion, leads to destruction.
Do you know !!
The kinetic energy of a body always positive.
Expression of kinetic energy
Suppose that a constant force

Work done by force
This work done by the force which makes a stationary body to move with a velocity
Kinetic energy
From this expression it is clear that the kinetic energy possessed by a moving body is directly proportional to its mass and to the square of its velocity, if velocity is doubled KE becomes 4 times.
KNOWLEDG NHANCER
Relation between kinetic energy and momentum :
A body of mass
The kinetic energy of the body,
or
or
(i) For same momentum :
K-energy varies inversely as the mass
(ii) For same K-energy :
Momentum varies directly as the square root of mass of the body.
CHECK POINT
(i) If a golf ball and a Ping-Pong ball both move with the same kinetic energy, can you say which has the greater speed? Explain in terms of K.E. Similarly, in a gaseous mixture of massive molecules and light molecules with the same average
(ii) How is it possible that a flock of birds in flight can have a momentum of zero but not have zero kinetic energy?
Check Your Answer
(i) The kinetic energy of an object depends on the mass and square of the velocity . As the kinetic enengy of a golf ball and a ping-pong ball is the same therefore a ping-pong ball has greater speed because its mass is less than a golf-ball. Similarly, in a gaseous mixture of massive molecules and light molecules with the same average K.E, the light molecules have the greater speed.
(ii) Momentum is a vector quantity having both magnitude and direction whereas kinetic energy is a scalar quantity having only magnitude. Momentum that is directional is capable of being cancelled entirely.
The vector sum of the momenta of a flock of birds in flight can be zero because of birds flying in different directions in the flock.
Each flying bird has some kinetic energy and the algebraic addition of the kinetic energies of all birds in the flock cannot be zero.
Illustration 7
If a stone of mass
Solution: From K.E.
Illustration 8
A scooter is moving with a velocity of
Solution: Kinetic energy is given by
Illustration 9
A bullet is fired from a gun. What will be the ratio of kinetic energy of bullet and gun ?
Solution: When a bullet is fired from a gun, the gun has same momentum backward, which the bullet has a forward momentum
So bullet has more K-energy than the gun.
Conservative And Non Conservative Forces
Nature has been gifted by several types of forces, coming into operation, now and then, as and when possible. To name a few, the wind force, the force of friction, the viscous drag, the gravitational force, the electric force, etc.
The forces which always tend to oppose the motion e.g., frictional forces, viscous forces, etc. always tend to dissipate energy when a body moves relative to another, in their presence i.e., work has always to be done against them, to move a body from one position to another, which cannot be recovered, after regaining the original position. These are hence known as non-conservative forces. At the same time, there are several forces which are conservative in nature and in which energy can be recovered, provided, the body is restored to its original configuration. Commonly encountered such forces are gravitational, elastic forces.
Hence we can define conservative and non-conservative forces as follows.
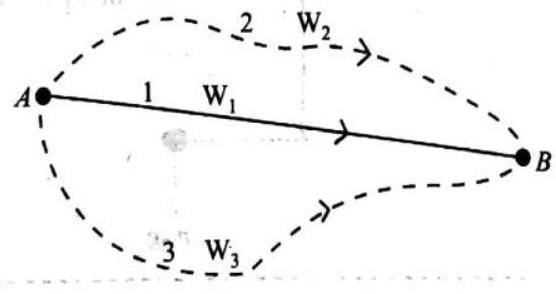
Example : Both blocks acquire the same gravitational potential energy,

Conservative Force and Work done
As we have already discussed in the previous chapter that work done by a conservative force doesn’t depend upon the path taken i.e. it only depends upon the initial and final positions of the body. There is another important very useful relation between work done by conservative force and potential energy. The work done by a conservative force is equal to the negative of change in the potential energy.
POTENTIAL ENERGY
Potential energy is energy due to position. If a body is in a position such that if it were released it would begin to move, it has potential energy. There are two common forms of potential energy, gravitational and elastic.
(i) Gravitational Potential Energy
When an object is allowed to fall from one level to a lower level it gains speed due to gravitational pull, i.e. it gains kinetic energy. Therefore, in possessing height, a body has the ability to convert its height into kinetic energy, i.e. it possesses potential energy.
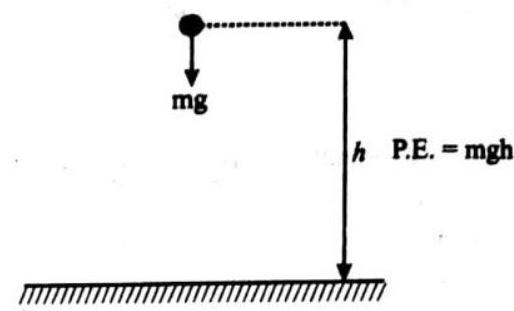
The magnitude of its gravitional potential energy is equivalen to the amount of work done by the weight of the body in causing the descent.
If a mass
Since
Note: The chosen level from which height is measured has no absolute position. It is, therefore, important to indicate clearly the zero P.E. level in any problem in which P.E. is to be calculated.
Do you know !!
It does not matter, what path is taken; work done to move a body between any two points in a vertical plane is equal to work done against gravity through the vertical distance between the points!
(ii) Elastic Potential Energy
This is a kind of potential energy which is due to a change in the shape of a body. The change in shape of a body can be brought about by stretching, compressing, bending and twisting the body. Some work has to be done to change the shape of a body. This work gets stored in the deformed body in the form of elastic potential energy. For example, the energy stored in a stretched rubber band or a spring is elastic potential energy and is equal to the work done in stretching the rubber band or spring. When this deformed body is released, it attains its original shape and the potential energy is converted into some other form, usually in kinetic energy. Elastic potential energy is never negative whether due to extension or to compression.
Consider a massless spring whose length is
by ’
So, the energy associated with the state of a elongation or compression of a spring is called elastic potential energy of spring or simply potential energy
Where ’
In which car will you be moving the fastest at the very bottom of the incline?
Check your answer
Of course, at any moment all cars have the same speed but the gravitational potential energy of the system of cars is least when the middle car is at the bottom - when the centre of mass of the system is lowest. Lowest potential energy means highest kinetic energy. So sit in the middle car for the finstest ride at the very bottom.
Conservation of Energy
According to this law, energy can only be converted from one form to another, it can neither be created nor destroyed. The total energy before and after the transformation always remains the same.
Conservation of Mechanical Energy
Kinetic and potential energy are both forms of mechanical energy. The total mechanical energy of a body or sywtem of bodies will be changed in value if :
(a) an external force other than weight causes work to be done (work done by weight is potential energy and is therefore already included in the total mechanical energy),
(b) some mechanical energy is converted into another form of energy (e.g. sound, heat, light etc.). Such a conversion of energy usually takes place when a sudden change in the motion of the system occurs. For instance, when two moving objects collide some mechanical energy is converted into sound energy which is heard as bang at impact. Another common example is the conversion of mechanical energy into heat energy when two rough objects rub against each other.
If neither (a) nor (b) occurs then the total mechanical energy of a system remains constant. This is the principle of conservation of Mechanical Energy can be expressed in the form :
The total mechanical energy (K.E. + P.E.) of a system remains constant provided that no external work is done and no mechanical energy is converted into another form of energy.
Examples :
(1) Body falling freely :
Considering earth as a body of zero mechanical energy, if a body of mass
So, potential energy at
Kinetic energy at
Total mechanical energy at
or
or
When the body reaches at point
Thus, the total mechanical energy remains conserved at every point on the path of a freely falling body.
(2) When the pendulum is pulled to position
At position
When the pendulum is released from position
When the pendulum swings from
Hence in the system of pendulum and earth, the energy is conserved. It is the potential energy, which changes to the kinetic energy and vice versa.
Illustration 10
A mass of
Solution :
(i) The initial energy of the body
Here, initially the body is at rest
and
(ii) When the body is at a height of
At this position, kinetic energy
or
Here the body is at height
Illustration 11
A body of mass
Solution : At a height of
After sometime the kinetic. energy is 450 joule, suppose at that instant potential energy is
or
or
Illustration 12
Starting at rest, the cart of figure slides frictionlessly to point
Solution : Considering its gravitational energy to have dropped to zero at
The m’s drop out, and the equation becomes
WORK-ENERGY THEOREM
According to the work-energy theorem, total work done on a system by forces (external, internal, conservative or non-conservative) equals the change in kinetic energy.
Where,
But work done by conservative forces equals the negative of change in potential energy,
So,
If
So, if non-conservative forces do not act then work done by external forces equals the change in mechanical energy and if there is no external force acting then mechanical energy of the system remains conserved.
Do you know !!
Work-energy theorem is particularly useful in calculation of minimum stopping force or minimum stopping distance. If a body is brought to a halt, the work done to do so is equal to the kinetic energy lost.
Illustrotion 13
A bullet leaving the nuzzle of a rifle barrel with a velocity
Solution : Let
For first plank :
Loss in
For second plank
Illustrotion 14
A particle of mass
Solution :
Initial velocity at
Final velocity at
Work done
Illustration 15
A force acts on a body of mass
Solution : Initial K.E.
Final K.E.
Work done
Hence, work done by force
Illustration 16
A block of mass
Solution : Alternatively, you can apply work-energy methods in a very precise way as follows :
By using Work-Energy theorem
For the block, in the system under consideration, the statement of work-energy theorem can be written as
Notice the difference between the “work done against friction” and the “work done by the frictional force”. In this example, work done against friction is
Motion In a Vertical Circle
Consider a particle of mass ’
At
At
Applying conservation of mechanical energy between
(Taking ’
Substituting in (ii), we get
Using equation (iii), tension at any point can be found by simply substituting the value of angle ’
At
At
Condition for just completing vertical circle :
Using
Similarly,
Condition for leaving circle :
At this point tension will be zero but velocity will not be zero.
Condition for oscillation :
When
Motion of a body on a smooth hemisphere : Consider a small body of mass ’
Using Newton’s
Applying conservation of energy between
When body leaves the contact,
Looping the loop : Consider a smooth inclined plane of vertical height
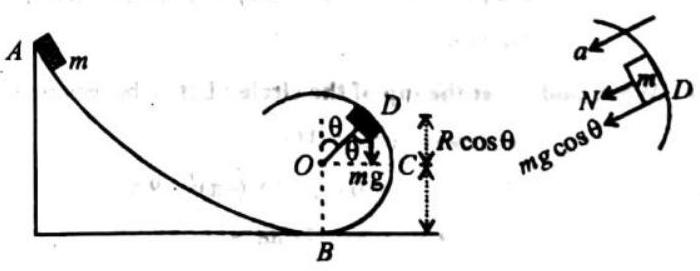
Using Newton’s
As it leaves the contact,
So,
Applying conservation of mechanical energy at
Solving (i) and (ii),
Also
Illustration 17
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow apherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motoreyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required to perform a vertical loop, if the radius of the chamber is
Solution : The motorcyclist is expected to drop down under the action of his weight, when he is at the uppermost point. However, it does not happen so. The reason is that at the uppermost point, the weight of the motorcyclist provides the necessary centripetal force in order to go round the vertical circle.
The minimum speed, the motor cyclist is required to possess at the uppermost point is given by
Here,
Illustration 18
A body weighing
Solution : Here,
Now, angular speed,
(a) When body is at the bottom of the circle : Let
(b) When body is at the top of the circle : Let
or
Illustration 19
A pendulum consisting of a small heavy bob suspended from a rigid support oscillates in a vertical plane. When the beb passes through the position of equilibrium, the rod is subjected to a tension equal to twice the weight of the hob, ’ fhrouthi what maximum angle from the vertical will the pendulum be deflected? Disregard the weight of the rod and the resiotanet of the air.
Solution : Suppose thatasmallbob of weight
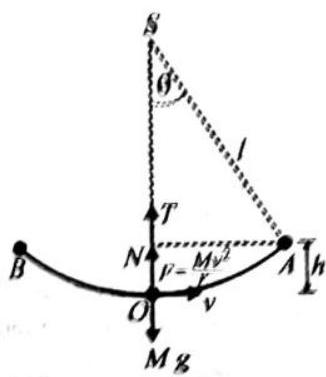
The resultant of these two forces provides the necessary centripetal force to the bob, so as to make it move along circular path of radius
Since
As the bob gets deflected from its equilibrium position, its velocity decreases. It goes up to the point
From the principle of conservation of energy, we have kinetic energy of the bob at the point
or
or
Illustrotion 20
A small sphere tied to the string of length
(a) Find the velocity of the sphere at the lowest position.
(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground? (take
Solution : (a) Let
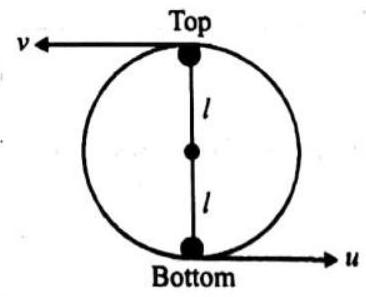
Radius of circle
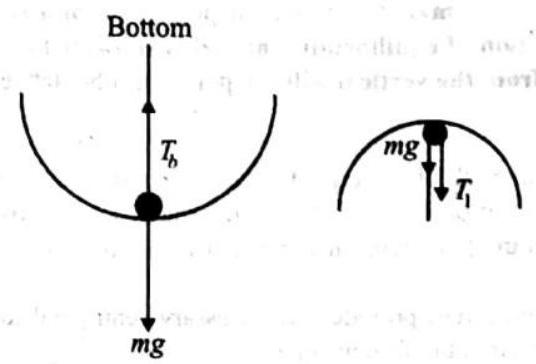
Using conservation of energy,
loss in
Using Eqs. (i) and (ii), we get
(b) After breaking away from the string, the sphere moves along a parabolic path, and strikes the ground at
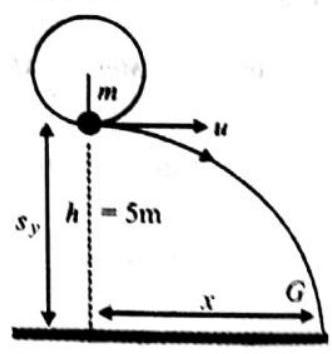
Let
The horizontal displacement
Hence the sphere hits the ground
Collisons
Collision is an event in which two or more than two bodies interact with one another for a short time and exchange momentum and kinetic energy. Collisions are of two types :
(i) Elastic collision
(ii) Inelastic collision
Do you know !!
Linear momentum is always conserved, whereas kinetic energy is conserved only in elastic collision.
Elastic Collision
A.collision in which there is no loss of kinetic energy is called elastic or perfectly elastic collision. The basic oharacteristics of perfectly elastic collision are
(i) linear momentum is conserved
(ii) kinetic energy is conserved
(iii) total energy is conserved
(iv) coefficient of restitution is unity
Elastic Collision in one Dimension
Let us discuss elastic collision is one dimension. Let two balls
Conserving linear momentum,
(Note : this is a vector equation so take care of sign)
Conserving kinetic energy,
From (i) and (ii), we get
Special Cases
(a) When
(b)
(c)
Coefficiant of Restitution
It is defined as the ratio of the velocity of separation to the velocity of approach. That is,
or,
Do you know !!
The collision in one dimension is also known as head-on collision.
Elastic Collision in two Dimensions
Suppose two balls
Conserving kinetic energy,
Conserving linear momentum along
Conserving linear momentum along
Inelastic Collision
In an inelastic collision kinetic energy is lost during collision. The basic characteristic of an inelastic collision are : ab? lalsog?
(i) linear momentum is conserved
(ii) kinetic energy is not conserved
(iii) total energy is conserved
(iv) coefficient of restitution is
For solving problems of inelastic collision we can use
And the loss in kinetic energy is given by
In completely inelastic collision the two bodies get stuck together and move with common velocity, that is why for perfectly inelastic collision;
Loss in K.E. is completely inelastic collision
Also, the fraction of K.E. lost is given by (when
Do you know !!
A collision in which colliding bodies stick together, is always an inelastic collision. It is because, Kinetic energy is never conserved in such collisions.
The bob
Check Your Answer
The positions of the bob of the pendulum and the target bob are shown in the fig. The bob of the pendulum will not rise as explained below:
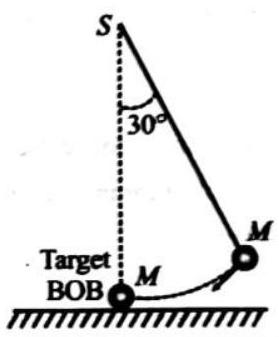
If the bob of the pendulum acquires a velocity, say
Illustration 21
A mass is released from a height
Solution : Take the mass as body 1 and the earth as body 2 . So
Using,
Illustration 22
Two balls each of mass
Solution : Here,
Now,
or,
Also,
or,
Thus, after the collision, the two balls bounce back with equal speeds
Illustration 23
A neutron having mass of
Solution : Here, mass of the neutron,
Initial velocity of the neutron,
Mass of the deutron,
and initial velocity of the deutron,
The mass of the composite particle i.e. triton,
As the neutron sticks to the deutron after the collision, the collision is inelastic in nature. For an inelastic collision, only the law of conservation of linear momentum holds. If
Illustration 24
A ball is dropped from rest at a height of
Solution : Here,
Let
From the relation :
Let
K.E. of the ball on reaching the ground,
On striking the ground, the ball loses
Therefore, K.E. possessed by the ball on bouncing from the ground
If
or
Suppose that after striking the ground, the ball bounces up to a height
Then, for the vertical motion of the ball after bouncing :
initial velocity,
and acceleration,
Now,
or
The loss in kinetic energy of the ball occurs, because of the fact that the collision between the ball and the ground is not perfectly elastic.
Power
In several situations, it is not enough only to know that how much work is done but it is also required that how quickly it is done i.e, it is also important to know the rate of work done by the force.
The time rate of doing work is defined as power
Power
Unit of Power
The unit of power is the joule per second and this is called the watt
1 Megawatt
Power was also measured earlier in a unit called horse power. Even these days, the unit of horse power is in common use.
1 horse power
The unit kilowatt-hour means one kilowatt of power supplied for one hour. It is, therefore, the unit of energy.
IDEA BOX

The Power of a moving vehicle
The power of a vehicle is defined as the rate at which the driving force is working.
Consider a vehicle moving at a constant speed
The distance moved in 1 second is
The work done by the driving force in 1 second is
Hence the power of the vehicle is
So, if
i.e. the power of a vehicle is given by multiplying the driving force by the velocity.
When the velocity is not constant this relationship gives the power at the instant when the velocity is
Do you know !!
Instantaneous power (P) of a body is defined as the dot product of force
KNOWLEDG NHANCER
Area under power-time curve gives the work done.
Illustration 25
What is the power of an engine which can lift 20 metric ton of coal per hour from a 20 metre deep mine ?
Solution : Mass,
Illustration 26
A student pulls a bucket of water in 1 minute from a
Solution : Work done by the student
Time duration of the work is
Hence, the power of student
Illustration 27
One coolie takes one minute to ralse a box through a height of 2 metre. Another one takes 30 second for the same job and does the same amount of work. Which one of the two has greater power and which one uses greater energy ?
Solution : Power of first coolie
Power of second coolie
So, the power of the second coolie is double that of the first.
Both the coolies spend the same amount of energy.
Aliter, we know that
For the same work,
or
Illustrotion 28
A 100W bulb operates for 5 hours. How much electric energy will it consume?
Solution : Work
EXERCISE 1
Fill in the Blanks
DIRECTIONS: Complete the following statements with an appropriate word/term to be filled in the blank space(s).
- The work done by the external force on a system equals the change in ____ energy.
- One horse-power
- An electric motor exerts a force of
- A one kilogram mass has a kinetic energy of one joule when its speed is ____ meter/sec.
- A truck and a car moving with the same kinetic energy are brought to rest by the application of brakes which provide equal retarding forces. The distance moved by the truck, in coming to rest, will then be ____ the distance moved by car.
- The work done in holding
- Two bodies of masses
- The energy possessed by the body due to its ____ called kinetic energy.
- Work done by a force is maximum when angle between force and displacement is ____
- Energy is a ____ quantity.
- Energy stored in an elongated rubber is ____
- Watt second is a unit of ____
- ____ energy can never be negative.
- When angle between force and displacement is obtuse, work done by the force is ____
True/False
DIRECTIONS: Read the following statements and write your answer as true or false.
- Work is always done on a body when it experiences an increase in energy through a mechanical influence.
- Work done by the resultant force is always equal to change in kinetic energy.
- A light and a heavy body, having equal momenta, have equal kinetic energies.
- Work done in the motion of a body over a closed loop is zero for every force in nature.
- More work is done in compressing a litre of air than a litre of water from a pressure of one atmosphere to three atmospheres.
- No work is done on a particle which remains at rest.
- A man rowing a boat up stream is at rest with respect to the shore, is doing no work.
- The total energy of a body in motion is equal to the work it can do in being brought to rest.
- A body cannot have momentum when its energy is zero.
- Kinetic energy of a body depends upon the direction of motion.
- Work done by friction can-never be positive.
- Work done by conservative force in round trip is zero.
- Gravitational force is non-conservative.
- Work done by conservative forces is equal to increase in potential energy.
- A man carrying a bucket of water, walking on a level road with a uniform velocity does no work.
Match the columns
DIRECTIONS: Each question contains statements given in two columns which have to be matched. Statements
1. A boy of mass
| Column I | Column II |
|---|---|
| (A) Force acting on the boy | (p) 550 |
| (B) Work done by the boy | (q) 3300 |
| (C) Gain of potential energy by the boy | (r) 33000 |
| (D) Power developed by the boy | (s) 220 |
2. Column I shows some devices and column II shows transformation of energy for which they are used. Then match the following.
| Column I | Column II |
|---|---|
| (A) Electric motor | (p) Electrical energy to heat energy |
| (B) Engine on an automobile | (q) Electrical energy to mechanical energy |
| (C) Electric heater | (r) Light energy to electrical energy |
| (D) Photocell | (s) Heat energy to mechanical energy. |
- In the situation shown in the figure, coefficient of friction between the block and ground is
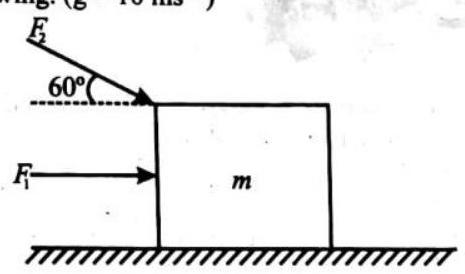
| Column I | Column II |
|---|---|
| (A) Magnitude of work done by |
(p) 20 J |
| (B) Magnitude of work done by |
(q) 30 J |
| (C) Magnitude of work done by friction | (r) 40 J |
| (D) Magnitude of increase in K.E of the block | (s) 50 J |
Very Short Answer Questions
DIRECTIONS: Give answer in one word or one sentence.
- A man raises a mass ’
- A mass
- Two bodies
- Ten identical balls are placed in contact on a smooth surface. If an eleventh identical ball moving with a speed ’
- Can a constant velocity be maintained in a body moving on a rough source without doing any work on it?
- Does the work done in raising a box on to a platform depends upon how fast it is raised up? If not, why?
- A man rowing a boat upstream is at rest with respect to the shore, is he doing work?
- A light body and a heavy body have the same momentum. Which one will have greater kinetic energy?
- A spring is cut into two equal halves. How is spring constant of each half affected?
- A truck and a car are moving with the same kinetic energy on a straight road. Their engines are simultaneously switched off. Which one will stop at a lesser distance?
Short Answer Questions
DIRECTIONS: Give answer in 2-3 sentences.
- Two springs
(a) they are stretched by the same amount,
(b) they are stretched by same force?
-
Calculate the work done to stretch a spring from
-
Two inclined frictionless tracks are gradual and the other steep meet at
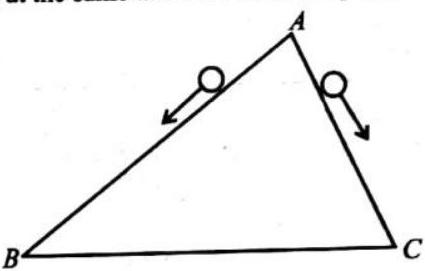
- What is an elastic collision? What will happen when
(i) a heavy body collides on a light mass at rest.
(ii) a light body collides on a heavy mass at rest.
- Show that in case of a freely falling body the total energy remains constant at every point in its paths.
- A motor pump is used to deliver water at a certain rate from a given pipe. To obtain ’
- Two masses, one
- Two masses, one
- The momentum of a body is increased by
Long Answer Questions
DIRECTIONS: Give answer in four to five sentences.
- Define work. Write its unit. How will you define 1 joule.
- What do you mean by energy? Explain different kinds of the mechanical energy.
- Define kinetic energy. Derive an expression for it.
- How will you define a collision. Define different kind of collision.
- Find expressions for the velocities of the colliding objects after an elastic collision.
- Explain conservative and non-conservative forces.
- Derive an expression for the velocity of an object undergoing a vertical circular motion at the highest point of its path.
EXERCISE 2
Multiple Choice Questions
DIRECTIONS : This section contains multiple choice questions. Each questions has 4 choices (a), (b), (c) and (d), out of which only one is correct.
- Which is not a unit of energy
(a) Watt second
(b) kilo watt hour
(c) watt
(d) joule
- kilowatt hour is the unit of
(a) time
(b) power
(c) energy
(d) force
- 1 kilowatt hour is equal to
(a) 1 joule
(c) 36 joule
(b) 100 joule
(d)
- A stone of mass
(a) The loss of gravitational potential energy by the stone is 1 joule
(b) The gain of gravitational potential energy by the stone is 1 joule
(c) The loss of gravitational potential energy is 9.8 joule
(d) The gain of gravitational potential energy is 9.8 joule
- The energy of
(a)
(b)
(c)
(d)
- A body of mass
(a)
(b)
(c)
(d)
- The kinetic energy of a body will become eight times if
(a) its mass is made four times
(b) its velocity is made four times
(c) both the mass and velocity are doubled
(d) both the mass and velocity are made four times
- For a body falling freely under gravity from a height
(a) only the potential energy goes on increasing
(b) only the kinetic energy goes on increasing
(c) both kinetic energy as well as potential energy go on increasing
(d) the kinetic energy goes on increasing while potential energy goes on decreasing
- A ball is dropped from a height of
(a)
(b)
(c)
(d)
- A
(a)
(b)
(c)
(d)
- The kinetic energy acquired by a body of mass ’
(a) directly proportional to mass
(b) inversely proportional to mass
(c) inversely proportional to mass
(d) independent of mass
- If a force
(a)
(b)
(c)
(d)
- The kinetic energy of a body becomes twice its initial value. The new momentum of the body will be
(a) 2 times
(b)
(c) 4 times
(d) unchanged
- A car weighing
(a)
(b)
(c)
(d) The information given is insufficient
- A uniform force of
(a)
(b)
(c)
(d)
- With what speed must a ball be thrown down for it to bounce
(a)
(b)
(c)
(d) The information given is incomplete
- The heart of a man pumps
(a)
(c)
(b)
(d)
- A cord is used to lower vertically a block of mass
(a)
(b)
(c)
(d) Mgd
- Figure shows the frictional force versus displacement for a particle in motion. The loss of kinetic energy (work done against frcition) in travelling over
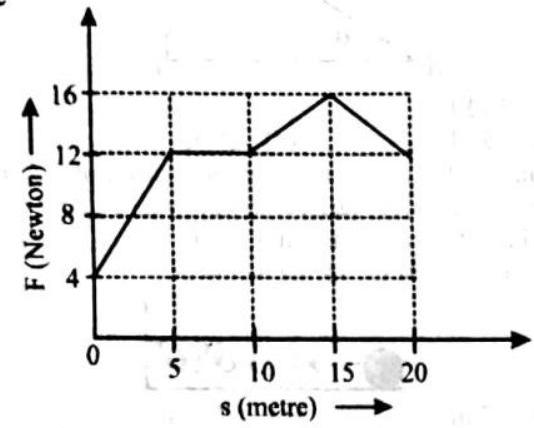
(a)
(b)
(c)
(d)
- Work done in time
(a)
(b)
(c)
(d)
- A man
(a)
(b)
(c)
(d)
- A man of weight
(a)
(b)
(c)
(d)
- Kinetic energy of a body moving with speed
(a)
(b)
(c)
(d)
- A weight-lifter lifts
(a)
(b)
(c)
(d)
- Two masses
(a)
(b)
(c)
(d)
- When you compress a coil spring you do work on it. The elastic potential energy
(a) increases
(b) decreases
(c) disappears
(d) remains the same
- If a stone of mass
(a)
(b)
(c) mgd
(d)
- No work is done when
(a) a nail is plugged into a wooden board
(b) a box is pushed along a horizontal floor
(c) there is no component of force parallel to the direction of motion
(d) there is no component of force normal to the direction of force
- Potential energy of your body is minimum when you
(a) are standing
(b) are sitting on a chair
(c) are sitting on the ground
(d) lie down on the ground
- The work done against gravity in moving the block a distance
(a)
(b) mgs
(c)
(d)
- A block of weight
(a)
(b) 0
(c)
(d)
- A child builds a tower from three blocks. The blocks are uniform cubes of side
(a)
(b)
(c)
(d)
- A car is moving with a constant speed of
(a)
(b)
(c)
(d)
- A particle of mass
(a)
(c)
(b)
(d)
- A body of mass
(a)
(b)
(c)
(d)
- A particle moves under the effect of a force
(a)
(b)
(c)
(d) zero
- A block is acted upon by a force, which is inversely proportional to the distance covered
(a)
(b)
(c)
(d) none of the above
- Two bodies
(a)
(b)
(c)
(d)
- A small body is projected in a direction inclined at
(a) zero
(b)
(c)
(d)
- If the linear momentum is increased by
(a)
(b)
(c)
(d)
- A wire suspended vertically from one of its ends is stretched by attaching a weight of
(a)
(b)
(c)
(d)
- Consider the following two statement
I. Linear momentum of a system of particles is zero.
II. Kinetic energy of a system of particles is zero. Then
(a) I implies II but II does not imply I.
(b) I does not imply II but II implies I.
(c) I implies II and II implies I.
(d) I does not imply II and II does not imply I.
- A bullet of mass ’
(a)
(b)
(c)
(d)
- A ball is dropped from a height
(a)
(c)
(b)
(d)
- A body of mass
(a)
(b)
(c)
(d)
- In figure, a carriage
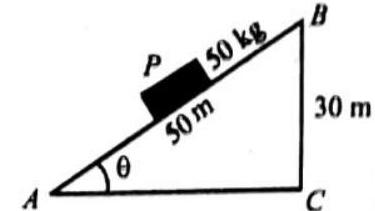
(a)
(b)
(c)
(d)
- A mass of
(a)
(b)
(c)
(d)
- A body of mass
(a)
(b)
(c)
(d)
More than one correct
DIRECTIONS: This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d), out of which One or More may be correct.
- The total energy of a swinging pendulum at any instant of time
(a) remains zero
(c) is same
(b) remains conserved
(d) is lost
- The power of a body doing 20 Joules of work in 5 seconds is
(a)
(b)
(c)
(d)
- 1 unit of electricity consumed is same as
(a)
(b)
(c)
(d)
- Which of the following is/are a scalar quantity?
(a) Acceleration
(b) Velocity
(c) Work done
(d) Energy
- No work is done by a force on an object if:
(a) the object moves in such a way that the point of application of the force remains fixed
(b) the object is stationary but the point of application of the force moves on the object
(c) the force is always perpendicular to its acceleration
(d) the force is always perpendicular to its velocity
- When a body is moving up with constant velocity:
(a) work done by force of gravity is positive
(b) work done by lifting force is positive
(c) work done by lifting force is negative
(d) work done by force of gravity is negative
- When two blocks connected by a spring move towards each other under mutual interaction:
(a) their momentum are equal and opposite
(b) their velocities are equal and opposite
(c) their accelerations are equal and opposite
(d) the force acting on them are equal and opposite.
- A particle is projected from a point at an angle with the horizontal at
- In which of the following are no work done by the force?
(a) A man walking upon a staircare
(b) A man carrying a bucket of water, walking on a level road with a uniform velocity.
(c) A drop of rain falling vertically with a constant velocity
(d) A man whirling a stone tied to a string in circle with a constant speed.
- A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that:
(a) the acceleration of the particle is constant
(b) the velocity of the particle is constant
(c) the particle moves in a circular path
(d) the kinetic energy of the particle is constant
- A body of mass
(a)
(b)
(c)
(d)
- A man of mass
(a) can never be less than
(b) is equal to
(c) is less than
(d) is greater than
- Which of the following are correct?
(a) The power of an agent is
(b) When a force retards the motion of a body, the work done is negative
(c) A body of weight 1 newton has a potential energy of 1 Joule relative to the ground when it is at a height of 1 metre
(d) A
- The figure given below shows how the net imteraction force between two particles A and B is related to the distance between them. When the distance between them varies from
(a) kinetic energy increases from
(b) potential enengy of the system increases from
(c) potential energy of the system increases from
(d) potential energy of the system increases form
Multiple Matching Questions
DIRECTIONS : Following question has four statements (A, B. C and D) given in Column I and four statements (a, r, s …. f) in Column II. Any given statement in Column I can have correct matching with one or more statement(s) griven in Column II. Match the entries in Column I with entries in Column II.
1.
| Column I | Column II |
|---|---|
| (A) Gravitational force | (p) Conservative |
| (B) Electrostatic force | (q) Non-consecutive |
| (C) Frictional force | (r) Act between surfaces in contact |
| (D) Viscous force | (s) Opposes relative motion |
| (t) Do not dissipate energy |
2. A particle of mass
| Column I | Column II |
|---|---|
| (A) Power of gravity at the highest point | (p) zero |
| (B) Power of gravity at the point of projection | (q) |
| (C) Work done by gravity during ascend | (r) |
| (D) Work done by gravity during descend | (s) negative |
| (t) positive |
Fill in the Blanks
I.
kinetic energy, velocity, mass, halved, one fourth
If the mass of a body is doubled, its (1) is also doubled and if the (2) of the body is halved, its kinetic energy gets (3). However if (4) of a body is doubled its kinetic energy becomes four times and if velocity of a body is halved, its kinetic energy becomes (5).
II. transformation, kinetic, change, potential, another
The (1) of one form of energy into (2) form of energy is known as (3) of energy. Suppose a stone is lying on the roof of a house. In this Position, all the energy of the stone is in the form of (4) energy. When the stone is dropped from the roof, it starts moving downwards towards the ground and the potential energy of the stone starts changing into (5) energy.
III. non-conservative, zero, conservative, non-zero.
The forces, work done by which do not depend on path followed but depend only on the initial and final position are called (1). Work done by these forces in round trip is (2) . On the other hand, the forces work done by which is path dependent are called (3).
Work done by these forces in round trip is (4).
Paragraph Based Questions
DIRECTIONS : Study the given paragraph(s) and answer the following questions.
PASSAGE-I
A block of mass
- The maximum compression in the spring is
(a)
(b)
(c)
(d)
- The velocity with which the block leaves the spring during return journey is
(a)
(c)
(b)
(d) zero
- Work done by friction in the round trip is
(a)
(b)
(c)
(d) zero
PASSAGE-II
Consider the situation shown in the figure. All surfaces are smooth, a particle is released from point

- How high will the particle rise above the ground after leaving from point
(a)
(b)
(c)
(d)
- How much time will the particle take to reach the ground after leaving from point
(a)
(b)
(c)
(d)
- What will be the horizontal distance travelled by the particle to reach the ground after leaving from point
(a)
(b)
(c)
(d)
PASSAGE-III
A pendulum bob of mass
- The maximum angle made by the string with the vertical is
(a)
(b)
(c)
(d)
- The maximum velocity of the
(a)
(b)
(c)
(d)
- The tension in the bob in the position of problem 7 will be
(a)
(b)
(c)
(d)
Assertions And Reasons
DIRECTIONS: Each of these questions contains an Assertion followed by reason. Read them carefully and answer the question on the basis of following options. You have to select the one that best describes the two statements.
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
1. Assertion : A moving hammer drives a nail into wood.
Reason : A moving hammer has potential energy.
2. Assertion : A man gets completely exhausted in trying to push a stationary wall.
Reason : Work done by the man on the wall is zero.
3. Assertion : The driver increases the speed of his car on approaching a hilly road.
Reason : To give more kinetic energy to the car so that it may go up against gravity.
4. Assertion : Winding up the spring of a toy car gives it energy for moving.
Reason : Work done in winding the spring get stored up as kinetic energý.
5. Assertion : A car engine convert heat energy into chemical energy.
Reason : A car burns fuel to get energy.
6. Assertion : The work done during a round trip is always zero.
7. Assertion : Work done in moving a body over a closed loop is zero for every force in nature.
Reason : Work done depends on nature of force.
8. Assertion : A person walking on horizontal road with a load on his head does no work.
Reason : No work is said to be done, if the directions of force and displacement of load are perpendicular to each other.
Hots Answer Questions
DIRECTIONS: Answer the following questions.
- It is generally much more difficult to stop a heavy truck than a light car when they move at the same speed. State a case in which the moving car could require more stopping force. (Consider relative times.)
- Why is a punch more forceful with a bare fist than with a boxing glove?
- A boxer can punch a heavy bag for more than an hour without tiring, but will tire quickly when boxing with an opponent for a few minutes. Why?
- Railroad cars are loosely coupled so that there is a noticeable time delay from the time the first car is moved and last cars gre moved from rest by the locomotive. Discuss the advisability of this loose coupling and slack between cars from an impulse-momentum point of view.
- A high-speed bus and an innocent bug have a head-on collision. The sudden change of momentum for the bug spatters it all over the windshield. Is the change in momentum of the bus greater, less, or the same as the change in momentum of the unfortunate bug?
- Why is it difficult for a firefighter to hold a hose that ejects large quantities of water at a high speed?
- You’re on a small raft next to a dock, and you jump from the raft only to fall into the water. What physics principle did you fail to take into account?
- Your friend says the conservation of momentum is violated when you step off a chair and gain momentum as you fall. What do you say?
- If a Mack truck and a Honda Civic have a head-on collision, which vehicle will experience the greater force of impact? The greater impulse ? The greater change in its momentum? The greater acceleration?
- Would a head-on collision between two cars be more damaging to the occupants if the cars stuck together or if the cars rebounded upon impact?
- Suppose there are three astronauts outside a space-ship, and two of them decide to pay catch using the third man. All the astronauts weigh the same on earth and are equally strong. The first astronaut throws the second one toward the third one and the game begins. Describe the motion of the astronauts as the game proceeds. How long will the game last?
- When a stationary uranium nucleus undergoes fission, it breaks into two unequal chunks that fly apart. What can you conclude about the momenta of the chunks? What can you conclude about the speed of the chunks?
- How is it possible that a flock of birds in flight can have a momentum of zero but not have zero kinetic energy?
- In determining the potential energy of Tenn’s drawn bow (figure), would it be an underestimate or an overestimate to multiply the force with which she holds the \to in its drawn position by the distance the pulled it? Why do we say the work done is the average force
- When a cannon with a long barrel is fired, the force of expanding gases acts on the cannonball for a longer distance. What effect does this have on the velocity of the emerging cannonball?
SOLUTIONS
EXERCISE - I
Fill In The Blanks
| 1. total | 2. 746 |
| 3. 20 | 4. |
| 5. the same | 6. zero |
| 7. |
8. motion |
| 9. |
10. Scalar |
| 11. potential energy | 12. energy |
| 13. kinetic | 14. negative |
True/False
| 1. True | 2. True | 3. False |
| 4. False | 5. True | 6. True |
| 7. True | 8. False | 9. True |
| 10. False | 11. False | 12. True |
| 13. False | 14. False | 15. True |
MATCH THE COLUMNS
- (A)
- (A)
- (A)
Work done by
Work done by
Work done by friction,
Very Short Answer Question
1. Work done against gravity is
2. Inelastic, as the two bodies are moving together after collision.
3. Energy
Heavier the mass, more will be momentum.
4. When the eleventh ball hits the first ball, the tenth ball starts moving with the same speed due to transfer of momentum in equal proportion.
5. No, work has to be done to compensate the energy loss due to friction.
6. Since, the gravitational force is conservative in nature, so work done against it depends only on initial and final points, not on time.
7. Yes, he is doing work to oppose the river current.
8.
9.
When it is cut into 2 equal halves, length of each half will be
10.
Here the retarding force
Since mass of the truck is more, so its frictional force will be more.
Short Answer Questions
1.
(a) For same stretch,
(b) For same force,
2.
3. Let
4. Elastic collision is defined as that collision in which both momentum and kinetic energy before and after collision are conserved. If two masses
given by
(i) If
(ii) If
5.
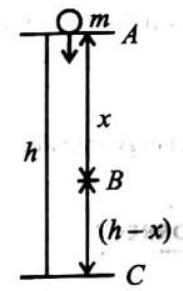
At
K.E.
At
Let
P.E.
It touches the ground.
If
Total energy remains constant at every point in the path of a freely falling body.
6. Let
To get
(a)
(b)
7. When dropped from same height, the two masses hit ground with same velocity.
8.
9. When momentum is increased by
EXERCISE-2
Multiple Choice Questions
1. (c)
2. (c)
3. (d)
4. (d)
5. (a)
6. (c)
7. (c)
8. (d)
9. (b)
10. (b)
11. (d)
12. (a)
13. (b)
14. (b)
15. (a)
16. (b)
17. (a)
18. (c)
19. (c)
20. (d)
21. (b)
22. (b)
23. (d)
24. (d)
25. (b)
26. (a)
27. (c)
28. (d)
29. (d)
30. (d)
31. (b)
32. (a)
33. (d)
34. (d)
35 (d) From
Velocity acquired in
Power
36. (b)
37. (d)
38. (c) As
39. (b) At the top of flight, horizontal component of velocity
40. (d) As
41. (c) Work done
42. (b) If
If
43. (c)
44. (d) As
45. (d) Applying the principle of conservation of linear momentum, we get
46. (b) Work done against gravity
Work done against friction
Total work done
47. (b)
48. (c) Fraction of energy transferred
More Than One Correct
1. (b, c)
2. (c, d)
3. (a, c)
4. (c, d)
5. (a, d)
6. (b, d)
7. (a, d) Net force acting on the system is zero, hence force as well as momentum of both the blocks are equal and opposite.
8.
Also
Hence all the graphs are correct.
9. (b, c, d)
10. (c, d) Acceleration and velocity change in direction, hence are not uniform.
11.
or
or
13. (a, b, c, d)
14. (b, d)
Multiple Matching Questions
- (A)
- (A)
Fill In The Passage
I. (1) kinetic energy
(2) mass
(3) halved
(4) velocity
(5) one fourth
II. (1) change
(2) another
(3) transformation
(4) potential
(5) kinetic
III. (1) conservative
(2) zero
(3) non-conservative
(4) non-zero.
Passage Based Questions
1. (b) By work-energy theorem, Work done by all the forces
or
or
2. (a)
or
3. (b) Work done by friction in round trip,
4. (c) Speed of particle at
For projectile motion of the particle,
5. (b) Let
at any instant,
When the particle strikes the ground,
or
or
but time cannot be negative, hence
6. (b) Now,
7. (b) For maxiumum angle, work done by
or
or
8. (a) Velocity is maximum when net force on the bob is zero.
Let the angle mode by the string with vertical at that instant be
or
By work energy theorem,
or
9. (d) At the position of maximum deflection,
using
We get
Assertion and Reasons
- (c)
- (a)
- (a)
- (c)
- (d)
- (d)
- (d)
- (a)
if
HOTS Subjective Questions
- If a moving truck or a car is brought to a stop then the change in momentum is brought to zero.
As both the truck and the car are traveling at the same speed but the truck is more heavier than the car therefore momentum of the truck is more and hence a greater force will be required to change its momentum to zero.
A moving car could require more stopping force if the time during which its momentum is brought to zero is reduced considerably. For example, if the time of impact is reduced by 10 , then force of impact is extended to 10 times.
-
A punch with a bare fist is more forceful than with a boxing glove. A boxing glove allows a longer time of impact thus decreasing the force of impact whereas a punch with a bare fist has smaller time of impact and hence it has greater force of impact.
-
When the boxer is punching a heavy bag, the bag provides impulse to stop the punches and reduce the momentum to zero. The boxer’s punch acts as action to the bag and the bag exerts an equal and opposite force of reaction to the boxer and thus stops the punches. Therefore the boxer can punch the bag for an hour without tiring.
While boxing with an opponent, punches are missed because the opponent bends sideways to protect himself and thus missed punches are in air. In this case air molecules will be providing impulse to stop the punches and that will be very small. There will be no enough impulse to bring the momentum to zero.
As a result the body of boxer will be pulled along with the punches and hence he will tire quickly.
- Railroad cars are loosely coupled so that there is a noticeable time delay from the time the first car is moved and last cars are moved from rest by the locomotive.
By the impulse-momentum relation
where
The mass of the locomotive and coupled cars is enormous so when locomotive moves from rest it acquires large momentum and this momentum is imparted to the cars through the loose coupling and slack between cars.
Such a large momentum will cause a great force of impact that might hurt the passengers inside the car.
The loose coupling allows a longer time of impact and thereby decreasing the force of impact considerably so that the passengers may be comfortable when cars gain momentum.
- A high-speed bus and an innocent bug have a head-on collision. The sudden change of momentum of the bus is the same as the change in momentum of the bug. This is because the momentum is conserved for all types of collisions. The mass of the bus is large hence its velocity will change by small amount after collision and as the mass of the bug is very small its velocity will change by large amount but the change in momentum of the bus and the bug will be the same.
- The water coming out a hose at high speed has a large momentum in the forward direction. In accordance with the conservation of momentum, the same amount of momentum is exerted on the hose pipe in the backward direction therefore a firefighter has to apply a large force to counter the backward momentum of hose and keep the hose in a stable position.
- A small raft is next to a dock. If someone jumps from the raft, he will fall into the water because he could not take into account the principle of the conservation of momentum. If someone jumps from the raft, he acquires momentum in the forward direction and hence the raft moves in the opposite direction gaining the momentum in backward direction so that the net change in the momentum may be zero as no external force acts here.
- There is no violation of the conservation of momentum when you step off a chair and gain momentum as you fall. When you are sitting on the chair the total momentum of the system is zero. When you fall you gain in momentum in one direction and the chair moves in the other direction, so that the net change in momentum of the system may be zero.
- If a Mack truck and a Honda Civic have a head on collision, both of them will experience the same force of impact, the same impulse and the same change in momentum. In any type of collision, the momentum of the system remains conserved. And by the impulse-momentum relation.
where
- A head-on collision between two cars will be more damaging to the occupants if the cars rebounded upon impact instead of sticking together. Because the impulse required to bring an object to a stop and then to throw it back again is greater than the impulse required merely to bring it to a stop. Thus impulse is greater when an object bounces and hence the damaging force is also greater.
- When the first astronaut throws the second one towards the third one, the first astronaut will be thrown in the opposite direction. This in accordance with the principle of momentum conservation.
When the second astronaut pushes the third astronaut he comes to rest and the third astronaut moves with the same velocity of the second.
The game will not last long because the astronaut will not meet together further.
- The forces involved in the fission of a uranium nucleus are internal force which means the net momentum of its flying chunks is the same as the momentum of the uranium nucleus before explosion. As the uranium nucleus is initially at rest therefore its net momentum is zero and hence the chunks fly apart exactly in opposite directions such that the sum of their momenta becomes zero.
Consider an uranium nucleus which is at rest
After fission it breaks into two chunks of masses

The momentum of each fragment is the same in magnitude but opposite in direction.
Thus,
or,
Now as the momentum of the two chunks is the same in magnitude therefore the speed of the lighter chunk will be greater and the speed of the heavier chunk will be smaller.
- Momentum is a vector quantity having both magnitude and direction whereas kinetic energy is a scalar quantity having only magnitude. Momentum that is directional is capable of being cancelled entirely.
The vector sum of the momenta of a flock of birds in flight can be zero because of birds flying in different directions in the flock.
Each flying bird has some kinetic energy and the algebraic addition of the kinetic energies of all birds in the flock cannot be zero.
- In determining the potential energy of Tenny’s drawn bow, it would be accurate to multiply the force with which she holds the \to in its drawn position by the distance she pulled it because work done (average force
- The velocity of the emerging cannonball fired from a cannon with a long barrel is greater because the force of expanding gases acts on the cannonball for a longer distance and hence the kinetic energy of the cannonball is more. It is evident from work - energy theorem.






