12.1 Introduction

In our daily life, many a times we compare two quantities of the same type. For example, Avnee and Shari collected flowers for scrap notebook. Avnee collected 30 flowers and Shari collected 45 flowers. So, we may say that Shari collected $45-30=15$ flowers more than Avnee.

Also, if height of Rahim is $150 cm$ and that of Avnee is $140 cm$ then, we may say that the height of Rahim is $150 cm-140 cm=10 cm$ more than Avnee. This is one way of comparison by taking difference.

If we wish to compare the lengths of an ant and a grasshopper, taking the difference does not express the comparison. The grasshopper’s length, typically $4 cm$ to $5 cm$ is too long as compared to the ant’s length which is a few mm. Comparison will be better if we try to find that how many ants can be placed one behind the other to match the length of grasshopper. So, we can say that 20 to 30 ants have the same length as a grasshopper.

Consider another example.

Cost of a car is ₹ 2,50,000 and that of a motorbike is ₹ 50,000. If we calculate the difference between the costs, it is ₹ $2,00,000$ and if we compare by division;

i.e. $\dfrac{2,50,000}{50,000}=\dfrac{5}{1}$

We can say that the cost of the car is five times the cost of the motorbike. Thus, in certain situations, comparison by division makes better sense than comparison by taking the difference. The comparison by division is the Ratio. In the next section, we shall learn more about ‘Ratios’.

12.2 Ratio

Consider the following:

Isha’s weight is $25 kg$ and her father’s weight is $75 kg$. How many times Father’s weight is of Isha’s weight? It is three times.

Cost of a pen is ₹ 10 and cost of a pencil is ₹ 2 . How many times the cost of a pen that of a pencil? Obviously it is five times.

In the above examples, we compared the two quantities in terms of ‘how many times’. This comparison is known as the Ratio. We denote ratio using symbol ‘:’

Consider the earlier examples again. We can say,

The ratio of father’s weight to Isha’s weight $=\dfrac{75}{25}=\dfrac{3}{1}=3: 1$

The ratio of the cost of a pen to the cost of a pencil $=\dfrac{10}{2}=\dfrac{5}{1}=5: 1$

Let us look at this problem.

In a class, there are 20 boys and 40 girls. What is the ratio of

(a) Number of girls to the total number of students.
(b) Number of boys to the total number of students.

Try These

1. In a class, there are 20 boys and 40 girls. What is the ratio of the number of boys to the number of girls?

2. Ravi walks $6 km$ in an hour while Roshan walks $4 km$ in an hour. What is the ratio of the distance covered by Ravi to the distance covered by Roshan?

First we need to find the total number of students, which is,

Number of girls + Number of boys $=20+40=60$.

Then, the ratio of number of girls to the total number of students is $\dfrac{40}{60}=\dfrac{2}{3}=2: 3$

Find the answer of part (b) in the similar manner.

Now consider the following example.

Length of a house lizard is $20 cm$ and the length of a crocodile is $4 m$.

“I am 5 times bigger than you”, says the lizard. As we can see this

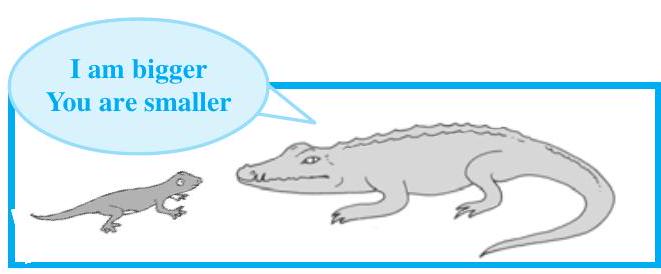
is really absurd. A lizard’s length cannot be 5 times of the length of a crocodile. So, what is wrong? Observe that the length of the lizard is in centimetres and length of the crocodile is in metres. So, we have to convert their lengths into the same unit.

Length of the crocodile $=4 m=4 \times 100=400 cm$.

Therefore, ratio of the length of the crocodile to the length of the lizard $=\dfrac{400}{20}=\dfrac{20}{1}=20: 1$.

Two quantities can be compared only if they are in the same unit.

Now what is the ratio of the length of the lizard to the length of the crocodile?

It is $\dfrac{20}{400}=\dfrac{1}{20}=1: 20$.

Observe that the two ratios $1: 20$ and $20: 1$ are different from each other. The ratio $1: 20$ is the ratio of the length of the lizard to the length of the crocodile whereas, $20: 1$ is the ratio of the length of the crocodile to the length of the lizard.

Now consider another example.

Length of a pencil is $18 cm$ and its diameter is $8 mm$. What is the ratio of the diameter of the pencil to that of its length? Since the length and the diameter of the pencil are given in different units, we first need to convert them into same unit.

Thus, length of the pencil $=18 cm$ $=18 \times 10 mm=180 mm$.

The ratio of the diameter of the pencil to that of the length of the pencil $=\dfrac{8}{180}=\dfrac{2}{45}=2: 45$.

Try These

1. Saurabh takes 15 minutes to reach school from his house and Sachin takes one hour to reach school from his house. Find the ratio of the time taken by Saurabh to the time taken by Sachin.

2. Cost of a toffee is 50 paise and cost of a chocolate is $₹ 10$. Find the ratio of the cost of a toffee to the cost of a chocolate.

3. In a school, there were 73 holidays in one year. What is the ratio of the number of holidays to the number of days in one year?

Think of some more situations where you compare two quantities of same type in different units.

We use the concept of ratio in many situations of our daily life without realising that we do so.

Compare the drawings A and B. B looks more natural than A. Why?

The legs in the picture A are too long in comparison to the other body parts. This is because we normally expect a certain ratio of the length of legs to the length of whole body.

Compare the two pictures of a pencil. Is the first one looking like a full pencil? No.

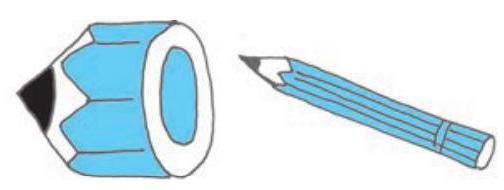
Why not? The reason is that the thickness and the length of the pencil are not in the correct ratio.

Same ratio in different situations :

Consider the following :

• Length of a room is $30 m$ and its breadth is $20 m$. So, the ratio of length of the room to the breadth of the room $=\dfrac{30}{20}=\dfrac{3}{2}=3: 2$
• There are 24 girls and 16 boys going for a picnic. Ratio of the number of girls to the number of boys $=\dfrac{24}{16}=\dfrac{3}{2}=3: 2$ The ratio in both the examples is $3: 2$.
• Note the ratios $30: 20$ and $24: 16$ in lowest form are same as $3: 2$. These are equivalent ratios.
• Can you think of some more examples having the ratio $3: 2$ ?

It is fun to write situations that give rise to a certain ratio. For example, write situations that give the ratio $2: 3$.

• Ratio of the breadth of a table to the length of the table is $2: 3$.
• Sheena has 2 marbles and her friend Shabnam has 3 marbles.

Then, the ratio of marbles that Sheena and Shabnam have is $2: 3$.

Can you write some more situations for this ratio? Give any ratio to your and 3. friends and ask them to frame situations.

Ravi and Rani started a business and invested money in the ratio $2: 3$. After one year the total profit was ₹ $4,00,000$.

Ravi said “we would divide it equally”, Rani said “I should get more as I have invested more”.

It was then decided that profit will be divided in the ratio of their investment.

Here, the two terms of the ratio $2: 3$ are 2

Sum of these terms $=2+3=5$

What does this mean?

This means if the profit is ₹ 5 then Ravi should get ₹ 2 and Rani should get $₹ 3$. Or, we can say that Ravi gets 2 parts and Rani gets 3 parts out of the 5 parts. i.e., Ravi should get $\dfrac{2}{5}$ of the total profit and Rani should get $\dfrac{3}{5}$ of the total profit.

If the total profit were ₹ 500

Ravi would get ₹ $\dfrac{2}{5} \times 500$=₹ $200$

and Rani would get $\dfrac{3}{5} \times 500$=₹ $300$

Now, if the profit were ₹ $4,00,000$ could you find the share of each?

Ravi’s share $\quad$=₹ $\dfrac{2}{5} \times 4,00,000$=₹ $1,60,000$

And Rani’s share =₹ $\dfrac{3}{5} \times 4,00,000$=₹ $2,40,000$

Can you think of some more examples where you have to divide a number of things in some ratio? Frame three such examples and ask your friends to solve them.

Let us look at the kind of problems we have solved so far.

Try These

1. Find the ratio of number of notebooks to the number of books in your bag.

2. Find the ratio of number of desks and chairs in your classroom.

3. Find the number of students above twelve years of age in your class. Then, find the ratio of number of students with age above twelve years and the remaining students.

4. Find the ratio of number of doors and the number of windows in your classroom.

5. Draw any rectangle and find the ratio of its length to its breadth.

Example 1 : Length and breadth of a rectangular field are $50 m$ and $15 m$ respectively. Find the ratio of the length to the breadth of the field.

Solution : Length of the rectangular field $=50 m$

Breadth of the rectangular field $=15 m$

The ratio of the length to the breadth is $50: 15$

The ratio can be written as $\dfrac{50}{15}=\dfrac{50 \div 5}{15 \div 5}=\dfrac{10}{3}=10: 3$

Thus, the required ratio is $10: 3$.

Example 2 : Find the ratio of $90 cm$ to $1.5 m$.

Solution : The two quantities are not in the same units. Therefore, we have to convert them into same units.

$1.5 m=1.5 \times 100 cm=150 cm$.

Therefore, the required ratio is $90: 150$.

$=\dfrac{90}{150}=\dfrac{90 \times 30}{150 \times 30}=\dfrac{3}{5}$

Required ratio is $3: 5$.

Example 3 : There are 45 persons working in an office. If the number of females is 25 and the remaining are males, find the ratio of:

(a) The number of females to number of males.
(b) The number of males to number of females.

Solution : Number of females $=25$

Total number of workers $=45$

Number of males $=45-25=20$

Therefore, the ratio of number of females to the number of males

$ =25: 20=5: 4 $

And the ratio of number of males to the number of females

$ =20: 25=4: 5 . $

(Notice that there is a difference between the two ratios $5: 4$ and $4: 5$ ).

Example 4 : Give two equivalent ratios of $6: 4$.

Solution : Ratio $6: 4=\dfrac{6}{4}=\dfrac{6 \times 2}{4 \times 2}=\dfrac{12}{8}$.

Therefore, $12: 8$ is an equivalent ratio of $6: 4$

Similarly, the ratio $6: 4=\dfrac{6}{4}=\dfrac{6 \times 2}{4 \times 2}=\dfrac{3}{2}$

So, $3: 2$ is another equivalent ratio of $6: 4$.

Therefore, we can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.

Write two more equivalent ratios of $6: 4$.

Example 5 : Fill in the missing numbers :

$ \dfrac{14}{21}=\dfrac{\square}{3}=\dfrac{6}{\square} $

Solution : In order to get the first missing number, we consider the fact that $21=3 \times 7$. i.e. when we divide 21 by 7 we get 3 . This indicates that to get the missing number of second ratio, 14 must also be divided by 7 .

When we divide, we have, $14 \div 7=2$

Hence, the second ratio is $\dfrac{2}{3}$.

Similarly, to get third ratio we multiply both terms of second ratio by 3 . (Why?)

Hence, the third ratio is $\dfrac{6}{9}$

Therefore, $\dfrac{14}{21}=\dfrac{\boxed{2}}{3}=\dfrac{6}{\boxed{9}}$ [These are all equivalent ratios.]

Example 6 : Ratio of distance of the school from Mary’s home to the distance of the school from John’s home is $2: 1$.

(a) Who lives nearer to the school?

(b) Complete the following table which shows some possible distances that Mary and John could live from the school.

(c) If the ratio of distance of Mary’s home to the distance of Kalam’s home from school is $1: 2$, then who lives nearer to the school?

Solution : (a) John lives nearer to the school (As the ratio is $2: 1$ ).

(b)

(c) Since the ratio is $1: 2$, so Mary lives nearer to the school.

Example 7 : Divide ₹ 60 in the ratio $1: 2$ between Kriti and Kiran.

Solution : The two parts are 1 and 2.

Therefore, sum of the parts $=1+2=3$.

This means if there are ₹ 3 , Kriti will get ₹ 1 and Kiran will get ₹ 2 . Or, we can say that Kriti gets 1 part and Kiran gets 2 parts out of every 3 parts.

Therefore, Kriti’s share $=\dfrac{1}{3} \times 60$ =₹ $20$

And Kiran’s share $=\dfrac{2}{3} \times 60$ =₹ $40$.

EXERCISE 12.1

1. There are 20 girls and 15 boys in a class.

(a) What is the ratio of number of girls to the number of boys?
(b) What is the ratio of number of girls to the total number of students in the class?

2. Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of

(a) Number of students liking football to number of students liking tennis.
(b) Number of students liking cricket to total number of students.

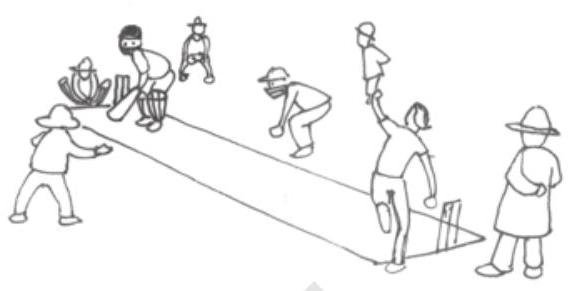
3. See the figure and find the ratio of

(a) Number of triangles to the number of circles inside the rectangle.
(b) Number of squares to all the figures inside the rectangle.
(c) Number of circles to all the figures inside the rectangle.

4. Distances travelled by Hamid and Akhtar in an hour are $9 km$ and $12 km$. Find the ratio of speed of Hamid to the speed of Akhtar.

5. Fill in the following blanks:

$\dfrac{15}{18}=\dfrac{\square}{6}=\dfrac{10}{\square}=\dfrac{\square}{30}$ [Are these equivalent ratios?]

6. Find the ratio of the following :

(a) 81 to 108
(b) 98 to 63
(c) 33 km to 121 km
(d) 30 minutes to 45 minutes

7. Find the ratio of the following:

(a) 30 minutes to 1.5 hours
(b) 40 cm to 1.5 m
(c) 55 paise to ₹ 1
(d) 500 mL to 2 litres

8. In a year, Seema earns $₹ 1,50,000$ and saves $₹ 50,000$. Find the ratio of

(a) Money that Seema earns to the money she saves.
(b) Money that she saves to the money she spends.

9. There are 102 teachers in a school of 3300 students. Find the ratio of the number of teachers to the number of students.

10. In a college, out of 4320 students, 2300 are girls. Find the ratio of

(a) Number of girls to the total number of students.
(b) Number of boys to the number of girls.
(c) Number of boys to the total number of students.

11. Out of 1800 students in a school, 750 opted basketball, 800 opted cricket and remaining opted table tennis. If a student can opt only one game, find the ratio of

(a) Number of students who opted basketball to the number of students who opted table tennis.
(b) Number of students who opted cricket to the number of students opting basketball.
(c) Number of students who opted basketball to the total number of students.

12. Cost of a dozen pens is $₹ 180$ and cost of 8 ball pens is $₹ 56$. Find the ratio of the cost of a pen to the cost of a ball pen.

13. Consider the statement: Ratio of breadth and length of a hall is $2: 5$. Complete the following table that shows some possible breadths and lengths of the hall.

14. Divide 20 pens between Sheela and Sangeeta in the ratio of $3: 2$.

15. Mother wants to divide $₹ 36$ between her daughters Shreya and Bhoomika in the ratio of their ages. If age of Shreya is 15 years and age of Bhoomika is 12 years, find how much Shreya and Bhoomika will get.

16. Present age of father is 42 years and that of his son is 14 years. Find the ratio of

(a) Present age of father to the present age of son.
(b) Age of the father to the age of son, when son was 12 years old.
(c) Age of father after 10 years to the age of son after 10 years.
(d) Age of father to the age of son when father was 30 years old.

12.3 Proportion

Consider this situation :

Raju went to the market to purchase tomatoes. One shopkeeper tells him that the cost of tomatoes is ₹ 40 for $5 kg$. Another shopkeeper gives the cost as 6 $kg$ for ₹ 42. Now, what should Raju do? Should he purchase tomatoes from the first shopkeeper or from the second? Will the comparison by taking the difference help him decide? No. Why not?

Think of some way to help him. Discuss with your friends.

Consider another example.

Bhavika has 28 marbles and Vini has 180 flowers. They want to share these among themselves. Bhavika gave 14 marbles to Vini and Vini gave 90 flowers to Bhavika. But Vini was not satisfied. She felt that she had given more flowers to Bhavika than the marbles given by Bhavika to her.

What do you think? Is Vini correct?

To solve this problem both went to Vini’s mother Pooja.

Pooja explained that out of 28 marbles,Bhavika gave 14 marbles to Vini.

Therefore, ratio is $14: 28=1: 2$.

And out of 180 flowers, Vini had given 90 flowers to Bhavika.

Therefore, ratio is $90: 180=1: 2$.

Since both the ratios are the same, so the distribution is fair.

Two friends Ashma and Pankhuri went to market to purchase hair clips. They purchased 20 hair clips for ₹ 30 . Ashma gave ₹ 12 and Pankhuri gave ₹ 18 . After they came back home, Ashma asked Pankhuri to give 10 hair clips to her. But Pankhuri said, “since I have given more money so I should get more clips. You should get 8 hair clips and I should get 12”.

Can you tell who is correct, Ashma or Pankhuri? Why?

Ratio of money given by Ashma to the money given by Pankhuri = ₹ $12: ₹ 18=2: 3$

According to Ashma’s suggestion, the ratio of the number of hair clips for Ashma to the number of hair clips for Pankhuri $=10: 10=1: 1$

According to Pankhuri’s suggestion, the ratio of the number of hair clips for Ashma to the number of hair clips for Pankhuri $=8: 12=2: 3$

Now, notice that according to Ashma’s distribution, ratio of hair clips and the ratio of money given by them is not the same. But according to the Pankhuri’s distribution the two ratios are the same.

Hence, we can say that Pankhuri’s distribution is correct.

Sharing a ratio means something!

Consider the following examples :

• Raj purchased 3 pens for ₹ 15 and Anu purchased 10 pens for ₹ 50. Whose pens are more expensive?

Ratio of number of pens purchased by Raj to the number of pens purchased by $Anu=3: 10$.

Ratio of their costs $=15: 50=3: 10$

Both the ratios $3: 10$ and $15: 50$ are equal. Therefore, the pens were purchased for the same price by both.

• Rahim sells $2 kg$ of apples for ₹ 180 and Roshan sells $4 kg$ of apples for $₹ 360$. Whose apples are more expensive?

Ratio of the weight of apples $=2 kg: 4 kg=1: 2$

Ratio of their cost =₹ $180: ₹ 360=6: 12=1: 2$

So, the ratio of weight of apples $=$ ratio of their cost.

Since both the ratios are equal, hence, we say that they are in proportion. They are selling apples at the same rate.

If two ratios are equal, we say that they are in proportion and use the symbol ‘::’ or ’ $=$ ’ to equate the two ratios.

For the first example, we can say $3,10,15$ and 50 are in proportion which is written as $3: 10:: 15: 50$ and is read as 3 is to 10 as 15 is to 50 or it is written as $3: 10=15: 50$.

For the second example, we can say 2, 4, 180 and 360 are in proportion which is written as $2: 4:: 180: 360$ and is read as 2 is to 4 as 180 is to 360 .

Let us consider another example.

A man travels $35 km$ in 2 hours. With the same speed would he be able to travel $70 km$ in 4 hours?

Now, ratio of the two distances travelled by the man is 35 to $70=1: 2$ and the ratio of the time taken to cover these distances is 2 to $4=1: 2$.

Hence, the two ratios are equal i.e. $35: 70=2: 4$.

Therefore, we can say that the four numbers $35,70,2$ and 4 are in proportion.

Hence, we can write it as $35: 70:: 2: 4$ and read it as 35 is to 70 as

2 is to 4 . Hence, he can travel $70 km$ in 4 hours with that speed.

Now, consider this example.

Cost of $2 kg$ of apples is ₹ 180 and a $5 kg$ watermelon costs ₹ 45 .

Now, ratio of the weight of apples to the weight of watermelon is $2: 5$.

Try These

Check whether the given ratios are equal, i.e. they are in proportion.

If yes, then write them in the proper form.

1. $1: 5$ and $3: 15$
2. $2: 9$ and $18: 81$
3. $15: 45$ and $5: 25$
4. $4: 12$ and $9: 27$
5. ₹ $10$ to ₹ $15$ and $4$ to $6$

And ratio of the cost of apples to the cost of the watermelon is $180: 45=4: 1$.

Here, the two ratios $2: 5$ and $180: 45$ are not equal,

i.e. $2: 5 \neq 180: 45$

Therefore, the four quantities 2, 5, 180 and 45 are not in proportion.

If two ratios are not equal, then we say that they are not in proportion. In a statement of proportion, the four quantities involved when taken in order are known as respective terms. First and fourth terms are known as extreme terms. Second and third terms are known as middle terms.

For example, in $35: 70:: 2: 4$;

$35,70,2,4$ are the four terms. 35 and 4 are the extreme terms. 70 and 2 are the middle terms.

Example 8 : Are the ratios $25 g: 30 g$ and $40 kg: 48 kg$ in proportion?

Solution : $25 g: 30 g=\dfrac{25}{30}=5: 6$

$40 kg: 48 kg=\dfrac{40}{48}=5: 6 \quad$ So, $25: 30=40: 48$.

Therefore, the ratios $25 g: 30 g$ and $40 kg: 48 kg$ are in proportion, i.e. $25: 30:: 40: 48$

The middle terms in this are 30, 40 and the extreme terms are 25, 48 .

Example 9 : Are 30, 40, 45 and 60 in proportion?

Solution : Ratio of 30 to $40=\dfrac{30}{40}=3: 4$.

Ratio of 45 to $60=\dfrac{45}{60}=3: 4$.

Since, $30: 40=45: 60$.

Therefore, 30, 40, 45, 60 are in proportion.

Example 10 : Do the ratios $15 cm$ to $2 m$ and $10 sec$ to 3 minutes form a proportion?

Solution : Ratio of $15 cm$ to $2 m=15: 2 \times 100(1 m=100 cm)$

$ =3: 40 $

Ratio of $10 sec$ to $3 min=10: 3 \times 60(1 min=60 sec)$

$ =1: 18 $

Since, $3: 40 \neq 1: 18$, therefore, the given ratios do not form a proportion.

EXERCISE 12.2

1. Determine if the following are in proportion.

(a) $15,45,40,120$
(b) $33,121,9,96$
(c) $24,28,36,48$
(d) $32,48,70,210$
(e) $4,6,8,12$
(f) $33,44,75,100$

2. Write True ( $T$ ) or False ( $F$ ) against each of the following statements :

(a) $16: 24:: 20: 30$
(b) $21: 6:: 35: 10$
(c) $12: 18:: 28: 12$
(d) $8: 9:: 24: 27$
(e) $5.2: 3.9:: 3: 4$
(f) $0.9: 0.36:: 10: 4$

3. Are the following statements true?

(a) 40 persons : 200 persons =₹ 15: ₹ 75
(b) 7.5 litres : 15 litres =5 kg: 10 kg
(c) 99 kg: 45 kg=₹ 44: ₹ 20
(d) 32 m: 64 m=6 sec: 12 sec
(e) 45 km: 60 km=12 hours : 15 hours

4. Determine if the following ratios form a proportion. Also, write the middle terms and extreme terms where the ratios form a proportion.

(a) 25 cm: 1 m and ₹ 40: ₹ 160
(b) 39 litres : 65 litres and 6 bottles : 10 bottles
(c) 2 kg: 80 kg and 25 g: 625 g
(d) 200 mL: 2.5 litre and ₹ 4: ₹ 50

12.4 Unitary Method

Consider the following situations:

• Two friends Reshma and Seema went to market to purchase notebooks. Reshma purchased 2 notebooks for ₹ 24 . What is the price of one notebook?

• A scooter requires 2 litres of petrol to cover $80 km$. How many litres of petrol is required to cover $1 km$ ?

These are examples of the kind of situations that we face in our daily life. How would you solve these?

Reconsider the first example: Cost of 2 notebooks is ₹ $24$.

Therefore, cost of 1 notebook =₹ $24 \div 2$=₹ $12$.

Now, if you were asked to find cost of 5 such notebooks. It would be = ₹ $12 \times 5$ = ₹ $60$

Reconsider the second example: We want to know how many litres are needed to travel $1 km$.

For $80 km$, petrol needed $=2$ litres.

Therefore, to travel $1 km$, petrol needed $=\dfrac{2}{80}=\dfrac{1}{40}$ litres.

Now, if you are asked to find how many litres of petrol are required to cover $120 km$ ?

Then petrol needed $=\dfrac{1}{40} \times 120$ litres $=3$ litres.

The method in which first we find the value of one unit and then the value of required number of units is known as Unitary Method.

Try These

1. Prepare five similar problems and ask your friends to solve them.

2. Read the table and fill in the boxes.

Time	Distance travelled by Karan	Distance travelled by Kriti
2 hours	8 km	6 km
1 hour	4 km	$\square$
4 hours	$\square$	$\square$

We see that,

Distance travelled by Karan in 2 hours $=8 km$

Distance travelled by Karan in 1 hour $=\dfrac{8}{2} km=4 km$

Therefore, distance travelled by Karan in 4 hours $=4 \times 4=16 km$

Similarly, to find the distance travelled by Kriti in 4 hours, first find the distance travelled by her in 1 hour.

Example 11 : If the cost of 6 cans of juice is ₹ 210 , then what will be the cost of 4 cans of juice?

Solution : Cost of 6 cans of juice =₹ $210$

Therefore, cost of one can of juice $=\dfrac{210}{6}$=₹ $35$

Therefore, cost of 4 cans of juice $=₹ 35 \times 4$=₹ $140$.

Thus, cost of 4 cans of juice is ₹ 140 .

Example 12 : A motorbike travels $220 km$ in 5 litres of petrol. How much distance will it cover in 1.5 litres of petrol?

Solution : In 5 litres of petrol, motorbike can travel $220 km$.

Therefore, in 1 litre of petrol, motor bike travels $=\dfrac{220}{5} km$

Therefore, in 1.5 litres, motorbike travels $=\dfrac{220}{5} \times 1.5 km$

$ =\dfrac{220}{5} \times \dfrac{15}{10} km=66 km . $

Thus, the motorbike can travel $66 km$ in 1.5 litres of petrol.

Example 13 : If the cost of a dozen soaps is ₹ 153.60 , what will be the cost of 15 such soaps?

Solution : We know that 1 dozen $=12$

Since, cost of 12 soaps =₹ $153.60$

Therefore, cost of 1 soap $=\dfrac{153.60}{12}$=₹ $12.80$

Therefore, cost of 15 soaps $=₹ 12.80 \times 15$=₹ $192$

Thus, cost of 15 soaps is ₹ 192 .

Example 14 : Cost of 105 envelopes is ₹ 350 . How many envelopes can be purchased for ₹ 100 ?

Solution : In ₹ 350, the number of envelopes that can be purchased $=105$

Therefore, in ₹ 1 , number of envelopes that can be purchased $=\dfrac{105}{350}$

Therefore, in ₹ 100 , the number of envelopes that can be

purchased $=\dfrac{105}{350} \times 100=30$

Thus, 30 envelopes can be purchased for ₹ 100 .]

Example 15 : A car travels $90 km$ in $2 \dfrac{1}{2}$ hours.

(a) How much time is required to cover $30 km$ with the same speed?
(b) Find the distance covered in 2 hours with the same speed.

Solution : (a) In this case, time is unknown and distance is known. Therefore, we proceed as follows :

$2 \dfrac{1}{2}$ hours $=\dfrac{5}{2}$ hours $=\dfrac{5}{2} \times 60$ minutes $=150$ minutes.

$90 km$ is covered in 150 minutes

Therefore, $1 km$ can be covered in $\dfrac{150}{90}$ minutes

Therefore, $30 km$ can be covered in $\dfrac{150}{90} \times 30$ minutes i.e. 50 minutes

Thus, $30 km$ can be covered in 50 minutes.

(b) In this case, distance is unknown and time is known. Therefore, we proceed as follows :

Distance covered in $2 \dfrac{1}{2}$ hours (i.e. $\dfrac{5}{2}$ hours) $=90 km$

Therefore, distance covered in 1 hour $=90 \div \dfrac{5}{2} km=90 \times \dfrac{2}{5}=36 km$

Therefore, distance covered in 2 hours $=36 \times 2=72 km$.

Thus, in 2 hours, distance covered is $72 km$.

EXERCISE 12.3

1. If the cost of $7 m$ of cloth is ₹ 1470 , find the cost of $5 m$ of cloth.

2. Ekta earns $₹ 3000$ in 10 days. How much will she earn in 30 days?

3. If it has rained $276 mm$ in the last 3 days, how many $cm$ of rain will fall in one full week (7 days)? Assume that the rain continues to fall at the same rate.

4. Cost of $5 kg$ of wheat is ₹ 91.50 .

(a) What will be the cost of $8 kg$ of wheat?
(b) What quantity of wheat can be purchased in ₹ 183 ?

5. The temperature dropped 15 degree celsius in the last 30 days. If the rate of temperature drop remains the same, how many degrees will the temperature drop in the next ten days?

6. Shaina pays $₹ 15000$ as rent for 3 months. How much does she has to pay for a whole year, if the rent per month remains same?

7. Cost of 4 dozen bananas is ₹ 180 . How many bananas can be purchased for $₹ 90$ ?

8. The weight of 72 books is $9 kg$. What is the weight of 40 such books?

9. A truck requires 108 litres of diesel for covering a distance of $594 km$. How much diesel will be required by the truck to cover a distance of $1650 km$ ?

10. Raju purchases 10 pens for $₹ 150$ and Manish buys 7 pens for $₹ 84$. Can you say who got the pens cheaper?

11. Anish made 42 runs in 6 overs and Anup made 63 runs in 7 overs. Who made more runs per over?

What have we discussed?

1. For comparing quantities of the same type, we commonly use the method of taking difference between the quantities.

2. In many situations, a more meaningful comparison between quantities is made by using division, i.e. by seeing how many times one quantity is to the other quantity. This method is known as comparison by ratio.

For example, Isha’s weight is $25 kg$ and her father’s weight is $75 kg$. We say that Isha’s father’s weight and Isha’s weight are in the ratio $3: 1$.

3. For comparison by ratio, the two quantities must be in the same unit. If they are not, they should be expressed in the same unit before the ratio is taken.

4. The same ratio may occur in different situations.

5. Note that the ratio $3: 2$ is different from $2: 3$. Thus, the order in which quantities are taken to express their ratio is important.

6. A ratio may be treated as a fraction, thus the ratio $10: 3$ may be treated as $\dfrac{10}{3}$.

7. Two ratios are equivalent, if the fractions corresponding to them are equivalent. Thus, $3: 2$ is equivalent to $6: 4$ or $12: 8.$

8. A ratio can be expressed in its lowest form. For example, ratio $50: 15$ is treated as $\dfrac{50}{15}$; in its lowest form $\dfrac{50}{15}=\dfrac{10}{3}$. Hence, the lowest form of the ratio $50: 15$ is $10: 3$.

9. Four quantities are said to be in proportion, if the ratio of the first and the second quantities is equal to the ratio of the third and the fourth quantities. Thus, 3,10 , 15,50 are in proportion, since $\dfrac{3}{10}=\dfrac{15}{50}$. We indicate the proportion by $3: 10:: 15: 50$, it is read as 3 is to 10 as 15 is to 50 . In the above proportion, 3 and 50 are the extreme terms and 10 and 15 are the middle terms.

10. The order of terms in the proportion is important. 3, 10, 15 and 50 are in proportion, but $3,10,50$ and 15 are not, since $\dfrac{3}{10}$ is not equal to $\dfrac{50}{15}$.

11. The method in which we first find the value of one unit and then the value of the required number of units is known as the unitary method. Suppose the cost of 6 cans is ₹ 210 . To find the cost of 4 cans, using the unitary method, we first find the cost of 1 can. It is $₹ \dfrac{210}{6}$ or $₹ 35$. From this, we find the price of 4 cans as $₹ 35 \times$ 4 or ₹ 140.