10.1 Introduction

When we talk about some plane figures as shown below we think of their regions and their boundaries. We need some measures to compare them. We look into these now.

10.2 Perimeter

Look at the following figures (Fig. 10.1). You can make them with a wire or a string.

If you start from the point $S$ in each case and move along the line segments then you again reach the point $S$. You have made a complete round of the

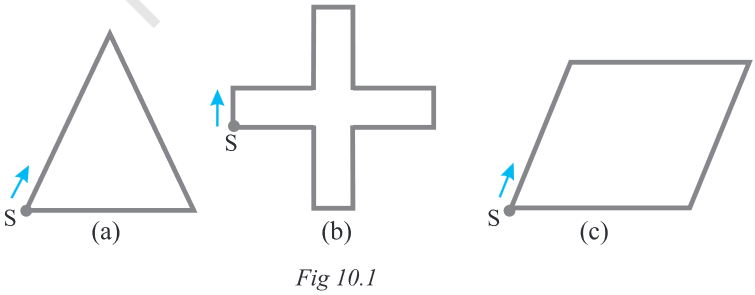
shape in each case (a), (b) & (c). The distance covered is equal to the length of wire used to draw the figure.

This distance is known as the perimeter of the closed figure. It is the length of the wire needed to form the figures.

The idea of perimeter is widely used in our daily life.

• A farmer who wants to fence his field.
• An engineer who plans to build a compound wall on all sides of a house.
• A person preparing a track to conduct sports.

All these people use the idea of ‘perimeter’.

Give five examples of situations where you need to know the perimeter.

Perimeter is the distance covered along the boundary forming a closed figure when you go round the figure once.

Try These

1. Measure and write the length of the four sides of the top of your study table.

AB= _______ cm
BC= _______ cm
CD= _______ cm
DA= _______ cm

Now, the sum of the lengths of the four sides

$=AB+BC+CD+DA$

$=$ _____ cm+ _____ cm+ _____ cm+ _____ cm

$=$ ______cm

What is the perimeter?

2. Measure and write the lengths of the four sides of a page of your notebook. The sum of the lengths of the four sides

$=AB+BC+CD+DA$

$=$ _____ cm+ _____ cm+ _____ cm+ _____ cm

$=$ ______cm

What is the perimeter of the page?

3. Meera went to a park $150 m$ long and $80 m$ wide. She took one complete round on its boundary. What is the distance covered by her?

4. Find the perimeter of the following figures:

So, how will you find the perimeter of any closed figure made up entirely of line segments? Simply find the sum of the lengths of all the sides (which are line segments).

10.2.1 Perimeter of a rectangle

Let us consider a rectangle $ABCD$ (Fig 10.2) whose length and breadth are $15 cm$ and $9 cm$ respectively. What will be its perimeter?

Perimeter of the rectangle $=$ Sum of the lengths of its four sides.

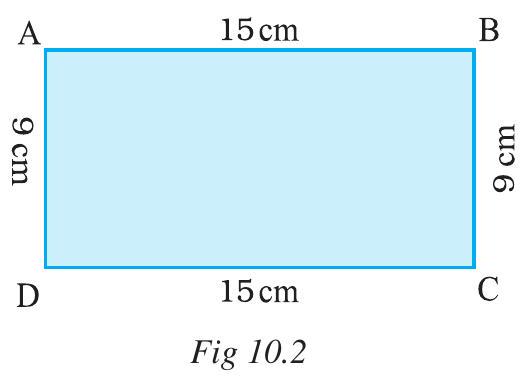
$ \begin{aligned} & =AB+BC+CD+DA \\ & =AB+BC+AB+BC \\ & =2 \times AB+2 \times BC \\ & =2 \times(AB+BC) \\ & =2 \times(15 cm+9 cm) \\ & =2 \times(24 cm) \\ & =48 cm \end{aligned} $

Remember that opposite sides of a rectangle are equal so AB = CD, AD = BC

Try These

Find the perimeter of the following rectangles:

Length of rectangle	Breadth of rectangle	Perimeter by adding all the sides	Perimeter by $2 \times($ Length + Breadth $)$
$25 cm$	$12 cm$	$=25 cm+12 cm$ $+25 cm+12 cm$ $=74 cm$	$=2 \times(25 cm+12 cm)$ $=2 \times(37 cm)$ $=74 cm$
$0.5 m$	$0.25 m$
$18 cm$	$15 cm$
$10.5 cm$	$8.5 cm$

Hence, from the said example, we notice that Perimeter of a rectangle $=$ length + breadth + length + breadth i.e. Perimeter of a rectangle $=\mathbf{2} \times($ length + breadth $)$

Let us now see practical applications of this idea :

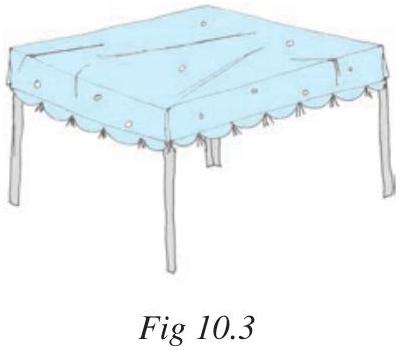
Example 1 : Shabana wants to put a lace border all around a rectangular table cover (Fig 10.3), $3 m$ long and $2 m$ wide. Find the length of the lace required by Shabana.

Solution : Length of the rectangular table cover $=3 m$

Breadth of the rectangular table cover $=2 m$

Shabana wants to put a lace border all around the table cover. Therefore, the length of the lace required will be equal to the perimeter of the rectangular table cover.

Now, perimeter of the rectangular table cover

$=2 \times($ length + breadth $)=2 \times(3 m+2 m)=2 \times 5 m=10 m$

So, length of the lace required is $10 m$.

Example 2 : An athlete takes 10 rounds of a rectangular park, $50 m$ long and $25 m$ wide. Find the total distance covered by him.

Solution : Length of the rectangular park $=50 m$

Breadth of the rectangular park $=25 m$

Total distance covered by the athlete in one round will be the perimeter of the park.

Now, perimeter of the rectangular park

$=2 \times($ length + breadth $)=2 \times(50 m+25 m)$

$=2 \times 75 m=150 m$

So, the distance covered by the athlete in one round is $150 m$.

Therefore, distance covered in 10 rounds $=10 \times 150 m=1500 m$

The total distance covered by the athlete is $1500 m$.

Example 3 : Find the perimeter of a rectangle whose length and breadth are $150 cm$ and $1 m$ respectively.

Solution : Length $=150 cm$

$ \text{ Breadth }=1 m=100 cm $

Perimeter of the rectangle

$=2 \times($ length + breadth $)$

$=2 \times(150 cm+100 cm)$

$=2 \times(250 cm)=500 cm=5 m$

Example 4 : A farmer has a rectangular field of length and breadth $240 m$ and $180 m$ respectively. He wants to fence it with 3 rounds of rope as shown in figure 10.4. What is the total length of rope he must use?

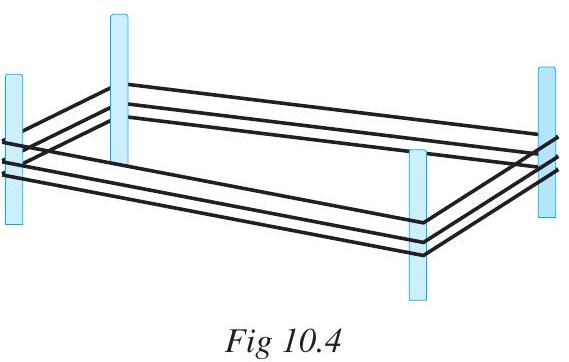
Solution: The farmer has to cover three times the perimeter of that field. Therefore, total length of rope required is thrice its perimeter.

Perimeter of the field $=2 \times($ length + breadth $)$

$ \begin{aligned} & =2 \times(240 m+180 m) \\ & =2 \times 420 m=840 m \end{aligned} $

Total length of rope required $=3 \times 840 m=2520 m$

Example 5 : Find the cost of fencing a rectangular park of length $250 m$ and breadth $175 m$ at the rate of ₹ 12 per metre.

Solution : Length of the rectangular park $=250 m$

Breadth of the rectangular park $=175 m$

To calculate the cost of fencing we require perimeter.

Perimeter of the rectangle $=2 \times($ length + breadth $)$

$ =2 \times(250 m+175 m) $

$ =2 \times(425 m)=850 m $

Cost of fencing $1 m$ of park $=₹ 12$

Therefore, the total cost of fencing the park

= ₹ $12 \times 850$=₹ $10200$

10.2.2 Perimeter of regular shapes

Consider this example.

Biswamitra wants to put coloured tape all around a square picture (Fig 10.5) of side $1 m$ as shown. What will be the length of the coloured tape he requires?

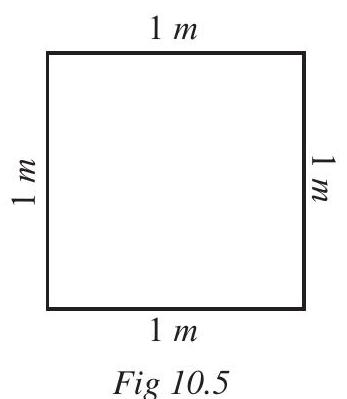
Since Biswamitra wants to put the coloured tape all around the square picture, he needs to find the perimeter of the picture frame.

Thus, the length of the tape required

$=$ Perimeter of square $=1 m+1 m+1 m+1 m=4 m$

Now, we know that all the four sides of a square are equal, therefore, in place of adding it four times, we can multiply the length of one side by 4 . Thus, the length of the tape required $=4 \times 1 m=4 m$

From this example, we see that

Perimeter of a square $=\mathbf{4} \times$ length of a side

Draw more such squares and find the perimeters.

Now, look at equilateral triangle (Fig 10.6) with each side equal to $4 cm$. Can we find its perimeter?

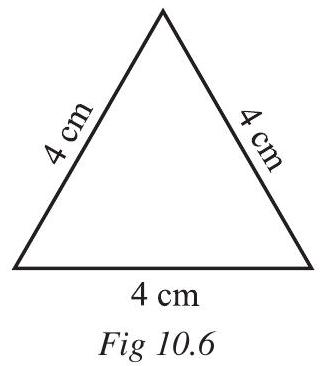
Perimeter of this equilateral triangle $=4+4+4 cm$

$ =3 \times 4 cm=12 cm $

So, we find that

Perimeter of an equilateral triangle $=3 \times$ length of a side

What is similar between a square and an equilateral triangle? They are figures having all the sides of equal length and all the angles of equal measure. Such figures are known as regular closed figures. Thus, a square and an equilateral triangle are regular closed figures.

Try These

Find various objects from your surroundings which have regular shapes and find their perimeters.

You found that,

Perimeter of a square $=4 \times$ length of one side

Perimeter of an equilateral triangle $=3 \times$ length of one side

So, what will be the perimeter of a regular pentagon?

A regular pentagon has five equal sides.

Therefore, perimeter of a regular pentagon $=5 \times$ length of one side and the perimeter of a regular hexagon will be _______ and of an octagon will be _______.

Example 6 : Find the distance travelled by Shaina if she takes three rounds of a square park of side $70 m$.

Solution : Perimeter of the square park $=4 \times$ length of a side $=4 \times 70 m=280 m$

Distance covered in one round $=280 m$

Therefore, distance travelled in three rounds $=3 \times 280 m=840 m$

Example 7 : Pinky runs around a square field of side $75 m$, Bob runs around a rectangular field with length $160 m$ and breadth $105 m$. Who covers more distance and by how much?

Solution : Distance covered by Pinky in one round $=$ Perimeter of the square

$ \begin{aligned} & =4 \times \text{ length of a side } \\ & =4 \times 75 m=300 m \end{aligned} $

Distance covered by Bob in one round $=$ Perimeter of the rectangle

$ \begin{aligned} & =2 \times(\text{ length }+ \text{ breadth }) \\ & =2 \times(160 m+105 m) \\ & =2 \times 265 m=530 m \end{aligned} $

Difference in the distance covered $=530 m-300 m=230 m$.

Therefore, Bob covers more distance by $230 m$.

Example 8 : Find the perimeter of a regular pentagon with each side measuring $3 cm$.

Solution : This regular closed figure has 5 sides, each with a length of $3 cm$. Thus, we get

Perimeter of the regular pentagon $=5 \times 3 cm=15 cm$

Example 9 : The perimeter of a regular hexagon is $18 cm$. How long is its one side?

Solution : Perimeter $=18 cm$

A regular hexagon has 6 sides, so we can divide the perimeter by 6 to get the length of one side.

One side of the hexagon $=18 cm \div 6=3 cm$

Therefore, length of each side of the regular hexagon is $3 cm$.

EXERCISE 10.1

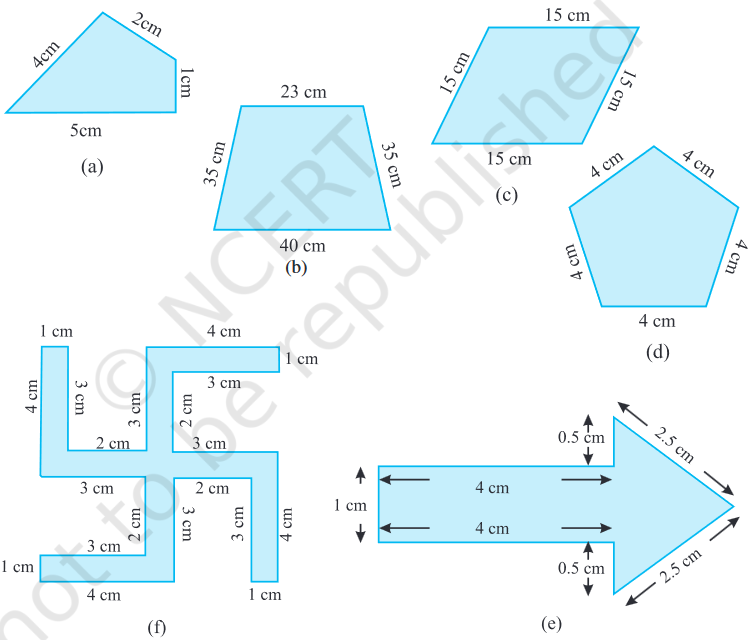
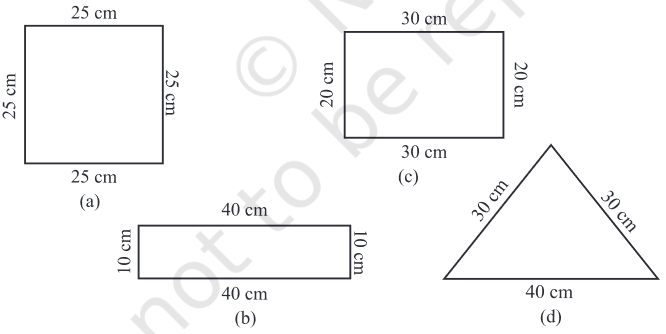
1. Find the perimeter of each of the following figures :

2. The lid of a rectangular box of sides $40 cm$ by $10 cm$ is sealed all round with tape. What is the length of the tape required?

3. A table-top measures $2 m 25 cm$ by $1 m 50 cm$. What is the perimeter of the table-top?

4. What is the length of the wooden strip required to frame a photograph of length and breadth $32 cm$ and $21 cm$ respectively?

5. A rectangular piece of land measures $0.7 km$ by $0.5 km$. Each side is to be fenced with 4 rows of wires. What is the length of the wire needed?

6. Find the perimeter of each of the following shapes :

(a) A triangle of sides $3 cm, 4 cm$ and $5 cm$.
(b) An equilateral triangle of side $9 cm$.
(c) An isosceles triangle with equal sides $8 cm$ each and third side $6 cm$.

7. Find the perimeter of a triangle with sides measuring $10 cm, 14 cm$ and $15 cm$.

8. Find the perimeter of a regular hexagon with each side measuring $8 m$.

9. Find the side of the square whose perimeter is $20 m$.

10. The perimeter of a regular pentagon is $100 cm$. How long is its each side?

11. A piece of string is $30 cm$ long. What will be the length of each side if the string is used to form :

(a) a square?
(b) an equilateral triangle?
(c) a regular hexagon?

12. Two sides of a triangle are $12 cm$ and $14 cm$. The perimeter of the triangle is $36 cm$. What is its third side?

13. Find the cost of fencing a square park of side $250 m$ at the rate of $₹ 20$ per metre.

14. Find the cost of fencing a rectangular park of length $175 m$ and breadth $125 m$ at the rate of ₹ 12 per metre.

15. Sweety runs around a square park of side $75 m$. Bulbul runs around a rectangular park with length $60 m$ and breadth $45 m$. Who covers less distance?

16. What is the perimeter of each of the following figures? What do you infer from the answers?

17. Avneet buys 9 square paving slabs, each with a side of $\frac{1}{2} m$. He lays them in the form of a square.

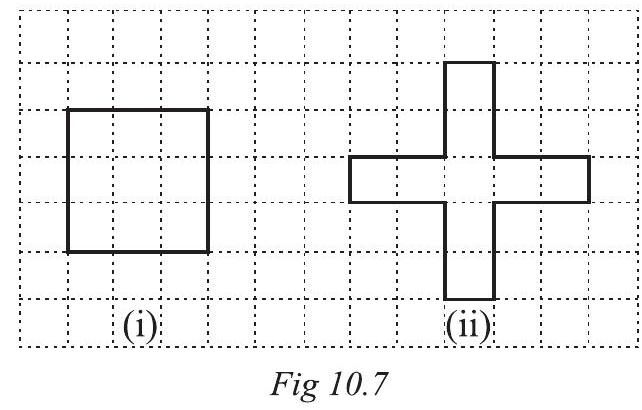
(a) What is the perimeter of his arrangement [Fig 10.7(i)]?
(b) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement [Fig 10.7 (ii)]?
(c) Which has greater perimeter?
(d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e. they cannot be broken.)

10.3 Area

Look at the closed figures (Fig 10.8) given below. All of them occupy some region of a flat surface. Can you tell which one occupies more region?

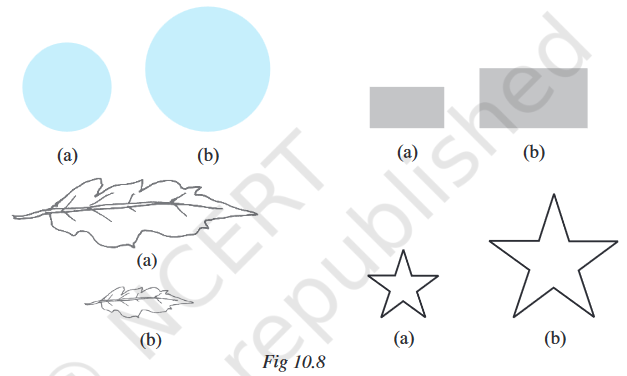
The amount of surface enclosed by a closed figure is called its area.

So, can you tell, which of the above figures has more area?

Now, look at the adjoining figures of Fig 10.9:

Which one of these has larger area? It is difficult to tell just by looking at these figures. So, what do you do?

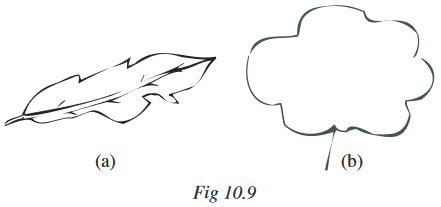
Place them on a squared paper or graph paper where every square measures $1 cm \times 1 cm$.

Make an outline of the figure.

Look at the squares enclosed by the figure. Some of them are completely enclosed, some half, some less than half and some more than half.

The area is the number of centimetre squares that are needed to cover it.

But there is a small problem : the squares do not always fit exactly into the area you measure. We get over this difficulty by adopting a convention :

• The area of one full square is taken as 1 sq unit. If it is a centimetre square sheet, then area of one full square will be $1 sq ~cm$.
• Ignore portions of the area that are less than half a square.
• If more than half of a square is in a region, just count it as one square.
• If exactly half the square is counted, take its area as $\frac{1}{2}$ sq unit.

Such a convention gives a fair estimate of the desired area.

Example 10 : Find the area of the shape shown in the figure 10.10.

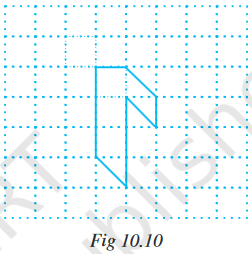
Solution : This figure is made up of line-segments.

Moreover, it is covered by full squares and half squares only. This makes our job simple.

(i) Fully-filled squares $=3$
(ii) Half-filled squares $=3$

Area covered by full squares

$=3 \times 1$ sq units $=3$ sq units

Total area $=4 \frac{1}{2}$ sq units.

Fig 10.10

Example 11 : By counting squares, estimate the area of the figure $10.9 b$.

Soultion : Make an outline of the figure on a graph sheet. (Fig 10.11)

Total area $=11+3 \times \frac{1}{2}+7=19 \frac{1}{2}$ sq units.

How do the squares cover it?

Example 12 : By counting squares, estimate the area of the figure $10.9 a$.

Soultion : Make an outline of the figure on a graph sheet. This is how the squares cover the figure (Fig 10.12).

Try These

1. Draw any circle on a graph sheet. Count the squares and use them to estimate the area of the circular region.

2. Trace shapes of leaves, flower petals and other such objects on the graph paper and find their areas.

EXERCISE 10.2

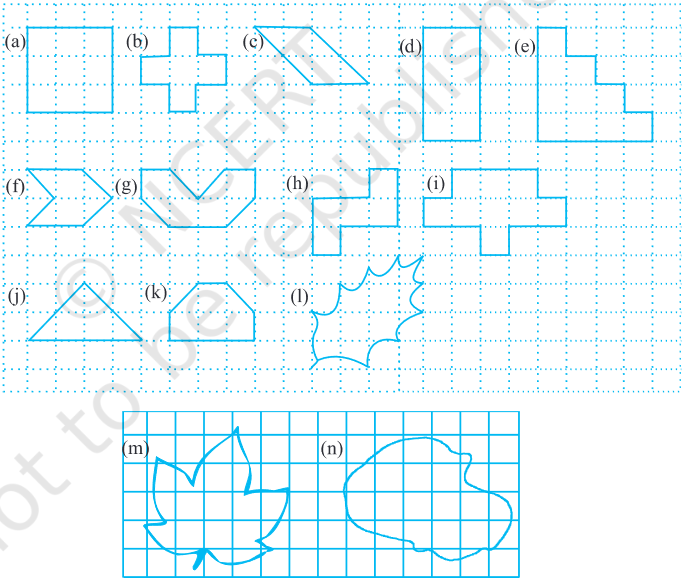
1. Find the areas of the following figures by counting square:

10.3.1 Area of a rectangle

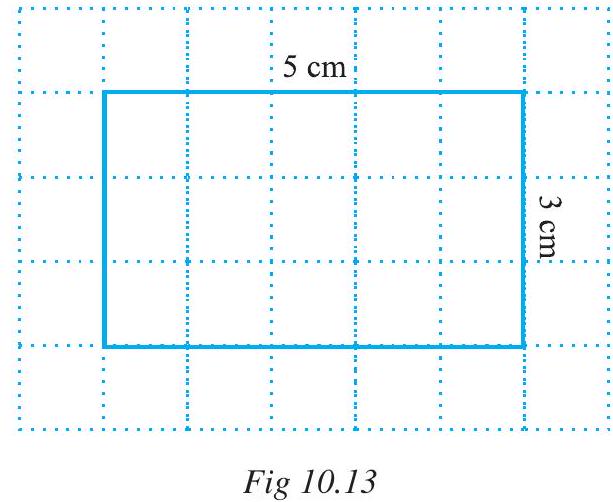
With the help of the squared paper, can we tell, what will be the area of a rectangle whose length is $5 cm$ and breadth is $3 cm$ ?

Draw the rectangle on a graph paper having $1 cm \times 1 cm$ squares (Fig 10.13). The rectangle covers 15 squares completely.

The area of the rectangle $=15 sq cm$ which can be written as $5 \times 3 sq cm$ i.e. (length $\times$ breadth).

The measures of the sides of some of the rectangles are given. Find their areas by placing them on a graph paper and counting the number of square.

We find,

Area of a rectangle $=($ length $\times$ breadth $)$

Without using the graph paper, can we find the area of a rectangle whose length is $6 cm$ and breadth is $4 cm$ ?

Yes, it is possible.

What do we infer from this?

We find that,

Area of the rectangle $=$ length $\times$ breadth $=6 cm \times 4 cm=24 sq cm$.

Try These

1. Find the area of the floor of your classroom.

2. Find the area of any one door in your house.

10.3.2 Area of a square

Let us now consider a square of side $4 cm$ (Fig 10.14).

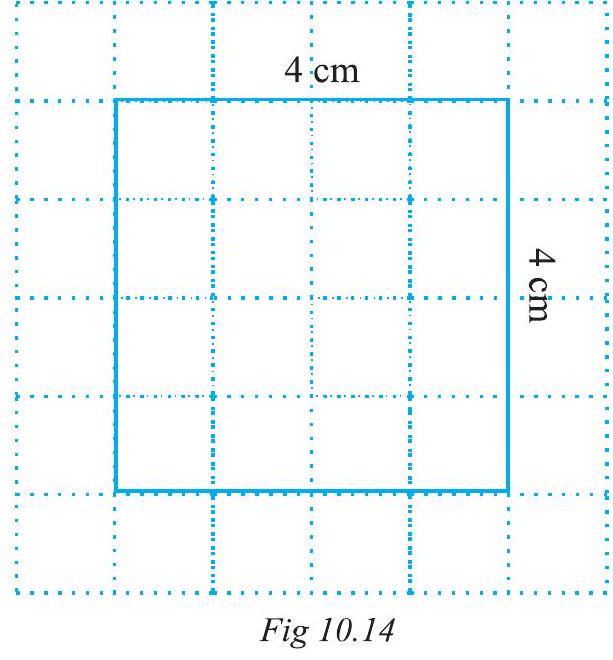
What will be its area?

If we place it on a centimetre graph paper, then what do we observe?

It covers 16 squares i.e. the area of the square $=16 sq cm=4 \times 4 sq cm$

Calculate areas of few squares by assuring length of one side of squares by yourself.

Find their areas using graph papers.

What do we infer from this?

We find that in each case,

Area of the square $=$ side $\times$ side

You may use this as a formula in doing problems.

Example 13 : Find the area of a rectangle whose length and breadth are $12 cm$ and $4 cm$ respectively.

Solution : Length of the rectangle $=12 cm$

Breadth of the rectangle $=4 cm$

Area of the rectangle $=$ length $\times$ breadth $=12 cm \times 4 cm=48 sq cm$.

Example 14 : Find the area of a square plot of side $8 m$.

Solution : Side of the square $=8 m$

Area of the square $=$ side $\times$ side

$ =8 m \times 8 m=64 sq m . $

Example 15 : The area of a rectangular piece of cardboard is $36 sq cm$ and its length is $9 cm$. What is the width of the cardboard?

Solution : Area of the rectangle $=36 sq cm$

Length $=9 cm$

Width $=$ ?

Area of a rectangle $=$ length $\times$ width

So, width $=\dfrac{\text{ Area }}{\text{ Length }}=\frac{36}{9}=4 cm$

Thus, the width of the rectangular cardboard is $4 cm$.

Example 16 : Bob wants to cover the floor of a room $3 m$ wide and $4 m$ long by squared tiles. If each square tile is of side $0.5 m$, then find the number of tiles required to cover the floor of the room.

Solution : Total area of tiles must be equal to the area of the floor of the room.

Length of the room $=4 m$

Breadth of the room $=3 m$

Area of the floor $=$ length $\times$ breadth $=4 m \times 3 m=12 sq m$

Area of one square tile $=$ side $\times$ side $=0.5 m \times 0.5 m$

$=0.25 sq m$

Number of tiles required $=\dfrac{\text{ Area of the floor }}{\text{ Area of one tile }}=\dfrac{12}{0.25}=\dfrac{1200}{25}=48$ tiles.

Example 17 : Find the area in square metre of a piece of cloth $1 m 25 cm$ wide and $2 m$ long.

Solution : Length of the cloth $=2 m$

Breadth of the cloth $=1 m 25 cm=1 m+0.25 m=1.25 m$

(since $25 cm=0.25 m$ )

Area of the cloth $=$ length of the cloth $\times$ breadth of the cloth

$ =2 m \times 1.25 m=2.50 sq~ m $

EXERCISE 10.3

1. Find the areas of the rectangles whose sides are :

(a) $3 cm$ and $4 cm$
(b) $12 m$ and $21 m$
(c) $2 km$ and $3 km$
(d) $2 m$ and $70 cm$

2. Find the areas of the squares whose sides are :

(a) $10 cm$
(b) $14 cm$
(c) $5 m$

3. The length and breadth of three rectangles are as given below :

(a) $9 m$ and $6 m$
(b) $17 m$ and $3 m$
(c) $4 m$ and $14 m$

Which one has the largest area and which one has the smallest?

4. The area of a rectangular garden $50 m$ long is $300 sq m$. Find the width of the garden.

5. What is the cost of tiling a rectangular plot of land $500 m$ long and $200 m$ wide at the rate of ₹ 8 per hundred sq $m$.?

6. A table-top measures $2 m$ by $1 m 50 cm$. What is its area in square metres?

7. A room is $4 m$ long and $3 m 50 cm$ wide. How many square metres of carpet is needed to cover the floor of the room?

8. A floor is $5 m$ long and $4 m$ wide. A square carpet of sides $3 m$ is laid on the floor. Find the area of the floor that is not carpeted.

9. Five square flower beds each of sides $1 m$ are dug on a piece of land $5 m$ long and 4 $m$ wide. What is the area of the remaining part of the land?

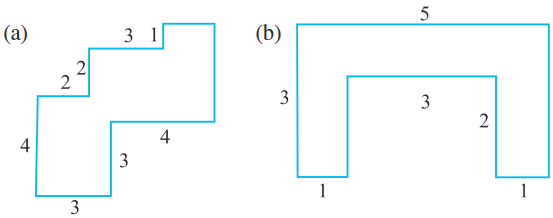
10. By splitting the following figures into rectangles, find their areas (The measures are given in centimetres).

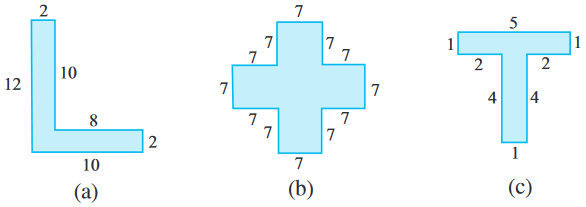
11. Split the following shapes into rectangles and find their areas. (The measures are given in centimetres)

12. How many tiles whose length and breadth are $12 cm$ and $5 cm$ respectively will be needed to fit in a rectangular region whose length and breadth are respectively:

(a) $100 cm$ and $144 cm$
(b) $70 cm$ and $36 cm$.

A challenge!

On a centimetre squared paper, make as many rectangles as you can, such that the area of the rectangle is $16 sq cm$ (consider only natural number lengths).

(a) Which rectangle has the greatest perimeter?
(b) Which rectangle has the least perimeter?

If you take a rectangle of area $24 sq cm$, what will be your answers?

Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter? With the least perimeter? Give example and reason.

What have we discussed?

1. Perimeter is the distance covered along the boundary forming a closed figure when you go round the figure once.

2. (a) Perimeter of a rectangle $=2 \times$ (length + breadth)

(b) Perimeter of a square $=4 \times$ length of its side

(c) Perimeter of an equilateral triangle $=3 \times$ length of a side

3. Figures in which all sides and angles are equal are called regular closed figures.

4. The amount of surface enclosed by a closed figure is called its area.

5. To calculate the area of a figure using a squared paper, the following conventions are adopted :

(a) Ignore portions of the area that are less than half a square.
(b) If more than half a square is in a region. Count it as one square.
(c) If exactly half the square is counted, take its area as $\frac{1}{2}$ sq units.

6. (a) Area of a rectangle $=$ length $\times$ breadth

(b) Area of a square $=$ side $\times$ side