Chapter 06 Integers
6.1 Introduction
Sunita’s mother has 8 bananas. Sunita has to go for a picnic with her friends. She wants to carry 10 bananas with her. Can her mother give 10 bananas to her? She does not have enough, so she borrows 2 bananas from her neighbour to be returned later. After giving 10 bananas to Sunita, how many bananas are left with her mother? Can we say that she has zero bananas? She has no bananas with her, but has to return two to her neighbour. So when she gets some more bananas, say 6 , she will return 2 and be left with 4 only.

Ronald goes to the market to purchase a pen. He has only ₹ 12 with him but the pen costs ₹ 15 . The shopkeeper writes ₹ 3 as due amount from him. He writes ₹ 3 in his diary to remember Ronald’s debit. But how would he remember whether ₹ 3 has to be given or has to be taken from Ronald? Can he express this debit by some colour or sign?
Ruchika and Salma are playing a game using a number strip which is marked from 0 to 25 at equal intervals.

To begin with, both of them placed a coloured token at the zero mark. Two coloured dice are placed in a bag and are taken out by them one by one. If the die is red in colour, the token is moved forward as per the number shown on throwing this die. If it is blue, the token is moved backward as per the number shown when this die is thrown. The dice are put back into the bag after each move so that both of them have equal chance of getting either die. The one who reaches the 25th mark first is the winner. They play the game. Ruchika gets the red die and gets four on the die after throwing it. She, thus, moves the token to mark four on the strip. Salma also happens to take out the red die and wins 3 points and, thus, moves her token to number 3.
In the second attempt, Ruchika secures three points with the red die and Salma gets 4 points but with the blue die. Where do you think both of them should place their token after the second attempt?
Ruchika moves forward and reaches $4+3$ i.e. the 7 th mark.

Whereas Salma placed her token at zero position. But Ruchika objected saying she should be behind zero. Salma agreed. But there is nothing behind zero. What can they do?
Salma and Ruchika then extended the strip on the other side. They used a blue strip on the other side.

Now, Salma suggested that she is one mark behind zero, so it can be marked as blue one. If the token is at blue one, then the position behind blue one is blue two. Similarly, blue three is behind blue two. In this way they decided to move backward. Another day while playing they could not find blue paper, so Ruchika said, let us use a sign on the other side as we are moving in opposite direction. So you see we need to use a sign going for numbers less than zero. The sign that is used is the placement of a minus sign attached to the number. This indicates that numbers with a negative sign are less than zero. These are called negative numbers.
Do This
(Who is where?)
Suppose David and Mohan have started walking from zero position in opposite directions. Let the steps to the right of zero be represented by ’ + ’ sign and to the left of zero represented by ‘-’ sign. If Mohan moves 5 steps to the right of zero it can be represented as +5 and if David moves 5 steps to the left of zero it can be represented as -5 . Now represent the following positions with + or - sign :
(a) 8 steps to the left of zero.
(b) 7 steps to the right of zero.
(c) 11 steps to the right of zero.
(d) 6 steps to the left of zero.
Do This
(Who follows me?)
We have seen from the previous examples that a movement to the right is made if the number by which we have to move is positive. If a movement of only 1 is made we get the successor of the number.
Write the succeeding number of the following :
| Number | Successor |
|---|---|
| 10 | |
| 8 | |
| -5 | |
| -3 | |
| 0 |
A movement to the left is made if the number by which the token has to move is negative.
If a movement of only 1 is made to the left, we get the predecessor of a number.

Now write the preceding number of the following:
| Number | Predecessor |
|---|---|
| 10 | |
| 8 | |
| 5 | |
| 3 | |
| 0 |
6.1.1 Tag me with a sign
We have seen that some numbers carry a minus sign. For example, if we want to show Ronald’s due amount to the shopkeeper we would write it as -3 .
Following is an account of a shopkeeper which shows profit and loss from the sale of certain items. Since profit and loss are opposite situations and if profit is represented by ’ + ’ sign, loss can be represented by ‘-’ sign.

Some of the situations where we may use these signs are :

The height of a place above sea level is denoted by a positive number. Height becomes lesser and lesser as we go lower and lower. Thus, below the surface of the sea level we can denote the height by a negative number.
Try These
Write the following numbers with appropriate signs:
(a) $100 m$ below sea level.
(b) $25^{\circ} C$ above $0^{\circ} C$ temperature.
(c) $15^{\circ} C$ below $0^{\circ} C$ temperature.
(d) any five numbers less than 0 .
If earnings are represented by ’ + ’ sign, then the spendings may be shown by a ‘-’ sign. Similarly, temperature above $0^{\circ} C$ is denoted a ’ + ’ sign and temperature below $0^{\circ} C$ is denoted by ‘-’ sign. For example, the temperature of a place $10^{\circ}$ below $0^{\circ} C$ is written as $-10^{\circ} C$.
6.2 Integers
The first numbers to be discovered were natural numbers i.e. 1, 2, 3, 4,.. If we include zero to the collection of natural numbers, we get a new collection of numbers known as whole numbers i.e. $0,1,2,3,4, \ldots$ You have studied these numbers in the earlier chapter. Now we find that there are negative numbers too. If we put the whole numbers and the negative numbers together, the new collection of numbers will look like $0,1,2,3,4,5, \ldots,-1,-2,-3$, $-4,-5, \ldots$ and this collection of numbers is known as Integers. In this collection, $1,2,3, \ldots$ are said to be positive integers and $-1,-2,-3, \ldots$ are said to be negative integers.
Let us understand this by the following figures. Let us suppose that the figures represent the collection of numbers written against them.
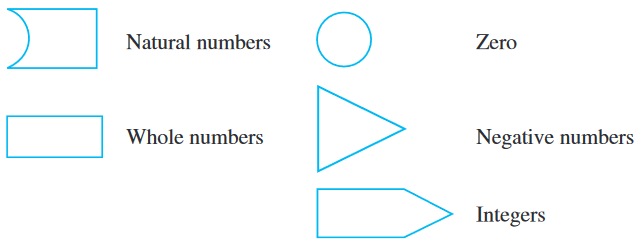
Then the collection of integers can be understood by the following diagram in which all the earlier collections are included :
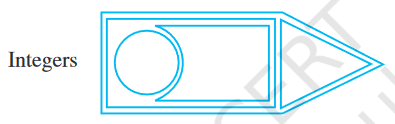
6.2.1 Representation of integers on a number line
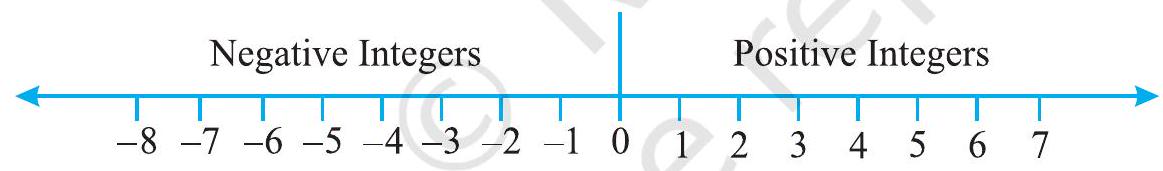
Draw a line and mark some points at equal distance on it as shown in the figure. Mark a point as zero on it. Points to the right of zero are positive integers and are marked $+1,+2,+3$, etc. or simply $1,2,3$ etc. Points to the left of zero are negative integers and are marked $-1,-2,-3$ etc.
In order to mark -6 on this line, we move 6 points to the left of zero. (Fig 6.1)
In order to mark +2 on the number line, we move 2 points to the right of zero. (Fig 6.2)
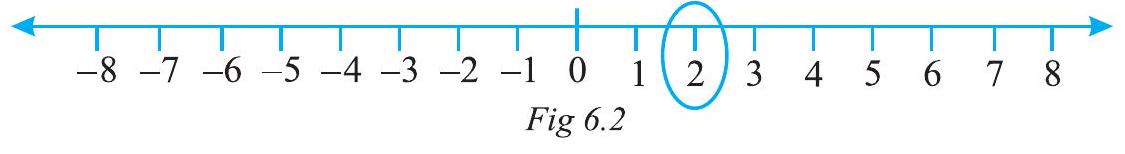
6.2.2 Ordering of integers
Raman and Imran live in a village where there is a step well. There are in all 25 steps down to the bottom of the well.
Try These
Mark -3, 7, -4, -8, -1 and -3 on the number line.
One day Raman and Imran went to the well and counted 8 steps down to water level. They decided to see how much water would come in the well during rains. They marked zero at the existing level of water and marked $1,2,3,4, \ldots$ above that level for each step. After the rains they noted that the water level rose up to the sixth step. After a few months, they noticed that the water level had fallen three steps below the zero mark. Now, they started thinking about marking the steps to note the fall of water level. Can you help them?
Suddenly, Raman remembered that at one big dam he saw numbers marked even below zero. Imran pointed out that there should be some way to distinguish between numbers which are above zero and below zero. Then Raman recalled that the numbers which were below zero had minus sign in front of them. So they marked one step below zero as -1 and two steps below zero as -2 and so on.
So the water level is now at -3 ( 3 steps below zero). After that due to further use, the water level went down by 1 step and it was at -4 . You can see that $-4<-3$.
Keeping in mind the above example, fill in the boxes using $>$ and $<$ signs.
Let us once again observe the integers which are represented on the number line.
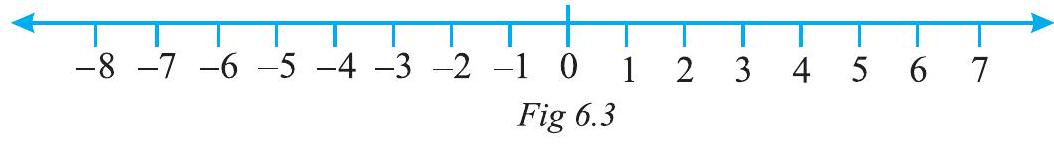
We know that $7>4$ and from the number line shown above, we observe that 7 is to the right of 4 (Fig 6.3).
Similarly, $4>0$ and 4 is to the right of 0 . Now, since 0 is to the right of -3 so, $0>-3$. Again, -3 is to the right of -8 so, $-3>-8$.
Thus, we see that on a number line the number increases as we move to the right and decreases as we move to the left.
Therefore, $-3<-2,-2<-1,-1<0,0<1,1<2,2<3$ so on.
Hence, the collection of integers can be written as…, $-5,-4,-3,-2,-1$, $0,1,2,3,4,5 \ldots$
Try These
Compare the following pairs of numbers using $>$ or $<$.
${}$ $ \begin{array}{rlrrl} 0 & \square -8 ; & -1 & \square & -15 \\ 5 & \square-5 ; & 11 & \square & 15 \\ 0 & \square \quad 6;& -20 & \square & 2 \end{array} $
From the above exercise, Rohini arrived at the following conclusions :
(a) Every positive integer is larger than every negative integer.
(b) Zero is less than every positive integer.
(c) Zero is larger than every negative integer.
(d) Zero is neither a negative integer nor a positive integer.
(e) Farther a number from zero on the right, larger is its value.
(f) Farther a number from zero on the left, smaller is its value.
Do you agree with her? Give examples.
Example 1 : By looking at the number line, answer the following questions : Which integers lie between -8 and -2 ? Which is the largest integer and the smallest integer among them?
Solution : Integers between -8 and -2 are $-7,-6,-5,-4,-3$. The integer -3 is the largest and -7 is the smallest.
If, I am not at zero what happens when I move?
Let us consider the earlier game being played by Salma and Ruchika.
Suppose Ruchika’s token is at 2. At the next turn she gets a red die which after throwing gives a number 3. It means she will move 3 places to the right of 2 .
Thus, she comes to 5 .

If on the other hand, Salma was at 1 , and drawn a blue die which gave her number 3 , then it means she will move to the left by 3 places and stand at -2 .

By looking at the number line, answer the following question:
Example 2 : (a) One button is kept at - 3. In which direction and how many steps should we move to reach at -9 ?
(b) Which number will we reach if we move 4 steps to the right of -6 .
Solution : (a) We have to move six steps to the left of -3 .
(b) We reach -2 when we move 4 steps to the right of -6 .
EXERCISE 6.1
1. Write opposites of the following:
(a) Increase in weight
(b) 30 km north
(c) 80 m east
(d) Loss of Rs 700
(e) 100 m above sea level
2. Represent the following numbers as integers with appropriate signs.
(a) An aeroplane is flying at a height two thousand metre above the ground.
(b) A submarine is moving at a depth, eight hundred metre below the sea level.
(c) A deposit of rupees two hundred.
(d) Withdrawal of rupees seven hundred.
3. Represent the following numbers on a number line:
(a) +5
(b) -10
(c) +8
(d) -1
(e) -6
4. Below figure is a vertical number line, representing integers. Observe it and locate the following points :
(a) If point $D$ is +8 , then which point is -8 ?
(b) Is point $G$ a negative integer or a positive integer?
(c) Write integers for points B and E.
(d) Which point marked on this number line has the least value?
(e) Arrange all the points in decreasing order of value.

5. Following is the list of temperatures of five places in India on a particular day of the year.

(a) Write the temperatures of these places in the form of integers in the blank column.
(b) Following is the number line representing the temperature in degree Celsius. Plot the name of the city against its temperature.

(c) Which is the coolest place?
(d) Write the names of the places where temperatures are above $10^{\circ} C$.
6. In each of the following pairs, which number is to the right of the other on the number line?
(a) 2,9
(b) -3,-8
(c) 0,-1
(d) -11,10
(e) -6,6
(f) 1,-100
7. Write all the integers between the given pairs (write them in the increasing order.)
(a) 0 and -7
(b) -4 and 4
(c) -8 and -15
(d) -30 and -23
8. (a) Write four negative integers greater than -20 .
(b) Write four integers less than -10 .
9. For the following statements, write True (T) or False (F). If the statement is false, correct the statement.
(a) -8 is to the right of -10 on a number line.
(b) -100 is to the right of -50 on a number line.
(c) Smallest negative integer is -1 .
(d) -26 is greater than -25 .
10. Draw a number line and answer the following :
(a) Which number will we reach if we move 4 numbers to the right of -2 .
(b) Which number will we reach if we move 5 numbers to the left of 1.
(c) If we are at -8 on the number line, in which direction should we move to reach -13 ?
(d) If we are at - 6 on the number line, in which direction should we move to reach -1 ?
6.3 Additon of Integers
Do This
(Going up and down)
In Mohan’s house, there are stairs for going up to the terrace and for going down to the godown.
Let us consider the number of stairs going up to the terrace as positive integer, the number of stairs going down to the godown as negative integer, and the number representing ground level as zero.
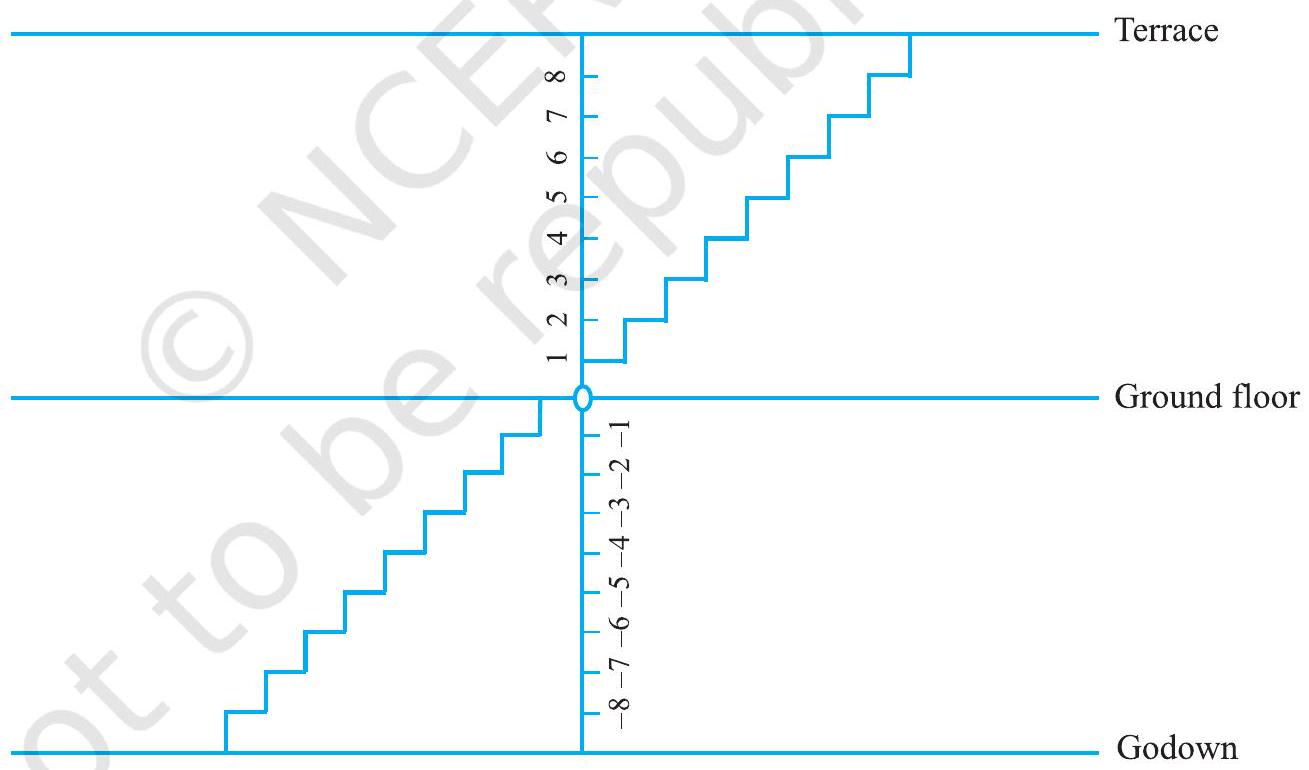
Do the following and write down the answer as integer :
(a) Go 6 steps up from the ground floor.
(b) Go 4 steps down from the ground floor.
(c) Go 5 steps up from the ground floor and then go 3 steps up further from there.
(d) Go 6 steps down from the ground floor and then go down further 2 steps from there.
(e) Go down 5 steps from the ground floor and then move up 12 steps from there.
(f) Go 8 steps down from the ground floor and then go up 5 steps from there.
(g) Go 7 steps up from the ground floor and then 10 steps down from there.
Ameena wrote them as follows :
(a) $+6$
(b) $-4$
(c) $(+5)+(+3)=+8$
(d) $(-6)+(-2)=-4$
(e) $(-5)+(+12)=+7$
(f) $(-8)+(+5)=-3$
(g) $(+7)+(-10)=17$
She has made some mistakes. Can you check her answers and correct those that are wrong?
Try These
Draw a figure on the ground in the form of a horizontal number line as shown below. Frame questions as given in the said example and ask your friends.

A Game
Take a number strip marked with integers from +25 to -25 .

Take two dice, one marked 1 to 6 and the other marked with three ’ + ’ signs and three ‘-’ signs.
Players will keep different coloured buttons (or plastic counters) at the zero position on the number strip. In each throw, the player has to see what she has obtained on the two dice. If the first die shows 3 and the second die shows - sign, she has -3 . If the first die shows 5 and the second die shows ’ + ’ sign, then, she has +5 .
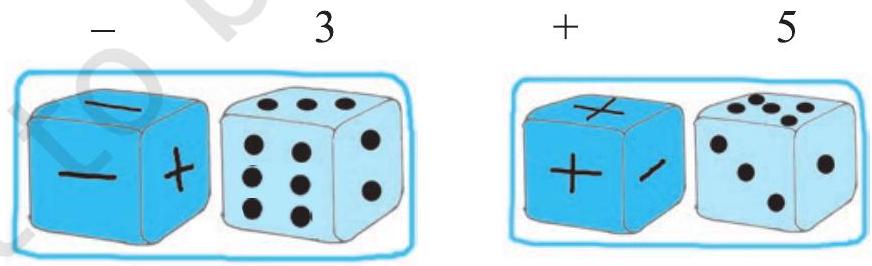
Whenever a player gets the + sign, she has to move in the forward direction (towards +25 ) and if she gets ’ - ’ sign then she has to move in the backward direction (towards -25 ).
Each player will throw both dice simultaneously. A player whose counter touches -25 is out of the game and the one whose counter touches +25 first, wins the game.
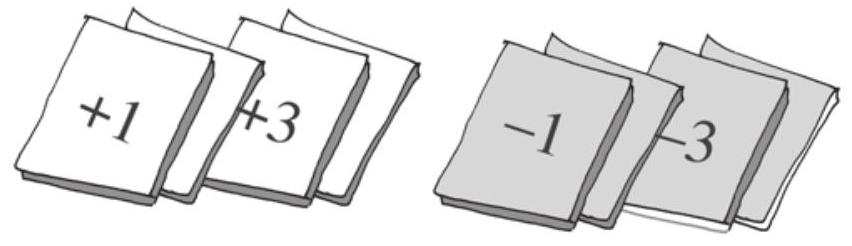
You can play the same game with 12 cards marked with $+1,+2,+3,+4$, +5 and +6 and $-1,-2, \ldots-6$. Shuffle the cards after every attempt.
Kamla, Reshma and Meenu are playing this game.
Kamla got $+3,+2,+6$ in three successive attempts. She kept her counter at the mark +11 .
Reshma got $-5,+3,+1$. She kept her counter at -1 . Meenu got $+4,-3,-2$ in three successive attempts; at what position will her counter be? At -1 or at +1 ?
Do This
Take two different coloured buttons like white and black. Let us denote one white button by $(+1)$ and one black button by ( -1$)$. A pair of one white button $(+1)$ and one black button $(-1)$ will denote zero i.e. $[1+(-1)=0]$
In the following table, integers are shown with the help of coloured buttons.
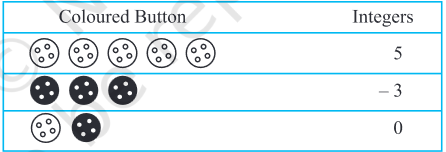
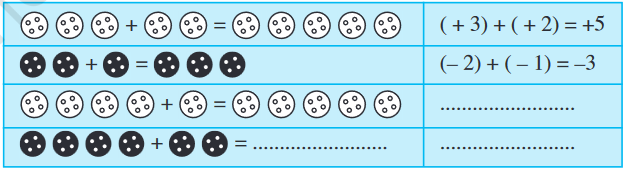
Let us perform additions with the help of the coloured buttons. Observe the following table and complete it.
Try These
Find the answers of the following additions:
(a) $(-11)+(-12)$
(b) $(+10)+(+4)$
(c) $(-32)+(-25)$
(d) $(+23)+(+40)$
You add when you have two positive integers like $(+3)+(+2)=+5[=3+2]$. You also add when you have two negative integers, but the answer will take a minus (-) sign like (-2) + (-1) = $-(\mathbf{2}+\mathbf{1})=\mathbf{- 3}$.
Now add one positive integer with one negative integer with the help of these buttons. Remove buttons in pairs i.e. a white button with a black button $[$ since $(+1)+(-1)=0]$. Check the remaining buttons.
(a) $(-4)+(+3)$
$=(-1)+(-3)+(+3)$
$=(-1)+0=-1$

(b) $(+4)+(-3)$
$ \begin{aligned} & =(+1)+(+3)+(-3) \\ & =(+1)+0=+1 \end{aligned} $

You can see that the answer of $4-3$ is 1 and $-4+3$ is -1 .
So, when you have one positive and one negative integer, you must subtract, but answer will take the sign of the bigger integer (Ignoring the signs of the numbers decide which is bigger). Some more examples will help :
(c) $(+5)+(-8)=(+5)+(-5)+(-3)=0+(-3)=(-3)$
(d) $(+6)+(-4)=(+2)+(+4)+(-4)=(+2)+0=+2$
Try These
Find the solution of the following:
(a) $(-7)+(+8)$
(b) $(-9)+(+13)$
(c) $(+7)+(-10)$
(d) $(+12)+(-7)$
6.3.1 Addition of integers on a number line
It is not always easy to add integers using coloured buttons. Shall we use number line for additions?
(i) Let us add 3 and 5 on number line.

On the number line, we first move 3 steps to the right from 0 reaching 3 , then we move 5 steps to the right of 3 and reach 8 . Thus, we get $3+5=8$ (Fig 6.4)
(ii) Let us add -3 and -5 on the number line.

On the number line, we first move 3 steps to the left of 0 reaching -3 , then we move 5 steps to the left of -3 and reach -8 . (Fig 6.5)
Thus, $(-3)+(-5)=-8$.
We observe that when we add two positive integers, their sum is a positive integer. When we add two negative integers, their sum is a negative integer.
(iii) Suppose we wish to find the sum of (+5) and (-3) on the number line. First we move to the right of 0 by 5 steps reaching 5 . Then we move 3 steps to the left of 5 reaching 2. (Fig 6.6)
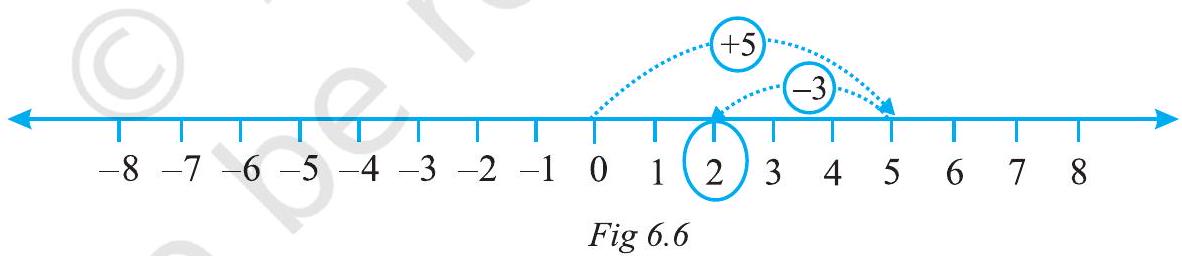
Thus, $(+5)+(-3)=2$
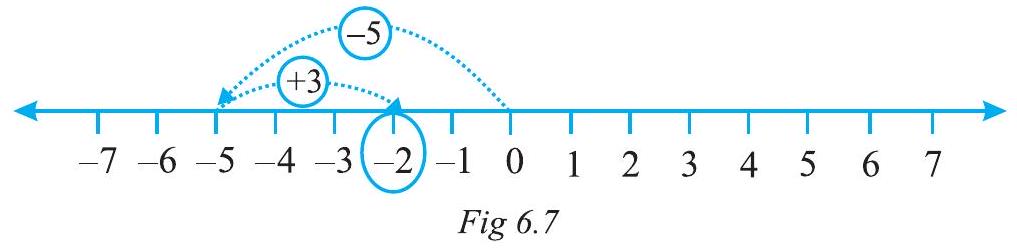
(iv) Similarly, let us find the sum of (-5) and (+3) on the number line.
First we move 5 steps to the left of 0 reaching -5 and then from this point we move 3 steps to the right. We reach the point -2 .
Thus, $(-5)+(+3)=-2$. (Fig 6.7)
Try These
1. Find the solution of the following additions using a number line :
(a) $(-2)+6$
(b) $(-6)+2$Make two such questions and solve them using the number line.
2. Find the solution of the following without using number line :
(a) $(+7)+(-11)$
(b) $(-13)+(+10)$
(c) $(-7)+(+9)$
(d) $(+10)+(-5)$Make five such questions and solve them.
When a positive integer is added to an integer, the resulting integer becomes greater than the given integer. When a negative integer is added to an integer, the resulting integer becomes less than the given integer.
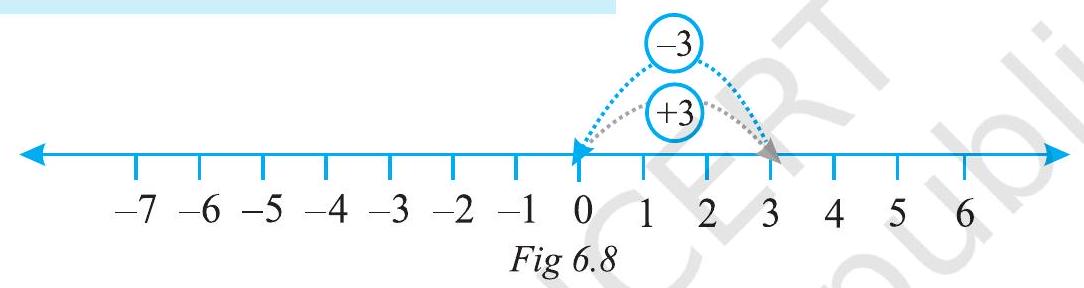
Let us add 3 and -3 . We first move from 0 to +3 and then from +3 , we move 3 points to the left. Where do we reach ultimately?
From the Figure 6.8, $3+(-3)=0$. Similarly, if we add 2 and -2 , we obtain the sum as zero.
Numbers such as 3 and - 3,2 and - 2, when added to each other give the sum zero. They are called additive inverse of each other.
What is the additive inverse of 6 ? What is the additive inverse of -7 ?
Example 3 : Using the number line, write the integer which is
(a) 4 more than -1
(b) 5 less than 3
Solution : (a) We want to know the integer which is 4 more than -1 . So, we start from -1 and proceed 4 steps to the right of -1 to reach 3 as shown below:
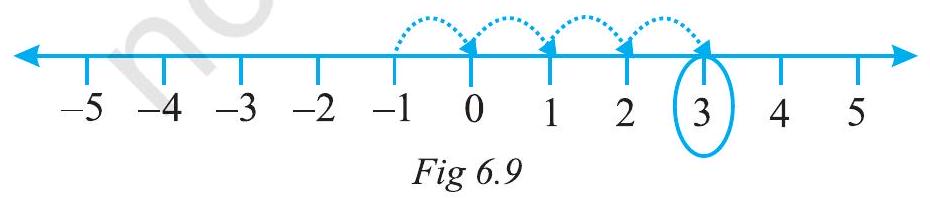
Therefore, 4 more than -1 is 3 (Fig 6.9).
(b) We want to know an integer which is 5 less than 3; so we start from 3 and move to the left by 5 steps and obtain -2 as shown below :

Therefore, 5 less than 3 is -2 . (Fig 6.10)
Example 4 : Find the sum of $(-9)+(+4)+(-6)+(+3)$
Solution : We can rearrange the numbers so that the positive integers and the negative integers are grouped together. We have
$ (-9)+(+4)+(-6)+(+3)=(-9)+(-6)+(+4)+(+3)=(-15)+(+7)=-8 $
Example 5 : Find the value of $(30)+(-23)+(-63)+(+55)$
Solution : $(30)+(+55)+(-23)+(-63)=85+(-86)=-1$
Example 6 : Find the sum of $(-10),(92),(84)$ and $(-15)$
Solution : $(-10)+(92)+(84)+(-15)=(-10)+(-15)+92+84$ $=(-25)+176=151$
EXERCISE 6.2
1. Using the number line write the integer which is :
(a) 3 more than 5
(b) 5 more than -5
(c) 6 less than 2
(d) 3 less than -2
2. Use number line and add the following integers :
(a) $9+(-6)$
(b) $5+(-11)$
(c) $(-1)+(-7)$
(d) $(-5)+10$
(e) $(-1)+(-2)+(-3)$
(f) $(-2)+8+(-4)$
3. Add without using number line :
(a) $11+(-7)$
(b) $(-13)+(+18)$
(c) $(-10)+(+19)$
(d) $(-250)+(+150)$
(e) $(-380)+(-270)$
(f) $(-217)+(-100)$
4. Find the sum of :
(a) 137 and - 354
(b) -52 and 52
(c) -312,39 and 192
(d) -50,-200 and 300
5. Find the sum :
(a) $(-7)+(-9)+4+16$
(b) $(37)+(-2)+(-65)+(-8)$
6.4 Subtraction of Integers with the help of a Number Line
We have added positive integers on a number line. For example, consider $6+2$. We start from 6 and go 2 steps to the right side. We reach at 8 . So, $6+2=8$. (Fig 6.11)
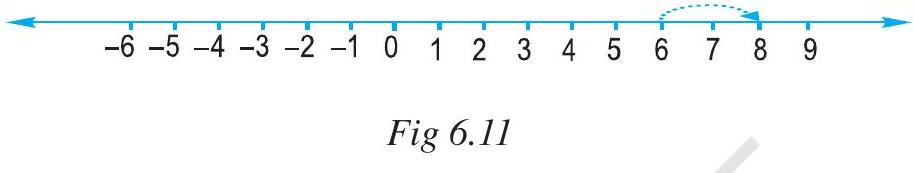
We also saw that to add 6 and (-2) on a number line we can start from 6 and then move 2 steps to the left of 6 . We reach at 4 . So, we have, $6+(-2)=4$. (Fig 6.12)
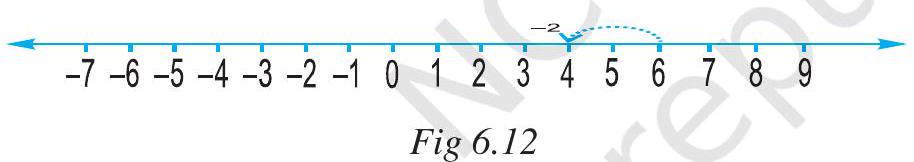
Thus, we find that, to add a positive integer we move towards the right on a number line and for adding a negative integer we move towards left.
We have also seen that while using a number line for whole numbers, for subtracting 2 from 6, we would move towards left. (Fig 6.13)
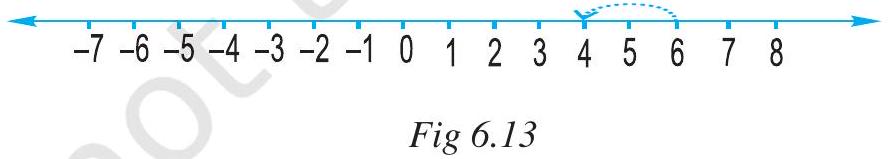
i.e. $6-2=4$
What would we do for $6-(-2)$ ? Would we move towards the left on the number line or towards the right?
If we move to the left then we reach 4.
Then we have to say $6-(-2)=4$. This is not true because we know $6-2=4$ and $6-2 \neq 6-(-2)$.
So, we have to move towards the right. (Fig 6.14)
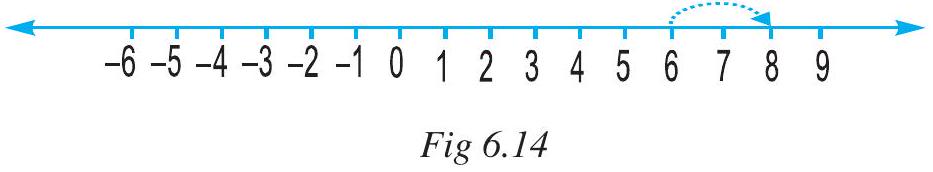
i.e. $6-(-2)=8$
This also means that when we subtract a negative integer we get a greater integer. Consider it in another way. We know that additive inverse of $(-2)$ is 2. Thus, it appears that adding the additive inverse of -2 to 6 is the same as subtracting $(-2)$ from 6.
We write $6-(-2)=6+2$.
Let us now find the value of $-5-(-4)$ using a number line. We can say that this is the same as $-5+(4)$, as the additive inverse of -4 is 4 .
We move 4 steps to the right on the number line starting from -5 . (Fig 6.15)
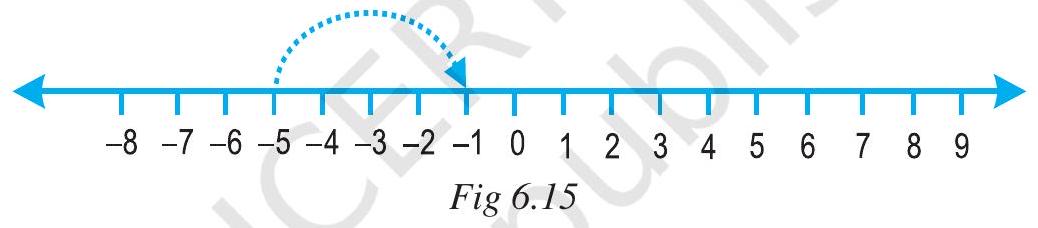
We reach at -1 .
i.e. $-5+4=-1$. Thus, $-5-(-4)=-1$.
Example 7 : Find the value of $-8-(-10)$ using number line
Solution : $-8-(-10)$ is equal to $-8+10$ as additive inverse of -10 is 10 . On the number line, from -8 we will move 10 steps towards right. (Fig 6.16)

We reach at 2 . Thus, $-8-(-10)=2$
Hence, to subtract an integer from another integer it is enough to add the additive inverse of the integer that is being subtracted, to the other integer.
Example 8 : Subtract ( -4$)$ from $(-10)$
Solution : $(-10)-(-4)=(-10)+($ additive inverse of -4$)$
$=-10+4=-6$
Example 9 : Subtract $(+3)$ from $(-3)$
Solution : $(-3)-(+3)=(-3)+($ additive inverse of +3$)$
$ =(-3)+(-3)=-6 $
EXERCISE 6.3
1. Find
(a) $35-(20)$
(b) $72-(90)$
(c) $(-15)-(-18)$
(d) $(-20)-(13)$
(e) $23-(-12)$
(f) $(-32)-(-40)$
2. Fill in the blanks with $>,<$ or $=$ sign.
(a) $(-3)+(-6)$ ______ $(-3)-(-6)$
(b) $(-21)-(-10)$ ______ $(-31)+(-11)$
(c) $45-(-11)$ ______ $57+(-4)$
(d) $(-25)-(-42)$ ______ $(-42)-(-25)$
3. Fill in the blanks.
(a) $(-8)+$ _____ $=0$
(b) $13+$ _____ $=0$
(c) $12+(-12)=$ _____
(d) $(-4)+$ _____ $=-12$
(e) _____ $-15=-10$
4. Find
(a) $(-7)-8-(-25)$
(b) $(-13)+32-8-1$
(c) $(-7)+(-8)+(-90)$
(d) $50-(-40)-(-2)$
What have we discussed?
1. We have seen that there are times when we need to use numbers with a negative sign. This is when we want to go below zero on the number line. These are called negative numbers. Some examples of their use can be in temperature scale, water level in lake or river, level of oil in tank etc. They are also used to denote debit account or outstanding dues.
2. The collection of numbers…,-4, $-3,-2,-1,0,1,2,3,4, \ldots$ is called integers.
So, $-1,-2,-3,-4, \ldots$ called negative numbers are negative integers and $1,2,3,4$, … called positive numbers are the positive integers.
3. We have also seen how one more than given number gives a successor and one less than given number gives predecessor.
4. We observe that
(a) When we have the same sign, add and put the same sign.
$\quad$ (i) When two positive integers are added, we get a positive integer [e.g. $(+3)+(+2)=+5$ ].
$\quad$ (ii) When two negative integers are added, we get a negative integer [e.g. $(-2)+(-1)=-3$ ].
(b) When one positive and one negative integers are added we subtract them as whole numbers by considering the numbers without their sign and then put the sign of the bigger number with the subtraction obtained. The bigger integer is decided by ignoring the signs of the integers [e.g. $(+4)+(-3)=+1$ and $(-4)+$ $(+3)=-1]$.
(c) The subtraction of an integer is the same as the addition of its additive inverse.
5. We have shown how addition and subtraction of integers can also be shown on a number line.










