Answer: (1)

Solution:

$a=\sin ^{-1}(\sin 5)=5-2 \pi$

and $b=\cos ^{-1}(\cos 5)=2 \pi-5$

$\therefore a^{2}+b^{2}=(5-2 \pi)^{2}+(2 \pi-5)^{2}$

$=8 \pi^{2}-40 \pi+50$

Answer: (4)

Solution:

Let probability of tail is $\frac{1}{3}$

$\Rightarrow$ Probability of getting head $=\frac{2}{3}$

$\therefore \quad$ Probability of getting 2 heads and 1 tail

$$ \begin{aligned} & =\left(\frac{2}{3} \times \frac{2}{3} \times \frac{1}{3}\right) \times 3 \\ & =\frac{4}{27} \times 3 \\ & =\frac{4}{9} \end{aligned} $$

Answer: (2)

Solution:

$\frac{a+b+68+44+40+60}{6}=55$

$212+a+b=330$

$\Rightarrow a+b=118$

$\frac{\sum x _i^{2}}{n}-(\bar{x})^{2}=194$

$\frac{a^{2}+b^{2}+(68)^{2}+(44)^{2}+(40)^{2}+(60)^{2}}{6}-(55)^{2}=194$

$=3219$

$11760+a^{2}+b^{2}=19314$

$\Rightarrow a^{2}+b^{2}=19314-11760$

$=7554$

$(a+b)^{2}-2 a b=7554$

From here $b=41.795$

$a+b=118$

$\Rightarrow a+b+2 b=118+83.59$

$=201.59$

Answer: (1)

Solution:

$a+d, a+7 d$ and $a+43 d$ are $1^{\text {st }}, 2^{\text {nd }}, 3^{\text {rd }}$ term of G.P.

$\frac{a+7 d}{a+d}=\frac{a+43 d}{a+7 d}$

$\Rightarrow(a+7 d)^{2}=(a+d)(a+43 d)$

$\Rightarrow a^{2}+49 d^{2}+14 d=a^{2}+44 a d+43 d^{3}$

$\Rightarrow 6 d^{2}=30 a d$

$\Rightarrow d^{2}=5 d$

$\Rightarrow d=0,5$

$a=1, d=5$

$S _{20}=\frac{20}{2}[2+(19) 5]$

$=10[95+2]$

$=970$

Answer: (4)

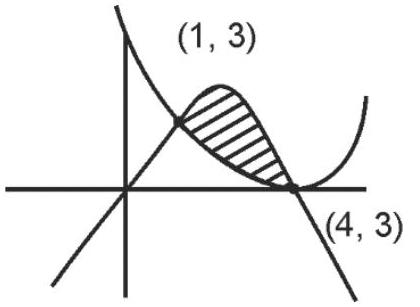
Solution:

Area $=\left|\int _1^{4}\left[(4-x)^{2}-\frac{(x-4)^{2}}{3}\right]\right| d x$

Area $=\left|4 x-\frac{x^{3}}{3}-\frac{(x-4)^{3}}{9}\right| _1^{4}$

$=\left|\left(16-\frac{64}{3}\right)-\left(4-\frac{1}{3}+\frac{27}{9}\right)\right|$

$=\left|16-\frac{64}{3}-4+\frac{1}{3}+3\right|$

$=|15-2|=6$

Answer: (3)

Solution:

Let $A=\left[\begin{array}{lll}x _1 & y _1 & z _1 \\ x _2 & y _2 & z _2 \\ x _3 & y _3 & z _3\end{array}\right]$

$$ \text { Given } A=\left[\begin{array}{l} 1 \tag{1}\ 0 \\ 1 \end{array}\right]=\left[\begin{array}{l} 2 \\ 0 \\ 2 \end{array}\right] $$

$$ \begin{aligned} & \therefore\left[\begin{array}{l} x _1+z _1 \\ x _2+z _2 \\ x _3+z _3 \end{array}\right]=\left[\begin{array}{l} 2 \\ 0 \\ 2 \end{array}\right] \\ & \therefore x _1+z _1=2 \ldots \text{(2)}\\ & \quad x _2+z _2=0 \ldots \text{(3)}\\ & x _3+z _3=0 \ldots \text{(4)} \end{aligned} $$

Given $A=\left[\begin{array}{c}-1 \\ 0 \\ 1\end{array}\right]=\left[\begin{array}{c}-4 \\ 0 \\ 4\end{array}\right]$

$\therefore\left[\begin{array}{l}-x _1+z _1 \\ -x _2+z _2 \\ -x _3+z _3\end{array}\right]=\left[\begin{array}{l}4 \\ 0 \\ 4\end{array}\right]$

$\Rightarrow-x _1+z _1=-4$

$-x _2+z _2=0$

$$ \begin{equation*} -x _3+z _3=4 \tag{6} \end{equation*} $$

Given $A=\left[\begin{array}{l}0 \\ 1 \\ 0\end{array}\right]=\left[\begin{array}{l}0 \\ 2 \\ 0\end{array}\right]$

$$ \therefore\left[\begin{array}{l} y _1 \\ y _2 \\ y _3 \end{array}\right]=\left[\begin{array}{l} 0 \\ 2 \\ 0 \end{array}\right] $$

$\therefore y _1=0, y _2=2, y _3=0$

$\therefore$ from (2), (3), (4), (5), (6) and (7)

$x _1=3, x _2=0, x _3=-1$

$y _1=0, y _2=2, y _3=0$

$z _1=-1, z _2=0, z _3=3$

$\therefore A=\left[\begin{array}{ccc}3 & 0 & -1 \\ 0 & 2 & 0 \\ -1 & 0 & 3\end{array}\right]$

$\therefore$ Now $(A-3 I)\left[\begin{array}{l}x \\ y \\ z\end{array}\right]=\left[\begin{array}{c}-1 \\ 2 \\ 3\end{array}\right]$

$\therefore\left[\begin{array}{rrr}0 & 0 & -1 \\ 0 & -1 & 0 \\ -1 & 0 & 0\end{array}\right]\left[\begin{array}{l}x \\ y \\ z\end{array}\right]=\left[\begin{array}{r}-1 \\ 2 \\ 3\end{array}\right]$

$\left[\begin{array}{l}-z \\ -y \\ -x\end{array}\right]=\left[\begin{array}{r}-1 \\ 2 \\ 3\end{array}\right]$

$[z=1],[y=-2],[x=-3]$

Answer: (1)

Solution:

$f$ is increasing function

$x<5 x<7 x$

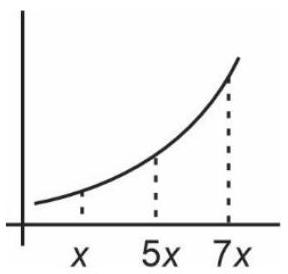
$f(x)<f(5 x)<f(7 x)$

$\frac{f(x)}{f(x)}<\frac{f(5 x)}{f(x)}<\frac{f(7 x)}{f(x)}$

$\lim _{x \rightarrow \infty} \frac{f(x)}{f(x)}<\lim _{x \rightarrow \infty} \frac{f(5 x)}{f(x)}<\lim _{x \rightarrow \infty} \frac{f(7 x)}{f(x)}$

$1<\lim _{x \rightarrow \infty} \frac{f(5 x)}{f(x)}<1 \Rightarrow \lim _{x \rightarrow \infty} \frac{f(5 x)}{f(x)}=1$

$\lim _{x \rightarrow \infty}\left(\frac{f(5 x)}{f(x)}-1\right)=0$

Answer: (1)

Solution:

$z _1+z _2=5$

$$ \begin{aligned} & z _1^{3}+z _2^{3}=20+15 i \\ & z _1^{3}+z _2^{3}=\left(z _1+z _2\right)^{3}-3 z _1 z _2\left(z _1+z _2\right) \\ & z _1^{3}+z _2^{3}=125-3 z _1 \cdot z _2(5) \\ & \Rightarrow 20+15 i=125-15 z _1 z _2 \\ & \Rightarrow 3 z _1 z _2=25-4-3 i \\ & 3 z _1 z _2=21-3 i \\ & z _1 \cdot z _2=7-i \\ & \left(z _1+z _2\right)^{2}=25 \\ & z _1^{2}+z _2^{2}=25-2(7-i) \\ & =11+2 i \\ & \left(z _1^{2}+z _2^{2}\right)^{2}=121-4+44 i \end{aligned} $$

$$ \begin{aligned} & \Rightarrow \quad z _1^{4}+z _2^{4}+2(7-i)^{2}=117+44 i \\ & \Rightarrow \quad z _1^{4}+z _2^{4}=117+44 i-2(49-1-14 i) \\ & =21+72 i \\ & \Rightarrow \quad\left|z _1^{4}+z _2^{4}\right|=75 \end{aligned} $$

Answer: (4)

Solution:

Take $e^{\sin x}=t(t>0)$

$\Rightarrow t-\frac{2}{t}=2$

$\Rightarrow \frac{t^{2}-2}{t}=2$

$\Rightarrow t^{2}-2 t-2=0$

$\Rightarrow t^{2}-2 t+1=3$

$\Rightarrow(t-1)^{2}=3$

$\Rightarrow t=1 \pm \sqrt{3}$

$\Rightarrow t=1 \pm 1.73$

$\Rightarrow t=2.73$ or -0.73 (rejected as $t>0$ )

$\Rightarrow e^{\sin x}=2.73$

$\Rightarrow \log _e e^{\sin x}=\log _e 2.73$

$\Rightarrow \sin x=\log _e 2.73>1$

So no solution.

Answer: (1)

Solution:

$(y-2)=m(x-8)$

$$ \begin{aligned} & \Rightarrow \quad x \text {-intercept } \\ & \Rightarrow \quad\left(\frac{-2}{m}+8\right) \\ & \Rightarrow y \text {-intercept } \\ & \Rightarrow(-8 m+2) \\ & \Rightarrow O A+O B=\frac{-2}{m^{2}}+8-8 m+2 \\ & f^{\prime}(m)=\frac{2}{m^{2}}-8=0 \\ & \Rightarrow m^{2}=\frac{1}{4} \end{aligned} $$

$$ \begin{aligned} & \Rightarrow m=\frac{-1}{2} \\ & \Rightarrow \quad f\left(\frac{-1}{2}\right)=18 \\ & \Rightarrow \text { Minimum }=18 \end{aligned} $$

Answer: (1)

Solution:

${ }^{6} C _m+2\left({ }^{6} C _{m+1}\right)+{ }^{6} C _{m+2}>{ }^{8} C _3$

${ }^{7} C _{m+1}+{ }^{7} C _{m+2}>{ }^{8} C _3$

${ }^{8} C _{m+2}>{ }^{8} C _3$

$\therefore m=2$

and ${ }^{n-1} P _3:{ }^{n} P _4=1: 8$

$\frac{(n-1)(n-2)(n-3)}{n(n-1)(n-2)(n-3)}=\frac{1}{8}$

$\therefore n=8$

$\therefore{ }^{n} P _{m+1}+{ }^{n+1} C _m={ }^{8} P _5+{ }^{9} C _2$

$=8 \times 7 \times 6 \times 5 \times 4+\frac{9 \times 8}{2}$

$=6756$

Answer: (3)

Solution:

$f(x)=e^{x^{3}-3 x+1}$

$$ \begin{aligned} & f^{\prime}(x)=e^{x^{3}-3 x+1} \cdot\left(3 x^{2}-3\right) \\ & =e^{x^{2}-3 x+1} \cdot 3(x-1)(x+1) \end{aligned} $$

For $x \in(-\infty,-1], f^{\prime}(x) \geq 0$

$\therefore f(x)$ is increasing function

$\therefore a=e^{-\infty}=0=f(-\infty)$

$$ b=e^{-1+3+1}=e^{3}=f(-1) $$

$$ \therefore P\left(4, e^{3}+2\right) $$

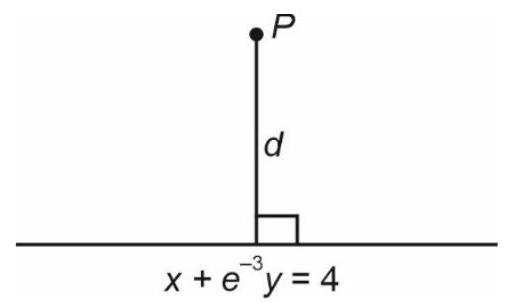
$d=\frac{\left(e^{3}+2\right)\left(e^{-3}\right)}{\sqrt{1+e^{-6}}}=\frac{1+2 e^{-3}}{\sqrt{1+e^{-6}}}=\frac{e^{3}+2}{\sqrt{e^{6}+1}}$

Answer: (1)

Solution:

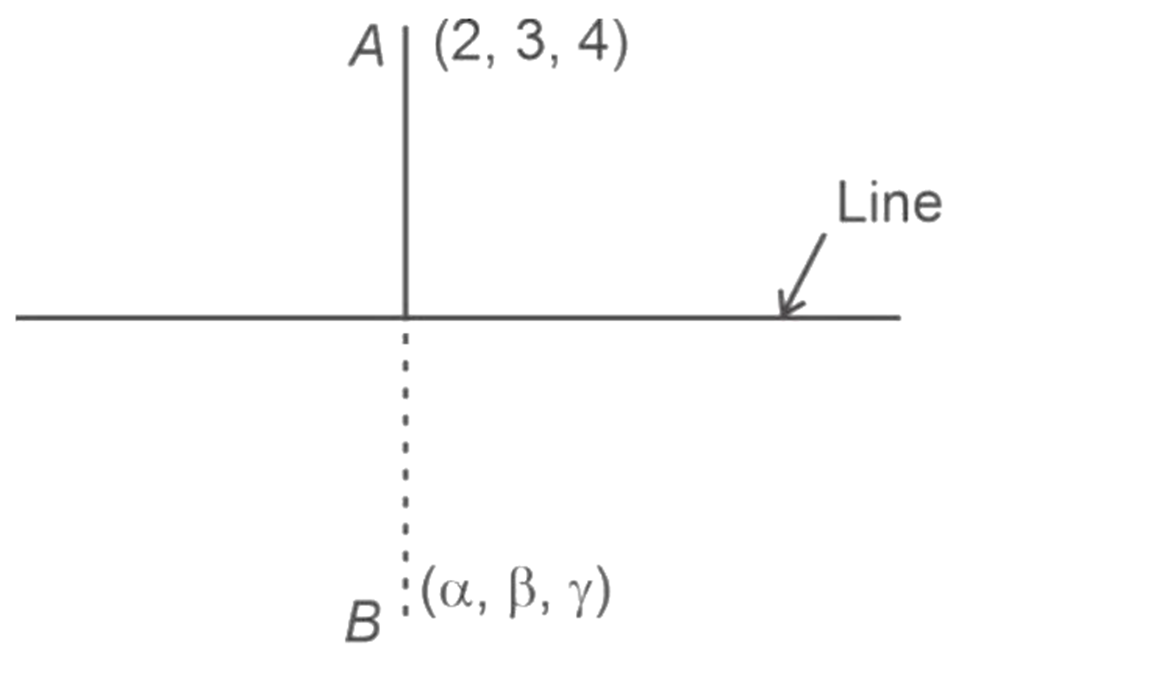
Take $\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\lambda$

$x=2 \lambda+1, y=3 \lambda+2, \quad z=4 \lambda+3$

$\overrightarrow{A B}=(\alpha-2) \hat{i}+(\beta-3) \hat{j}+(\gamma-4) \hat{k}$

Now,

$(\alpha-2) \cdot 2+(\beta-3) \cdot 3+(\gamma-4) \cdot 4=0$

$2 \alpha-4+3 \beta-9+4 \gamma-16=0$

$\Rightarrow 2 \alpha+3 \beta+4 \gamma=29$

Answer: (4)

Solution:

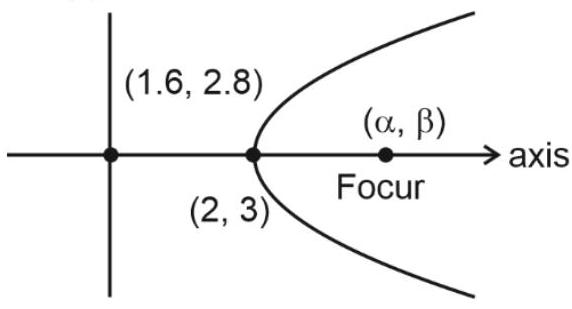
Slope of axis $=\frac{1}{2}$

$y-3=\frac{1}{2}(x-2)$

$\Rightarrow 2 y-6=x-2$

$\Rightarrow 2 y-x-4=0$

$2 x+y-6=0$

$4 x+2 y-12=0$

$\alpha+1.6=4 \Rightarrow \alpha=2.4$

$\beta+2.8=6 \Rightarrow \beta=3.2$

Ellipse passes through $(2.4,3.2)$

$\Rightarrow \frac{\left(\frac{24}{10}\right)^{2}}{a^{2}}+\frac{\left(\frac{32}{10}\right)^{2}}{b^{2}}=1$

Also $1-\frac{a^{2}}{b^{2}}=\frac{1}{2}$

$\frac{a^{2}}{b^{2}}=\frac{1}{2}$

$\frac{144}{25} b^{2}+\frac{256}{25} a^{2}=a^{2} b^{2}$

$\frac{144}{25}+\frac{256}{25} \times \frac{1}{2}=a^{2}$

$\Rightarrow \frac{(128+144)}{25}=a^{2} \Rightarrow \frac{272}{25}=a^{2}$

$\Rightarrow b^{2}=\frac{2 \times 272}{25}$

Latus rectum $=\frac{2 b^{2}}{a}$

(Latus rectum) ${ }^{2}$

$$ =\frac{4 b^{4}}{a^{2}}=4\left(\frac{b^{2}}{a^{2}}\right) b^{2}=\frac{8 \times 272 \times 2}{25}=\frac{4352}{25} $$

Answer: (15)

Solution:

$\int _0^{\pi} \frac{x^{2} \sin x \cdot \cos x}{\sin ^{4} x+\cos ^{4} x} d x$

$$ =\int _0^{\frac{\pi}{2}} \frac{\sin x \cos x}{\sin ^{4} x+\cos ^{4} x}\left(x^{2}-(\pi-x)^{2}\right) d x $$

$$ =\int _0^{\frac{\pi}{2}} \frac{\sin x \cdot \cos x\left(2 \pi x-\pi^{2}\right)}{\sin ^{4} x+\cos ^{4} x} x $$

$=2 \pi \int _0^{\frac{\pi}{2}} \frac{x \sin x \cos x}{\sin ^{4} x+\cos ^{4} x} d x-\pi^{2} \int _0^{\frac{\pi}{2}} \frac{\sin x \cos x}{\sin ^{4} x+\cos ^{4} x} d x$

$=2 \pi \cdot \frac{\pi}{4} \int _0^{\frac{\pi}{2}} \frac{\sin x \cos x}{\sin ^{4} x+\cos ^{4} x} d x-\pi^{2} \int _0^{\frac{\pi}{2}} \frac{\sin x \cos x}{\sin ^{4} x+\cos ^{4} x} d x$

$=-\frac{\pi^{2}}{2} \int _0^{\frac{\pi}{2}} \frac{\sin x \cos x}{\sin ^{4} x+\cos ^{4} x} d x$

$=-\frac{\pi^{2}}{2} \int _0^{\frac{\pi}{2}} \frac{\sin x \cos x d x}{1-2 \sin ^{2} x+\cos ^{2} x}$

$=-\frac{\pi^{2}}{2} \int _0^{\frac{\pi}{2}} \frac{\frac{1}{2} \sin 2 x}{1-\frac{1}{2} \sin ^{2} 2 x} d x$

$=-\frac{\pi^{2}}{2} \int _0^{\frac{\pi}{2}} \frac{\sin 2 x}{2-\sin ^{2} 2 x} d x$

$=-\frac{\pi^{2}}{2} \int _0^{\frac{\pi}{2}} \frac{\sin 2 x}{1+\cos ^{2} 2 x} d x$

Let $\cos 2 x=t$

$=-\frac{\pi^{2}}{2} \int _1^{-1} \frac{1}{2} d t$

$=-\frac{\pi^{2}}{4} \int _{-1}^{1} \frac{d t}{1+t^{2}}$

$=-\frac{\pi^{2}}{4} \cdot \frac{\pi}{2}=-\frac{\pi^{3}}{8}$

$\therefore \quad \frac{120}{\pi^{3}}\left|-\frac{\pi^{3}}{8}\right|=15$

Answer: (136)

Solution:

After giving 2 apples to each child 15 apples left now 15 apples can be distributed in ${ }^{15+3-1} C _2={ }^{17} C _2$ ways

$=\frac{17 \times 16}{2}=136$

Answer: (0)

Solution:

$\because \quad R$ is symmetric relation

$\Rightarrow \quad(y, x) \in R \forall(x, y) \in R$

$(x, y) \in R \Rightarrow 2 x=3 y$ and $(y, x) \in R \Rightarrow 3 x=2 y$

Which holds only for $(0,0)$

Which does not belongs to $R$.

$\therefore \quad$ Value of $n=0$

Answer: (7)

Solution:

$|A|=2$

$$ \begin{aligned} & \underbrace{\operatorname{adj}(\operatorname{adj}(\operatorname{adj} \ldots(a)))} _{2024 \text { times }}=|A|^{(n-1)^{2024}} \\ & =|A|^{2^{2024}} \\ & =2^{2^{2024}} \\ & 2^{2024}=\left(2^{2}\right) 2^{2022}=4(8)^{674}=4(9-1)^{674} \\ & \Rightarrow \quad 2^{2024} \equiv 4(\bmod 9) \\ & \Rightarrow \quad 2^{2024} \equiv 9 m+4, \quad m \leftarrow \text { even } \\ & 2^{9 m+4} \equiv 16 \cdot\left(2^{3}\right)^{3 m} \equiv 16(\bmod 9) \\ & \equiv 7 \end{aligned} $$