Answer: (1)

Solution:

General term of series

$$ \Rightarrow \quad T _r=\frac{r}{1-3 r^{2}+r^{4}} $$

$$ \begin{aligned} & =\frac{r}{\left(r^{4}-2 r^{2}+1\right)-r^{2}}=\frac{r}{\left(r^{2}-1\right)^{2}-r^{2}} \\ & =\frac{r}{\left(r^{2}-r-1\right)\left(r^{2}+r-1\right)}=\frac{\frac{1}{2}\left[\left(r^{2}+r-1\right)-\left(r^{2}-r-1\right)\right]}{\left(r^{2}-r-1\right)\left(r^{2}+r-1\right)} \\ & =\frac{1}{2}\left[\frac{1}{r^{2}-r-1}-\frac{1}{r^{2}+r-1}\right] \end{aligned} $$

Sum of 10 terms $\Rightarrow$

$\sum _{r=1}^{10} T _r=\frac{1}{2}\left[\frac{1}{-1}-\frac{1}{1}\right]+\frac{1}{2}\left[\frac{1}{1}-\frac{1}{5}\right]+\frac{1}{2}\left[\frac{1}{5}-\frac{1}{11}\right]+\ldots$

$$ +\frac{1}{2}\left[\frac{1}{89}-\frac{1}{109}\right] $$

Telescopic sum

$$ \Rightarrow \frac{1}{2}\left[-1-\frac{1}{109}\right]=\frac{1}{2}\left(\frac{-110}{109}\right)=\frac{-55}{109} $$

Answer: (1)

Solution:

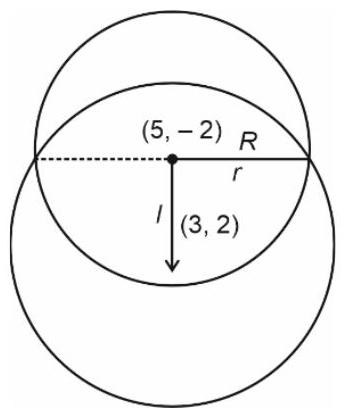
$2 x+3 y=12$

$3 x-2 y=5$

Point of intersection $\equiv(3,2)$

$\therefore$ centre is $(3,2)$

$I=\sqrt{4+16}=2 \sqrt{5}$

$R^{2}+R^{2}=r^{2}$

$\Rightarrow 20+(25+4-13)=r^{2}$

$\Rightarrow 20+16=r^{2}$

$\Rightarrow r=6$

Answer: (3)

Solution:

Total balls in urn $=15+10+60+15=100$ balls 2 balls are taken with replacement

So, probability that 1 ball is red and

1 ball is white $=\frac{{ }^{15} C _1 \times{ }^{10} C _1}{{ }^{100} C _2}$

$\frac{15 \times 10 \times 2}{100 \times 99}=\frac{300}{100 \times 99}=\frac{3}{99}=\frac{1}{33}$

Answer: (2)

Solution:

$\lim _{x \rightarrow 0} \frac{e^{|2 \sin x|}-2|\sin x|-1}{x^{2}}$

$$ =\lim _{x \rightarrow 0} \frac{1+|2 \sin x|+\frac{|2 \sin x|^{2}}{2}+\ldots \infty-2|\sin x|-1}{x^{2}} $$

$=\lim _{x \rightarrow 0} \frac{2 \sin ^{2} x+\ldots}{x^{2}}$

$=2$

Answer: (3)

Solution:

4 letter words formed by

DISTRIBUTION

$D \rightarrow 1$

I $\rightarrow 3$

$S \rightarrow 1$

$T \rightarrow 2$

$R \rightarrow 1$

$B \rightarrow 1$

$U \rightarrow 1$

$O \rightarrow 1$

$N \rightarrow 1$

(i) 4 alike $=0$

(ii) 3 alike +1 diff $={ }^{1} C _1 \times{ }^{8} C _1 \times \frac{4 !}{3 !}$

(iii) $2 A B C$ type

$\Rightarrow{ }^{2} C _1 \cdot{ }^{8} C _2 \cdot \frac{4 !}{2 !}$

(iv) $2 A 2 B={ }^{2} C _2 \cdot{ }^{4} C _2$

(v) $A B C D$ type : ${ }^{9} C _4 \times 4$ !

$\Rightarrow$ Total $=3734$

Answer: (1)

Solution:

$\vec{p} \times \vec{b}-\vec{c} \times \vec{b}=0$

$$ \begin{aligned} & (\vec{p}-\vec{c}) \times \vec{b}=0 \\ & \Rightarrow \vec{b} | \vec{p}-\vec{c} \end{aligned} $$

$\Rightarrow \vec{b}=\lambda(\vec{p}-\vec{c})$

$\Rightarrow k \vec{b}+\vec{c}=\vec{p}$

$\vec{p}=\hat{i}(4 k+1)+\hat{j}(k-3)+\hat{k}(7 k+4)$

$\vec{p} \cdot \vec{a}=0$

$(4 k+1) 3+(k-3) 1+(7 k+4)(-2)=0$

$12 k+3+k-3-14 k-8=0$

$\Rightarrow k=-8$

$\therefore \vec{p}=-31 \hat{i}-11 \hat{j}-52 \hat{k}$

$\vec{p} \cdot(\hat{i}-\hat{j}-\hat{k})=-31+11+52=-31+63$

$=32$

Answer: (4)

Solution:

$y \frac{d x}{d y}=x(\ln x-\ln y+1), x>0, y>0$

$\frac{d x}{d y}=\frac{x}{y}\left(\ln \left(\frac{x}{y}\right)+1\right)$

$\frac{x}{y}=t \Rightarrow x=t y$

$\Rightarrow \frac{d x}{d y}=t+y \frac{d t}{d y}$

$\Rightarrow t+y \frac{d t}{d y}=t \ln t+t$

$\Rightarrow \frac{d t}{t \ln t}=\frac{d y}{y}$

$\Rightarrow \ln (\ln t)=\ln y+c$

$\Rightarrow \ln \left(\ln \frac{x}{y}\right)=\ln y+c$

at $x=e, y=1$

$\Rightarrow \ln (\ln e)=\ln 1+C$

$\Rightarrow c=0$

$\Rightarrow \ln \left(\ln \frac{x}{y}\right)=\ln y$ $\Rightarrow \ln \left(\frac{x}{y}\right)=y$

$\left|\log _e\left(\frac{x}{y}\right)\right|=y \quad$ as $y>0$

Answer: (1)

Solution:

$f(x)=\frac{4 x+3}{6 x-4}$

$g(x)=f(f(x))$

$=\frac{4\left(\frac{4 x+3}{6 x-4}\right)+3}{6\left(\frac{4 x+3}{6 x-4}\right)-4}=\frac{16 x+12+18 x-12}{24 x+18-24 x+16}$

$=\frac{34 x}{34}=x$

$g(g(g(g(x))))=x$

Answer: (4)

Solution:

$f^{\prime}(x)=\left|\begin{array}{ccc}3 x^{2} & 2 x^{2}+1 & 1+3 x \\ 6 x & 2 x & x^{3}+6 \\ 3 x^{2}-1 & 4 & x^{2}-2\end{array}\right|+$

$$ \left|\begin{array}{ccc} x^{3} & 4 x & 1+3 x \\ 3 x^{2}+2 & 2 & x^{3}+6 \\ x^{3}-x & 0 & x^{2}-2 \end{array}\right|+\left|\begin{array}{ccc} x^{3} & 2 x^{2}+1 & 3 \\ 3 x^{2}+2 & 2 x & 3 x^{2} \\ x^{3}-x & 4 & 2 x \end{array}\right| $$

Now, $f(0)=\left|\begin{array}{lll}0 & 1 & 1 \\ 2 & 0 & 6 \\ 0 & 4 & -2\end{array}\right|=12$

and $f^{\prime}(0)=\left|\begin{array}{ccc}0 & 1 & 1 \\ 0 & 0 & 6 \\ -1 & 4 & -2\end{array}\right|+\left|\begin{array}{ccc}0 & 0 & 1 \\ 2 & 2 & 6 \\ 0 & 0 & -2\end{array}\right|+\left|\begin{array}{lll}0 & 1 & 3 \\ 2 & 0 & 0 \\ 0 & 4 & 0\end{array}\right|$

$$ =-6+0+24=18 $$

$\Rightarrow 2 f(0)+f^{\prime}(0)=2 \times 12+18=42$

Answer: (3)

Solution:

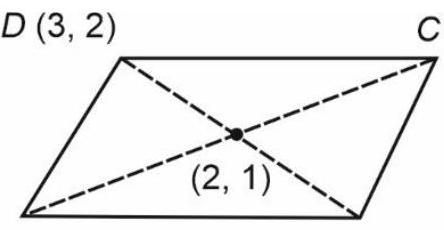
$A(\alpha, \beta)$

B $(1,0)$

Using mid point formula

$\alpha+\gamma=4$

$\beta+\rho=2$

$\alpha+\beta+\gamma+\rho=6$

$\therefore 2(\alpha+\beta+\gamma+\rho)=12$

Answer: (4)

Solution:

Let $g(x)=p x+q$

Since $f(x)$ is continuous at $x=0$

$\Rightarrow g(0)=\lim _{x \rightarrow 0^{+}}\left(\frac{x+1}{x+2}\right)^{1 / x}=0$

$\Rightarrow g(x)=p x \quad(q=0)$

Now, $f^{\prime}(1)=f(-1)$

$y=\left(\frac{1+x}{2+x}\right)^{1 / x}$

$\Rightarrow \ln y=\frac{1}{x} \ln \left(\frac{1+x}{2+x}\right)$

$\frac{1}{y} d y=\frac{-1}{x^{2}} \ln \left(\frac{1+x}{2+x}\right)+\frac{1}{x} \times \frac{1}{\left(\frac{1+x}{2+x}\right)} \times \frac{(x+2)-(x+1)}{(2+x)^{2}}$

at $x=1$

$f(1)=\left(\frac{2}{3}\right)\left[-\ln \left(\frac{2}{3}\right)+\frac{3}{2}\left(\frac{1}{9}\right)\right]$

$$ \begin{aligned} & =\frac{-2}{3} \ln \left(\frac{2}{3}\right)+\frac{1}{9} \\ & \Rightarrow f(-1)=-P=\frac{-2}{3} \ln \left(\frac{2}{3}\right)+\frac{1}{9} \\ & \Rightarrow p=\frac{2}{3} \ln \left(\frac{2}{3}\right)-\frac{1}{9} \\ & g(3)=3 p=2 \ln \left(\frac{2}{3}\right)-\frac{1}{3}=\ln \left(\frac{4}{9}\right)+\log e^{(-1 / 3)} \\ & \Rightarrow \ln \left(\frac{4}{9 e^{1 / 3}}\right) \end{aligned} $$

Answer: (2)

Solution:

$\vec{\tau}=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 5 \\ -1 & 3 & 2\end{array}\right|=\hat{i}(6-15)-\hat{j}(4+5)+\hat{k}(6+3)$

$=-9 \hat{i}-9 \hat{j}+9 \hat{k}$

$\therefore$ Required line $(L): \frac{x-5}{1}=\frac{y+4}{1}=\frac{z-3}{-1}=\lambda$

$x=\lambda+5, y=\lambda-4, z=3-\lambda$

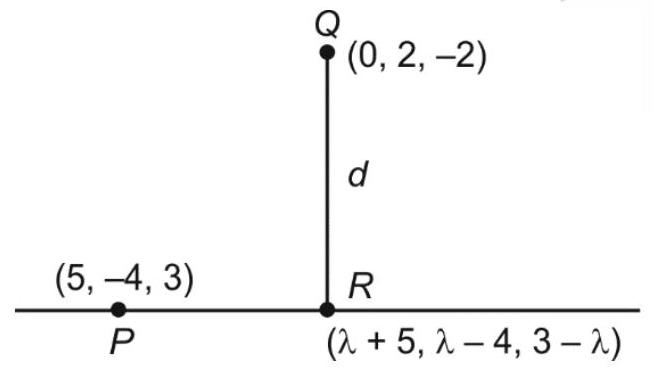
$\overrightarrow{Q R} \cdot \vec{I}=(\lambda+5) \cdot 1+(\lambda-6) \cdot 1+(3-\lambda+2)(-1)=0$

$\Rightarrow \lambda+5+\lambda-6-5+\lambda=0$

$\Rightarrow 3 \lambda=6$

$\Rightarrow \lambda=2$

$\therefore \quad R(7,-2,1)$

$\therefore \quad Q R=\sqrt{49+16+9}$

$=\sqrt{74}$

Answer: (2)

Solution:

$z=\frac{\pi}{4}(1+i)^{4}\left[\frac{1+\pi+\pi+1}{i(1+\pi)-\sqrt{\pi}+\sqrt{\pi}}\right]$

$=\frac{\pi}{4}(1+i)^{4} \frac{2}{(i)}=\frac{\pi}{2} \frac{(1+i)^{4}}{i}=\frac{-\pi}{2} i(1+i)^{4}$

$|z|=\left|-\frac{\pi}{2}\right||i||1+i|^{4}=\left(\frac{\pi}{2}\right)(1)(\sqrt{2})^{4}=2 \pi$

$z=\frac{-\pi}{2}(-4 i)=2 \pi i \Rightarrow \arg (z)=\frac{\pi}{2}$

$\Rightarrow \beta=\frac{2 \pi}{\frac{\pi}{2}}=4$

Also, $(1-i)^{x}=2^{x}$

$\Rightarrow$ Taking modulus both sides

$\Rightarrow(\sqrt{2})^{x}=2^{x} \Rightarrow(\sqrt{2})^{x}=0$

$\Rightarrow$ at $x=0$

$\Rightarrow 1$ solution $\Rightarrow \alpha=1$

$\Rightarrow$ Perpendicular distance from $(1,4)$

$\left|\frac{4(1)-3(4)-7}{5}\right|=\left|\frac{4-12-7}{5}\right|=3$

Answer: (3)

Solution:

Given $\frac{a x^{2}+2(a+1) x+9 a+4}{x^{2}-8 x+32}<0 \quad \forall x \in \mathbb{R}$

In $x^{2}-8 x+32$, we have $D=64-128<0$

$\therefore x^{2}-8 x+32>0 \quad \forall x \in \mathbb{R}$ $\Rightarrow a x^{2}+2(a+1) x+9 a+4<0 \quad \forall x \in \mathbb{R}$

$\Rightarrow a<0$ and $D<0$

$\because$ Question has asked for positive integral values of $a$

$\therefore \quad|S|=0$

Answer: (4)

Solution:

Let $\sin A=\alpha$

$$ \begin{aligned} & \sin B=\beta \\ & \sin C=\gamma \\ & A+B+C=\pi \\ & \Rightarrow(\alpha+\beta)^{2}-\gamma^{2}=3 \alpha \beta \\ & \Rightarrow \alpha^{2}+\beta^{2}-\alpha \beta=\gamma^{2} \\ & \Rightarrow \alpha^{2}+\beta^{2}-\gamma^{2}=\alpha \beta \\ & \Rightarrow \frac{\alpha^{2}+\beta^{2}-\gamma^{2}}{2 \alpha \beta}=\frac{1}{2} \\ & \Rightarrow \cos C=\frac{1}{2} \Rightarrow C=60^{\circ} \\ & \Rightarrow \sin C=\frac{\sqrt{3}}{2}=\gamma \end{aligned} $$

Answer: (118)

Solution:

$(1+x)\left(1-x^{2}\right)\left(1+\frac{3}{x}+\frac{3}{x^{2}}+\frac{1}{x^{3}}\right)^{5}$

$$ \begin{aligned} & \Rightarrow \quad(1+x)^{2}(1-x) \frac{\left(x^{3}+3 x^{2}+3 x+1\right)^{5}}{x^{15}} \\ & \Rightarrow \frac{(1+x)^{2}(1-x)\left[(x+1)^{3}\right]^{5}}{x^{15}}=\frac{(1-x)(1+x)^{17}}{x^{15}} \\ & \Rightarrow \text { Coefficient of } x^{3} \Rightarrow x^{18} \text { in }(1-x)(1+x)^{17} \\ & \Rightarrow(1+x)^{17}-x(1+x)^{17} \\ & \Rightarrow 0-x\left({ }^{17} C _{17} x^{17}\right)={ }^{-17} C _{17}=-1 \end{aligned} $$

and coefficient of $x^{-13} \Rightarrow x^{2}$ in $(1-x)(1+x)^{17}$

$\Rightarrow(1+x)^{17}-x(1+x)^{17}$

$$ \begin{aligned} & \Rightarrow \quad{ }^{17} C _2-{ }^{17} C _1=17 \times 8-17 \\ &=17 \times 7=119 \\ & \Rightarrow \text { sum }=119-1=118 \end{aligned} $$

Answer: (13)

Solution:

$R={(1,2),(2,3),(2,4)}$

for reflexive, we need to add,

$(1,1),(2,2),(3,3),(4,4)$

for symmetric

if $(1,2) \in R$

then $(2,1) \in R$

if $(2,3) \in R$

then $(3,2) \in R$

if $(2,4) \in R$

then $(4,2) \in R$

So set becomes

${(1,1),(2,2),(3,3),(4,4),(1,2),(2,1),(2,3),(3,2), (2,4),(4,2)}$

for transitive

As $(1,2) \in R$

$(2,3) \in R$

then $(1,3) \in R$ then $(3,1) \in R$ (for symmetric)

$\&(1,2) \in R$

$(2,4) \in R$

then $(1,4) \in R$ then $(4,1) \in R$ (for symmetric) $(3,2) \in R$

$(2,4) \in R$

then $(3,4) \in R$ then $(4,3) \in R$ (for symmetric)

so set $S={(1,1),(2,2),(3,3),(4,4),(1,2),(2,1),(2,3),(3,2),(2,4),(4,2),(1,3),(3,1),(1,4),(4,1), (3,4),(4,3)}$

so 13 new elements are added

$\Rightarrow n=13$

Answer: (167)

Solution:

$|\vec{c}|^{2}=9(|\vec{a} \times \vec{b}|)^{2}+|\vec{b}|^{2}+0$

$|\vec{c}|^{2}=9(16-4)+16$

$$ {\because|\vec{a} \times \vec{b}|^{2}=|\vec{a}|^{2}|\vec{b}|^{2}-(\vec{a} \cdot \vec{b})^{2} } $$

$|\vec{C}|^{2}=124$

$|\vec{c}|=\sqrt{124}$

$\vec{c}=(3(\vec{a} \times \vec{b}))-\vec{b}$

$\vec{c} \cdot \vec{b}=-|\vec{b}|^{2}=-16$

$4 \times \sqrt{124} \cos \alpha=-16$

$\cos \alpha=\frac{-4}{\sqrt{124}}=\frac{-2}{\sqrt{31}}$

$\sin \alpha=\sqrt{1-\frac{4}{31}}$

$\sin \alpha=\sqrt{\frac{27}{31}}$

Then, $192 \sin ^{2} \alpha=192 \times \frac{27}{31}$

$\approx 167.2$

Answer: (58)

Solution:

$x-2 y+z=-4$

$2 x+\alpha y+3 z=5$

$3 x-y+\beta z=3$

$\Delta _2=\left|\begin{array}{ccc}1 & -4 & 1 \\ 2 & 5 & 3 \\ 3 & 3 & \beta\end{array}\right|=0$

$(5 \beta-9)+4(2 \beta-9)-9=0$

$13 \beta=54$

$\beta=\frac{54}{13}$

$\Delta _3=\left|\begin{array}{ccc}1 & -2 & -4 \\ 2 & \alpha & 5 \\ 3 & -1 & 3\end{array}\right|=0$

$(3 \alpha+5)+2(-9)-4(-2-3 \alpha)=0$

$3 \alpha+5-18+8+12 \alpha=0$

$\Rightarrow \alpha=\frac{1}{3}$

$12 \alpha+13 \beta=4+13 \times \frac{54}{13}$

$=58$