JEE Main 12 Jan 2019 Morning Question 3
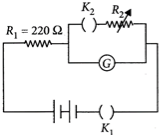
Question: The galvanometer deflection, when key $ K _1 $ is closed but $ K _2 $ is open, equals $ {\theta_0}, $ (see figure). On closing $ K _2 $ also and adjusting $ R _2 $ to $ 5\Omega , $ the deflection in galvanometer becomes $ \frac{{\theta_0}}{5}. $ The resistance of the galvanometer is, then, given by [Neglect the internal resistance of battery] [JEE Main Online Paper Held On 12-Jan-2019 Morning]
Options:
A) $ 25\Omega $
B) $ 22\Omega $
C) $ 5\Omega $
D) $ 12\Omega $
Show Answer
Answer:
Correct Answer: B
Solution:
Initially, let $ I _1 $ be the current through G. then $ I _1=\frac{V}{220+G}. $
After the key $ K _2 $ is closed, the circuit is shown as Apply KVL on loop 1,
$ 5I _3=GI _4\Rightarrow I _3=\frac{GI _4}{5} $ Also, $ I _3+I _4=I _2 $
$ \Rightarrow $ $ ( \frac{G}{5}+1 )I _4=I _2 $
$ \Rightarrow $ $ I _4=\frac{V}{( R _1+\frac{5G}{G+5} )( \frac{G+5}{5} )} $ For a galvanometer, $ I\propto \theta $ So, $ \frac{I _1}{I _4}=\frac{{\theta_0}}{{\theta_0}/5}\Rightarrow 5=\frac{V}{220+G}\frac{R _1(G+5)+5G}{5V} $
$ \Rightarrow $ $ 25(220+G)=(220)(G+5)+5G $
$ \Rightarrow $ $ 25(220)+20G=220G+1100 $
$ \Rightarrow $ $ 200G=4400\Rightarrow G=22\Omega $










