JEE Main 12 Jan 2019 Morning Question 19
Question: In a meter bridge, the wire of length 1 m has a non-uniform cross-section such that the variation $ \frac{dR}{dl} $ of its resistance R with length l is $ \frac{dR}{dl}\propto \frac{1}{\sqrt{l}}. $ Two equal resistances are connected as shown in the figure. The galvanometer has zero deflection when the jockey is at point P. What is the length AP? [JEE Main Online Paper Held On 12-Jan-2019 Morning]
Options:
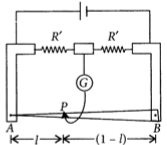
A) 0.35 m
B) 0.2 m
C) 0.25 m
D) 0.3 m
Show Answer
Answer:
Correct Answer: C
Solution:
Let AP be the length $ l $ $ \frac{dR}{dl}\propto \frac{1}{\sqrt{l}},dR=K\frac{dl}{\sqrt{l}} $
Taking integration on both the sides $ \int _{{}}^{{}}{dR}=K\int _{{}}^{{}}{\frac{1}{\sqrt{l}}dl} $ $ R=2K{l^{1/2}}=2K $ $ (\because l=1m) $
Balancing point will divide the resistance in equal part. So, l will be correspond to $ K(\Omega ) $ .
$ \therefore $ $ K=2K\sqrt{l} $ or $ l=0.25m $










