JEE Main 12 Jan 2019 Morning Question 10
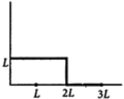
Question: The position vector of the centre of mass $ \vec{r}cm $ of an asymmetric uniform bar of negligible area of cross-section as shown in figure is [JEE Main Online Paper Held On 12-Jan-2019 Morning]
Options:
A) $ \vec{r},cm=\frac{11}{8}L\hat{x}+\frac{3}{8}L,\hat{y} $
B) $ \vec{r},cm=\frac{13}{8}L\hat{x}+\frac{5}{8}L,\hat{y} $
C) $ \vec{r},cm=\frac{3}{8}L\hat{x}+\frac{11}{8}L,\hat{y} $
D) $ \vec{r},cm=\frac{5}{8}L\hat{x}+\frac{13}{8}L,\hat{y} $
Show Answer
Answer:
Correct Answer: B
Solution:
-
$ {{\vec{r}}_1}=L(\hat{x}+\hat{y}) $ $ {{\vec{r}}_2}=2L\hat{x}+\frac{L}{2}\hat{y} $ $ {{\vec{r}}_3}=2.5L\hat{x} $ $ {{\vec{r}} _{cm}}=\frac{m _1{{{\vec{r}}}_1}+m _2{{{\vec{r}}}_2}+m _3{{{\vec{r}}}_3}}{m _1+m _2+m _3} $
Let $ m _2=m, $ so $ m _3=m $ and $ m _1=2m $
$ \therefore $ $ {{\vec{r}} _{cm}}=\frac{1}{4}[ 2L(\hat{x}+\hat{y})+( 2L\hat{x}+\frac{L}{2}\hat{y} )+2.5L\hat{x} ] $ $ =\frac{1}{4}(6.5\hat{x}+2.5\hat{y})=\frac{13L}{8}\hat{x}+\frac{5L}{8}\hat{y}. $










