JEE Main 12 Jan 2019 Morning Question 25
Question: Let $ P(4,-4) $ and $ Q(9,6) $ be two points on the parabola, $ y^{2}=4x $ and let X be any point on the arc POQ of this parabola, where O is the vertex of this parabola, such that the area of APXQ is maximum. Then this maximum area (in sq. units) is [JEE Main Online Paper Held On 12-Jan-2019 Morning]
Options:
A) $ \frac{125}{2} $
B) $ \frac{125}{4} $
C) $ \frac{625}{4} $
D) $ \frac{75}{2} $
Show Answer
Answer:
Correct Answer: B
Solution:
- The correct option is C $ \frac{125}{4} $ Cosider the parabola ${y^2}$ = ${4x}$
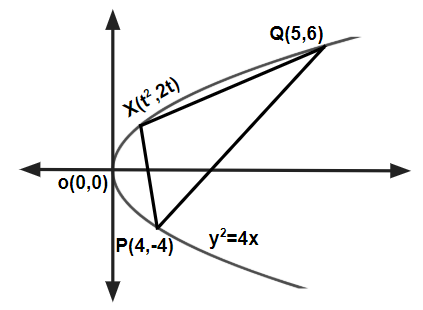
$ \begin{aligned} \text{Let the coordinates of point } X \text{ be } (t^2, 2t) & \\ \therefore \text{ area of } \triangle PXQ &= \begin{vmatrix} t^2 & 2t & 1 \\ 4 & -4 & 1 \\ 9 & 6 & 1 \end{vmatrix} \\ \Rightarrow A &= \frac{1}{2} \left[ t^2(-4 - 6) - 2t(4 - 9) + 1(24 + 36) \right] \\ &= \frac{1}{2} \left[ -10t^2 + 10t + 60 \right] \\ \Rightarrow A &= 5(-t^2 + t + 6) \\ \Rightarrow \frac{dA}{dt} &= 5(-2t + 1) = 0 \\ \Rightarrow t &= \frac{1}{2} \\ \therefore \text{ minimum area } &= 5 \left( -\frac{1}{4} + \frac{1}{2} + 6 \right) \\ &= \frac{125}{4} \text{ sq. units} \end{aligned} $










