JEE Main 12 Jan 2019 Evening Question 26
Question: Two particles A, B are moving on two concentric circles of radii $ R _1 $ and $ R _2 $ with equal angular speed $ \omega $ . At t = 0, their positions and direction of motion are shown in the figure. The relative velocity $ {{\vec{v}} _{A}}-{{\vec{v}} _{B}} $ at $ t=\frac{\pi }{2\omega } $ is given by [JEE Main Online Paper Held On 12-Jan-2019 Evening]
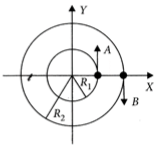
Options:
A) $ -\omega (R _1+R _2)\hat{i} $
B) $ \omega (R _1-R _2)\hat{i} $
C) $ \omega (R _2-R _1)\hat{i} $
D) $ -\omega (R _1+R _2)\hat{i} $
Show Answer
Answer:
Correct Answer: C
Solution:
The angle transversed in time $ \frac{\pi }{2\omega } $ is $ \theta =\omega t=\frac{\omega \pi }{2\omega }=\frac{\pi }{2} $ i.e., at $ t=\frac{\pi }{2\omega }, $
the position of two particles is shown in the figure
$ \therefore $ The relative velocity $ {{\vec{v}} _{A}}-{{\vec{v}} _{B}} $ is $ =-R _1\omega \hat{i}-(-R _2\omega \hat{i}) $ $ =\omega (R _2-R _1)\hat{i} $










