Work Power and Energy 4 Question 1
2. A wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from
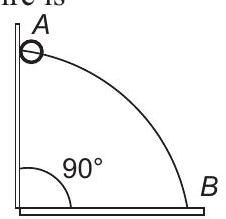
(a) always radially outwards
(b) always radially inwards
(c) radially outwards initially and radially inwards later
(d) radially inwards initially and radially outwards later
Show Answer
Answer:
Correct Answer: 2. (c)
Solution:
Using conservation of energy
Radial force equation is
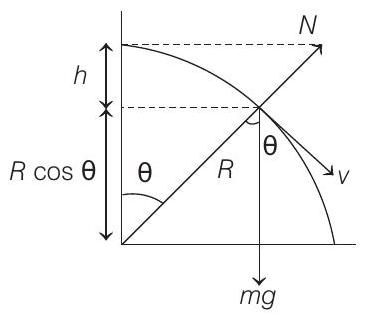
Here,
So, normal force act radially outward on bead, if






